はじめに
一般化極値(GEV)分布はワイブル、グンベル、フレシェを含む極値分布ファミリーからなるメタ分布です。定常過程の極値分布をモデル化するのに用います。それは、裾の振る舞い(極めて頻度の低い極端な状態)で必要とされる先験的な決定なしで、例えば、年間の最大風速、年間のトラックによる橋梁の最大荷重などについてのモデル化です。
以下のコール[2001(注1)]によるパラメータ化では、最大値のGEV分布
G(x) = exp([1- ξ (( x - μ)/ σ)] -1/ξ)
ξ < 0 :上位のテイルで折り返すワイブル分布(右端が有限)
ξ = 0 : テイルの両側を折り返さないグンベル分布
ξ > 0 :下位のテイルで折り返すフレシェ分布 このシェイプパラメータξ でパラメータ化はSciPyでは符号が反対に(cという変数)使われている。最小値の分布は、負のデータの最大分布を観察することによって検討される。
私たちは、コールが使ったポートピリーの年間最大海面の水位データの例を用いて、それ以前の(確率の)頻度主義の結果と比較します。
コールの極値の統計モデル
母数化で三つのタイプの分布を包含しているという意味で一般化されている。
Stuart Coles. An introduction to statistical modeling of extreme values. Springer Series in Statistics. Springer, London, England, 2001 edition, August 2001. ISBN 978-1-85233-459-8.
ここで展開するサンプルコードはpymc-experimentalを必要としていますが、これは現在開発中のもので、pymcのディストリビューションには含まれていません。(2023年4月現在)パッケージツールcondaからはレポジトリにないためインストールできません。以下は開発プロジェクトのgithubです。 https://github.com/pymc-devs/pymc-experimental#questions. コードを実行する場合は、pipを使ってインストールしてください。 pip install git+https://github.com/pymc-devs/pymc-experimental.git
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pymc_experimental.distributions as pmx
import pytensor.tensor as pt
from arviz.plots import plot_utils as azpu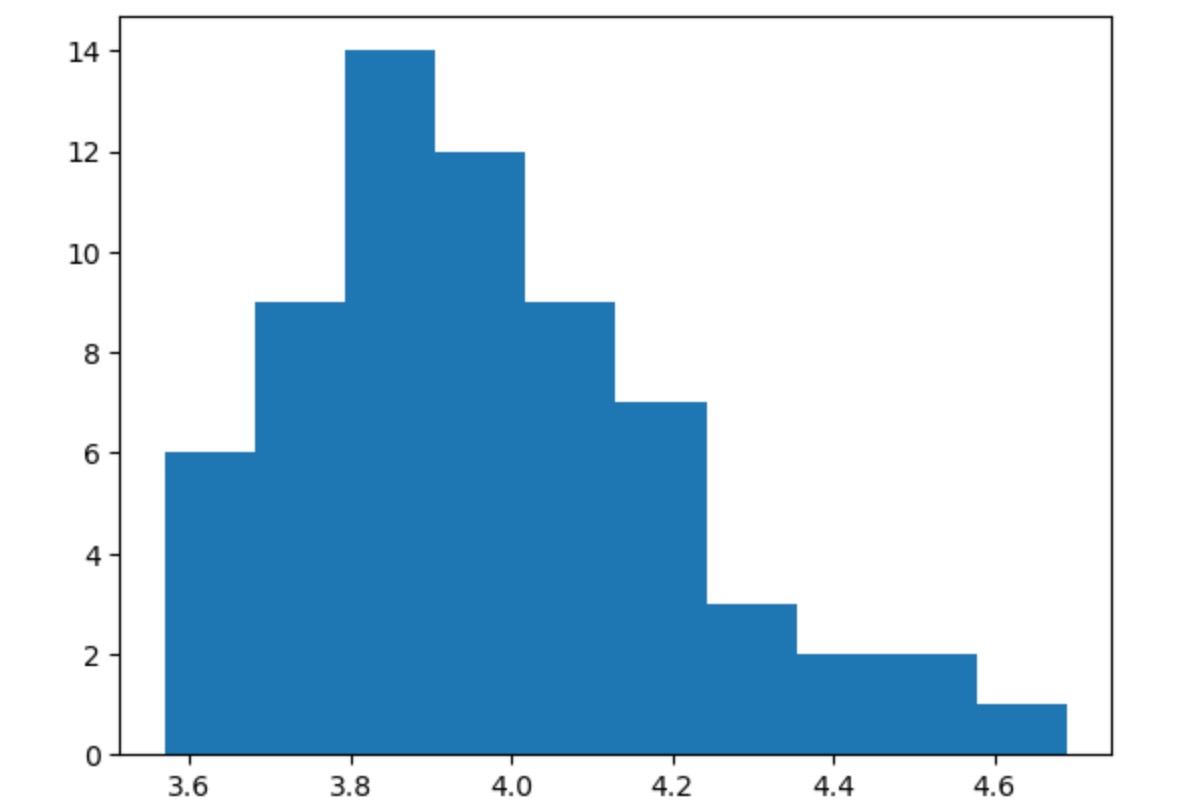
モデル化と予測
モデル化において二つのことを行います。
- 有益な事前情報がない上で、GEVパラメータのパラメータの推定
- 10年のリターンレベルの予測
不確実なパラメータによる極値の予測はベイジアンの設定では、簡単に成し遂げます。この簡易さを、カプラーニとオブリエンが遭遇した頻度主義の設定による計算の困難さと比較するのは興味深いことです。どのケースでもpを越えるの確率の予測値は、以下で与えられます。
xp = μ - σ{ 1 - [-log(1 - p)]}/ξこれはパラメータ値の決定関数です。そしてモデルのコンテキストでは、pm.Deterministc()を使って実行できます。
これを考慮して、10年のリターン値 p = 1/10 とします。
p = 1/10上のヒストグラムの簡単なレビューから事前に推定したモデルを設定します。
- μ : ネガティブな結果を制限した標準偏差の正規(Normal)分布より現実に考慮できるものはない。
- σ:正に違いなく、微小値です。それで標準偏差のユニットとしてHalfNormalを使います。
- ξ: テイルの振る舞いに関しては不可知論者です。ゼロを中心に物理的に±0.6の境界を持つゼロ近辺に密集させます。
# Optionally centre the data, depending on fitting and divergences
# cdata = (data - data.mean())/data.std()
with pm.Model() as model:
# Priors
μ = pm.Normal("μ", mu=3.8, sigma=0.2)
σ = pm.HalfNormal("σ", sigma=0.3)
ξ = pm.TruncatedNormal("ξ", mu=0, sigma=0.2, lower=-0.6, upper=0.6)
# Estimation
gev = pmx.GenExtreme("gev", mu=μ, sigma=σ, xi=ξ, observed=data)
# Return level
z_p = pm.Deterministic("z_p", μ - σ / ξ * (1 - (-np.log(1 - p)) ** (-ξ)))事前予測チェック
私たちが選択した事前の推定がデータの範囲をどれくらいカバーするか探ってみましょう。
idata = pm.sample_prior_predictive(samples=1000, model=model)
az.plot_ppc(idata, group="prior", figsize=(12, 6))
ax = plt.gca()
ax.set_xlim([2, 6])
ax.set_ylim([0, 2]);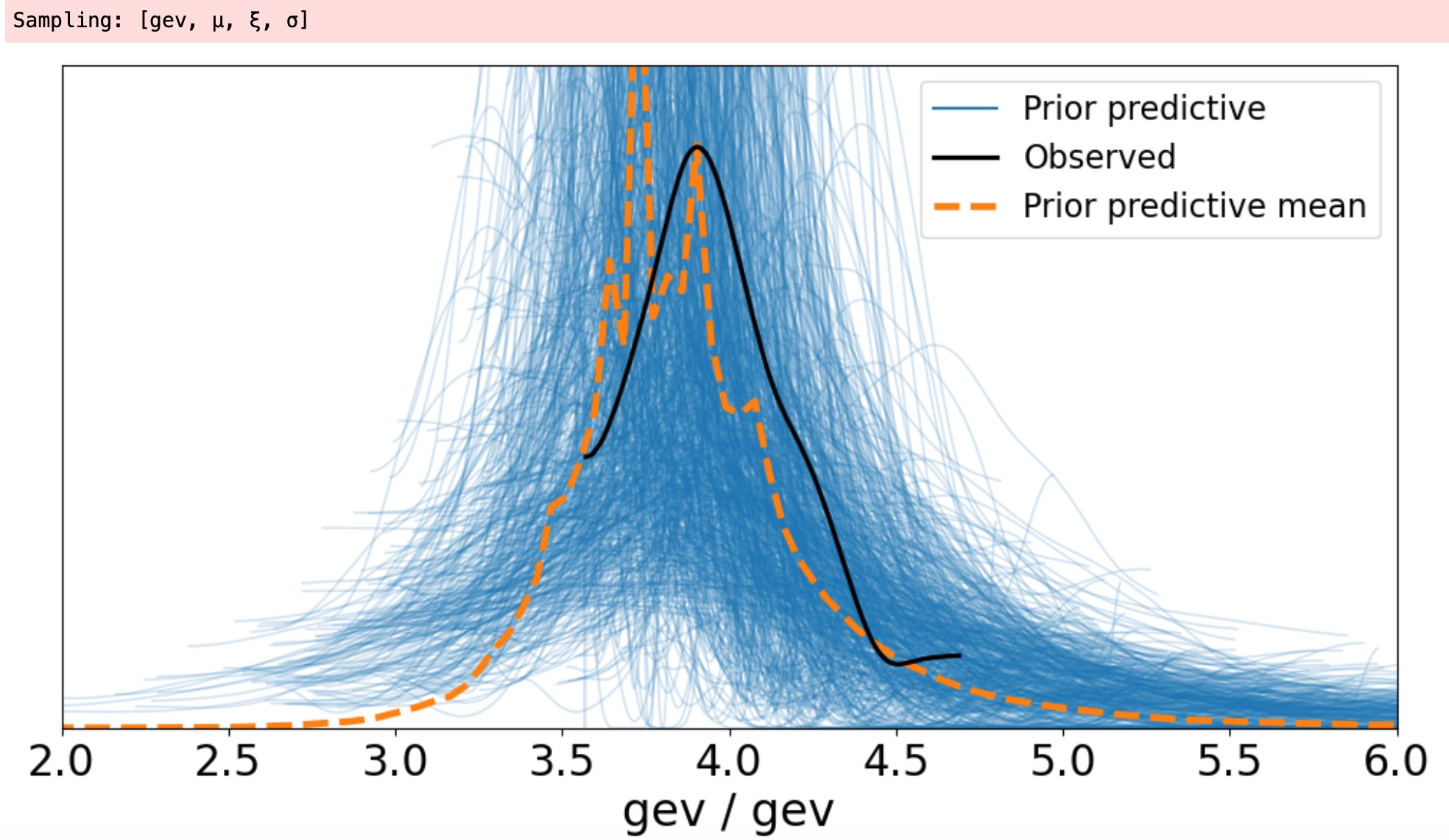
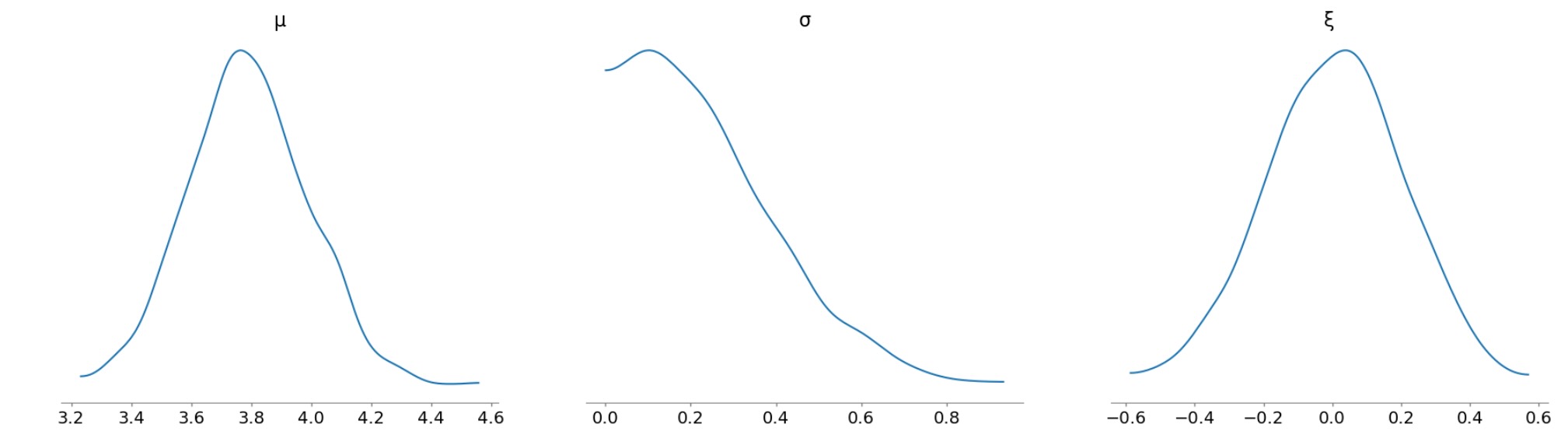
plot_posterior()関数を使って、パラメータのサンプル値を見ることができます。しかし、idataオブジェクトを渡し、"事前"のグループを特定することになります。
az.plot_posterior(
idata, group="prior", var_names=["μ", "σ", "ξ"], hdi_prob="hide", point_estimate=None
);
推定
魔法の推論ボタンを押します。
with model:
trace = pm.sample(
5000,
cores=4,
chains=4,
tune=2000,
initvals={"μ": -0.5, "σ": 1.0, "ξ": -0.1},
target_accept=0.98,
)
# add trace to existing idata object
idata.extend(trace)
az.plot_trace(idata, var_names=["μ", "σ", "ξ"], figsize=(12, 12));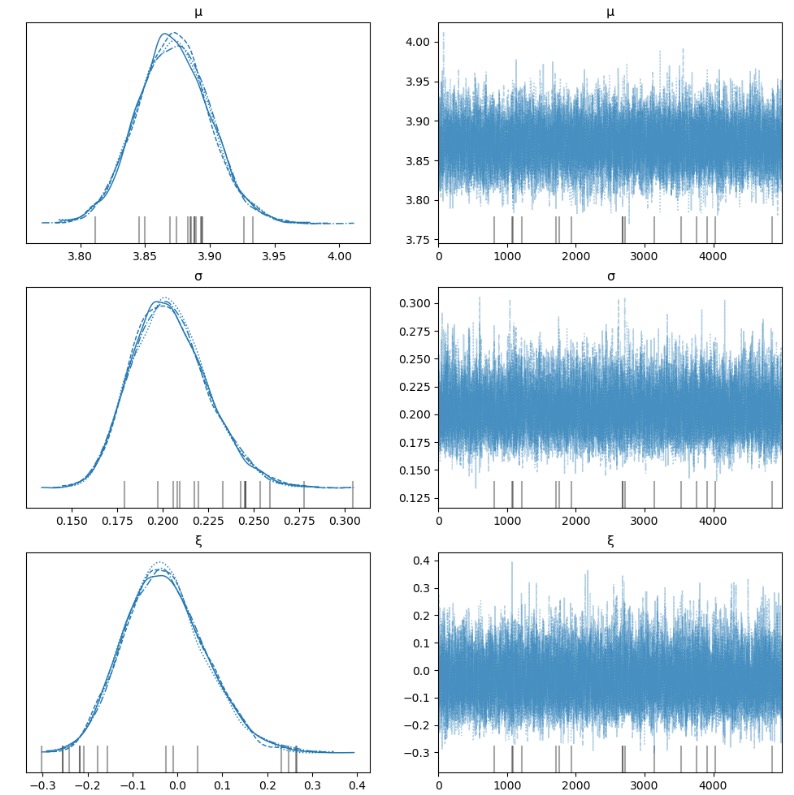
発散
トレースは発散を見せています。パラメータをサポートするために境界に接近した時に、HMC/NUTSサンプラーは問題が生じます。GEVの境界が ξ の符号を変えるので、この問題を解決するために変換を提案するのが困難になります。一つの可能な変換ーBox-Coxー が、Bali[2003]によって提案されています。しかし、CapraniとOBrien[2010]は、最大尤度の推定でさえも数値的に不安定になることを発見しています。いづれのケースでも発散の問題を緩和するために推薦するのは、
- 対象の受動率を増加させる
- より有益な事前情報を得て、特にシェイプパラメータを物理的に適切な値に制限する。典型的にはξ ⊂ [-0.5, 0.5 ]
- テイルを惹きつける領域を決定し、その分布を直接使用する。
推論
95%の信頼できるパラメータの内部範囲の推定は、
az.hdi(idata, hdi_prob=0.95)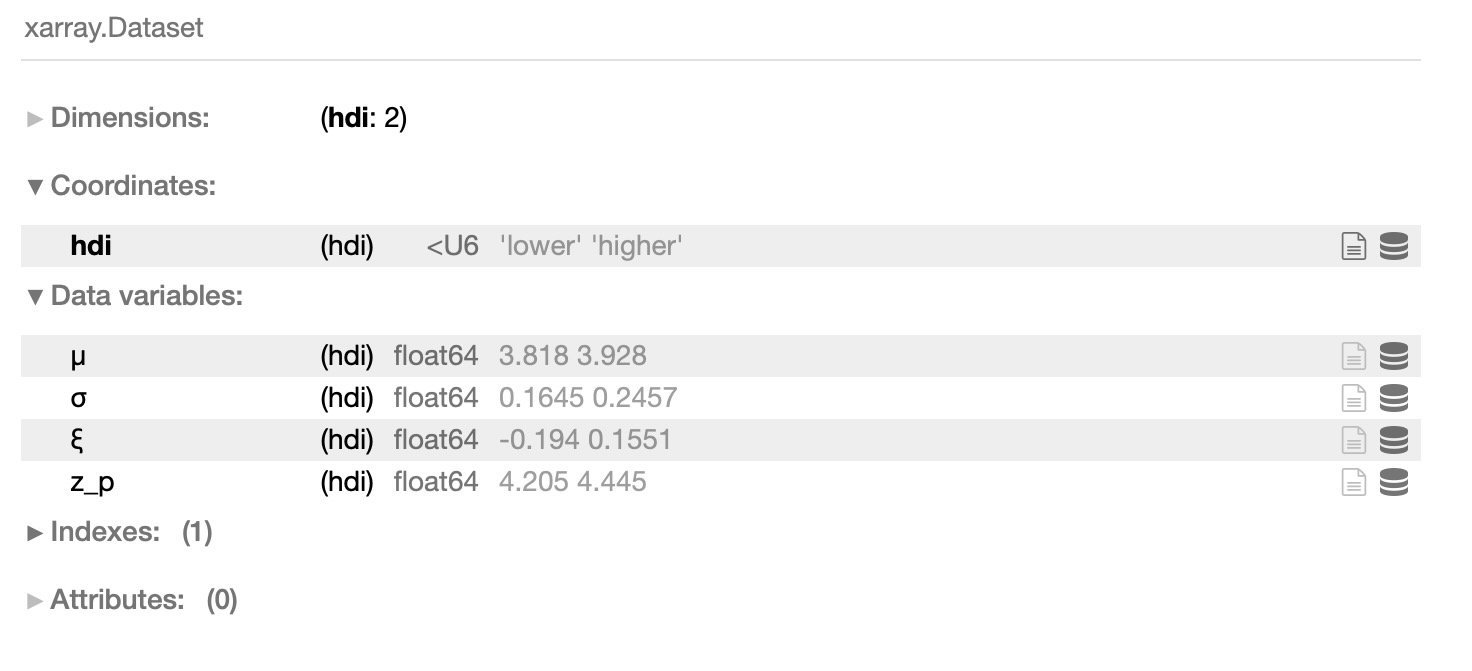
予測分布の試験は、(正規を仮定する必要はなく)パラメータの変異性を考慮します。
az.plot_posterior(idata, hdi_prob=0.95, var_names=["z_p"], round_to=4);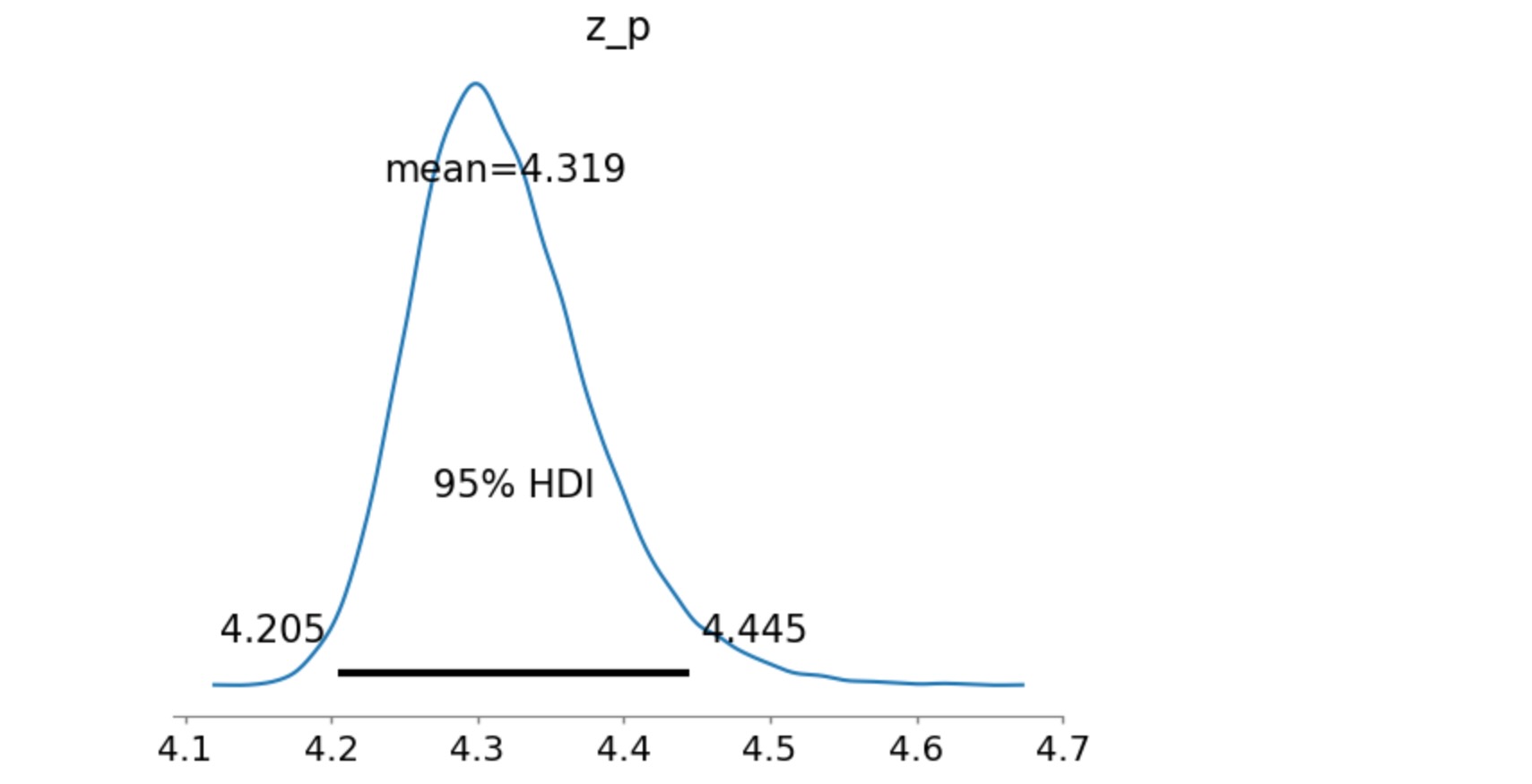
そのようにデータが影響しているかを見るために、Zp の事前と事後予測を比較しましょう。
z.plot_dist_comparison(idata, var_names=["z_p"]);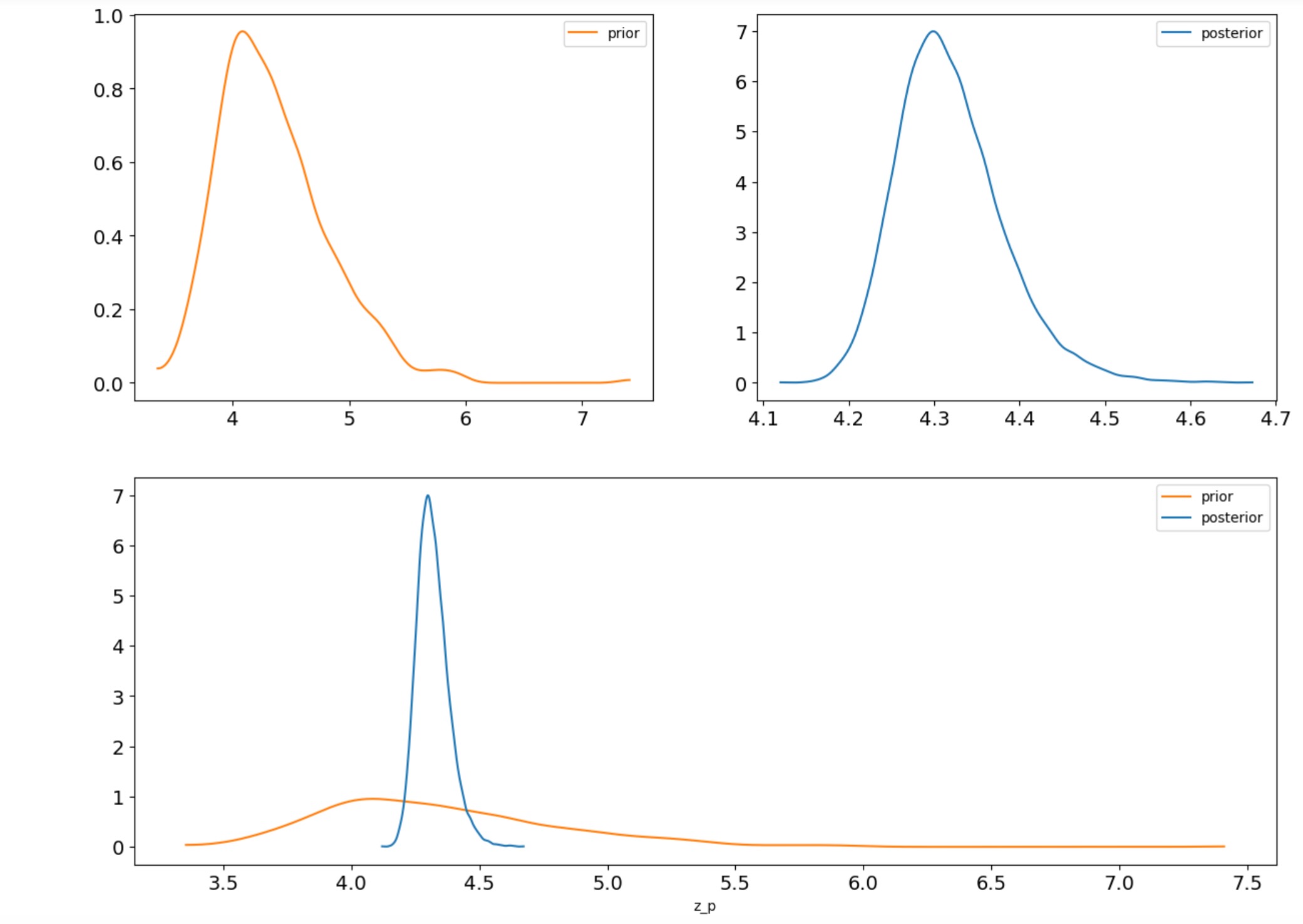
比較
コール[2001]による結果を比較するために、私たちは、事後分布(最大事後推定 またはMAP)のモードを使って最大尤度の推定(MLE)を概算します。事前分布が事後推定の周りで適切に平坦な場合に、まとまります。
コール[2001]によるMLEの結果は

推定の共分散行列は

私たちの推論からMLEの推定を抽出することは、何か試験可能な配列を扱うために、任意のArvizの背後関数にアクセスすることを必要とします。
_, vals = az.sel_utils.xarray_to_ndarray(idata["posterior"], var_names=["μ", "σ", "ξ"])
mle = [azpu.calculate_point_estimate("mode", val) for val in vals]
mle[3.871685835613608, 0.20104686595697233, -0.03366355398308349]idata["posterior"].drop_vars("z_p").to_dataframe().cov().round(6)| μ | σ | ξ | |
|---|---|---|---|
| μ | 0.000778 | 0.000179 | -0.000767 |
| σ | 0.000179 | 0.000445 | -0.000583 |
| ξ | -0.000767 | -0.000583 | 0.008216 |
結果はよく適合しています。しかし、ベイジアン設定でこれを実行する利点は、本質的に自由なパラメータの完全な事後接合分布とリターンレベルを得ることです。これを、ゆるい正規性の仮定とコール[2001]が行った分散教分散行列を得るための計算努力と比較してみなさい。
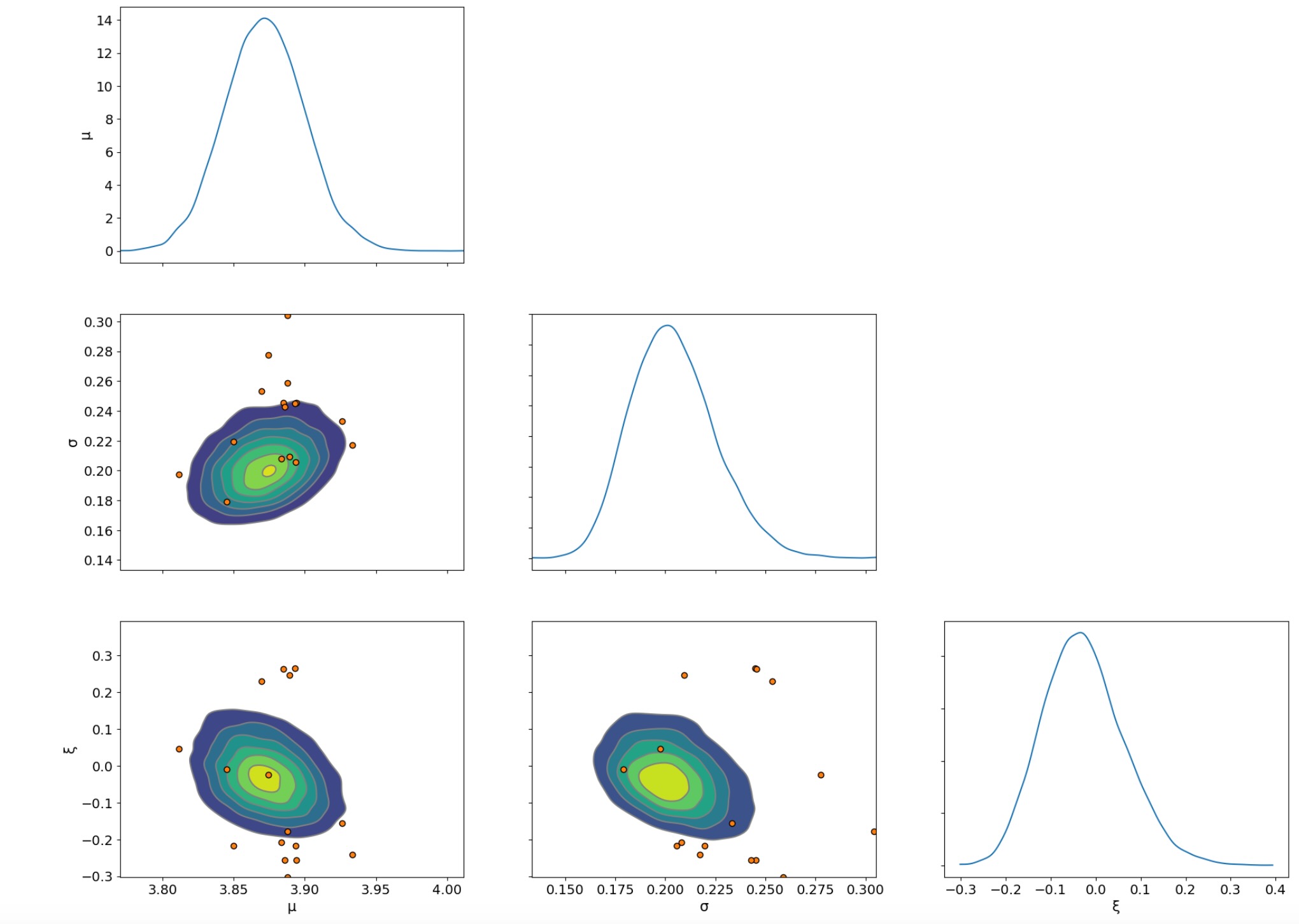
最後に、ペアのプロットを試験して、発散している状態で推論することの困難さをみてみます。
az.plot_pair(idata, var_names=["μ", "σ", "ξ"], kind="kde", marginals=True, divergences=True);
製作者
著者:Colin Caprani. 2021年10月
参考文献
- Stuart Coles. An introduction to statistical modeling of extreme values. Springer Series in Statistics. Springer, London, England, 2001 edition, August 2001. ISBN 978-1-85233-459-8.
- Colin C. Caprani and Eugene J. OBrien. The use of predictive likelihood to estimate the distribution of extreme bridge traffic load effect. Structural Safety, 32(2):138–144, 2010.
- Turan G. Bali. The generalized extreme value distribution. Economics Letters, 79(3):423–427, 2003.
- Colin C. Caprani and Eugene J. OBrien. Estimating extreme highway bridge traffic load effects. In Hitoshi Furuta, Dan M Frangopol, and Masanobu Shinozuka, editors, Proceedings of the 10th International Conference on Structural Safety and Reliability (ICOSSAR2009), 1 – 8. CRC Press, 2010.