観測値に対抗する推論：COVID-19が原因の超過死者数の計算

　因果推論と観測値に対抗する(counterfactual:注1)思考は本当に興味深いものですが、複雑なトピックです。それでもやはり相対的に簡単な例を通してその考えを理解するために前進することができます。ここではその概念とpyMCを用いたベイジアン因果推論の実績的な実装に焦点を当てます。

　私たちはこれを使うことを考えさせられますが、しかしCOVID-19が原因の超過死者数の計算を例にするのは重要なことです。個々の論旨の考えは強力にグーグルの(causalimpact:注2)因果関係への影響(Brodersen et al.[2015])と重複しています。実際に私たちは、イングランドとウェールズからのデータを使ってCOVID-19が始まってからの超過死者数を見積ることを試みます。超過死者数は以下のように定義します。

超過死者数 = 報告された死者数　ー　　予想死者数
　　　　　(ノイズ付きの実際の死者） 　(観測されていない事実に逆らったデータ）

　超過死者数について主張するために、因果推論/観測値に対抗する推論を必要とします。死者数は、世界の現実の(ノイズと遅延を含む)観測できる測定した事実だけが報告されますが、予想死者数は、我々の時間軸上では実現することがないため測定できません。それは、予想死者数が、"いったい何が起こっているのか?"を問うことができる状況での、実際には観測されなかったデータ(counterfactual)の思考実験です。

全体のストラテジー

実際にこれについてどのように進めましょう？私たちはこのストラテジーに従います。

1. 全ての原因による死者数の報告データ、同様にいくつかの適当な予測変数を取り込みます。

• 月毎の平均温度
• 季節効果のモデルを使った年間の月
• 任意の線形トレンド下のモデルを使った時間

2. covidの事前と事後のデータを分離します。これは重要なステップです。私たちは、COVID-19前のデータに基づく観測値に対抗した予測を構築できるように、私たちがわかっているCOVID-19前の状況に基づくモデルを提案したいのです。

3. 事前データセットに基づいてモデルパラメータを見積ります。

4. COVID-19以前の期間でのモデルによる死者数の予測。これはcounterfactualではなく、すでに観測済みのデータを説明するのにどれくらいモデルが有用であるかを教えてくれます。

5. 観測値に対抗する推論(Counterfactual inference) - 私たちは事実に対抗した予測を構築するためのモデルを使います。仮にCOVID-19がなかったとしたら、私たちはその後の将来何を見ることになったのか？　これは有名なdo-operator(注3)を使うことによってアーカイブすることができます。私たちはサンプルデータがない事後予測でこれを行います。

6. 観測値に対抗した推論、報告された死者数と比較して超過死者数を計算します。

モデル化のストラテジー

　私たちはモデリングに対して多くの異なるアプローチを取ります。時系列データを取り扱うために、時系列モデリングのアプローチを使うことが賢明です。例えば、グーグル社のCausalInpactはベイジアン構造時系列モデルを使います。しかし私たちは多くの代替の時系列モデルを選択することができます。

　しかし、このケーススタディの焦点は、時系列モデルの特定よりむしろ、観測値に対抗した推論であるため、時系列モデルについて簡単な線形回帰アプローチを選択します。（これについてはMartin [2021]を参照してください。注4）

因果推論の免責

　読者は、私たちがここでできる因果性を主張することには、もちろん限界があることを認識しているでしょう。

　私たちが、仮に一定期間に宣伝した状況でのマーケティング例を取り扱って、超過売上についての推論を作りたいならば、宣伝期間に起きた他の因子に関して説明する調査が終了していれば、強力な因果性を主張できます。

　同様に、イングランドとウェールズで2020年1月以後、UKで変化した他の多くのことがあります。そのため、私たちが信頼度を上げたいならば、他の実現可能な関連因子を説明する必要があります。

　最後に、私たちは、x人が直接COVID-19によって死亡した、とは断言しません。超過死者の概念の長所は、全ての死因から私たちが予測した超過分を読み取ることです。そのようにしてCOVID-19ウイルスによる直接の死者だけでなく、ウィルスによって後で生じる全ての影響と、例えば、注意の有効性をカバーします。

import calendar
import os

import arviz as az
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns
import xarray as xr

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

役立つ関数をいくつか定義します。

def ZeroSumNormal(name, *, sigma=None, active_dims=None, dims, model=None):
    model = pm.modelcontext(model=model)

    if isinstance(dims, str):
        dims = [dims]

    if isinstance(active_dims, str):
        active_dims = [active_dims]

    if active_dims is None:
        active_dims = dims[-1]

    def extend_axis(value, axis):
        n_out = value.shape[axis] + 1
        sum_vals = value.sum(axis, keepdims=True)
        norm = sum_vals / (pt.sqrt(n_out) + n_out)
        fill_val = norm - sum_vals / pt.sqrt(n_out)
        out = pt.concatenate([value, fill_val], axis=axis)
        return out - norm

    dims_reduced = []
    active_axes = []
    for i, dim in enumerate(dims):
        if dim in active_dims:
            active_axes.append(i)
            dim_name = f"{dim}_reduced"
            if name not in model.coords:
                model.add_coord(dim_name, length=len(model.coords[dim]) - 1, mutable=False)
            dims_reduced.append(dim_name)
        else:
            dims_reduced.append(dim)

    raw = pm.Normal(f"{name}_raw", sigma=sigma, dims=dims_reduced)
    for axis in active_axes:
        raw = extend_axis(raw, axis)
    return pm.Deterministic(name, raw, dims=dims)


def format_x_axis(ax, minor=False):
    # major ticks
    ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y %b"))
    ax.xaxis.set_major_locator(mdates.YearLocator())
    ax.grid(which="major", linestyle="-", axis="x")
    # minor ticks
    if minor:
        ax.xaxis.set_minor_formatter(mdates.DateFormatter("%Y %b"))
        ax.xaxis.set_minor_locator(mdates.MonthLocator())
        ax.grid(which="minor", linestyle=":", axis="x")
    # rotate labels
    for label in ax.get_xticklabels(which="both"):
        label.set(rotation=70, horizontalalignment="right")


def plot_xY(x, Y, ax):
    quantiles = Y.quantile((0.025, 0.25, 0.5, 0.75, 0.975), dim=("chain", "draw")).transpose()

    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.025, 0.975]),
        fill_kwargs={"alpha": 0.25},
        smooth=False,
        ax=ax,
    )
    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.25, 0.75]),
        fill_kwargs={"alpha": 0.5},
        smooth=False,
        ax=ax,
    )
    ax.plot(x, quantiles.sel(quantile=0.5), color="C1", lw=3)


# default figure sizes
figsize = (10, 5)

# create a list of month strings, for plotting purposes
month_strings = calendar.month_name[1:]

データの取り込み

　私たちの目的のために、イングランドとウェールズで報告された(月毎の)死者数を取得します。このデータは国立統計局のデータセット、イングランドとウェールズの月次登録死者から利用できます。2006年から2022年の間のデータをダウンロードし、一つのcsvファイルに集計します。Met局からUKの気温平均のデータセットを取得し、予測用に月次のUKの気温データの平均を追加します。

try:
    df = pd.read_csv(os.path.join("..", "data", "deaths_and_temps_england_wales.csv"))
except FileNotFoundError:
    df = pd.read_csv(pm.get_data("deaths_and_temps_england_wales.csv"))

df["date"] = pd.to_datetime(df["date"])
df = df.set_index("date")

# split into separate dataframes for pre and post onset of COVID-19
pre = df[df.index < "2020"]
post = df[df.index >= "2020"]

データ視覚化

プロットした時系列は、死者数に季節要因があることを明白に示しており、そして年毎に死者数の平均が増加していることが想定できます。

ax = sns.lineplot(data=df, x="date", y="deaths", hue="pre")
format_x_axis(ax)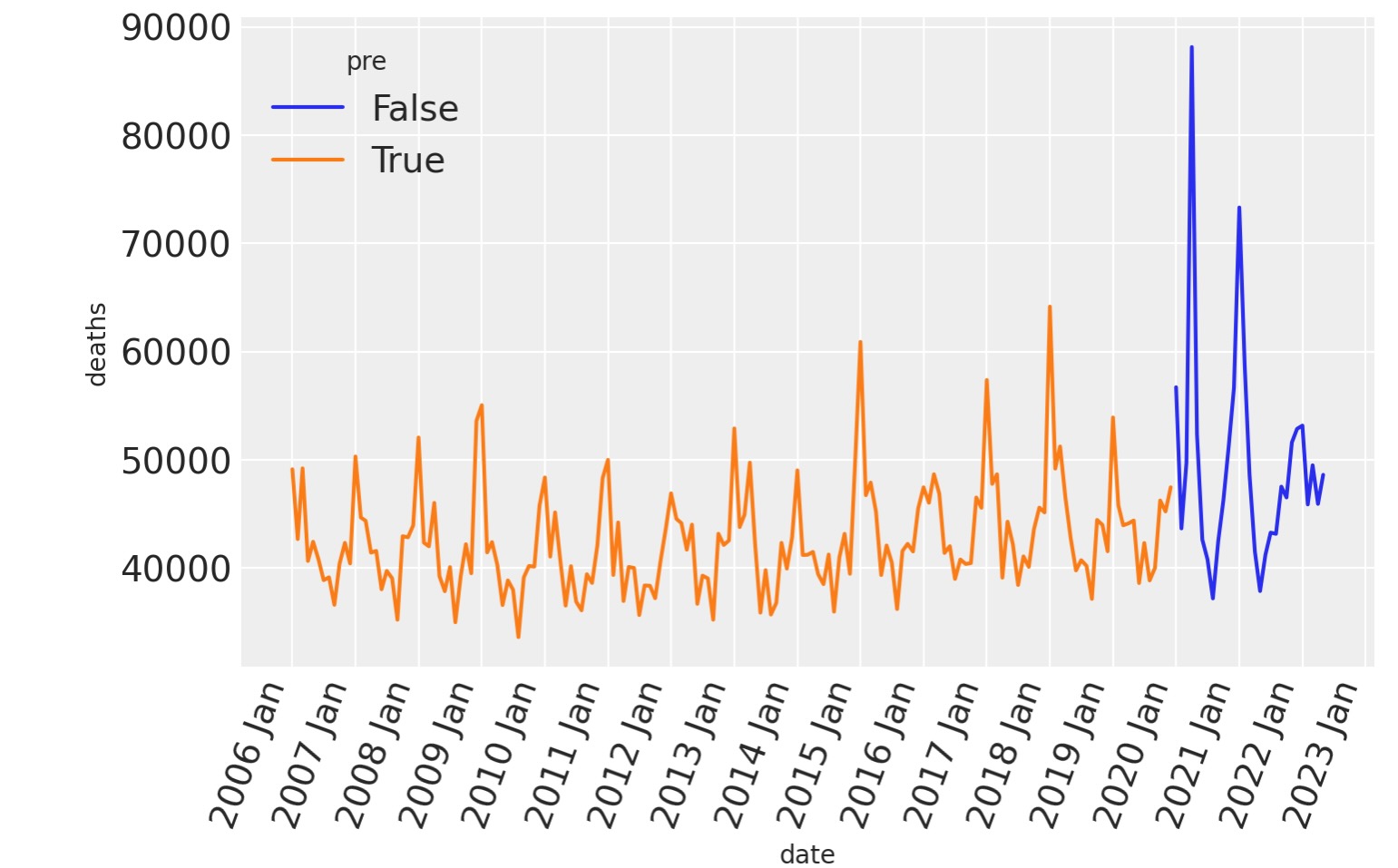

季節要因

年を色分けして月毎の関数として死者数をプロットすることで季節パターンをより緊密に見てみましょう。夏よりも冬の季節の方がより死者が多いのではないかという死者数に季節トレンドがあるのではないかという考えを確認します。私たちは1月の死者数が多いことがわかります。2月に下がった後、3月に再度戻ります。これは以下の組み合わせのためようです。

• 一月に登録されている実際は12月に発生した死者を押し戻す（push-back）。
• または、2月に亡くなった多くの脆弱な人々は、潜在的に寒い条件のせい1月に倒れていた状況が、先延ばし（pull-forward）になった。

　色付けは、年に関して主要な影響を持っておりーそれは年毎の死者数のベースラインが増加しているーという私たちの懸念をサポートします。

ax = sns.lineplot(data=pre, x="month", y="deaths", hue="year", lw=3)
ax.set(title="Pre COVID-19 data");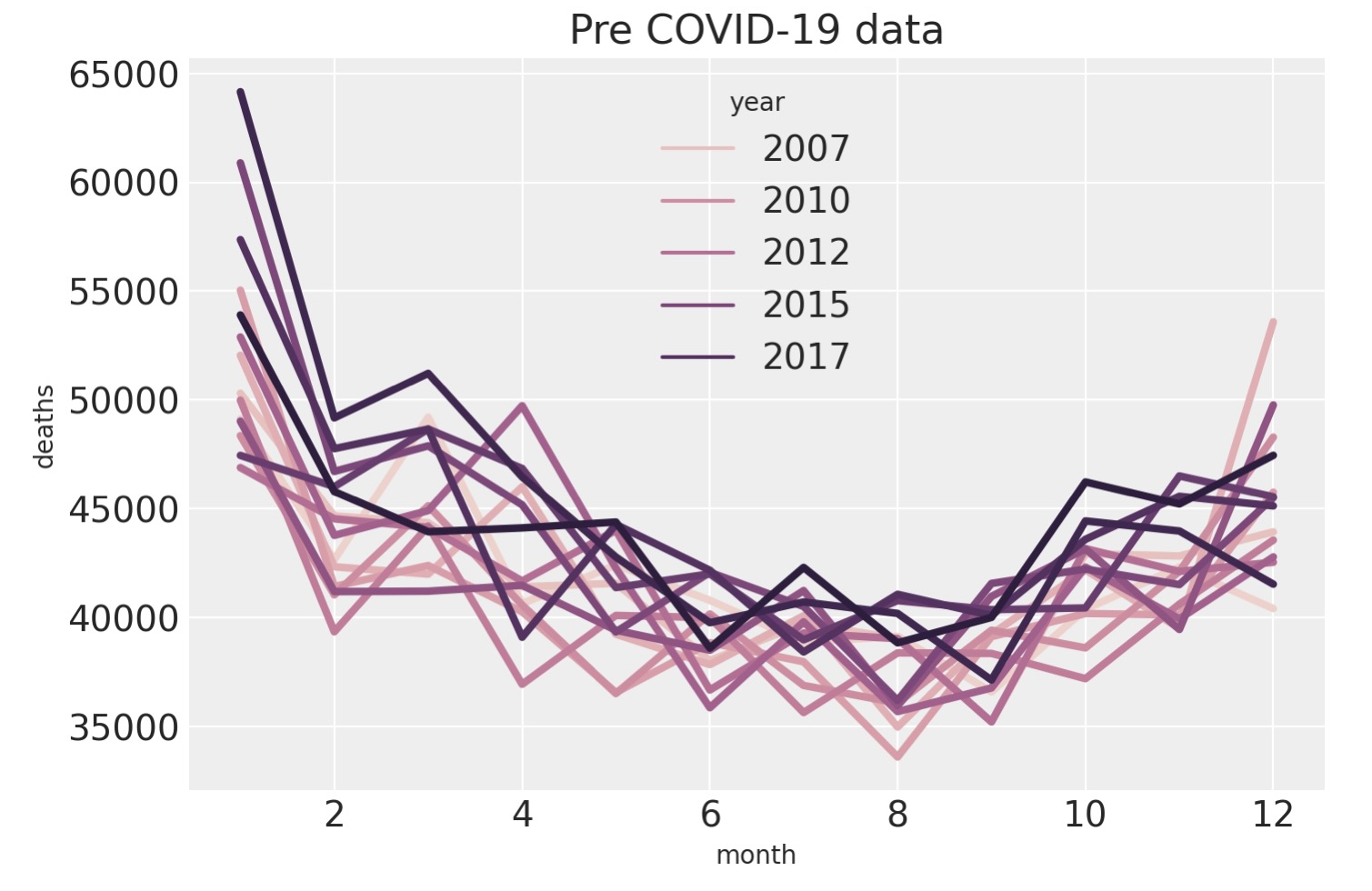

線形トレンド

COVID-19以前の時間上の死者の総数をプロットすることで緊密にみてみましょう。ここに幾らか変わりやすさはありますが、予測が報告された死者数の幾らかの分散を捉えるために、線形トレンドを追加しているようです。そしてそれゆえ、報告された死者数のよりよいモデルを生み出します。

annual_deaths = pd.DataFrame(pre.groupby("year")["deaths"].sum()).reset_index()
sns.regplot(x="year", y="deaths", data=annual_deaths);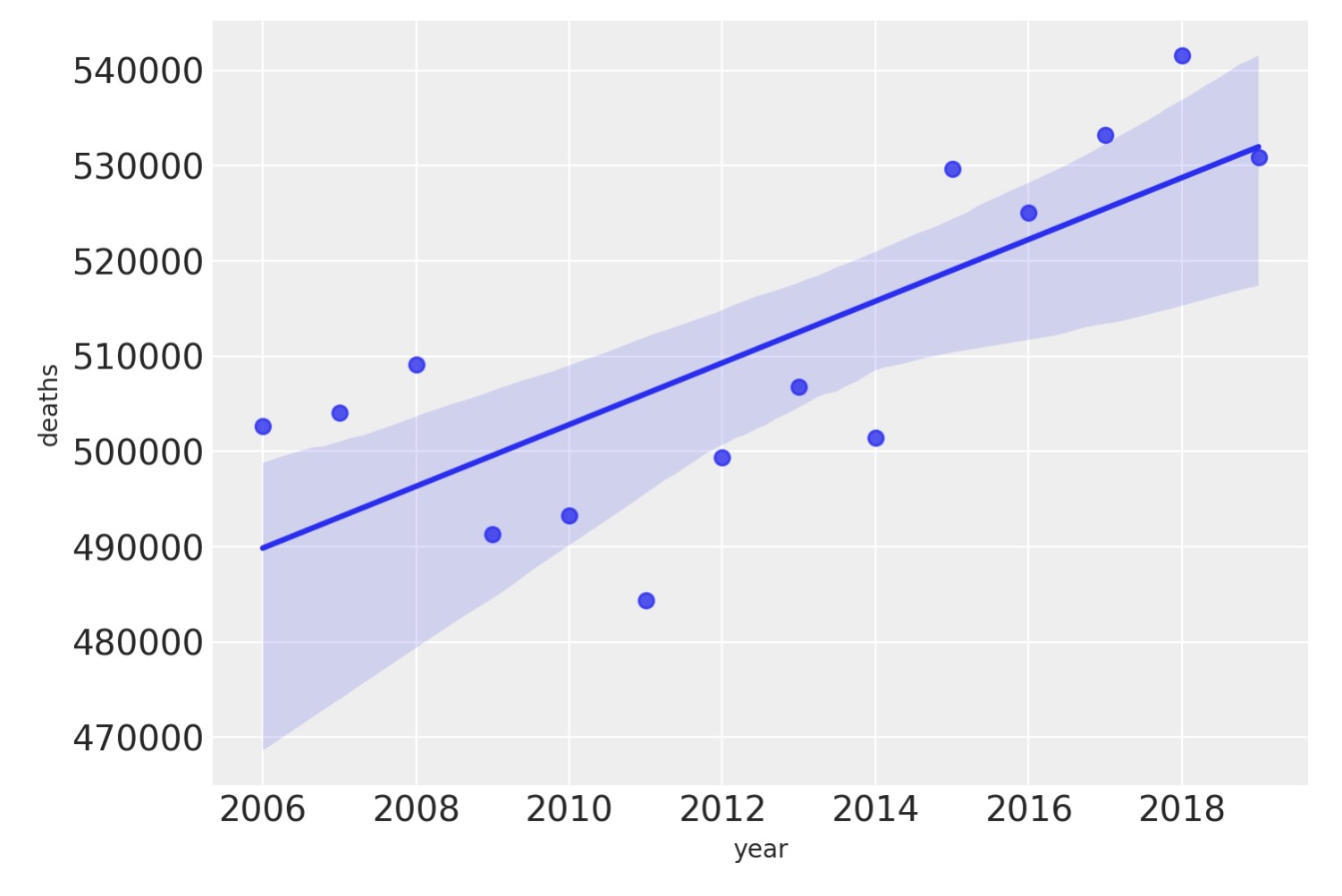

死に関する気温の影響

　事前データ、それのみに注目すると、月毎の平均気温と、死者数の間に負の関係があるのは明白です。広い範囲の気温の領域でこの死者数は気温に関してU字型の関係を持っておりことが明白です。しかし、イングランドとウェールズの気候は、このカーブの低い側だけをみます。それにもかかわらず、その関係はおおよそ二次方程式の近似がもっともらしい、しかし私たちの目的には線形な関係が開始する位置として適当なようです。

fig, ax = plt.subplots(1, 2, figsize=figsize)
sns.regplot(x="temp", y="deaths", data=pre, scatter_kws={"s": 40}, order=1, ax=ax[0])
ax[0].set(title="Linear fit (pre COVID-19 data)")
sns.regplot(x="temp", y="deaths", data=pre, scatter_kws={"s": 40}, order=2, ax=ax[1])
ax[1].set(title="Quadratic fit (pre COVID-19 data)");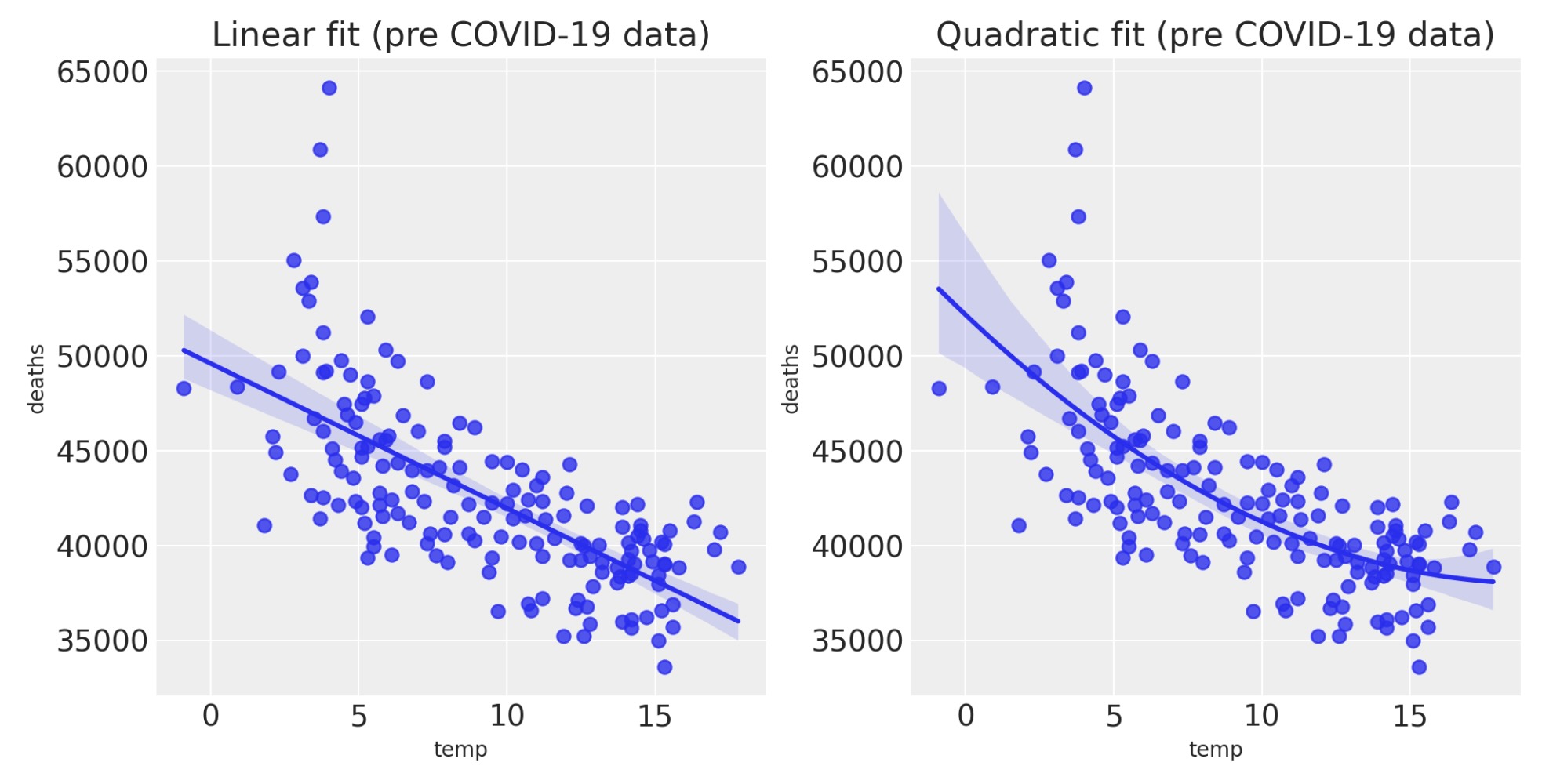

私たちのモデルの気温係数の事前の定義を使って、この関係の傾きをテストしてみましょう。

# NOTE: results are returned from higher to lower polynomial powers
slope, intercept = np.polyfit(pre["temp"], pre["deaths"], 1)
print(f"{slope:.0f} deaths/degree")

-764 deaths/degree

　これを元にして気温と死者数の間の関係だけに焦点を当てるならば、月次の平均気温７６４°から１度増加するごとに、死者数が減少することを予想します。そのため、気温の影響のための係数を事前に定義することにより、この図を使うことができます。

モデリング

　私たちは、時間経過上で切片と線形のトレンド、（各月の）季節の偏差、月次の平均気温により、報告された死者数を予測するつもりです。そうこれはかなり分かりやすい線形モデルです。特筆すべきことは、私たちは、パラメータの同一性が確認できるように一つモデルの自由度を減少させるために、正規に分布された月次の偏差を平均値０を持つように変換することです。

with pm.Model(coords={"month": month_strings}) as model:

    # observed predictors and outcome
    month = pm.MutableData("month", pre["month"].to_numpy(), dims="t")
    time = pm.MutableData("time", pre["t"].to_numpy(), dims="t")
    temp = pm.MutableData("temp", pre["temp"].to_numpy(), dims="t")
    deaths = pm.MutableData("deaths", pre["deaths"].to_numpy(), dims="t")

    # priors
    intercept = pm.Normal("intercept", 40_000, 10_000)
    month_mu = ZeroSumNormal("month mu", sigma=3000, dims="month")
    linear_trend = pm.TruncatedNormal("linear trend", 0, 50, lower=0)
    temp_coeff = pm.Normal("temp coeff", 0, 200)

    # the actual linear model
    mu = pm.Deterministic(
        "mu",
        intercept + (linear_trend * time) + month_mu[month - 1] + (temp_coeff * temp),
        dims="t",
    )
    sigma = pm.HalfNormal("sigma", 2_000)
    # likelihood
    pm.TruncatedNormal("obs", mu=mu, sigma=sigma, lower=0, observed=deaths, dims="t")

pm.model_to_graphviz(model)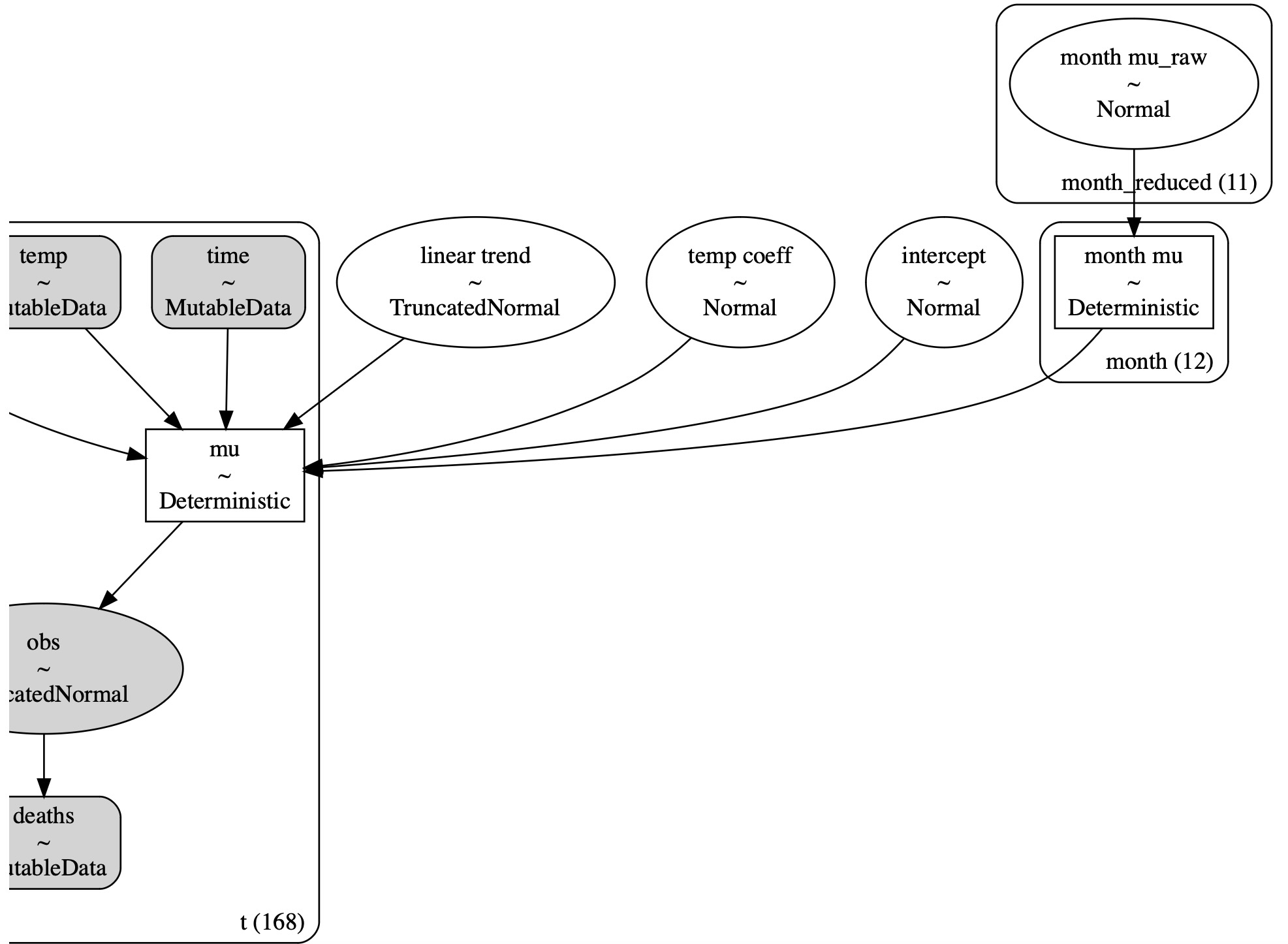

事前予測チェック

ベイジアンワークフローの一部として、任意の観測データを取得する前に、モデルが探索する結果を見るために事前予測をプロットします。

with model:
    idata = pm.sample_prior_predictive(random_seed=RANDOM_SEED)


fig, ax = plt.subplots(figsize=figsize)

plot_xY(pre.index, idata.prior_predictive["obs"], ax)
format_x_axis(ax)
ax.plot(pre.index, pre["deaths"], label="observed")
ax.set(title="Prior predictive distribution in the pre COVID-19 era")
plt.legend();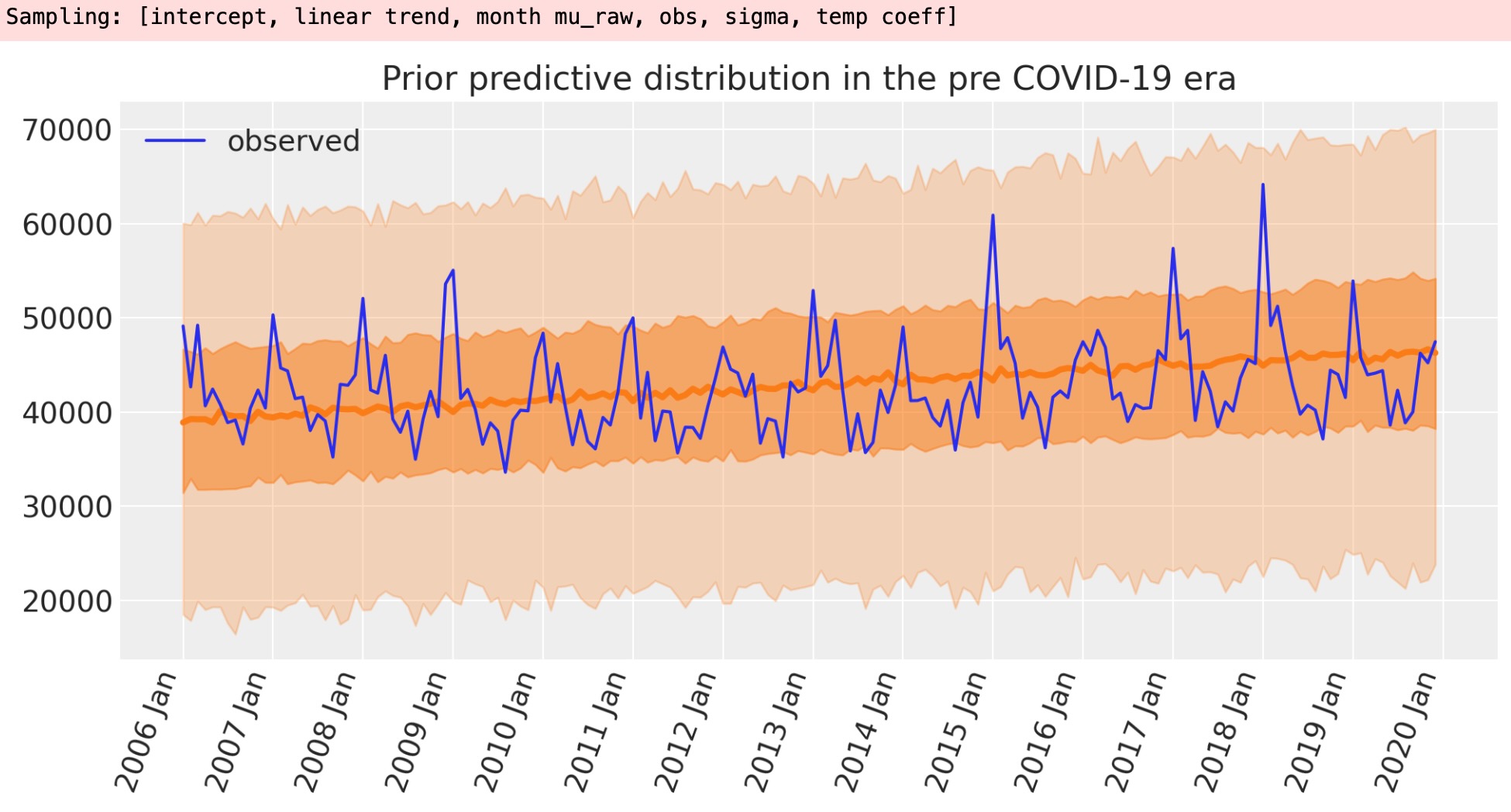

これは適切であるようです。

• 事前の死者数は、観測値の中央に見えます。
• 事前に与えられた、死者数の予測範囲は全く広範囲で、モデルに過剰な制限を与えそうにありません。
• モデルは各月で負の死者数を予測しません。

私たちは、Arviz事前予測チェックプロットすることでより詳細にこれを見ることができます。再度、私たちには、観測値の分布が、実際の観測値の中央にありながら、より拡散していることがわかります。これは、事前の制限がありすぎずに、上位と下位の事後予測に組織的に影響しそうにないことを私たちが知っているように有益です。

az.plot_ppc(idata, group="prior");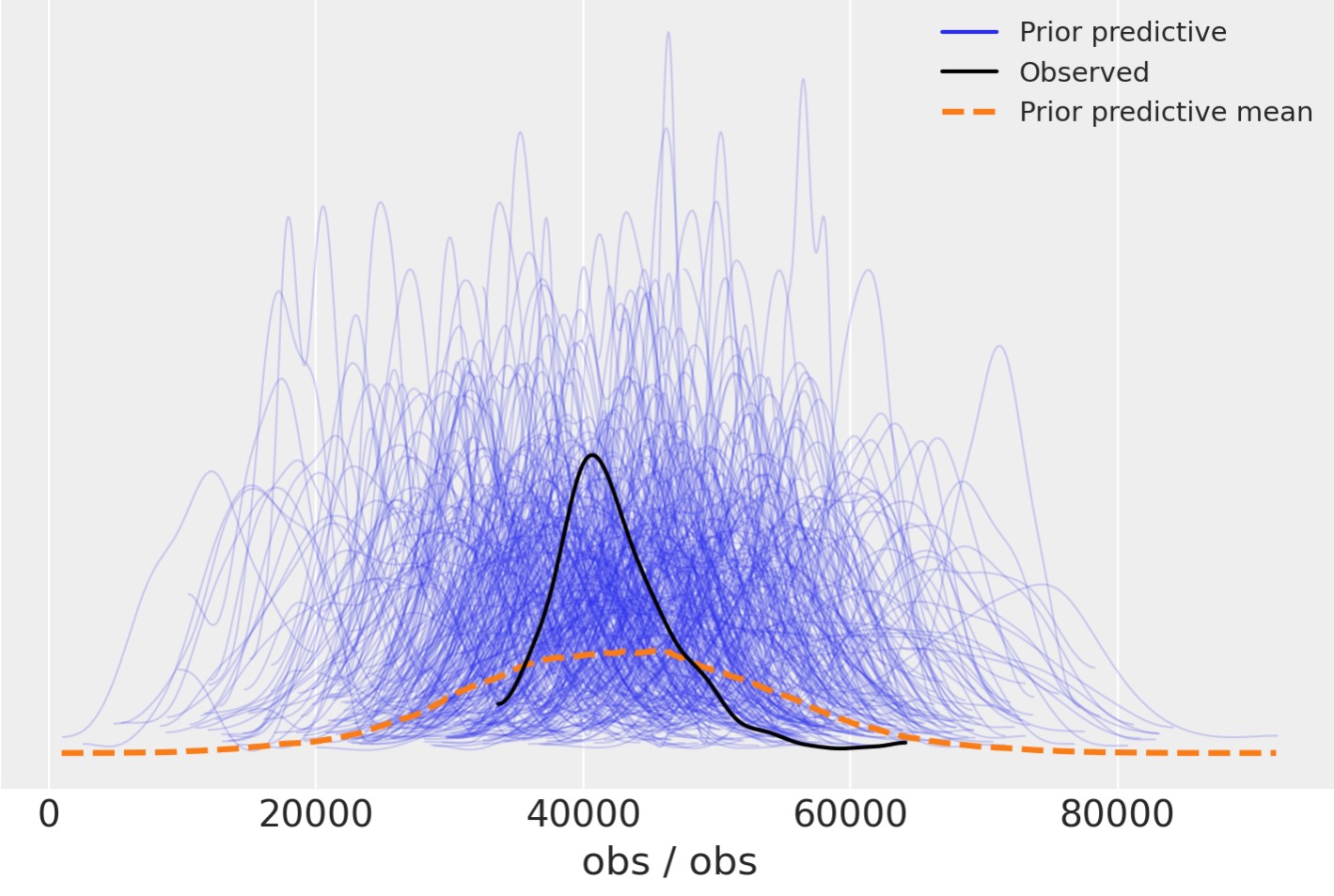

推論

事後分布のためのサンプルを出力します。これがCOVID-19以前のデータのみで実行していることを覚えておいてください。

with model:
    idata.extend(pm.sample(random_seed=RANDOM_SEED))

az.plot_trace(idata, var_names=["~mu", "~month mu_raw"]);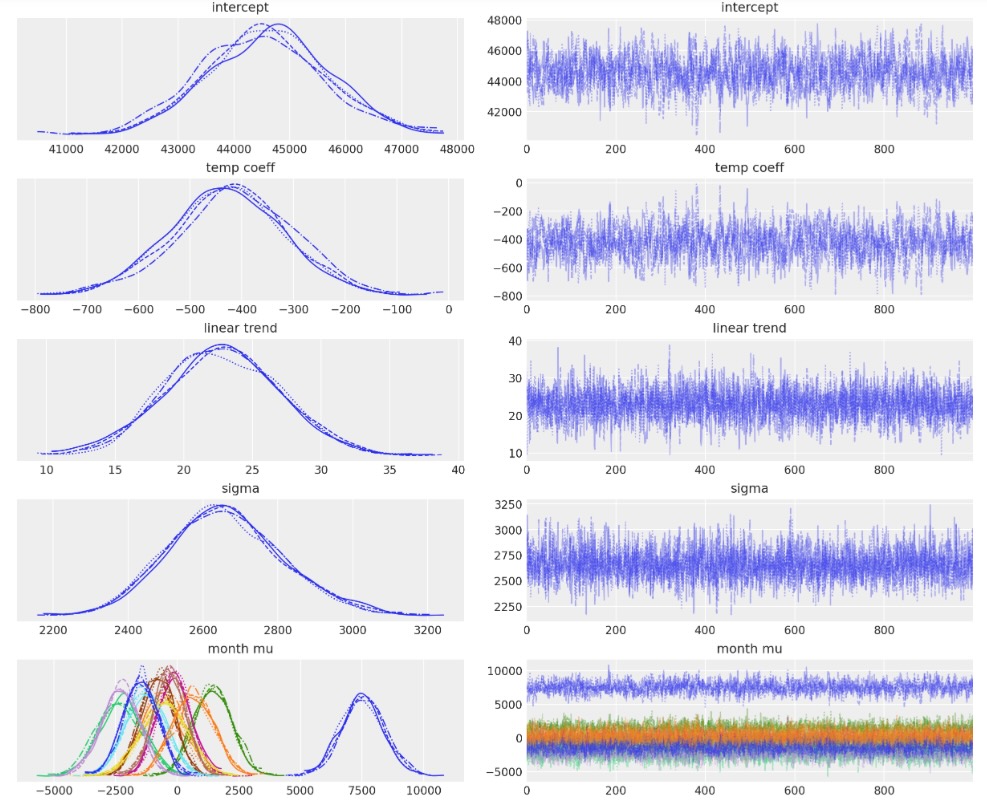

季節の影響に焦点を当てるために異なった方法で、月次の偏差の事後予測をみてみましょう。

az.plot_forest(idata.posterior, var_names="month mu", figsize=figsize);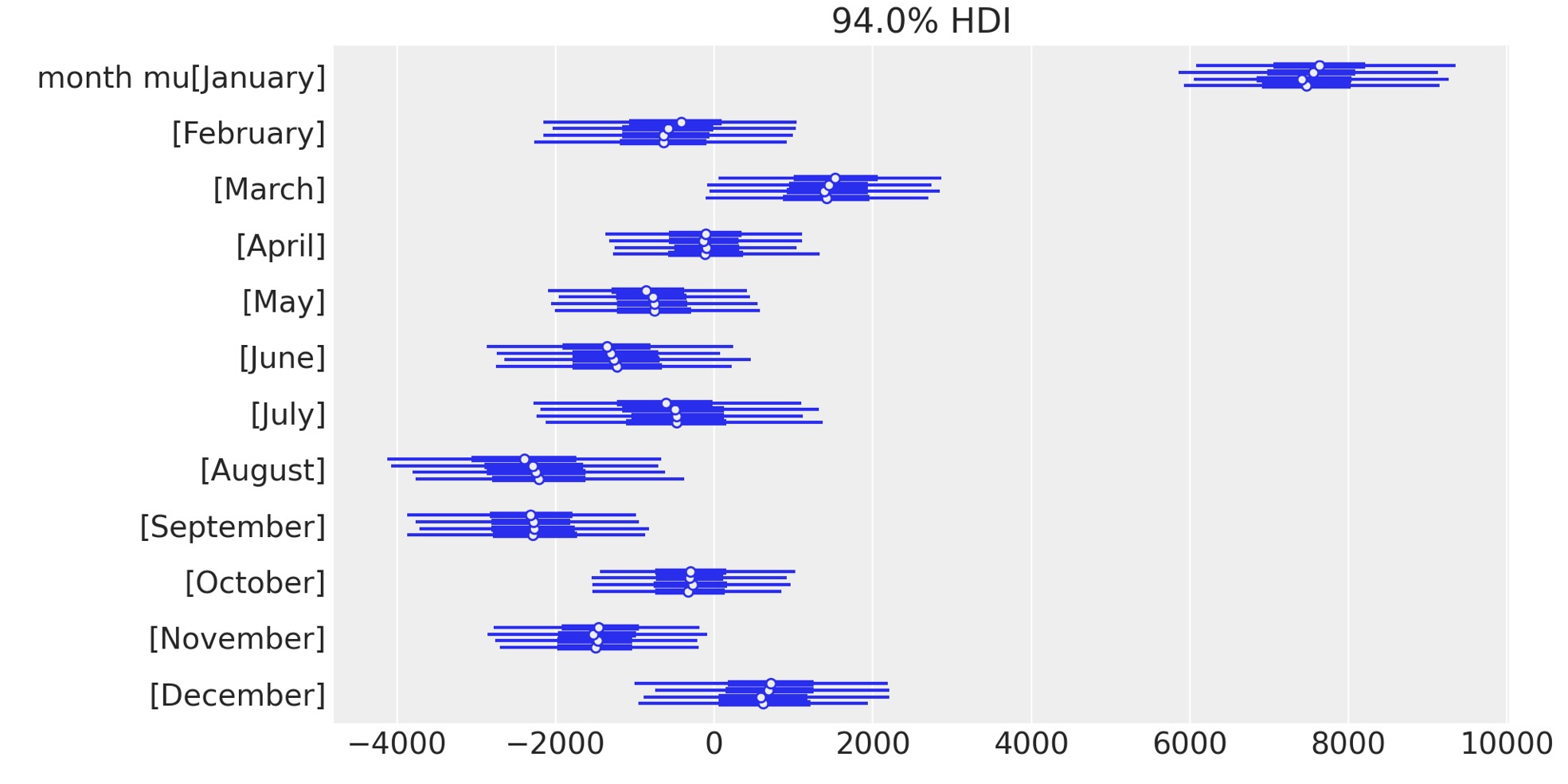

事後予測チェック

他のベイジアンワークフローの重要な側面は、モデルの事後予測をプロットすることです。それは、どれくらいうまくモデルがすでに観測されたデータに適合できるか見ることができます。この点で、モデルが簡単すぎるか、それともうまく適合しているかどうかを決定することができます。

with model:
    idata.extend(pm.sample_posterior_predictive(idata, random_seed=RANDOM_SEED))


fig, ax = plt.subplots(figsize=figsize)

az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.95, smooth=False)
ax.plot(pre.index, pre["deaths"], label="observed")
format_x_axis(ax)
ax.set(title="Posterior predictive distribution in the pre COVID-19 era")
plt.legend();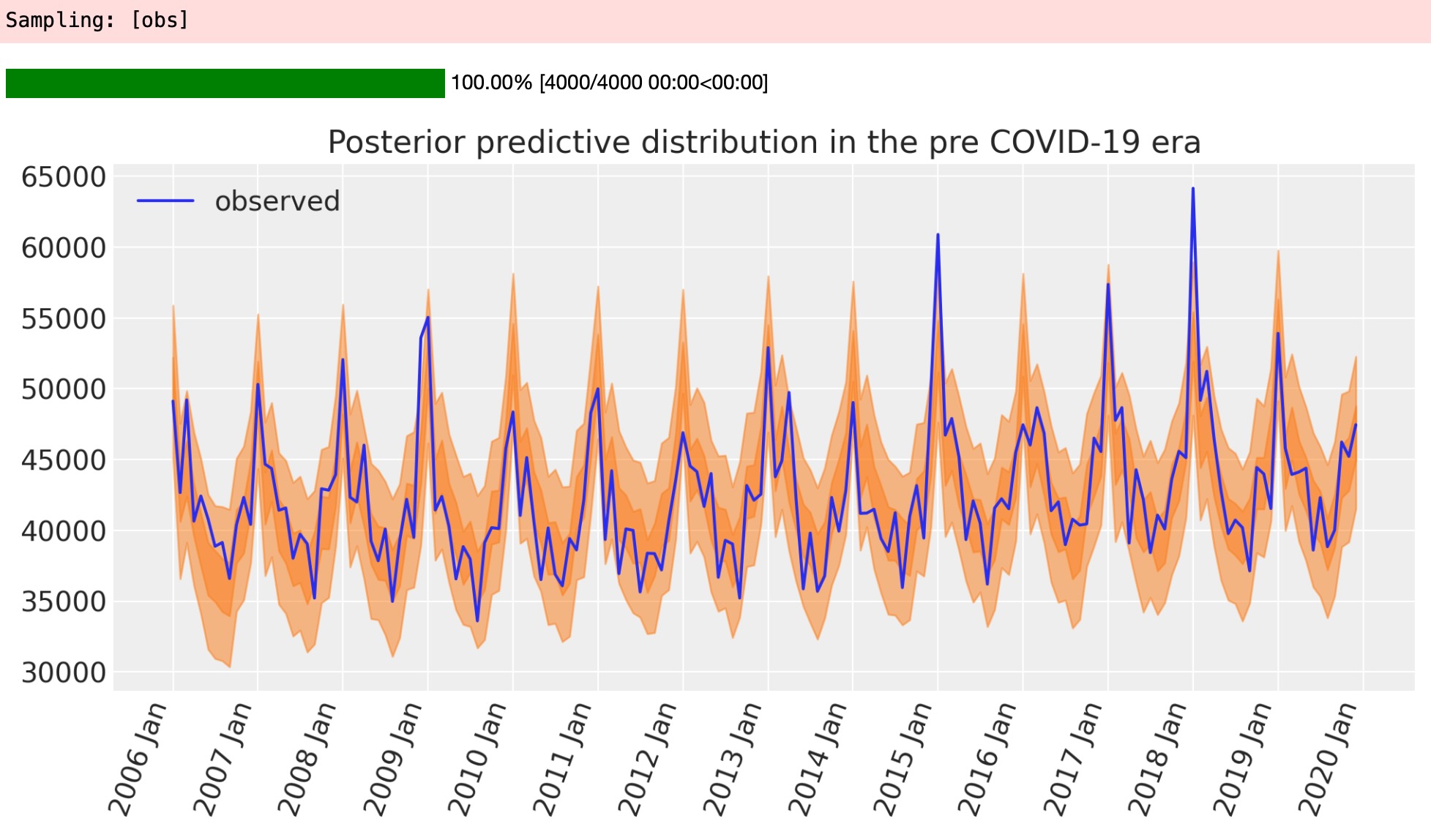

別のチェックをやりましょう。しかし、季節の影響に焦点を当てます。私たちは、年の月の関数として死の上のプロットを再現します。そして、完全な混乱からプロットを維持するために、事後平均だけをプロットします。このように、これは事後予測のチェックではなく、事後の観測値のチェックです。

temp = idata.posterior["mu"].mean(dim=["chain", "draw"]).to_dataframe()
pre = pre.assign(deaths_predicted=temp["mu"].values)

fig, ax = plt.subplots(1, 2, figsize=figsize, sharey=True)
sns.lineplot(data=pre, x="month", y="deaths", hue="year", ax=ax[0], lw=3)
ax[0].set(title="Observed")
sns.lineplot(data=pre, x="month", y="deaths_predicted", hue="year", ax=ax[1], lw=3)
ax[1].set(title="Model predicted mean");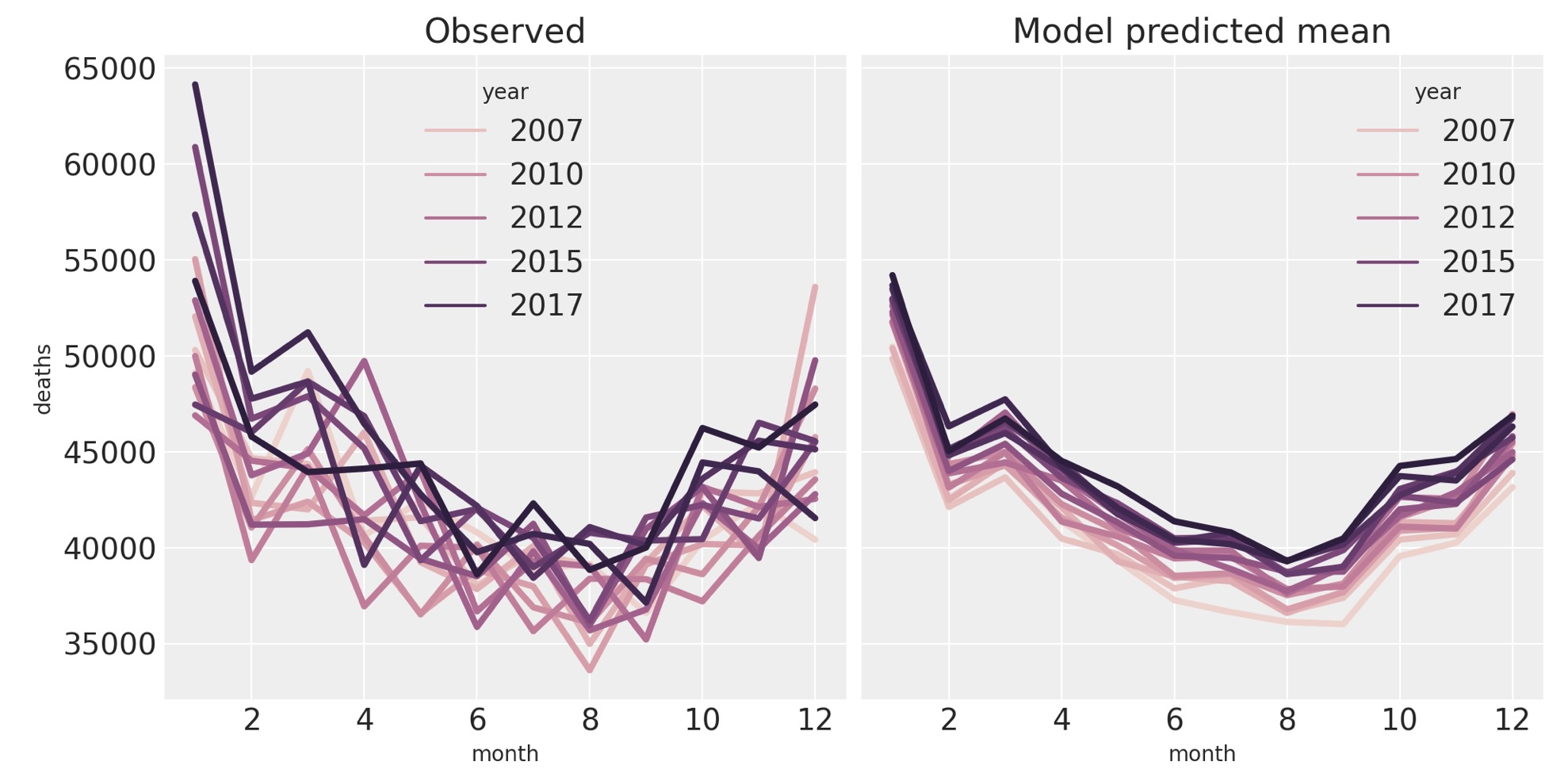

モデルは、データの特性を捉えることがかなり良くできています。右の図は月と年の主要な影響を明白に見ることができます。しかしながら、一月の左のデータでは、モデルがとらえていない何か興味深いことが起きていることがわかります。これは、年と月の間の相互作用を追加するモデルで捉えることができるかもしれません。この左の図は読者の演習とします。

超過死者数：Covid前

この段階は厳密には必要ありません。しかし、超過死者数の方式を事前期間のモデルの事前予測に適用できます。これはどの程度良いモデルとして検査できるかという理由で有益です。

# convert deaths into an XArray object with a labelled dimension to help in the next step
deaths = xr.DataArray(pre["deaths"].to_numpy(), dims=["t"])

# do the calculation by taking the difference
excess_deaths = deaths - idata.posterior_predictive["obs"]

fig, ax = plt.subplots(figsize=figsize)
# the transpose is to keep arviz happy, ordering the dimensions as (chain, draw, t)
az.plot_hdi(pre.index, excess_deaths.transpose(..., "t"), hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, excess_deaths.transpose(..., "t"), hdi_prob=0.95, smooth=False)
format_x_axis(ax)
ax.axhline(y=0, color="k")
ax.set(title="Excess deaths, pre COVID-19");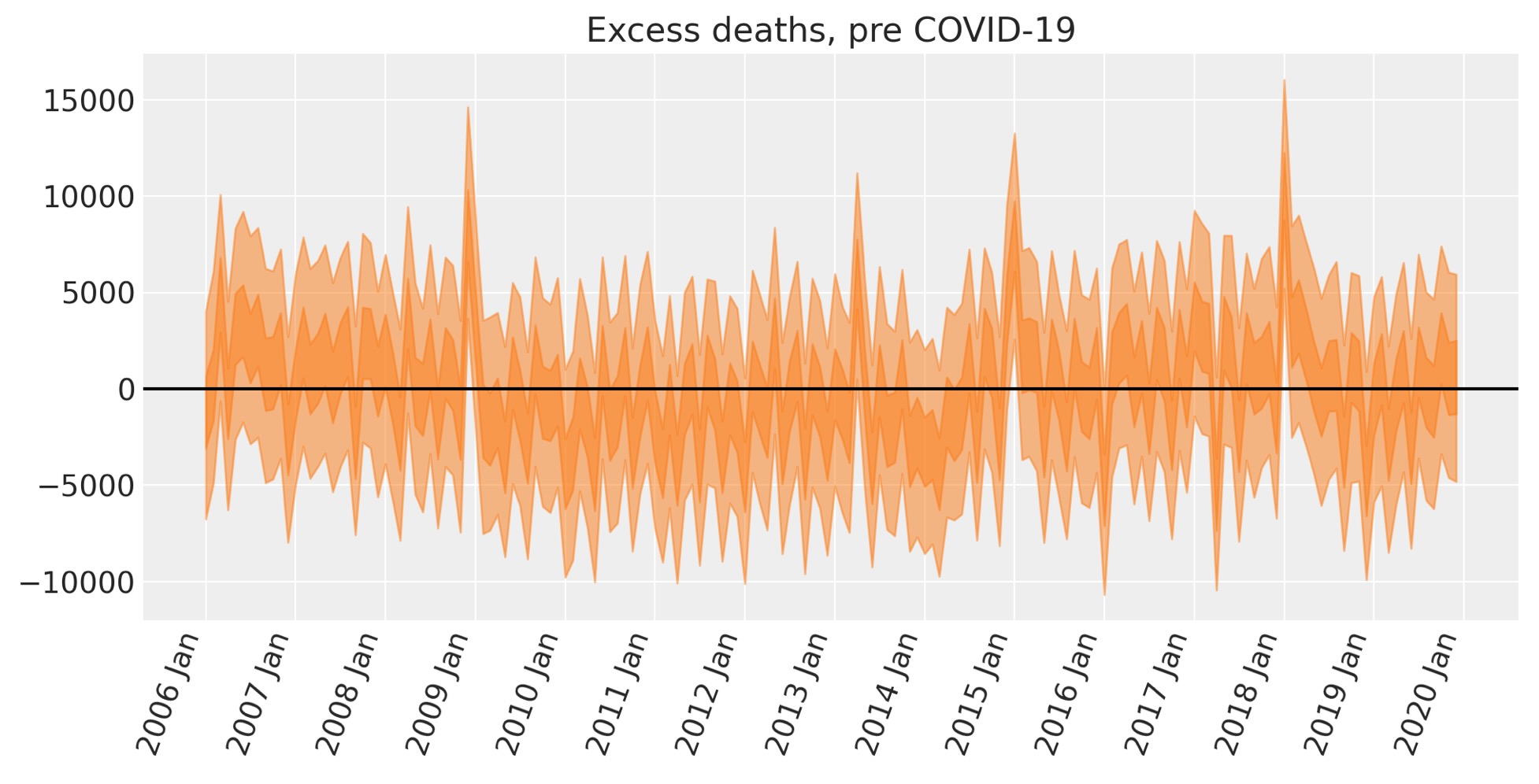

ここで、超過死者数はゼロより大きいことが最もらしい状況において、いくつかのスパイクを見ることができます。そうした機会は、私たちが予測できるa)季節の影響、b)線形の増加トレンド、c)冬場の寒さの影響の上下になります。

もし私たちが関心があるならば、これについて説明するかもしれない追加の兆候についての仮説を生成することを開始できます。ある考えは、共通の風邪の蔓延、または月の最低気温、それは平均値で捉えることのできない追加の予測情報の追加を含んでいます。

　私たちはまた一方で、モデルが全く捉えることのできない追加の一時的トレンドがあるのは見ることができます。ゼロの事後平均から低い頻度で組織的にドリフトすることがあります。それは潜在的に時間軸上で脆弱な集団の大きさの変化が原因となって、私たちが予期した兆候では全く捉えることのできないデータの中で追加の相違があるということです。

　しかし、COVID-19期間で超過の死者数を捉えることが私たちの厳密な目的です。そのため、ここでの第一の意図は、観測値に対抗する（counterfactual）思考なので、報告された死者数に関して最も包括的なモデルを作らずに、先へ進みます。

観測値に対抗する推論

それでは、通常の実務上の'仮の事態'のシナリオで、報告された死者数の予測モデルを使います。

　月と時間と一時的データ事後のデータフレームからモデルを更新し、私たちがこの’観測値に対抗する’(counterfactual)シナリオで観測する報告された死者数を予測するために、事後予測サンプリングを実行します。私たちはこれを'予測(フォーキャスティング)'とも呼びます。

with model:
    pm.set_data(
        {
            "month": post["month"].to_numpy(),
            "time": post["t"].to_numpy(),
            "temp": post["temp"].to_numpy(),
        }
    )
    counterfactual = pm.sample_posterior_predictive(
        idata, var_names=["obs"], random_seed=RANDOM_SEED
    )

fig, ax = plt.subplots(figsize=figsize)

plot_xY(post.index, counterfactual.posterior_predictive["obs"], ax)
format_x_axis(ax, minor=True)
ax.plot(post.index, post["deaths"], label="reported deaths")
ax.set(title="Counterfactual: Posterior predictive forecast of deaths if COVID-19 had not appeared")
plt.legend();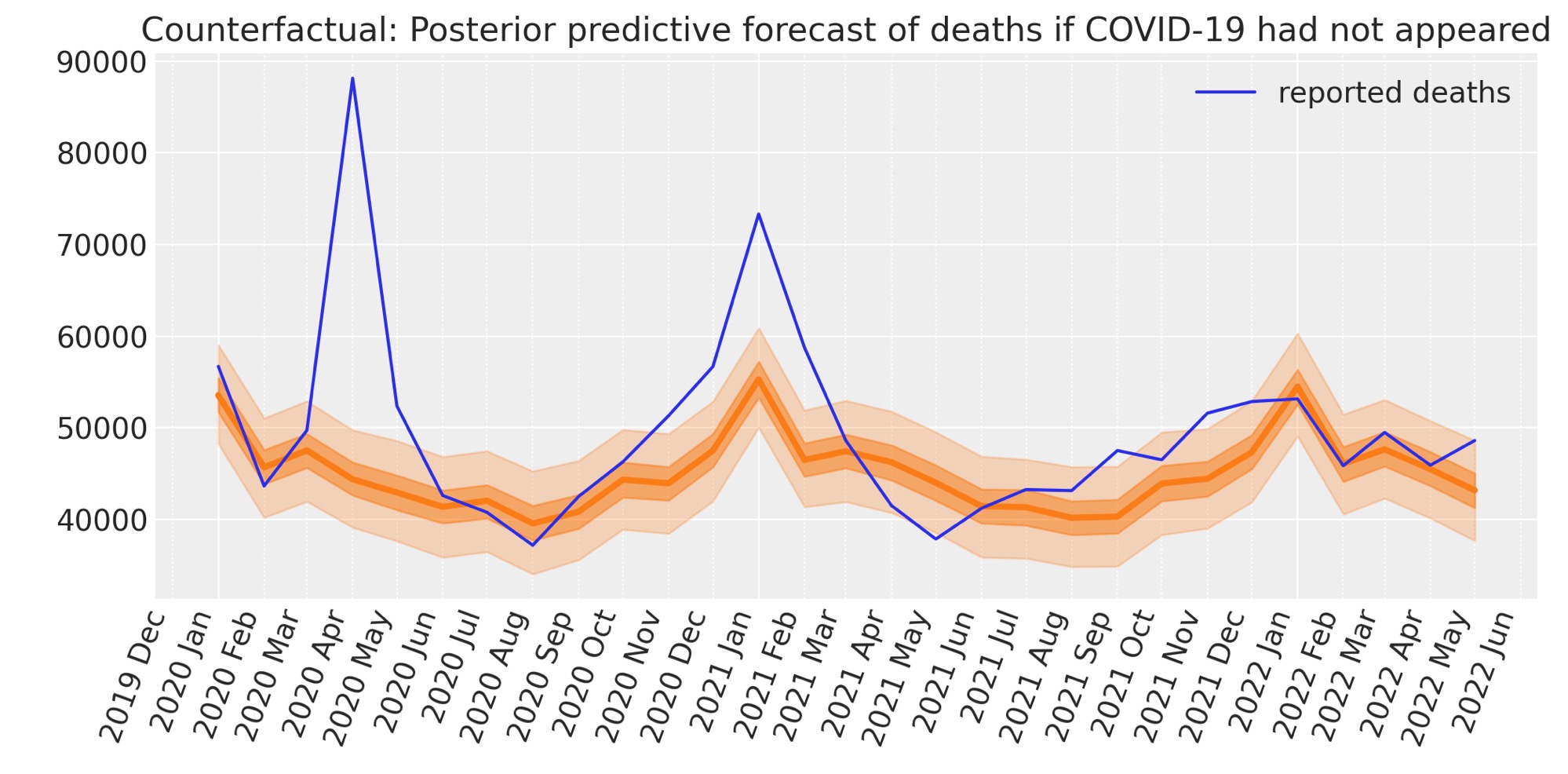

　私たちは、今、超過死者数の計算に必要な要素を持っています。すなわち、報告された死者数とCOVID-19期間の以前から事後までに変化がなかった時に何人の死者数が出たのかベイジアン観測に対抗する(counterfactual)予測です。

超過死者数：Covidが始まってからの超過死者数

　それでは、観測値に対抗するシナリオ下での予測された死者数を使います。そして、超過死者数の観測値に対抗する予期値で提案する報告された死者数と比較します。

# convert deaths into an XArray object with a labelled dimension to help in the next step
deaths = xr.DataArray(post["deaths"].to_numpy(), dims=["t"])

# do the calculation by taking the difference
excess_deaths = deaths - counterfactual.posterior_predictive["obs"]

そして、超過死者数の合計を簡単に計算できます。

# calculate the cumulative excess deaths
cumsum = excess_deaths.cumsum(dim="t")

fig, ax = plt.subplots(2, 1, figsize=(figsize[0], 9), sharex=True)

# Plot the excess deaths
# The transpose is to keep arviz happy, ordering the dimensions as (chain, draw, t)
plot_xY(post.index, excess_deaths.transpose(..., "t"), ax[0])
format_x_axis(ax[0], minor=True)
ax[0].axhline(y=0, color="k")
ax[0].set(title="Excess deaths, since COVID-19 onset")

# Plot the cumulative excess deaths
plot_xY(post.index, cumsum.transpose(..., "t"), ax[1])
format_x_axis(ax[1], minor=True)
ax[1].axhline(y=0, color="k")
ax[1].set(title="Cumulative excess deaths, since COVID-19 onset");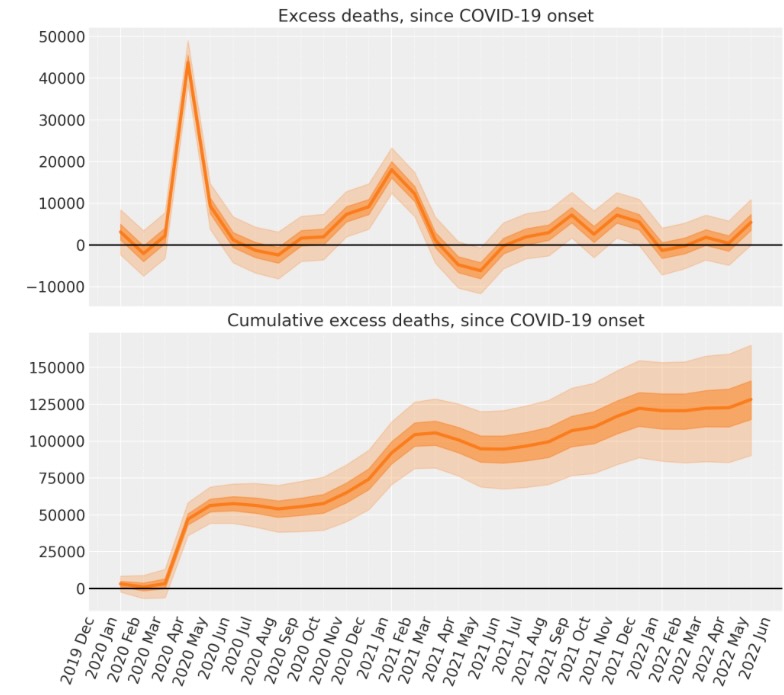

　さて、結果を得ました ー pyMCによる観測値に対抗するベイジアン推論が終了しました。私たちはいくつかのステップを実行しました。

• 単純な線形回帰モデルを作りました。
• COVID-19前のデータを元にモデルのパラメータを推定しました。事前と事後予測のチェックを実行しました。モデルは相当うまく適合ていますが、将来、モデルを改良する余地があります。
• 将来(COVID-19期間)に、何も起きなかったと仮定して、何が起きそうかの”観測に対抗する予測”を作るためにモデルを使いました。
• 報告死者数と私たちの’観測値に対抗する予測死者数を比較することで、’超過死者数（と超過死者の合算）を計算しました。

　もちろん、悪いニュースは、最後のデータポイント(2022年5月）にあるように、イングランドとウェールズの超過死者数は再度、上昇を開始したということです。