準備
ここでベイジアン加法回帰ツリー(BART)のコードを実行させるには、Python3.8(3.7<= python < 3.11)の環境が必要です。
注)BARTには PyMC-BART と Python 3.8が必要
この項のコードを動かすにはPyMC-BARTが必要です。PyMC-BARTはPyMCのフレームワークを拡張しています。BARTのバージョンは、0.4.0
Python 3.11ではなく、実行環境をPython3.8に変更し、python38環境にpip を使ってインストールしてください。
pip install pymc-bartなお、Python 3.8環境のインストールと切り替えは以下のTensorFlowの記事を参考にしてください。TensorFlowの実行環境のためにPython3.8の環境構築とJupyterからの3.8環境への切り替えの設定方法について解説しています。
下のログは、パッケージマネージャのcondaを使ってpython3.8の環境に切り替えた後、上のpipを使ってpyMC-BARTをインストールした例です。
(base) MacBook-Air:~ username$ conda activate python38
(python38) MacBook-Air:~ username$ pip install pymc-bart
Collecting pymc-bart
Downloading pymc_bart-0.4.0-py3-none-any.whl (25 kB)
Collecting pymc>=5.0.0
Using cached pymc-5.3.1-py3-none-any.whl (446 kB)
Collecting arviz
Downloading arviz-0.15.1-py3-none-any.whl (1.6 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.6/1.6 MB 3.4 MB/s eta 0:00:00
Collecting matplotlib<=3.5.2
Using cached matplotlib-3.5.2-cp38-cp38-macosx_11_0_arm64.whl (7.2 MB)
Collecting numba
Downloading numba-0.57.0-cp38-cp38-macosx_11_0_arm64.whl (2.5 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 2.5/2.5 MB 3.2 MB/s eta 0:00:00
Requirement already satisfied: packaging>=20.0 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (23.0)
Requirement already satisfied: cycler>=0.10 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (0.11.0)
Requirement already satisfied: pyparsing>=2.2.1 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (3.0.9)
Requirement already satisfied: kiwisolver>=1.0.1 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (1.4.4)
Requirement already satisfied: numpy>=1.17 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (1.22.3)
Requirement already satisfied: pillow>=6.2.0 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (9.4.0)
Requirement already satisfied: fonttools>=4.22.0 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (4.25.0)
Requirement already satisfied: python-dateutil>=2.7 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from matplotlib<=3.5.2->pymc-bart) (2.8.2)
Collecting pytensor<2.12,>=2.11.0
Downloading pytensor-2.11.2.tar.gz (3.5 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 3.5/3.5 MB 3.4 MB/s eta 0:00:00
Installing build dependencies ... done
Getting requirements to build wheel ... done
Installing backend dependencies ... done
Preparing metadata (pyproject.toml) ... done
Requirement already satisfied: typing-extensions>=3.7.4 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from pymc>=5.0.0->pymc-bart) (4.5.0)
Requirement already satisfied: cloudpickle in ./anaconda3/envs/python38/lib/python3.8/site-packages (from pymc>=5.0.0->pymc-bart) (2.2.1)
Requirement already satisfied: cachetools>=4.2.1 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from pymc>=5.0.0->pymc-bart) (5.3.0)
Collecting fastprogress>=0.2.0
Downloading fastprogress-1.0.3-py3-none-any.whl (12 kB)
Collecting scipy>=1.4.1
Downloading scipy-1.10.1-cp38-cp38-macosx_12_0_arm64.whl (28.8 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 28.8/28.8 MB 3.0 MB/s eta 0:00:00
Requirement already satisfied: pandas>=0.24.0 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from pymc>=5.0.0->pymc-bart) (1.5.3)
Collecting xarray>=0.21.0
Downloading xarray-2023.1.0-py3-none-any.whl (973 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 973.1/973.1 kB 3.2 MB/s eta 0:00:00
Collecting xarray-einstats>=0.3
Downloading xarray_einstats-0.5.1-py3-none-any.whl (28 kB)
Requirement already satisfied: setuptools>=60.0.0 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from arviz->pymc-bart) (65.6.3)
Collecting h5netcdf>=1.0.2
Downloading h5netcdf-1.1.0-py2.py3-none-any.whl (26 kB)
Requirement already satisfied: importlib-metadata in ./anaconda3/envs/python38/lib/python3.8/site-packages (from numba->pymc-bart) (6.1.0)
Collecting llvmlite<0.41,>=0.40.0dev0
Downloading llvmlite-0.40.0-cp38-cp38-macosx_11_0_arm64.whl (28.1 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 28.1/28.1 MB 852.6 kB/s eta 0:00:00
Requirement already satisfied: h5py in ./anaconda3/envs/python38/lib/python3.8/site-packages (from h5netcdf>=1.0.2->arviz->pymc-bart) (3.6.0)
Requirement already satisfied: pytz>=2020.1 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from pandas>=0.24.0->pymc>=5.0.0->pymc-bart) (2023.3)
Collecting filelock
Downloading filelock-3.12.0-py3-none-any.whl (10 kB)
Collecting etuples
Downloading etuples-0.3.9.tar.gz (30 kB)
Preparing metadata (setup.py) ... done
Collecting cons
Downloading cons-0.4.5.tar.gz (26 kB)
Preparing metadata (setup.py) ... done
Collecting logical-unification
Downloading logical-unification-0.4.6.tar.gz (31 kB)
Preparing metadata (setup.py) ... done
Collecting miniKanren
Downloading miniKanren-1.0.3.tar.gz (41 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 41.3/41.3 kB 347.9 kB/s eta 0:00:00
Preparing metadata (setup.py) ... done
Requirement already satisfied: six>=1.5 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from python-dateutil>=2.7->matplotlib<=3.5.2->pymc-bart) (1.15.0)
Requirement already satisfied: zipp>=0.5 in ./anaconda3/envs/python38/lib/python3.8/site-packages (from importlib-metadata->numba->pymc-bart) (3.15.0)
Collecting toolz
Downloading toolz-0.12.0-py3-none-any.whl (55 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 55.8/55.8 kB 519.5 kB/s eta 0:00:00
Collecting multipledispatch
Downloading multipledispatch-0.6.0-py3-none-any.whl (11 kB)
Building wheels for collected packages: pytensor, cons, logical-unification, etuples, miniKanren
Building wheel for pytensor (pyproject.toml) ... done
Created wheel for pytensor: filename=pytensor-2.11.2-cp38-cp38-macosx_11_0_arm64.whl size=3675444 sha256=94e8f1f5d37f99730bdc86fda29ba11385f8291d6ff0f7610bfc2191ca537dd2
Stored in directory: /Users/username/Library/Caches/pip/wheels/4e/41/e3/4bcf700ff213d5097c71fa06623e2cc25b8e20e560367c22bd
Building wheel for cons (setup.py) ... done
Created wheel for cons: filename=cons-0.4.5-py3-none-any.whl size=9115 sha256=78a8988741931bc55fbdc83c8f967b435bccfb33d9c31fd12c9e18d9945fbf29
Stored in directory: /Users/username/Library/Caches/pip/wheels/7f/7d/7f/60404727e7315590ed31801adc1534189bb14d0907b550b1d6
Building wheel for logical-unification (setup.py) ... done
Created wheel for logical-unification: filename=logical_unification-0.4.6-py3-none-any.whl size=13911 sha256=c0aa3f4deb0280b33467dfeab8fef8806ca4ae4299de054d4b20b1a4b70e33f4
Stored in directory: /Users/username/Library/Caches/pip/wheels/3a/ba/c0/41870a2550bb5c7f7d584882da204a2f570f3da7f939921b8a
Building wheel for etuples (setup.py) ... done
Created wheel for etuples: filename=etuples-0.3.9-py3-none-any.whl size=12617 sha256=2aca3c951b95cd85e8a397535d771d45475b25960dd346886af150fb6a73e1fc
Stored in directory: /Users/username/Library/Caches/pip/wheels/8f/31/a4/d168fd2653f35b4977d06a7607985b941daae136a3eda13042
Building wheel for miniKanren (setup.py) ... done
Created wheel for miniKanren: filename=miniKanren-1.0.3-py3-none-any.whl size=23910 sha256=6b94904e16e460c699d5ef2d97da8628a9d48825da7dcfa5aa8a58a51ef09e4e
Stored in directory: /Users/username/Library/Caches/pip/wheels/06/83/f0/bf4f50c0e6bfab8ae0860cb6e4a029a8a5346e3c1c38d926e6
Successfully built pytensor cons logical-unification etuples miniKanren
Installing collected packages: toolz, scipy, multipledispatch, llvmlite, filelock, fastprogress, numba, matplotlib, logical-unification, h5netcdf, xarray, cons, xarray-einstats, etuples, miniKanren, arviz, pytensor, pymc, pymc-bart
Attempting uninstall: matplotlib
Found existing installation: matplotlib 3.7.1
Uninstalling matplotlib-3.7.1:
Successfully uninstalled matplotlib-3.7.1
Successfully installed arviz-0.15.1 cons-0.4.5 etuples-0.3.9 fastprogress-1.0.3 filelock-3.12.0 h5netcdf-1.1.0 llvmlite-0.40.0 logical-unification-0.4.6 matplotlib-3.5.2 miniKanren-1.0.3 multipledispatch-0.6.0 numba-0.57.0 pymc-5.3.1 pymc-bart-0.4.0 pytensor-2.11.2 scipy-1.10.1 toolz-0.12.0 xarray-2023.1.0 xarray-einstats-0.5.1
(python38) MacBook-Air:~ username$
イントロダクション
from pathlib import Path
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb
from sklearn.model_selection import train_test_split
%config InlineBackend.figure_format = "retina"
print(f"Running on PyMC v{pm.__version__}")Running on PyMC v5.3.1RANDOM_SEED = 5781
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")BART 概要
ベイジアン加法回帰ツリー(以下BART)は、ノンパラメトリック回帰アプローチです。任意の共変量Xをもち、モデル Yにそれらを使用するならば(事前を除外して)BARTモデルは以下のように関連づけられます。
Y = f(X) + εここで、モデルfの回帰ツリーの総計を使います。εはノイズです。もっとも典型的な例ではεは正規に分布N(0,σ)します。以下のよに記します。
Y 〜 N(μ = BART(X),σ)原理的に、ツリーの総計をモデルに使うことにその他、関連した制限はありません。例えば、私たちは次をのように
Y 〜 Poisson(μ = BART(X))BARTがベイジアンである一つの理由は、事前に回帰ツリーを超えて使うことです。事前(分布)は、そうしたリーフの値がゼロに近いあさいツリーを好む方法で定義されます。鍵になる考えは、単一のBARTツリーは、データを適合するのにとても良いわけではなく、しかし、それらのツリーを合計した時に良い結果と融通のきく近似を得られます。
BARTと石炭の採掘
BARTを例題でよく理解するために、古いけれども、貴重な石炭の採掘における事故のデータセットを使います。PyMCでは古典的な例の一つです。オリジナルのPyMCの例にあるように、二つのポワソン分布からなるスイッチポイント(転換点)として、代わりにこの問題を考えます。ポワソンレスポンスによるノンパラメトリック回帰として、この問題を考えていきます。(これは通常、ポワソン過程、またはコックス過程という用語で議論されます。しかし、それらの技術背景がなくても大丈夫です)。ガウス過程による同様の例として、1(ハイパーリンク)及び2(ハイパーリンク)があります。私たちのデータは、日付の単一のコラムによるデータなので、事前の処理が必要になります。データを分離します。
try:
coal = np.loadtxt(Path("..", "data", "coal.csv"))
except FileNotFoundError:
coal = np.loadtxt(pm.get_data("coal.csv"))# discretize data
years = int(coal.max() - coal.min())
bins = years // 4
hist, x_edges = np.histogram(coal, bins=bins)
# compute the location of the centers of the discretized data
x_centers = x_edges[:-1] + (x_edges[1] - x_edges[0]) / 2
# xdata needs to be 2D for BART
x_data = x_centers[:, None]
# express data as the rate number of disaster per year
y_data = histPyMCではBART変数は、他のランダム変数と同様に定義できます。一つの重要な相違は、私たちのXsとYσの変数を BARTの変数に渡す必要があります。この情報は、ツリーをサンプリングするときに使います。ツリーの合計を超える事前は、かなり大きいので、私たちのデータからはどのような情報もなしに、これは不可能なタスクになります。
ここで、合計が20ツリーを超えて使おうとする場合も明白になります。20のような少ない数のツリーは、このような簡易モデルでも十分です。そして、特にモデル化の早い段階で、モデルが私たちの問題に良い考えとなるようにより力把握するためにできる限る素早く少数のことを試みようとするときに、より複雑なモデルでも素早い近似になるので、非常にうまく働きます。一旦、モデルについてもっと確からしいそれらのケースでは、m を増加させることで、近似を改善できるように、文献内では、数値が10,100または200のようなよい結果のレポートを見つけることは共通になります。
with pm.Model() as model_coal:
μ_ = pmb.BART("μ_", X=x_data, Y=np.log(y_data), m=20)
μ = pm.Deterministic("μ", pm.math.exp(μ_))
y_pred = pm.Poisson("y_pred", mu=μ, observed=y_data)
idata_coal = pm.sample(random_seed=RANDOM_SEED)
結果を調べる前にもっと詳しく議論する必要があります。BART変数は、常に現実の線上でサンプルされます。原理的には、-♾️から♾️までの値を取ることができることを意味します。このように、標準一般化線形モデルのために実行したように、値を変換する必要があるかもしれません。例えば、model_coalでは、私たちは、pm.math.exp(μ_)を計算します。なぜならポワソン分布は0から♾️までの予期値を持ちます。これは通常のやり方です。新規さは、log(Y)をとった前のモデルで実行したように、私たちがYの値への逆変換を適用する必要があるかもしれません。これを実行する主要な理由は、Yの値は、ツリーの合計とリーフノードの変異のために適当な初期値を得るためのものです。このように、逆変換の適用は、効果と結果の正確さを改善する簡単な方法です。すべての可能な尤度に対して、これを実行すべきでしょうか?Noです。もし、私たちが、正規ステューデントTや非対称ラプラスのような分布の位置パラメータのために、BARTを使うならば、これらのパラメータのサポートが実際の線であるように何もする必要がありません。非凡な例外はベルヌーイ尤度です。(n=1の二項分布)、このケースでは、ロジスティック関数をBART変数に適用する必要があります。しかし、そのYの逆変換は適用する必要がありません。PyMC-BARTはこの特別なケースに注意を払っています。
OK,model_coalの結果を見てましょう。
_, ax = plt.subplots(figsize=(10, 6))
rates = idata_coal.posterior["μ"] / 4
rate_mean = rates.mean(dim=["draw", "chain"])
ax.plot(x_centers, rate_mean, "w", lw=3)
ax.plot(x_centers, y_data / 4, "k.")
az.plot_hdi(x_centers, rates, smooth=False)
az.plot_hdi(x_centers, rates, hdi_prob=0.5, smooth=False, plot_kwargs={"alpha": 0})
ax.plot(coal, np.zeros_like(coal) - 0.5, "k|")
ax.set_xlabel("years")
ax.set_ylabel("rate");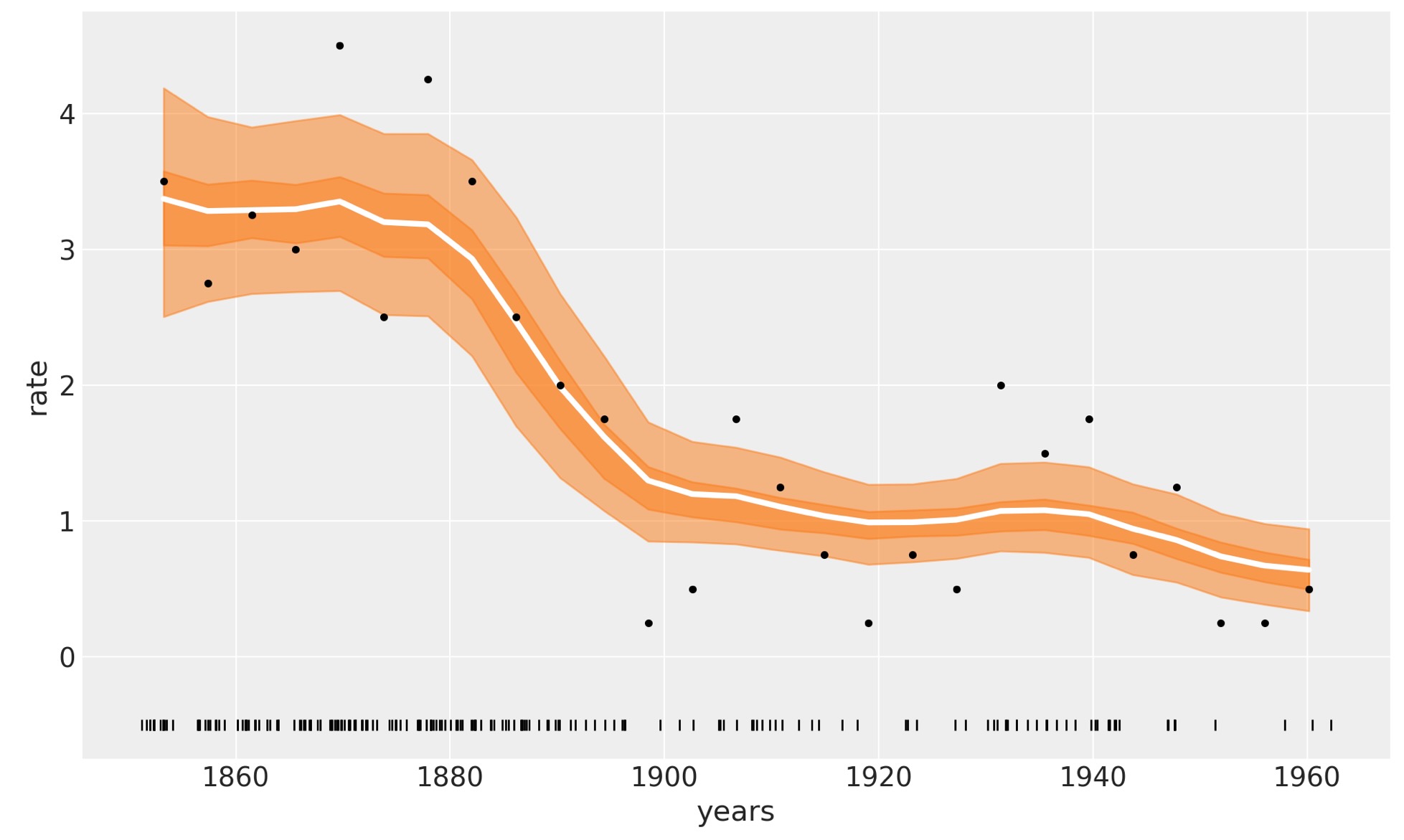
以下の図の白線は、事故の中間レートを示しています。濃いオレンジの幅は、HDI 50%、薄い方は94%を提供しています。1880年から1900年の間の炭鉱事故の急速な減少を見ることができます。オリジナルのPyMCの紹介の概要の例とこれらの結果を比較することを気にしないでください。
前の図で白線は、4000事後出力の平均です。そしてそれらの各事後出力は、m=20を超えた合計になります。
以下の図は、μの事後から二つのサンプルを表示しています。これらの関数はスムースではないことがわかります。これは構いません、回帰ツリーを使う直接の結果です。ツリーはステップを描く関数のように見ることができます。
このように、BARTを使うときに、ステップ関数が私たちの問題を近似するのに、十分であると仮定していることを知る必要があります。実際はこれは稀なケースです。なぜなら、私たちは、通常、50,100または200のような値の多くのツリーを合計しています。追加で、私たちは、しばしば事後分布を超えて平均します。例えガウス過程(スプライン)の例のように実際の平滑化関数を使わない時でも、これはすべて、"ステップ平滑化"させます。良い理論的な結果は、m->♾️の極限でBART事前分布は、微分的な(noehearedifferentiable) ガウス過程に収束することを教えます。
以下の図は事後からのμの二つのサンプルを表示しています。
plt.step(x_data, rates.sel(chain=0, draw=[3, 10]).T);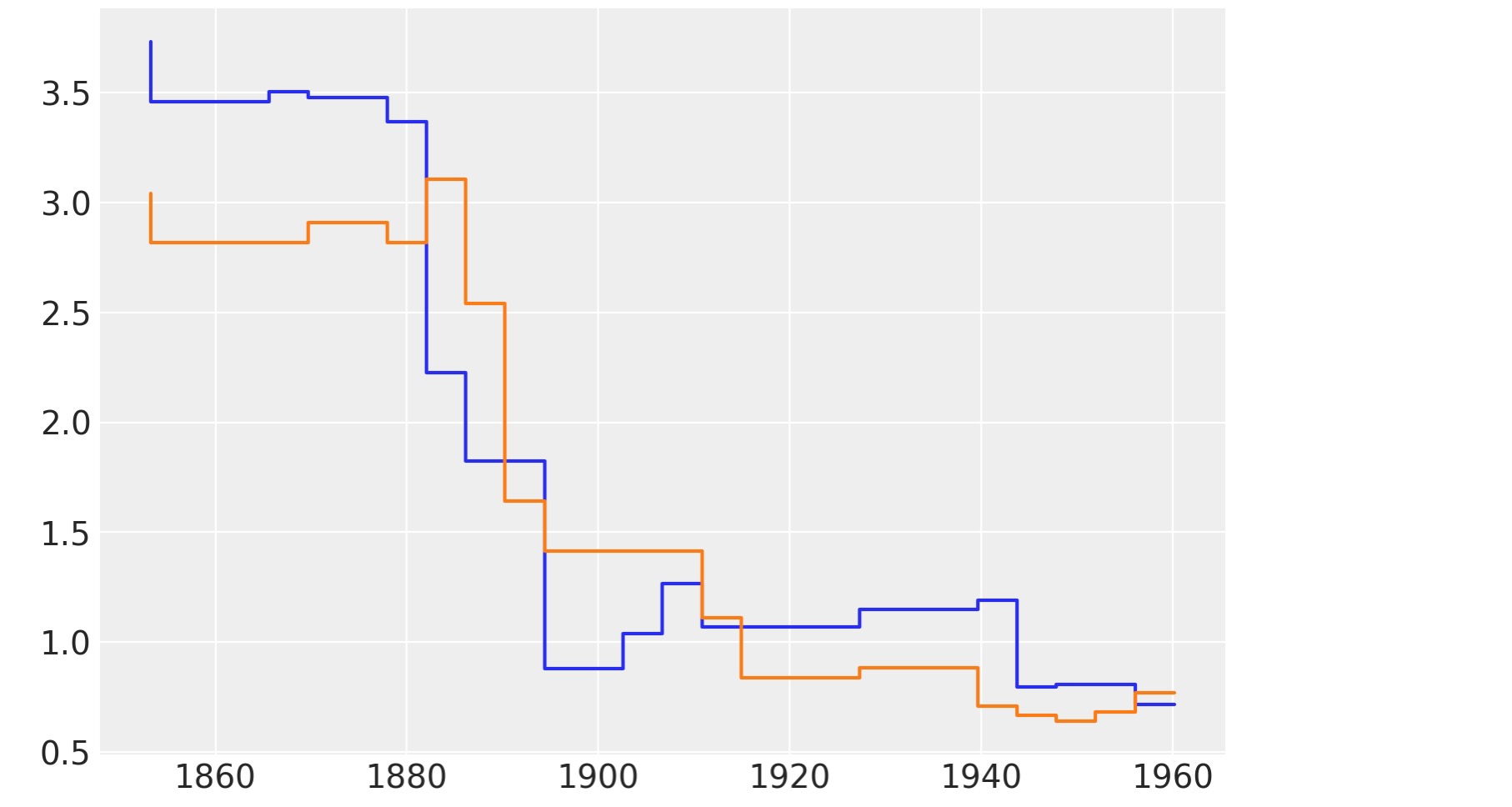
次の図はm三つのツリーを表示します。これは、完全にそれ自身によるとても良い近似ではなく、非常に簡単な関数であることがわかります。個別のツリーの調査は、一般的にBARTを実行するときは必要ありません。BART内部の働きをかなり直感的に得ることができるため単にそれらを図示します。
bart_trees = μ_.owner.op.all_trees
for i in [0, 1, 2]:
plt.step(x_data[:, 0], [bart_trees[0][i].predict(x) for x in x_data])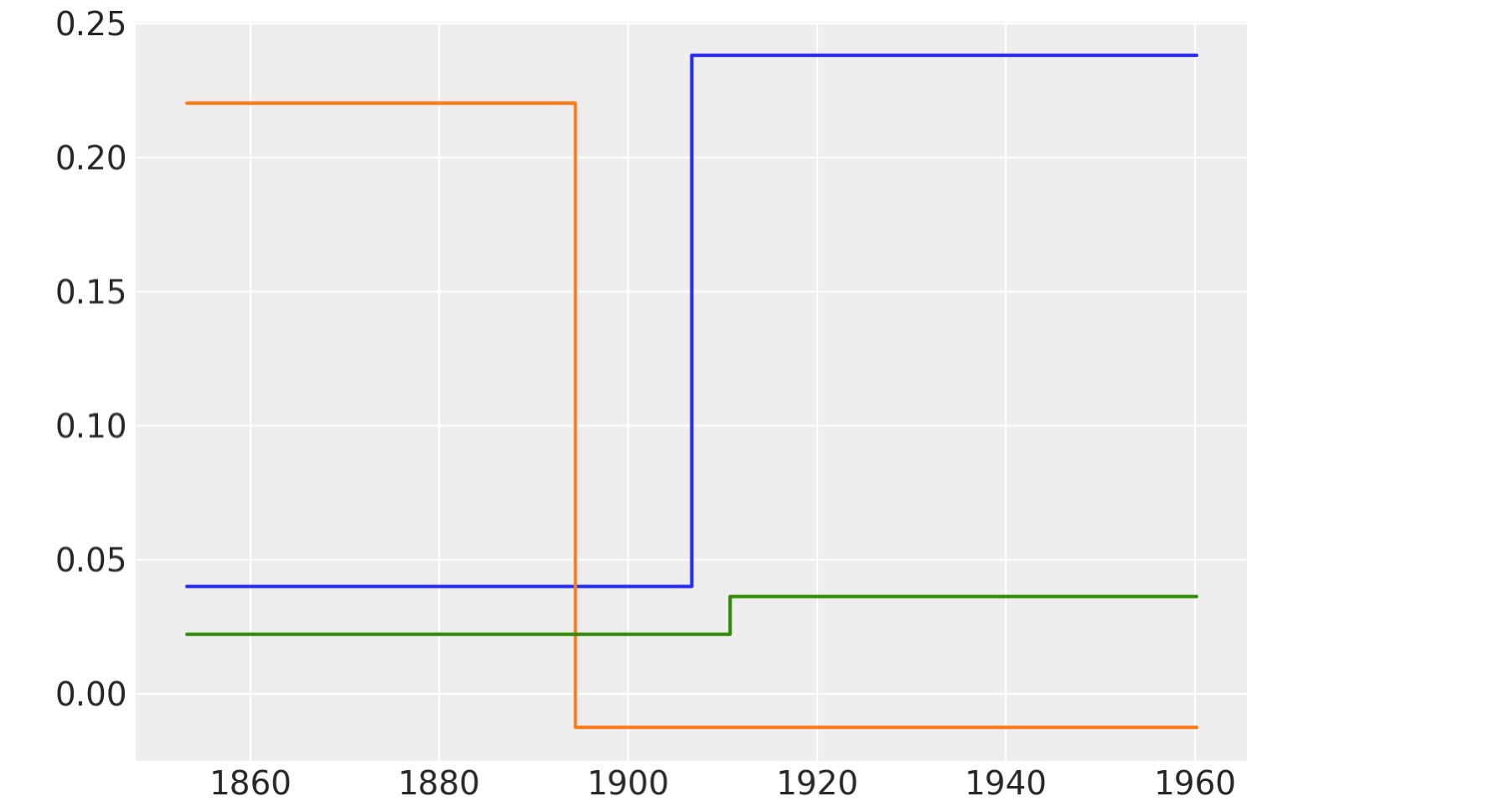
自転車とBART
PyMCで提案するBARTのその他の特徴を探検するために。ここで異なる例に移ります。この例では、年間の自転車のレンタル数についてデータを扱います。そしてその日の時間、温度、湿度、そして平日か休日かという四つの変分を選択します。これは、bike_sharing_datasetのサブセットです。
try:
bikes = pd.read_csv(Path("..", "data", "bikes.csv"))
except FileNotFoundError:
bikes = pd.read_csv(pm.get_data("bikes.csv"))
features = ["hour", "temperature", "humidity", "workingday"]
X = bikes[features]
Y = bikes["count"]with pm.Model() as model_bikes:
α = pm.Exponential("α", 1)
μ = pmb.BART("μ", X, np.log(Y), m=50)
y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y)
idata_bikes = pm.sample(compute_convergence_checks=False, random_seed=RANDOM_SEED)
診断の収束
BARTモデルのサンプリングの収束を調べるために、2段階のアプローチを取ります。
- 非BART変数(model_bikesのαのように)のために、R-hat(<=1.01), ESS(<100 x チェイン数)、トレース図、またはより良いランク図を使うのと同様に数的診断を調べるように、標準の推薦に従います。
- BART変数のために、pmb.plot_convergence関数を使うことを推薦します。
私たちはそのようなチェックを次に見ることができます。
az.plot_trace(idata_bikes, var_names=["α"], kind="rank_bars");
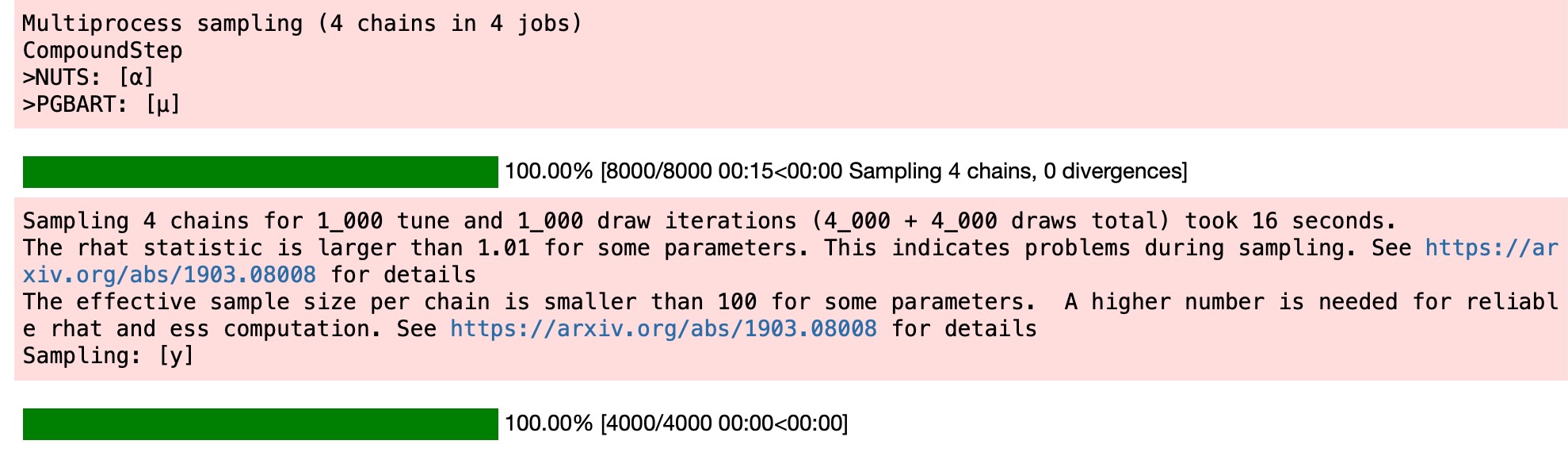
pmb.plot_convergence(idata_bikes, var_name="μ");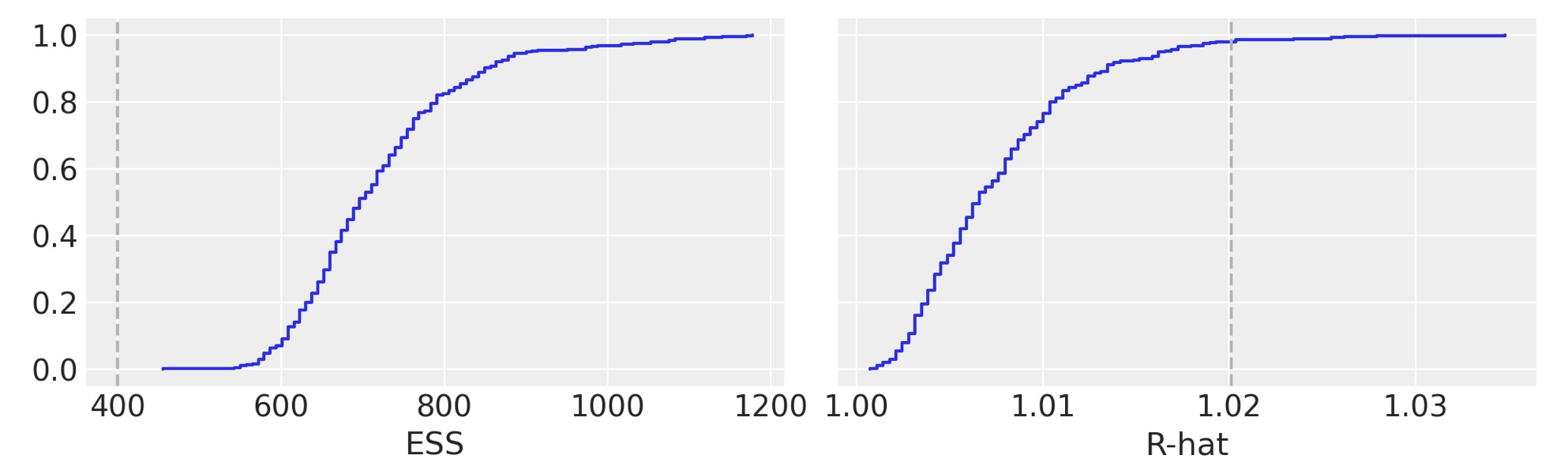
BARTの文脈では、BART変数の診断は、非BART変数の診断より、重要ではないと考えられています。主要な引数は、潜在的な変数の個別の予測が、直接的な興味にならず、その代わりに如何にうまく全体の関数や回帰を見積もるかについてだけ注意を払うべきです。
私たちは、ベイジアンワークフローの重要な一部として、BART変数の収束を調べることを代わりに熟考します。pmb.plot_convergence関数を使う主要な理由は、通常、BART変数が、大きなベクターであり、(観測単位で分布を見積もる)そして、このように大きな数値の診断を調べる必要があります。追加で、R-hatの閾値1.01は、難しい閾値ではなくこの値は、少数のR-hatsが試験されるか一つを仮定することで選択されます。そして、もし、大きな数値のR-hatを観測するならば、たとえ私たちの推論に間違いがないとしても、それらの少数は閾値1.01(または私たちが選んだどのような閾値)より大きくなることが予期されます。その理由のために、公平な分析は多重の比較調整を含むべきです。そして、pmb.plot_convergenceがあなたのために自動的にそのことを実行します。ではどのように出力を読みましょう?私たちは、二つのパネルを持ちます。一つはESS,もう一つはR-hat用です。青い線は、それらの値のための実感的な蓄積の分布、ESSのために点線の上に完全な曲線を必要とします。そしてR-hatのために、点線の下で完全になるように曲線を必要とします。前の図の中で、私たちは閾値の上で少数の値を持つESSとR-hatのために、それを無駄にしているのを見ることができます。
私たちの結果は無駄ですか?もっともありそうにないことです。しかし、もう少し出力させる必要があるのは確かです。
部分的に依存した図
私たちのモデルの結果を解釈するのに役立つように、部分的に依存する図を使います。これは、予測値の上でともに異なる周辺効果を表示するある種の図です。それは、他のすべての共分散の平均であるYの共に異なるXiの効果です。この種の図は、BARTの除外するものではありません。しかし、それらは、しばしばBARTの文脈で使用されます。PyMC-BARTは予測データからこの図を作るためにユーティリティ関数を提供しています。
pmb.plot_dependence(μ, X=X, Y=Y, grid=(2, 2), func=np.exp);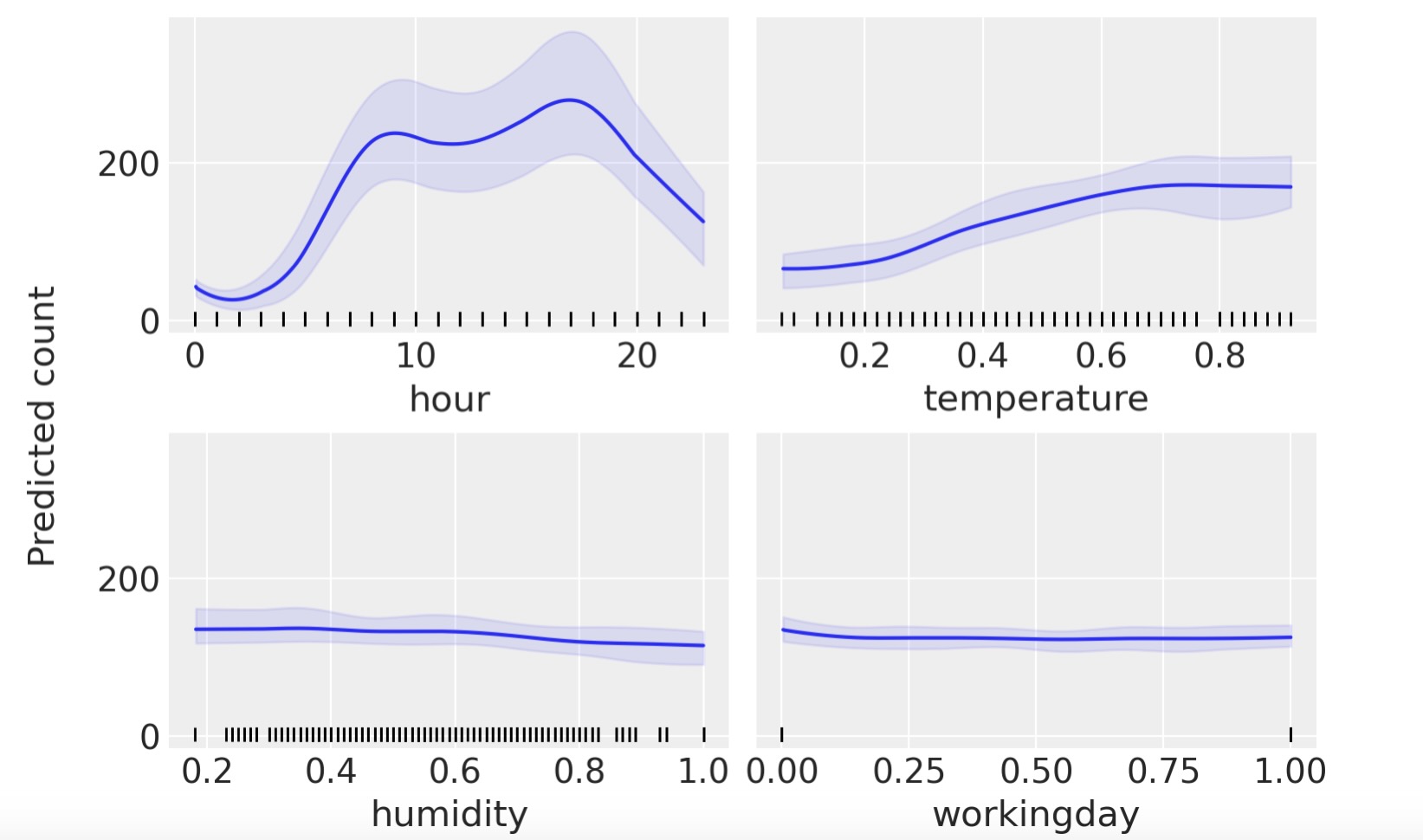
この図から私たちは、予測値の共変量の主要な効果を見ることができます。これは、単調な増減効果に反して複雑な関係の回復することができるので、非常に有用です。例えば、hourの共変量にとって、深夜に最小となる、8と17の周りで二つの頂点を見ることができます。
部分的な依存図を解釈するときに、この図の過程について注意する必要があります。最初に、変数が独立であることを仮定しています。例えば、hourの結果を計算するときに、温度の効果を制限しなけれなりません。そして、これは、hour=0での部分的に独立した値を計算することを意味します。私たちは、温度のすべての観測データを持っているので、これは、実際は深夜に計測されていない温度を含んでも良く、低い温度が高い温度よりも相応しいこと与えます。もし共変量(covariate)の値の半数が予想値に正に関連しており、他の半分が負に関連しているならば、私たちは平均値だけを見ていることになります。部分依存図は、それらの寄与が相互に除外され、平坦になります。これは、pmb.plot_dependence(…,kind="ice")による個別の条件予測図を使うことで、解決できる問題です。すべてのこの仮定は、私たちのモデルではなく、部分依存図の仮定であることを注記します。実際、BARTは変数を相互に簡単に適合できます。BARTの事前は、高次の相互に規則化されるけれども)。もっと機械学習モデルの解釈では"解釈できる機械学習"本を調べることができます。[Molnah, 2019]
最後に、他の回帰法のように、個別の変数で見ている結果が、他の変数を含んだ条件であるときは注意すべきです。例えば、湿度がほとんど平坦である間は、この共変量は自転車を使う数値には小さい影響しかないことを意味します。これは、湿度と温度が任意の拡張で相関しているケースになります。一旦私たちのモデルに温度をを含めると湿度が多すぎる追加情報にはなりません。再度、例題のモデルの適合を試みてください。しかし、今回は湿度が単一の共変量として、その後hourを単一の共変量(covariate)として再度モデルを適合を試みてください。この単一変数のモデルの結果は、hour 共変量の前回の図と非常に似ていますが、湿度の共変量では似ていないことがわかります。
変数の重要性
前のセクションで見たように、部分依存図は、視覚化し、各共変量がどのくらい予測結果に寄与するかという考えを提供できます。しかしBARTそれ自身は、変数の重要せを見積もるのに単純なヒューリスティック(経験)を導きます。それは変数が、何回、すべての回帰ツリーに含まれるかを簡単に数えることです。直感的には、もし変数が縦横であれば、重要性が低い変数より高い頻度で適合ツリーの中に現れます。このヒューリスティックスは実際は、妥当な結果を生むように見えます。この手続きを理論に適合させすぎていることはありません。少なくとも今のところは。
以下の図は、スケールが0から1までの相対的な重要さをと個別の重要さの合計が1であることを表示します。それを見ると、少なくともこのケースでは、相対的に重要な性質は部分依存図と一致します。
追加で、PyMC-BARTは、変数の重要性にアクセスするための斬新な方法を提供します。あなたは、下のパネルの例を見ることができます。x軸は共変量の数であり、y軸は、完全なモデルと制限されたモデルのに相応しい予測間のピアソン相関係数の二乗です。それらは、変数のサブセットだけです。その成分は、上のパネルに表示されているように、以下の相対的に変数の重要性の順序を含んでいます。こうしてこの例では、共変量の数は、1.hour, 2.hour と温度、3.hour,温度、湿度となります。最後に、4は、hour,温度、湿度、平日、すなわち、完全なモデルを意味します。しかし、私たちが見る次の図は、単一の成分、hour、のモデルであっても完全なモデルに非常に近いものになっています。さらに、二つの成分、hour,温度からなるモデルは、平均で完全なモデルと区別がつきません。エラーの値は事後予測分布から94% HDIを表します。これらの相関を計算することに注意するのは重要です。私たちはモデルを再サンプルさせず、制限されたモデルの予測の代わりに、完全なモデルから変数を取り除くことで近似します。
pmb.plot_variable_importance(idata_bikes, μ, X, samples=100);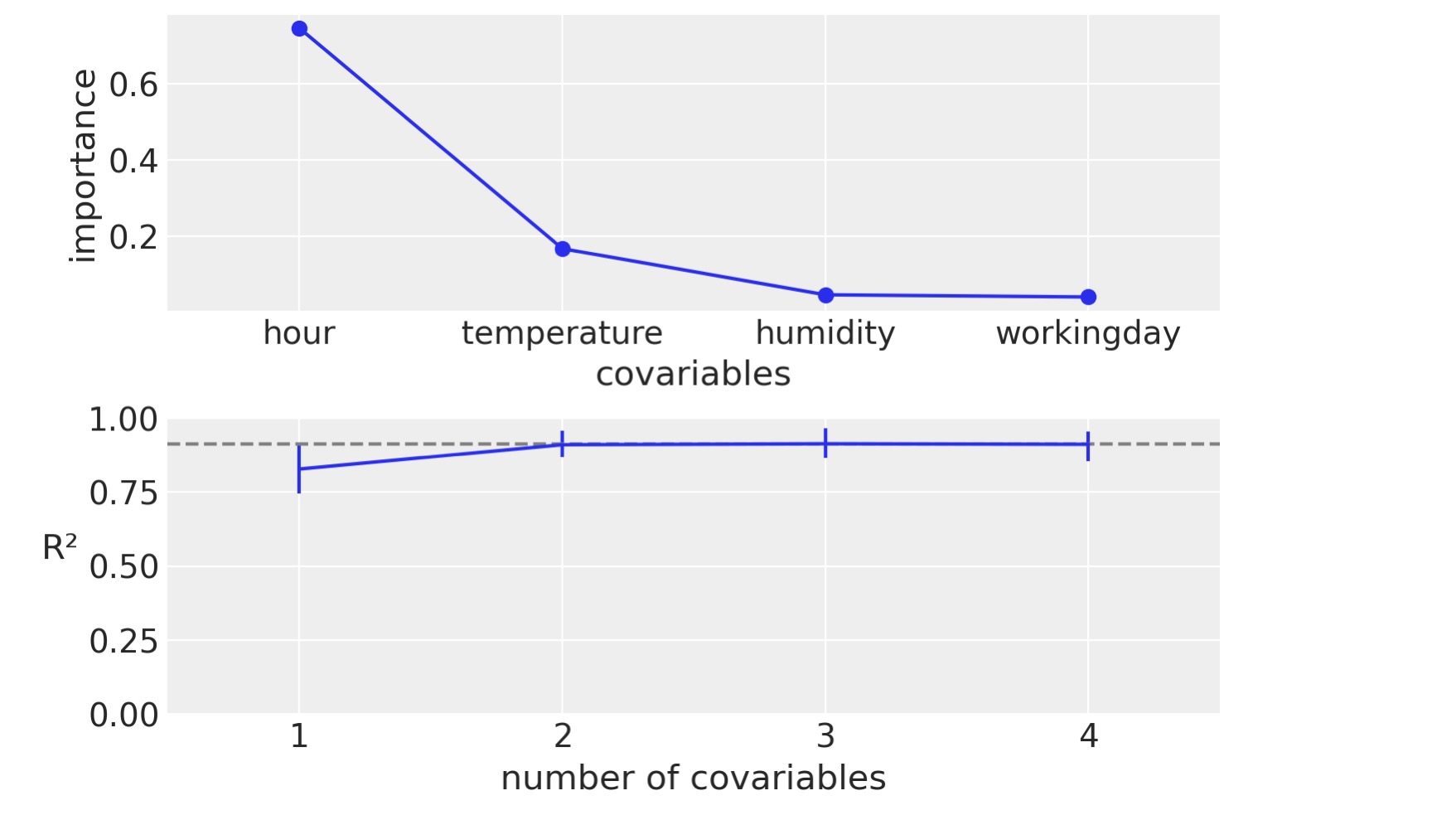
分離予測
このセクションでは、BARTによる分離予測の方法をお見せします。前に使ったものと同じデータセットを使いますが、今回は、トレーニング用とテストセットようにデータを分離します。トレーニングセットをモデルに適合させるために使い、テストセットをモデルを評価するために使います。
回帰
回帰問題としてモデル化することから始めましょう。この文脈では、データをトレーニング用とテストセット用にランダムに分割します。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=RANDOM_SEED)ここで、上のように同じモデルを適合しますが、今回は、共変量のため共有変数を使います。それによってそれらを取り替えて分離予測を生成します。
with pm.Model() as model_oos_regression:
X = pm.MutableData("X", X_train)
Y = Y_train
α = pm.Exponential("α", 1)
μ = pmb.BART("μ", X, np.log(Y))
y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y, shape=μ.shape)
idata_oos_regression = pm.sample(random_seed=RANDOM_SEED)
posterior_predictive_oos_regression_train = pm.sample_posterior_predictive(
trace=idata_oos_regression, random_seed=RANDOM_SEED
)
次にモデルのデータを事後予測分布からのサンプルと交換します。
with model_oos_regression:
X.set_value(X_test)
posterior_predictive_oos_regression_test = pm.sample_posterior_predictive(
trace=idata_oos_regression, random_seed=RANDOM_SEED
)
最後に、事後予測分布を観測データと比較できます。
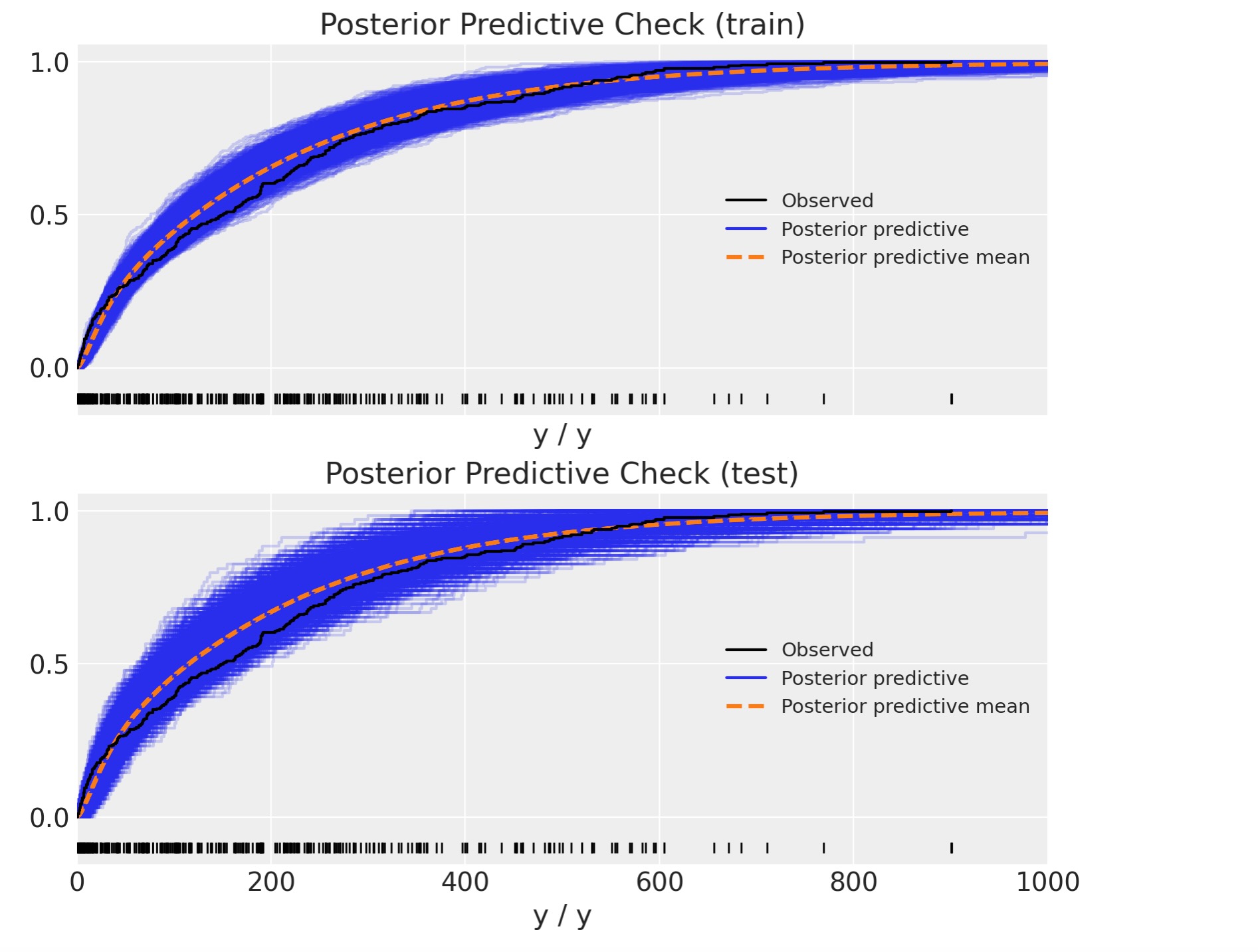
結果は全く妥当に見えています。
時系列
hourの特徴を使って時系列の観点から同じデータを見ることができます。この視点では、情報が漏洩しないようにデータの順序が変わらないように確認する必要があります。こうして、hour特徴を使って、トレーニング、テスト用に分離を定義します。
train_test_hour_split = 19
train_bikes = bikes.query("hour <= @train_test_hour_split")
test_bikes = bikes.query("hour > @train_test_hour_split")
X_train = train_bikes[features]
Y_train = train_bikes["count"]
X_test = test_bikes[features]
Y_test = test_bikes["count"]同じモデルを実行します。(しかし異なる入力データで)そして、上のように分離予測を生成します。
with pm.Model() as model_oos_ts:
X = pm.MutableData("X", X_train)
Y = Y_train
α = pm.Exponential("α", 1 / 10)
μ = pmb.BART("μ", X, np.log(Y))
y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y, shape=μ.shape)
idata_oos_ts = pm.sample(random_seed=RANDOM_SEED)
posterior_predictive_oos_ts_train = pm.sample_posterior_predictive(
trace=idata_oos_ts, random_seed=RANDOM_SEED
)
分離予測を生成します。
with model_oos_ts:
X.set_value(X_test)
posterior_predictive_oos_ts_test = pm.sample_posterior_predictive(
trace=idata_oos_ts, random_seed=RANDOM_SEED
)
上と同様に、事後予測分布と観測データを比較します。
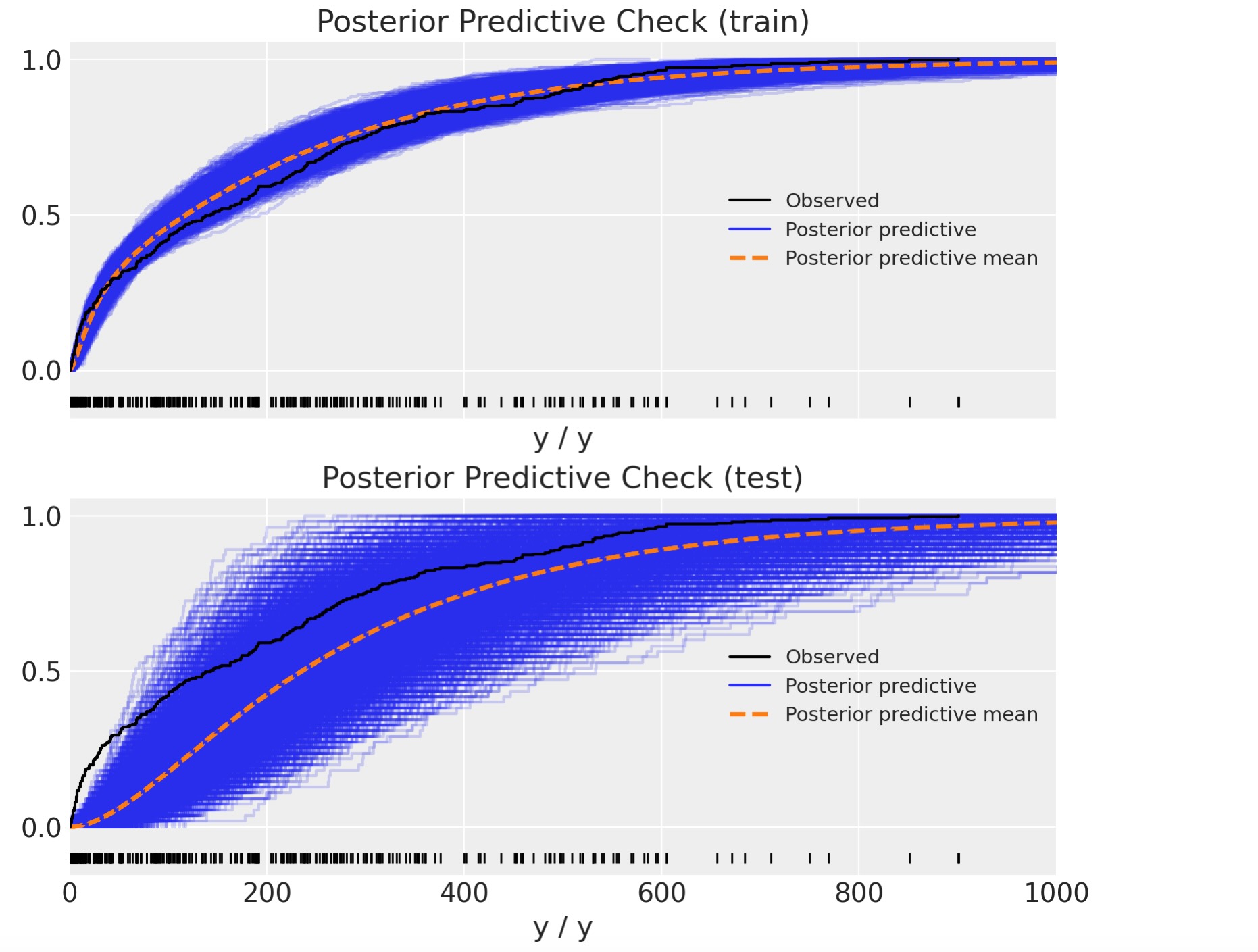
これは、正しいように見えません。テストセットの予測は奇妙に見えます。何が起きたか理解するために、時系列の予測を図示することができます。
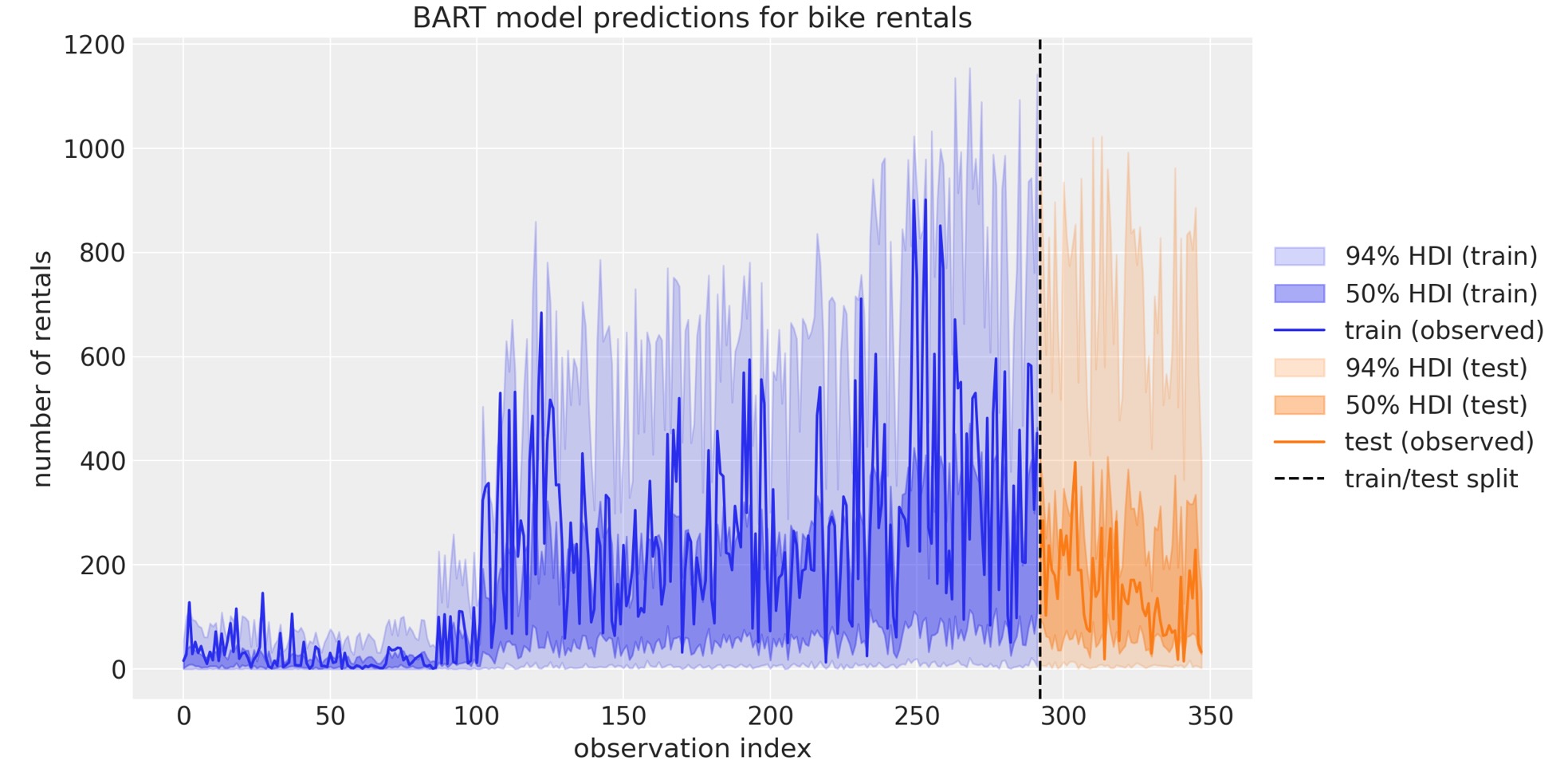
この図は、テストセットの悪い振る舞い背後にある季節への理解に役立ちます。私たちが見た初期モデルから変数の重要性ランキングを思い出してください。そこではhourがもっとも重要な予測変数でした。一方、私たちのトレーニングデータは、hourの値は19(トレーニングとテストの閾値なので)までしかありません。BARTはデータの分離の方法を学習するので、例えば、20と22の間のhourの値は微分できません。両方の値が19より大きいことに注意しなければなりません。これは、BARTを使うときに理解するために非常に重要なことです。もし、トレンド成分があるならば、時系列予測にBARTを使うべきでないことを、これが説明しています。このケースでは、最初にデータをトレンドを外した方が良く、残りをBARTでモデルします。そして、違ったモデルでトレンドをモデル化します。
製作者
著者:Osvaldo Martin 2021年 12月
更新:Osvaldo Martin 2022 5月
更新:Osvaldo Martin 2022年 9月
更新:Osvalso Martin 2022年 11月
更新:Juan Orduz 2023年 1月 分離予測 の章を追加
更新: Osvaldo Martin 2023年 3月
参考文献
- Christoph Molnar. Interpretable Machine Learning. Christoph Molnar, 2019.
- Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, and Osvaldo A Martin. Bayesian additive regression trees for probabilistic programming.
- Osvaldo A Martin, Ravin Kumar, and Junpeng Lao. Bayesian Modeling and Computation in Python. Chapman and Hall/CRC, 2021.
