分割時系列分析

このノートブックは、簡単なベイジアン分割時系列分析の導出方法に焦点を当てます。これは、すべての処置ユニットに介入を適用する場合、擬似実験の設定(quasi-experimental seting)に役立ちます。

　例えば、Webサイトの変更が実施される場合、Webサイト変更に伴う影響（causal impact）を知りたくなります。そのときこの変更が、選択的とランダムに、Webサイトユーザーのテストグループに適用されるならば、A/Bテストアプローチを使って原因を主張することができるでしょう。

　しかし、Webサイトの変更がWebサイトのすべてのユーザーに公開されたならば、あなたはそのグループをコントロールすることはできません。このケースでは、あなたはもしWebサイトが変更されなかったら、何が起きていたかという、Counterfactualを直接、測定することはありません。このケースでは、あなたが”良い”時系列のデータを持っていれば、分割時系列アプローチを使うことができるかもしれません。

　興味のある読者は、直接、優秀なテキストブック"The Effect[Huntigton-Klein 2021]"の１７章の"event studies"を当たってください。その著者は、分割時系列を好んでいます。

因果DAG

分割時系列のための簡単な因果のDAGを以下に記します、しかし、より一般的なDAGは[Huntington-Klein 2021]を参照してください。端的には、

• 処置と時間(時間経過における他の因子)による影響の結果
• 処置は時間によって因果的に影響を受ける

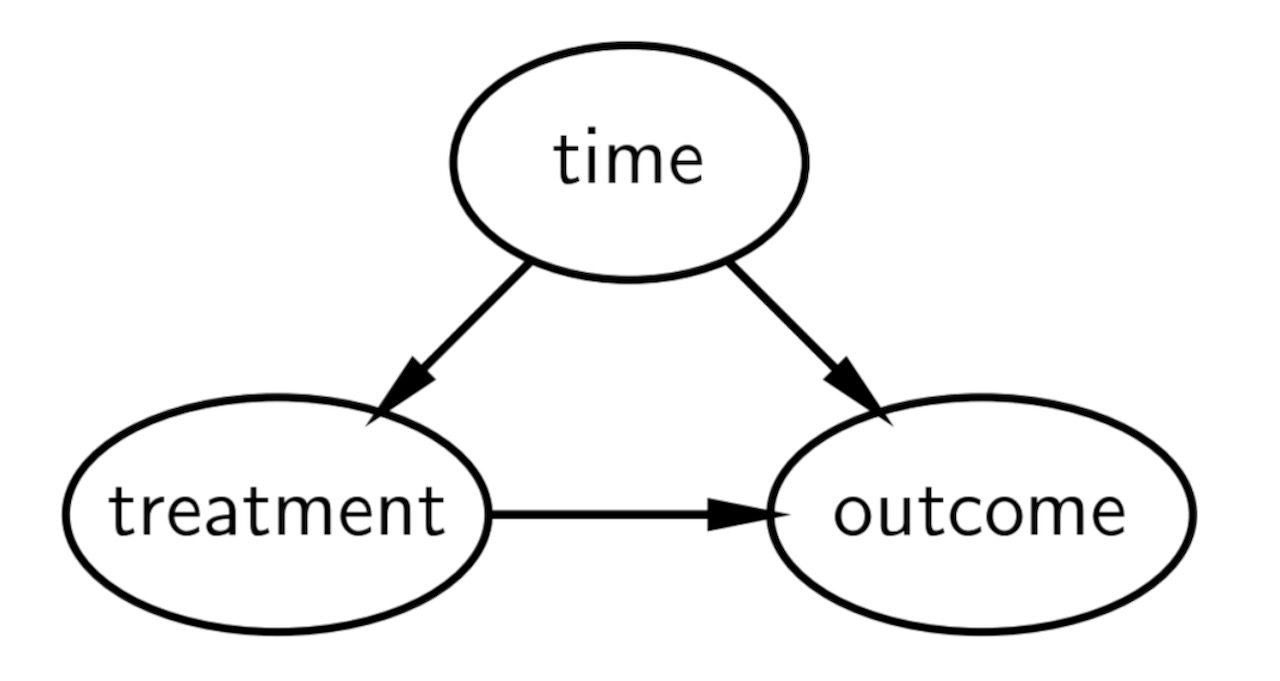
　直感的に、アプローチのロジックを記します。

• 私たちは、時間による変化の結果がわかっています。
• 私たちが、処置の前にどのように時間経過で結果が変化するかのモデルを構築する場合、処置が実施されなかったら何が起こるかを予期してcounterfactualの予測を行うことができます。
• 私たちは、このcounterfactualを介入が起きた時からの観測結果と比較することができます。もし不一致があれば、これを介入による(causal impact)影響としてみなすことができます。

　介入と同じ時点で起きた他の最もらしい原因を省けるならば、これは妥当です。これは、介入からの時間がもっと経過すると、より扱いにくくなります。なぜなら、代替駅な説明を提供する他の関連事象が発生するかもしれないからです。

　これは急には分かり難いならば、下の例のデータをチェックすることを勧めます。その後、このセクションに戻ってください。

import arviz as az
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import xarray as xr

from scipy.stats import norm

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

ここで、任意の役立つ関数を定義しましょう。

def format_x_axis(ax, minor=False):
    # major ticks
    ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y %b"))
    ax.xaxis.set_major_locator(mdates.YearLocator())
    ax.grid(which="major", linestyle="-", axis="x")
    # minor ticks
    if minor:
        ax.xaxis.set_minor_formatter(mdates.DateFormatter("%Y %b"))
        ax.xaxis.set_minor_locator(mdates.MonthLocator())
        ax.grid(which="minor", linestyle=":", axis="x")
    # rotate labels
    for label in ax.get_xticklabels(which="both"):
        label.set(rotation=70, horizontalalignment="right")


def plot_xY(x, Y, ax):
    quantiles = Y.quantile((0.025, 0.25, 0.5, 0.75, 0.975), dim=("chain", "draw")).transpose()

    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.025, 0.975]),
        fill_kwargs={"alpha": 0.25},
        smooth=False,
        ax=ax,
    )
    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.25, 0.75]),
        fill_kwargs={"alpha": 0.5},
        smooth=False,
        ax=ax,
    )
    ax.plot(x, quantiles.sel(quantile=0.5), color="C1", lw=3)


# default figure sizes
figsize = (10, 5)

データ生成

　この例に焦点を当てると、分割時系列アプローチを使うことにで原因を主張することができます。とても簡単なモデルだけを必要とする、任意の相対的に簡単な合成データを使って実行します。

treatment_time = "2017-01-01"
β0 = 0
β1 = 0.1
dates = pd.date_range(
    start=pd.to_datetime("2010-01-01"), end=pd.to_datetime("2020-01-01"), freq="M"
)
N = len(dates)


def causal_effect(df):
    return (df.index > treatment_time) * 2


df = (
    pd.DataFrame()
    .assign(time=np.arange(N), date=dates)
    .set_index("date", drop=True)
    .assign(y=lambda x: β0 + β1 * x.time + causal_effect(x) + norm(0, 0.5).rvs(N))
)
df

120 rows × 2 columns

# Split into pre and post intervention dataframes
pre = df[df.index < treatment_time]
post = df[df.index >= treatment_time]

fig, ax = plt.subplots()
ax = pre["y"].plot(label="pre")
post["y"].plot(ax=ax, label="post")
ax.axvline(treatment_time, c="k", ls=":")
plt.legend();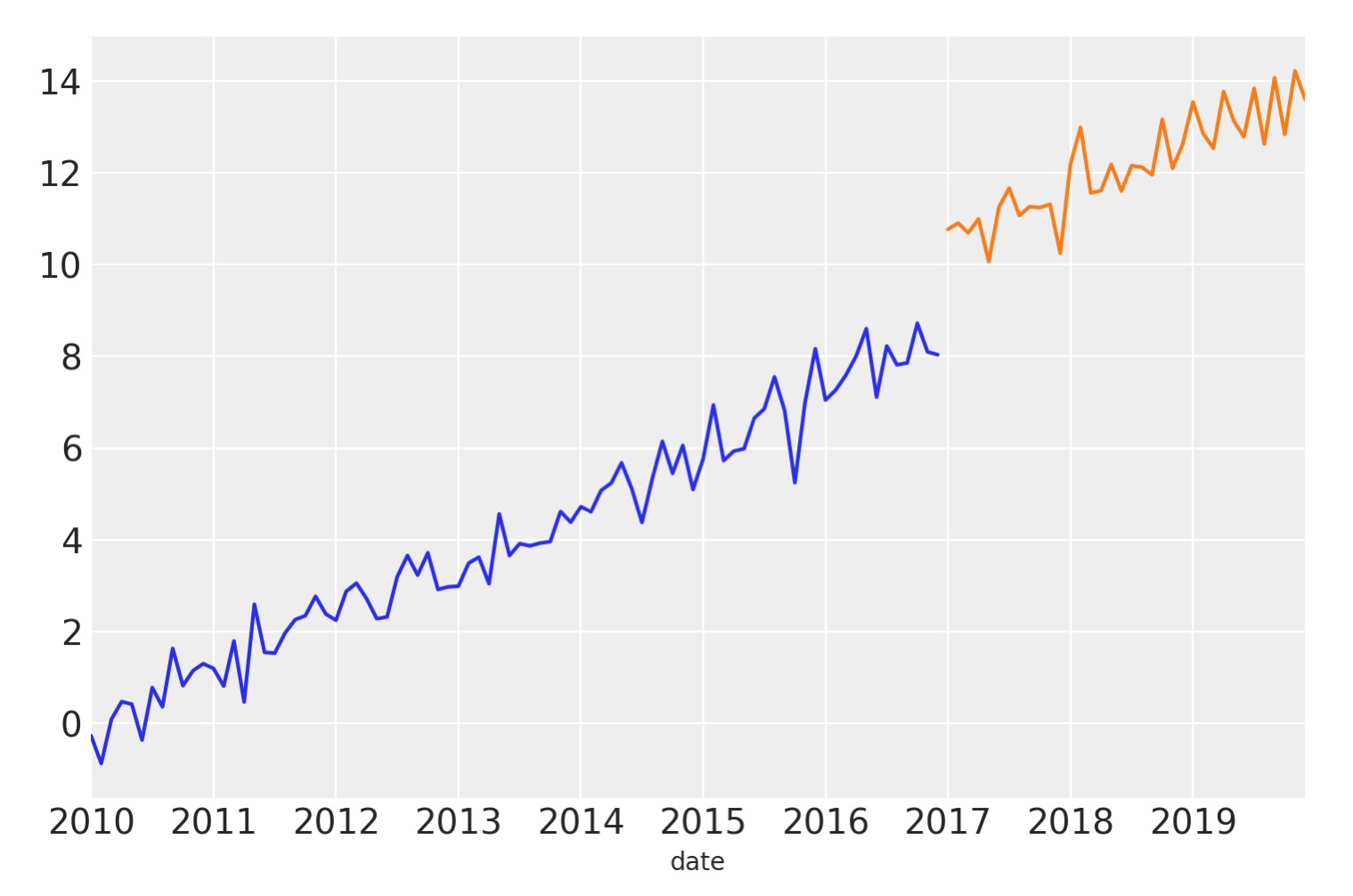

　この簡単なデータセットでは、上側へのノイズを含んだ線形のトレンドを得ます。そして、このデータは合成なので、介入時の結果で段階的に増加することがわかっています。そしてその結果は時間に一定です。

モデリング

　ここで、簡単な線形モデルを構築します。'もし介入が適用されていなければ、何が発生していたか'の予測の妥当な処理である、終端のある介入前のデータでモデルの構築していることを覚えておいてください。他の方法では、切片、傾きまたは、結果が発散しているか一定であるかに関する変化のような、介入後の観測値の任意の様相をモデル化しません。

with pm.Model() as model:
    # observed predictors and outcome
    time = pm.MutableData("time", pre["time"].to_numpy(), dims="obs_id")
    # priors
    beta0 = pm.Normal("beta0", 0, 1)
    beta1 = pm.Normal("beta1", 0, 0.2)
    # the actual linear model
    mu = pm.Deterministic("mu", beta0 + (beta1 * time), dims="obs_id")
    sigma = pm.HalfNormal("sigma", 2)
    # likelihood
    pm.Normal("obs", mu=mu, sigma=sigma, observed=pre["y"].to_numpy(), dims="obs_id")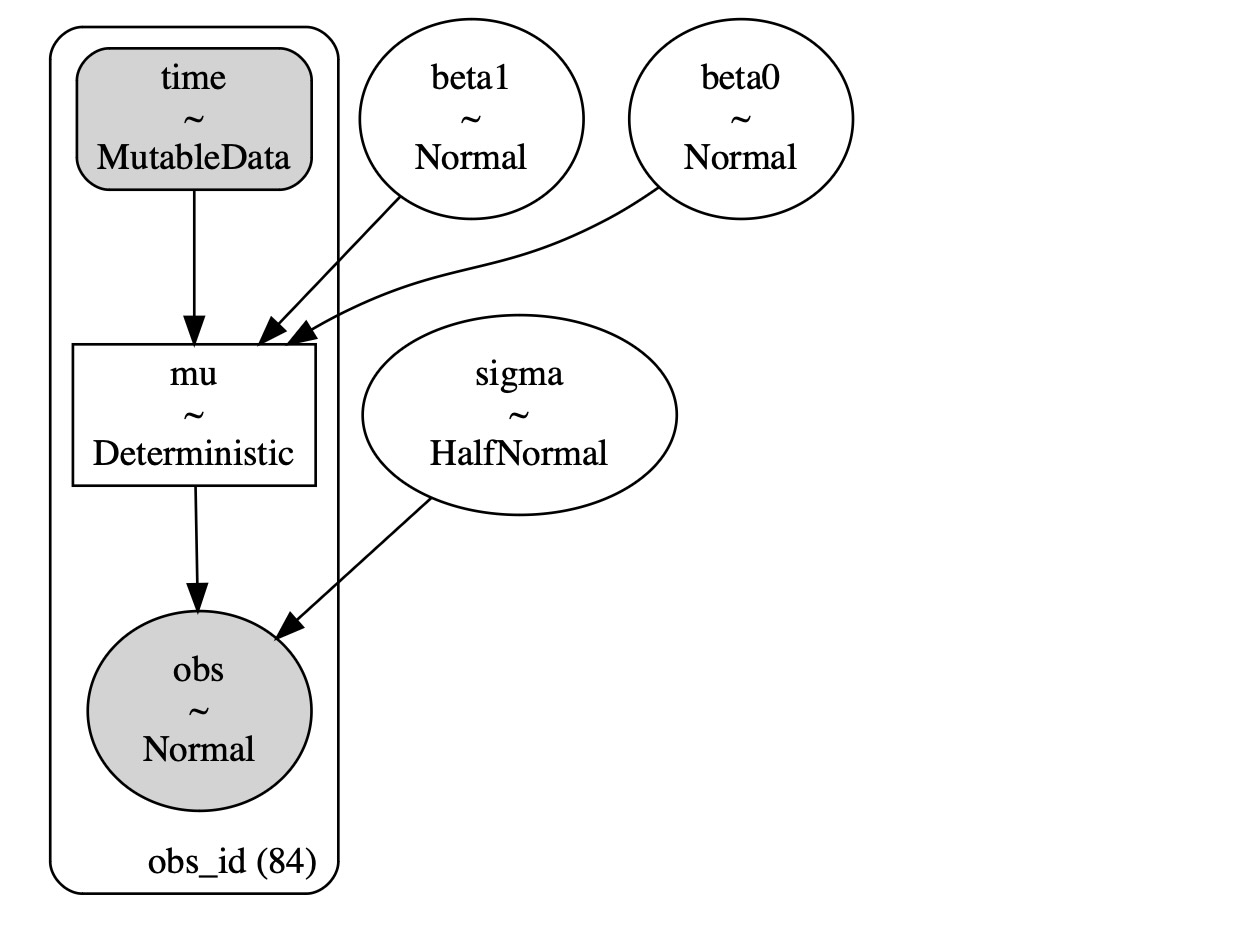

事前予測チェック

　ベイジアンワークフローの一部として、私たちは、任意の観測データを持つ前に、どのような結果をモデルが見つけるかがわかるために事前予測を図示します。

with model:
    idata = pm.sample_prior_predictive(random_seed=RANDOM_SEED)

fig, ax = plt.subplots(figsize=figsize)

plot_xY(pre.index, idata.prior_predictive["obs"], ax)
format_x_axis(ax)
ax.plot(pre.index, pre["y"], label="observed")
ax.set(title="Prior predictive distribution in the pre intervention era")
plt.legend();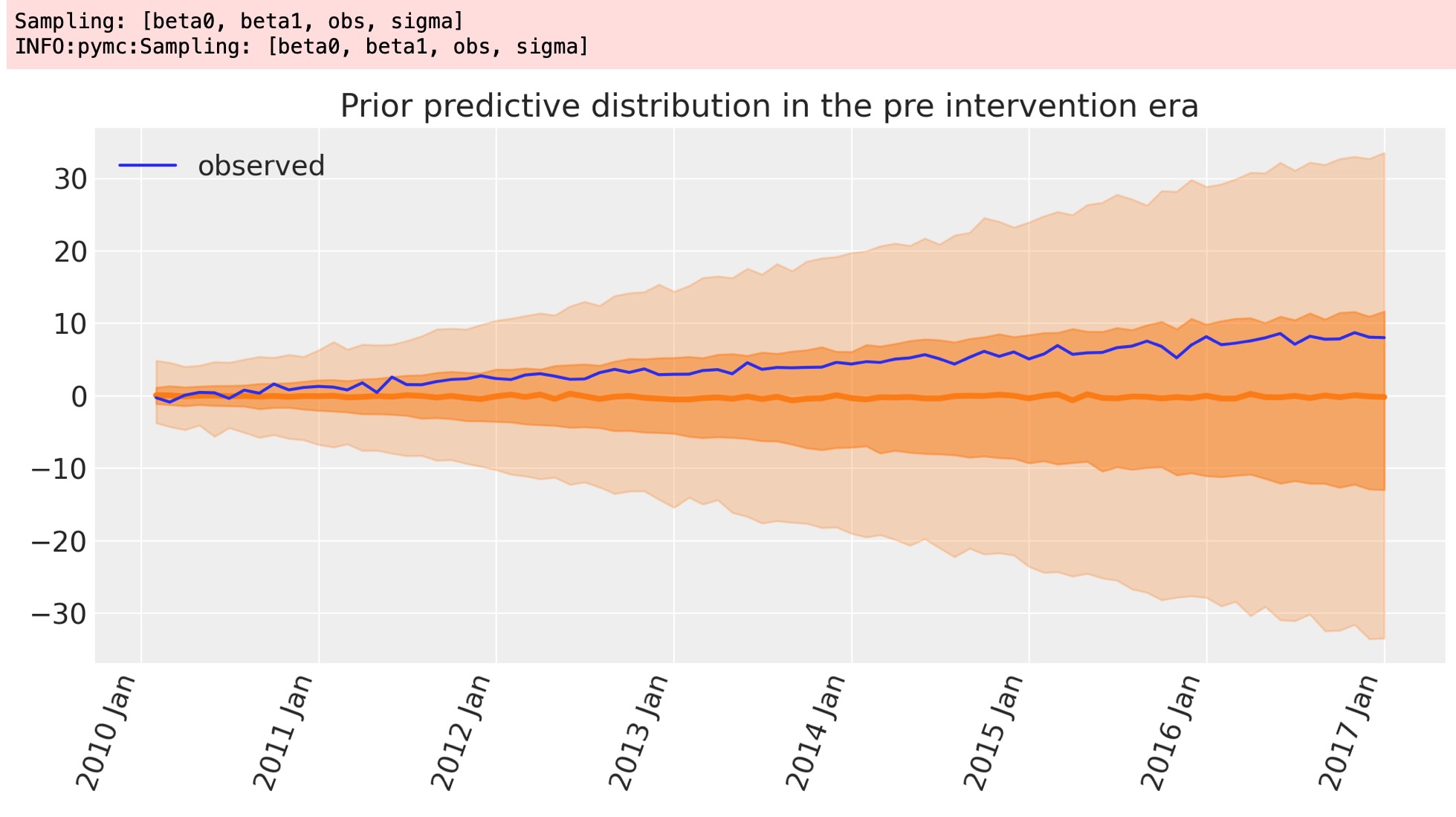

　これは、切片と傾きを覆う事前分布が、実際のデータを容易に含んでいる予測観測値を導くのに十分な幅があり、妥当に見えます。これは、特別な事前の選択が、事後パラメータの見積もりを過度に制限しないことを意味します。

推論

　事後分布にサンプルを出力します。そして、私たちが、介入前のデータだけでこれを処理していることを覚えておいてください。

with model:
    idata.extend(pm.sample(random_seed=RANDOM_SEED))

az.plot_trace(idata, var_names=["~mu"]);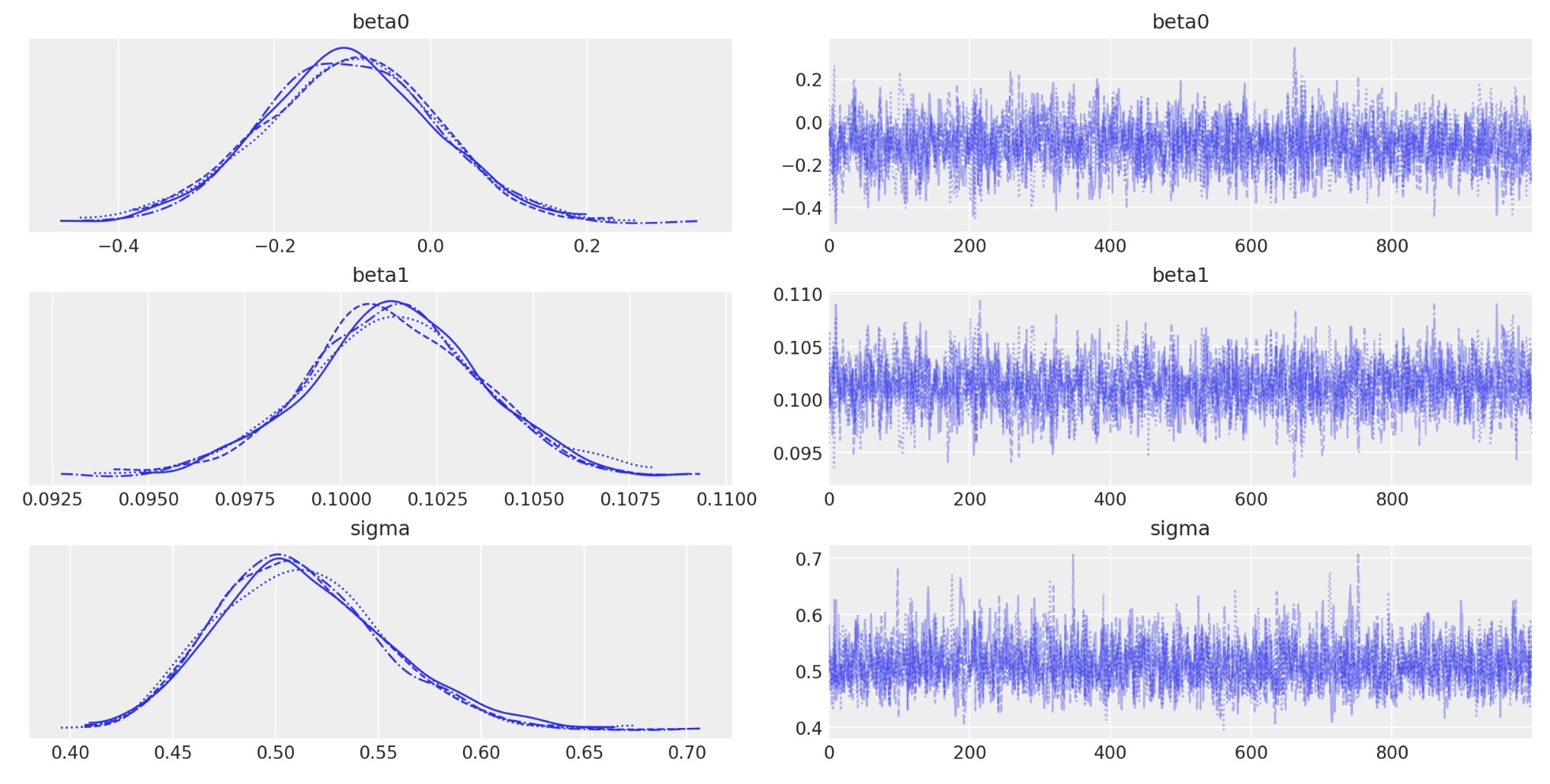

事後予測チェック

　ベジアンワークフローの別の重要な様相は、モデルの事後予測を図示することです。モデルがどれくらい上手く既に観測したデータを回復できるか見せてくれます。それは、モデルが簡単すぎるか、またはよくできているかどうかを決定することができるポイントです。

with model:
    idata.extend(pm.sample_posterior_predictive(idata, random_seed=RANDOM_SEED))

fig, ax = plt.subplots(figsize=figsize)

az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.95, smooth=False)
ax.plot(pre.index, pre["y"], label="observed")
format_x_axis(ax)
ax.set(title="Posterior predictive distribution in the pre intervention era")
plt.legend();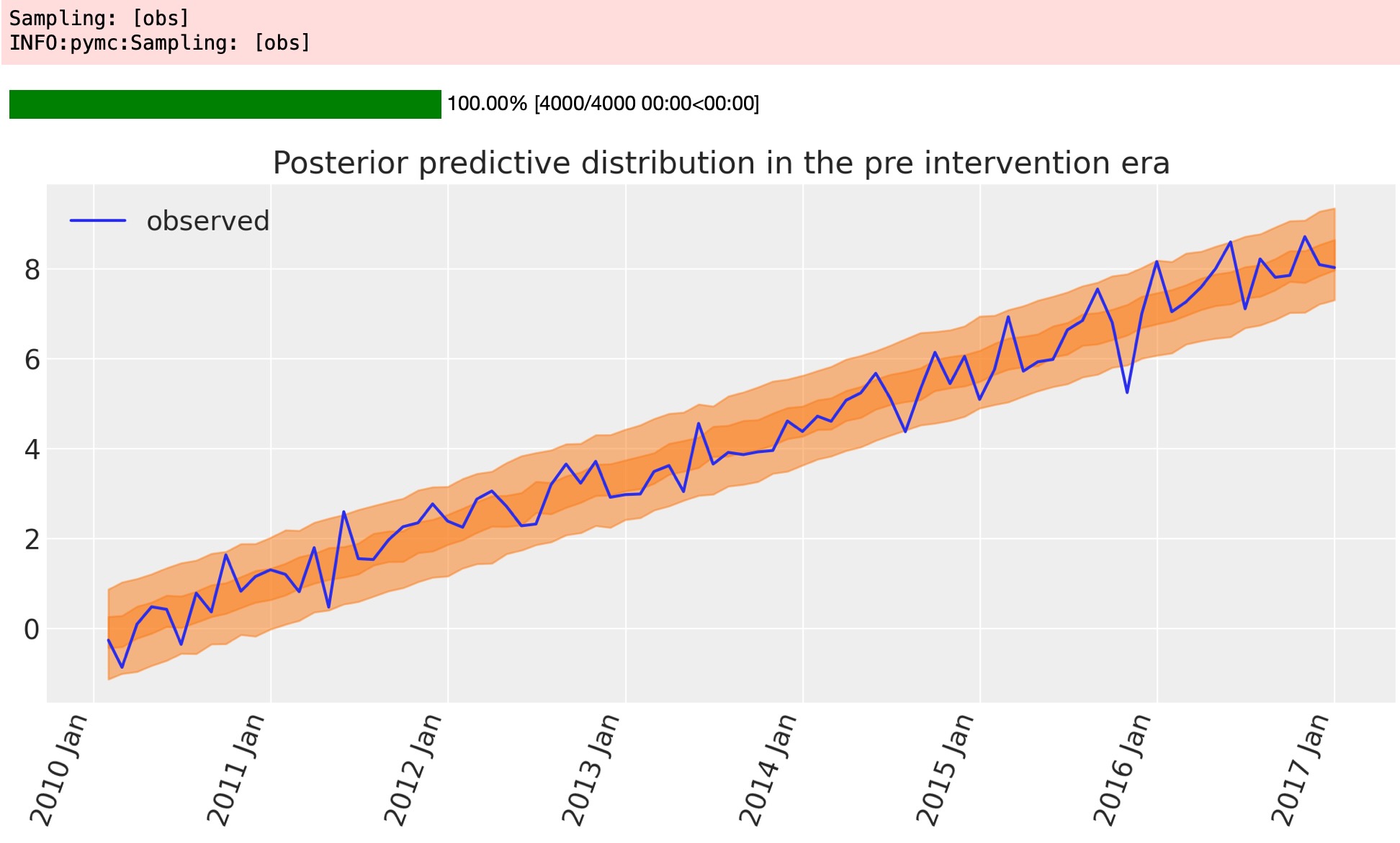

　次のステップは厳密には不要ですが、モデルが回復したものとエラーが見えるデータ間の相違を計算することができます。介入前のデータを復元するために予期できない不可能性を識別するのに使うことができます。

# convert outcome into an XArray object with a labelled dimension to help in the next step
y = xr.DataArray(pre["y"].to_numpy(), dims=["obs_id"])

# do the calculation by taking the difference
excess = y - idata.posterior_predictive["obs"]

fig, ax = plt.subplots(figsize=figsize)
# the transpose is to keep arviz happy, ordering the dimensions as (chain, draw, time)
az.plot_hdi(pre.index, excess.transpose(..., "obs_id"), hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, excess.transpose(..., "obs_id"), hdi_prob=0.95, smooth=False)
format_x_axis(ax)
ax.axhline(y=0, color="k")
ax.set(title="Residuals, pre intervention");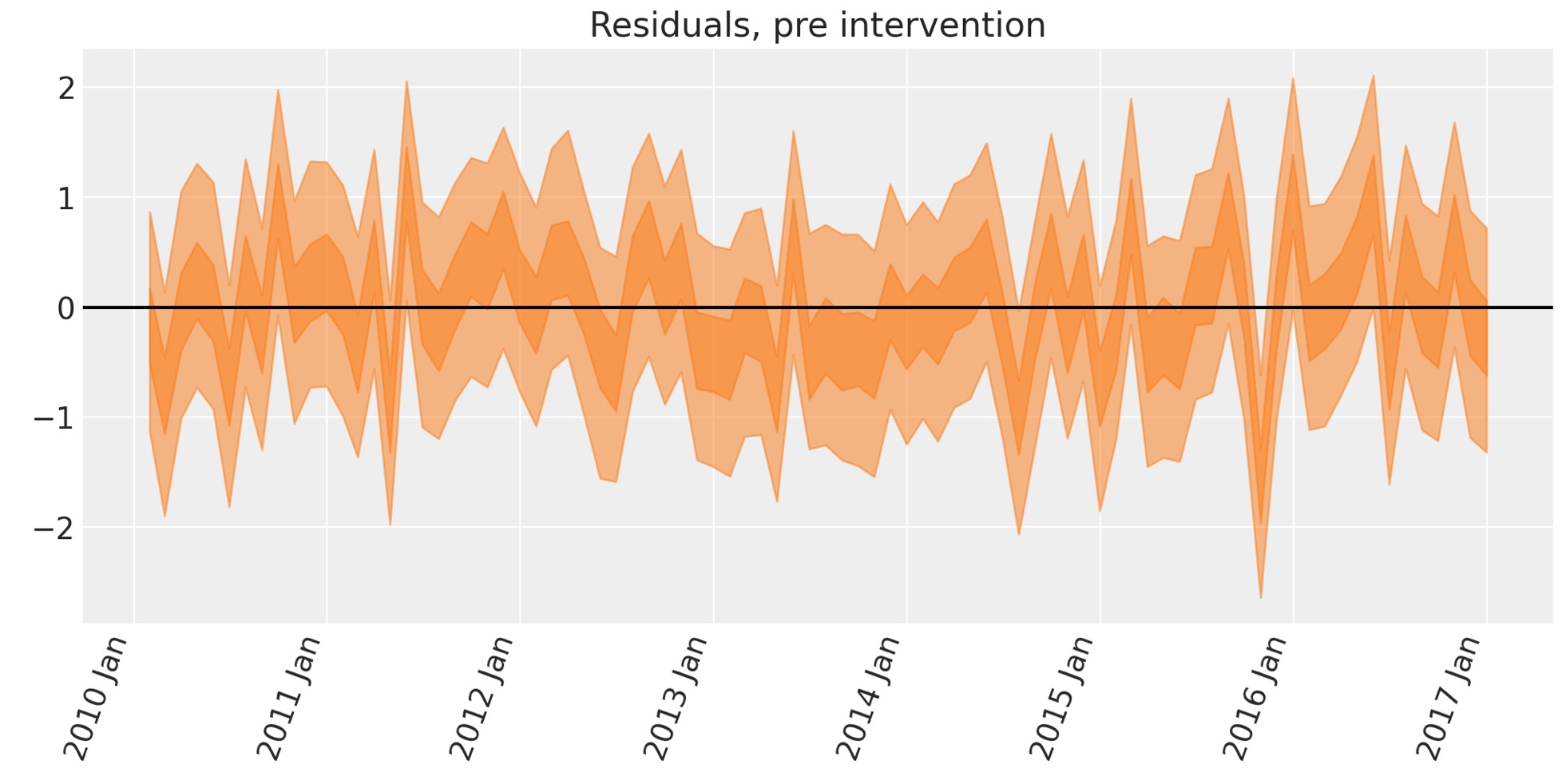

Counterfactual推論

　ここで、介入がなかった時のwhat ifシナリオの観測した結果の予測のためにモデルを使います。

　そのため、Counerfactualシナリオで観測した介入後のデータフレームからtimeデータでモデルを更新します。私たちはこれを”forecasting”と呼びます。

with model:
    pm.set_data(
        {
            "time": post["time"].to_numpy(),
        }
    )
    counterfactual = pm.sample_posterior_predictive(
        idata, var_names=["obs"], random_seed=RANDOM_SEED
    )

fig, ax = plt.subplots(figsize=figsize)

plot_xY(post.index, counterfactual.posterior_predictive["obs"], ax)
format_x_axis(ax, minor=False)
ax.plot(post.index, post["y"], label="observed")
ax.set(
    title="Counterfactual: Posterior predictive forecast of outcome if intervention not taken place"
)
plt.legend();

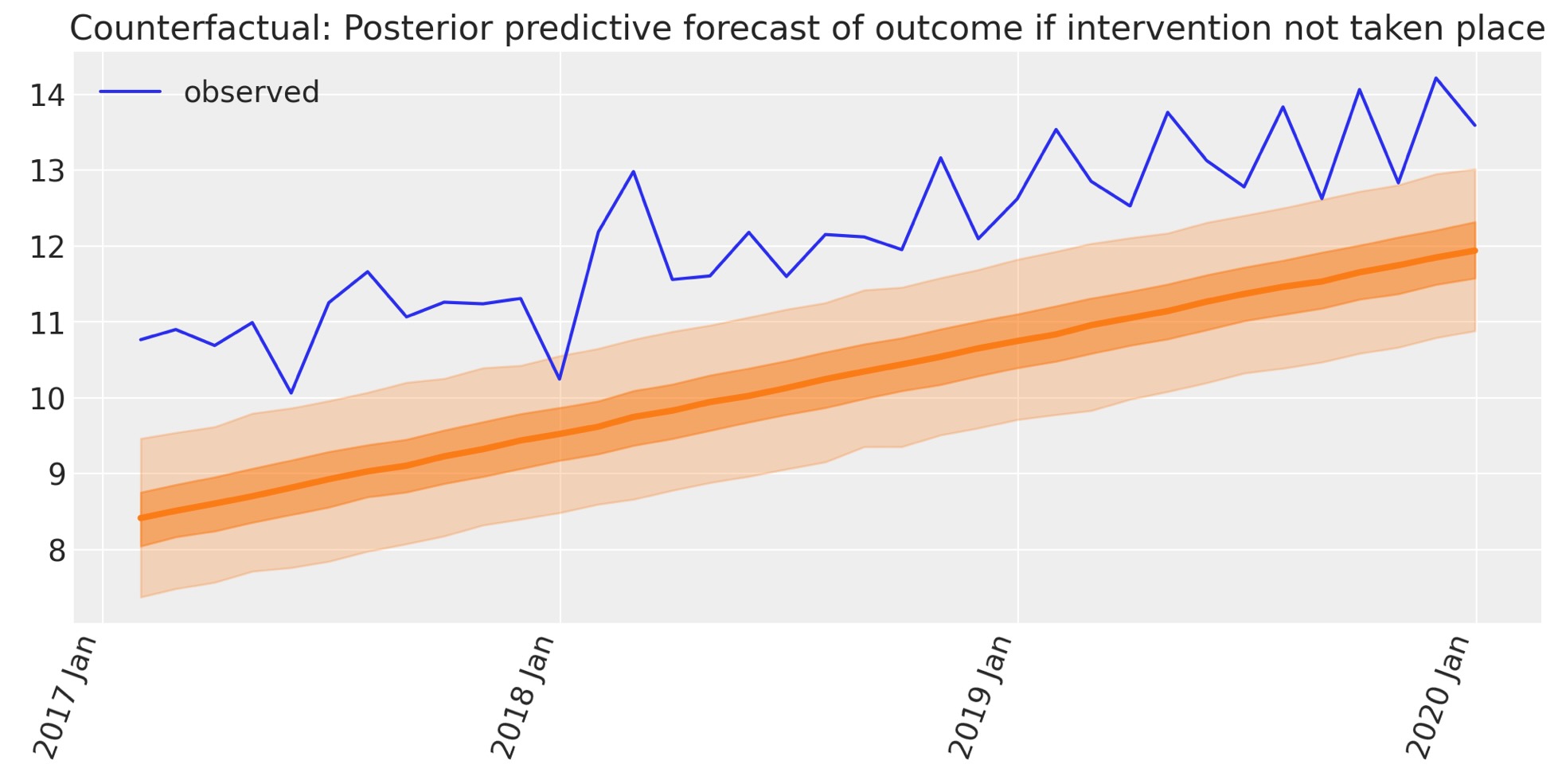
　私たちはここで、因果の影響の計算に必要な成分を所有します。これは、簡単にベイジアンcounterfactual予測と観測値の間の相違です。

介入後の因果の影響 Causal Impact

　ここで、私たちは、counerfactualシナリオ下での結果の予測を使います。そして、counterfactual予測を提案するために結果に観測値と比較します。

# convert outcome into an XArray object with a labelled dimension to help in the next step
outcome = xr.DataArray(post["y"].to_numpy(), dims=["obs_id"])

# do the calculation by taking the difference
excess = outcome - counterfactual.posterior_predictive["obs"]

　そして、累積の因果の影響を簡単に計算できます。

# calculate the cumulative causal impact
cumsum = excess.cumsum(dim="obs_id")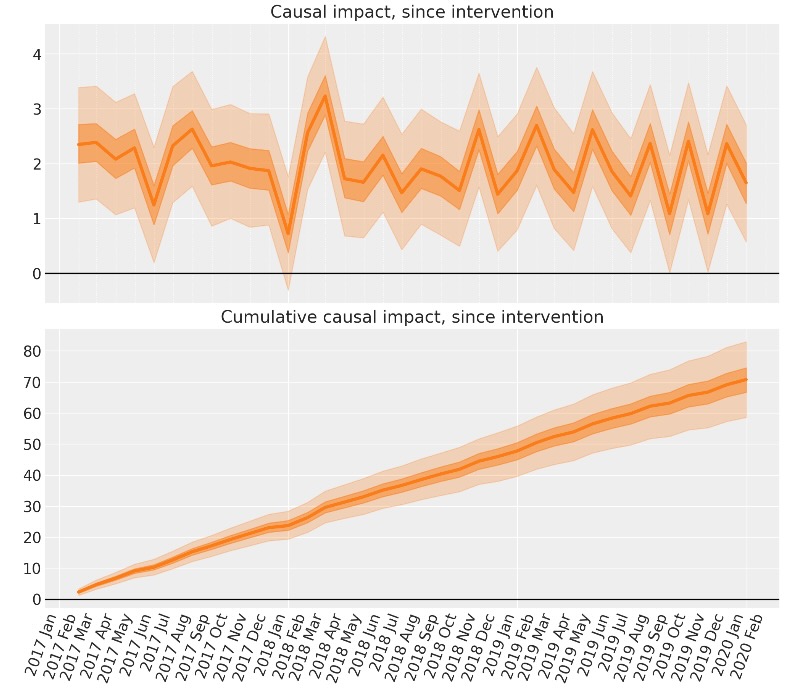

fig, ax = plt.subplots(2, 1, figsize=(figsize[0], 9), sharex=True)

# Plot the excess
# The transpose is to keep arviz happy, ordering the dimensions as (chain, draw, t)
plot_xY(post.index, excess.transpose(..., "obs_id"), ax[0])
format_x_axis(ax[0], minor=True)
ax[0].axhline(y=0, color="k")
ax[0].set(title="Causal impact, since intervention")

# Plot the cumulative excess
plot_xY(post.index, cumsum.transpose(..., "obs_id"), ax[1])
format_x_axis(ax[1], minor=False)
ax[1].axhline(y=0, color="k")
ax[1].set(title="Cumulative causal impact, since intervention");

　そして、結果を得ました。私たちは、分割時系列アプローチを使ってPyMCで任意のベイジアンcounterfactual予測を実行しました。私たちが実施したいくつかのステップは、

• 時系列を予測するために、簡単なモデルの構築
• 介入前のデータを元にしたモデルまぱメータの推定。事前の実行と事後の予測チェック。モデルがかなり良いことを注記します。
• もし介入が発生していなければ、介入後の時間で何が起きたかのcounterfactual予測を作るためにモデルを使いました。
• 観測した結果と介入がないケースでのcounterfactual予測結果を比較することで、因果の影響を計算しました。

　もちろん、多くのケースで分割時系列アプローチは、現実の世界の設定をもっと含むことができます。例えば、季節にような、もっと一時的な構造です。もし、そうならば、単に線形回帰モデルではなく、特別な時系列モデルを使いたいかもしれません。追加の任意の設計は事前と事後の介入の終端からなるのでなく、介入が実施前、実施、実施後(ABAデザインとして知られる)の状態でに終端も含目ることができます。