因子分析

　因子分析は、潜在的な変数に符号化された多変量データの低いランクの構造を識別するためのに確率モデルとして広く使われてきました。主成分分析と密接に関係しており、事前分布にそれらの潜在的変数を仮定していることだけ異なります。根底にあるガウス変数を線形変換して完全に記述できる線形ガウスモデルは良い例です。どのように因子分析が他のモデルに関係しているか高いレベルで見るために、GhahramaniとRoweisによって公開されたこの図を調べることができます。

import arviz as az
import matplotlib
import numpy as np
import pymc as pm
import pytensor.tensor as pt
import scipy as sp
import seaborn as sns
import xarray as xr

from matplotlib import pyplot as plt
from matplotlib.lines import Line2D
from numpy.random import default_rng
from xarray_einstats import linalg
from xarray_einstats.stats import XrContinuousRV

print(f"Running on PyMC3 v{pm.__version__}")

Running on PyMC3 v5.3.1

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

np.set_printoptions(precision=3, suppress=True)
RANDOM_SEED = 31415
rng = default_rng(RANDOM_SEED)

シミュレートするデータの生成

　少数の例を通して実行するため、最初にいくつかのデータを生成します。潜在的な変数はガウシアンではないので、データは因子分析モデルによって仮定された正確な生成過程にしたがいません。実際はkの潜在変数を持つノイズのある線形関数である、N(横列)、d行(縦列）の観測データセットを仮定します。

n = 250
k_true = 4
d = 10

　次のコードセルは、潜在変数の配列Mの作成と、線形変換Qを通じてデータを生成します。そのとき、行列積 QMは、変数パラメータerr_sdによって操作される加法ガウスノイズに影響を与えます。

err_sd = 2
M = rng.binomial(1, 0.25, size=(k_true, n))
Q = np.hstack([rng.exponential(2 * k_true - k, size=(d, 1)) for k in range(k_true)]) * rng.binomial(
    1, 0.75, size=(d, k_true)
)
Y = np.round(1000 * np.dot(Q, M) + rng.standard_normal(size=(d, n)) * err_sd) / 1000

　私たちがデータを生成する方法のために、コラムY間の相関を説明する共分散行列は、QQtと等しくなります。PCAの原理的な仮定と因子分析は、Qtが完全な列ではないことです。私たちは、共分散行列を図示目すれば、この兆候を見ることができます。

plt.figure(figsize=(4, 3))
sns.heatmap(np.corrcoef(Y));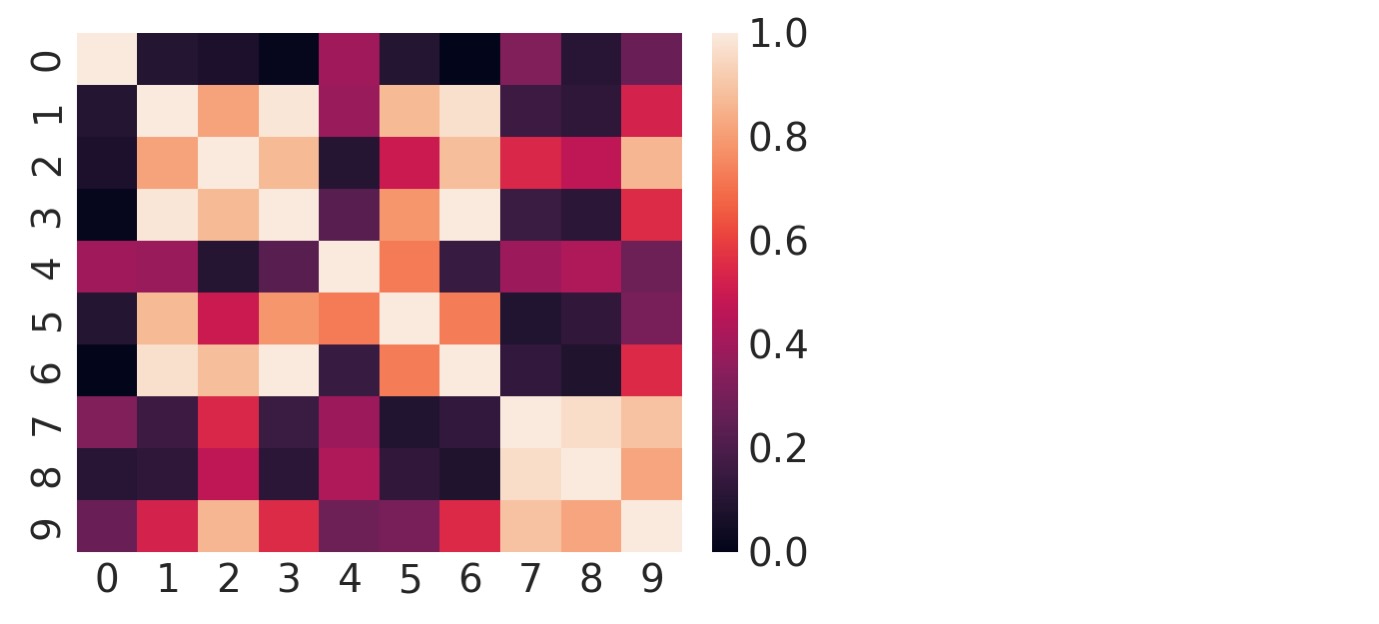

十分に長い間、目を凝らしてみると、明確にコラムがお互いに線形関数のような領域であることがわかります。

モデル

　確率PCAと因子分析はPyMC discourseのトピックの共通の源です。下にリンクされている投稿は、問題の異なる様相を取り扱っています。

• 大きなデータセットのためのminibatched FA
• FAの欠損値の取り扱い
• FA/PPCAの識別

直接の実装

　因子分析のためのモデルは、確率行列の因子化

　Ψは対角行列です。下付の文字は行列の次元を示しています。確率PCAは、Ψ　= σ 2 I でセットされる変量です。基礎的な実装は、(この要点から)次のセルで、示されます。信じられないことに、モデルの適合には必要とされない性質です。

k = 2

coords = {"latent_columns": np.arange(k), "rows": np.arange(n), "observed_columns": np.arange(d)}

with pm.Model(coords=coords) as PPCA:
    W = pm.Normal("W", dims=("observed_columns", "latent_columns"))
    F = pm.Normal("F", dims=("latent_columns", "rows"))
    psi = pm.HalfNormal("psi", 1.0)
    X = pm.Normal("X", mu=pt.dot(W, F), sigma=psi, observed=Y, dims=("observed_columns", "rows"))

    trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)  # target_accept=0.9

この点で、サンプルを外れることと収束のチェックの誤りに関して、すでにいくつかの警告があります。下のトレース図でより詳しい問題を見ることができます。。この図は、各チェインのサンプルを超えて評価される平均と同じように、行列Wの単一のエントリーのための各サンプラーチェインにより、取られる経路を示しています。

for i in trace.posterior.chain.values:
    samples = trace.posterior["W"].sel(chain=i, observed_columns=3, latent_columns=1)
    plt.plot(samples, label="Chain {}".format(i + 1))
    plt.axhline(samples.mean(), color=f"C{i}")
plt.legend(ncol=4, loc="upper center", fontsize=12, frameon=True), plt.xlabel("Sample");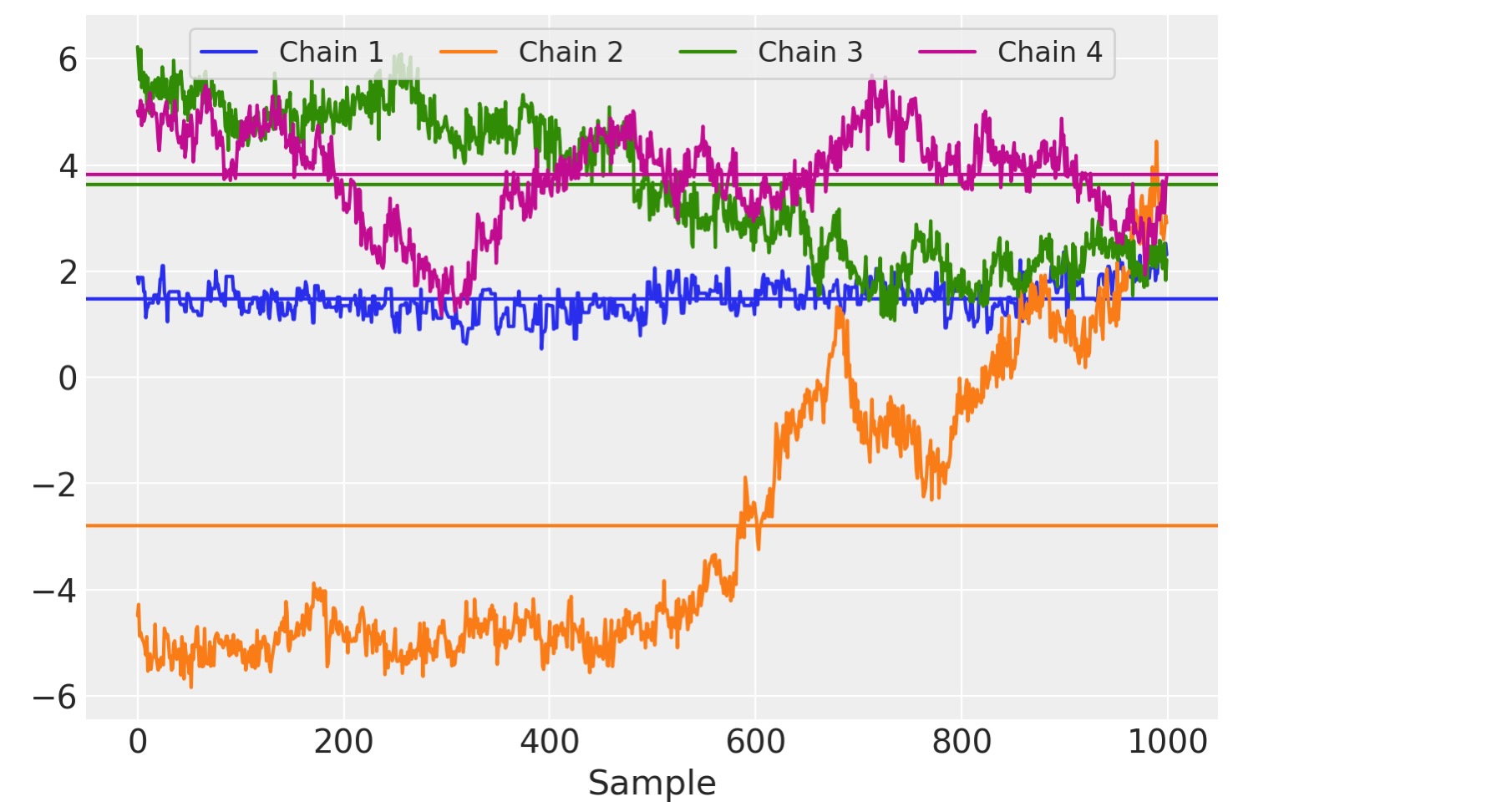

　各チェインは異なるサンプル平均を持つように見えます、サンプリング回数を超えた長い範囲のトレンドとして現れる、チェインを横切る自己回帰の大きな処理を見ることができます。任意のチェインは、うまく発散しています。このモデルのためにMCMCを使うことで,その主張のためのより詳しい証拠を与えることは、最適ではありません。

　このモデルの様式の主要な不利な点の一つは、識別性の欠如です。このモデルが表現するように、尤度XにとってのWF積の問題は、任意の逆行列Ωに対して、P (X |W,F)＝P(X| WΩ, Ω^-1 F). WとFの事前が大きすぎるか、小さすぎるかどちらかにならないように、Ωを制限するので、因子と読み込みは、回転され、反射され、そして、モデルの尤度を変更することなく影響されます。実行中にドリフトするためのパラメータ化のためでさえ、サンプラーを実行させている間に起こることを予測します、そして上の高い自己送還をもつWのトレース図を出力します。

代替のパラメータ化

　これは、Wの様式を次のように制約することで固定化できます。

• 低位の三角
• 正の対角の増加

　非スクエアな行列を満たすために、expand_block_triangularを適合することができます。この関数はpm.expand_packed_triangularの模倣です。しかし、後半でだけスクエア行列のパックされたバージョンで、動作します。(別の言い方をすると、私たちのモデルで　d = k、前半は非スクエア行列を使います。

def expand_packed_block_triangular(d, k, packed, diag=None, mtype="pytensor"):
    # like expand_packed_triangular, but with d > k.
    assert mtype in {"pytensor", "numpy"}
    assert d >= k

    def set_(M, i_, v_):
        if mtype == "pytensor":
            return pt.set_subtensor(M[i_], v_)
        M[i_] = v_
        return M

    out = pt.zeros((d, k), dtype=float) if mtype == "pytensor" else np.zeros((d, k), dtype=float)
    if diag is None:
        idxs = np.tril_indices(d, m=k)
        out = set_(out, idxs, packed)
    else:
        idxs = np.tril_indices(d, k=-1, m=k)
        out = set_(out, idxs, packed)
        idxs = (np.arange(k), np.arange(k))
        out = set_(out, idxs, diag)
    return out

　私たちは、また、主要な対角に沿った増加するエントリーによる正の対角行列を作るのに役立つ他の関数を定義します。

def makeW(d, k, dim_names):
    # make a W matrix adapted to the data shape
    n_od = int(k * d - k * (k - 1) / 2 - k)

    # trick: the cumulative sum of z will be positive increasing
    z = pm.HalfNormal("W_z", 1.0, dims="latent_columns")
    b = pm.HalfNormal("W_b", 1.0, shape=(n_od,), dims="packed_dim")
    L = expand_packed_block_triangular(d, k, b, pt.ones(k))
    W = pm.Deterministic("W", pt.dot(L, pt.diag(pt.extra_ops.cumsum(z))), dims=dim_names)
    return W

　これらの変更により、モデルを再構築し、MCMCのサンプラーを再度、実行します。

with pm.Model(coords=coords) as PPCA_identified:
    W = makeW(d, k, ("observed_columns", "latent_columns"))
    F = pm.Normal("F", dims=("latent_columns", "rows"))
    psi = pm.HalfNormal("psi", 1.0)
    X = pm.Normal("X", mu=pt.dot(W, F), sigma=psi, observed=Y, dims=("observed_columns", "rows"))
    trace = pm.sample(tune=2000)  # target_accept=0.9

for i in range(4):
    samples = trace.posterior["W"].sel(chain=i, observed_columns=3, latent_columns=1)
    plt.plot(samples, label="Chain {}".format(i + 1))

plt.legend(ncol=4, loc="lower center", fontsize=8), plt.xlabel("Sample");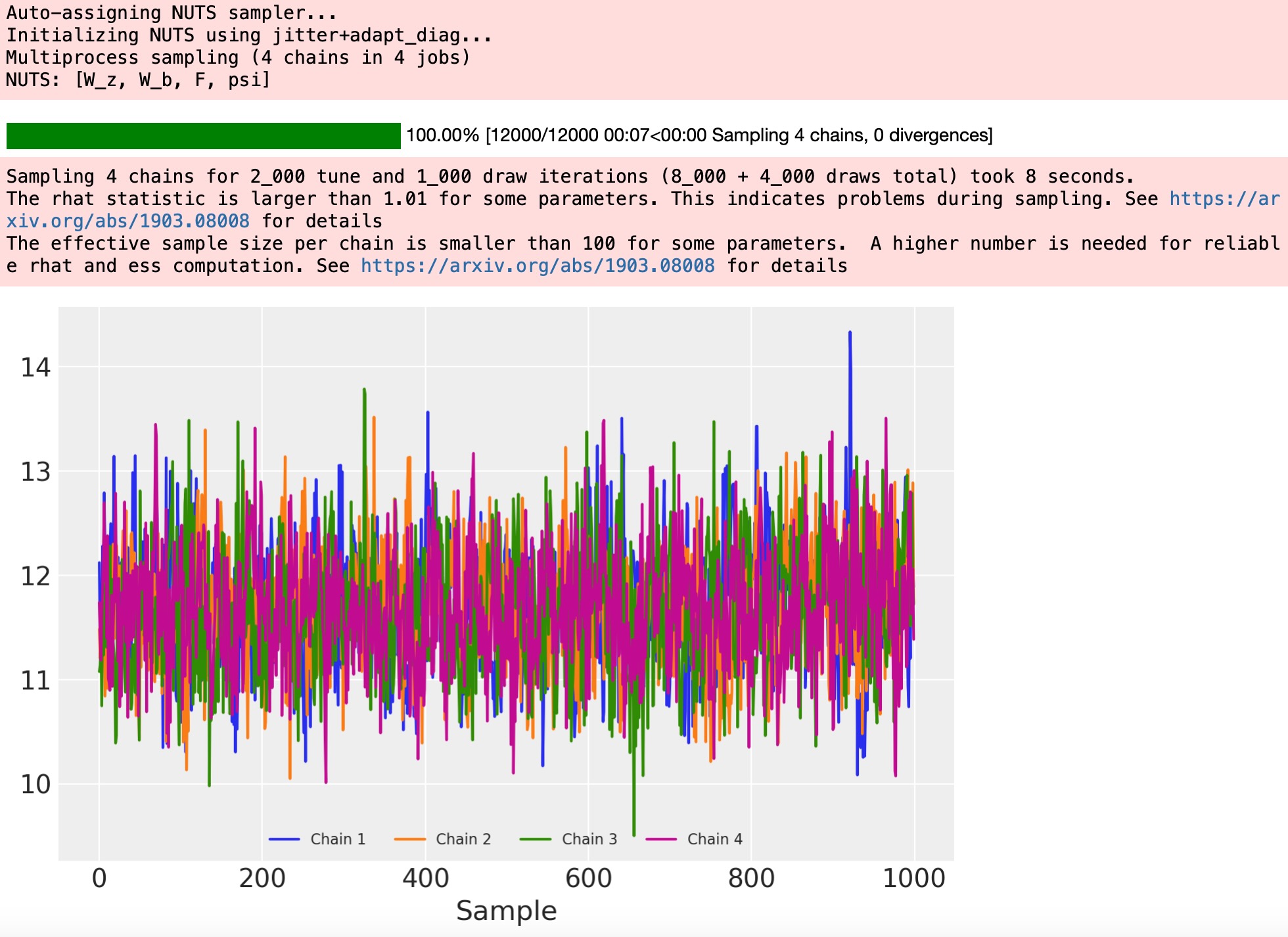

　W(とF)ここで、サンプラーチェインの間で比較するように、識別できる事後分布を得ます。

　Fのk x nパラメータは全てサンプルされる必要があるため、サンプリングは、非常に大きい数字nに対して、全く高価になります。加えて、観測データポイントXiと関連する潜在値 Fi間のリンクは、ミニバッチ(mini-batch)によるストリーミング推論が実行できないことを意味しています。このアプローチはしばしば、定期的に実行する(amortize)推論として記述されます。しかし、Fの事前を固定することは、柔軟なモデル化とは認められません。　Fij 〜N(0,1）に合わせて、

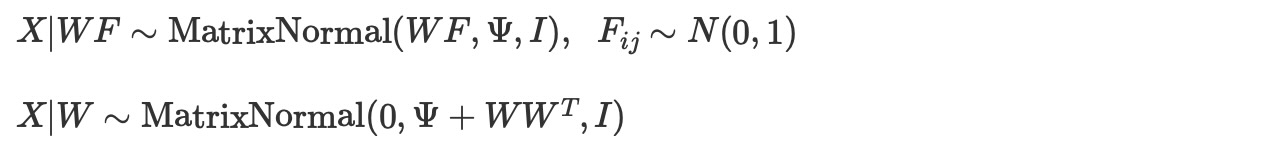
　もしあなたが正規分布行列に馴染みがないならば、行列の値をランダム変数にする他変量ガウスを拡張することを考えてみてください。そのとき、列間の相関と行間の相関は、正規行列で特徴づけられる二つの分離した共分散行列によって取り扱うことができます。ここで、Fiを周辺の外n持つモデルの様式のために私たちの記述を簡単にします。Fiを明確に統合するには、ADVIとFullRQnkADVI近似の高速計算のために観測のバッチ処理をイネーブルにします。

coords["observed_columns2"] = coords["observed_columns"]
with pm.Model(coords=coords) as PPCA_scaling:
    W = makeW(d, k, ("observed_columns", "latent_columns"))
    Y_mb = pm.Minibatch(Y.T, batch_size=50)  # MvNormal parametrizes covariance of columns, so transpose Y
    psi = pm.HalfNormal("psi", 1.0)
    E = pm.Deterministic(
        "cov",
        pt.dot(W, pt.transpose(W)) + psi * pt.diag(pt.ones(d)),
        dims=("observed_columns", "observed_columns2"),
    )
    X = pm.MvNormal("X", 0.0, cov=E, observed=Y_mb)
    trace_vi = pm.fit(n=50000, method="fullrank_advi", obj_n_mc=1).sample()

結果

　MCMCを使って計算した事後とVIを比較する場合、(少なくとも私たちが注目する特別なパラメータ)二つの分布が近いことを認識します。しかし、それらの平均値は異なっています。MCMCチェインの全ては相互に承認し、ADVIの予測は遠く離れてはいません。

col_selection = dict(observed_columns=3, latent_columns=1)
ax = az.plot_kde(
    trace_vi.posterior["W"].sel(**col_selection).squeeze().values,
    label="FR-ADVI posterior",
    plot_kwargs={"alpha": 0},
    fill_kwargs={"alpha": 0.5, "color": "red"},
)
for i in trace.posterior.chain.values:
    mcmc_samples = trace.posterior["W"].sel(chain=i, **col_selection).values
    az.plot_kde(
        mcmc_samples,
        label="MCMC posterior for chain {}".format(i + 1),
        plot_kwargs={"color": f"C{i}"},
    )

ax.set_title(rf"PDFs of $W$ estimate at {col_selection}")
ax.legend(loc="upper right");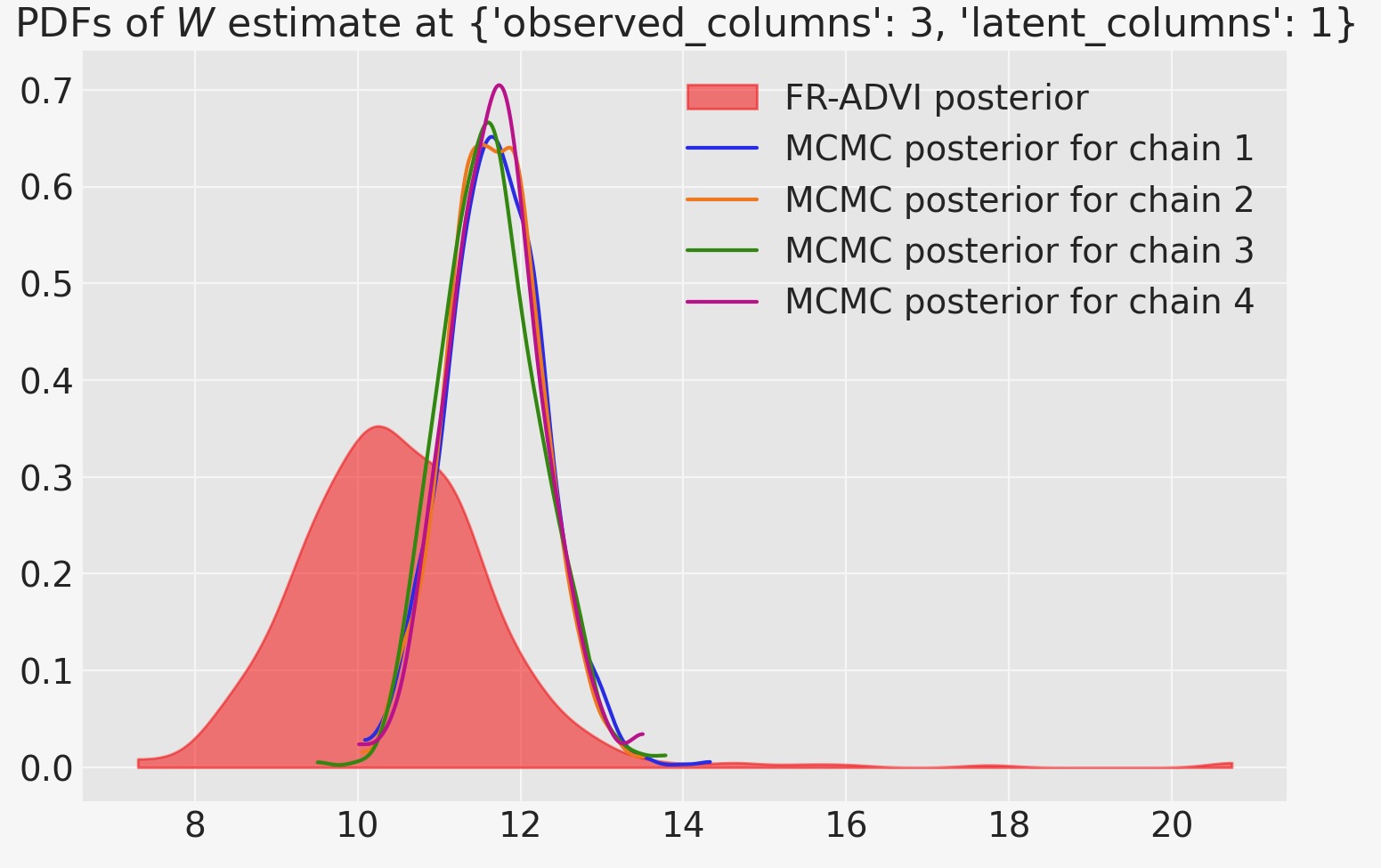

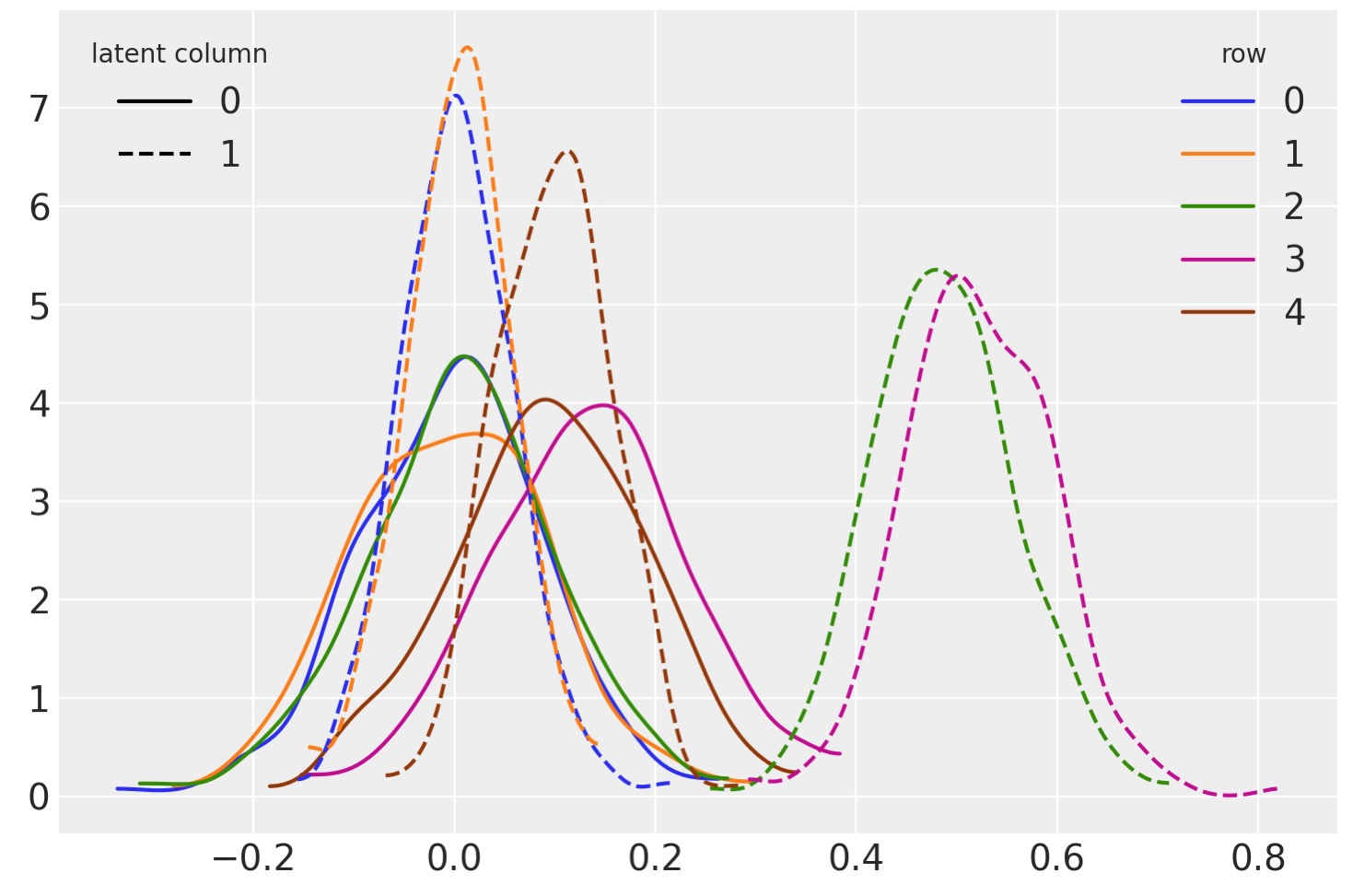
Fの事後識別子

　行列Fは、因子分析の典型的な関心です。そして、しばしば次元縮約のための特徴行列として使用されます。しかし、Fはモデルを簡単に適合させるために、境界化します。そしてここでは元に戻します。これは、実際、最小二乗の演習です。

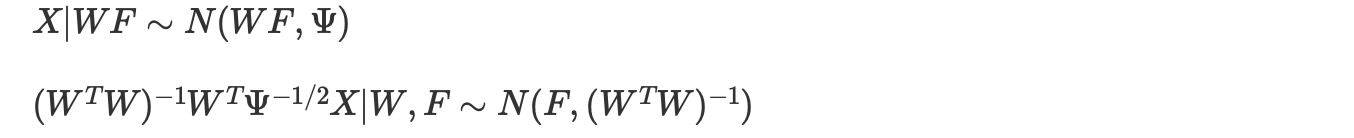
　ここで、私たちのモデル下で多変量正規である、Fの事後表現に適切に変換することで、標準正規分布からランダム変数を出力します。

# configure xarray-einstats
def get_default_dims(dims, dims2):
    proposed_dims = [dim for dim in dims if dim not in {"chain", "draw"}]
    assert len(proposed_dims) == 2
    if dims2 is None:
        return proposed_dims


linalg.get_default_dims = get_default_dims

post = trace_vi.posterior
obs = trace.observed_data

WW = linalg.inv(
    linalg.matmul(
        post["W"], post["W"], dims=("latent_columns", "observed_columns", "latent_columns")
    )
)
WW_W = linalg.matmul(
    WW,
    post["W"],
    dims=(("latent_columns", "latent_columns2"), ("latent_columns", "observed_columns")),
)
F_mu = xr.dot(1 / np.sqrt(post["psi"]) * WW_W, obs["X"], dims="observed_columns")
WW_chol = linalg.cholesky(WW)
norm_dist = XrContinuousRV(sp.stats.norm, xr.zeros_like(F_mu))  # the zeros_like defines the shape
F_sampled = F_mu + linalg.matmul(
    WW_chol,
    norm_dist.rvs(),
    dims=(("latent_columns", "latent_columns2"), ("latent_columns", "rows")),
)

fig, ax = plt.subplots()
ls = ["-", "--"]
for i in range(2):
    for j in range(5):
        az.plot_kde(
            F_sampled.sel(latent_columns=i, rows=j).squeeze().values,
            plot_kwargs={"color": f"C{j}", "ls": ls[i]},
            ax=ax,
        )
legend = ax.legend(
    handles=[Line2D([], [], color="k", ls=ls[i], label=f"{i}") for i in range(2)],
    title="latent column",
    loc="upper left",
)
ax.add_artist(legend)
ax.legend(
    handles=[Line2D([], [], color=f"C{i}", label=f"{i}") for i in range(5)],
    title="row",
    loc="upper right",
);