import random
import arviz as az
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import scipy.optimize
from matplotlib.lines import Line2D
from pymc.sampling.jax import sample_blackjax_nuts, sample_numpyro_nuts
from scipy.stats import multivariate_normalベイジアン代入法と 欠測の度合い
欠測値データの分析は因果推論の学習への入り口です。
欠測データによって困らせられる任意の分析の鍵となる特徴の一つは、という欠測の特質を決定する仮定です。すなわち、私たちのデータのギャップの理由は何なのか?それらは無視できるのか?なぜ心配すべきか?このノートブックでは、最大尤度予測とベイジアン代入法の技術を使うことで欠測データの取り扱い方を見ていきます。これは、counterfactualケースの予測と欠測データの存在で予測を決定する仮定について疑問のドアを開きます。
私たちは、従業員の満足度調査の分析例を考えることによって、固い討議を実施します。そしてどのように異なった労働条件が回答と非回答に寄与するかデータを見ていきます。
%config InlineBackend.figure_format = 'retina' # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)欠測データの分類法
ルービンの有名な分類法は、三つの基本的なオプションの選択によりこの問題に答えます。
- 完全にランダムな欠測(MCAR)
- ランダムな欠測(MAR)
- 非ランダムな欠測(MNAR)
これらの各パラダイムは、欠測データのパターンに関しての条件確率の用語で明白に定義してまとめられます。最初のパターンは危惧は最も小さくなります。MCARの仮定は、実現データが観測値と観測されなかったデータの両方に無関係な方法で、データが欠測している状態です。Φで示す状況の偶然の環境によって欠測します。
P( M=1 | Yobs,Ymiss, Φ) = P( M= 1|Φ )ここで2番目のパターン(MAR)は、欠測の理由が、観測データと状況の環境の関数にできるのことを認めます。時にこれは無視できる欠測のケースと呼ばれます。なぜなら、予測を観測データを基礎にした良い信念で進めることができます。それらは正確さを失う可能性がありますが、推論は正しくなります。
P( M=1 | Yobs,Ymiss, Φ) = P( M= 1|Yobs,Φ )もっとも無法な欠測データのソートは、欠測が、観測データの何らかの外側の働きで、恒等式が乖離してまとめることができない場合です。代入の努力とより一般的な見積もりは、この最後のケースでは、混乱させるリスクのせいでもっと困難になります。これは無視できない欠測のケースです。
P( M=1 | Yobs,Ymiss, Φ)これらの仮定は、いづれかの分析を開始する前に設定します。それらは検証できず継承されます。あなたの分析は、どのくらい各仮定が、それらを適用するために探し出す文脈でもっともらしいかに依存して、成立するかまたは不成立になります。例えば、別の種類の欠測データは、"切り詰めた検閲データのベイジアン回帰"(ハイパーリンク)で討議される 体系的な検閲からの結果になります。そのようなケースでは、検閲の理由が欠測パターンを決定します。
雇用者満足度調査
クレイグ・エンダーズの欠測データ分析の応用 [2022] の説明に従います。そして雇用者満足度調査のデータセットで作業します。このデータセットは、従業員の労働条件と満足度の報告を測定したいくつかの合成からなります。特に注記すると、自由裁量(empower)、仕事満足度(workstat)、二つの合成調査、従業員の指導の状況(climate)、そして彼らの上司の資質の関係(lmx)になります。
鍵となる疑問は、何の仮定が私たちの欠測データを決定しているかです。
try:
df_employee = pd.read_csv("../data/employee.csv")
except FileNotFoundError:
df_employee = pd.read_csv(pm.get_data("employee.csv"))
df_employee.head()| employee | team | turnover | male | empower | lmx | worksat | climate | cohesion | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.0 | 1 | 32.0 | 11.0 | 3.0 | 18.0 | 3.5 |
| 1 | 2 | 1 | 1.0 | 1 | NaN | 13.0 | 4.0 | 18.0 | 3.5 |
| 2 | 3 | 1 | 1.0 | 1 | 30.0 | 9.0 | 4.0 | 18.0 | 3.5 |
| 3 | 4 | 1 | 1.0 | 1 | 29.0 | 8.0 | 3.0 | 18.0 | 3.5 |
| 4 | 5 | 1 | 1.0 | 0 | 26.0 | 7.0 | 4.0 | 18.0 | 3.5 |
# Percentage Missing
df_employee[["worksat", "empower", "lmx"]].isna().sum() / len(df_employee)worksat 0.047619
empower 0.161905
lmx 0.041270
dtype: float64# Patterns of missing Data
df_employee[["worksat", "empower", "lmx"]].isnull().drop_duplicates().reset_index(drop=True)| worksat | empower | lmx | |
|---|---|---|---|
| 0 | False | False | False |
| 1 | False | True | False |
| 2 | True | True | False |
| 3 | False | False | True |
| 4 | True | False | False |
fig, ax = plt.subplots(figsize=(20, 7))
ax.hist(df_employee["empower"], bins=30, ec="black", color="cyan", label="Empowerment")
ax.hist(df_employee["lmx"], bins=30, ec="black", color="yellow", label="LMX")
ax.hist(df_employee["worksat"], bins=30, ec="black", color="green", label="Work Satisfaction")
ax.set_title("Employee Satisfaction Survey Results", fontsize=20)
ax.legend();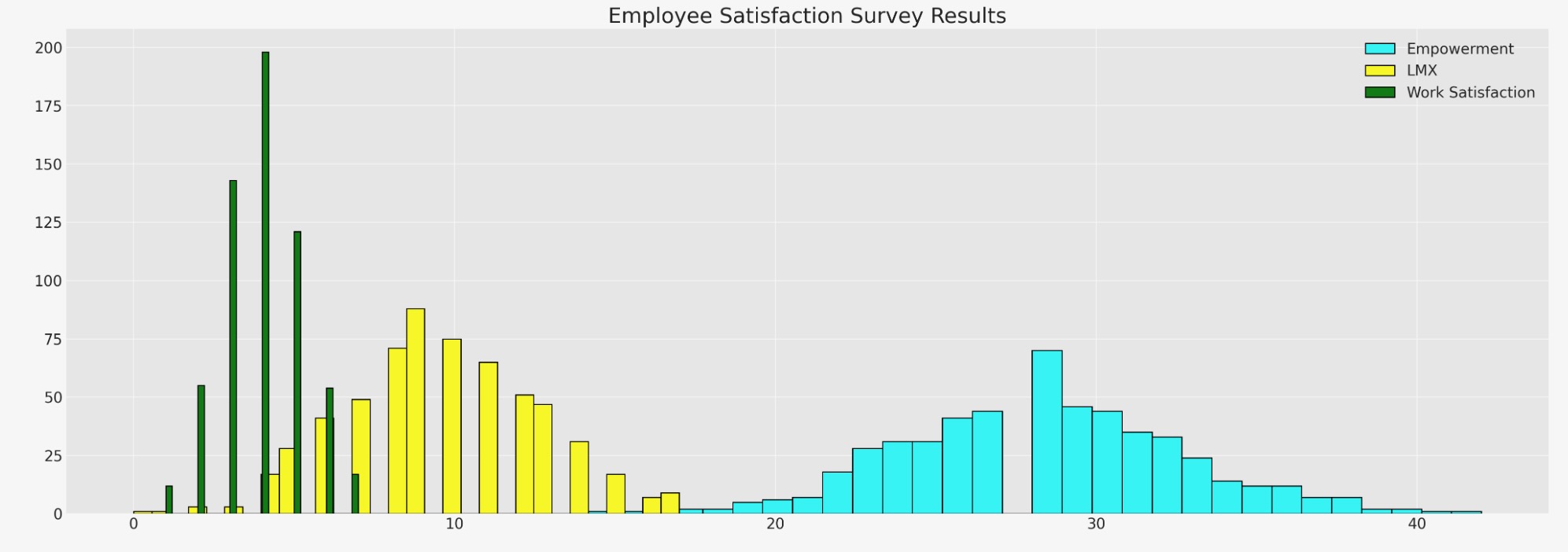
ここで、従業員数のヒストグラムを見ます。変数の関係と、どのように一つのギャップが他の値によって打ち込まれるか、をよりよく理解するために代入を望む、データにギャップがあります。
FIML:最大尤度の完全な情報この欠測データを取り扱う方法は、代入法ではありません。多重正規分布のパラメータを予測するために最大尤度予測を使います。それは、私たちの観測データを生成する最も良い方法です。源データセット内に欠測データを持つ事実を反映したまっすぐなMLEアプローチより少し巧妙です。しかし、基本的に、同じ考えに基づいてます。私たちは最もよく観測データに適合するように、私たちの多重正規分布のパラメータを最適化します。
手続きは、データをそれらを欠測のパターンに分離し、私たちが最大化したい最高の対数尤度に寄与するものとして、各分離を扱うことによって ことによって働きます。私たちは、それらの寄与を多重正規分布への適合を予測するために結合します。
data = df_employee[["worksat", "empower", "lmx"]]
def split_data_by_missing_pattern(data):
# We want to extract our the pattern of missing-ness in our dataset
# and save each sub-set of our data in a structure that can be used to feed into a log-likelihood function
grouped_patterns = []
patterns = data.notnull().drop_duplicates().values
# A pattern is whether the values in each column e.g. [True, True, True] or [True, True, False]
observed = data.notnull()
for p in range(len(patterns)):
temp = observed[
(observed["worksat"] == patterns[p][0])
& (observed["empower"] == patterns[p][1])
& (observed["lmx"] == patterns[p][2])
]
grouped_patterns.append([patterns[p], temp.index, data.iloc[temp.index].dropna(axis=1)])
return grouped_patterns
def reconstitute_params(params_vector, n_vars):
# Convenience numpy function to construct mirrored COV matrix
# From flattened params_vector
mus = params_vector[0:n_vars]
cov_flat = params_vector[n_vars:]
indices = np.tril_indices(n_vars)
cov = np.empty((n_vars, n_vars))
for i, j, c in zip(indices[0], indices[1], cov_flat):
cov[i, j] = c
cov[j, i] = c
cov = cov + 1e-25
return mus, cov
def optimise_ll(flat_params, n_vars, grouped_patterns):
mus, cov = reconstitute_params(flat_params, n_vars)
# Check if COV is positive definite
if (np.linalg.eigvalsh(cov) < 0).any():
return 1e100
objval = 0.0
for obs_pattern, _, obs_data in grouped_patterns:
# This is the key (tricky) step because we're selecting the variables which pattern
# the full information set within each pattern of "missing-ness"
# e.g. when the observed pattern is [True, True, False] we want the first two variables
# of the mus vector and we want only the covariance relations between the relevant variables from the cov
# in the iteration.
obs_mus = mus[obs_pattern]
obs_cov = cov[obs_pattern][:, obs_pattern]
ll = np.sum(multivariate_normal(obs_mus, obs_cov).logpdf(obs_data))
objval = ll + objval
return -objval
def estimate(data):
n_vars = data.shape[1]
# Initialise
mus0 = np.zeros(n_vars)
cov0 = np.eye(n_vars)
# Flatten params for optimiser
params0 = np.append(mus0, cov0[np.tril_indices(n_vars)])
# Process Data
grouped_patterns = split_data_by_missing_pattern(data)
# Run the Optimiser.
try:
result = scipy.optimize.minimize(
optimise_ll, params0, args=(n_vars, grouped_patterns), method="Powell"
)
except Exception as e:
raise e
mean, cov = reconstitute_params(result.x, n_vars)
return mean, cov
fiml_mus, fiml_cov = estimate(data)
print("Full information Maximum Likelihood Estimate Mu:")
display(pd.DataFrame(fiml_mus, index=data.columns).T)
print("Full information Maximum Likelihood Estimate COV:")
pd.DataFrame(fiml_cov, columns=data.columns, index=data.columns)Full information Maximum Likelihood Estimate Mu:
| worksat | empower | lmx | |
|---|---|---|---|
| 0 | 3.983351 | 28.595211 | 9.624485 |
Full information Maximum Likelihood Estimate COV:
| worksat | empower | lmx | |
|---|---|---|---|
| worksat | 1.568676 | 1.599817 | 1.547433 |
| empower | 1.599817 | 19.138522 | 5.428954 |
| lmx | 1.547433 | 5.428954 | 8.934030 |
提案分布からのサンプリング
私たちは関心のある他の特徴を予測するために提案分布からサンプルし、観測データに逆らってテストできます。
mle_fit = multivariate_normal(fiml_mus, fiml_cov)
mle_sample = mle_fit.rvs(10000)
mle_sample = pd.DataFrame(mle_sample, columns=["worksat", "empower", "lmx"])
mle_sample.head()| worksat | empower | lmx | |
|---|---|---|---|
| 0 | 4.463236 | 29.007710 | 8.673368 |
| 1 | 4.571793 | 31.950366 | 7.298634 |
| 2 | 2.260706 | 29.139802 | 5.037035 |
| 3 | 3.235741 | 33.336789 | 12.926463 |
| 4 | 3.474920 | 29.081055 | 10.118566 |
これは、観測データに逆らって提案分布と比較することができます。
fig, ax = plt.subplots(figsize=(20, 7))
ax.hist(
mle_sample["empower"],
bins=30,
ec="black",
color="cyan",
alpha=0.2,
label="Inferred Empowerment",
)
ax.hist(mle_sample["lmx"], bins=30, ec="black", color="yellow", alpha=0.2, label="Inferred LMX")
ax.hist(
mle_sample["worksat"],
bins=30,
ec="black",
color="green",
alpha=0.2,
label="Inferred Work Satisfaction",
)
ax.hist(data["empower"], bins=30, ec="black", color="cyan", label="Observed Empowerment")
ax.hist(data["lmx"], bins=30, ec="black", color="yellow", label="Observed LMX")
ax.hist(data["worksat"], bins=30, ec="black", color="green", label="Observed Work Satisfaction")
ax.set_title("Inferred from MLE fit: Employee Satisfaction Survey Results", fontsize=20)
ax.legend()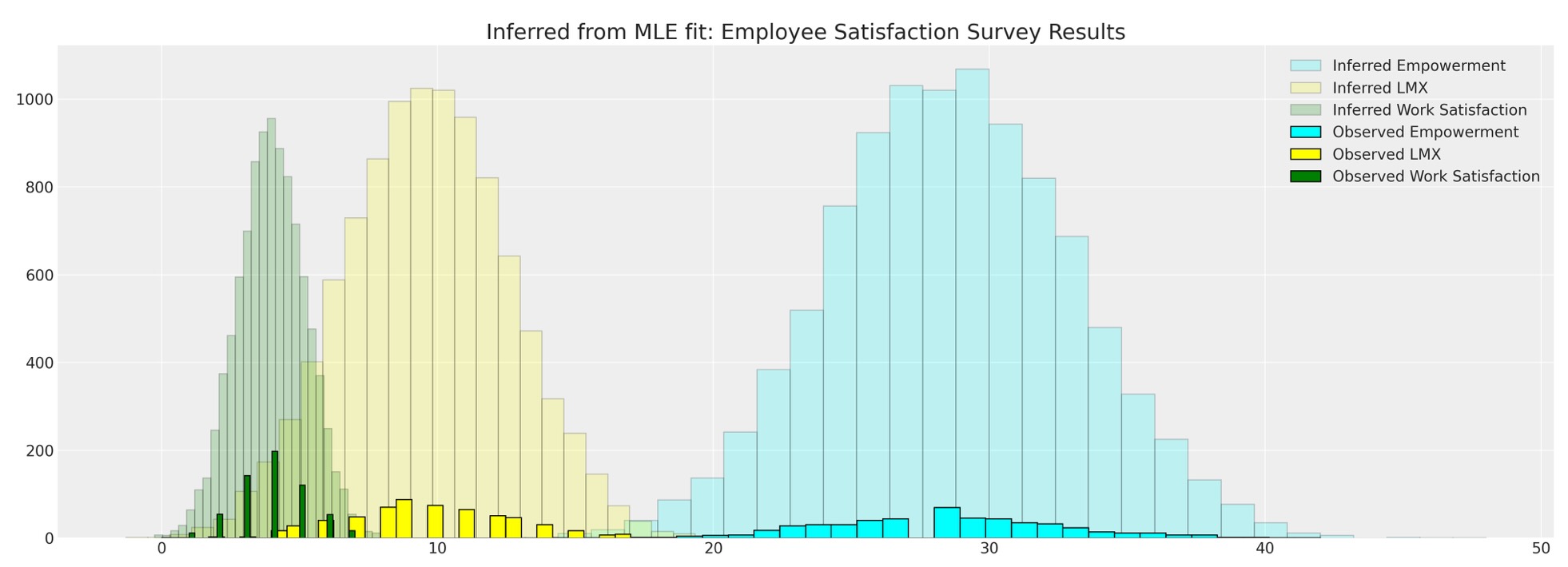
代入メトリックスデータ間の相関
私たちは、サンプルから関心のその他の特徴も計算することができます。例えば、私たちは、当該の変数間の相関について知りたくなるかもしれません。
pd.DataFrame(mle_sample.corr(), columns=data.columns, index=data.columns)| worksat | empower | lmx | |
|---|---|---|---|
| worksat | 1.000000 | 0.294727 | 0.415648 |
| empower | 0.294727 | 1.000000 | 0.411302 |
| lmx | 0.415648 | 0.411302 | 1.000000 |
ブートストラップ精度分析
私たちは、結束の異なる仕様下で、ブートストラップサンプルに対して予測したパラメータを検証することを求めて構いません。
data_200 = df_employee[["worksat", "empower", "lmx"]].dropna().sample(200)
data_200.reset_index(inplace=True, drop=True)
sensitivity = {}
n_missing = np.linspace(30, 100, 5) # Change or alter the range as desired
bootstrap_iterations = 100 # change to large number running a real analysis in this case
for n in n_missing:
sensitivity[int(n)] = {}
sensitivity[int(n)]["mus"] = []
sensitivity[int(n)]["cov"] = []
for i in range(bootstrap_iterations):
temp = data_200.copy()
for m in range(int(n)):
i = random.choice(range(200))
j = random.choice(range(3))
temp.iloc[i, j] = np.nan
try:
fiml_mus, fiml_cov = estimate(temp)
sensitivity[int(n)]["mus"].append(fiml_mus)
sensitivity[int(n)]["cov"].append(fiml_cov)
except Exception as e:
nextここで、いろいろな欠測データ間に対して最大尤度パラメータ予測を図示します。このアプローチは任意の代入法へ適用できます。
fig, axs = plt.subplots(1, 3, figsize=(20, 7))
for n in sensitivity.keys():
temp = pd.DataFrame(sensitivity[n]["mus"], columns=["worksat", "empower", "lmx"])
for col, ax in zip(temp.columns, axs):
ax.hist(
temp[col], alpha=0.1, ec="black", label=f"Missing: {np.round(n/200, 2)}, Mean: {col}"
)
ax.legend()
ax.set_title(f"Bootstrap Distribution for Mean:\n{col}")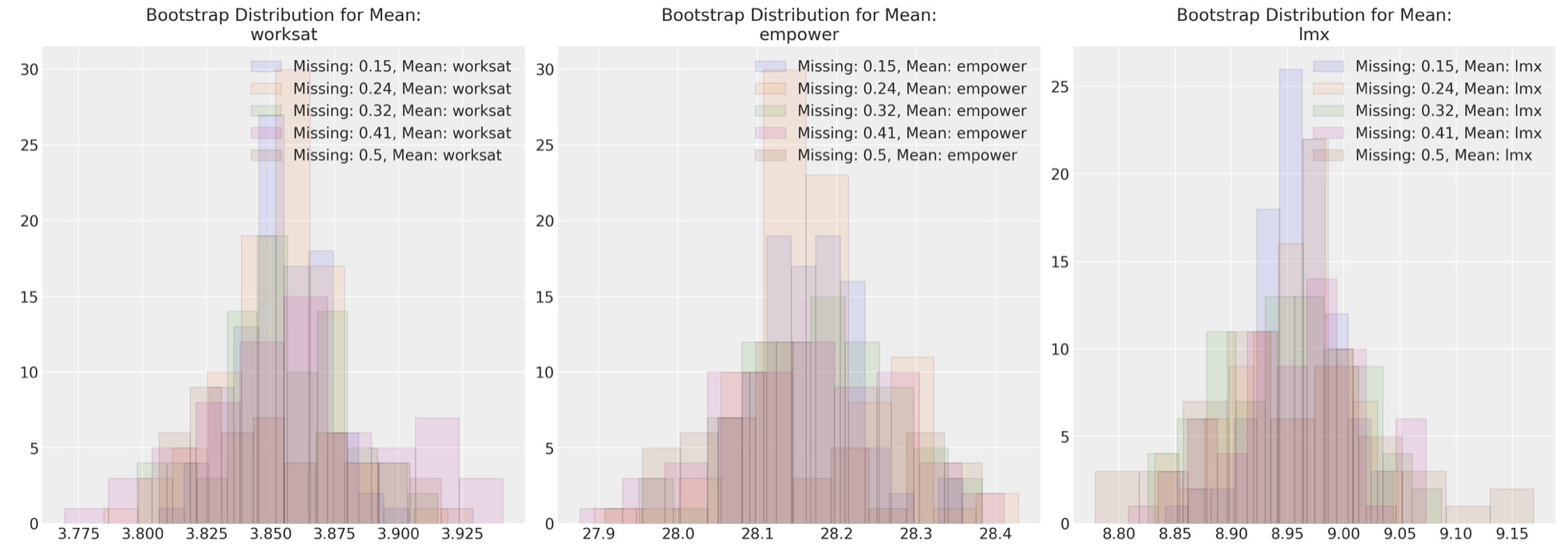
これらの図は、私たちの多重正規分布のパラメータ予測のやり方が、如何に欠測データの度合いを修正するの全く頑丈であるかを示します。代替的な欠測データの管理方法の下で、同様のシミュレーション演習を試みるのに役立つ演習です。
ベイジアン代入法
次に、同じ問題にベイズの方法を適用します。しかしここで私たちは、事後予測分布を使って、欠測データを直接代入するのを見ます。代入のベイジアンアプローチは、私たちが上で見たものより異なる趣向です。私たちは、データ生成分布のパラメータを単に学習するのではなく、ベイズの過程は、MCMCサンプリング過程を通じて、特別な欠測エントリーに欠測データを直接代入しいます。
import pytensor.tensor as pt
with pm.Model() as model:
# Priors
mus = pm.Normal("mus", 0, 1, size=3)
cov_flat_prior, _, _ = pm.LKJCholeskyCov("cov", n=3, eta=1.0, sd_dist=pm.Exponential.dist(1))
# Create a vector of flat variables for the unobserved components of the MvNormal
x_unobs = pm.Uniform("x_unobs", 0, 100, shape=(np.isnan(data.values).sum(),))
# Create the symbolic value of x, combining observed data and unobserved variables
x = pt.as_tensor(data.values)
x = pm.Deterministic("x", pt.set_subtensor(x[np.isnan(data.values)], x_unobs))
# Add a Potential with the logp of the variable conditioned on `x`
pm.Potential("x_logp", pm.logp(rv=pm.MvNormal.dist(mus, chol=cov_flat_prior), value=x))
idata = pm.sample_prior_predictive()
idata = pm.sample()
idata.extend(pm.sample(random_seed=120))
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
pm.model_to_graphviz(model)

az.plot_posterior(idata, var_names=["mus", "cov"]);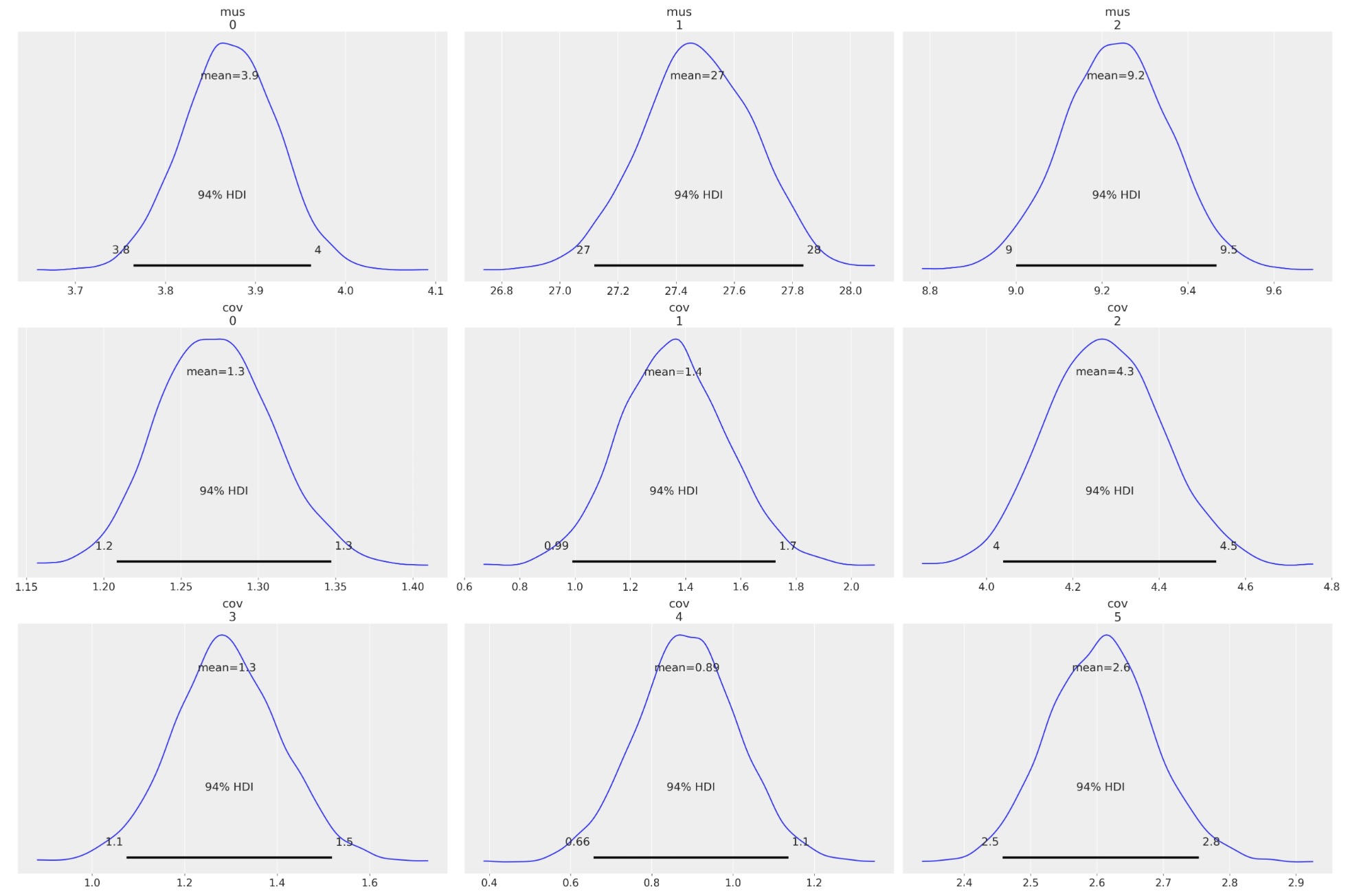
az.summary(idata, var_names=["mus", "cov", "x_unobs"])| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| mus[0] | 3.871 | 0.053 | 3.765 | 3.962 | 0.001 | 0.000 | 5831.0 | 3414.0 | 1.0 |
| mus[1] | 27.474 | 0.195 | 27.118 | 27.837 | 0.003 | 0.002 | 5355.0 | 3347.0 | 1.0 |
| mus[2] | 9.232 | 0.124 | 9.000 | 9.466 | 0.002 | 0.001 | 6012.0 | 3406.0 | 1.0 |
| cov[0] | 1.272 | 0.037 | 1.208 | 1.347 | 0.000 | 0.000 | 5916.0 | 3077.0 | 1.0 |
| cov[1] | 1.356 | 0.195 | 0.990 | 1.725 | 0.003 | 0.002 | 5349.0 | 3024.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| x_unobs[153] | 29.823 | 4.074 | 22.025 | 37.210 | 0.043 | 0.031 | 8853.0 | 3061.0 | 1.0 |
| x_unobs[154] | 2.554 | 1.087 | 0.565 | 4.572 | 0.018 | 0.013 | 3514.0 | 1845.0 | 1.0 |
| x_unobs[155] | 29.979 | 4.063 | 22.747 | 37.834 | 0.044 | 0.031 | 8392.0 | 2674.0 | 1.0 |
| x_unobs[156] | 29.567 | 4.213 | 21.055 | 37.167 | 0.042 | 0.030 | 9832.0 | 2601.0 | 1.0 |
| x_unobs[157] | 27.454 | 3.922 | 20.261 | 35.200 | 0.042 | 0.030 | 8710.0 | 2719.0 | 1.0 |
167 rows × 9 columns
imputed_dims = data.shape
imputed = data.values.flatten()
imputed[np.isnan(imputed)] = az.summary(idata, var_names=["x_unobs"])["mean"].values
imputed = imputed.reshape(imputed_dims[0], imputed_dims[1])
imputed = pd.DataFrame(imputed, columns=[col + "_imputed" for col in data.columns])
imputed.head(10)| worksat_imputed | empower_imputed | lmx_imputed | |
|---|---|---|---|
| 0 | 3.000 | 32.000 | 11.000 |
| 1 | 4.000 | 29.452 | 13.000 |
| 2 | 4.000 | 30.000 | 9.000 |
| 3 | 3.000 | 29.000 | 8.000 |
| 4 | 4.000 | 26.000 | 7.000 |
| 5 | 4.017 | 27.922 | 10.000 |
| 6 | 5.000 | 29.107 | 11.000 |
| 7 | 3.000 | 22.000 | 9.000 |
| 8 | 2.000 | 23.000 | 6.863 |
| 9 | 4.000 | 32.000 | 9.000 |
fig, axs = plt.subplots(1, 3, figsize=(20, 7))
axs = axs.flatten()
for col, col_i, ax in zip(data.columns, imputed.columns, axs):
ax.hist(data[col], color="red", label=col, ec="black", bins=30)
ax.hist(imputed[col_i], color="cyan", alpha=0.3, label=col_i, ec="black", bins=30)
ax.legend()
ax.set_title(f"Imputed Distribution and Observed for {col}")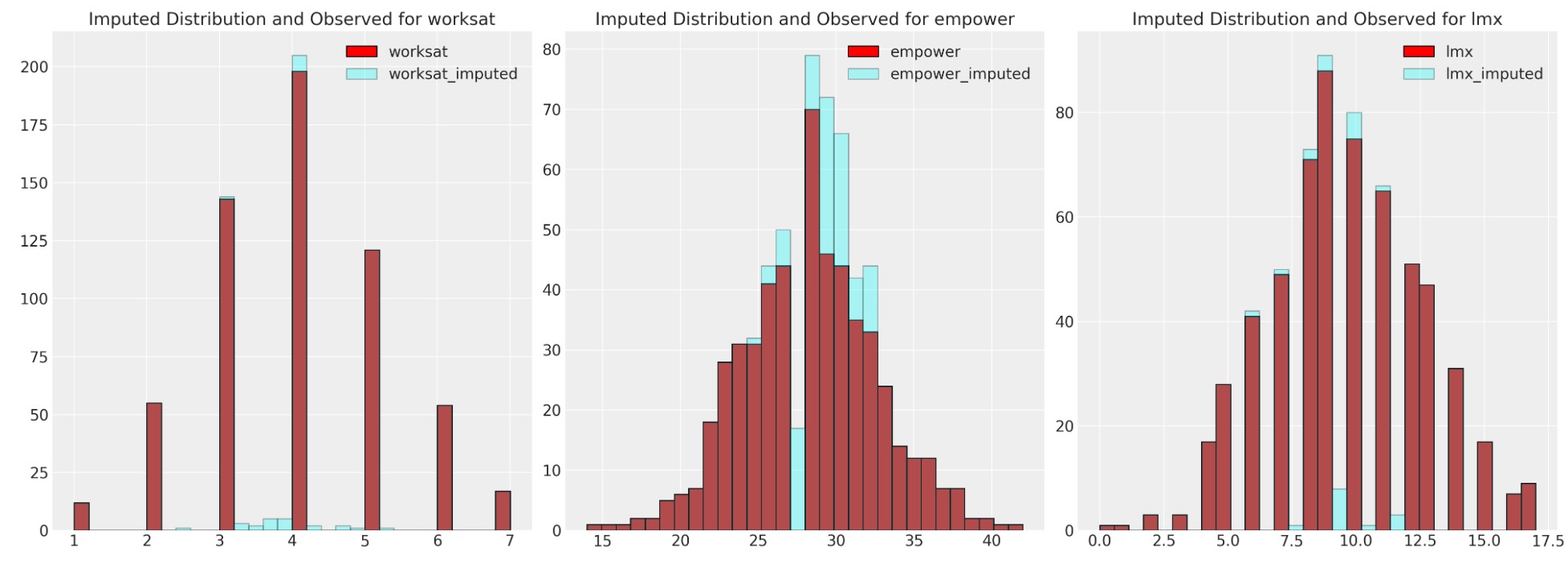
pd.DataFrame(az.summary(idata, var_names=["cov_corr"])["mean"].values.reshape(3, 3))
/Users/tanakayoshinobu/anaconda3/lib/python3.10/site-packages/arviz/stats/diagnostics.py:592: RuntimeWarning: invalid value encountered in double_scalars (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.000 | 0.302 | 0.424 |
| 1 | 0.302 | 1.000 | 0.405 |
| 2 | 0.424 | 0.405 | 1.000 |
これらの結果は、上のFIMLアプローチとして認められています。その結果はエンダーの応用結束データ分析で報告されています。
チェインされた方程式によるベイズ代入
これまでのところ代入のための他変量アプローチを見てきました。それは、私たちのデータセットを同じ分布から出力された集まりとして各変数を取り扱います。しかし、それは、私たちが分析することにに関心を持つ特別に中心的な関係がある場合、しばしば役立つもっと柔軟なアプローチがあります。
従業員のデータセットに着目すると、私たちは、lmx,climate,maleそしてempower間の関係を検査します。そこで私たちが注目するのは何がやりがいになるのかです。私たちの性別の変数maleは、完全に規定され、代入される必要がないことを思い出してください。だから私たちは、連結分布を分解できます。
f(em,lmx,climate,male) =f(emp|lmx,climate,male)・f(lmx|climate,male)・f(climate|male)・f(male)*それは個別の回帰方程式、または、もっと一般的に各自要求される条件モデルの成分モデルに分離できます。
empower = α2 + β3 male + γ4 + β lmx
lmx = α1 + β1 climate + β2 male
climate = α0 + β0 male私たちは、これらの方程式の各自に、保存している代入データセットを順番に代入します。そしてそれを先の次のモデル化の演習に送ります。変数のいくつかが2度現れているため、これはわずかに複雑さを追加します。一つは、中心的な回帰の予測として、もう一つはそれら自身の成分モデルの尤度項として。
PyMC代入
上で見たように、私たちは、特別なサンプリング分布を使って、結束データの値を代入するためにPyMCを使うことができます。チェインした方程式んpケースでは、これは少し巧妙になります。なぜなら一つの方程式の回帰にlmxのためのデータと尤度の観測データの両方を使いたくなるかもしれません。
それはまた、結束データに代入するために使うであろうサンプリング分布を決めるのに、問題になります。私たちはここで、私たちの主要な回帰の予測項に代入するために、代わりに正規サンプリング分布と様式を使う例をお見せします。
data = df_employee[["lmx", "empower", "climate", "male"]]
lmx_mean = data["lmx"].mean()
lmx_min = data["lmx"].min()
lmx_max = data["lmx"].max()
lmx_sd = data["lmx"].std()
cli_mean = data["climate"].mean()
cli_min = data["climate"].min()
cli_max = data["climate"].max()
cli_sd = data["climate"].std()
priors = {
"climate": {"normal": [lmx_mean, lmx_sd, lmx_sd], "uniform": [lmx_min, lmx_max]},
"lmx": {"normal": [cli_mean, cli_sd, cli_sd], "uniform": [cli_min, cli_max]},
}
def make_model(priors, normal_pred_assumption=True):
coords = {
"alpha_dim": ["lmx_imputed", "climate_imputed", "empower_imputed"],
"beta_dim": [
"lmxB_male",
"lmxB_climate",
"climateB_male",
"empB_male",
"empB_climate",
"empB_lmx",
],
}
with pm.Model(coords=coords) as model:
# Priors
beta = pm.Normal("beta", 0, 1, size=6, dims="beta_dim")
alpha = pm.Normal("alphas", 10, 5, size=3, dims="alpha_dim")
sigma = pm.HalfNormal("sigmas", 5, size=3, dims="alpha_dim")
if normal_pred_assumption:
mu_climate = pm.Normal(
"mu_climate", priors["climate"]["normal"][0], priors["climate"]["normal"][1]
)
sigma_climate = pm.HalfNormal("sigma_climate", priors["climate"]["normal"][2])
climate_pred = pm.Normal(
"climate_pred", mu_climate, sigma_climate, observed=data["climate"].values
)
else:
climate_pred = pm.Uniform("climate_pred", 0, 40, observed=data["climate"].values)
if normal_pred_assumption:
mu_lmx = pm.Normal("mu_lmx", priors["lmx"]["normal"][0], priors["lmx"]["normal"][1])
sigma_lmx = pm.HalfNormal("sigma_lmx", priors["lmx"]["normal"][2])
lmx_pred = pm.Normal("lmx_pred", mu_lmx, sigma_lmx, observed=data["lmx"].values)
else:
lmx_pred = pm.Uniform("lmx_pred", 0, 40, observed=data["lmx"].values)
# Likelihood(s)
lmx_imputed = pm.Normal(
"lmx_imputed",
alpha[0] + beta[0] * data["male"] + beta[1] * climate_pred,
sigma[0],
observed=data["lmx"].values,
)
climate_imputed = pm.Normal(
"climate_imputed",
alpha[1] + beta[2] * data["male"],
sigma[1],
observed=data["climate"].values,
)
empower_imputed = pm.Normal(
"emp_imputed",
alpha[2] + beta[3] * data["male"] + beta[4] * climate_pred + beta[5] * lmx_pred,
sigma[2],
observed=data["empower"].values,
)
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(random_seed=120))
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
return idata, model
idata_uniform, model_uniform = make_model(priors, normal_pred_assumption=False)
idata_normal, model_normal = make_model(priors, normal_pred_assumption=True)
pm.model_to_graphviz(model_uniform)
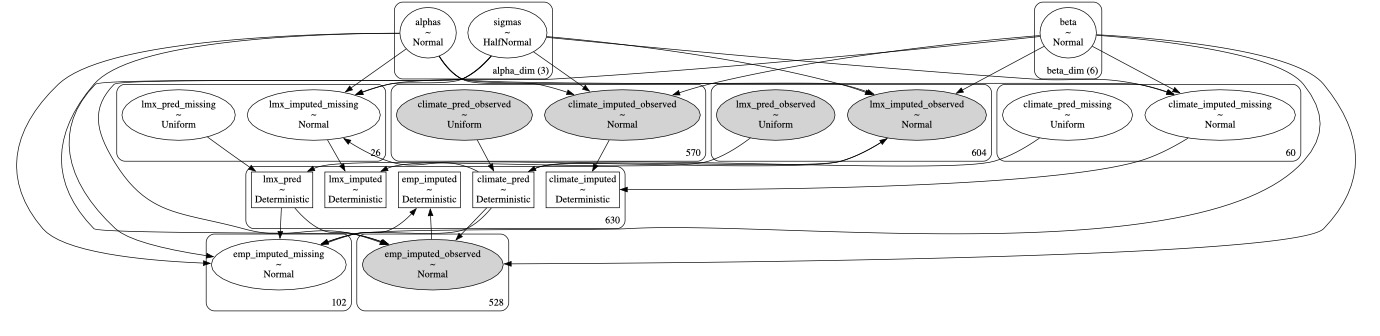
idata_normalarviz.InferenceData
モデル適合
次に私たちの回帰モデルへのパラメータの適合を調査します。そして、どのようにそれらが代入スキームの事前仕様に依存するか観察します。
az.summary(idata_normal, var_names=["alphas", "beta", "sigmas"], stat_focus="median")| median | mad | eti_3% | eti_97% | mcse_median | ess_median | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|
| alphas[lmx_imputed] | 9.059 | 0.464 | 7.818 | 10.357 | 0.016 | 3674.002 | 3059.0 | 1.0 |
| alphas[climate_imputed] | 19.775 | 0.155 | 19.337 | 20.200 | 0.005 | 4299.703 | 2929.0 | 1.0 |
| alphas[empower_imputed] | 17.931 | 0.651 | 16.018 | 19.814 | 0.019 | 3540.997 | 2918.0 | 1.0 |
| beta[lmxB_male] | 0.441 | 0.158 | 0.003 | 0.862 | 0.004 | 6520.515 | 2738.0 | 1.0 |
| beta[lmxB_climate] | 0.017 | 0.023 | -0.045 | 0.078 | 0.001 | 3648.868 | 3021.0 | 1.0 |
| beta[climateB_male] | 0.701 | 0.208 | 0.094 | 1.275 | 0.007 | 4336.455 | 3304.0 | 1.0 |
| beta[empB_male] | 1.646 | 0.212 | 1.053 | 2.234 | 0.005 | 5651.396 | 3037.0 | 1.0 |
| beta[empB_climate] | 0.203 | 0.028 | 0.125 | 0.281 | 0.001 | 3930.174 | 3294.0 | 1.0 |
| beta[empB_lmx] | 0.599 | 0.040 | 0.484 | 0.712 | 0.001 | 3399.791 | 3300.0 | 1.0 |
| sigmas[lmx_imputed] | 3.021 | 0.060 | 2.867 | 3.194 | 0.001 | 6148.600 | 3037.0 | 1.0 |
| sigmas[climate_imputed] | 4.015 | 0.080 | 3.806 | 4.254 | 0.002 | 6123.862 | 3448.0 | 1.0 |
| sigmas[empower_imputed] | 3.816 | 0.081 | 3.591 | 4.051 | 0.002 | 4552.885 | 2953.0 | 1.0 |
az.summary(idata_uniform, var_names=["alphas", "beta", "sigmas"], stat_focus="median")| median | mad | eti_3% | eti_97% | mcse_median | ess_median | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|
| alphas[lmx_imputed] | 9.165 | 0.405 | 8.075 | 10.221 | 0.010 | 3712.879 | 3193.0 | 1.0 |
| alphas[climate_imputed] | 19.777 | 0.157 | 19.337 | 20.229 | 0.003 | 5584.873 | 3324.0 | 1.0 |
| alphas[empower_imputed] | 18.829 | 0.629 | 17.059 | 20.685 | 0.021 | 2822.068 | 2760.0 | 1.0 |
| beta[lmxB_male] | 0.442 | 0.163 | -0.016 | 0.905 | 0.004 | 7222.639 | 2857.0 | 1.0 |
| beta[lmxB_climate] | 0.012 | 0.019 | -0.041 | 0.066 | 0.001 | 3629.087 | 2869.0 | 1.0 |
| beta[climateB_male] | 0.696 | 0.218 | 0.081 | 1.316 | 0.006 | 5271.275 | 2932.0 | 1.0 |
| beta[empB_male] | 1.635 | 0.214 | 1.031 | 2.229 | 0.005 | 5579.792 | 3541.0 | 1.0 |
| beta[empB_climate] | 0.206 | 0.024 | 0.135 | 0.273 | 0.001 | 3117.189 | 3655.0 | 1.0 |
| beta[empB_lmx] | 0.487 | 0.044 | 0.368 | 0.615 | 0.001 | 2614.049 | 2661.0 | 1.0 |
| sigmas[lmx_imputed] | 3.023 | 0.055 | 2.872 | 3.189 | 0.001 | 7020.907 | 2916.0 | 1.0 |
| sigmas[climate_imputed] | 4.019 | 0.082 | 3.796 | 4.270 | 0.003 | 5017.521 | 2733.0 | 1.0 |
| sigmas[empower_imputed] | 3.782 | 0.082 | 3.561 | 4.020 | 0.003 | 4269.148 | 3075.0 | 1.0 |
どのようにサンプリング分布の選択が、私たちの二つのモデルを横切ってベータ係数の異なるパラメータの予測を誘導するか見ることができます。二つの代入はパラメータのレベルで広い範囲を認めます。しかし、それらが暗黙にわかりやすく異なります。
az.plot_forest(
[idata_normal, idata_uniform],
var_names=["beta"],
kind="ridgeplot",
model_names=["Gaussian Sampling Distribution", "Uniform Sampling Distribution"],
figsize=(10, 8),
)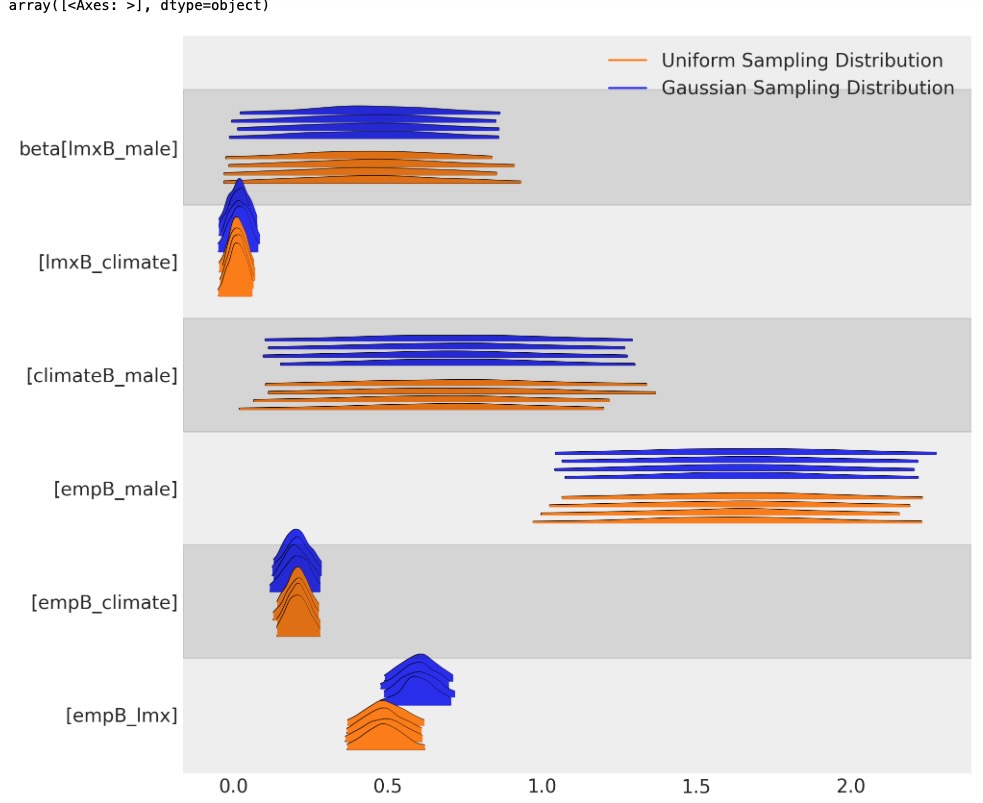
この相違は、事後予測分布のダウンストリームの影響です。私たちはここで、予測期間のサンプリング分布が、私たちの主要な回帰方程式の事後予測適合に影響するか見ることができます。
事後予測分布
az.plot_ppc(idata_uniform)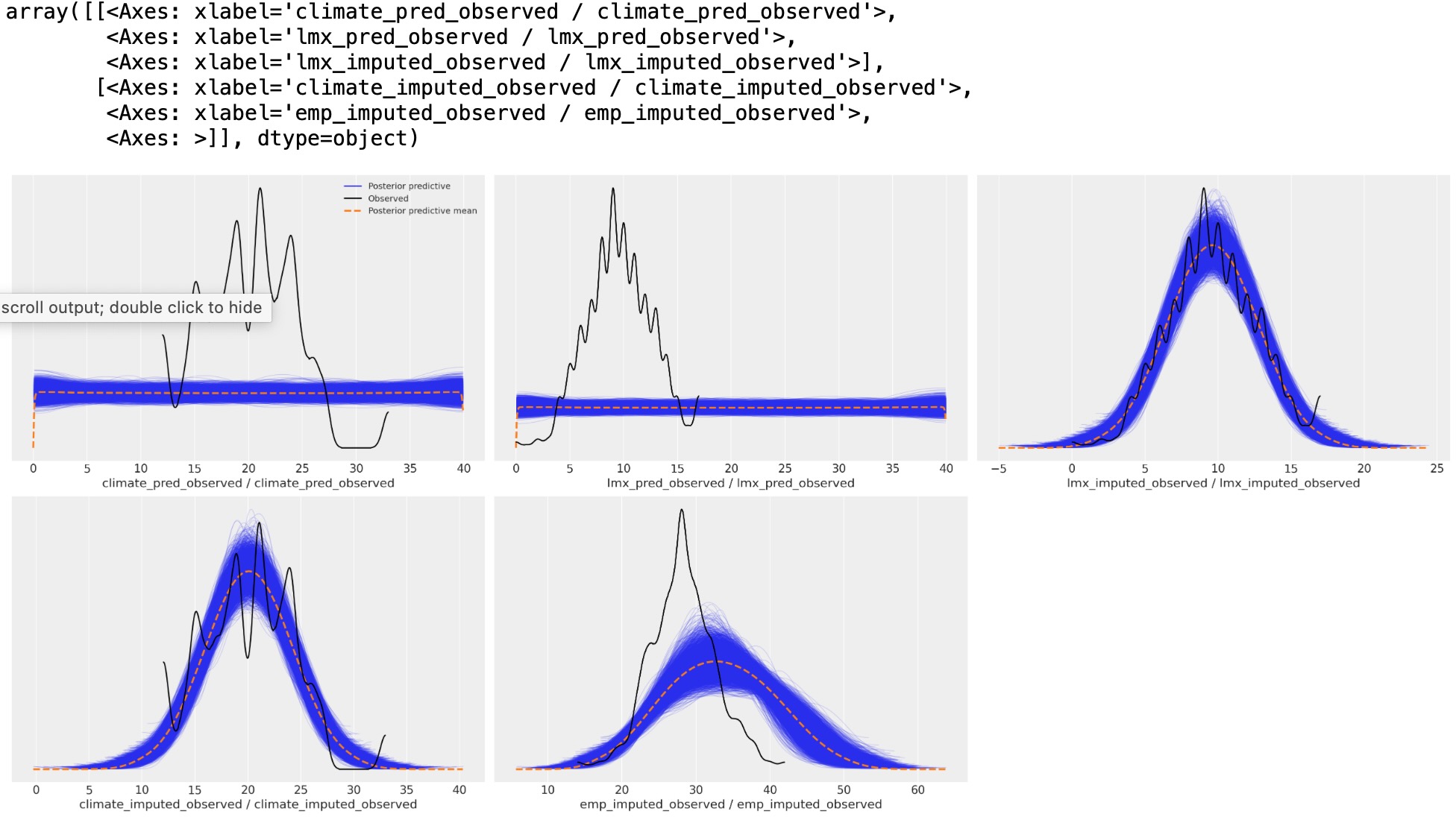
az.plot_ppc(idata_normal)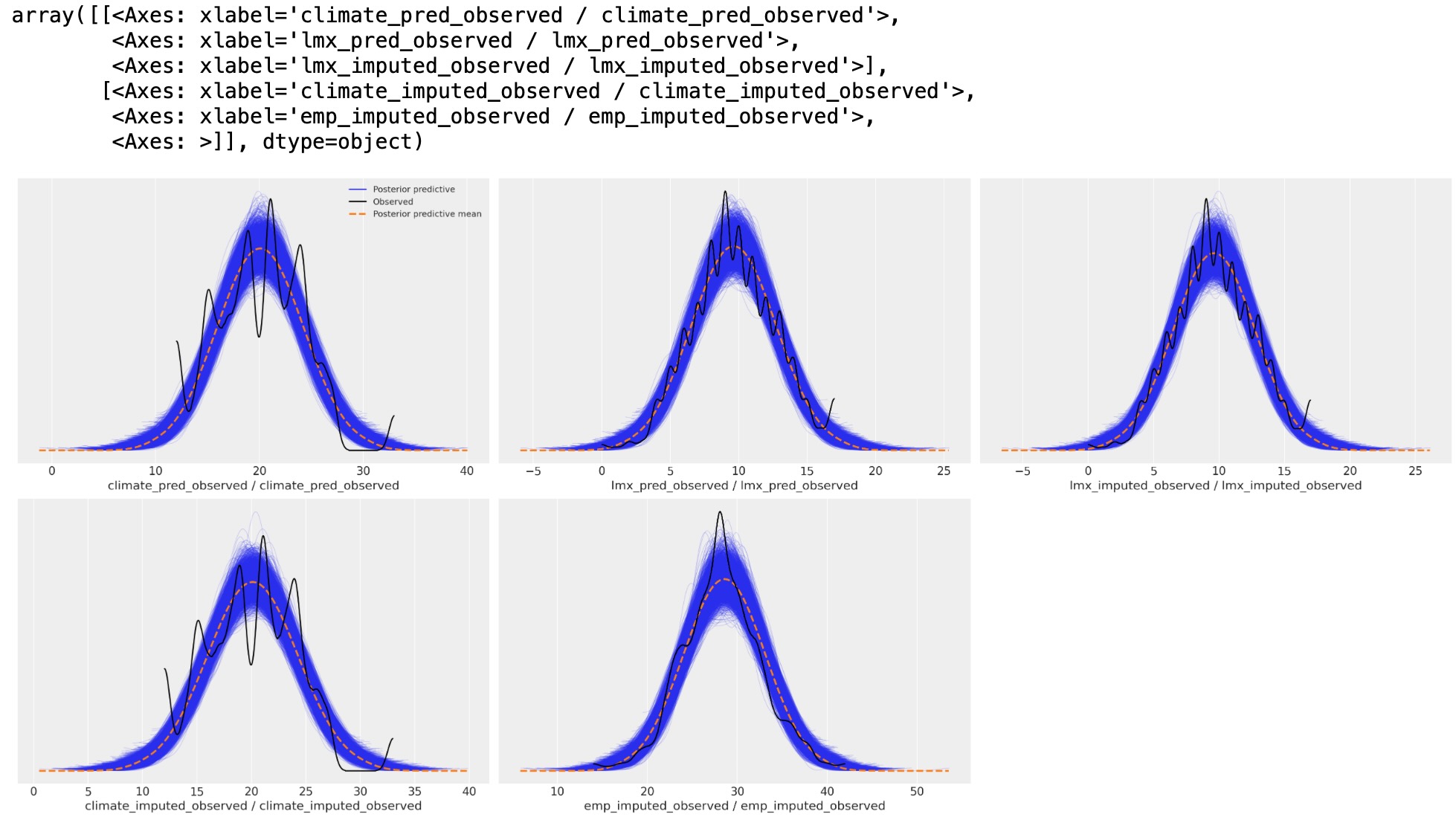
事後予測分布の過程
上では私たちは、単一のPyMCモデルの文脈で尤度項の数を見積もりました。これらの尤度は、私たちのempowerに対する主要な回帰方程式の予測として使われる変数の欠損項の代入値を決定するハイパーパラメータを制限します。しかし、手動でもっとシーケンシャルな代入も実行することができます。そこでは、付随した回帰方程式を分離してモデルにし、順番に各変数への代入値を抽出し、その後、主要な回帰方程式への代入値で簡単な回帰を実行します。
私たちは、ここで、各回帰方程式と観測データの引数のために代入値を抽出する方法を示します。
def get_imputed(idata, data):
imputed_data = data.copy()
imputed_climate = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"climate_imputed"
].mean(axis=1)
mask = imputed_data["climate"].isnull()
imputed_data.loc[mask, "climate"] = imputed_climate.values[imputed_data[mask].index]
imputed_lmx = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"lmx_imputed"
].mean(axis=1)
mask = imputed_data["lmx"].isnull()
imputed_data.loc[mask, "lmx"] = imputed_lmx.values[imputed_data[mask].index]
imputed_emp = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"emp_imputed"
].mean(axis=1)
mask = imputed_data["empower"].isnull()
imputed_data.loc[mask, "empower"] = imputed_emp.values[imputed_data[mask].index]
assert imputed_data.isnull().sum().to_list() == [0, 0, 0, 0]
imputed_data.columns = ["imputed_" + col for col in imputed_data.columns]
return imputed_data
imputed_data_uniform = get_imputed(idata_uniform, data)
imputed_data_normal = get_imputed(idata_normal, data)
imputed_data_normal.head(5)| imputed_lmx | imputed_empower | imputed_climate | imputed_male | |
|---|---|---|---|---|
| 0 | 11.0 | 32.000000 | 18.0 | 1 |
| 1 | 13.0 | 29.447382 | 18.0 | 1 |
| 2 | 9.0 | 30.000000 | 18.0 | 1 |
| 3 | 8.0 | 29.000000 | 18.0 | 1 |
| 4 | 7.0 | 26.000000 | 18.0 | 0 |
私たちは、ここで各欠損セルのための予測値を代入するために、平均値を使います。しかし、事後予測分布の多くの最もらしい値を使ってある種、敏感な分析を実行します。
代入データセットの図示
ここで、私たちは、どのように異なるサンプリング分布が代入のパターンに影響を与えるか、示すためにそれらの観測データに逆らった代入値を図示します。
joined_uniform = pd.concat([imputed_data_uniform, data], axis=1)
joined_normal = pd.concat([imputed_data_normal, data], axis=1)
for col in ["lmx", "empower", "climate"]:
joined_uniform[col + "_missing"] = np.where(joined_uniform[col].isnull(), 1, 0)
joined_normal[col + "_missing"] = np.where(joined_normal[col].isnull(), 1, 0)
def rand_jitter(arr):
stdev = 0.01 * (max(arr) - min(arr))
return arr + np.random.randn(len(arr)) * stdev
fig, axs = plt.subplots(1, 3, figsize=(20, 8))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
ax2 = axs[2]
## Derived from MV norm fit.
z = multivariate_normal(
[lmx_mean, joined_uniform["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]
).pdf(joined_uniform[["imputed_lmx", "imputed_empower"]])
ax.scatter(
rand_jitter(joined_uniform["imputed_lmx"]),
rand_jitter(joined_uniform["imputed_empower"]),
c=joined_uniform["empower_missing"],
cmap=cm.winter,
ec="black",
s=50,
)
ax.set_title("Relationship between LMX and Empowerment \n after Uniform Imputation", fontsize=20)
ax.tricontour(joined_uniform["imputed_lmx"], joined_uniform["imputed_empower"], z)
ax.set_xlabel("Leader-Member-Exchange")
ax.set_ylabel("Empowerment")
custom_lines = [
Line2D([0], [0], color=cm.winter(0.0), lw=4),
Line2D([0], [0], color=cm.winter(0.9), lw=4),
]
ax.legend(custom_lines, ["Observed", "Missing - Imputed Empowerment Values"])
z = multivariate_normal(
[lmx_mean, joined_normal["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]
).pdf(joined_normal[["imputed_lmx", "imputed_empower"]])
ax2.scatter(
rand_jitter(joined_normal["imputed_lmx"]),
rand_jitter(joined_normal["imputed_empower"]),
c=joined_normal["empower_missing"],
cmap=cm.autumn,
ec="black",
s=50,
)
ax2.set_title("Relationship between LMX and Empowerment \n after Gaussian Imputation", fontsize=20)
ax2.tricontour(joined_normal["imputed_lmx"], joined_normal["imputed_empower"], z)
ax2.set_xlabel("Leader-Member-Exchange")
ax2.set_ylabel("Empowerment")
custom_lines = [
Line2D([0], [0], color=cm.autumn(0.0), lw=4),
Line2D([0], [0], color=cm.autumn(0.9), lw=4),
]
ax2.legend(custom_lines, ["Observed", "Missing - Imputed Empowerment Values"])
ax1.hist(
joined_normal["imputed_empower"],
label="Gaussian Imputed Empowerment",
bins=30,
color="slateblue",
ec="black",
)
ax1.hist(
joined_uniform["imputed_empower"],
label="Uniform Imputed Empowerment",
bins=30,
color="cyan",
ec="black",
)
ax1.hist(
joined_normal["empower"], label="Observed Empowerment", bins=30, color="magenta", ec="black"
)
ax1.legend()
ax1.set_title("Imputed & Observed Empowerment", fontsize=20);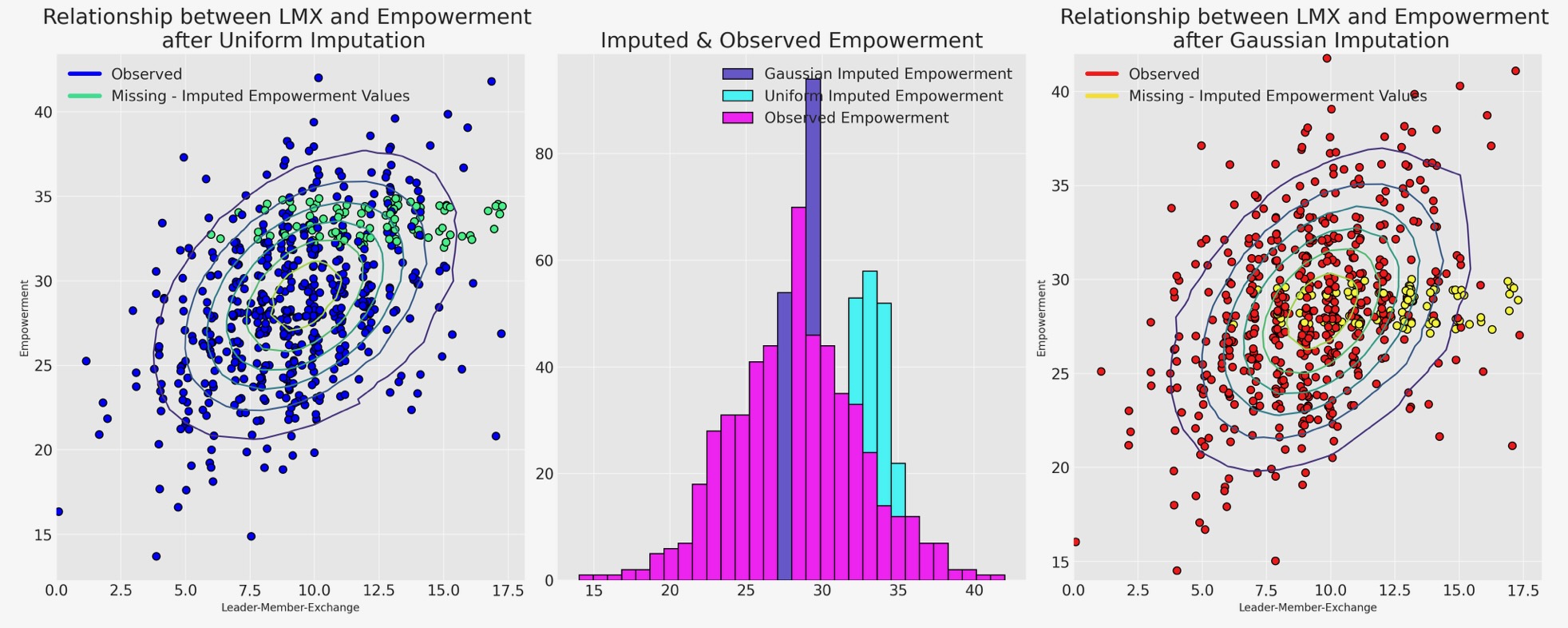
サンプリング分布の最高の選択は、最もらしい代入を相違して導きます。処理するモデルの選択は、私たちのデータの欠測の理由を管理する方法(決定する)の仮定によって左右されます。
階層構造とデータ代入
私たちの雇用者のデータセットは、私たちが今まで試験してきたものよりもっと粒状です。特にそれらが100または雇用者の集まりで作るそうしたチームがあります。私たちは、その満足さの傾向の度合いはどれくらいか、または不完全な調査のスコアはローカルチーム環境のせいか、これは、欠測データのパターンの因子になるか、と思います。私たちは、報告されたチームによる充実度のスコアを試験し、それら報告されたlmxのスコアによって各チーム内の予測された回帰線を図示します。
heatmap = df_employee.pivot("employee", "team", "empower").dropna(how="all")
heatmap = pd.concat(
[heatmap[~heatmap[col].isnull()][col].reset_index(drop=True) for col in heatmap.columns], axis=1
)
with pd.option_context("format.precision", 2):
display(heatmap.style.background_gradient(cmap="Blues"));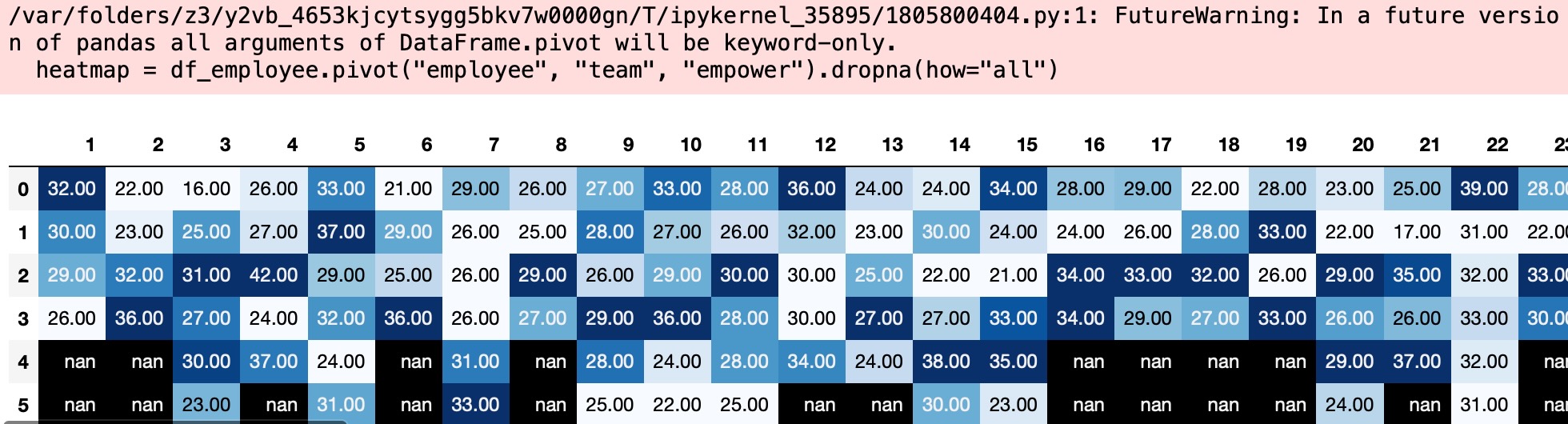
fits = [] x = np.linspace(0, 20, 100) fig, ax = plt.subplots(figsize=(20, 7)) for team in df_employee["team"].unique(): temp = df_employee[df_employee["team"] == team][["lmx", "empower"]].dropna() fit = np.polyfit(temp["lmx"], temp["empower"], 1) y = fit[0] * x + fit[1] fits.append(fit) ax.plot(x, y, alpha=0.6) ax.scatter(rand_jitter(temp["lmx"]), rand_jitter(temp["empower"]), color="black", ec="white") ax.set_title("Simple Regression fits by Team \n Empower ~ LMX", fontsize=20) ax.set_xlabel("Leader-Member-Exchange (LMX)") ax.set_ylabel("Empowerment") ax.set_ylim(0, 45);
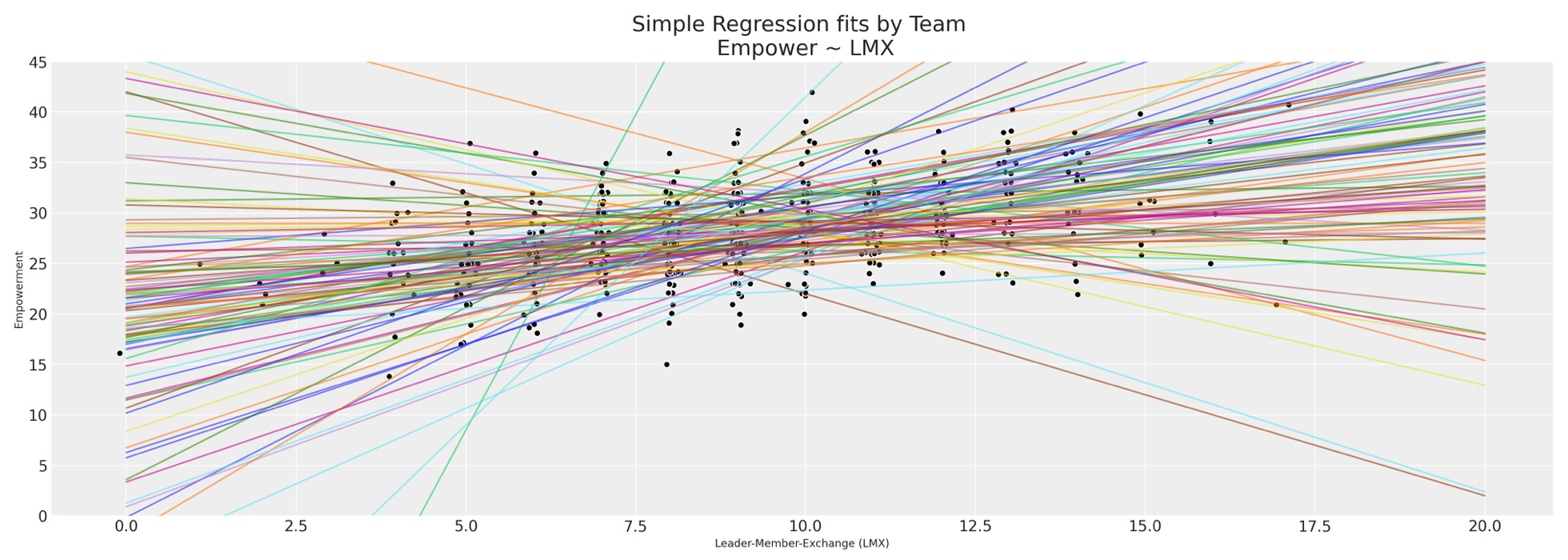
異なるチームを横断して、しかし各チームの限定した観測値を見ているので、充実度と労働環境の間に不均一な関係がある、少なくとも提案された回帰線には十分な広がりがあります。これは、階層ベイズモデルの完全な使用ケースです。
team_idx, teams = pd.factorize(df_employee["team"], sort=True)
employee_idx, _ = pd.factorize(df_employee["employee"], sort=True)
coords = {"team": teams, "employee": np.arange(len(df_employee))}
with pm.Model(coords=coords) as hierarchical_model:
# Priors
company_beta_lmx = pm.Normal("company_beta_lmx", 0, 1)
company_beta_male = pm.Normal("company_beta_male", 0, 1)
company_alpha = pm.Normal("company_alpha", 20, 2)
team_alpha = pm.Normal("team_alpha", 0, 1, dims="team")
team_beta_lmx = pm.Normal("team_beta_lmx", 0, 1, dims="team")
sigma = pm.HalfNormal("sigma", 4, dims="employee")
# Imputed Predictors
mu_lmx = pm.Normal("mu_lmx", 10, 5)
sigma_lmx = pm.HalfNormal("sigma_lmx", 5)
lmx_pred = pm.Normal("lmx_pred", mu_lmx, sigma_lmx, observed=df_employee["lmx"].values)
# Combining Levels
alpha_global = pm.Deterministic("alpha_global", company_alpha + team_alpha[team_idx])
beta_global_lmx = pm.Deterministic(
"beta_global_lmx", company_beta_lmx + team_beta_lmx[team_idx]
)
beta_global_male = pm.Deterministic("beta_global_male", company_beta_male)
# Likelihood
mu = pm.Deterministic(
"mu",
alpha_global + beta_global_lmx * lmx_pred + beta_global_male * df_employee["male"].values,
)
empower_imputed = pm.Normal(
"emp_imputed",
mu,
sigma,
observed=df_employee["empower"].values,
)
idata_hierarchical = pm.sample_prior_predictive()
# idata_hierarchical.extend(pm.sample(random_seed=1200, target_accept=0.99))
idata_hierarchical.extend(
sample_blackjax_nuts(draws=20_000, random_seed=500, target_accept=0.99)
)
pm.sample_posterior_predictive(idata_hierarchical, extend_inferencedata=True)
pm.model_to_graphviz(hierarchical_model)注意:ModuleNotFoundError: No module named 'blackjax'
python環境にblackjaxがインストールされておらず、NUTSが、blackjaxモジュールを要求した場合は、以下のコマンドを実行ししてパッケージをインストールしてください。
conda config --add channels conda-forge
conda config --set channel_priority strict
conda insall blackjax
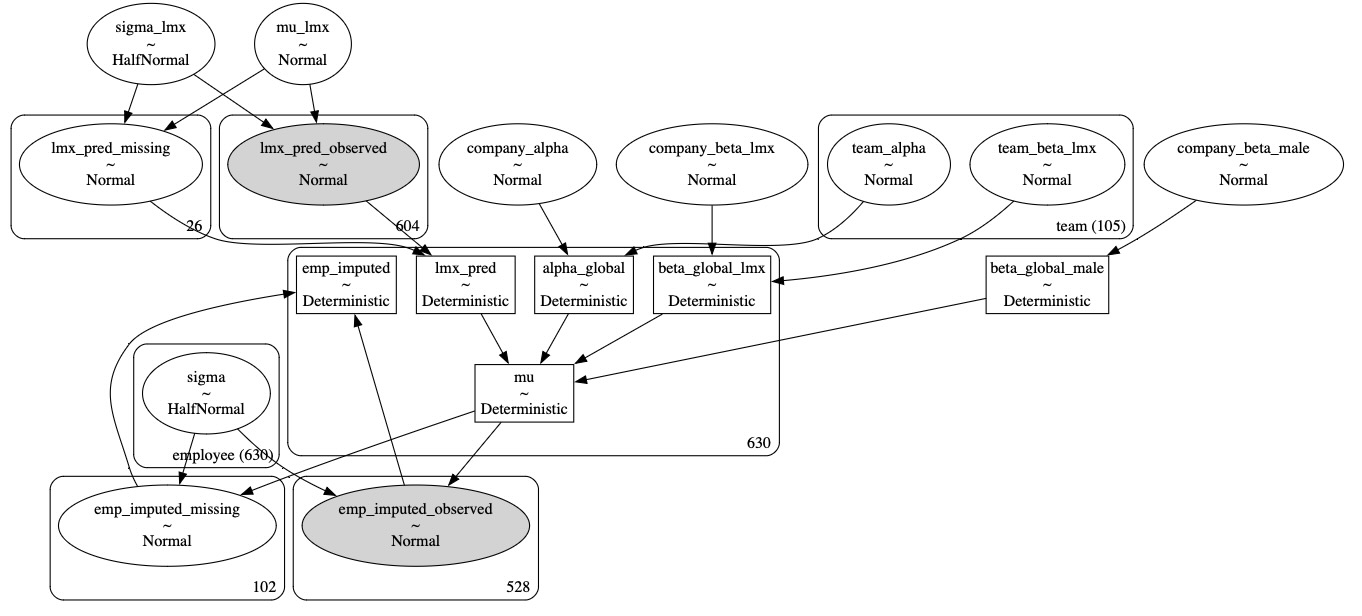
idata_hierarchicalarviz.InferenceData
任意の収束チェック
az.plot_trace(
idata_hierarchical,
var_names=["company_alpha", "team_alpha", "company_beta_lmx", "team_beta_lmx"],
kind="rank_vlines",
);
az.plot_energy(idata_hierarchical, figsize=(20, 7));
モデル適合の検査
summary = az.summary(
idata_hierarchical,
var_names=[
"company_alpha",
"team_alpha",
"company_beta_lmx",
"company_beta_male",
"team_beta_lmx",
],
)
summary| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| company_alpha | 20.871 | 0.543 | 19.870 | 21.931 | 0.033 | 0.024 | 265.0 | 608.0 | 1.01 |
| team_alpha[1] | -0.277 | 0.949 | -1.995 | 1.551 | 0.032 | 0.022 | 898.0 | 2847.0 | 1.00 |
| team_alpha[2] | -0.066 | 0.998 | -1.951 | 1.785 | 0.025 | 0.018 | 1559.0 | 3185.0 | 1.00 |
| team_alpha[3] | -0.577 | 0.937 | -2.319 | 1.194 | 0.024 | 0.017 | 1500.0 | 3285.0 | 1.00 |
| team_alpha[4] | -0.210 | 1.016 | -2.172 | 1.618 | 0.026 | 0.019 | 1477.0 | 2825.0 | 1.00 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| team_beta_lmx[101] | 0.158 | 0.211 | -0.240 | 0.544 | 0.013 | 0.009 | 269.0 | 949.0 | 1.01 |
| team_beta_lmx[102] | 0.415 | 0.203 | 0.026 | 0.788 | 0.011 | 0.008 | 326.0 | 1054.0 | 1.00 |
| team_beta_lmx[103] | -0.140 | 0.207 | -0.536 | 0.244 | 0.012 | 0.008 | 314.0 | 929.0 | 1.01 |
| team_beta_lmx[104] | -0.160 | 0.187 | -0.522 | 0.181 | 0.010 | 0.007 | 324.0 | 1167.0 | 1.01 |
| team_beta_lmx[105] | 0.077 | 0.390 | -0.551 | 0.884 | 0.018 | 0.013 | 506.0 | 1011.0 | 1.01 |
213 rows × 9 columns
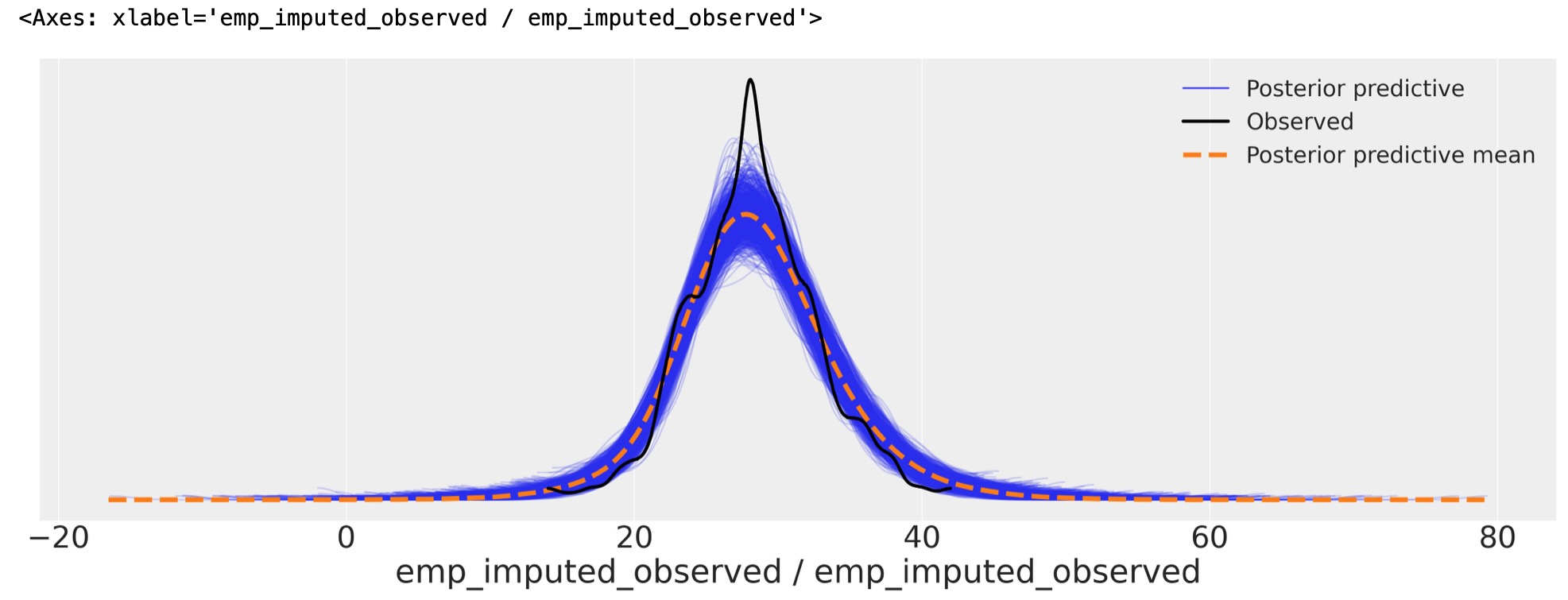
az.plot_ppc(
idata_hierarchical, var_names=["emp_imputed_observed"], figsize=(20, 7), num_pp_samples=1000
)
代入の異種パターン
因果推論の疑問を考えている時は、ローカル因子の混乱させる影響に注意を払います。これは、代入するときにもまた必要とされます。私たちはここで、チーム特有の切片の選択を示します。特別なチームに属していることは、上記のあなたの充実度、あるいは下記会社レベルの切片項の総平均をシフトすることを提案します。これら環境のローカルな影響は、欠測値を代入するときに説明するために探索することです。
ax = az.plot_forest(
idata_hierarchical,
var_names=["team_beta_lmx"],
coords={"team": [1, 20, 22, 30, 50, 70, 76, 80, 100]},
figsize=(20, 15),
kind="ridgeplot",
combined=True,
ridgeplot_alpha=0.4,
hdi_prob=True,
)
ax[0].axvline(0)
ax[0].set_title("Team Contribution to the marginal effect of LMX on Empowerment", fontsize=20);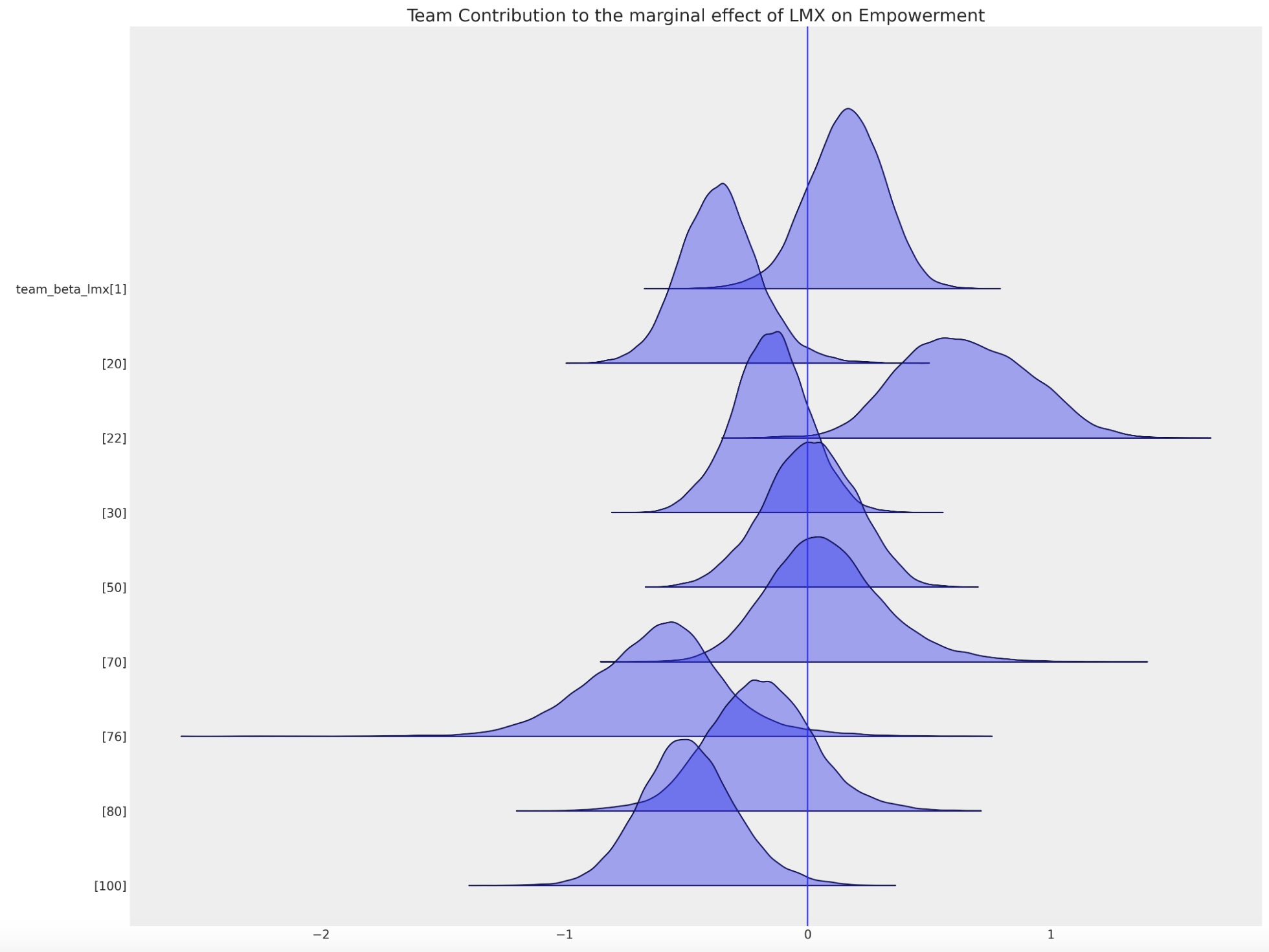
このローカルな差異を取り込む能力は、代入値のパターンにも影響します。
imputed_data = df_employee[["lmx", "empower", "climate"]]
imputed_lmx = az.extract(idata_hierarchical, group="posterior_predictive", num_samples=1000)[
"lmx_pred"
].mean(axis=1)
mask = imputed_data["lmx"].isnull()
imputed_data.loc[mask, "lmx"] = imputed_lmx.values[imputed_data[mask].index]
imputed_emp = az.extract(idata_hierarchical, group="posterior_predictive", num_samples=1000)[
"emp_imputed"
].mean(axis=1)
mask = imputed_data["empower"].isnull()
imputed_data.loc[mask, "empower"] = imputed_emp.values[imputed_data[mask].index]
imputed_data.columns = ["imputed_" + col for col in imputed_data.columns]
joined = pd.concat([imputed_data, df_employee], axis=1)
joined["check"] = np.where(joined["empower"].isnull(), 1, 0)
mosaic = """AAAABB"""
fig, axs = plt.subplot_mosaic(mosaic, sharex=False, figsize=(20, 7))
axs = [axs[k] for k in axs.keys()]
axs[0].scatter(
joined["imputed_lmx"],
joined["imputed_empower"],
c=joined["check"],
cmap=cm.winter,
ec="black",
s=40,
)
z = multivariate_normal([10, joined["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]).pdf(
joined[["imputed_lmx", "imputed_empower"]]
)
axs[0].tricontour(joined["imputed_lmx"], joined["imputed_empower"], z)
axs[1].hist(joined["imputed_empower"], ec="black", label="Imputed", color="limegreen", bins=30)
axs[1].hist(joined["empower"], ec="black", label="observed", color="blue", bins=30)
axs[1].set_title("Empowerment Distributions Imputed \n with Team Informed Estimates", fontsize=20)
axs[0].set_xlabel("Leader Member Exchange - LMX")
axs[0].set_ylabel("Empowerment")
axs[0].set_title("Empowerment Imputed \n with Team Informed Estimates", fontsize=20)
axs[1].legend();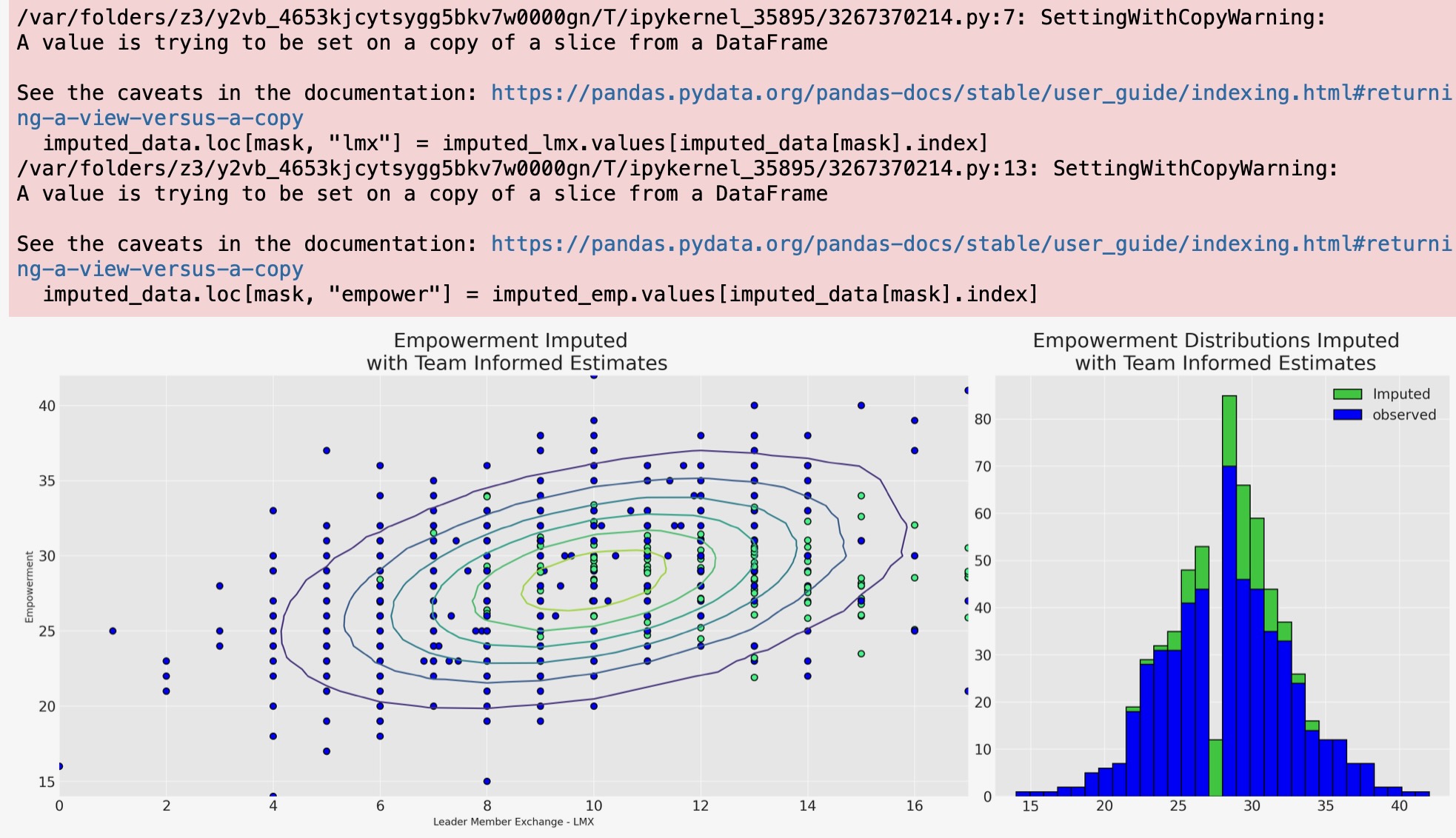
チーム固有の情報が、lmxとmaleの関数として広い広がりの幅広い範囲の充実度の値を代入することを私たちに認めることは、階層モデルから明白です。これは、すべての力関係がローカルなので、もっと説得力があります。そしてこの潜在的なモデルは各従業員の労働条件によって知らされます。そのように私たちの階層モデルは、欠測報告に対して確率的な権限を与える値がもっと微妙な違いの視点にあると考えられることができます。階層代入モデルは、二つの方法で”情報を借ります”(i) 個別のチームの予測は、大域的な予測にへ引っ張られ、欠測値はチームの力学の私たちの測定を重視して代入されます。
結論
私たちは、ここで、欠測データを代入するために多重のアプローチを見てきました。私たちは、欠測値のデータの理由が、急には明らかにならず、どのくらい異なった雇用者が、彼らの管理者との特別な関係のもとで異なった理由を持つかで与えられる例に焦点を当ててきました。しかし、ここで適用されたその技術は全く一般的です。
代入するための多重正規アプローチは、多くのケースで驚くべきことにうまく働きます。しかし、もっと鋭利なアプローチはチェインした方程式の連続した仕様です。ここでのベイジアンアプローチは、最新技術です。なぜなら私たちは、代入方程式の成分モデルのように簡単な回帰モデルよりも全く自由に使えます。各方程式では、尤度項と私たちが許容するサンプリング分布を超えて事前分布の選択を自由にできます。私たちはまた、それらが欠測データのパターンを制限する限り私たちのデータの重視する自然のクラスターに階層構造を追加することができます。
この一般的な点は重要です。ベイジアンアプローチの柔軟性は、なぜデータが欠測したかについて理論の適当な複雑さへ仕立てることができます。同様の考えはcounterfactual推論に関連した予測過程に適用します。私たちが、なぜデータが欠測したかの理論を開発すればするほど、もっと私たちは、理論の巧妙さを取り込むために、柔軟なモデル化のフレームワークを必要とします。ベイジアンモデリングは、この理論の構築と評価のループにとって、見事なツールです。
製作者
著者:Nathaniel Forde 2023年2月
参考文献
- Craig Enders K. Applied Missing Data Analysis. The Guilford Press, 2022.