import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
print(f"Running on PyMC v{pm.__version__}")Running on PyMC v5.0.1%load_ext watermark
az.style.use("arviz-darkgrid")連続モンテカルロ - ベイズ計算の近似
ベイジアン計算の近似法は、尤度関数が対話的で評価にコストがかかるケースで、事後予測分布のために開発された技術の集合体です。これは、尤度関数が分析の一部ではないことを意味せず、単に尤度関数を近似します。ここで、その名称ををABC法とします。
ABCは、生物学システムのような正確な研究の範囲で複雑な現象をモデル化する時に役に立ちます。そのようなモデルはしばしば観測されないランダムな量を含みます。それは尤度関数を特徴づけるのが難しく、しかし、データはモデルからシミュレートできます。
これらの方法は一般的形式は以下のとおりです
- 事前提案分布π(θ)からパラメータθをサンプルします
- θの関数を使って、データセットyをシミュレートします。そして観測データセットy0と同じ次元のデータセットを返します。
- 許容閾値εと距離関数dを使って検査データセットy0とシミュレートデータセットを比較します。
距離関数のあるケースでは、二つの統計の結果間のd(S(y0),S(y)),を計算されます。すべてのデータセットの距離を計算する問題を避けて、
結果として、分布π(θ|d(y0,y)) <= εからサンプルパラメータを得ます。
もし、εが、十分小さいならば、この分布は、事後分布π(θ|y0)の良い近似になります。
サンプルしたパラメータを提案分布Φ(θ(i))の系列を通して広めることで、連続モンテカルロABCは、反復して事前を事後に変形処理します。受容パラメータθの重みは次のように
w(i) ∝ π(θ(i)) / Φ(θ(i))伝統的なSMC、言い換えれば、多重の極値を持つ分布からサンプルする能力、の優位性を組み合わせます、しかし、尤度関数を評価する必要はありません。
(Lintusaari,2016),(Toni,T., 2008), (Nunez,Prangle, 2015)
古き良きガウス適合
PyMCでABCの使用法を記すために、ガウシアンデータの平均と標準偏差をとても簡単に見積もる例から始めます。
data = np.random.normal(loc=0, scale=1, size=1000)ガウス尤度を使う通常の環境下では明らかに、非常にうまく働きます。しかし、この例の目的には手に負えません。ノートブックはここで終わります。全てはとても退屈です。それで、代わりにシミュレータを定義します。通常のデータに対する非常にまっすぐなシミュレータは、偽の乱数生成器です。現実の世界のシミュレータは、もっとも何かの愛好家になります。
def normal_sim(rng, a, b, size=1000):
return rng.normal(a, b, size=size)一般的に、pYMC3でABCモデルを定義すると、他のPyMC3モデルの定義と非常に似たものになります。二つの重要な相違は、私たちがsimulator分布を定義する必要があるのと、kernel="ABC"でsample_smcを使う必要があることです。Simulatorは、合成データを生成する関数を通って一般的なインターフェイスとして働きます。そのパラメータは、観測データ、オプションの距離関数と統計結果。以下のコードは、私たちがデフォルトの距離で使っているgaussian_kernel, summary_statisticのsortです。名称がsortで提案されているsortは、距離を計算する前にデータをソートします。
最後に、SMC-ABCはシミュレーションデータをストアするオプションを提案します。これは、シミュレータが評価するには高価であるため、扱いやすくできます。そして、事後予測チェックのための例としてシミュレートしたデータを使うことを求めて良いでしょう。
with pm.Model() as example:
a = pm.Normal("a", mu=0, sigma=5)
b = pm.HalfNormal("b", sigma=1)
s = pm.Simulator("s", normal_sim, params=(a, b), sum_stat="sort", epsilon=1, observed=data)
idata = pm.sample_smc()
idata.extend(pm.sample_posterior_predictive(idata))
サンプラーがとてもよく実行したことを plot_traceによって判断します。この簡単なモデルによって与えられたことは驚くことではありません。とにかく、平坦な順位の図を見て、安心させられます。
az.plot_trace(idata, kind="rank_vlines");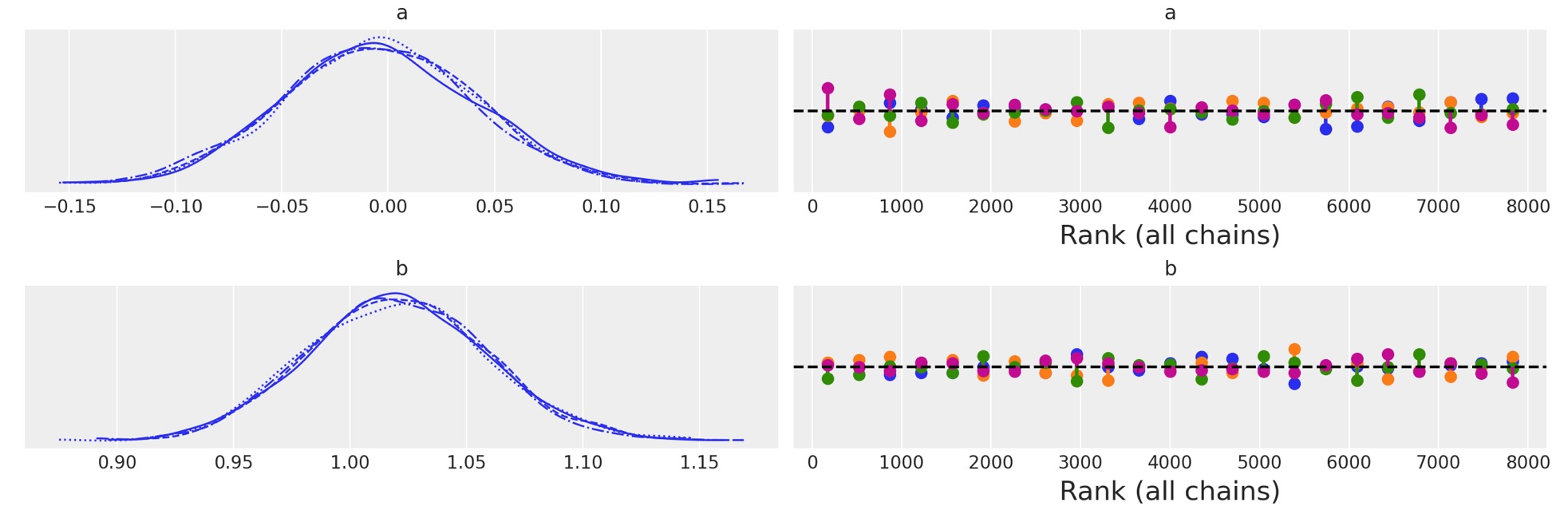
az.summary(idata, kind="stats")| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| a | -0.004 | 0.046 | -0.092 | 0.079 |
| b | 1.020 | 0.039 | 0.946 | 1.090 |
事後予測チェックは、全体的によく適合しエチルことを示しています。合成データは、観測したものより重いテイルを持っています。あなたが、もっと狭まく適合させたければ、εの値を減らすことを求めてかまいません。
az.plot_ppc(idata, num_pp_samples=500);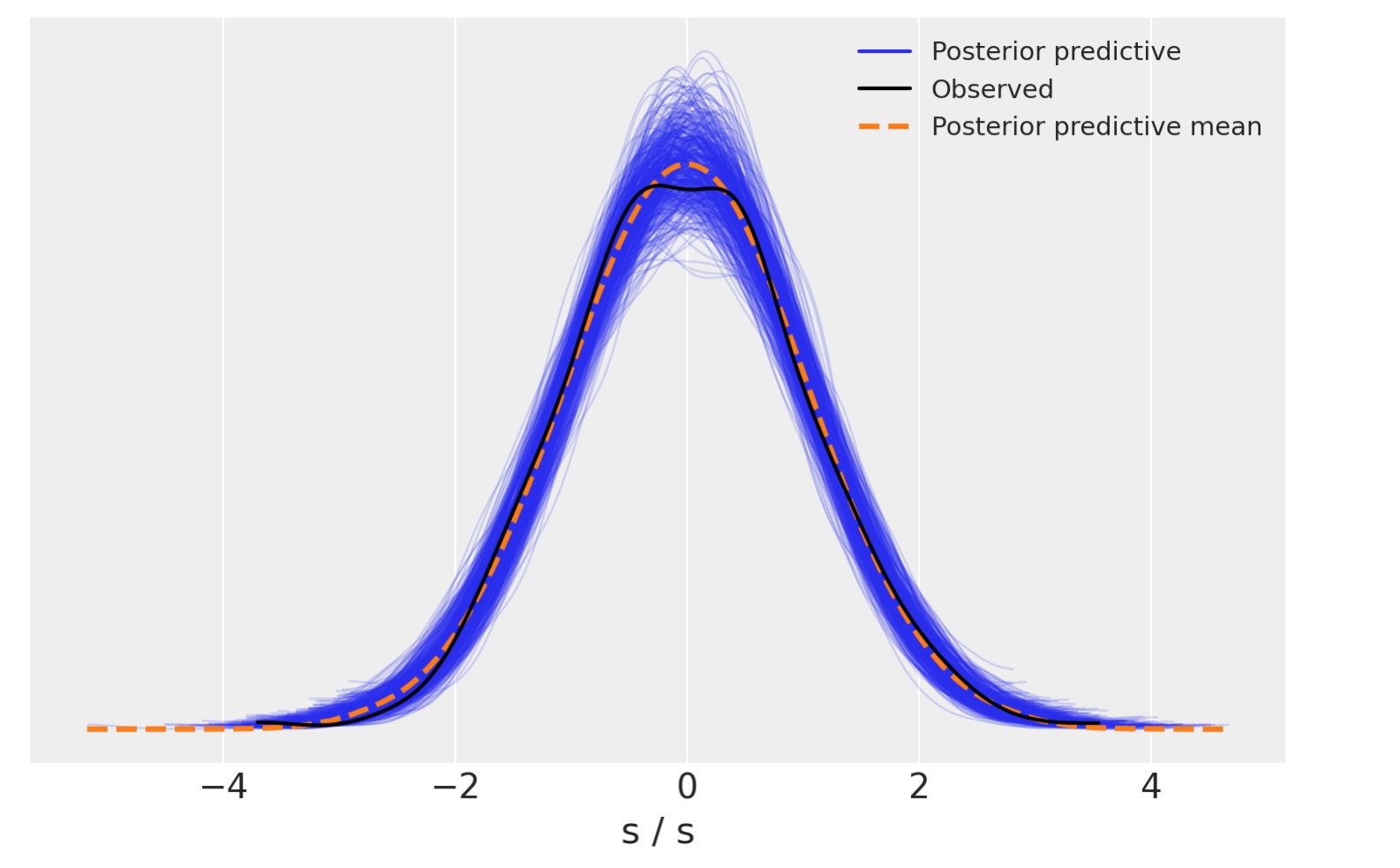
Lotka-Volterra
捕食者/獲物の相互作用がある時の二つの種の個体数がどのように変化するかを記述する Lotka-Volterraは、よく知られた生物学のモデルです。(A Biologist's Guide to Mathematical Modeling in Ecology and Evolution,Otto and Day,2007). 例えば、うさぎと狐。それぞれの種の初期個体数を与え、この常微分方程式の積分は、両個体数の変化の進行の曲線を記述します。
- a は、うさぎの、狐がいない時の自然増加率。
- b は、捕食によるうさぎの自然致死率
- c は、うさぎがいない時の狐の自然致死率
- d は、何匹の捉えられたうさぎが、新しい狐を生み出すかを記述する因子
SMCーABCとODEsは本質的に特別ではないことに注意してください。原理的にシミュレータはどのようなコードの種にもなることができ、与えられたパラメータセットでフェイクデータを生成できます。
from scipy.integrate import odeint
# Definition of parameters
a = 1.0
b = 0.1
c = 1.5
d = 0.75
# initial population of rabbits and foxes
X0 = [10.0, 5.0]
# size of data
size = 100
# time lapse
time = 15
t = np.linspace(0, time, size)
# Lotka - Volterra equation
def dX_dt(X, t, a, b, c, d):
"""Return the growth rate of fox and rabbit populations."""
return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])
# simulator function
def competition_model(rng, a, b, size=None):
return odeint(dX_dt, y0=X0, t=t, rtol=0.01, args=(a, b, c, d))観測データとしてそれを使うために、シミュレータ関数を使うことで、任意のノイズが追加されたデータセットを得ます。
# function for generating noisy data to be used as observed data.
def add_noise(a, b):
noise = np.random.normal(size=(size, 2))
simulated = competition_model(None, a, b) + noise
return simulated# plotting observed data.
observed = add_noise(a, b)
_, ax = plt.subplots(figsize=(12, 4))
ax.plot(observed[:, 0], "x", label="prey")
ax.plot(observed[:, 1], "x", label="predator")
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.set_title("Observed data")
ax.legend();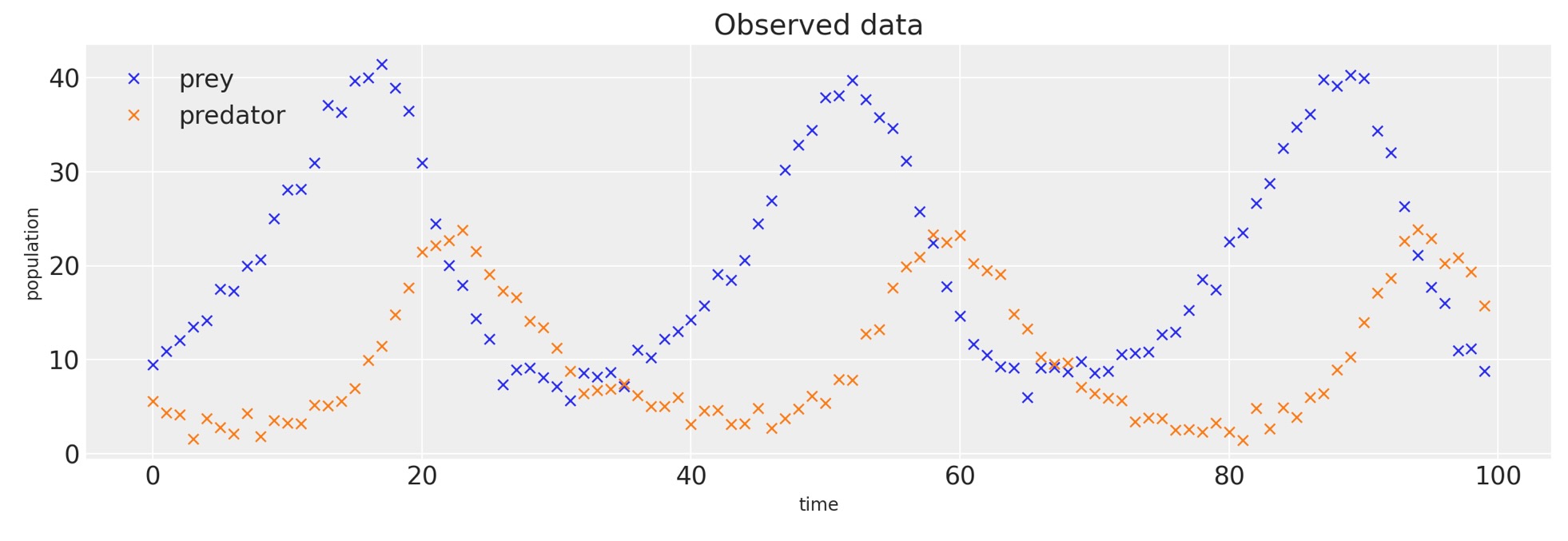
最初の例として、尤度関数を特定する代わりに、pm.Simuklator()を使います。
with pm.Model() as model_lv:
a = pm.HalfNormal("a", 1.0)
b = pm.HalfNormal("b", 1.0)
sim = pm.Simulator("sim", competition_model, params=(a, b), epsilon=10, observed=observed)
idata_lv = pm.sample_smc()
az.plot_trace(idata_lv, kind="rank_vlines");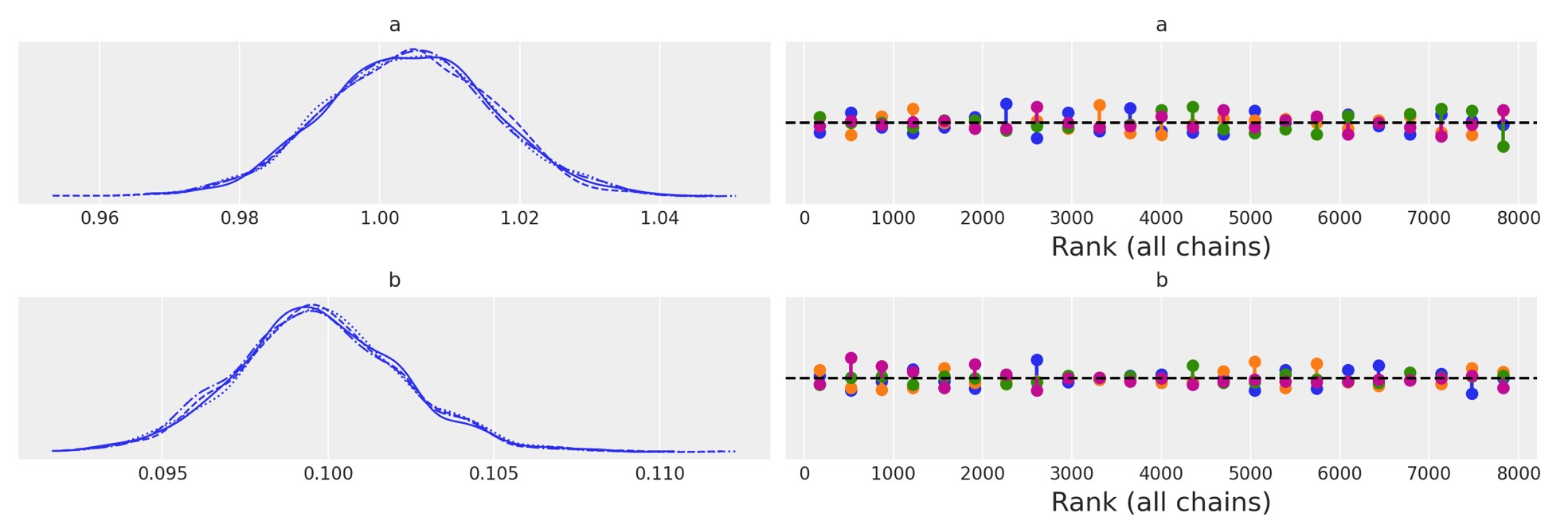
az.plot_posterior(idata_lv);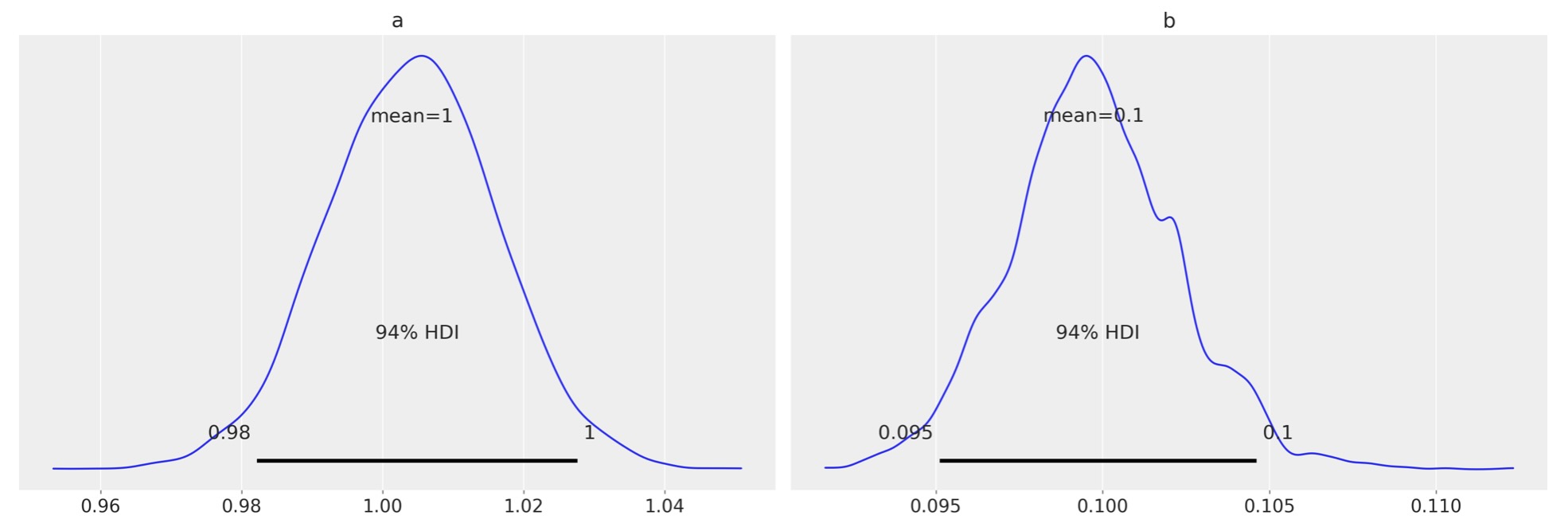
# plot results
_, ax = plt.subplots(figsize=(14, 6))
posterior = idata_lv.posterior.stack(samples=("draw", "chain"))
ax.plot(observed[:, 0], "o", label="prey", c="C0", mec="k")
ax.plot(observed[:, 1], "o", label="predator", c="C1", mec="k")
ax.plot(competition_model(None, posterior["a"].mean(), posterior["b"].mean()), linewidth=3)
for i in np.random.randint(0, size, 75):
sim = competition_model(None, posterior["a"][i], posterior["b"][i])
ax.plot(sim[:, 0], alpha=0.1, c="C0")
ax.plot(sim[:, 1], alpha=0.1, c="C1")
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.legend();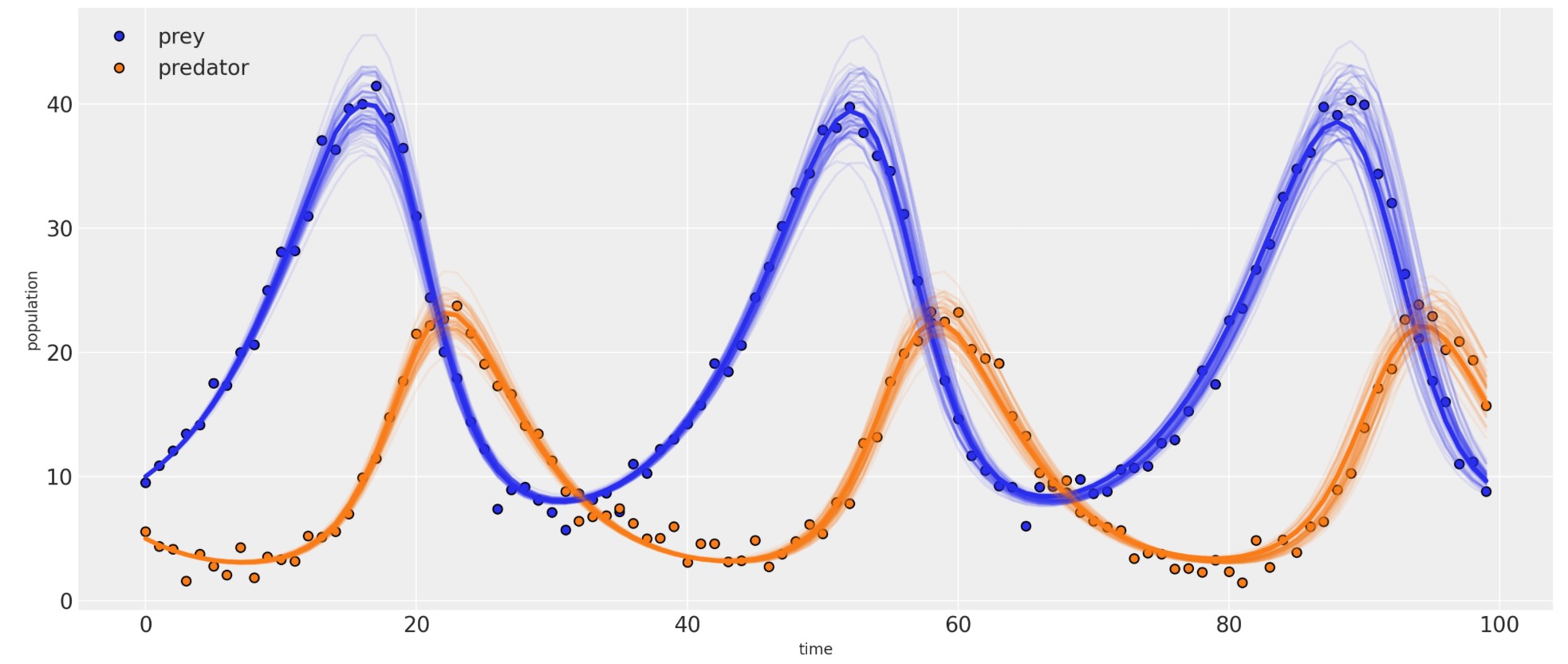
参考文献
- Osvaldo A Martin, Ravin Kumar, and Junpeng Lao. Bayesian Modeling and Computation in Python. Chapman and Hall/CRC, 2021.