生存分析は、事象への時間分布を研究することです。その範囲は、薬事、生物、工学、社会科学を横断して多くの領域に応用されます。このチュートリアルは、適合の仕方とPyMCを使ってpythonで、ベイジアン生存モデルの分析を示します。
私たちは、RのHSAURパッケージ乳房切除のデータセットの分析によってそれらの概念を記述します。
import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
from matplotlib import pyplot as plt
from pymc.distributions.timeseries import GaussianRandomWalk
from pytensor import tensor as T
print(f"Running on PyMC v{pm.__version__}")Running on PyMC v5.0.1RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")try:
df = pd.read_csv("../data/mastectomy.csv")
except FileNotFoundError:
df = pd.read_csv(pm.get_data("mastectomy.csv"))
df.event = df.event.astype(np.int64)
df.metastasized = (df.metastasized == "yes").astype(np.int64)
n_patients = df.shape[0]
patients = np.arange(n_patients)df.head()| time | event | metastasized | |
|---|---|---|---|
| 0 | 23 | 1 | 0 |
| 1 | 47 | 1 | 0 |
| 2 | 69 | 1 | 0 |
| 3 | 70 | 0 | 0 |
| 4 | 100 | 0 | 0 |
n_patients44各横列は、乳房切除の手術を受けた女性の乳がんの診断から観測値を表します。横列、timeは、観察された女性の手術後の時間を表示しています。横列eventは女性が、観察期間で亡くなったかどうかを示しています。横列のmetastasized(転移)は、癌が手術前に転移したかどうかを表しています。
このチュートリアルは、乳房切除後の生存時間と、癌が転移したかどうかの関係を分析します。
生存分析の短期集中講座
最初に、少し理論を紹介します。もし、ランダム変数Tが、私たちが研究する事象への時間であれば、生存分析は、第一に生存関数を考えます。
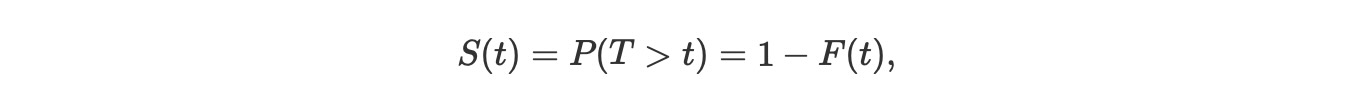
ここで、FはTのCDFです。それは数学的に、生存関数のhazard rate λ(t)の項を説明するのに便利です。hazard率は、まだ発生していない事象が、与えられた時間tで発生するリアルタイムの確率です。それは、
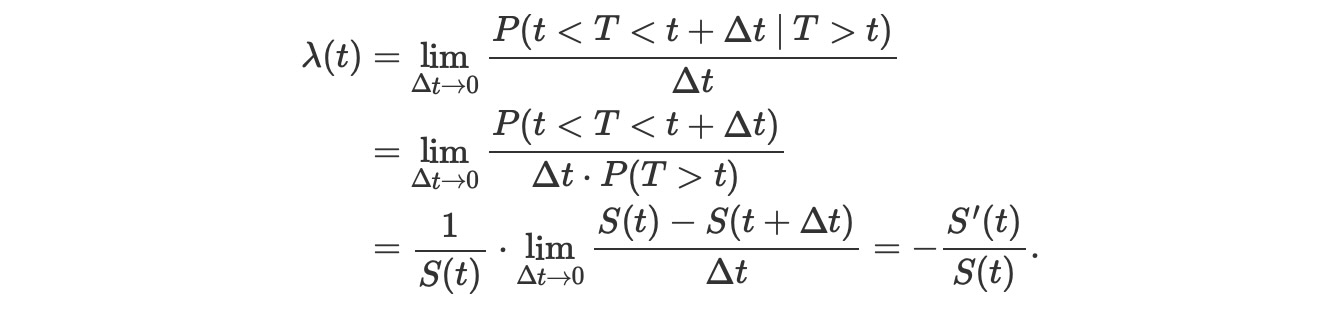
以下で示す生存関数のためのこの微分方程式を解くには、
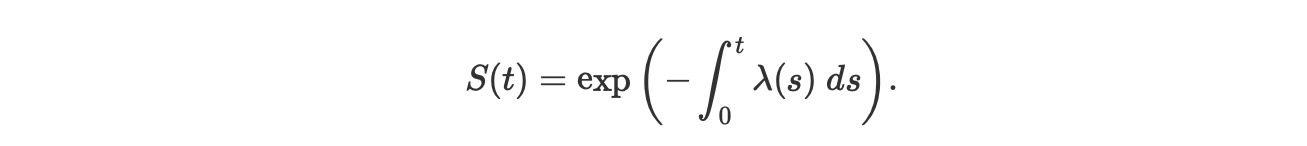
この生存関数の表現は、累積、hazard関数を示します。
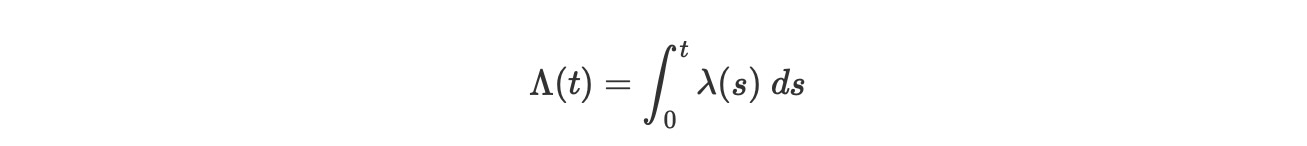
は、生存分析の重要な量です。便利なようにS(t) = exp(ーΛ(t))とおきます。
生存関数の重要な、しかし、微妙な点は、検閲censoringです。私たちが見積もるのに関心を向ける量であるけれども、手術と死亡の間の時間です。私たちはすべての案件で脂肪を観察するのではありません。私たちが分析を実行する時間の点では、私たちの案件のいくつかは、ありがたいことにまだ生存しています。私たちの乳房切除の研究のケースでは、df.eventはもし、死亡案件が観察された場合、1、死亡が観察されなければゼロになります。
df.event.mean()0.5909090909090909私たちの観察の40%超が、検閲されました。私たちは、観察の経過時間を視覚化し、どの観察が検閲されたか下に示します。
fig, ax = plt.subplots(figsize=(8, 6))
ax.hlines(
patients[df.event.values == 0], 0, df[df.event.values == 0].time, color="C3", label="Censored"
)
ax.hlines(
patients[df.event.values == 1], 0, df[df.event.values == 1].time, color="C7", label="Uncensored"
)
ax.scatter(
df[df.metastasized.values == 1].time,
patients[df.metastasized.values == 1],
color="k",
zorder=10,
label="Metastasized",
)
ax.set_xlim(left=0)
ax.set_xlabel("Months since mastectomy")
ax.set_yticks([])
ax.set_ylabel("Subject")
ax.set_ylim(-0.25, n_patients + 0.25)
ax.legend(loc="center right");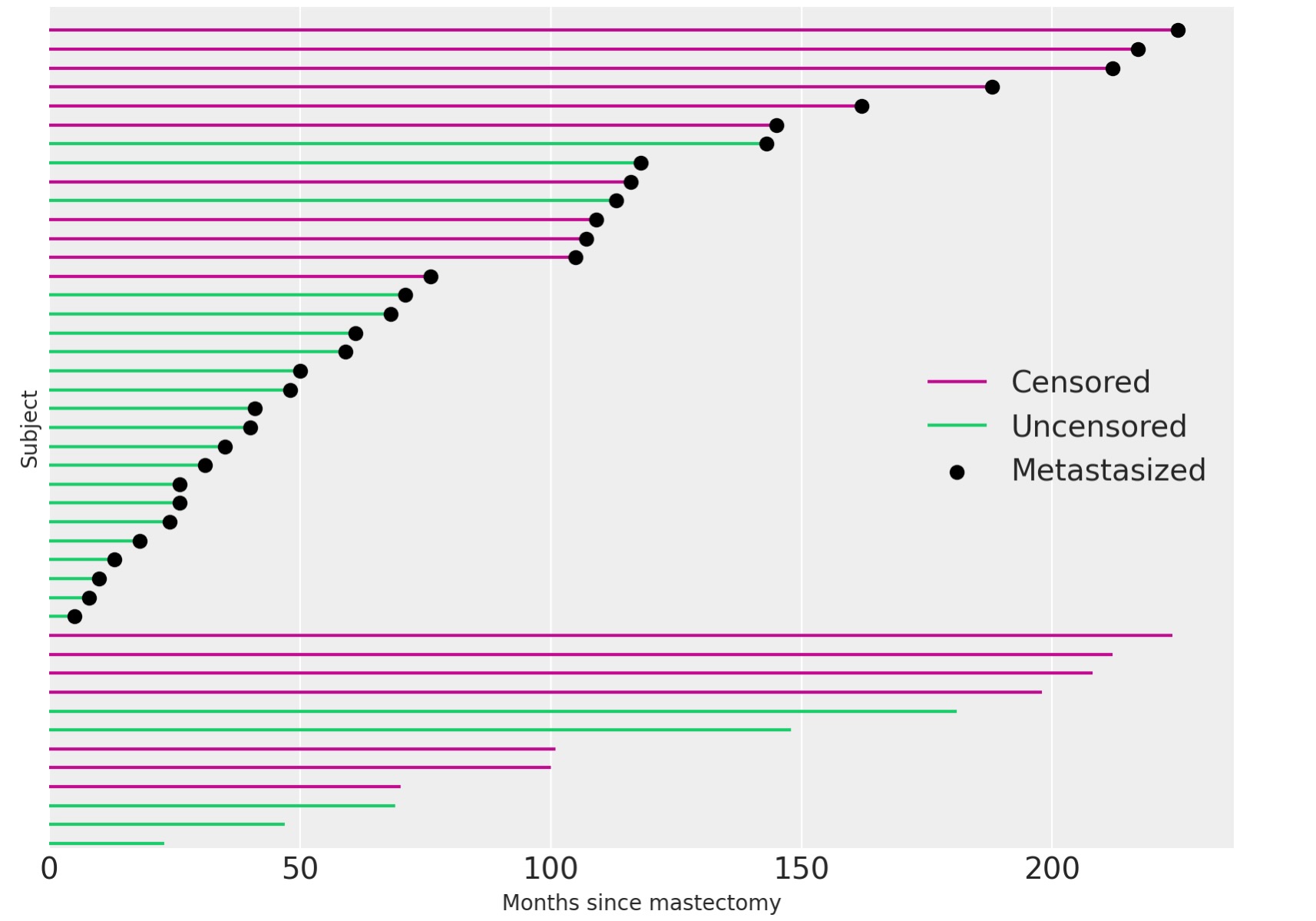
観察が、検閲されたとき(df.eventがゼロ)、df.timeはその案件で生存時間を持ちません。私たちがそのような検閲された観察から結論できるすべては、案件の真の生存時間、df.timeを超えることです。
これは、このチュートリアルの目的のためには、十分な基礎的な生存分析理論です。もっと広範囲な紹介は、Aalen et al[Aalen Odd, Ornulf Borgan, Hakon Gjessing. Survival and event history analysis:a process point of view.Springer 2008]を調べてください。
ベイジアン比例ハザードモデル
生存分析の最も基本的な二つの見積もりは、生存関数の Kaplan-Meierの見積もりと、累積ハザード関数のNelson-Aalen 見積もりです。しかし、私たちは生存時間における転移の影響を理解したいので、危険回帰モデルがより適当です。おそらく、共通に使用される危険回帰モデルは、COxの釣り合った(比例した)ハザードモデルです。このモデルでは、もし、私たちが、共変量Xと回帰係数βを持つならば、ハザード率は下のようにモデル化されます。
λ(t) = λ0(t) exp( xβ )ここで、λ0(t)は、共変量xとは独立したハザードのベースライン。この例では、共変量は、一次元ベクターdf.metastasizedです。
多くの回帰状況と違い、xは切片に対応する定数の項は含まれません。もし、xが、切片に対応する定数を含むならば、モデルは同一であることが確認できなくなります。この同一であることが確認できなくなることを記述するために、下を考えます。
λ(t) = λ0(t) exp(β0 + xβ ) = λ0(t) exp(β0) exp(xβ) もし、β^0 = β0 + δ 、 λ^0 = λ0(t) exp( - δ) ならば, この時、λ(t) = λ^0(t) exp(β^0 + xβ) 、同様に、識別できない β0 でモデルを作ります。
コックスモデルで、ベイジアン推論を実行するために、私たちは、βとλ0で事前を特徴づけなければなりません。私たちは、βの正規事前分布を、β〜N(μ、σ2)、ここでμβ〜N(0、100) 、σβ〜U(0,10)
λ0(t)の相応しい事前分布は、はっきりしません。私たちは、セミパラメトリック事前分布を選択します。そこで、λ0(t)は一片の定数関数です。この事前の要求は、私たちに、終点でのインターバル内の疑問であるSj <= t <= sj+1 時間の範囲を分離することを要求します。この分割で、λ0(t)= λj、もしsj <= t <= sj+1. λ0(t)はこの様式を持って、制限されます。私たちが実行するすべては、λjがN-1個の事前を選択することです。私たちは、独立した不明確な事前 λj〜Gammma(10 -2, 10 -2). 私たちの乳房切除例では、各インターバルを3ヶ月で作ります。
interval_length = 3
interval_bounds = np.arange(0, df.time.max() + interval_length + 1, interval_length)
n_intervals = interval_bounds.size - 1
intervals = np.arange(n_intervals)私たちは、どのように死亡と検閲された観察がこれらのインターバルに分布されるかを見ます。
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(
df[df.event == 0].time.values,
bins=interval_bounds,
lw=0,
color="C3",
alpha=0.5,
label="Censored",
)
ax.hist(
df[df.event == 1].time.values,
bins=interval_bounds,
lw=0,
color="C7",
alpha=0.5,
label="Uncensored",
)
ax.set_xlim(0, interval_bounds[-1])
ax.set_xlabel("Months since mastectomy")
ax.set_yticks([0, 1, 2, 3])
ax.set_ylabel("Number of observations")
ax.legend();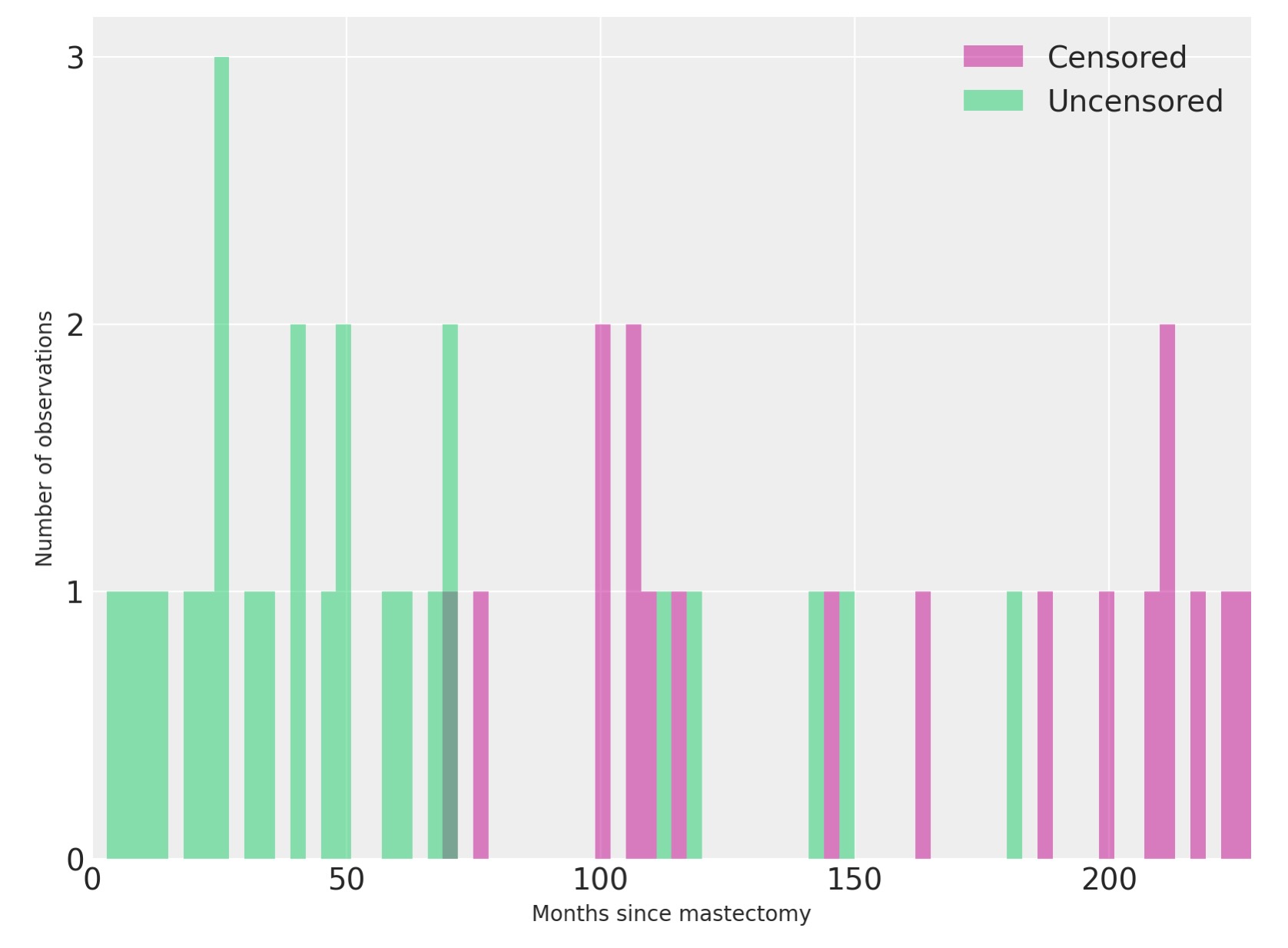
βとλ0(t)の選択した事前分布では、私たちは、ここで、どのようにモデルがpymcのMCMCシミュレーションを使って適合するかを示します。鍵になる観察は、一片の固定の比例したハザードモデルが、ポワソン回帰モデルと緊密に関係していることです。(モデルは識別しませんが、パラメータβやλでなく、観察データだけに依存した因子によって尤度は異なります。より詳細は、German RodriguezのWWS509 コースノートを見てください)。
私たちは、j番目のインターバルで、i番目の案件が、死亡かどうかを元にした指示変数を定義します。
dij = { 1 もし、事例 i がインターバル jで 死亡
0 それ以外last_period = np.floor((df.time - 0.01) / interval_length).astype(int)
death = np.zeros((n_patients, n_intervals))
death[patients, last_period] = df.event私たちは、また、tijをi番目の案件がj番目のインターバルで危険になる時間の量として定義します。
exposure = np.greater_equal.outer(df.time.to_numpy(), interval_bounds[:-1]) * interval_length
exposure[patients, last_period] = df.time - interval_bounds[last_period]
最後に、j番目のインターバルで、i番目の案件によって招かれる危険をλij = λj exp(xβ) として示します。
私たちは、平均tij λijのポワソンランダム変数をdij で近似します。この近似は、以下のpuMcモデルで導かれます。
coords = {"intervals": intervals}
with pm.Model(coords=coords) as model:
lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims="intervals")
beta = pm.Normal("beta", 0, sigma=1000)
lambda_ = pm.Deterministic("lambda_", T.outer(T.exp(beta * df.metastasized), lambda0))
mu = pm.Deterministic("mu", exposure * lambda_)
obs = pm.Poisson("obs", mu, observed=death)私たちはここで、モデルからサンプルします。
n_samples = 1000
n_tune = 1000with model:
idata = pm.sample(
n_samples,
tune=n_tune,
target_accept=0.99,
random_seed=RANDOM_SEED,
)
私たちは、誰の癌が、乳房切除されたかの案件のハザード率を葯1、誰の癌が乳房切除されなかったかの率を半分になっているのを見ます。
np.exp(idata.posterior["beta"]).mean()- array(2.43598147)
- Coordinates: (0)
- Indexes: (0)
- Attributes: (0)
az.plot_posterior(idata, var_names=["beta"]);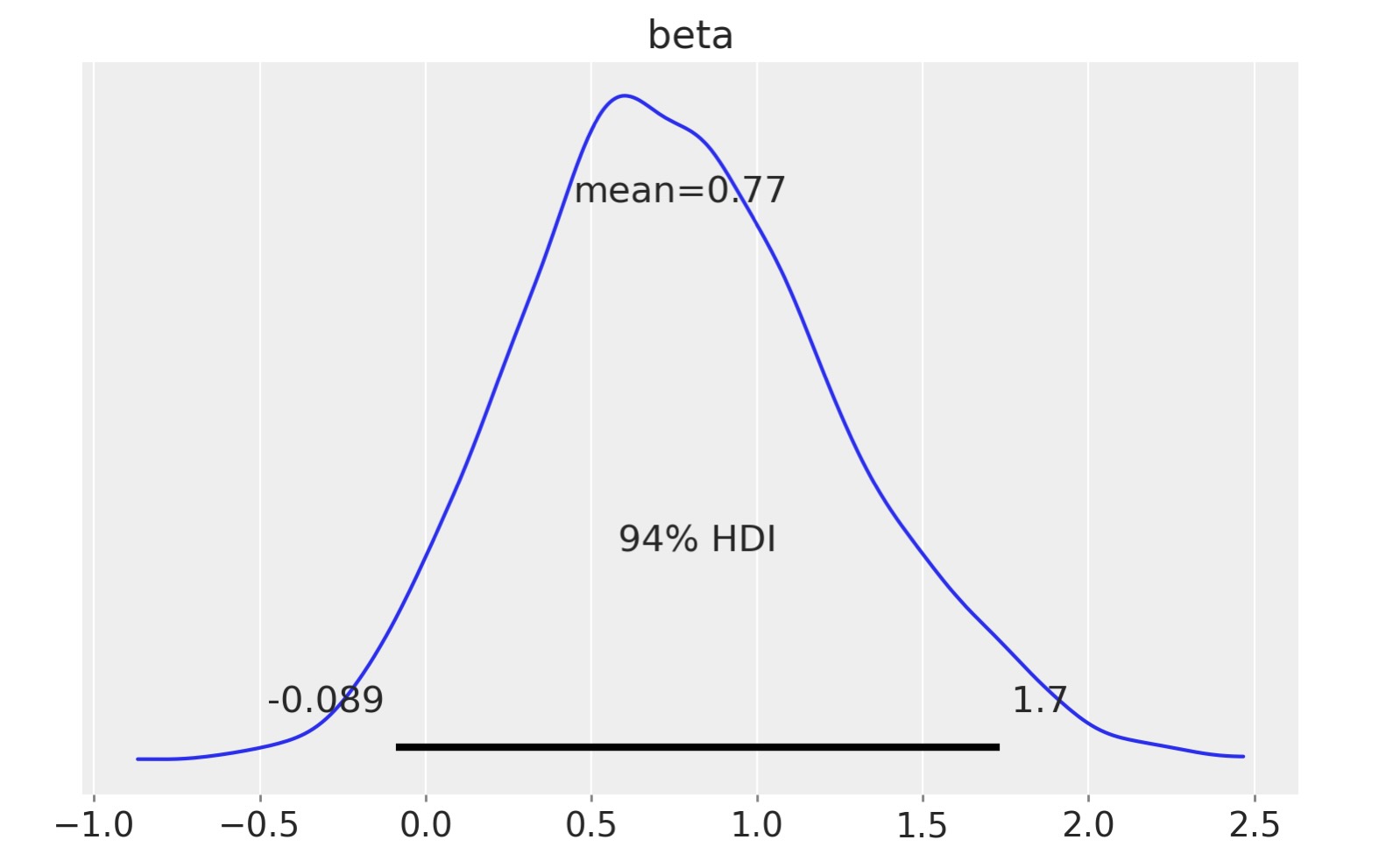
az.plot_autocorr(idata, var_names=["beta"]);
私たちはここで、累積ハザードと生存関数の両方で、乳房切除の影響を試験します。
base_hazard = idata.posterior["lambda0"]
met_hazard = idata.posterior["lambda0"] * np.exp(idata.posterior["beta"])def cum_hazard(hazard):
return (interval_length * hazard).cumsum(axis=-1)
def survival(hazard):
return np.exp(-cum_hazard(hazard))
def get_mean(trace):
return trace.mean(("chain", "draw"))fig, (hazard_ax, surv_ax) = plt.subplots(ncols=2, sharex=True, sharey=False, figsize=(16, 6))
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(base_hazard),
ax=hazard_ax,
smooth=False,
color="C0",
fill_kwargs={"label": "Had not metastasized"},
)
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(met_hazard),
ax=hazard_ax,
smooth=False,
color="C1",
fill_kwargs={"label": "Metastasized"},
)
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(base_hazard)), color="darkblue")
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(met_hazard)), color="maroon")
hazard_ax.set_xlim(0, df.time.max())
hazard_ax.set_xlabel("Months since mastectomy")
hazard_ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
hazard_ax.legend(loc=2)
az.plot_hdi(interval_bounds[:-1], survival(base_hazard), ax=surv_ax, smooth=False, color="C0")
az.plot_hdi(interval_bounds[:-1], survival(met_hazard), ax=surv_ax, smooth=False, color="C1")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(base_hazard)), color="darkblue")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(met_hazard)), color="maroon")
surv_ax.set_xlim(0, df.time.max())
surv_ax.set_xlabel("Months since mastectomy")
surv_ax.set_ylabel("Survival function $S(t)$")
fig.suptitle("Bayesian survival model");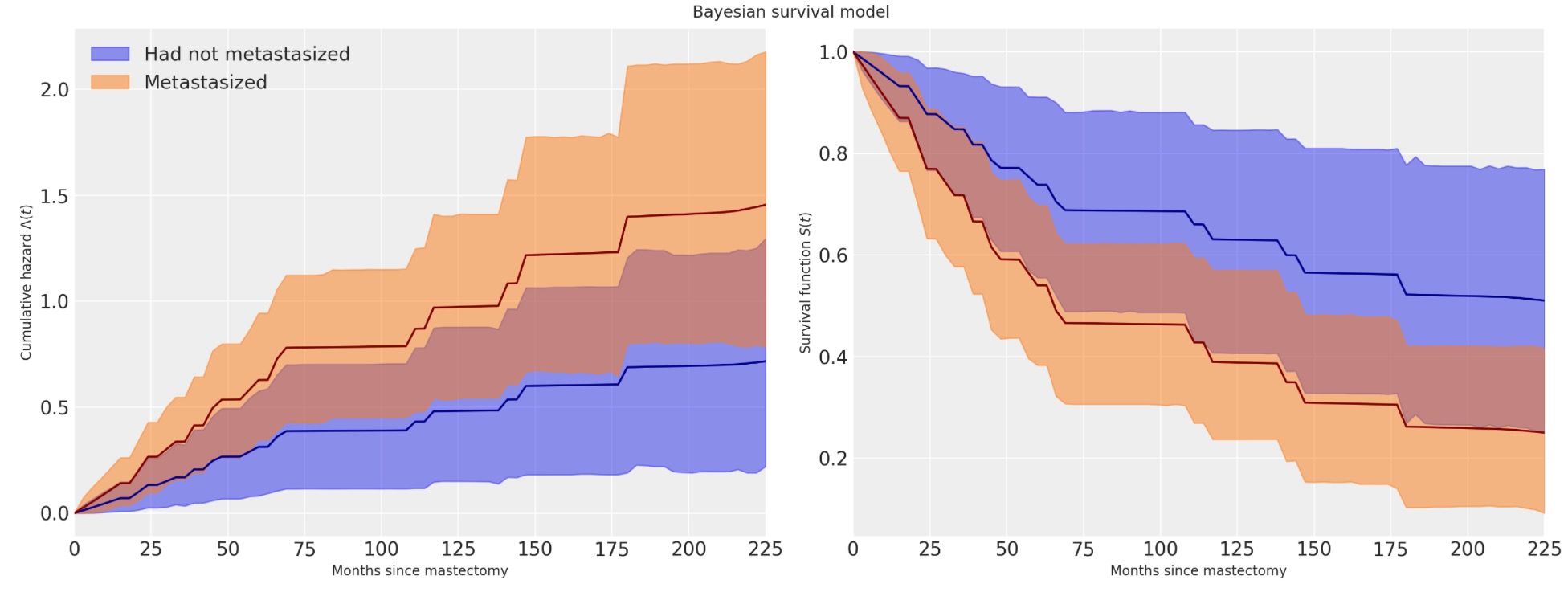
私たちは、乳房切除の案件のために累積ハザードが初期にもっと急速に増加するのを見ます。その後、ベースラインの累積ハザードを並列に大雑把に増加します。
これらの図はまた、各関数のインターバルとして95%上位の事後密度を表示しています。pymcを使ったベイジアンモデル適合の 明確な優位性の一つは、私たちの見積もりの不確実性の量を継承することです。
時間変化の影響
モデルの一方の優位性は、その柔軟性の構築です。上の図から、私たちは追加のハザード時間経過による転移のためだと信じるのが妥当です。ガンガ転移を持った時、乳房切除の後で急速にハザード率が増加することがもっともらしく見えます。しかし、時間経過により転移のリスクは減少していきます。私たちは、回帰変数を時間経過で変化させることによって、この機構をモデルに組み込みます。もし、sj <= t <= Sj+1 時間変化係数モデルでは、私たちは、λ(t) = λj exp(xβ)とおきます。回帰係数の順番は、β1,β2,…βN-1様式正規ランダムウォーク β1〜N(0,1), βj | βj-1〜N(βj-1,1).
私たちはPymcに以下のようにこのモデルを実装します。
coords = {"intervals": intervals}
with pm.Model(coords=coords) as time_varying_model:
lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims="intervals")
beta = GaussianRandomWalk("beta", init_dist=pm.Normal.dist(), sigma=1.0, dims="intervals")
lambda_ = pm.Deterministic("h", lambda0 * T.exp(T.outer(T.constant(df.metastasized), beta)))
mu = pm.Deterministic("mu", exposure * lambda_)
obs = pm.Poisson("obs", mu, observed=death)このモデルでサンプル出力を実行します。
with time_varying_model:
time_varying_idata = pm.sample(
n_samples,
tune=n_tune,
return_inferencedata=True,
target_accept=0.99,
random_seed=RANDOM_SEED,
)
az.plot_forest(time_varying_idata, var_names=["beta"]);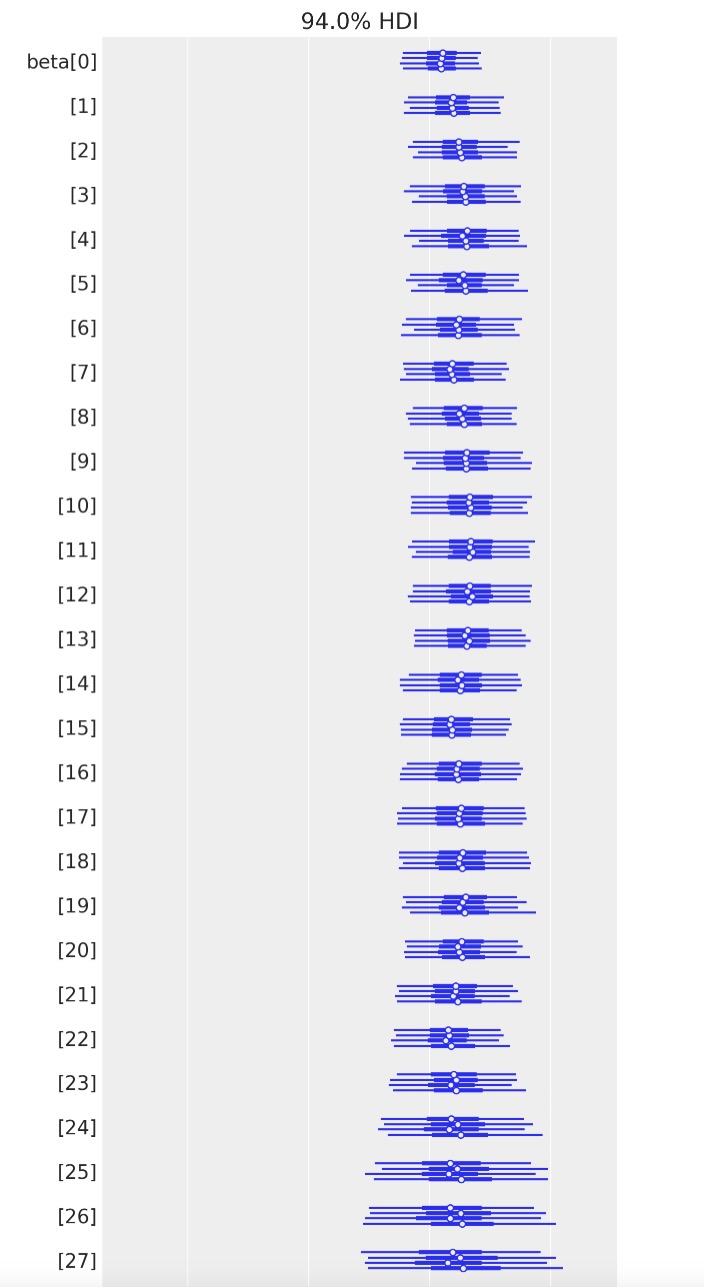
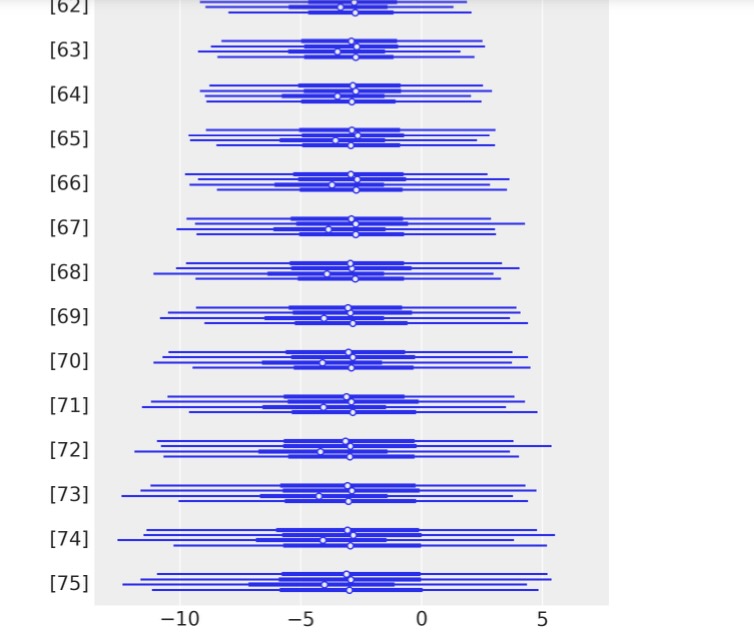
初期値のβj >0以下、時間経過でβjを図示したものから、転移のせいでハザード率が増加し、しかし、結局、このリスクはβj < 0で減少していくことを示しているのがわかります。
fig, ax = plt.subplots(figsize=(8, 6))
beta_eti = time_varying_idata.posterior["beta"].quantile((0.025, 0.975), dim=("chain", "draw"))
beta_eti_low = beta_eti.sel(quantile=0.025)
beta_eti_high = beta_eti.sel(quantile=0.975)
ax.fill_between(interval_bounds[:-1], beta_eti_low, beta_eti_high, color="C0", alpha=0.25)
beta_hat = time_varying_idata.posterior["beta"].mean(("chain", "draw"))
ax.step(interval_bounds[:-1], beta_hat, color="C0")
ax.scatter(
interval_bounds[last_period[(df.event.values == 1) & (df.metastasized == 1)]],
beta_hat.isel(intervals=last_period[(df.event.values == 1) & (df.metastasized == 1)]),
color="C1",
zorder=10,
label="Died, cancer metastasized",
)
ax.scatter(
interval_bounds[last_period[(df.event.values == 0) & (df.metastasized == 1)]],
beta_hat.isel(intervals=last_period[(df.event.values == 0) & (df.metastasized == 1)]),
color="C0",
zorder=10,
label="Censored, cancer metastasized",
)
ax.set_xlim(0, df.time.max())
ax.set_xlabel("Months since mastectomy")
ax.set_ylabel(r"$\beta_j$")
ax.legend();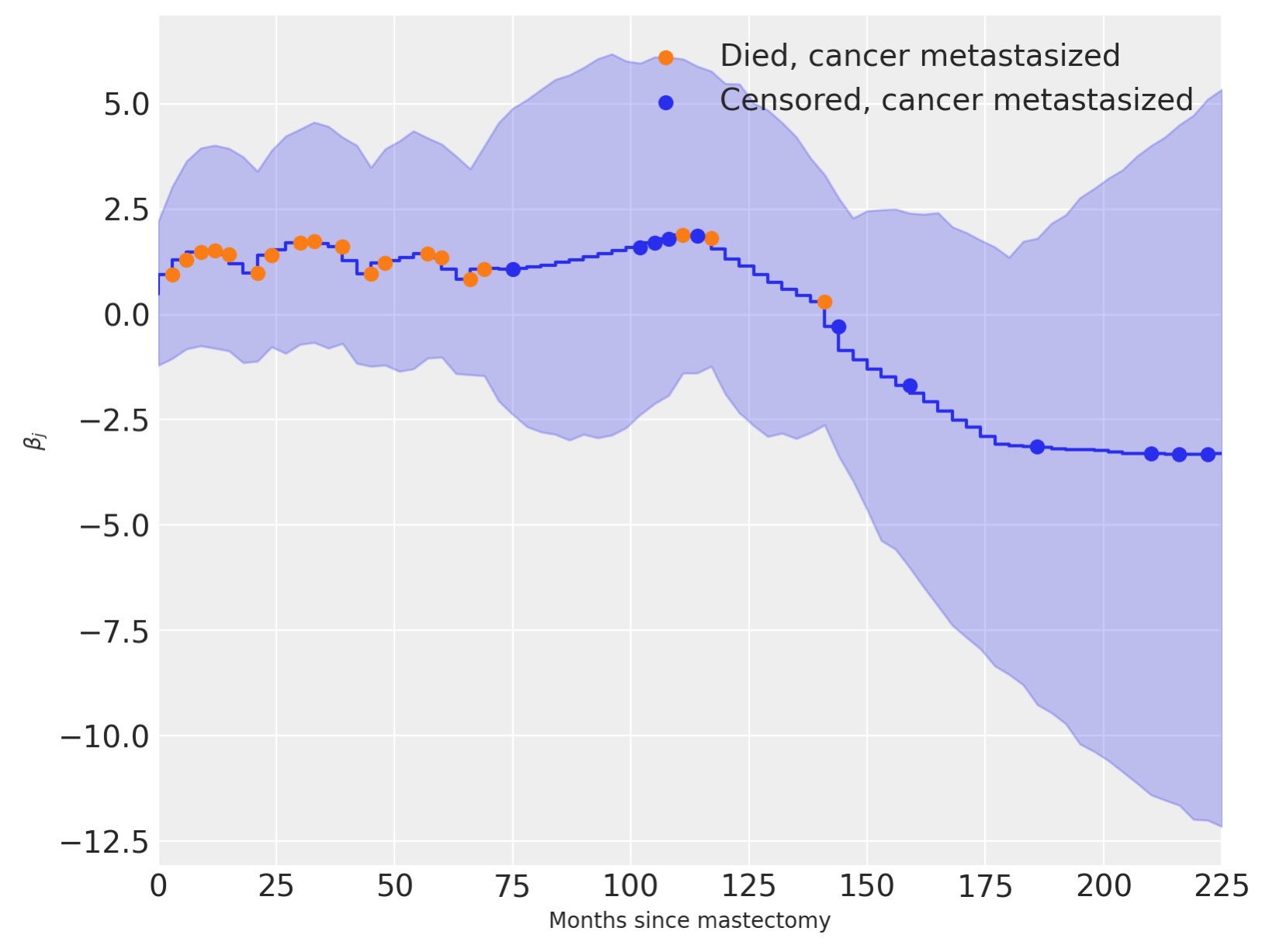
12の事例のうち、3件だけが、研究期間で、生存中に癌が転移して死亡している点で与えられる、係数βjは乳房切除の後、100ヶ月の周辺で急速に減少を始めます。これは妥当なように見えます。
私たちの累積ハザードの予測の変化と、生存関数が時間変化の影響に起因していることもまた、以下の図から全く明らかです。
tv_base_hazard = time_varying_idata.posterior["lambda0"]
tv_met_hazard = time_varying_idata.posterior["lambda0"] * np.exp(
time_varying_idata.posterior["beta"]
)fig, ax = plt.subplots(figsize=(8, 6))
ax.step(
interval_bounds[:-1],
cum_hazard(base_hazard.mean(("chain", "draw"))),
color="C0",
label="Had not metastasized",
)
ax.step(
interval_bounds[:-1],
cum_hazard(met_hazard.mean(("chain", "draw"))),
color="C1",
label="Metastasized",
)
ax.step(
interval_bounds[:-1],
cum_hazard(tv_base_hazard.mean(("chain", "draw"))),
color="C0",
linestyle="--",
label="Had not metastasized (time varying effect)",
)
ax.step(
interval_bounds[:-1],
cum_hazard(tv_met_hazard.mean(dim=("chain", "draw"))),
color="C1",
linestyle="--",
label="Metastasized (time varying effect)",
)
ax.set_xlim(0, df.time.max() - 4)
ax.set_xlabel("Months since mastectomy")
ax.set_ylim(0, 2)
ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
ax.legend(loc=2);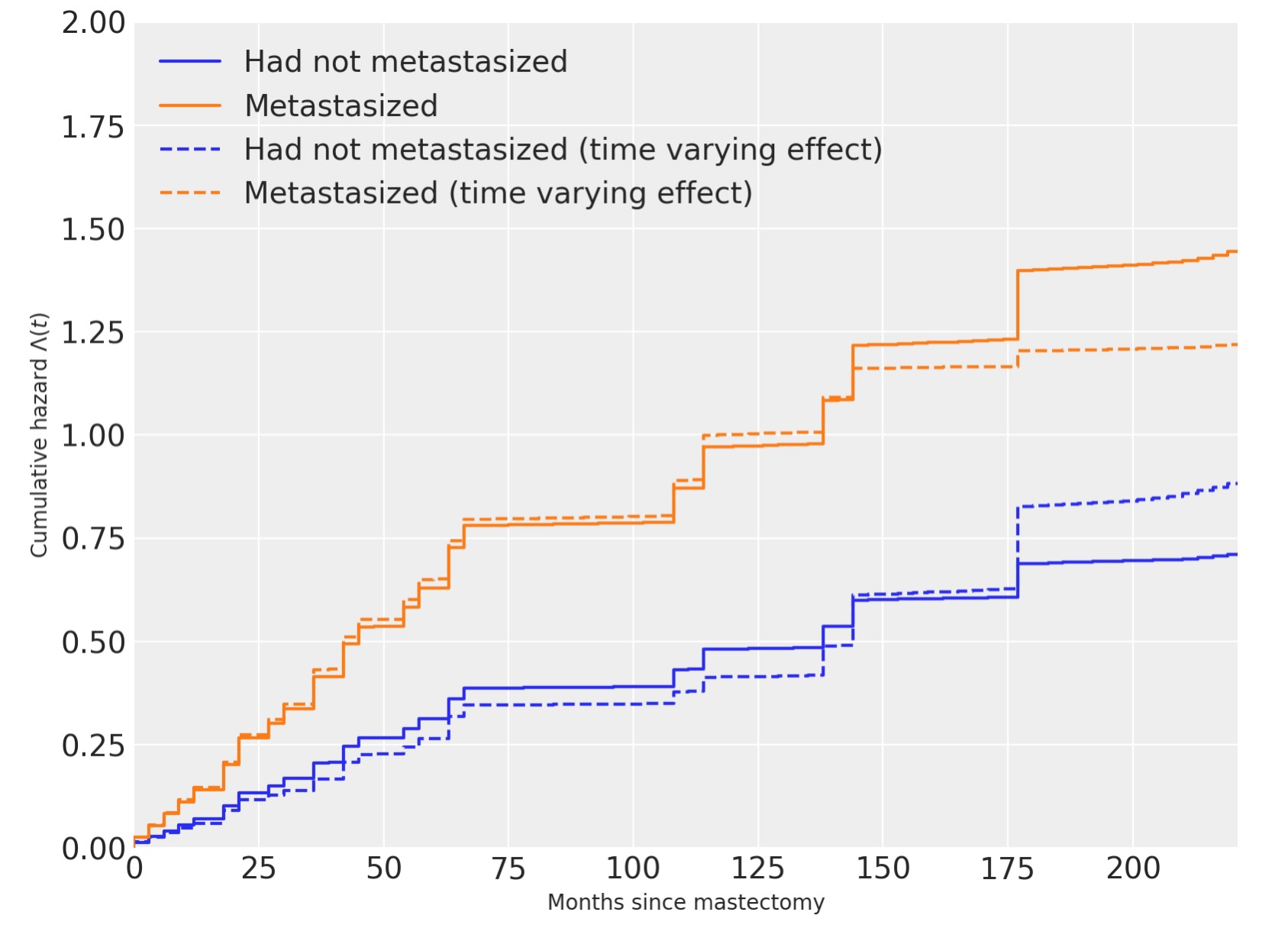
fig, (hazard_ax, surv_ax) = plt.subplots(ncols=2, sharex=True, sharey=False, figsize=(16, 6))
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(tv_base_hazard),
ax=hazard_ax,
color="C0",
smooth=False,
fill_kwargs={"label": "Had not metastasized"},
)
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(tv_met_hazard),
ax=hazard_ax,
smooth=False,
color="C1",
fill_kwargs={"label": "Metastasized"},
)
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(tv_base_hazard)), color="darkblue")
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(tv_met_hazard)), color="maroon")
hazard_ax.set_xlim(0, df.time.max())
hazard_ax.set_xlabel("Months since mastectomy")
hazard_ax.set_ylim(0, 2)
hazard_ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
hazard_ax.legend(loc=2)
az.plot_hdi(interval_bounds[:-1], survival(tv_base_hazard), ax=surv_ax, smooth=False, color="C0")
az.plot_hdi(interval_bounds[:-1], survival(tv_met_hazard), ax=surv_ax, smooth=False, color="C1")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(tv_base_hazard)), color="darkblue")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(tv_met_hazard)), color="maroon")
surv_ax.set_xlim(0, df.time.max())
surv_ax.set_xlabel("Months since mastectomy")
surv_ax.set_ylabel("Survival function $S(t)$")
fig.suptitle("Bayesian survival model with time varying effects");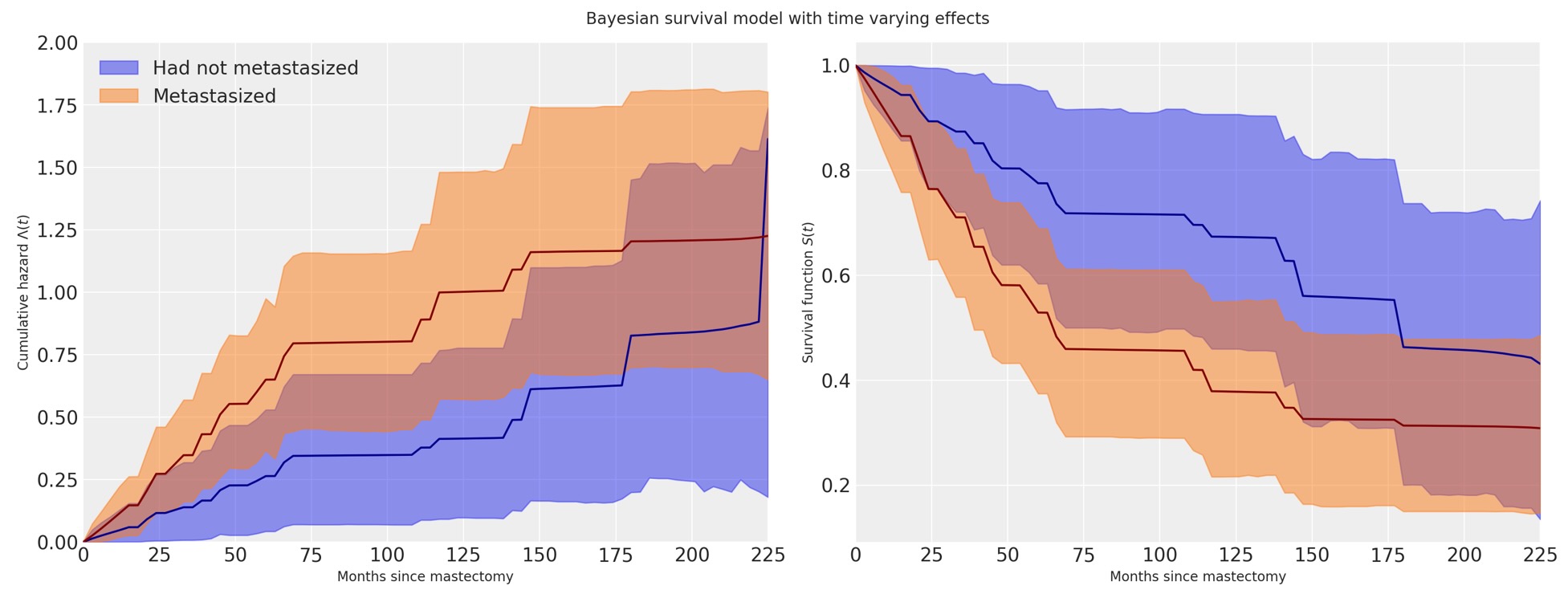
私たちは現実には、生存分析と生存分析へのベイジアンアプローチの両方の表面を引っ掻いただけです。ベイジアン生存分析のより詳しい情報はIbrahim et alで利用できます。(例えば、オリジナルか時間変化モデルのどちらか一方で、個別の短所を説明することを求めて良い。)
このチュートリアルは、IPython notebookとして利用できます。最初にここにあるブログ投稿に対応しています。
製作者
著書:Austin Rochfold
更新:Fernand Irarrazaval 2022年 6月 PyMC v4
更新:Chris Fonnesbeck 2023年 1月 PyMC v5