因子モデルは一般的に小さな数値の観測できない”因子”を発見することを試みることです。それは、たくさんの観測変数の変化の相当な部分に影響します。そして、それらは主成分分析のような次元縮約技術に関係しています。動的因子モデルは、観測していない因子の動的な変換を明白にモデル化します。そして、それはしばしば、時系列データに適用されます。
マクロ経済の同時性指標は、ビジネスサイクルの共通の成分を取り込むためにデザインされます。そのような成分は、同時に多くのマクロ経済変数に影響することを仮定しています。同時性指標(例えば、同時性経済指標のインデックスindex of Coincident Economic Indicatorsの見積もりと使用は、動的因子モデルの先行します。いくつかの影響のある論文 Stcks and Watson81989,1991)はそれらの理論的基礎を提供するために動的因子モデルを使っています。
以下、私たちは Stock Watson(1991)モデルの KimとNelson(1999)が見つけた取り扱いに従います。動的因子モデルを形式化するために、最大尤度によってパラメータを見積もり、同時性指標を生成します。
マクロ経済データ
共通に振る舞う四つのマクロ経済変数(これらの変数のバージョンはFREDで利用できます。以下で使われる系列のIDは、括弧で示されます)を考えることによって、同時性指標を生成します。
- Industrial Production(IPMAM) 工業生産
- Real aggregate income(excluding transfer payments)(W875RX1)
- Manufactuaring and trade sales(CMRMTSPL)
- Employees on non-farm payrolls(PAYEMS)
すべてのケースで、データは月次変化し、季節を調整して、1972-2005の期間をとっています。
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
np.set_printoptions(precision=4, suppress=True, linewidth=120)from pandas_datareader.data import DataReader
# Get the datasets from FRED
start = '1979-01-01'
end = '2014-12-01'
indprod = DataReader('IPMAN', 'fred', start=start, end=end)
income = DataReader('W875RX1', 'fred', start=start, end=end)
sales = DataReader('CMRMTSPL', 'fred', start=start, end=end)
emp = DataReader('PAYEMS', 'fred', start=start, end=end)
# dta = pd.concat((indprod, income, sales, emp), axis=1)
# dta.columns = ['indprod', 'income', 'sales', 'emp'](注)pandas-datareader
pandas-datareaderを使います。pandasのパッケージには含まれていません。pandas-datareaderとして独立したパッケージとしてインストールしてください。
conda install pandas-datareader
注意:FREDの最近の更新(8/12/15) 時系列CMRMTSPLは、1997年に開始するよう切り詰められています。これは、CMRMTSLは継ぎ合わせの系列に起因した、多分間違いです。早期の終端は、HMRMT系列からであり、遅い終端は、CMRMTによって定義されます。
これは(02/11/16)から正しくなっており、しかし、系列は、下に示されるように、HMRMTとCMRMTから手作業で構築されています。
# HMRMT = DataReader('HMRMT', 'fred', start='1967-01-01', end=end)
# CMRMT = DataReader('CMRMT', 'fred', start='1997-01-01', end=end)# HMRMT_growth = HMRMT.diff() / HMRMT.shift()
# sales = pd.Series(np.zeros(emp.shape[0]), index=emp.index)
# # Fill in the recent entries (1997 onwards)
# sales[CMRMT.index] = CMRMT
# # Backfill the previous entries (pre 1997)
# idx = sales.loc[:'1997-01-01'].index
# for t in range(len(idx)-1, 0, -1):
# month = idx[t]
# prev_month = idx[t-1]
# sales.loc[prev_month] = sales.loc[month] / (1 + HMRMT_growth.loc[prev_month].values)dta = pd.concat((indprod, income, sales, emp), axis=1)
dta.columns = ['indprod', 'income', 'sales', 'emp']
dta.index.freq = dta.index.inferred_freqdta.loc[:, 'indprod':'emp'].plot(subplots=True, layout=(2, 2), figsize=(15, 6));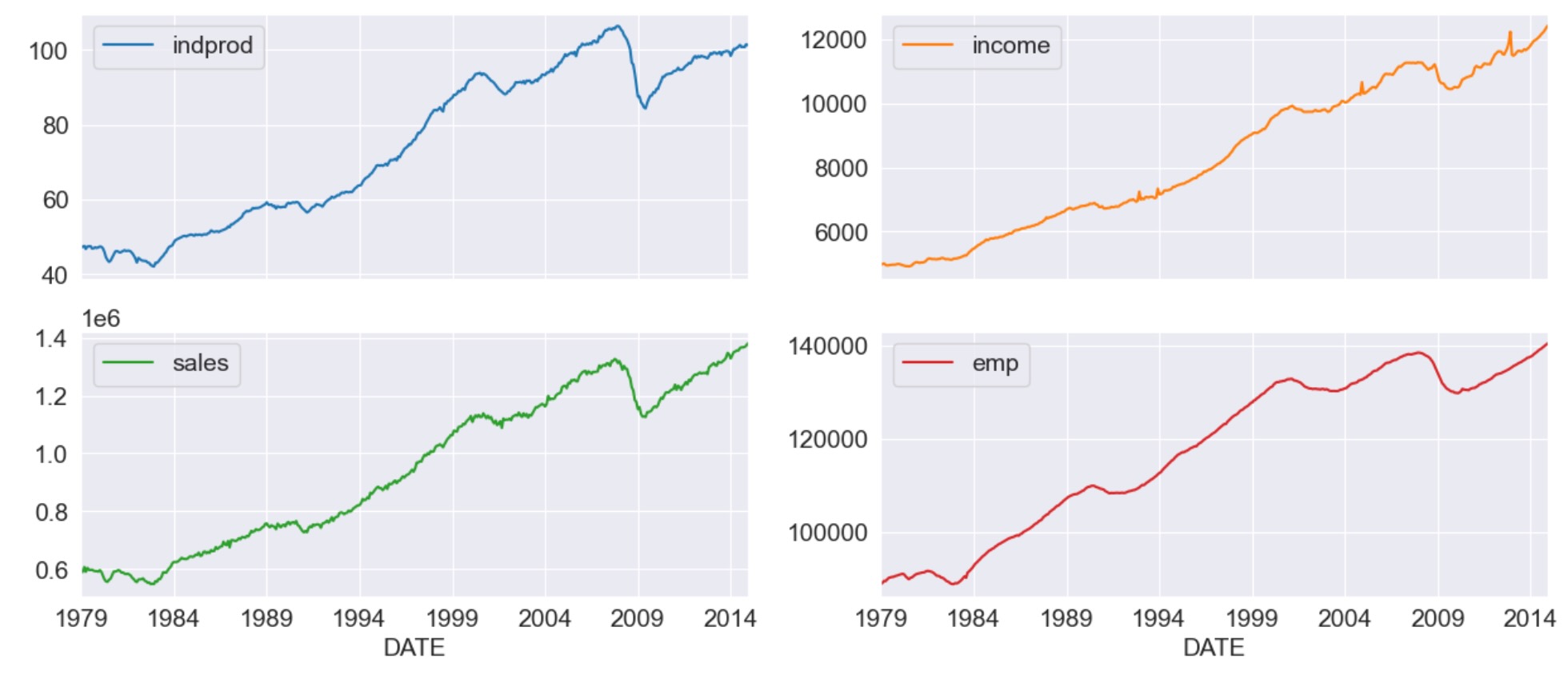
StockとWatson(1991)は、彼らのデータセットを、それらは、各系列のunit rootの帰無仮説を拒否できないだけでなく、それらは、系列が共統合されていた強力な証拠が見つからない、と報告しています。
結果として、彼らは、動作を落として正規化した、最初の変数の相違(対数の)を使ってモデルを見積ることを提案しています。
# Create log-differenced series
dta['dln_indprod'] = (np.log(dta.indprod)).diff() * 100
dta['dln_income'] = (np.log(dta.income)).diff() * 100
dta['dln_sales'] = (np.log(dta.sales)).diff() * 100
dta['dln_emp'] = (np.log(dta.emp)).diff() * 100
# De-mean and standardize
dta['std_indprod'] = (dta['dln_indprod'] - dta['dln_indprod'].mean()) / dta['dln_indprod'].std()
dta['std_income'] = (dta['dln_income'] - dta['dln_income'].mean()) / dta['dln_income'].std()
dta['std_sales'] = (dta['dln_sales'] - dta['dln_sales'].mean()) / dta['dln_sales'].std()
dta['std_emp'] = (dta['dln_emp'] - dta['dln_emp'].mean()) / dta['dln_emp'].std()
動的因子
因子モデルの一般動学は、次のようにかけます。
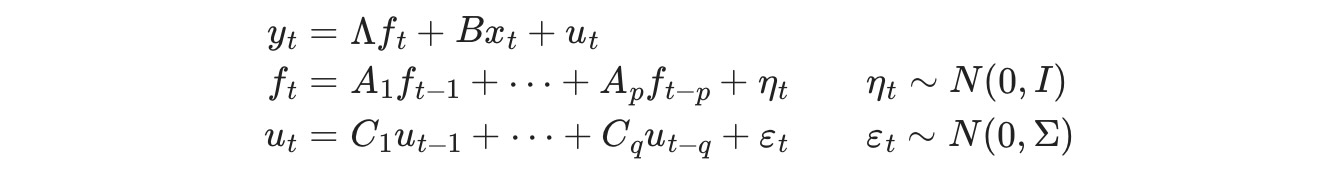
ここで、ytは観測データ、ftは観測されない因子、(ベクター自己回帰として発達),xtは外因性の変数、utはエラー、または"特異点"過程(utはオプションとして自己回帰が許されます)。 Λ行列は、しばしば、"因子読み込み"の行列として、参照されます。因子エラー項の変数は、観測されない因子の識別子を確認するために行列の識別用に設定されます。
このモデルは、状態空間形式に送られ、観測されない因子はカルマンフィルターで推定されます。尤度は、再帰フィルタリングの積で評価されます。そして最大尤度の推定はパラメータの推定に使用されます。
モデル仕様
この応用の特別な動的因子モデルは、AR(2)過程に従うことを仮定した観測されていない一つの因子を持ちます。イノベーションεt は、各式に関連した独立したエラー項で、独立していることを仮定しています。utは独立AR(2)過程に従います。
このようにここで考えられる仕様は、
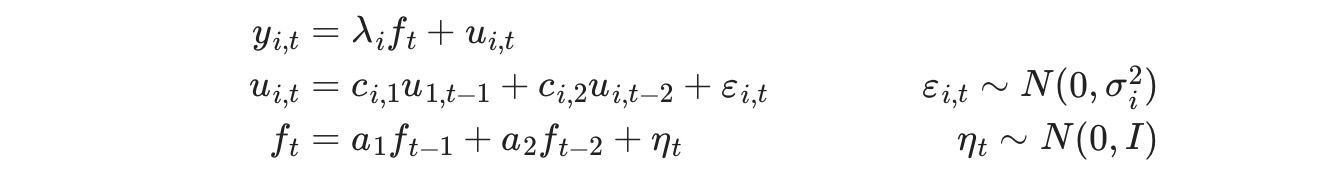
ここで、i は次のいづれかです。[indprod, income, sales, emp]
このモデルは、statsmodelに組み込まれている"動的因子"(DynamicFactor)モデルを使って形式化できます。特に、私たちは、次の仕様を持っています。
- k_factors = 1 (観測されない因子)
- factor_order = 2 (AR(2)過程に従う)
- error_var = False (VARとして連結するよりむしろ独立したAR過程としてエラーを出力)
- error_order = 2(エラーは2次の自己回帰AR(2)過程)
- error_cov_type ='diagonal'(イノベーションは非相関)
一旦、モデルが生成されると、パラメータは最大尤度で推定されます。これは、fit()メソッドを使って実行されます。
注意:データを動作を落として正規化していることを思い出してください。これは、以下に続く結果を解釈するのに重要になります。
余談:Kim とNelsonの彼らの実証に例では、実際、雇用変数が因子の遅延した値への依存を許容する少し異なるモデルを考えています。このモデルは、組み込まれているDynamicFactorクラスに適合しません。しかし、新しいパラメータの要求と制限を実装するサブクラスを使うことで適合させることができます。下の Appendix Aを参照してくさい。
パラメータの推定
多変量モデルは相対的に多くのパラメータを持つことができます。そして、ローカルな最小値を避けて、最大尤度を見つけることは難しくなります。この問題の緩和を試みるため、Scipyで利用できる修正Powell法を(詳細は最小化の論文を見てください)使って初期最大化ステップ(モデルが定義した最初のパラメータから)を実行します。標準LBFGS最適化法では、結果のパラメータは、その後、開始のパラメータとして使用されます。
# Get the endogenous data
endog = dta.loc['1979-02-01':, 'std_indprod':'std_emp']
# Create the model
mod = sm.tsa.DynamicFactor(endog, k_factors=1, factor_order=2, error_order=2)
initial_res = mod.fit(method='powell', disp=False)
res = mod.fit(initial_res.params, disp=False)
推定
一旦、モデルが推定されると、私たちが分析と推定に使うことができるふたつの成分があります。
- 推定パラメータ
- 推定因子
パラメータ
解釈するのが難しい多くの観測変数と観測因子があるモデルですが、推定パラメータはモデルの結果の理解に役立ちます。
この困難さの一つの理由は、因子の読み込みと観測されない因子間の識別の問題に起因します。簡単に分かる識別の問題は、読み込みと因子の符号です。下に表示している均衡モデルでは、すべての読み込んだ因子と観測されない因子の反対の符号からの結果になってます。
ここで、モデルの影響の簡単な解釈の一つは、観測されない因子に固執することです。私たちは、相当な影響を示していることを、見つけます。
print(res.summary(separate_params=False))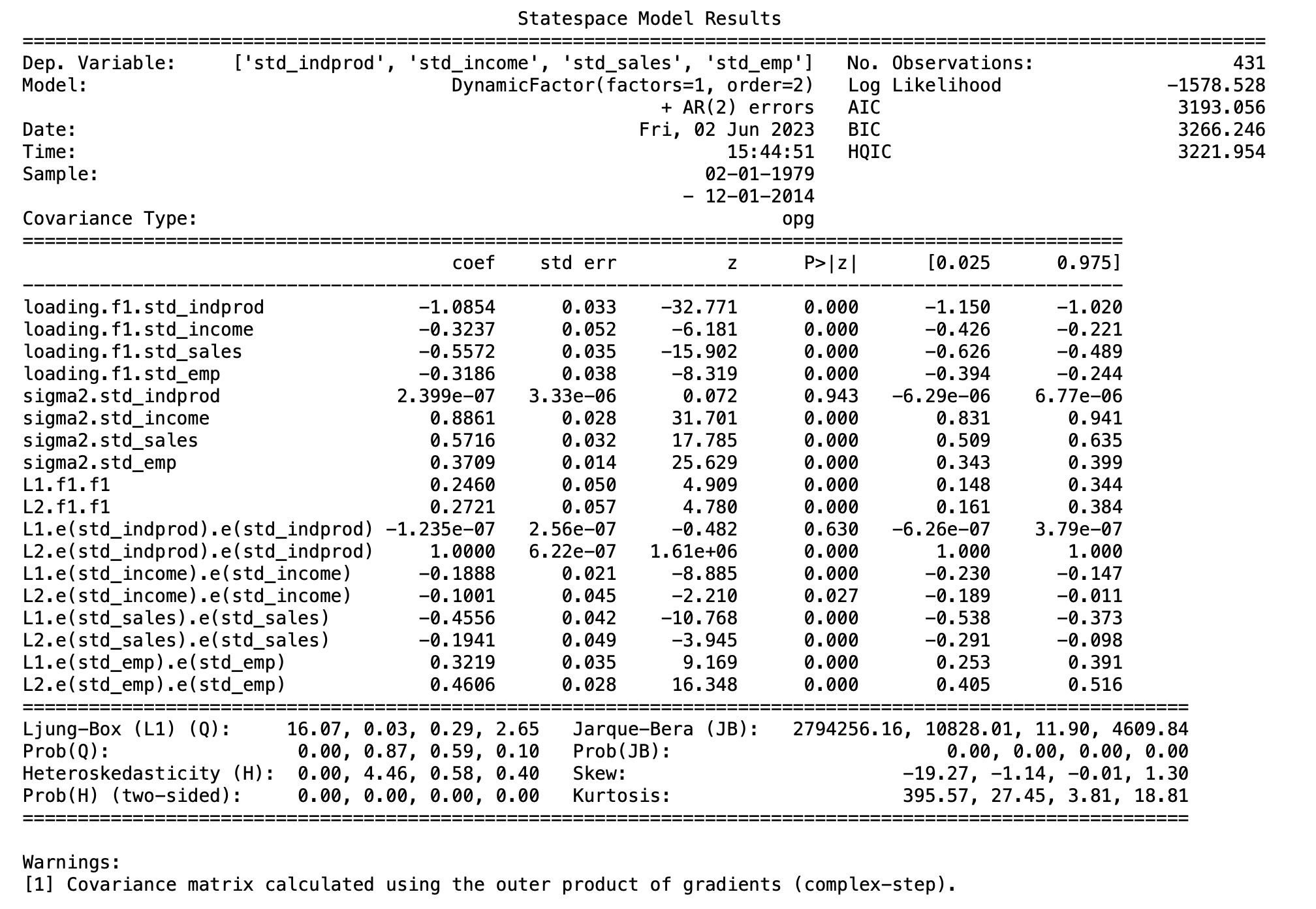
推定因子
観測されない因子を図示するのは役立ちますが、ふたつの理由で考えているより役立たないかもしれません。
- 上に記述した、符号に関係した識別問題
- データが異なっているので、推定因子は、オリジナルデータでなく、異なるデータの変異を説明します。
これらは、同時性指標が生成される理由です。
USリセッションのNBER指標に加えて、これらの予約で観測されない因子が下に図示されます。因子は、ビジネスサイクルの活動のいくつかの段階を取り出すのに成功していることがわかります。
fig, ax = plt.subplots(figsize=(13,3))
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, res.factors.filtered[0], label='Factor')
ax.legend()
# Retrieve and also plot the NBER recession indicators
rec = DataReader('USREC', 'fred', start=start, end=end)
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);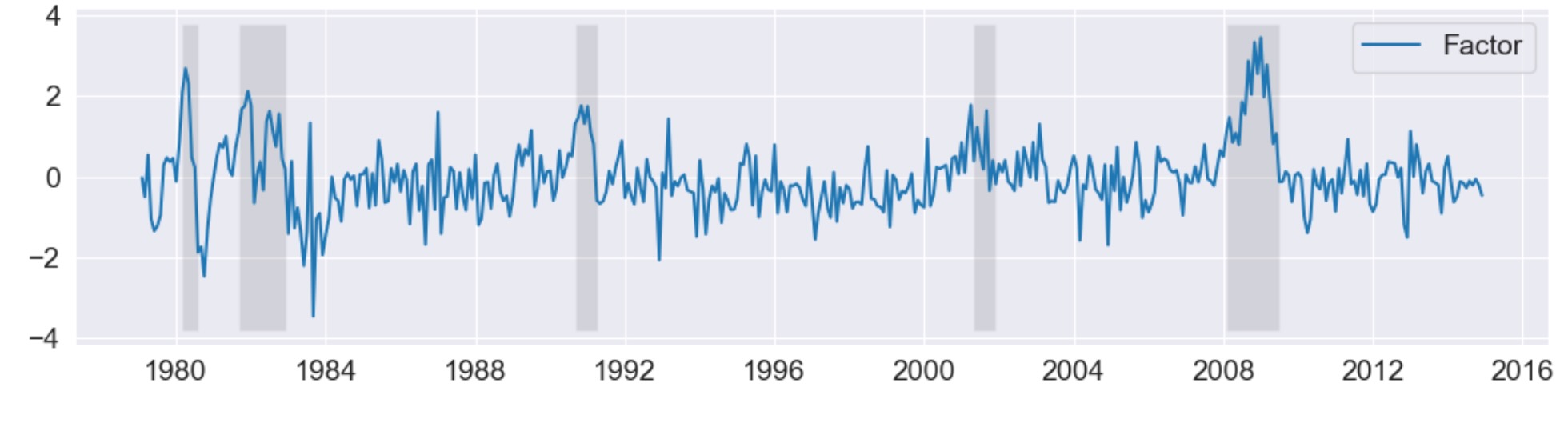
事後予測
ここで、同時性指標の助言により、私たちはモデルの結果を解釈することができますが、それらは、推定された因子により、何が取り込まれたか判別する、役にたつ一般的なアプローチです。与えられたものとして推定因子を取ることによって、それらを各観測した変数に回帰させ、決定した係数を保存して、各因子が分散の相当の部分を説明する変数とそうでない変数を判別することができます。
もっと多くの変数と因子を持つモデルでは、これは、時に解釈を因子に貸与することができます。(例えば、一つの因子が第一の現実の変数にロードされ、その他は正規の変数で)
四つの内因性の変数と、一つの因子だけを持つこのモデルでは、R2値の簡易なテーブルに分類するのは簡単です。しかし、より大きなモデルでは、そうではありません。この理由により、バーチャートがしばしば使われます。図から、私たちは因子が、売り上げと雇用の変異の大部分と工業生産指数の多くの変異を説明していることが簡単にわかります。それは収入を説明するには役立ちません。
res.plot_coefficients_of_determination(figsize=(8,2));
同時性指標
上に記述したように、このモデルのゴールは、マクロ経済の現在の状態を理解するために使用する、解釈できる系列を作ることでした。これは、同時指標が何かをデザイン(設計)することです。それは下のように構築されます。構築の説明に関心がある読者のために、KimとNelson(1999), StockとWatson(1991)を参照してください。
本質的に、実施することは、因子の平均の再構築です。私たちは、それを、フィラデルフィアFederal Reserve Bank(FRED のUSPHCI)によって発表された同時指標と比較します。
usphci = DataReader('USPHCI', 'fred', start='1979-01-01', end='2014-12-01')['USPHCI']
usphci.plot(figsize=(13,3));
dusphci = usphci.diff()[1:].values
def compute_coincident_index(mod, res):
# Estimate W(1)
spec = res.specification
design = mod.ssm['design']
transition = mod.ssm['transition']
ss_kalman_gain = res.filter_results.kalman_gain[:,:,-1]
k_states = ss_kalman_gain.shape[0]
W1 = np.linalg.inv(np.eye(k_states) - np.dot(
np.eye(k_states) - np.dot(ss_kalman_gain, design),
transition
)).dot(ss_kalman_gain)[0]
# Compute the factor mean vector
factor_mean = np.dot(W1, dta.loc['1972-02-01':, 'dln_indprod':'dln_emp'].mean())
# Normalize the factors
factor = res.factors.filtered[0]
factor *= np.std(usphci.diff()[1:]) / np.std(factor)
# Compute the coincident index
coincident_index = np.zeros(mod.nobs+1)
# The initial value is arbitrary; here it is set to
# facilitate comparison
coincident_index[0] = usphci.iloc[0] * factor_mean / dusphci.mean()
for t in range(0, mod.nobs):
coincident_index[t+1] = coincident_index[t] + factor[t] + factor_mean
# Attach dates
coincident_index = pd.Series(coincident_index, index=dta.index).iloc[1:]
# Normalize to use the same base year as USPHCI
coincident_index *= (usphci.loc['1992-07-01'] / coincident_index.loc['1992-07-01'])
return coincident_index以下、US リセッションと同時指標USPHCIの比較に加えて、計算した同時指標を図示します。
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
coincident_index = compute_coincident_index(mod, res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, label='Coincident index')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);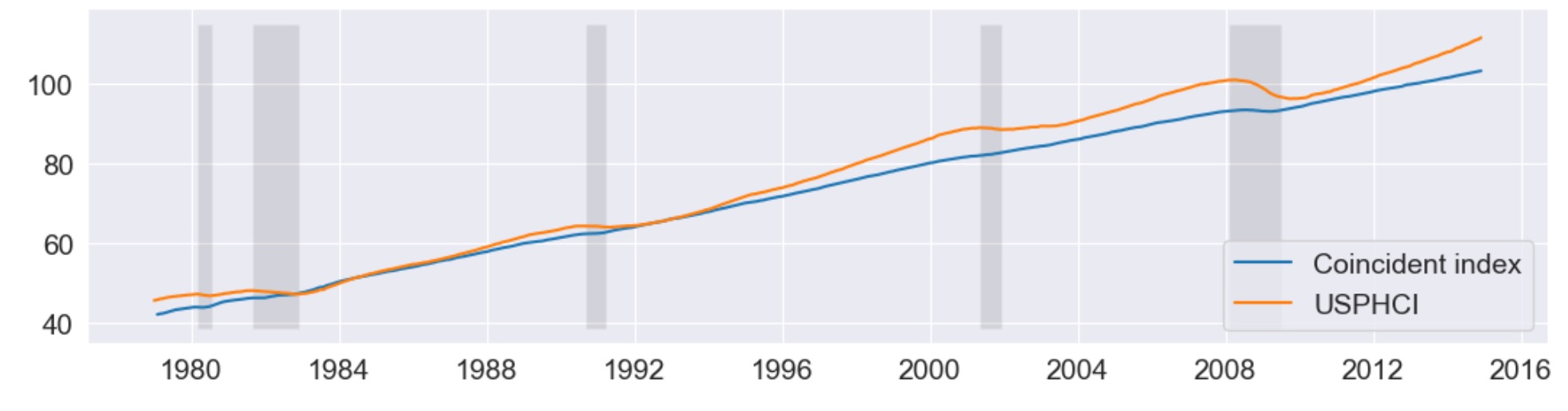
Appendix 1:動的因子モデルの拡張
次のようにする前の指標を思い出してください。
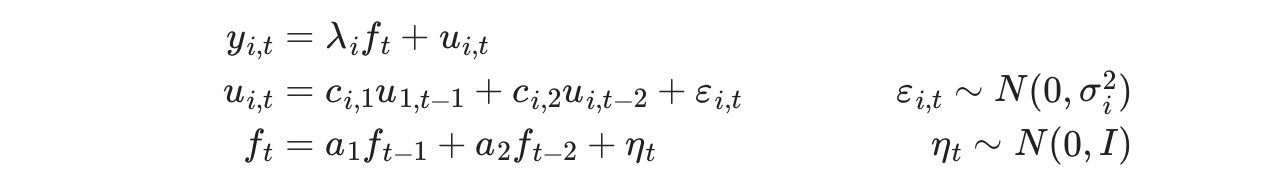
状態空間形式で書かれた、モデルの前の仕様は、以下の観測式

変換式は

DynamicFactorモデルは、状態空間の表記の設定を取り扱います。そして、DynaicFactor.uodateメソッドは、適当な位置に、適合したパラメータの値で満たします。
拡張した仕様は、employmentを因子の遅延した値への依存を許容したいことを除けば、前の例と同じです。これはyemp,t式を変更して生成します。ここに、
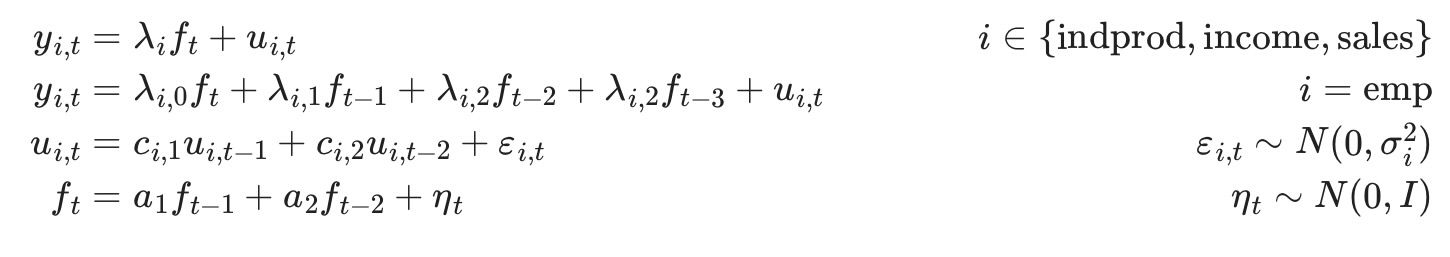
ここで、一致する観測式は以下のようになります。

二つの新しい状態変数,ft-2,ft-3を導入したことに注意してください。変換式を更新する必要があることを示しています。

このモデルは、DynamicFactorクラスによるout-of-boxを取り扱うことができません。しかし、適当な方法による状態空間表記を改める時に、サブクラスを作ることで、取り扱うことができるようになります。最初に、もし私たちがfactor_order=4に設定したならば、私たちは、したかったことをほぼ終了したことを注記します。このケースでは、観測式の最後の行は、
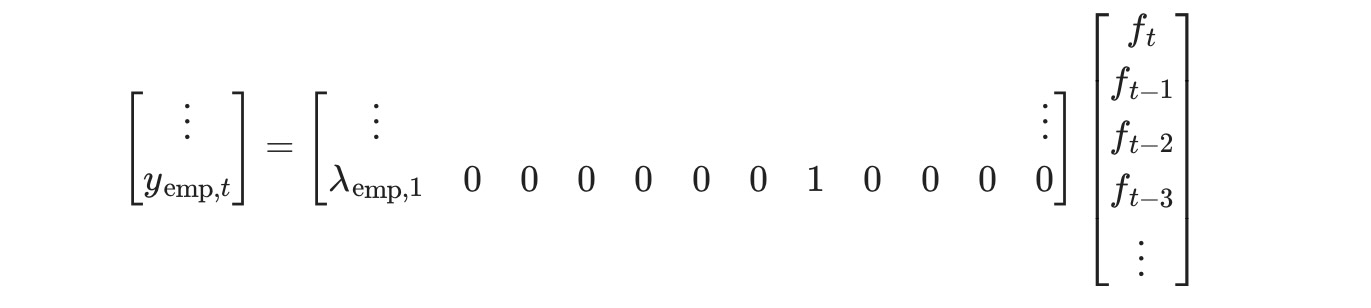
そして、変換式の最初の行は、
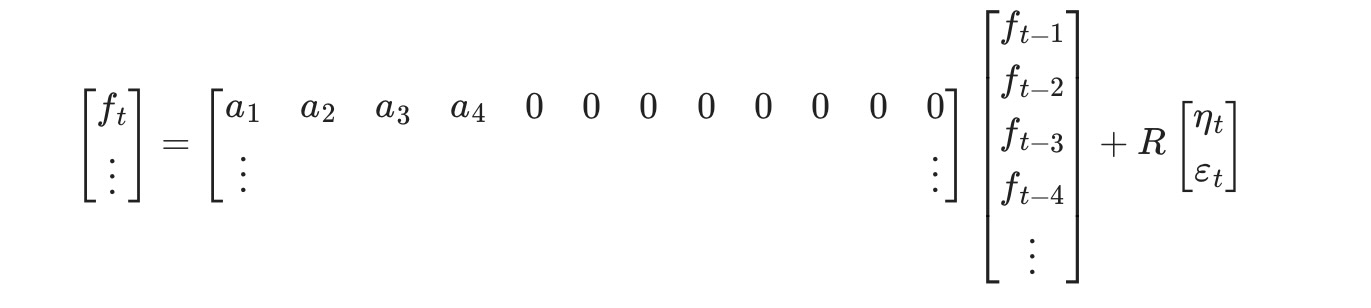
私たちがしたいことに対して、以下の相違があります。
- 上の状況で、λemp,jは、強制的に0 j>0 になり、それらはパラメータとして推定されます。
- 私たちは、AR(2)により、因子を変換したいだけです。しかし、上の状況下では、AR(4)になります
私たちのストラテジーは、DynamicFactorのサブクラスを作り、factor_order=4を仮定して、それに仕事の大部分を実行させます。私たちが実際にそのサブクラスで実行させることは、それらふたつの問題を修正することだけです。
最初に、これはサブクラスの全体のコードです。下に議論します。最初から下に定義され、除外されるメソッドはありません。実際、メソッド、init,start_parmss, param_names,transform_param,untransform_params,そしてupdateは、DynamicFactorクラスに限らず、statsmodelのすべての状態空間の核になる形式です。
from statsmodels.tsa.statespace import tools
class ExtendedDFM(sm.tsa.DynamicFactor):
def __init__(self, endog, **kwargs):
# Setup the model as if we had a factor order of 4
super(ExtendedDFM, self).__init__(
endog, k_factors=1, factor_order=4, error_order=2,
**kwargs)
# Note: `self.parameters` is an ordered dict with the
# keys corresponding to parameter types, and the values
# the number of parameters of that type.
# Add the new parameters
self.parameters['new_loadings'] = 3
# Cache a slice for the location of the 4 factor AR
# parameters (a_1, ..., a_4) in the full parameter vector
offset = (self.parameters['factor_loadings'] +
self.parameters['exog'] +
self.parameters['error_cov'])
self._params_factor_ar = np.s_[offset:offset+2]
self._params_factor_zero = np.s_[offset+2:offset+4]
@property
def start_params(self):
# Add three new loading parameters to the end of the parameter
# vector, initialized to zeros (for simplicity; they could
# be initialized any way you like)
return np.r_[super(ExtendedDFM, self).start_params, 0, 0, 0]
@property
def param_names(self):
# Add the corresponding names for the new loading parameters
# (the name can be anything you like)
return super(ExtendedDFM, self).param_names + [
'loading.L%d.f1.%s' % (i, self.endog_names[3]) for i in range(1,4)]
def transform_params(self, unconstrained):
# Perform the typical DFM transformation (w/o the new parameters)
constrained = super(ExtendedDFM, self).transform_params(
unconstrained[:-3])
# Redo the factor AR constraint, since we only want an AR(2),
# and the previous constraint was for an AR(4)
ar_params = unconstrained[self._params_factor_ar]
constrained[self._params_factor_ar] = (
tools.constrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[constrained, unconstrained[-3:]]
def untransform_params(self, constrained):
# Perform the typical DFM untransformation (w/o the new parameters)
unconstrained = super(ExtendedDFM, self).untransform_params(
constrained[:-3])
# Redo the factor AR unconstrained, since we only want an AR(2),
# and the previous unconstrained was for an AR(4)
ar_params = constrained[self._params_factor_ar]
unconstrained[self._params_factor_ar] = (
tools.unconstrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[unconstrained, constrained[-3:]]
def update(self, params, transformed=True, **kwargs):
# Peform the transformation, if required
if not transformed:
params = self.transform_params(params)
params[self._params_factor_zero] = 0
# Now perform the usual DFM update, but exclude our new parameters
super(ExtendedDFM, self).update(params[:-3], transformed=True, **kwargs)
# Finally, set our new parameters in the design matrix
self.ssm['design', 3, 1:4] = params[-3:]それで正確に何をしたのでしょうか。
"__init__
ここでの重要なステップは、私たちが操作する基礎の動的因子モデルを特徴づけることです。特に、上に記述したように、因子のために最終的にはAR(2)モデルになりますが、私たちは、factor_order=4で初期化します。私たちはまた、いくつかの一般的な設定に関連したタスクを実行します。
"start_params"
start_paramsは最適化の初期値として使います。私たちは、三つの新しいパラメータを追加しているので、それらをパスする必要があります。もし、これを実行しなければ、最適化は、三つの要素のデフォルトの値で開始します。
"param_names"
parame_namesは、色々な場所で使われます。しかし、特に結果クラスで使われます。下に、全体の結果のまとめを得ます。それは、すべてのパラメータが関連する名前を持つ時に可能になります。
"transform_param" and "untransferm_param"
オプティマイザは制約なく、可能なパラメータの値を選択します。それは、通常は必要とされない、(例えば、分散は負の値にならないので)そして、transform_paramは、オプティマイザで使われる制限のない値を、モデルに適切な制限のない値に変換するのに使用されます。分散項は普通、二乗され、(正になるように強制的に)AR遅延係数は、しばしば定常モデルに導くのを制限されます。untransform_paramは、逆の操作に使われます。(そして、開始パラメータは通常モデルに適切な値を特徴付ける点で重要です。そして、私たちは、最適化ルーチンを始める前にオプティマイザに適当な値に変換する必要があります。)
私たちは、私たちの新しいパラメータを変換、または逆変換する必要がない時でさえ、(読み込みは理論的には、任意の値を取り得ます)、私たちは、ふたつの理由でこのコードを修正する必要があります。
- DynamicFactorクラスのバージョンは、私たちが今もっているものより、三つの少ないパラメータを予期しています。少なくとも、私たちは三つの新しいパラメータを取り扱う必要があります。
- DynamicFactorクラスのバージョンは、それがAR(4)モデルなので、因子遅延係数を定常になるよう制限します。私たちは、実際にはAR(2)モデルをもっているので、再度、制限を実行する必要があります。私たちはまた、最後のふたつの自己回帰係数をここでゼロに設定します。
"update"
私たちが、新しいupdateメソッドを規定する必要がある、もっとも重要な理由は、状態空間形式の中に置く必要のある三つの新しいパラメータがあるためです。特に、私たちは、三つの新しいパラメータを状態空間で表す以外は、親のDynamicFactor.updateクラスにすべてのパラメータの配置の取り扱いを任せます。そして、その時、最後の三つを手動で置きます。
# Create the model
extended_mod = ExtendedDFM(endog)
initial_extended_res = extended_mod.fit(maxiter=1000, disp=False)
extended_res = extended_mod.fit(initial_extended_res.params, method='nm', maxiter=1000)
print(extended_res.summary(separate_params=False))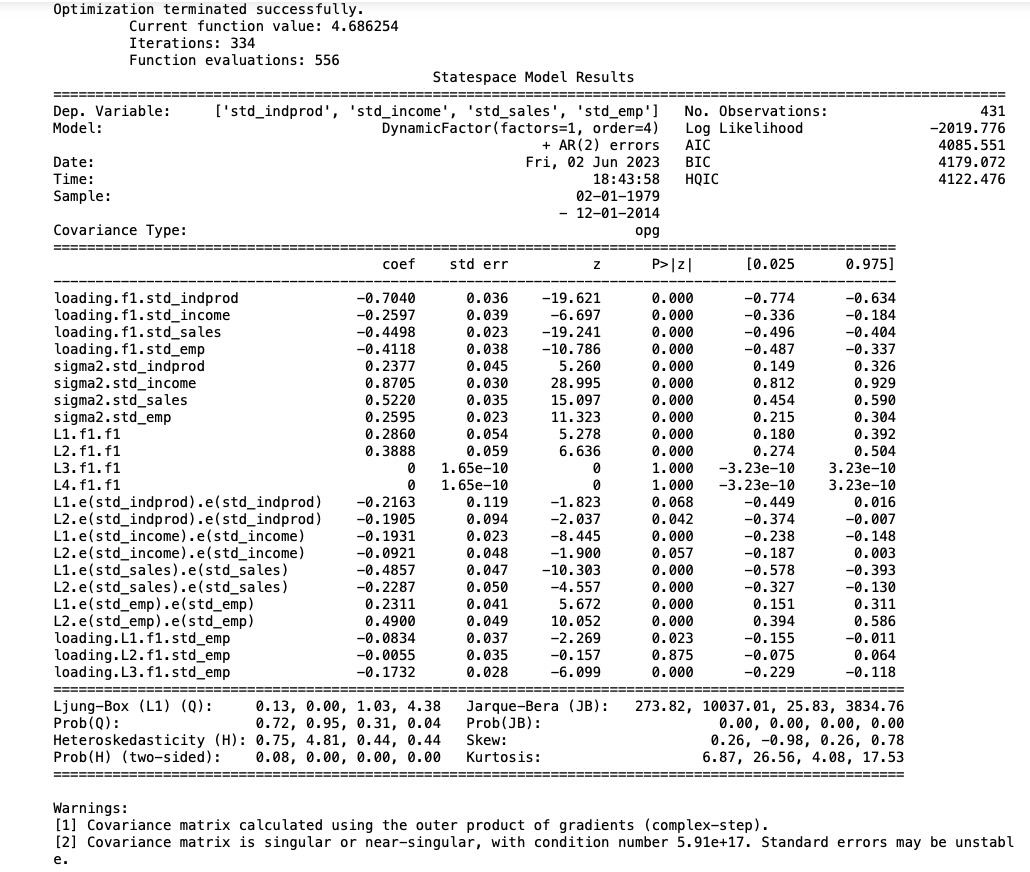
このモデルは、尤度を増加させますが、追加の三つのパラメータが不当な扱いを受けるAICとBICの尺度より好まれます。
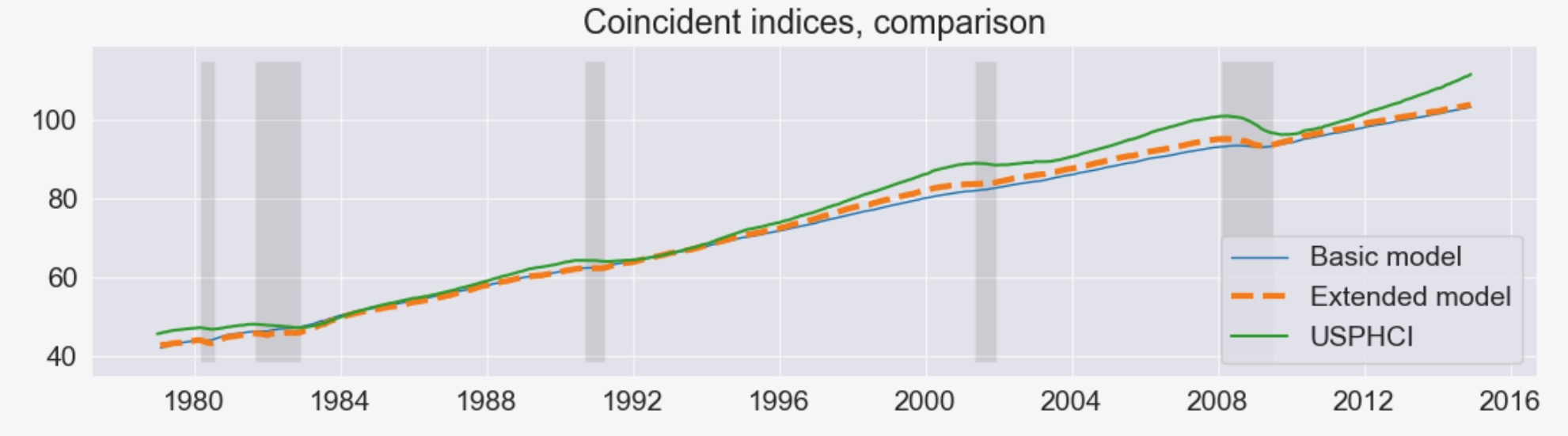
さらには、定性的な結果は変わりません。私たちがR2チャート、新しい同時性指標の更新から見たように、それらの両方は、実際に以前の結果と一致しています。
extended_res.plot_coefficients_of_determination(figsize=(8,2));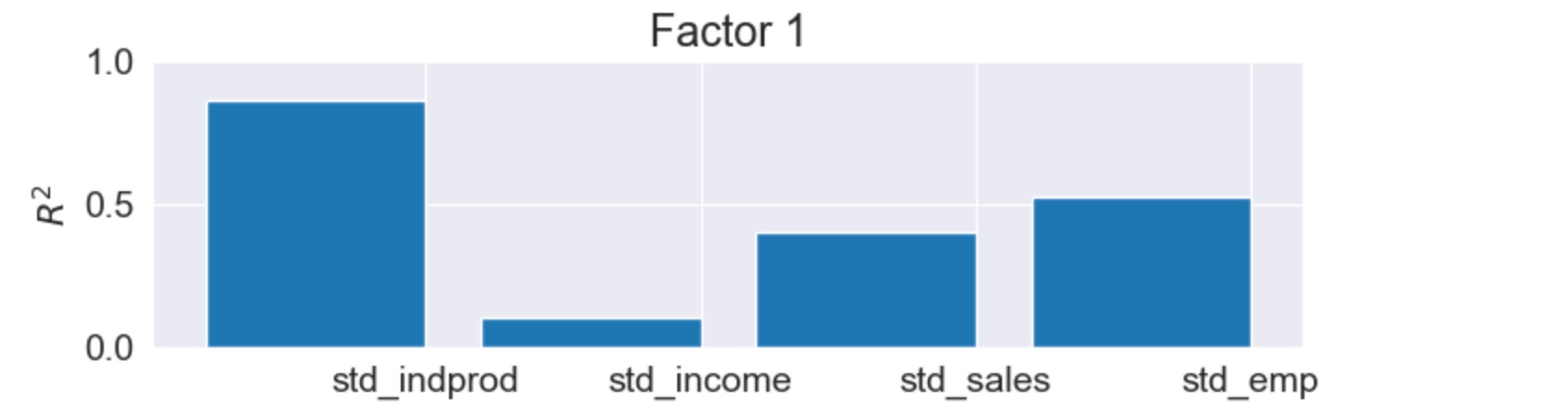
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
extended_coincident_index = compute_coincident_index(extended_mod, extended_res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, '-', linewidth=1, label='Basic model')
ax.plot(dates, extended_coincident_index, '--', linewidth=3, label='Extended model')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
ax.set(title='Coincident indices, comparison')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);