このノートブックはレジームの変化と動的回帰モデルを推定するために、statsmodelsのマルコフ・スイッチングモデルを使う例を提供します。それは、Stataのマルコフスイッチングの論文の例です。ここで(http://www.stata.com/manuals14/tsmswitch.pdf.)参照できます。
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
# NBER recessions
from pandas_datareader.data import DataReader
from datetime import datetime
usrec = DataReader(
"USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)区間切り替えのあるフェデラル・ファンンド・レート
最初の例は、一定の区間の周りのノイズとフェデラルファンドレートをモデル化します。しかし、区間は異なるレジーム間で変化します。このモデルは簡単に、
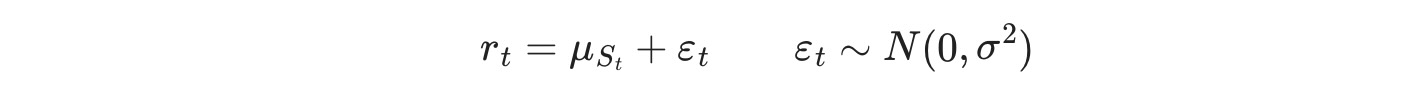
ここで St ⊆ { 0,1 }, レジーム遷移は次に従います。
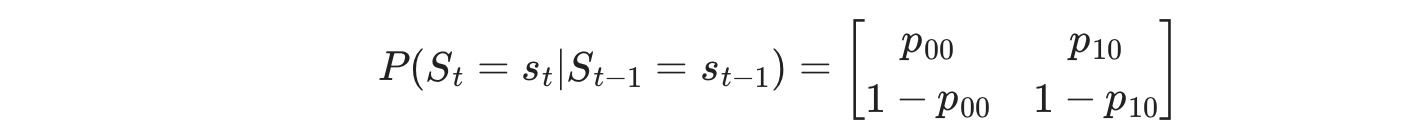
私たちは、このモデルのパラメータを最大尤度: p00 ,p10, μ0, μ1, σ2によって推定します。
この例で使うデータはここで(https://www.stata-press.com/data/r14/usmacro.)取得できます。
# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import fedfunds
dta_fedfunds = pd.Series(
fedfunds, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS")
)
# Plot the data
dta_fedfunds.plot(title="Federal funds rate", figsize=(12, 3))
# Fit the model
# (a switching mean is the default of the MarkovRegession model)
mod_fedfunds = sm.tsa.MarkovRegression(dta_fedfunds, k_regimes=2)
res_fedfunds = mod_fedfunds.fit()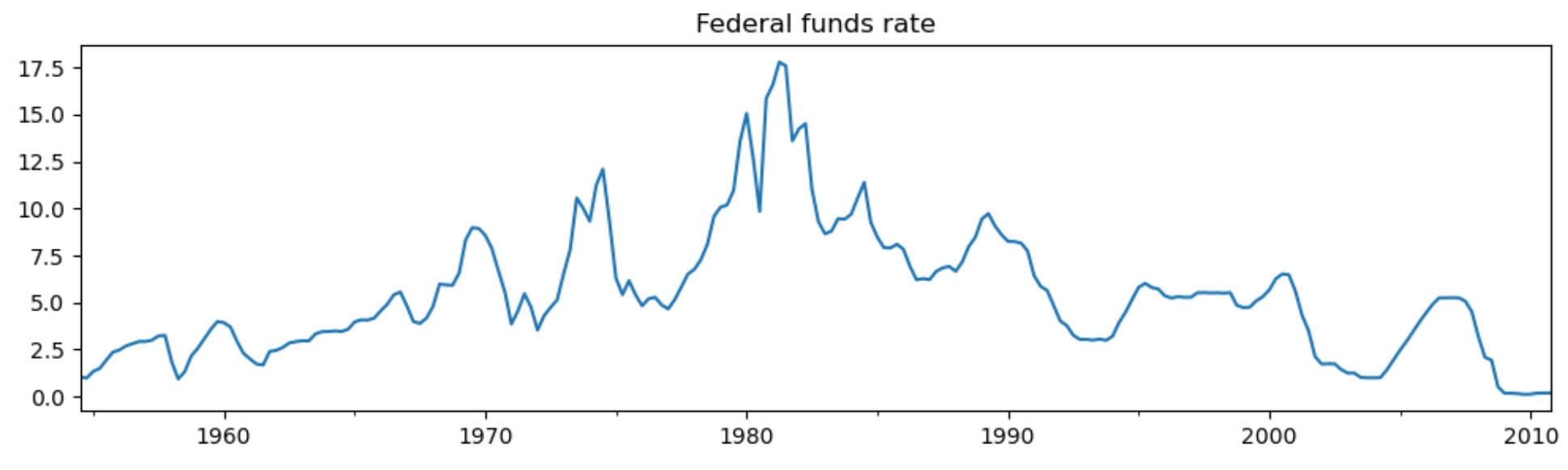
res_fedfunds.summary()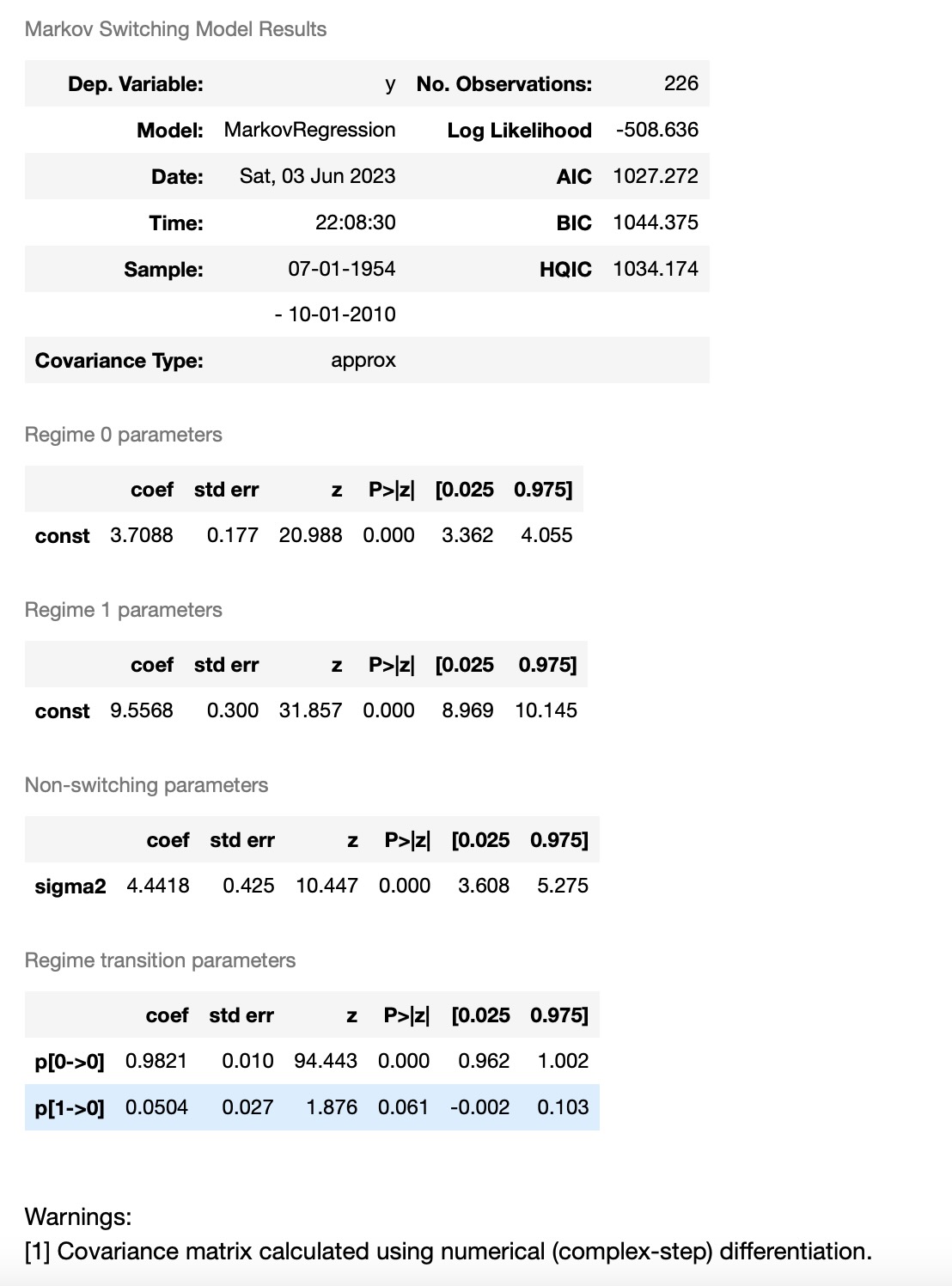
出力結果から、最初のレジーム("低レジーム")のフェデラルファンドレートの平均は、3.7、"高レジーム"は、9.6 と推定されます。下はスムース化した高レジームの確率です。モデルは、1980年代が高いフェデラルファンドレートが存在していた期間であると示しています。
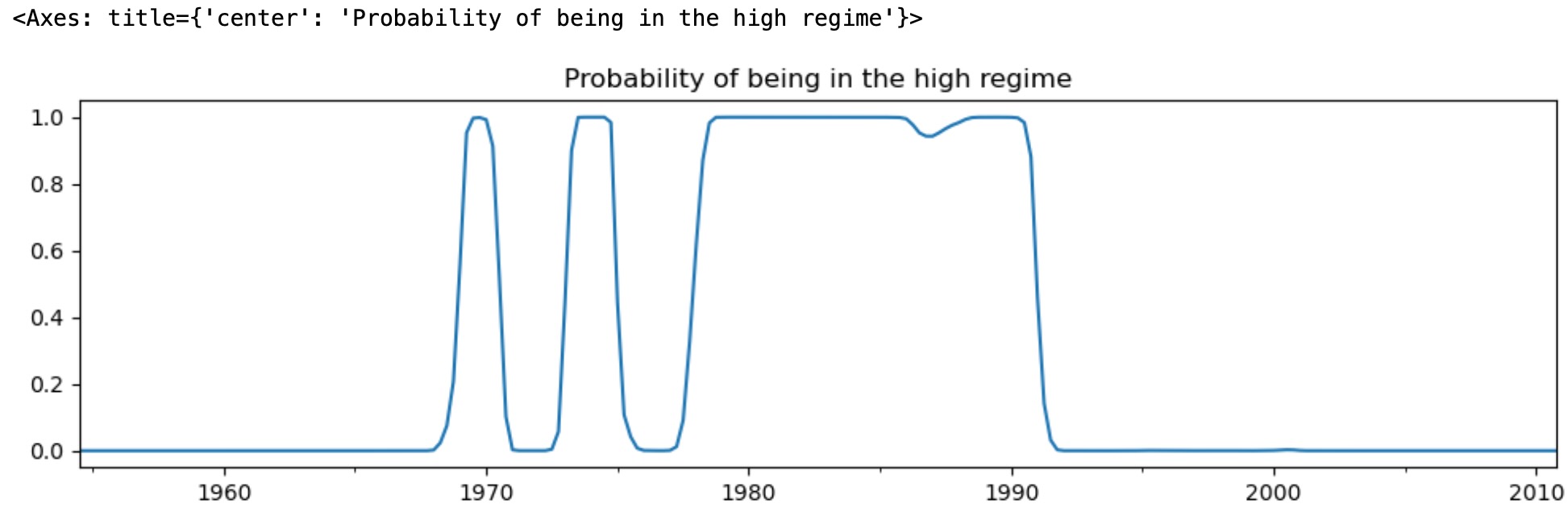
res_fedfunds.smoothed_marginal_probabilities[1].plot(
title="Probability of being in the high regime", figsize=(12, 3)
)
推定遷移確率から私たちは、低レジームと高レジーム推定期間を計算することができます。
print(res_fedfunds.expected_durations)[55.85400626 19.85506546]低レジームが約14年持続することを予期し、高レジームが約5年だけ持続することが予測されます
区間切り替えのあるフェデラル・ファンンド・レートと遅延従属変数
2番目の例は、フェデラルファンドレートの遅延した値を含み、前の例を補います。
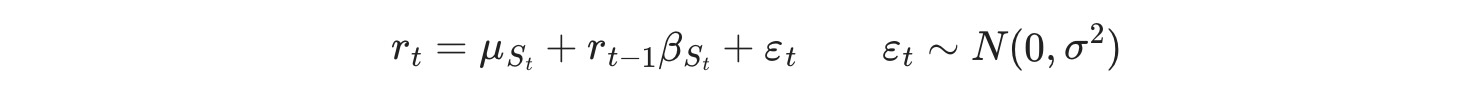
ここで St ⊆ { 0,1 }, レジーム遷移は次に従います。
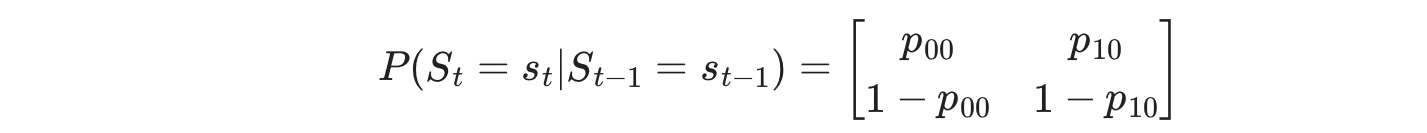
私たちは、このモデルのパラメータを最大尤度: p00 ,p10, μ0, μ1, σ2によって推定します。
# Fit the model
mod_fedfunds2 = sm.tsa.MarkovRegression(
dta_fedfunds.iloc[1:], k_regimes=2, exog=dta_fedfunds.iloc[:-1]
)
res_fedfunds2 = mod_fedfunds2.fit()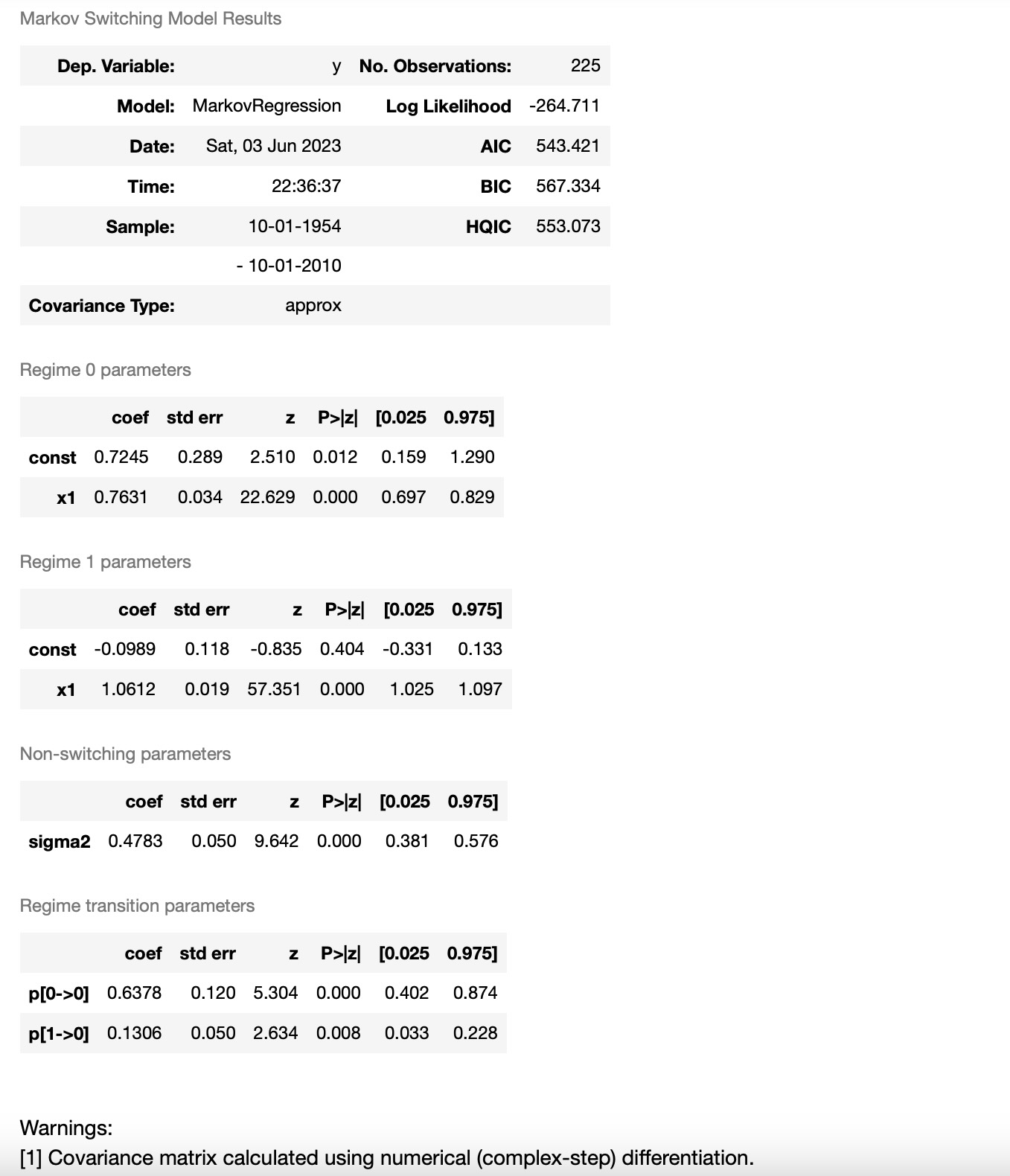
これらは、出力結果から気づくことがいくつかあります。
- 情報の基準は大幅に減少しました。このモデルが前のモデルよりもよく適合していることを示しています。
- レジームの解釈は、区間の期間が切り替わったことです。今最初のレジームがより高い区間で、2番目のレジームがより低い区間を持ちます。
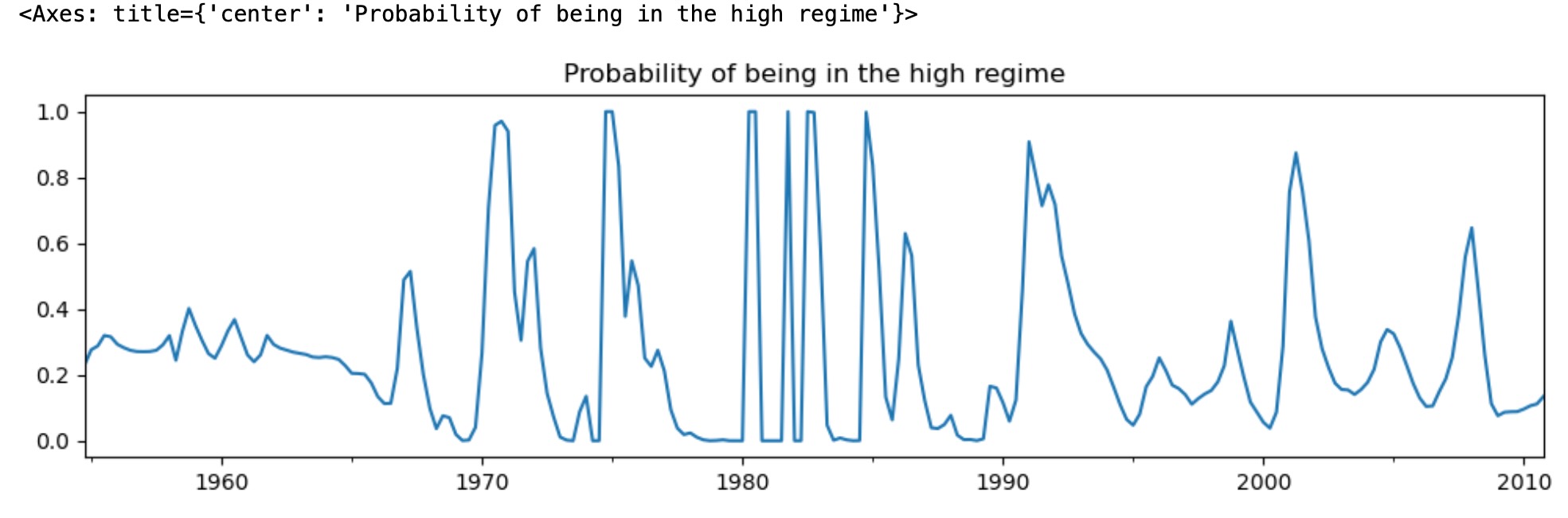
高レジーム状態のスムース化確率を検証することで、もっと変動することがわかります。
res_fedfunds2.smoothed_marginal_probabilities[0].plot(
title="Probability of being in the high regime", figsize=(12, 3)
)
最後に各レジームの予測期間は少し減少します。
print(res_fedfunds2.expected_durations)[2.76105188 7.65529154]2または3レジームのテイラールール
私たちは、どちらがよりよくデータに適合するか判るように2と3のレジーム両方があるテイラータイプのルールの切り替えを推定するために、ふたつの追加の外因性の変数ー生産ギャップの尺度とインフレーションの尺度を含みます。
なぜならモデルは、しばしば推定するのが難しく、3レジームモデルでは、私たちは20回ランダムサーチを反復し、結果を改良するために、開始パラメータの詳しいサーチに費やします。
# Get the additional data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import ogap, inf
dta_ogap = pd.Series(ogap, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))
dta_inf = pd.Series(inf, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))
exog = pd.concat((dta_fedfunds.shift(), dta_ogap, dta_inf), axis=1).iloc[4:]
# Fit the 2-regime model
mod_fedfunds3 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=2, exog=exog)
res_fedfunds3 = mod_fedfunds3.fit()
# Fit the 3-regime model
np.random.seed(12345)
mod_fedfunds4 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=3, exog=exog)
res_fedfunds4 = mod_fedfunds4.fit(search_reps=20)res_fedfunds3.summary()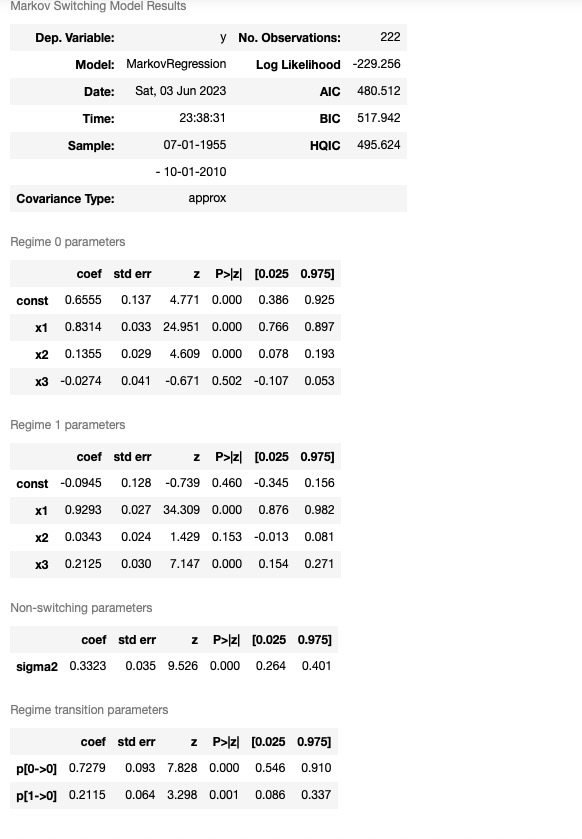
res_fedfunds4.summary()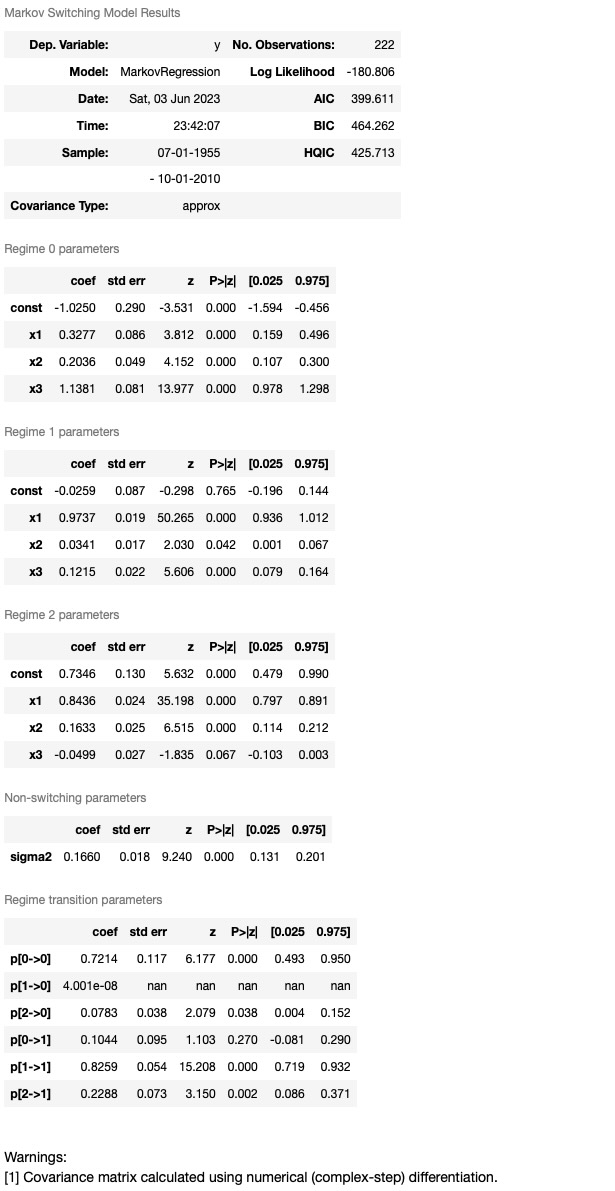
低い情報の基準のせいで、低、中、高、金利レジームの解釈で、私たちは3ー状態モデルを好むかもしれません。各レジームのスムース化した確率は下に図示されます。
fig, axes = plt.subplots(3, figsize=(10, 7))
ax = axes[0]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-interest rate regime")
ax = axes[1]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-interest rate regime")
ax = axes[2]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-interest rate regime")
fig.tight_layout()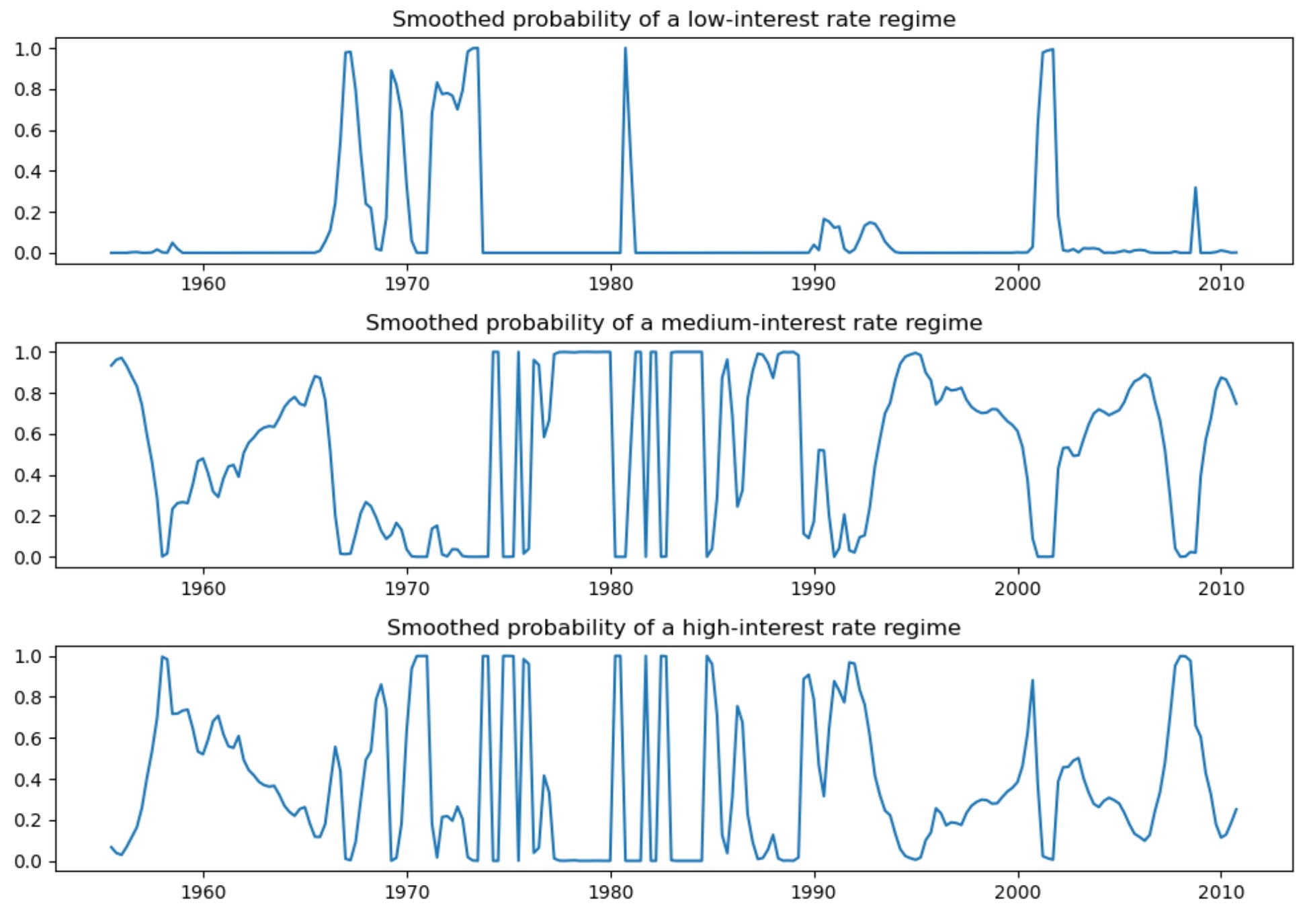
分散の切り替え
私たちはまた分散切り替えを調整します。特に次のモデルを考えます。
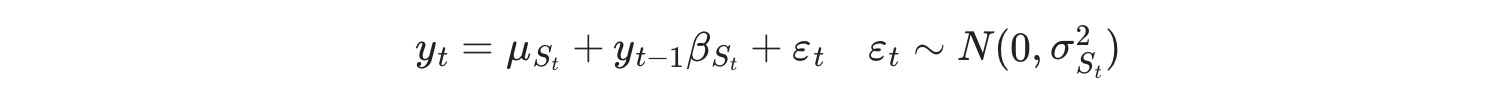
私たちは、このモデルのパラメータを推定するために、最大尤度を使います。: p00 ,p10, μ0, μ1 , β0 , β1 , σ02,σ12
アプリケーションは株式の絶対リターンです。
# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import areturns
dta_areturns = pd.Series(
areturns, index=pd.date_range("2004-05-04", "2014-5-03", freq="W")
)
# Plot the data
dta_areturns.plot(title="Absolute returns, S&P500", figsize=(12, 3))
# Fit the model
mod_areturns = sm.tsa.MarkovRegression(
dta_areturns.iloc[1:],
k_regimes=2,
exog=dta_areturns.iloc[:-1],
switching_variance=True,
)
res_areturns = mod_areturns.fit()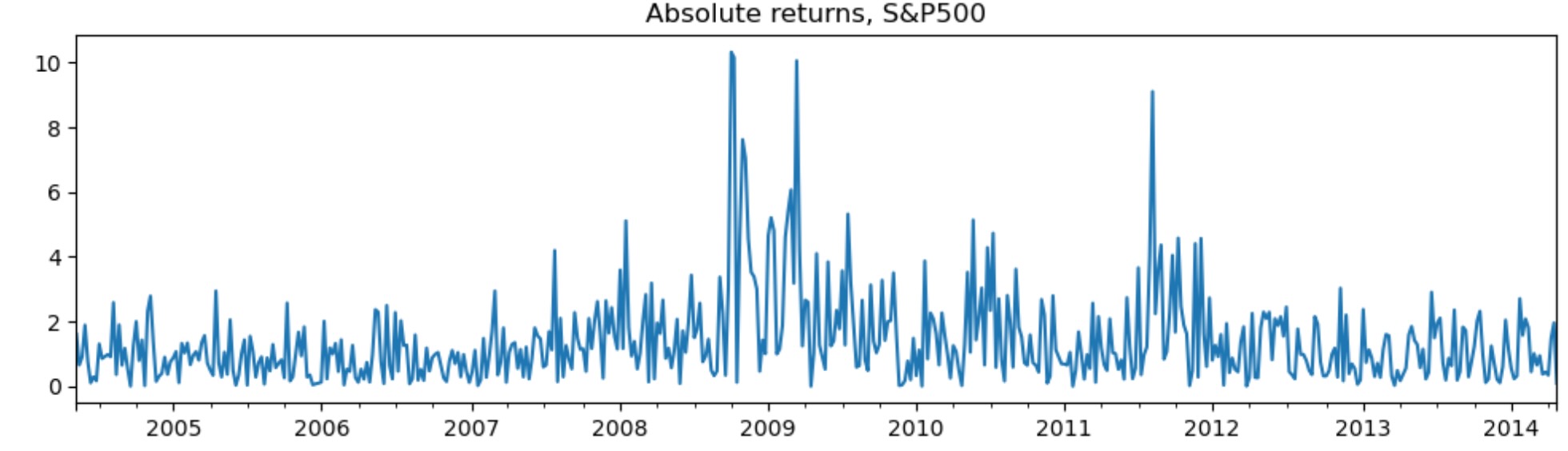
res_areturns.summary()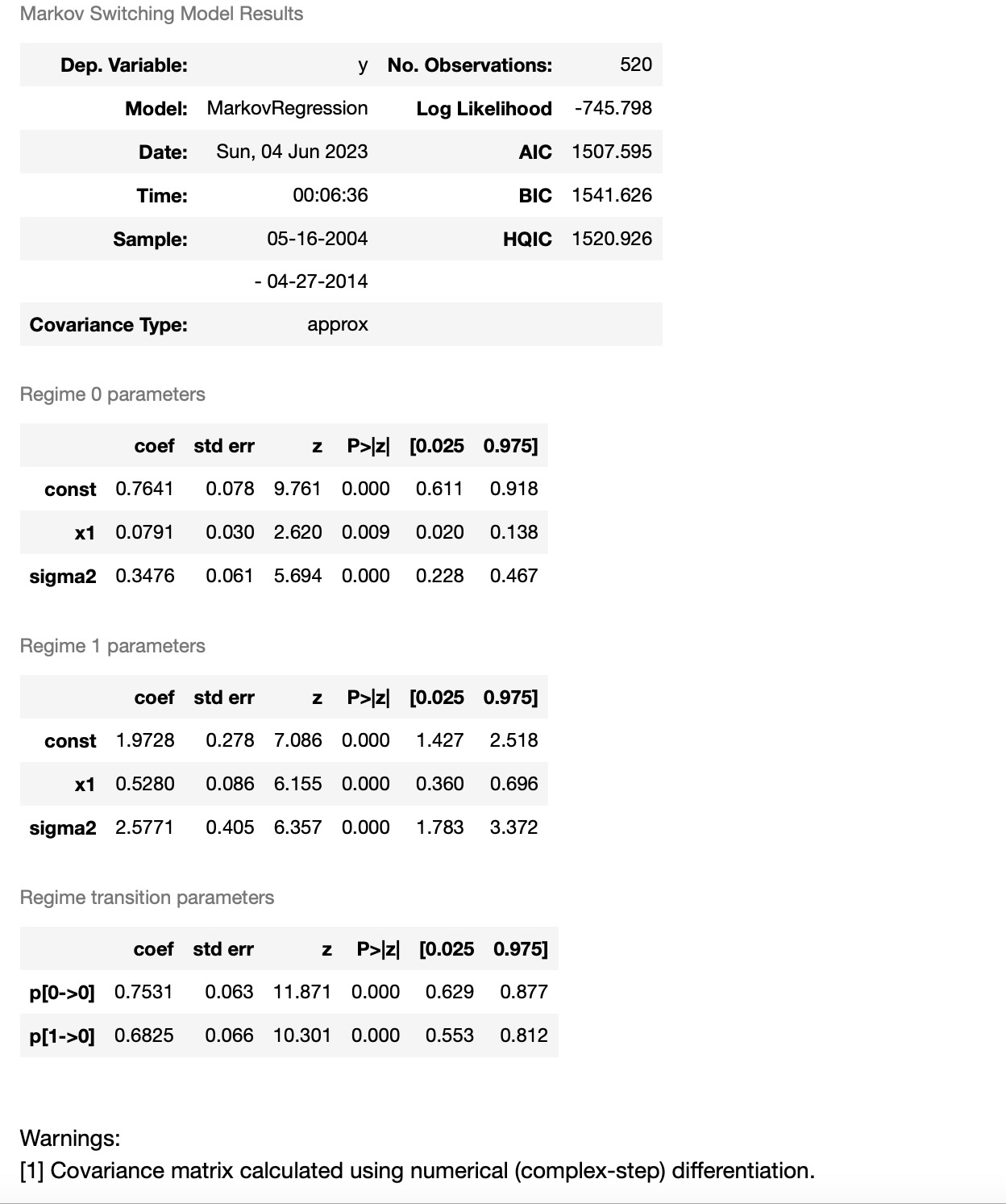
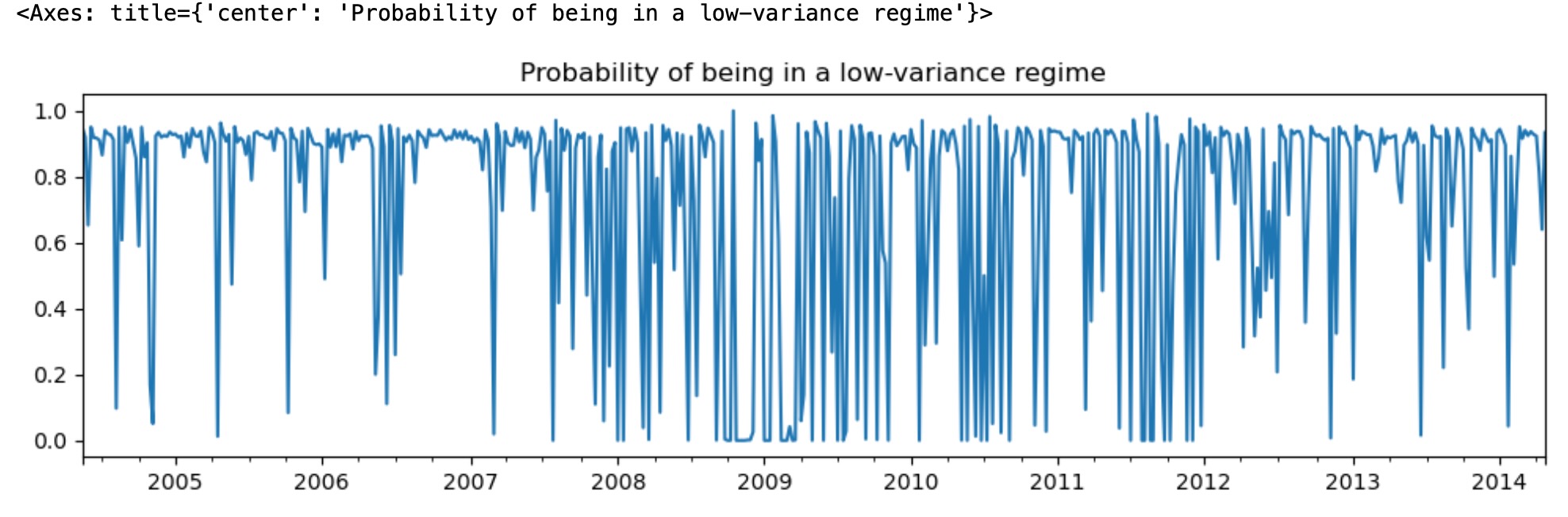
最初のレジームは低い分散のレジーム、そして2番目のレジームは高い分散のレジームです。下に私たちは低い分散レジームにある確率を図示します。2008年から2012年まで、経済を案内する一つのレジームの明確な徴候は見えません。
res_areturns.smoothed_marginal_probabilities[0].plot(
title="Probability of being in a low-variance regime", figsize=(12, 3)
)