この例は、主成分分析と部分最小二乗回帰を toy データセットで比較します。私たちのゴールは、対象がデータの中で任意の方向に強く相関している場合、いかにPLSがPCRより優れているかを説明することです。
PCRは二つのステップからなる回帰です。最初にPCAがトレーニングデータに適用されます。可能なら次元縮約を実行します。その後、回帰が変換したサンプルでトレイニングされます。PCAでは変換は純粋に、対象に対する情報が何も使われないことを意味する、教師なし(unsupervised)です。この結果、PCRは、対象が低い分散の方向に強く相関しているようなデータセットでは貧弱な性能になります。本当に、PCAの次元縮約はデータを低い次元の空間へ投影します。そこで投影したデータの分散は、各次元軸で貪欲に最大化されます。それにもかかわらず、対象への最大予測力は、低い分散の方向で紛失します。そして最終的な回帰は、それらに影響を与えることができません。
PLSは、変換と回帰両方です。そして、PCRとよく似ています。それは、線形回帰を変換データに適用する前に、サンプルに次元縮約を適用します。PCRとの主要な相違は、PLS変換が教師あり(supervised)ということです。それゆえ、この例で見るように、私たちが議論した問題に悩むことはありません。
データ
私たちは、二つの特徴の簡単なデータを作ることで開始します。PCRとPLSに入る前に、私たちは、このデータセットの二つの主成分、言い換えると、データのもっとも大きい分散を説明する二つの方向、を表示するためにPCA予測に適合させます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
rng = np.random.RandomState(0)
n_samples = 500
cov = [[3, 3], [3, 4]]
X = rng.multivariate_normal(mean=[0, 0], cov=cov, size=n_samples)
pca = PCA(n_components=2).fit(X)
plt.scatter(X[:, 0], X[:, 1], alpha=0.3, label="samples")
for i, (comp, var) in enumerate(zip(pca.components_, pca.explained_variance_)):
comp = comp * var # scale component by its variance explanation power
plt.plot(
[0, comp[0]],
[0, comp[1]],
label=f"Component {i}",
linewidth=5,
color=f"C{i + 2}",
)
plt.gca().set(
aspect="equal",
title="2-dimensional dataset with principal components",
xlabel="first feature",
ylabel="second feature",
)
plt.legend()
plt.show()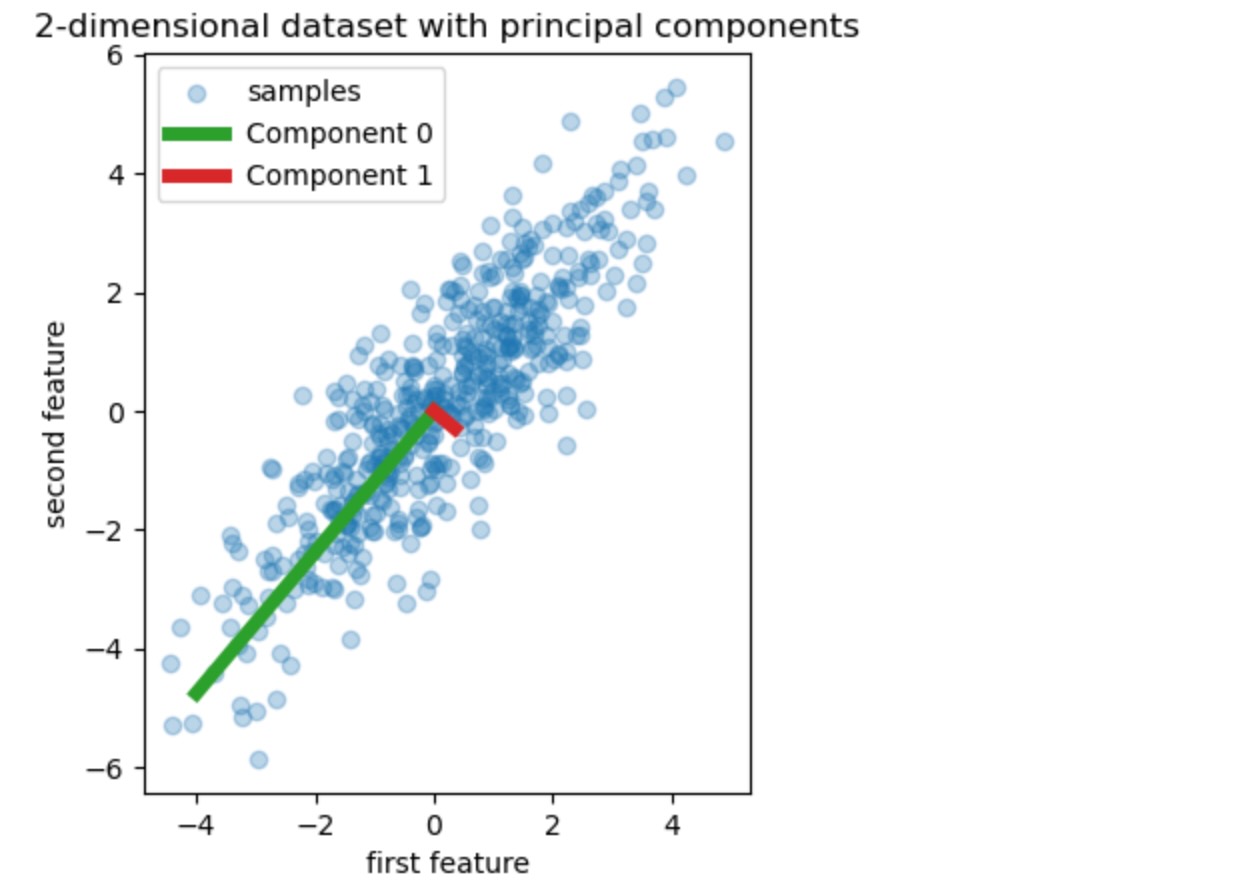
この例の目的のために、私たちはここで、小さな変位のある方向で強い相関のある対象y を定義します。これを終わらせるために、私たちは2番目の成分状上にXを投影します。そしてあるノイズをそれに追加します。
y = X.dot(pca.components_[1]) + rng.normal(size=n_samples) / 2
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(X.dot(pca.components_[0]), y, alpha=0.3)
axes[0].set(xlabel="Projected data onto first PCA component", ylabel="y")
axes[1].scatter(X.dot(pca.components_[1]), y, alpha=0.3)
axes[1].set(xlabel="Projected data onto second PCA component", ylabel="y")
plt.tight_layout()
plt.show()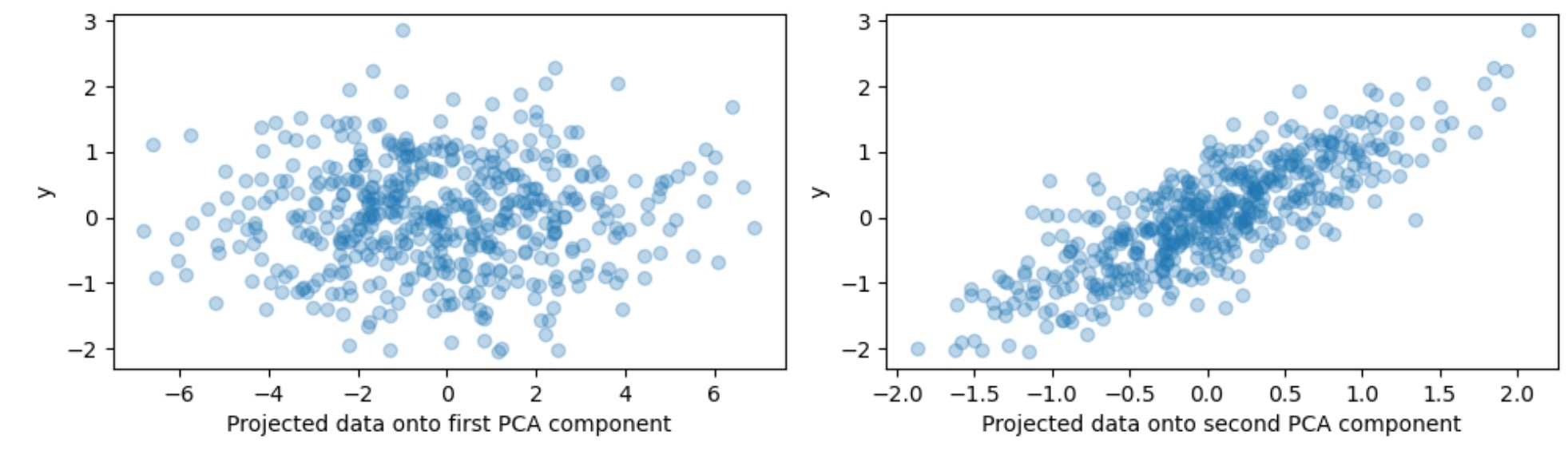
一つの成分の投影と予測力
私たちは、二つの回帰PCRとPLSをここで作ります、そして説明のために、成分の数を1に設定します。良い演習で推薦されているように、データをPCRのPCAステップへ送る前に、最初に私たちはそれを標準化します。PLS予測は内蔵のスケーリング能力を持っています。
両モデルに、私たちは、対象に対して最初の成分に投影したデータを図示します。両方のケースで、投影データは、トレーニングデータとして回帰に使用されます。
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import PLSRegression
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)
pcr = make_pipeline(StandardScaler(), PCA(n_components=1), LinearRegression())
pcr.fit(X_train, y_train)
pca = pcr.named_steps["pca"] # retrieve the PCA step of the pipeline
pls = PLSRegression(n_components=1)
pls.fit(X_train, y_train)
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(pca.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[0].scatter(
pca.transform(X_test), pcr.predict(X_test), alpha=0.3, label="predictions"
)
axes[0].set(
xlabel="Projected data onto first PCA component", ylabel="y", title="PCR / PCA"
)
axes[0].legend()
axes[1].scatter(pls.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[1].scatter(
pls.transform(X_test), pls.predict(X_test), alpha=0.3, label="predictions"
)
axes[1].set(xlabel="Projected data onto first PLS component", ylabel="y", title="PLS")
axes[1].legend()
plt.tight_layout()
plt.show()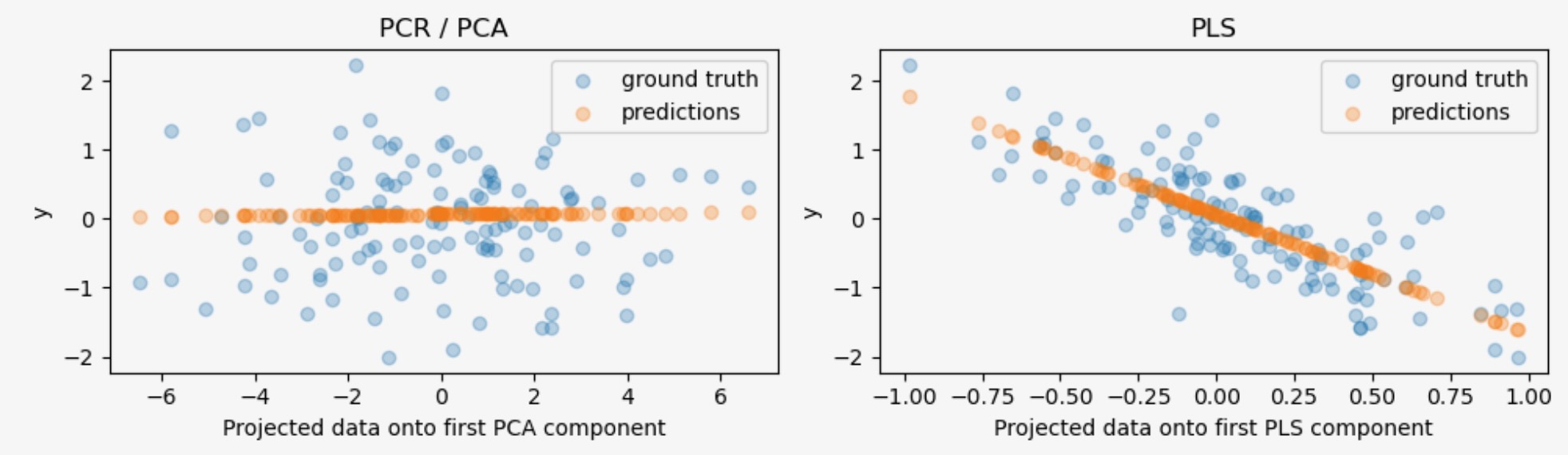
予測のようにPCRの教師なしPCA変換は、それがもっとも大きな予測方向であるにもかかわらず、2番目の成分、いわば、もっとも低い分散の方向を失くしています。これは、PCAが完全に教師なし変換のためです。そして、投影データが対象に対して低い予測力を持つ結果になります。
一方で、PLS回帰は、もっとも低い分散の影響を取り込んで管理します。変換の間に対象の情報を使えることに感謝してください。それは、この方向が実際にもっとも大きく予測できることが認識できます。私たちは、最初のPLS成分が対象に対して負に相関していることを注意します。それは固有値の符号が恣意的な事実から来ています。
私たちは、両方の予測のR二乗スコアを出力します。それはこのケースでは、PCRよりPLSの方がより代替良い代替として、更なる確認になります。負のR二乗はPCRが、対象の平均を簡単に予測する回帰より悪い性能を出すことを示しています。
print(f"PCR r-squared {pcr.score(X_test, y_test):.3f}")
print(f"PLS r-squared {pls.score(X_test, y_test):.3f}")PCR r-squared -0.026 PLS r-squared 0.658