TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。
PCMCIはここに記述されています: J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996
PCMCIのより進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。
このチュートリアルは、線形のラグに収束するLinearMediationクラス、同様に 同時に起こる因果の影響と影響の分析を説明しています。理論的背景については、以下の論文を参照してください;Runge, Jakob, Vladimir Petoukhov, Jonathan F. Donges, Jaroslav Hlinka, Nikola Jajcay, Martin Vejmelka, David Hartman, Norbert Marwan, Milan Paluš, and Jürgen Kurths. 2015. “Identifying Causal Gateways and Mediators in Complex Spatio-Temporal Systems.” Nature Communications 6: 8502. https://doi.org/10.1038/ncomms9502.
注記1:上記論文は、ここで拡張しているラグ付きのケースだけをカバーしています。
注記2:潜在変数とより深い機能を含む一般的な線形、非線形の因果分析は、CausalEffectクラスを使います。そしてそのチュートリアルは、以下の記事を参照してください。しかし、LinearMediationクラスはもっと速くそのタスクを処理します。
最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.models import LinearMediation, Prediction因果の結果と影響
前のセクションは、因果のリンクの推定に関して配慮しました。このセクションでは、私たちは、どのように時系列グラフが、RungeがNature Communication 2015でより詳細に議論したように、線形のフレームワークで因果の結果と影響を評価に使うことができるかを議論します。
注記:一般的な因果分析については、CαusalEffectクラスとチュートリアルを参照してください。
単純な因果チェインの以下のモデルを考えます。
Xt = ηtx
Yt = 0.5 Xt-1 + η
Zt = 0.5Yt - 0.5 Xt-1 + ηtz np.random.seed(42)
# links_coeffs = {0: [],
# 1: [((0, -1), 0.5)],
# 2: [((1, -1), 0.5)],
# }
def lin_f(x): return x
links_coeffs = {0: [((0,-1), 0.8, lin_f)],
1: [((1,-1), 0.8, lin_f), ((0, -1), 0.5, lin_f)],
2: [((2,-1), 0.8, lin_f), ((1, 0), 0.5, lin_f), ((0, -1), -0.25, lin_f)],
}
var_names = [r"$X$", r"$Y$", r"$Z$"]
data, _ = toys.structural_causal_process(links_coeffs, T=1000)
true_parents = toys._get_true_parent_neighbor_dict(links_coeffs)
# Initialize dataframe object, specify variable names
dataframe = pp.DataFrame(data,
var_names=var_names)
med = LinearMediation(dataframe=dataframe)
med.fit_model(all_parents=true_parents, tau_max=4)私たちはここの真の親を基礎にした線形影響モデルを適合します。実際は、これらは専門家の知識で知られるか、または因果の発見メソッド(例えばPCMCIplus)で推定されるかのどちらかになります。
#parents = toys.dag_to_links(graph_output_from_pcmciplus)
#print(parents)全体で指向性のあるグラフを提供する必要があることに注意してください、言い換えると、全ての終端が方向がある必要があります。そしてそれらは 0-0(指向性のない)またはx-x(衝突)することはできません。
もし、線形モデルの仮定が、適用され、因果の充分さが満たされるならば、標準時系列(LinearMediationクラスのデフォルト)から推定したXt-r -> Ytのリンク係数は、ある標準偏差Xt-rの混乱が原因によるYtの推定値の変化と一致します。Xt-2 -> Zのリンク係数をチェックしましょう。
print ("Link coefficient (0, -2) --> 2: ", med.get_coeff(i=0, tau=-2, j=2))Link coefficient (0, -2) --> 2: 0.0
リンク係数はダイレクトリンクの非ゼロだけです。しかし、ダイレクトリンクはlag -1で発生します。
print ("Link coefficient (0, -1) --> 2: ", med.get_coeff(i=0, tau=-1, j=2))Link coefficient (0, -1) --> 2: -0.05504267290234566
あなたは、以下のようにリンク係数の行列を取得できます。
val_matrix = med.get_val_matrix(symmetrize=True)
print(val_matrix)[[[ 0. 0.81202835 0. 0. 0. ] [ 0. 0.24447189 0. 0. 0. ] [ 0. -0.05504267 0. 0. 0. ]] [[ 0. 0. 0. 0. 0. ] [ 0. 0.80636579 0. 0. 0. ] [ 0.26667124 0. 0. 0. 0. ]] [[ 0. 0. 0. 0. 0. ] [ 0.26667124 0. 0. 0. 0. ] [ 0. 0.80217797 0. 0. 0. ]]]
あなたはダイレクトリンクの結果によって終端を色付けしたグラフを図示できます。同時に起こる終端だけが、二つのノード間で図示できるので、一つのval_matrix値だけがあります。これは、エントリーが対称:val_matrix[i,j,0] = val_matrixj,i,0]である必要があることを意味します。ここに私たちは、すべてがゼロの同時性エントリーval_matrix[i,j,0] symmetrize = Trueを経由してゼロでない値のval_matrix[j,i,0]へ設定することによって実行します。
# Get graph array from parents dictionary
graph = toys.links_to_graph(true_parents)
tp.plot_graph(graph=graph, val_matrix=val_matrix); plt.show()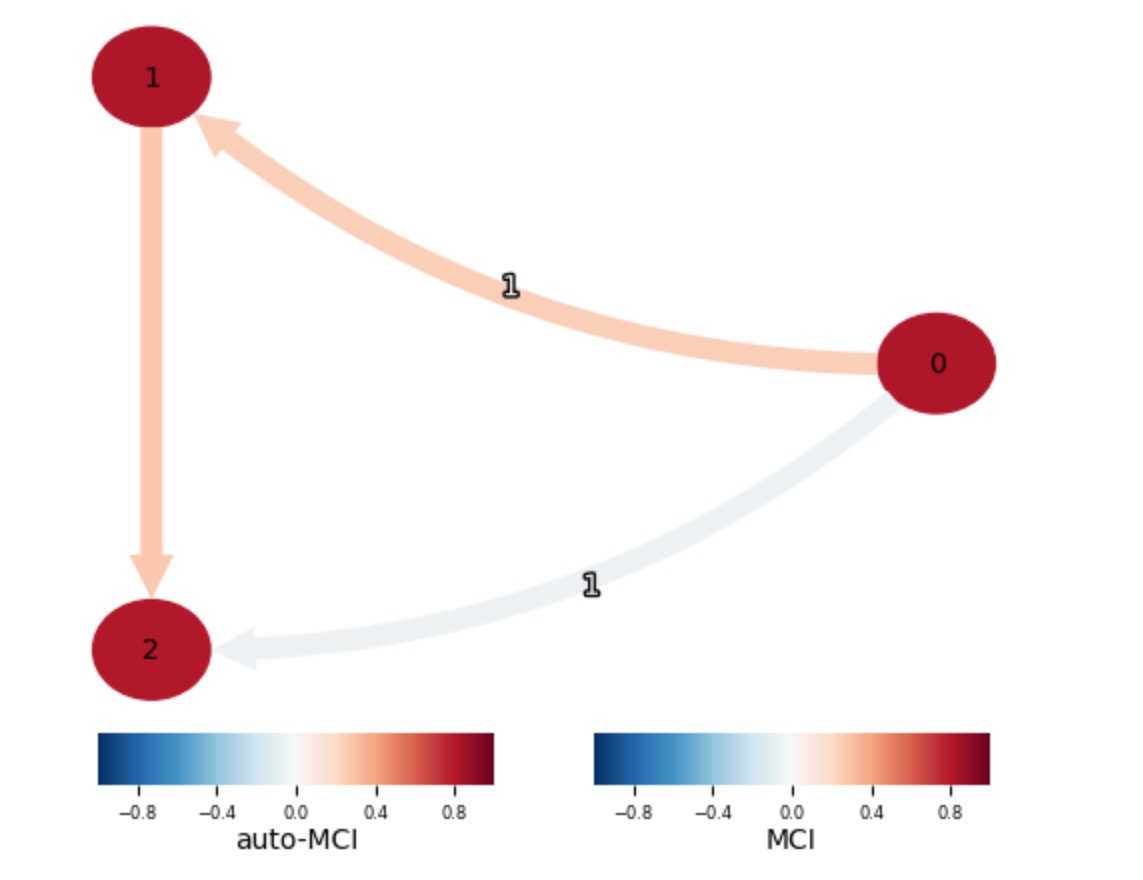
(総)因果の影響は、追加で、間接的な影響を評価します。そして、二つの変数間の全ての可能なパスの間のリンク係数の積の総和によって単純に計算されます。例えば、ここではXt-2 -> Ztへの因果の影響は、
print ("Causal effect (0, -2) --> 2: ", med.get_ce(i=0, tau=-2, j=2))Causal effect (0, -2) --> 2: 0.06895563457475423
影響した因果の結果は、因果への中間変数の寄与の量で表されます。例えば、Xt-2 -> Ztの因果のYの寄与を見てみましょう。
print ("Mediated Causal effect (0, -2) --> 2 through 1: ", med.get_mce(i=0, tau=-2, j=2, k=1))Mediated Causal effect (0, -2) --> 2 through 1: 0.1578058647179413
Yは正の符号で因果に影響を及ぼすので、MCEは大きくなります。影響分析は直接リンクばかりでなく、間接パスでも量を測るための強力なツールです。これは、"一つの過程で他の二つの間の因果のメカニズムがどれくらい重要なのか?"のような疑問に答えることができます。trigramite.plottingモジュールは、時系列グラフ内、集合のネットワーク内の両方で因果の経路を可視化するため機能があります。ここで、私たちはXt-4とZtの間の全ての因果経路を見ていきます。
i=0; tau=4; j=2
graph_data = med.get_mediation_graph_data(i=i, tau=tau, j=j)
tp.plot_mediation_time_series_graph(
var_names=var_names,
path_node_array=graph_data['path_node_array'],
tsg_path_val_matrix=graph_data['tsg_path_val_matrix']
)
tp.plot_mediation_graph(
var_names=var_names,
path_val_matrix=graph_data['path_val_matrix'],
path_node_array=graph_data['path_node_array'],
); plt.show()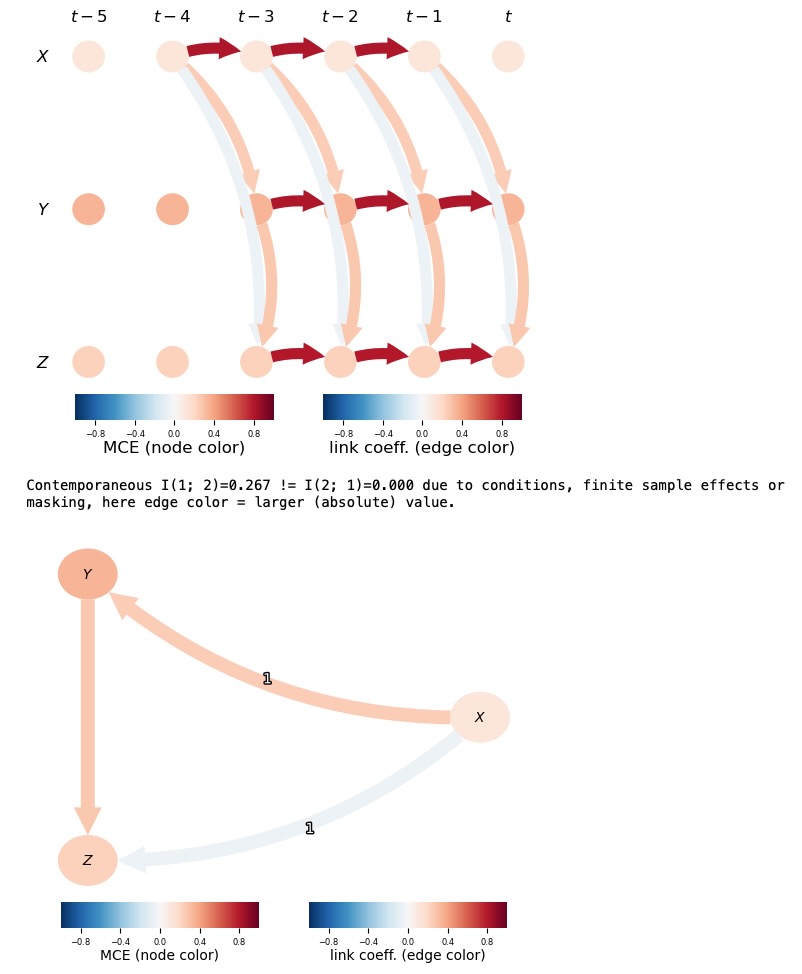
両方の図で、ノードの色は、変数の影響を表し、リンクの色はリンク係数を表します。下側のパネルは、もっと複雑な経路の可視化を容易にします。しかし、時間と変数を横切る経路がわかりにくくなります。
因果と影響分析は、もっと総計を測ることができます。平均因果(ACE)は、全体のシステムで単一の変数の影響がどれくらい強いか量を測ります。そして平均因果感受性(ACS)は、単一の変数がシステムの他の場所への入力の揺らぎにより、どれくらい強く影響するか量を測ります。最後に、平均因果の影響度(ACME)は、単一の変数が任意の二つの過程間で因果にどれくらい強く影響するか、量を測ることができます。Runge と他の人達による, Nature Communications(2015)では、これらの尺度が、因果の尺度が代替的により優れて解釈できることを示すために、伝統的な複雑なネットワークの尺度と比較されています。例えば、間の中心的な役割は、特定のノードへの最短経路の平均値を与えます。しかし、因果の最短経路を取る必要はなく、間は因果の重みを厳密に考慮に入れる必要はありません。
print ("Average Causal Effect X=%.2f, Y=%.2f, Z=%.2f " % tuple(med.get_all_ace()))
print ("Average Causal Susceptibility X=%.2f, Y=%.2f, Z=%.2f " % tuple(med.get_all_acs()))
print ("Average Mediated Causal Effect X=%.2f, Y=%.2f, Z=%.2f " % tuple(med.get_all_amce()))Average Causal Effect X=0.37, Y=0.28, Z=0.00 Average Causal Susceptibility X=0.00, Y=0.26, Z=0.39 Average Mediated Causal Effect X=0.00, Y=0.17, Z=0.00
デフォルトで、自己ループは、これらの尺度から除外されることに注意してください。Mediationクラスは、線形の因果だけをサポートします。非線形の効果のための問題は、扱いにくく、もっと深い機能を提供しているCausalEffectsクラスで扱うことができます。しかし、LinearMediationクラスは、もっと高速です。
ブートストラップ信頼度
LinearMediationクラスの最も大きな機能は、あなたがブートストラップ手続きを経た信頼度を取得できることです。これは、最初にfit_model_bootstrap(...)を適用することが必要です。ここで自由パラメータは、boot_blocklengthがサンプルの重属性を説明するために使われます。
med.fit_model_bootstrap(boot_blocklength=1, seed=42, boot_samples=100)<tigramite.models.LinearMediation at 0x144e4c1c0>
# Get Causal effect and 90% confidence interval
print(med.get_ce(i=0, tau=2, j=2))
print(med.get_bootstrap_of(function='get_ce',
function_args={'i':0, 'tau':2, 'j':2}, conf_lev=0.9))0.06895563457475423 [0.05538271 0.08424146]
# Get Average Mediated Causal Effect and 90% confidence intervals
print(med.get_all_amce())
print(med.get_bootstrap_of(function='get_all_amce',
function_args={}, conf_lev=0.9))[0.00000000e+00 1.71227525e-01 2.77555756e-16] [[0.00000000e+00 1.54668834e-01 0.00000000e+00] [0.00000000e+00 1.82662878e-01 3.35842465e-16]]
