TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。
PCMCIはここに記述されています: J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996
PCMCIのさらに進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。
このチュートリアルは、部分相関の条件独立性テスト(ParCorrWLS)の重みづけた最小二乗変分に適用する方法を説明します。それは分散不均一性を処理するように設計されます。例えば、線形ガウスセットのエラー項の一定でない変異。理論液背景は、以下の論文を参照してください。
W. Günther, U. Ninad, J. Wahl, J. Runge, Conditional Independence Testing with Heteroskedastic Data and Applications to Causal Discovery, Advances in neural information processing systems 35 (2022)
後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.parcorr_wls import ParCorrWLS
from scipy import stats1. 分散不均一性
よく知られている部分相関テスト(ParCorr)の基づくある仮定は、不均一性です。エラー項の変分が一定であることを意味します。私たちは、この仮定が、違反する場合の状況に関心があります。例えば、私たちは、不均一データについて考えることを欲します。このケースで変数は、例えば、サンプリングインデックスまたは、一つまたは多重影響する変数の値に依存することができます。一つの影響ある変数の分散の線形従属性について考えるかもしれません。しかし関係は、多くの異なる機能の様式を取ることができます。
ParCorrは不均一データに対しては信頼性がなくなります。最小二乗(OLS)推定の共分散行列なので、静的なテストを計算するために使います。それは、この設定に一致せずに隔たることができます。
現実のデータの不均一なソースは、多方面にわたります。例えば、環境科学では、異なった地域での降雨は、例えば場所でスケールされたノイズのような、システムの他の変数によっても説明できない異なる分散を示します。そうした問題は、異なる貯水池の集計データによって紹介することができます。そして、貯水池の場所に充分によく相関する変数を追加するのでなく、季節効果は、また、不均一性を取り入れることができます。
構造因果モデルで不均一性をモデル化するために、私たちは、ノイズ変数のスケーリング関数として示します。ドメインX=X1 x X2 x…x Xn上で、結合分布Px, 有限の多くのランダム変数V=(x1,…xd)を考えます。その時、以下のSCMからnサンプルに関心を持ちます。
X:= fi(Pa(Xti)) + hi(H(Xti)) . Niここで、fiは線形関数、 t ⊆ Γ はサンプルインデックスの略です。私たちは不均一関数si: X x Γ -> R > 0. を持ちます。ノイズ変数 Niは独立標準ガウス分布を仮定します。変数Xtの親のセットは、Pa(Xt)で示されます。そして、不均一性を誘導する変数のセットは、H(Xt) ⊆ Pa(Xt) ∪ {t} によって示されます。それは、空のセットにすることもできます。さらに、私たちは、因果関係が時間上で安定しているという制約を設けます。例えば、Pa(Xt)の親のセットは関数fiと同様に、時間に依存しません。
ParCorrWLS:分散不均一性データにおける条件独立テスト
一般データ
私たちは、標準部分相関テストが、OLS回帰ステップを基礎にしているために、不均一ノイズに対して、敏感であることがわかります。そこで、私たちは、OLS回帰を重みづけ最小二乗(WLS)アプローチに取り替えることを提案します。それは、一定でないエラーの分散も取り扱えることが知られています。
WLSの考えは、各データポイントが真の回帰線からどれくらい離れているかに依存して、再度重みづけを実行することです。それらの高い分散のエラーよりももっと情報のある低い分散をエラーが持つことをデータポイントに仮定することは妥当です。そこで、理想的考えは、重みは、関連するエラーの逆分散として選択されます。
分散関数推定
一般的に、私たちは、重要な真実の分散がわかることを望みます。そこでは、私たちは、不均一変数の条件分散関数の近似を持ちます。私たちは、上のSCMの簡単なバージョンでのアプローチを説明します。すなわち、私たちは次のこと考えます
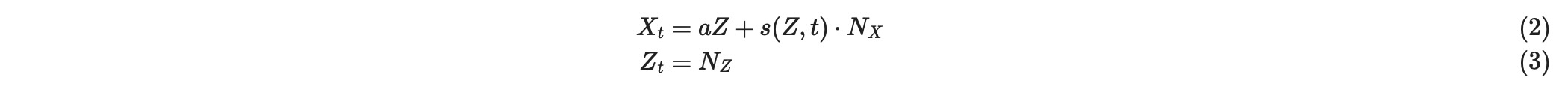
ここで、aは、定数で、NxとNzは標準正規独立ノイズ項です。
Xのため、私たちはここで、s2 = var(Xt|Z=x)を近似します。
そのため、私たちは、[1]のアプローチと同様に、条件分散のために剰余(残余)を基礎にしたノンパラメトリック推定を使います。Var(X|Z) = E(X - E[Z{Z])2 |Z|の識別による動機づけ、とこれは、Zに関して(X-aZ)2 の回帰であることに注意します。最初のステップは、二乗剰余(X-aZ)2を得るためにOLS回帰を使います。その後、私たちは、これらZの剰余を回帰のために、ノンパラメトリック回帰メソッドを使います。そして、そこでは、Zの値に近いKの剰余の線形の組み合わせを使うことで、条件平均を予測します。サンプリングしたインデックス依存不均一性は、これは、ウインドウアプローチに変わります。それは特に、剰余を二乗してスムース化します。
私たちは、不均一性のソースに関する知識を依拠していることに注意してください。これは、ユーザーに提供できる専門家の知識です。
アプリケーションの例
親に依存した分散不均一性
toyデータの生成
以下の過程に従って時系列データを生成することを考えます。
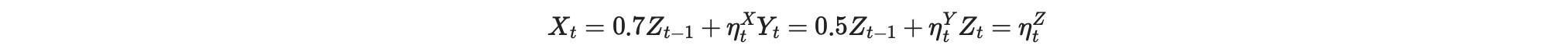
ここで、η〜 N(0,1), しかし ηX、ηY〜 N(0,σ(Zt-1)). XとYは両方不均一であることに注意してください。言い換えると、分散は、ラグ1のZの値で変化します。分散はZに依存するので、私たちは、これを親依存不均一性を呼びます。以下のσ(.)は、関数generate_parent_dependent_stdsを使って生成されます。
時間依存の不均一性のケースは、以下でカバーされます。
random_state = np.random.RandomState(42)
T = 500
N = 3
def generate_data(generate_stds, random_state):
data = np.zeros((T, N))
Z = random_state.standard_normal(T+1)
data[:, 2] = Z[1:]
stds_matrix = np.ones((T,N))
stds = generate_stds(Z, T)
stds_matrix[:, 0] = stds
stds_matrix[:, 1] = stds
noise_X = random_state.normal(0, stds, T)
noise_Y = random_state.normal(0, stds, T)
data[:, 0] = 0.7*Z[:T] + noise_X
data[:, 1] = 0.7*Z[:T] + noise_Y
return data, stds_matrix, noise_X, noise_Y
def generate_parent_dependent_stds(Z, T):
stds = np.ones(T) + 5*(1 + Z[:T])*(1+Z[:T]>0)
return stds
data, stds_matrix, noise_X, noise_Y = generate_data(generate_parent_dependent_stds, random_state)
# Initialize dataframe object, specify time axis and variable names
var_names = [r'$X$', r'$Y$', r'$Z$']
dataframe = pp.DataFrame(data,
datatime = {0:np.arange(len(data))},
var_names=var_names)最初に、私たちは、時系列を図示します。これは、関数tp.plot_timeseriesで実行できます。
時系列の図示と不均一性の可視化
tp.plot_timeseries(dataframe); plt.show()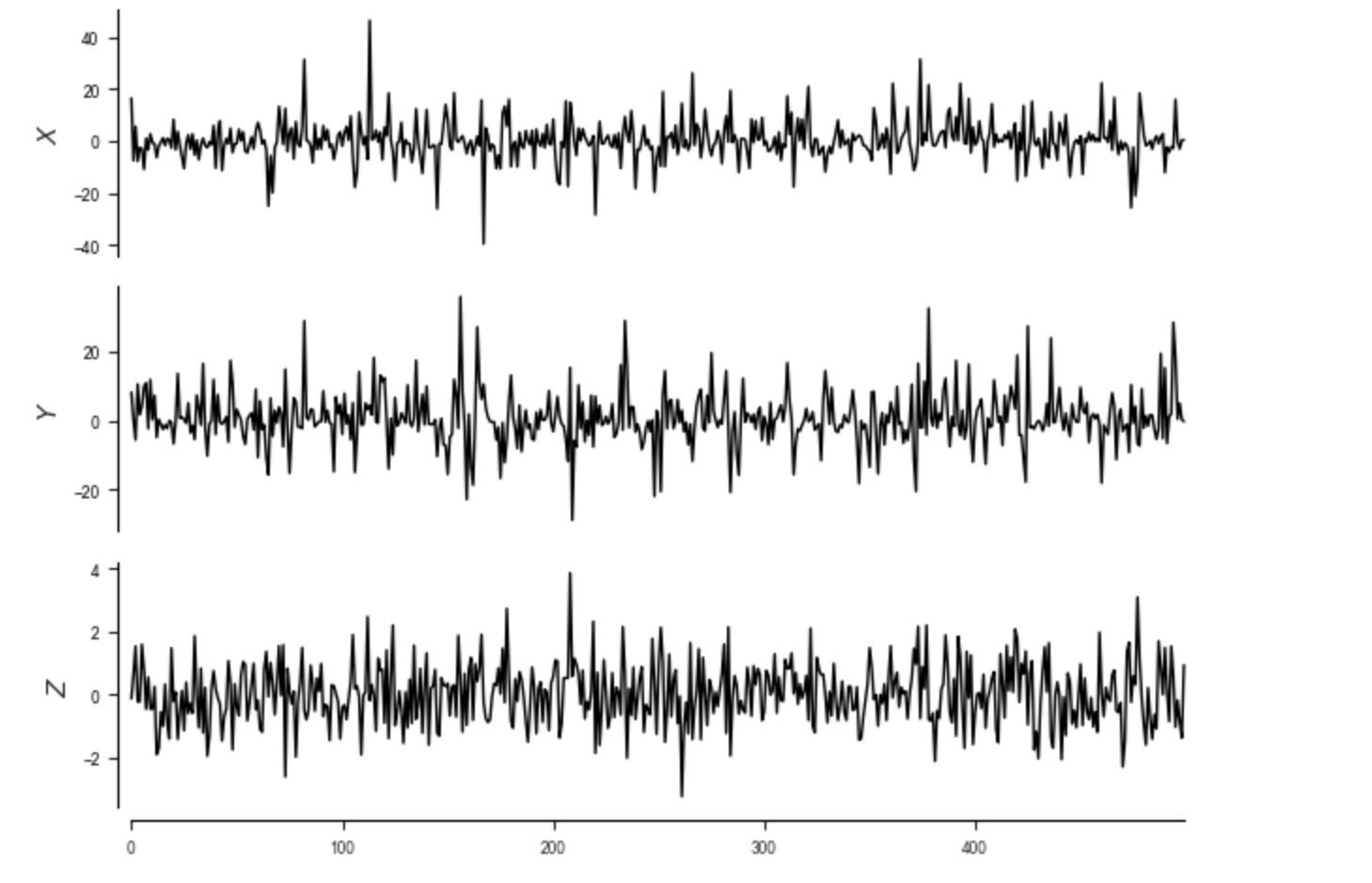
私たちは、ηX vs Zと ηY とZ を不均一な関係性を可視化して図示します。
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs = axs.ravel()
axs[0].scatter(data[:-1, 2], noise_X[1:], color="black")
axs[0].set_xlabel(r'$Z_{t-1}$')
axs[0].set_ylabel(r'$\eta_t^X$')
axs[1].scatter(data[:-1, 2], noise_Y[1:], color="black")
axs[1].set_xlabel(r'$Z_{t-1}$')
axs[1].set_ylabel(r'$\eta_t^Y$')
plt.show()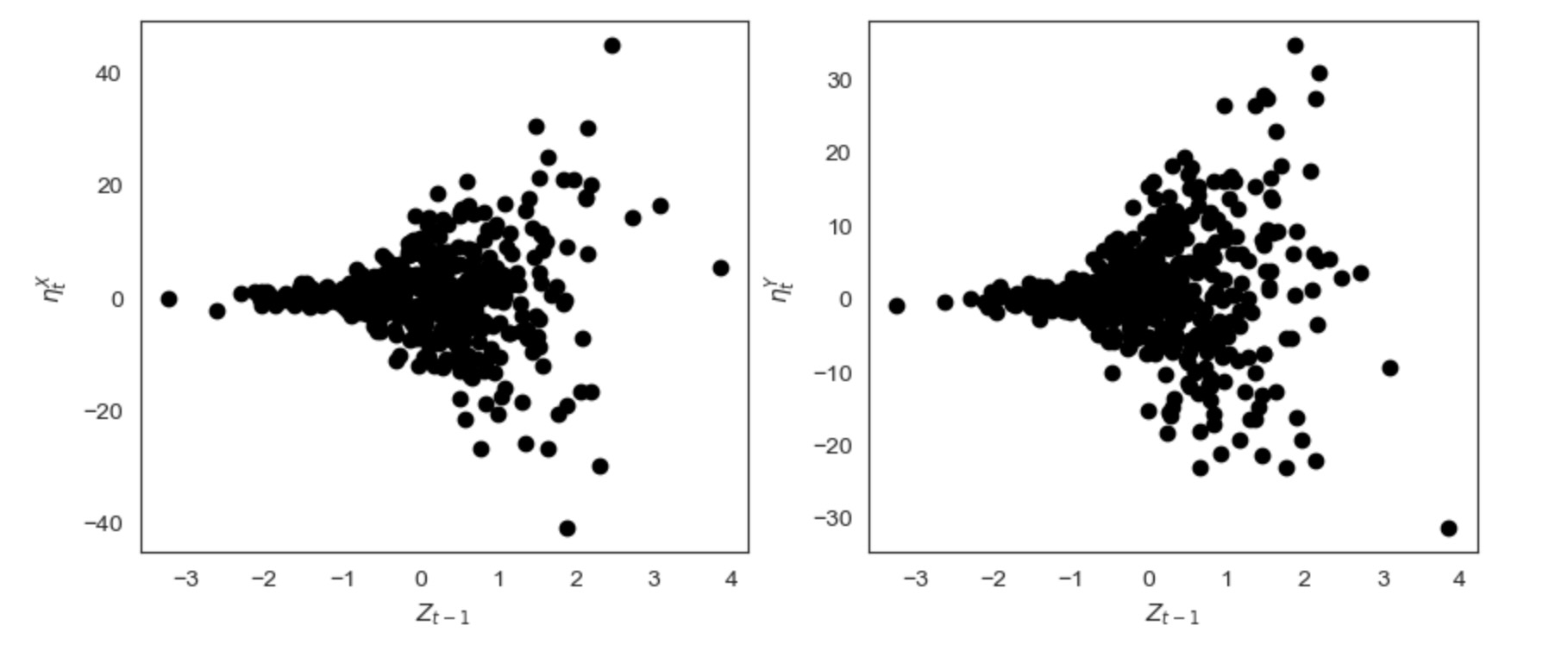
ParCorrWLS条件独立テスト
与えられたZでXとYの独立性をテストするために、私たちは、ParCorrWLS条件独立テストを選択します。このテストは不均一データの線形依存性のテストに最適です。
私たちは、分散関数を知らないので、それを近似する必要があります。このケースでは、ParCorrWLSは辞書の様式で、どのノードが不均一なノイズを持ち、他のノードがどのようなラグでを持つかを特徴づける、不均一性の関係に関する専門家の知識を私たちに要求します。
さらに、私たちは、Window_sizeパラメータを設定することができます。それは、分散推定ステップにおいて、二乗余剰をスムーシングするのにいくつの近傍を取り扱います。詳しくは、セクション2.2を参照してください。
expert_knowledge = {0: [(2, -1)], 1: [(2, -1)]}
parcorr_wls = ParCorrWLS(expert_knowledge=expert_knowledge,
window_size=50,
significance='analytic')
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr_wls,
verbosity=1)pcmci.verbosity = 1
results = pcmci.run_pcmciplus(tau_min=0, tau_max=2, pc_alpha=0.01)
#results = pcmci.run_pcmci(tau_max=8, pc_alpha=None, alpha_level=0.01)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr_wls
tau_min = 1
tau_max = 2
pc_alpha = [0.01]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X$ has 1 link(s):
($Y$ -1): max_pval = 0.00098, min_val = -0.148
Variable $Y$ has 1 link(s):
($Z$ -1): max_pval = 0.00216, min_val = 0.137
Variable $Z$ has 0 link(s):
##
## Step 2: PC algorithm with contemp. conditions and MCI tests
##
Parameters:
independence test = par_corr_wls
tau_min = 0
tau_max = 2
pc_alpha = 0.01
contemp_collider_rule = majority
conflict_resolution = True
reset_lagged_links = False
max_conds_dim = None
max_conds_py = None
max_conds_px = None
max_conds_px_lagged = None
fdr_method = none
## Significant links at alpha = 0.01:
Variable $X$ has 0 link(s):
Variable $Y$ has 1 link(s):
($Z$ -1): pval = 0.00216 | val = 0.137
Variable $Z$ has 0 link(s):ここで、私たちは、学習したDAGを図示するのに、tp.plot_graphを使うことができます。
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()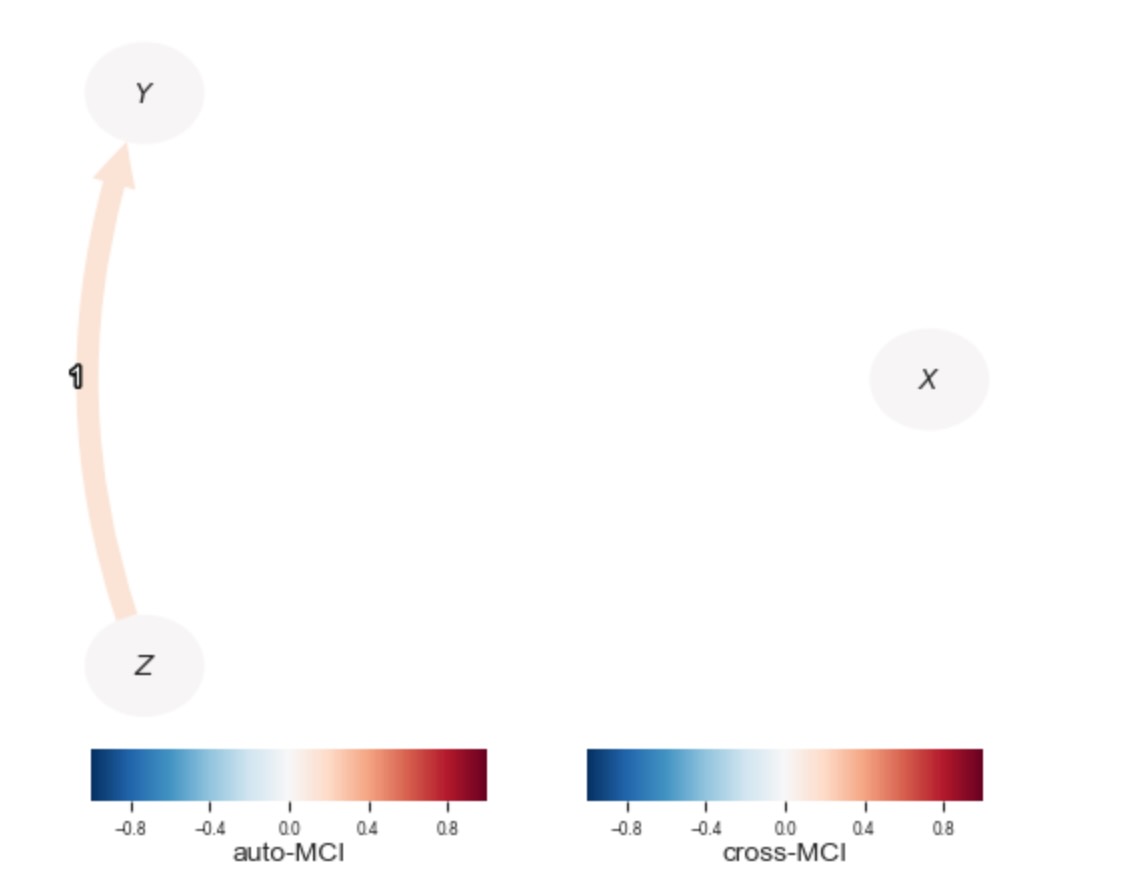
重要な真実の重みとParCorrWLSの比較
専門家の知識をもとにした分散の近似の代わりに、パラメータgt_std_matrixを使って、各観測値に対する重要な真実をParCorrWLSに供給することは可能です。しかし、一般的に、そうした知識は、取得するのが困難で、おそらくtoy-データ用だけとして知られています。
parcorr_wls_gt = ParCorrWLS(gt_std_matrix=stds_matrix,
significance='analytic')
pcmci_gt = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr_wls_gt,
verbosity=0)
pcmci_gt.verbosity = 0
results_gt = pcmci_gt.run_pcmciplus(tau_min=0, tau_max=2, pc_alpha=0.01)
tp.plot_graph(
val_matrix=results_gt['val_matrix'],
graph=results_gt['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()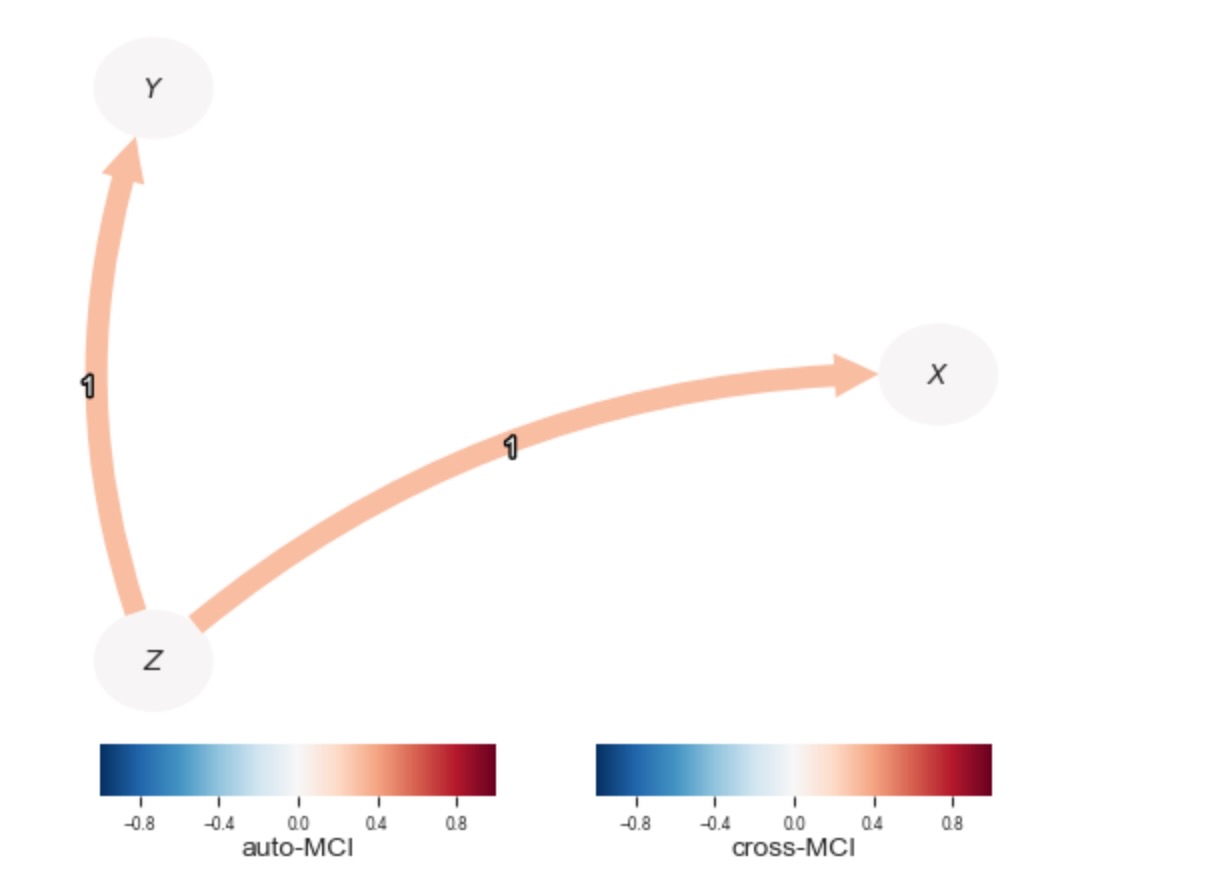
ParCorrとの比較
ParCorrWLSの有用性を直感的に得るために、私たちは、標準ParCorr条件独立テストと出力を比較します。
parcorr = ParCorr(significance='analytic')
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)
pcmci_parcorr.verbosity = 0
results_parcorr = pcmci_parcorr.run_pcmciplus(tau_min=0, tau_max=2, pc_alpha=0.01)tp.plot_graph(
val_matrix=results_parcorr['val_matrix'],
graph=results_parcorr['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()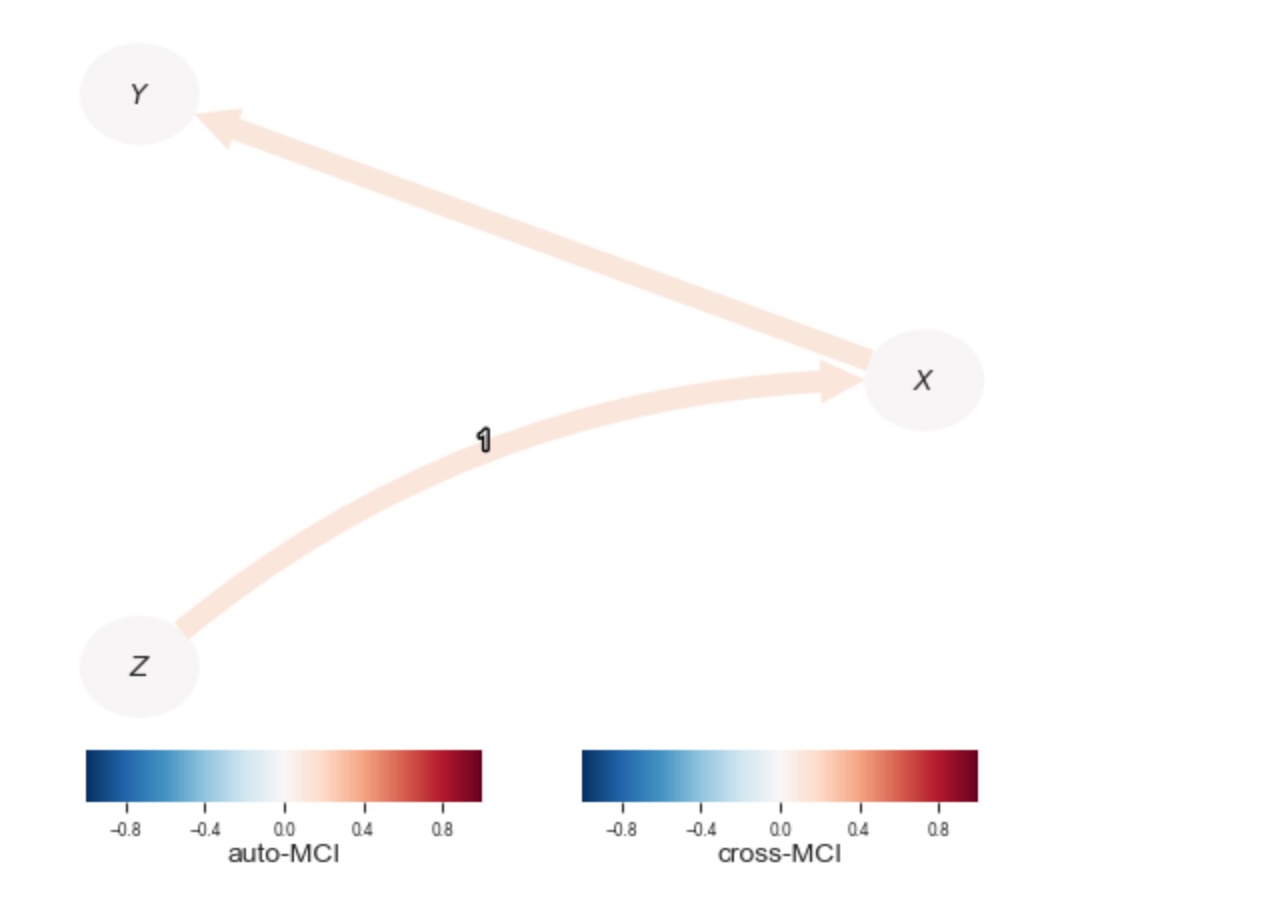
私たちは、標準部分相関テストが、ZとYの間のリンクを回復できないことがわかります。XからYへの間違ったリンクが見つけられます。
時間(またはサンプリングインデックス)依存不均一性
私たちが、生成したデータから以下の過程を再度考えてみます。
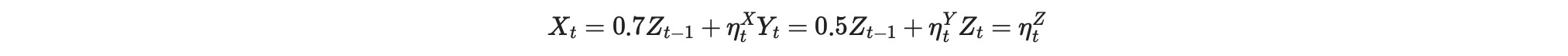
ここで、ηt 〜 N(0,1), しかし ηtX、ηtY 〜 N(0,1). 再度、注意します。XとYは両方不均一です。しかし、この時はtに反応します。例えば、時間またはサンプリングインデックス。私たちのコードでは、σ(.)は関数generate_time_dependent_stdsを使って生成されます。
random_state = np.random.RandomState(42)
def generate_time_dependent_stds(Z, T):
stds = np.array([1 + 0.018*t for t in range(T)])
return stds
data, stds_matrix, noise_X, noise_Y = generate_data(generate_time_dependent_stds, random_state)
# Initialize dataframe object, specify time axis and variable names
var_names = [r'$X$', r'$Y$', r'$Z$']
dataframe = pp.DataFrame(data,
datatime = {0:np.arange(len(data))},
var_names=var_names)再度、上のように、私たちは、関数tp.plot_timeseriesを使って時系列を図示します。
tp.plot_timeseries(dataframe); plt.show()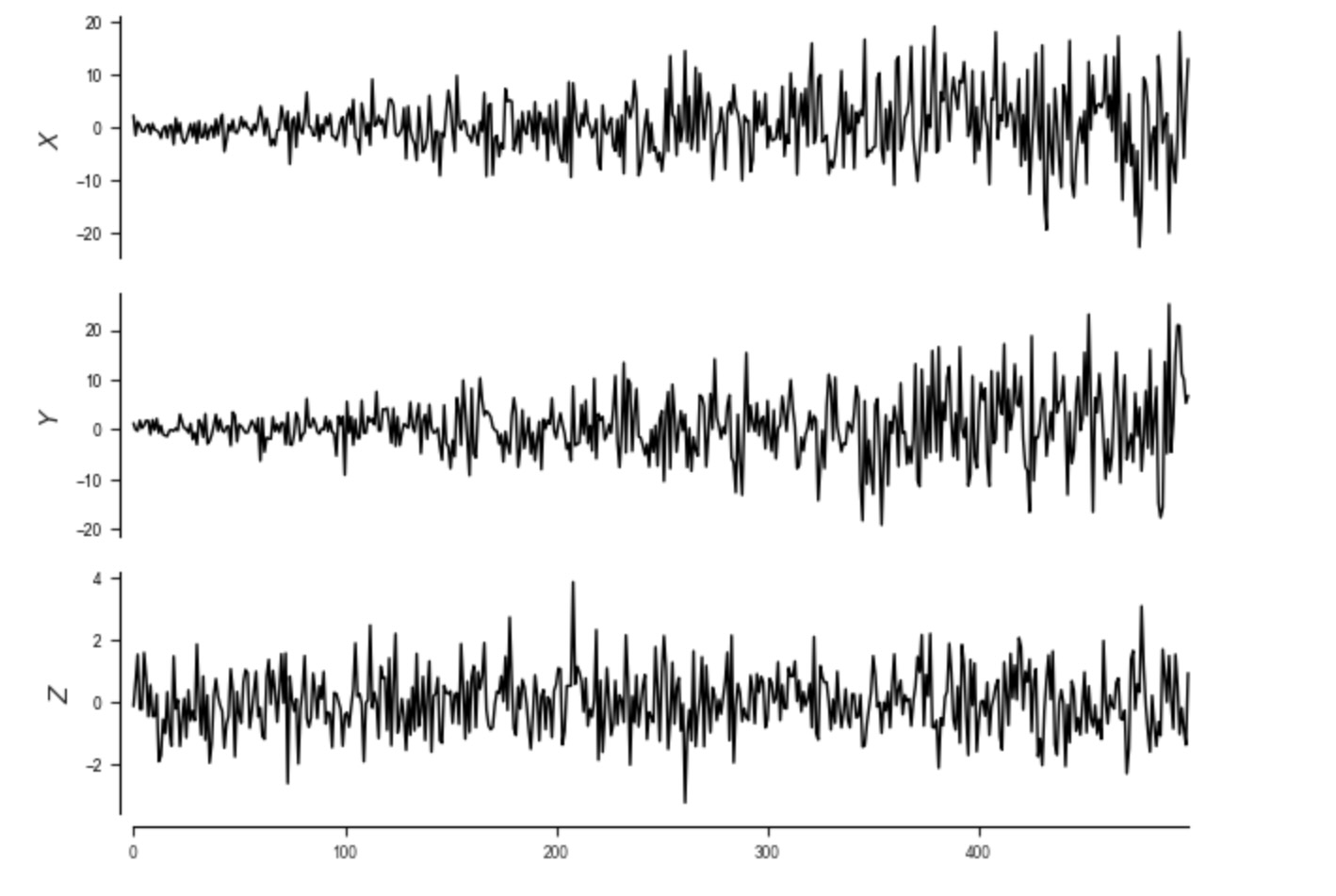
ここで、私たちはすでに、時系列プロットから、不均一性を疑うことができます。しかし、私たちはまた、分散不均一性が親のせいではないことを確認するために、時間軸上の間で、ηX とηYを図示します。
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs = axs.ravel()
axs[0].scatter(np.linspace(0, T, T), noise_X, color="black")
axs[0].set_xlabel('time')
axs[0].set_ylabel(r'$\eta_t^X$')
axs[1].scatter(np.linspace(0, T, T), noise_Y, color="black")
axs[1].set_xlabel('time')
axs[1].set_ylabel(r'$\eta_t^Y$')
plt.show()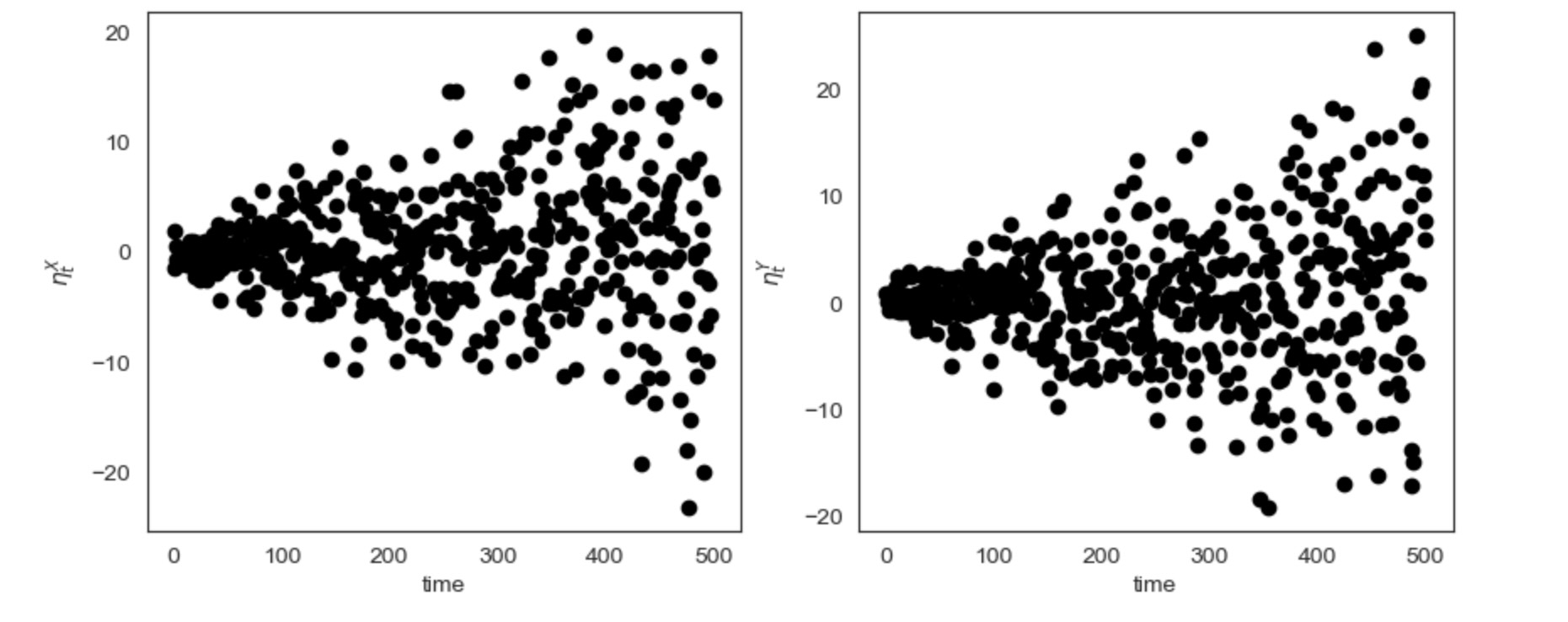
もし、私たちが、データ内に時間に依存した不均一性を処理するならば、私たちは再度、Zで与えられるXとYの独立性をテストするために、ParCorrWLS条件独立テスを選択します。時間に依存した不均一性の専門家の知識は、親に依存した不均一性のために上で実行したのと同様の方法でPArCorrWLSに渡すことができます。もし、私たちが、時間に依存した不均一性によって影響されるすべての変数を特等づけたいならば、私たちは、文字列’time-dependent heteroskedasity’をParCorrWLSのパラメータexpert_knowledgeに渡すことができます。しかし、不均一性が現れる各個別のノードを特徴づけることもまた可能です。このケースでは私たちは、ノードインデックスをキーにした辞書を使います。そして、その項目は一つの要素のリストからなります:['time-dependent heteroskedasticity']. 再度、私たちはまた、wondow_sizeパラメータを設定します。
expert_knowledge = {0: ["time-dependent heteroskedasticity"], 1: ["time-dependent heteroskedasticity"]}
parcorr_wls = ParCorrWLS(expert_knowledge=expert_knowledge,
window_size=50,
significance='analytic')
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr_wls,
verbosity=1)pcmci.verbosity = 1
results = pcmci.run_pcmciplus(tau_min=0, tau_max=2, pc_alpha=0.01)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr_wls
tau_min = 1
tau_max = 2
pc_alpha = [0.01]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X$ has 1 link(s):
($Z$ -1): max_pval = 0.00019, min_val = 0.167
Variable $Y$ has 1 link(s):
($Z$ -1): max_pval = 0.00002, min_val = 0.188
Variable $Z$ has 0 link(s):
##
## Step 2: PC algorithm with contemp. conditions and MCI tests
##
Parameters:
independence test = par_corr_wls
tau_min = 0
tau_max = 2
pc_alpha = 0.01
contemp_collider_rule = majority
conflict_resolution = True
reset_lagged_links = False
max_conds_dim = None
max_conds_py = None
max_conds_px = None
max_conds_px_lagged = None
fdr_method = none
## Significant links at alpha = 0.01:
Variable $X$ has 1 link(s):
($Z$ -1): pval = 0.00019 | val = 0.167
Variable $Y$ has 1 link(s):
($Z$ -1): pval = 0.00002 | val = 0.188
Variable $Z$ has 0 link(s):tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()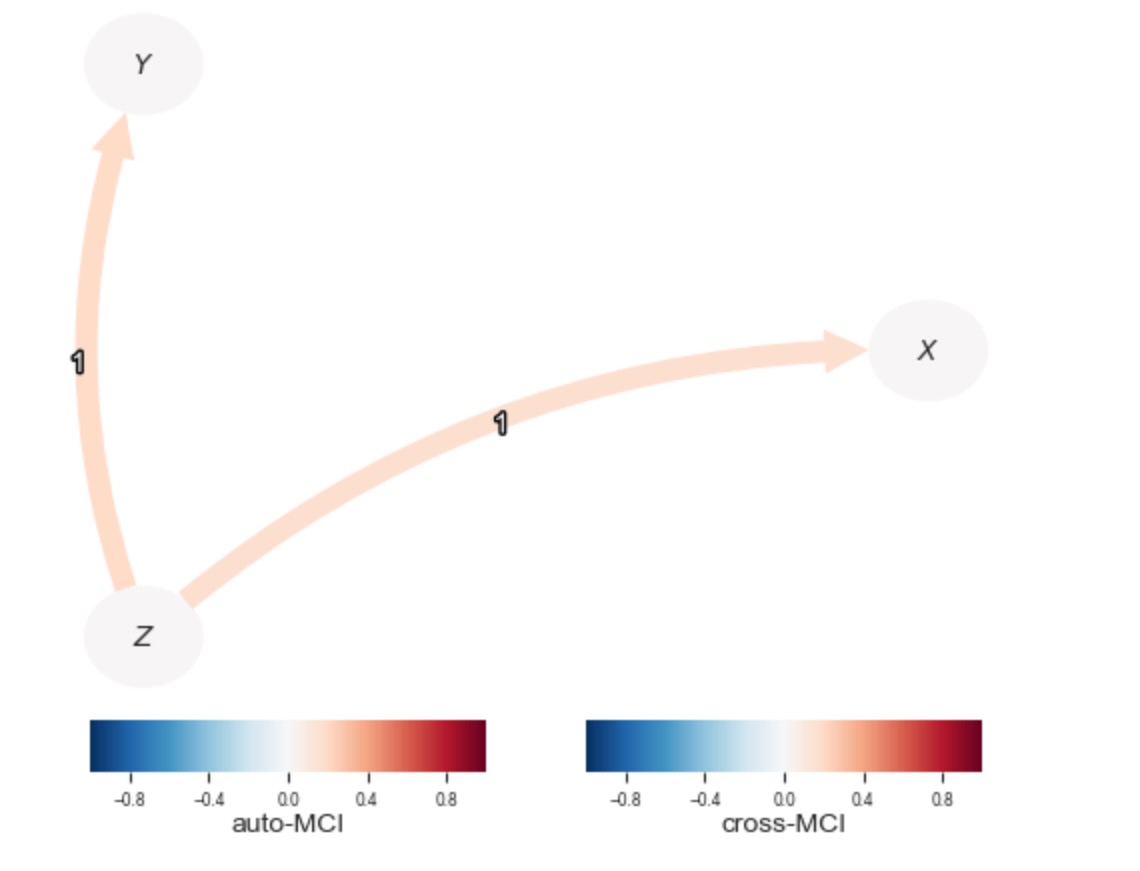
ParCorrLSとの比較
時間依存不均一性のケースでは、私たちは、標準ParCorrテストの性能の劣化を予期しました。これは、下の図で、ZからXへのリンクが発見されないことからもわかります。
parcorr = ParCorr(significance='analytic')
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)
pcmci_parcorr.verbosity = 0
results_parcorr = pcmci_parcorr.run_pcmciplus(tau_min=0, tau_max=2, pc_alpha=0.01)tp.plot_graph(
val_matrix=results_parcorr['val_matrix'],
graph=results_parcorr['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()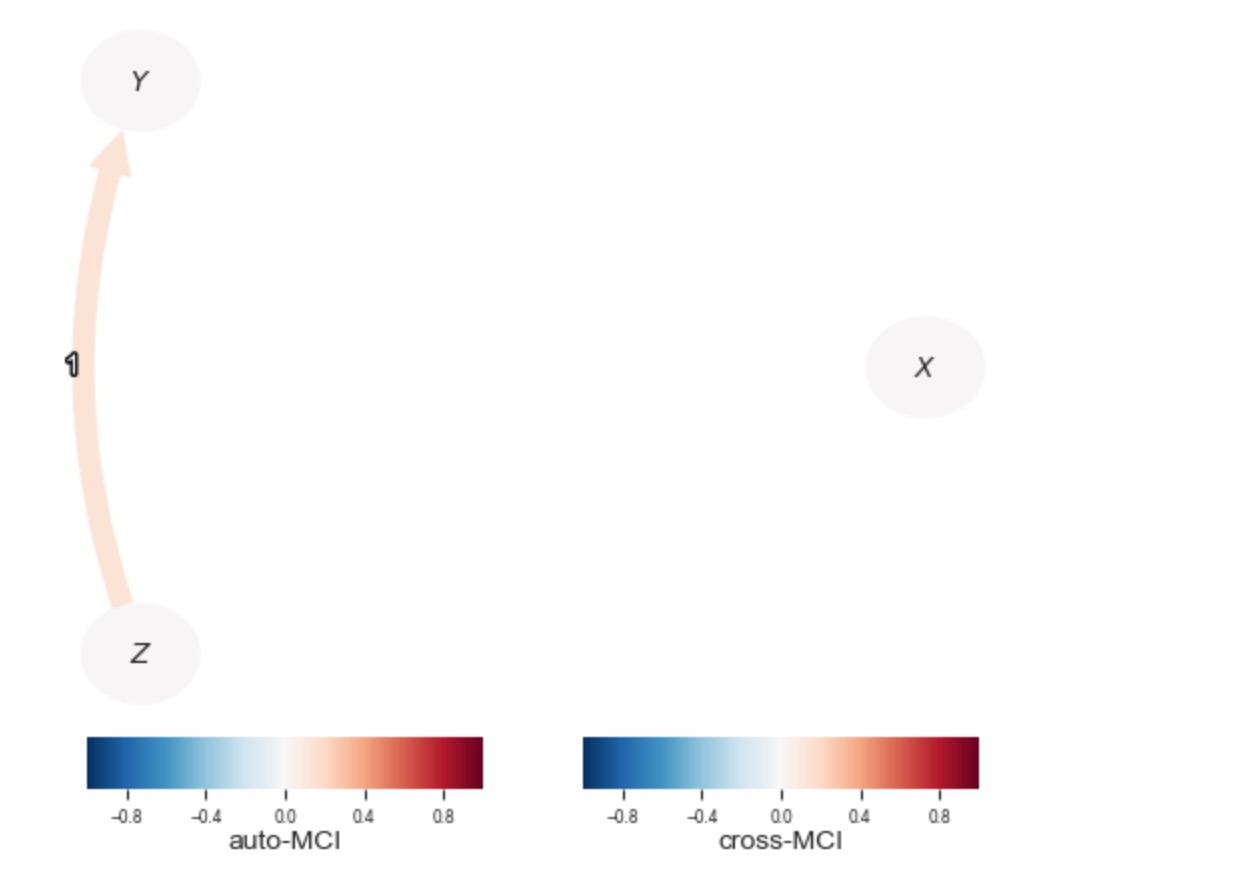
参考文献
[1] P. M. Robinson. Asymptotically efficient estimation in the presence of heteroskedasticity of unknown form. Econometrica: Journal of the Econometric Society, pages 875–891, 1987.