TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。
PCMCIはここに記述されています: J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996
PCMCIのさらに進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。
このチュートリアルは、欠測値とマスキングを例を通して説明します。理論的背景は以下の論文を参照してください。
Runge, Jakob. 2018. “Causal Network Reconstruction from Time Series: From Theoretical Assumptions to Practical Estimation.” Chaos: An Interdisciplinary Journal of Nonlinear Science 28 (7): 075310.
最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.models import LinearMediation, Prediction欠測値
Tigramiteは、安定して結束値を取り扱います。例えば、結束値がデータ内で、999として示していると、DataFrame(…,missing_flag=999.)とフラグをつけることができます。その時、持続して遅延時間は取り扱われますが、任意の変数内で発生した結束値の全てのサンプルの時間間隔は、破棄されます。
注記:バージョン5以前では、DatraFrameは、2*tau_maxまでの全ての遅延で、その後に起きるサンプルを破棄するのが、デフォルトの設定でした。これは、隔たりを避けるための意図でした。しかし、これは、結束値がランダムに発生しないデータへの隔たりを導くだけなので、この設定は過度に保守的で、破棄するサンプルが多すぎることになります。こうして、バージョン5以来、DatFrameを初期化するための別のパラメータがあり、remove_missing_upto_maxlag = Falseがデフォルトです。
np.random.seed(1)
data = np.random.randn(100, 3)
for t in range(1, 100):
data[t, 0] += 0.7*data[t-1, 0]
data[t, 1] += 0.8*data[t-1, 1] + 0.8*data[t-1,0]
data[t, 2] += 0.8*data[t-1, 2] + 0.8*data[t-1,1]
# Randomly mark 10% of values as missing values in variable 2
data[np.random.permutation(100)[:10], 2] = 999.
# Initialize dataframe object, specify time axis and variable names
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']
dataframe = pp.DataFrame(data,
datatime = np.arange(len(data)),
var_names=var_names,
missing_flag=999.)
tp.plot_timeseries(dataframe); plt.show()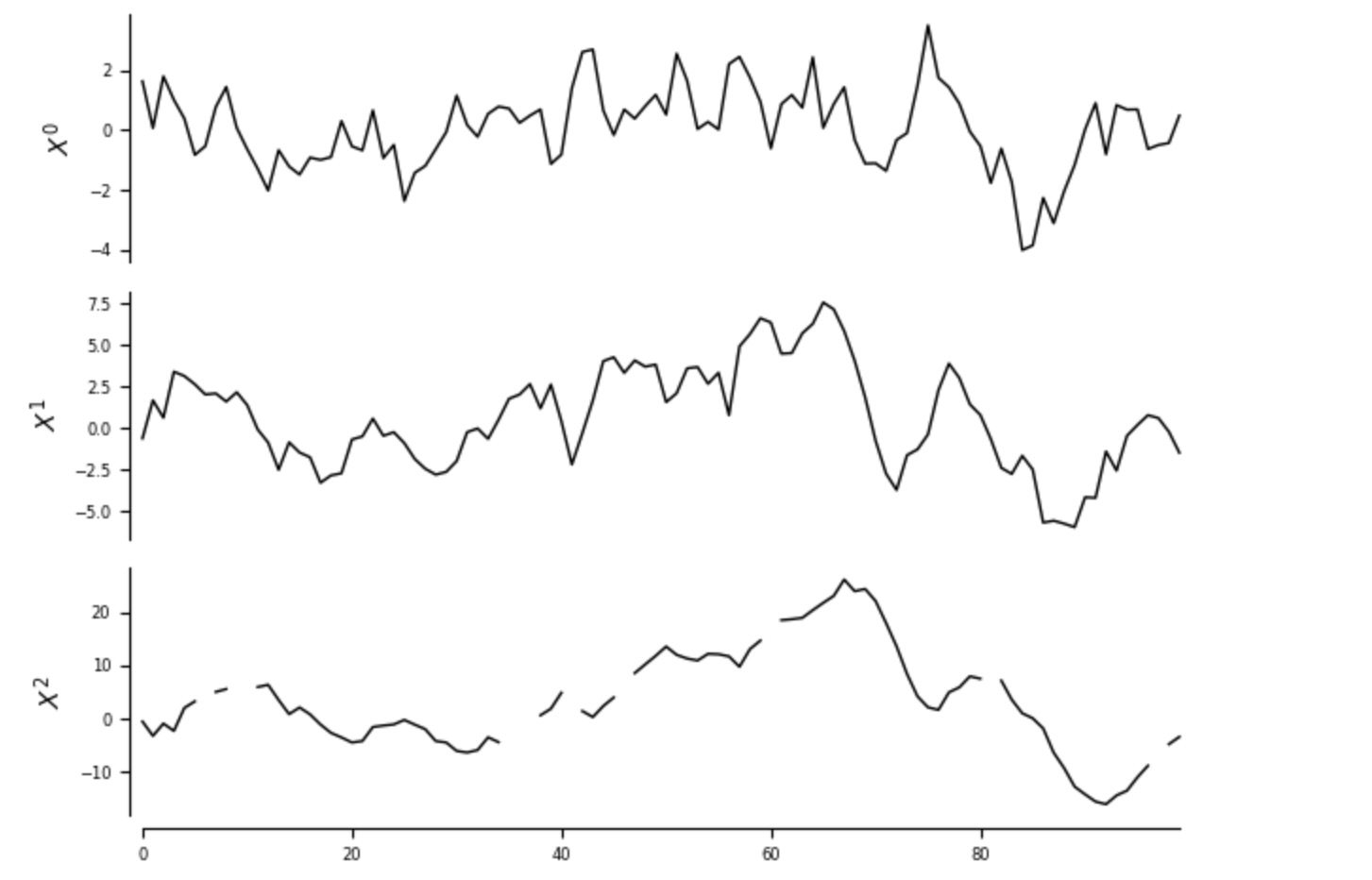
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr(verbosity=3), verbosity=4)
results = pcmci_parcorr.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Initialize conditional independence test
Parameters:
independence test = par_corr
significance = analytic
##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 2
pc_alpha = [0.2]
max_conds_dim = None
max_combinations = 1
## Variable $X^0$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^0$ (1/6):
Constructed array of shape (2, 96) from
X = [(0, -1)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.688 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.688
No conditions of dimension 0 left.
Link ($X^0$ -2) -?> $X^0$ (2/6):
Constructed array of shape (2, 96) from
X = [(0, -2)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.449 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.449
No conditions of dimension 0 left.
Link ($X^1$ -1) -?> $X^0$ (3/6):
Constructed array of shape (2, 96) from
X = [(1, -1)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.355 | pval = 0.00039
Subset 0: () gives pval = 0.00039 / val = 0.355
No conditions of dimension 0 left.
Link ($X^1$ -2) -?> $X^0$ (4/6):
Constructed array of shape (2, 96) from
X = [(1, -2)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.248 | pval = 0.01470
Subset 0: () gives pval = 0.01470 / val = 0.248
No conditions of dimension 0 left.
Link ($X^2$ -1) -?> $X^0$ (5/6):
Constructed array of shape (2, 86) from
X = [(2, -1)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.152 | pval = 0.16123
Subset 0: () gives pval = 0.16123 / val = 0.152
No conditions of dimension 0 left.
Link ($X^2$ -2) -?> $X^0$ (6/6):
Constructed array of shape (2, 86) from
X = [(2, -2)]
Y = [(0, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.129 | pval = 0.23578
Subset 0: () gives pval = 0.23578 / val = 0.129
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^0$ has 5 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.688
($X^0$ -2): max_pval = 0.00000, min_val = 0.449
($X^1$ -1): max_pval = 0.00039, min_val = 0.355
($X^1$ -2): max_pval = 0.01470, min_val = 0.248
($X^2$ -1): max_pval = 0.16123, min_val = 0.152
Testing condition sets of dimension 1:
Link ($X^0$ -1) -?> $X^0$ (1/5):
Constructed array of shape (3, 96) from
X = [(0, -1)]
Y = [(0, 0)]
Z = [(0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.585 | pval = 0.00000
Subset 0: ($X^0$ -2) gives pval = 0.00000 / val = 0.585
No conditions of dimension 1 left.
Link ($X^0$ -2) -?> $X^0$ (2/5):
Constructed array of shape (3, 96) from
X = [(0, -2)]
Y = [(0, 0)]
Z = [(0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.052 | pval = 0.61676
Subset 0: ($X^0$ -1) gives pval = 0.61676 / val = -0.052
Non-significance detected.
Link ($X^1$ -1) -?> $X^0$ (3/5):
Constructed array of shape (3, 96) from
X = [(1, -1)]
Y = [(0, 0)]
Z = [(0, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.018 | pval = 0.86238
Subset 0: ($X^0$ -1) gives pval = 0.86238 / val = 0.018
Non-significance detected.
Link ($X^1$ -2) -?> $X^0$ (4/5):
Constructed array of shape (3, 96) from
X = [(1, -2)]
Y = [(0, 0)]
Z = [(0, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.006 | pval = 0.95598
Subset 0: ($X^0$ -1) gives pval = 0.95598 / val = 0.006
Non-significance detected.
Link ($X^2$ -1) -?> $X^0$ (5/5):
Constructed array of shape (3, 86) from
X = [(2, -1)]
Y = [(0, 0)]
Z = [(0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.001 | pval = 0.99188
Subset 0: ($X^0$ -1) gives pval = 0.99188 / val = -0.001
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^0$ has 1 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.585
Algorithm converged for variable $X^0$
## Variable $X^1$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^1$ (1/6):
Constructed array of shape (2, 96) from
X = [(0, -1)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.725 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.725
No conditions of dimension 0 left.
Link ($X^0$ -2) -?> $X^1$ (2/6):
Constructed array of shape (2, 96) from
X = [(0, -2)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.790 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.790
No conditions of dimension 0 left.
Link ($X^1$ -1) -?> $X^1$ (3/6):
Constructed array of shape (2, 96) from
X = [(1, -1)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.903 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.903
No conditions of dimension 0 left.
Link ($X^1$ -2) -?> $X^1$ (4/6):
Constructed array of shape (2, 96) from
X = [(1, -2)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.776 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.776
No conditions of dimension 0 left.
Link ($X^2$ -1) -?> $X^1$ (5/6):
Constructed array of shape (2, 86) from
X = [(2, -1)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.534 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.534
No conditions of dimension 0 left.
Link ($X^2$ -2) -?> $X^1$ (6/6):
Constructed array of shape (2, 86) from
X = [(2, -2)]
Y = [(1, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.431 | pval = 0.00003
Subset 0: () gives pval = 0.00003 / val = 0.431
No conditions of dimension 0 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^1$ has 6 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.903
($X^0$ -2): max_pval = 0.00000, min_val = 0.790
($X^1$ -2): max_pval = 0.00000, min_val = 0.776
($X^0$ -1): max_pval = 0.00000, min_val = 0.725
($X^2$ -1): max_pval = 0.00000, min_val = 0.534
($X^2$ -2): max_pval = 0.00003, min_val = 0.431
Testing condition sets of dimension 1:
Link ($X^1$ -1) -?> $X^1$ (1/6):
Constructed array of shape (3, 96) from
X = [(1, -1)]
Y = [(1, 0)]
Z = [(0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.780 | pval = 0.00000
Subset 0: ($X^0$ -2) gives pval = 0.00000 / val = 0.780
No conditions of dimension 1 left.
Link ($X^0$ -2) -?> $X^1$ (2/6):
Constructed array of shape (3, 96) from
X = [(0, -2)]
Y = [(1, 0)]
Z = [(1, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.451 | pval = 0.00000
Subset 0: ($X^1$ -1) gives pval = 0.00000 / val = 0.451
No conditions of dimension 1 left.
Link ($X^1$ -2) -?> $X^1$ (3/6):
Constructed array of shape (3, 96) from
X = [(1, -2)]
Y = [(1, 0)]
Z = [(1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.191 | pval = 0.06359
Subset 0: ($X^1$ -1) gives pval = 0.06359 / val = -0.191
No conditions of dimension 1 left.
Link ($X^0$ -1) -?> $X^1$ (4/6):
Constructed array of shape (3, 96) from
X = [(0, -1)]
Y = [(1, 0)]
Z = [(1, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.736 | pval = 0.00000
Subset 0: ($X^1$ -1) gives pval = 0.00000 / val = 0.736
No conditions of dimension 1 left.
Link ($X^2$ -1) -?> $X^1$ (5/6):
Constructed array of shape (3, 86) from
X = [(2, -1)]
Y = [(1, 0)]
Z = [(1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.181 | pval = 0.09800
Subset 0: ($X^1$ -1) gives pval = 0.09800 / val = -0.181
No conditions of dimension 1 left.
Link ($X^2$ -2) -?> $X^1$ (6/6):
Constructed array of shape (3, 86) from
X = [(2, -2)]
Y = [(1, 0)]
Z = [(1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.113 | pval = 0.30104
Subset 0: ($X^1$ -1) gives pval = 0.30104 / val = -0.113
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^1$ has 5 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.780
($X^0$ -1): max_pval = 0.00000, min_val = 0.725
($X^0$ -2): max_pval = 0.00000, min_val = 0.451
($X^1$ -2): max_pval = 0.06359, min_val = 0.191
($X^2$ -1): max_pval = 0.09800, min_val = 0.181
Testing condition sets of dimension 2:
Link ($X^1$ -1) -?> $X^1$ (1/5):
Constructed array of shape (4, 96) from
X = [(1, -1)]
Y = [(1, 0)]
Z = [(0, -1), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.856 | pval = 0.00000
Subset 0: ($X^0$ -1) ($X^0$ -2) gives pval = 0.00000 / val = 0.856
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^0$ -1) -?> $X^1$ (2/5):
Constructed array of shape (4, 96) from
X = [(0, -1)]
Y = [(1, 0)]
Z = [(1, -1), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.654 | pval = 0.00000
Subset 0: ($X^1$ -1) ($X^0$ -2) gives pval = 0.00000 / val = 0.654
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^0$ -2) -?> $X^1$ (3/5):
Constructed array of shape (4, 96) from
X = [(0, -2)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.078 | pval = 0.45596
Subset 0: ($X^1$ -1) ($X^0$ -1) gives pval = 0.45596 / val = 0.078
Non-significance detected.
Link ($X^1$ -2) -?> $X^1$ (4/5):
Constructed array of shape (4, 96) from
X = [(1, -2)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.013 | pval = 0.90014
Subset 0: ($X^1$ -1) ($X^0$ -1) gives pval = 0.90014 / val = -0.013
Non-significance detected.
Link ($X^2$ -1) -?> $X^1$ (5/5):
Constructed array of shape (4, 86) from
X = [(2, -1)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.051 | pval = 0.64715
Subset 0: ($X^1$ -1) ($X^0$ -1) gives pval = 0.64715 / val = -0.051
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^1$ has 2 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.780
($X^0$ -1): max_pval = 0.00000, min_val = 0.654
Algorithm converged for variable $X^1$
## Variable $X^2$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^2$ (1/6):
Constructed array of shape (2, 86) from
X = [(0, -1)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.277 | pval = 0.00994
Subset 0: () gives pval = 0.00994 / val = 0.277
No conditions of dimension 0 left.
Link ($X^0$ -2) -?> $X^2$ (2/6):
Constructed array of shape (2, 86) from
X = [(0, -2)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.401 | pval = 0.00013
Subset 0: () gives pval = 0.00013 / val = 0.401
No conditions of dimension 0 left.
Link ($X^1$ -1) -?> $X^2$ (3/6):
Constructed array of shape (2, 86) from
X = [(1, -1)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.782 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.782
No conditions of dimension 0 left.
Link ($X^1$ -2) -?> $X^2$ (4/6):
Constructed array of shape (2, 86) from
X = [(1, -2)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.864 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.864
No conditions of dimension 0 left.
Link ($X^2$ -1) -?> $X^2$ (5/6):
Constructed array of shape (2, 77) from
X = [(2, -1)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.979 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.979
No conditions of dimension 0 left.
Link ($X^2$ -2) -?> $X^2$ (6/6):
Constructed array of shape (2, 77) from
X = [(2, -2)]
Y = [(2, 0)]
Z = []
extraZ = []
with missing values = 999.0 removed
val = 0.936 | pval = 0.00000
Subset 0: () gives pval = 0.00000 / val = 0.936
No conditions of dimension 0 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^2$ has 6 link(s):
($X^2$ -1): max_pval = 0.00000, min_val = 0.979
($X^2$ -2): max_pval = 0.00000, min_val = 0.936
($X^1$ -2): max_pval = 0.00000, min_val = 0.864
($X^1$ -1): max_pval = 0.00000, min_val = 0.782
($X^0$ -2): max_pval = 0.00013, min_val = 0.401
($X^0$ -1): max_pval = 0.00994, min_val = 0.277
Testing condition sets of dimension 1:
Link ($X^2$ -1) -?> $X^2$ (1/6):
Constructed array of shape (3, 69) from
X = [(2, -1)]
Y = [(2, 0)]
Z = [(2, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.872 | pval = 0.00000
Subset 0: ($X^2$ -2) gives pval = 0.00000 / val = 0.872
No conditions of dimension 1 left.
Link ($X^2$ -2) -?> $X^2$ (2/6):
Constructed array of shape (3, 69) from
X = [(2, -2)]
Y = [(2, 0)]
Z = [(2, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.538 | pval = 0.00000
Subset 0: ($X^2$ -1) gives pval = 0.00000 / val = -0.538
No conditions of dimension 1 left.
Link ($X^1$ -2) -?> $X^2$ (3/6):
Constructed array of shape (3, 77) from
X = [(1, -2)]
Y = [(2, 0)]
Z = [(2, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.746 | pval = 0.00000
Subset 0: ($X^2$ -1) gives pval = 0.00000 / val = 0.746
No conditions of dimension 1 left.
Link ($X^1$ -1) -?> $X^2$ (4/6):
Constructed array of shape (3, 77) from
X = [(1, -1)]
Y = [(2, 0)]
Z = [(2, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.915 | pval = 0.00000
Subset 0: ($X^2$ -1) gives pval = 0.00000 / val = 0.915
No conditions of dimension 1 left.
Link ($X^0$ -2) -?> $X^2$ (5/6):
Constructed array of shape (3, 77) from
X = [(0, -2)]
Y = [(2, 0)]
Z = [(2, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.707 | pval = 0.00000
Subset 0: ($X^2$ -1) gives pval = 0.00000 / val = 0.707
No conditions of dimension 1 left.
Link ($X^0$ -1) -?> $X^2$ (6/6):
Constructed array of shape (3, 77) from
X = [(0, -1)]
Y = [(2, 0)]
Z = [(2, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.461 | pval = 0.00003
Subset 0: ($X^2$ -1) gives pval = 0.00003 / val = 0.461
No conditions of dimension 1 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^2$ has 6 link(s):
($X^2$ -1): max_pval = 0.00000, min_val = 0.872
($X^1$ -1): max_pval = 0.00000, min_val = 0.782
($X^1$ -2): max_pval = 0.00000, min_val = 0.746
($X^2$ -2): max_pval = 0.00000, min_val = 0.538
($X^0$ -2): max_pval = 0.00013, min_val = 0.401
($X^0$ -1): max_pval = 0.00994, min_val = 0.277
Testing condition sets of dimension 2:
Link ($X^2$ -1) -?> $X^2$ (1/6):
Constructed array of shape (4, 77) from
X = [(2, -1)]
Y = [(2, 0)]
Z = [(1, -1), (1, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.986 | pval = 0.00000
Subset 0: ($X^1$ -1) ($X^1$ -2) gives pval = 0.00000 / val = 0.986
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^1$ -1) -?> $X^2$ (2/6):
Constructed array of shape (4, 77) from
X = [(1, -1)]
Y = [(2, 0)]
Z = [(2, -1), (1, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.795 | pval = 0.00000
Subset 0: ($X^2$ -1) ($X^1$ -2) gives pval = 0.00000 / val = 0.795
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^1$ -2) -?> $X^2$ (3/6):
Constructed array of shape (4, 77) from
X = [(1, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.015 | pval = 0.90125
Subset 0: ($X^2$ -1) ($X^1$ -1) gives pval = 0.90125 / val = 0.015
Non-significance detected.
Link ($X^2$ -2) -?> $X^2$ (4/6):
Constructed array of shape (4, 69) from
X = [(2, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.342 | pval = 0.00463
Subset 0: ($X^2$ -1) ($X^1$ -1) gives pval = 0.00463 / val = 0.342
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^0$ -2) -?> $X^2$ (5/6):
Constructed array of shape (4, 77) from
X = [(0, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.013 | pval = 0.91292
Subset 0: ($X^2$ -1) ($X^1$ -1) gives pval = 0.91292 / val = -0.013
Non-significance detected.
Link ($X^0$ -1) -?> $X^2$ (6/6):
Constructed array of shape (4, 77) from
X = [(0, -1)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.150 | pval = 0.20014
Subset 0: ($X^2$ -1) ($X^1$ -1) gives pval = 0.20014 / val = -0.150
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^2$ has 3 link(s):
($X^2$ -1): max_pval = 0.00000, min_val = 0.872
($X^1$ -1): max_pval = 0.00000, min_val = 0.782
($X^2$ -2): max_pval = 0.00463, min_val = 0.342
Algorithm converged for variable $X^2$
## Resulting lagged parent (super)sets:
Variable $X^0$ has 1 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.585
Variable $X^1$ has 2 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.780
($X^0$ -1): max_pval = 0.00000, min_val = 0.654
Variable $X^2$ has 3 link(s):
($X^2$ -1): max_pval = 0.00000, min_val = 0.872
($X^1$ -1): max_pval = 0.00000, min_val = 0.795
($X^2$ -2): max_pval = 0.00463, min_val = 0.342
##
## Step 2: MCI algorithm
##
Parameters:
independence test = par_corr
tau_min = 0
tau_max = 2
max_conds_py = None
max_conds_px = None
link ($X^0$ -1) -?> $X^0$ (1/8):
with conds_y = [ ]
with conds_x = [ ($X^0$ -2) ]
Constructed array of shape (3, 96) from
X = [(0, -1)]
Y = [(0, 0)]
Z = [(0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.585 | pval = 0.00000 [cached]
link ($X^0$ -2) -?> $X^0$ (2/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^0$ -3) ]
Constructed array of shape (4, 96) from
X = [(0, -2)]
Y = [(0, 0)]
Z = [(0, -1), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = -0.048 | pval = 0.64516
link ($X^1$ 0) o?o $X^0$ (3/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^1$ -1) ($X^0$ -1) ]
Constructed array of shape (4, 96) from
X = [(1, 0)]
Y = [(0, 0)]
Z = [(0, -1), (1, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.072 | pval = 0.48950
link ($X^1$ -1) -?> $X^0$ (4/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^1$ -2) ($X^0$ -2) ]
Constructed array of shape (5, 96) from
X = [(1, -1)]
Y = [(0, 0)]
Z = [(0, -1), (1, -2), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.091 | pval = 0.38447
link ($X^1$ -2) -?> $X^0$ (5/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^1$ -3) ($X^0$ -3) ]
Constructed array of shape (5, 96) from
X = [(1, -2)]
Y = [(0, 0)]
Z = [(0, -1), (1, -3), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = 0.048 | pval = 0.64957
link ($X^2$ 0) o?o $X^0$ (6/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
Constructed array of shape (6, 69) from
X = [(2, 0)]
Y = [(0, 0)]
Z = [(0, -1), (2, -1), (1, -1), (2, -2)]
extraZ = []
with missing values = 999.0 removed
val = -0.068 | pval = 0.59118
link ($X^2$ -1) -?> $X^0$ (7/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^2$ -2) ($X^1$ -2) ($X^2$ -3) ]
Constructed array of shape (6, 70) from
X = [(2, -1)]
Y = [(0, 0)]
Z = [(0, -1), (2, -2), (1, -2), (2, -3)]
extraZ = []
with missing values = 999.0 removed
val = -0.118 | pval = 0.34583
link ($X^2$ -2) -?> $X^0$ (8/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^2$ -3) ($X^1$ -3) ($X^2$ -4) ]
Constructed array of shape (6, 71) from
X = [(2, -2)]
Y = [(0, 0)]
Z = [(0, -1), (2, -3), (1, -3), (2, -4)]
extraZ = []
with missing values = 999.0 removed
val = 0.007 | pval = 0.95741
link ($X^0$ 0) o?o $X^1$ (1/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^0$ -1) ]
Constructed array of shape (4, 96) from
X = [(0, 0)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.072 | pval = 0.48950 [cached]
link ($X^0$ -1) -?> $X^1$ (2/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ($X^0$ -2) ]
Constructed array of shape (4, 96) from
X = [(0, -1)]
Y = [(1, 0)]
Z = [(1, -1), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.654 | pval = 0.00000 [cached]
link ($X^0$ -2) -?> $X^1$ (3/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^0$ -3) ]
Constructed array of shape (5, 96) from
X = [(0, -2)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = 0.098 | pval = 0.34941
link ($X^1$ -1) -?> $X^1$ (4/8):
with conds_y = [ ($X^0$ -1) ]
with conds_x = [ ($X^1$ -2) ($X^0$ -2) ]
Constructed array of shape (5, 96) from
X = [(1, -1)]
Y = [(1, 0)]
Z = [(0, -1), (1, -2), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.560 | pval = 0.00000
link ($X^1$ -2) -?> $X^1$ (5/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^1$ -3) ($X^0$ -3) ]
Constructed array of shape (6, 96) from
X = [(1, -2)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1), (1, -3), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = 0.151 | pval = 0.15061
link ($X^2$ 0) o?o $X^1$ (6/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
Constructed array of shape (6, 69) from
X = [(2, 0)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1), (2, -1), (2, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.057 | pval = 0.65168
link ($X^2$ -1) -?> $X^1$ (7/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^2$ -2) ($X^1$ -2) ($X^2$ -3) ]
Constructed array of shape (7, 70) from
X = [(2, -1)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1), (2, -2), (1, -2), (2, -3)]
extraZ = []
with missing values = 999.0 removed
val = -0.250 | pval = 0.04498
link ($X^2$ -2) -?> $X^1$ (8/8):
with conds_y = [ ($X^1$ -1) ($X^0$ -1) ]
with conds_x = [ ($X^2$ -3) ($X^1$ -3) ($X^2$ -4) ]
Constructed array of shape (7, 71) from
X = [(2, -2)]
Y = [(1, 0)]
Z = [(1, -1), (0, -1), (2, -3), (1, -3), (2, -4)]
extraZ = []
with missing values = 999.0 removed
val = 0.057 | pval = 0.64695
link ($X^0$ 0) o?o $X^2$ (1/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^0$ -1) ]
Constructed array of shape (6, 69) from
X = [(0, 0)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -2), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = -0.068 | pval = 0.59118 [cached]
link ($X^0$ -1) -?> $X^2$ (2/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^0$ -2) ]
Constructed array of shape (6, 69) from
X = [(0, -1)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -2), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = -0.135 | pval = 0.28206
link ($X^0$ -2) -?> $X^2$ (3/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^0$ -3) ]
Constructed array of shape (6, 69) from
X = [(0, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -2), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = -0.188 | pval = 0.13451
link ($X^1$ 0) o?o $X^2$ (4/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^1$ -1) ($X^0$ -1) ]
Constructed array of shape (6, 69) from
X = [(1, 0)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -2), (0, -1)]
extraZ = []
with missing values = 999.0 removed
val = 0.057 | pval = 0.65168 [cached]
link ($X^1$ -1) -?> $X^2$ (5/8):
with conds_y = [ ($X^2$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^1$ -2) ($X^0$ -2) ]
Constructed array of shape (6, 69) from
X = [(1, -1)]
Y = [(2, 0)]
Z = [(2, -1), (2, -2), (1, -2), (0, -2)]
extraZ = []
with missing values = 999.0 removed
val = 0.731 | pval = 0.00000
link ($X^1$ -2) -?> $X^2$ (6/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^1$ -3) ($X^0$ -3) ]
Constructed array of shape (7, 69) from
X = [(1, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -2), (1, -3), (0, -3)]
extraZ = []
with missing values = 999.0 removed
val = 0.152 | pval = 0.23139
link ($X^2$ -1) -?> $X^2$ (7/8):
with conds_y = [ ($X^1$ -1) ($X^2$ -2) ]
with conds_x = [ ($X^2$ -2) ($X^1$ -2) ($X^2$ -3) ]
Constructed array of shape (6, 63) from
X = [(2, -1)]
Y = [(2, 0)]
Z = [(1, -1), (2, -2), (1, -2), (2, -3)]
extraZ = []
with missing values = 999.0 removed
val = 0.415 | pval = 0.00108
link ($X^2$ -2) -?> $X^2$ (8/8):
with conds_y = [ ($X^2$ -1) ($X^1$ -1) ]
with conds_x = [ ($X^2$ -3) ($X^1$ -3) ($X^2$ -4) ]
Constructed array of shape (7, 58) from
X = [(2, -2)]
Y = [(2, 0)]
Z = [(2, -1), (1, -1), (2, -3), (1, -3), (2, -4)]
extraZ = []
with missing values = 999.0 removed
val = 0.238 | pval = 0.08553
## Significant links at alpha = 0.01:
Variable $X^0$ has 1 link(s):
($X^0$ -1): pval = 0.00000 | val = 0.585
Variable $X^1$ has 2 link(s):
($X^0$ -1): pval = 0.00000 | val = 0.654
($X^1$ -1): pval = 0.00000 | val = 0.560
Variable $X^2$ has 2 link(s):
($X^1$ -1): pval = 0.00000 | val = 0.731
($X^2$ -1): pval = 0.00108 | val = 0.415マスキング
結束値と異なり、マスキングは、状況によって、サンプルを含めるか除外するかに使うことができます。オプションパラメータmaskとmask_typeを使うことによって適用します。
mask: は、オプション引数で、DataFrameオブジェクトを初期化するときに渡すことができます。dataと同じシェイプのnumpy配列です。そして、値0(または偽)または1(または真)を含んでいます。この方法でdataの各エントリーは、0または1に関連します。ここで、0はエントリーがマスクされないこと、1はマスクされることになることを意味します。mask_typeは、オプション引数で、条件独立性テストオブジェクトを初期化するときに、例えば、ParCorrに渡すことができます。それは、文字列で、x,yとzの文字を任意に組み合わせることができます。もし、mask_typeが、Noneとして左辺が未定ならば、そのときmaskは使用されません。mask_typeは、変数の種類を、マスクがアクティブになっていて、条件独立性テストのそれらの役割によって決定します。
詳細は以下のようになります。
機械的に何をマスクするか
X = Xt-riが、与えられたZ={Xt-rkk,Xt-ril,…}でY=Xtjの条件独立かどうかのテストを考えます。この特別なZは、単に説明のためです。Zは、空かまたは、一つの成分を持ちます。個別のサンプルは、こうしてsn=(Xn-ri,Xnj,Xn-rkk,Xn-ril,…) 2 * τmax ≦ n ≦ t (それは2.τmaxで、MCIテストが、遅延変数の親を条件とすると 2.τmaxではない)になります。そのとき、マスキングの機能は、もし、少なくとも次のうちのひとつの条件が真のときに、テストからサンプルsnが除外されます。
- Xn-riが、
maskによってマスクされるように、mask_typeに文字xが印付けられます。 - Xnjが、
maskによってマスクされるように、mask_typeに文字yが印付けられます。 - Xn-rkkまたはXn-rlまたは,…が、
maskによってマスクされるように、mask_typeに文字zが印づけられます。
直感的に、サンプルsは、条件独立性テストから除外されます。もし、i)そのエントリーの一つが、maskによってマスクされるように印しづけられ、そして、ii)このエントリーが、X-型(またはy-型、z-型)の変数に一致しており、そしてmask_typeが、マスキングがX-型(またはY-型、z-型)変数にアクティブにされることを示しています。
例1
私たちは全ての値Xsiに、mask_type=yを選択してマスクをかけ、sは時間範囲[t0,t1]の中にないものとして、印をつけます。その後、Y-型の変数に一致するエントリーのサンプルにだけが、残りの時間ステップから取られます。上の表記で、それらのt0≦n ≦ t1だけが残ります。しかし、これら残りのサンプルにとって、X型またはZ型に一致するエトリーは、時間ウィンドウ[t0,t1]の外から取って良いことに注意してください。例えば、Xt0-1iの値は[t0,t1]の外側の時間のインデックスを含むけれども、もし、X=Xt-1iであれば、サンプルst0=(Xt0-1i,Xt0j,Xt0-rkk,Xt0-τil,…)は、保持されます。
これは、 [Kretschmer et al.,2016]に記述されているように、異なるケースの本質的なものです。単独のインターバル[t0,t1]は、一年の12月-2月に対応するいくつかのインターバルで取り替えられます。
[Kretschmer et al., 2016] Kretschmer, M., Coumou, D., Donges, J. F., and Runge, J. (01 Jun. 2016). Using causal effect networks to analyze different arctic drivers of midlatitude winter circulation. Journal of Climate, 29(11):4069 – 4081. https://doi.org/10.1175/JCLI-D-15-0654.1.
例2
例1と同じマスクで、mask_type=xyを選択します。そのとき、例1で無視された全てのサンプルは、ここでもまた無視されます。加えて、t0 ≦ n ≦ t0 + τ -1のときにサンプルsnもまた無視されます。そのため、もし、τ = 0であれば、それ以上のサンプルは無視されません。もし、τ = 1 ならば、単独のサンプルst0は、さらに無視されます。もし、τ = 2 ならば、二つのサンプル st0とst0+1がさらに無視されます。そしてそのように続きます。これは、まだxを含んでいることを示し、さらに、もし、τmaxが大きく選択された場合、mask_typeに z を含んでいることは、強力に残りのサンプル数を減少することを示しています。
これを説明するために、ページ4073最後のパラグラフからページ4074の最初のパラグラフ[Kretschmer et al., 2016]を見てください。そして、もし、mask_typeが、yの代わりにxyだったとすると、何が起きるか見てください。ここで、Y=PoVt であり、Zは空です。τ = 1にとって、X= EA-snow t-1. もし、mask_typeがxy だったら、EA-snowもまた12月-2月に制限されます。したがって、各年は、3サンプルのうち二つだけが寄与します。(月次の間隔で)。二つのサンプルは、(2月のPoV、1月のEA-snow),(1月のPoV、12月のEA-snow). τ - 3であれば、X=EA-snowそして、2月のPoVが11月のEAーsnowと対になる必要がるため、サンプルは離れません。それは、マスクのないインターバル12月ー2月が範囲外になります。同様に1月(12月)のPoVは、10月(9月)のEA-snowと対になる必要があります。その両方は、マスクのないインターバルの範囲外です。
何のマスクを使うことができるか
因果ステーショナリティーに関して背景知識が利用できます。特に、正確な因果メカニズムがステーショナリーのために信頼されるように、時間範囲を規定することが許容されます。これは、次の図で説明されます。全体の時系列(例えばマスキングのない)のPCMCIの実行は、基礎になる因果構造は、全体の時系列を超えて、同じところにとどまる、という仮定を暗黙に作ります。図の上の部分を見てください。ユーザーは、しかし、因果の構造は時間経過で変化するという背景知識を持っています。例えば、二つのレジーム間で、図の下の部分に示されるように、6ヶ月ごとに交代します。(図は、これら二つのレジームを図示されているように、冬と夏として参照します。)。そのようなケースでは、マスキングは、異なるレジームを別々に分析します。
この例は、[Kretschmer et al.,2016]の応用と同様です。そこでは、mask_type=yの使用は、PCMCIAで対象変数、変数は12月-2月に制限されます、この因果ドライバーを探索するだけの結果になります。潜在的な因果ドライバーは、しかし、12月-2月期だけではありません。もし、この例のmask_typeがxyであれば、その時、潜在底な因果ドライバーは、12月-2月に制限されます。もし、mask_typeがxyzならば、追加の対象変数と因果ドライバー、条件付き変数は12月-2月期に制限されます。
例3 (コード付き)
以下は、私たちは、基礎となる因果ドライバーが、冬の半年と夏の半年で参照される二つのレジーム間を交代するデータを生成します。特に、二つのレジームは、一つの因果の影響が、二つのレジームの反対のサインになる点が異なります。
# Masking demo: We consider time series where the one part is generated by a different
# causal process than the other part.
np.random.seed(42)
T = 1000
data = np.random.randn(T, 2)
data_mask = np.zeros(data.shape)
for t in range(1, T):
# print t % 365
if (t % 365) < 3*30 or (t % 365) > 8*30:
# Winter half year
data[t, 0] += 0.4*data[t-1, 0]
data[t, 1] += 0.3*data[t-1, 1] + 0.9*data[t-1, 0]
else:
# Summer half year
data_mask[[t, t-1]] = True
data[t, 0] += 0.4*data[t-1, 0]
data[t, 1] += 0.3*data[t-1, 1] - 0.9*data[t-1, 0]
T, N = data.shape
# print data_mask[:100, 0]
dataframe = pp.DataFrame(data, mask=data_mask)
tp.plot_timeseries(dataframe, figsize=(8,3), grey_masked_samples='data'); plt.show()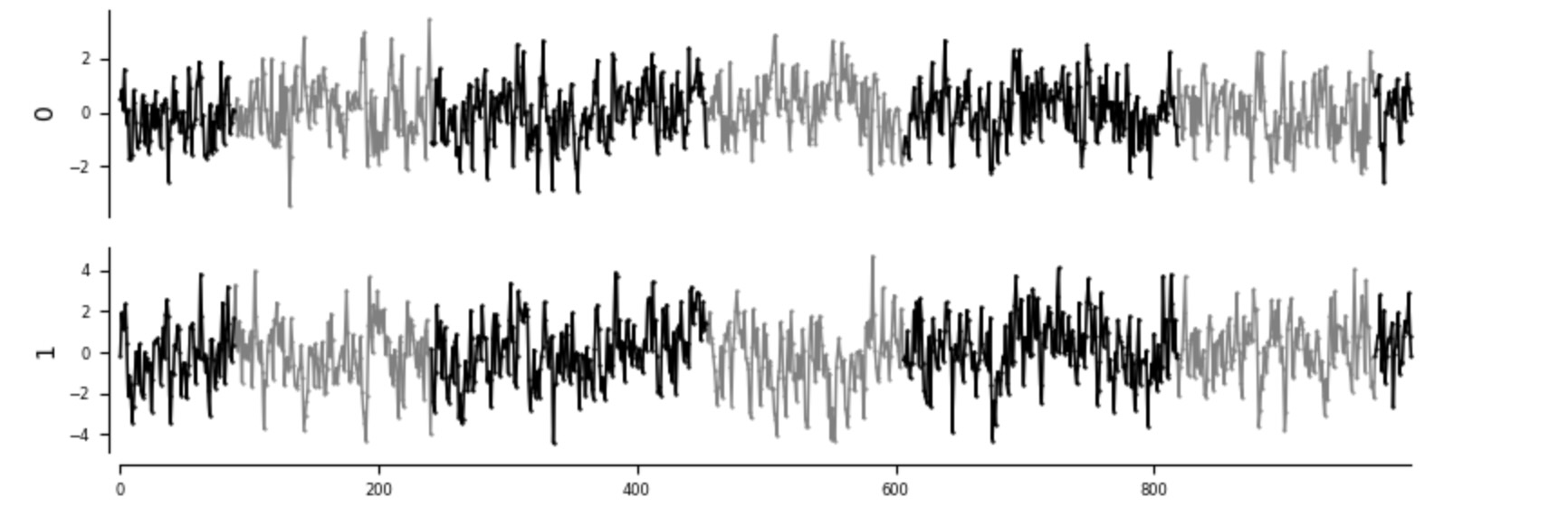
# Setup analysis
def run_and_plot(cond_ind_test, fig_ax, aspect=20):
pcmci = PCMCI(dataframe=dataframe, cond_ind_test=cond_ind_test)
results = pcmci.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level=0.01)
tp.plot_graph(fig_ax = fig_ax, val_matrix=results['val_matrix'],
graph=results['graph'], var_names=var_names,
node_aspect=aspect, node_size=0.02
); plt.show()# Causal graph of whole year yields no link because effects average out
fig = plt.figure(figsize=(3,2)); ax=fig.add_subplot(111)
run_and_plot(ParCorr(mask_type=None), (fig, ax))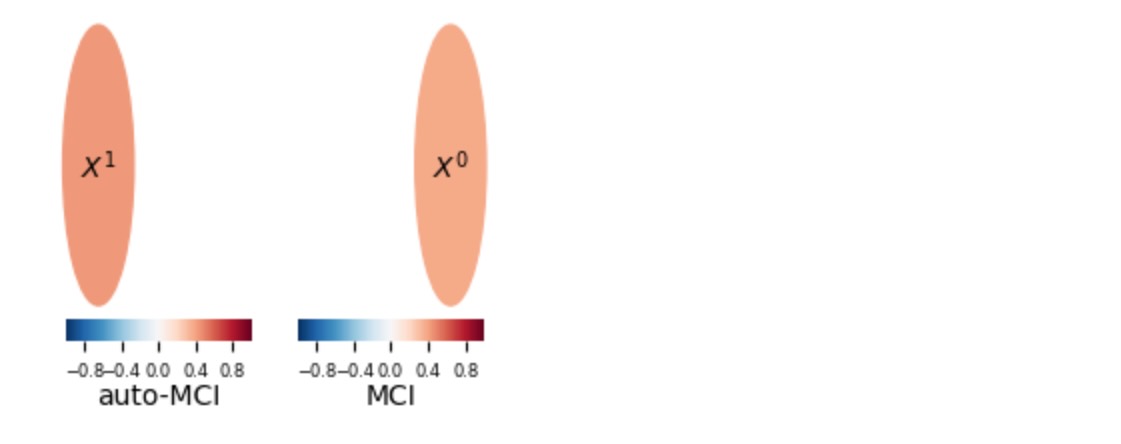
# Causal graph of winter half only gives positive link
fig = plt.figure(figsize=(3,2)); ax=fig.add_subplot(111)
run_and_plot(ParCorr(mask_type='y'), (fig, ax))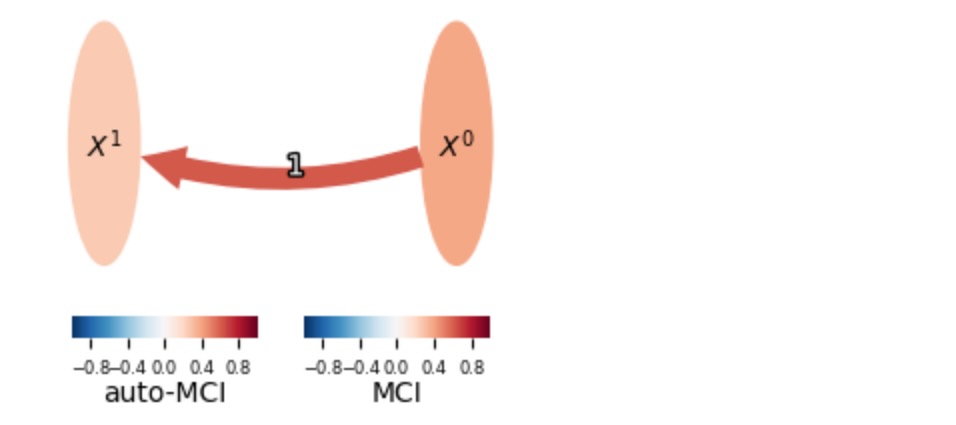
# Causal graph of summer half only gives negative link
fig = plt.figure(figsize=(3,2)); ax=fig.add_subplot(111)
dataframe.mask[0] = (dataframe.mask[0] == False)
run_and_plot(ParCorr(mask_type='y'), (fig, ax))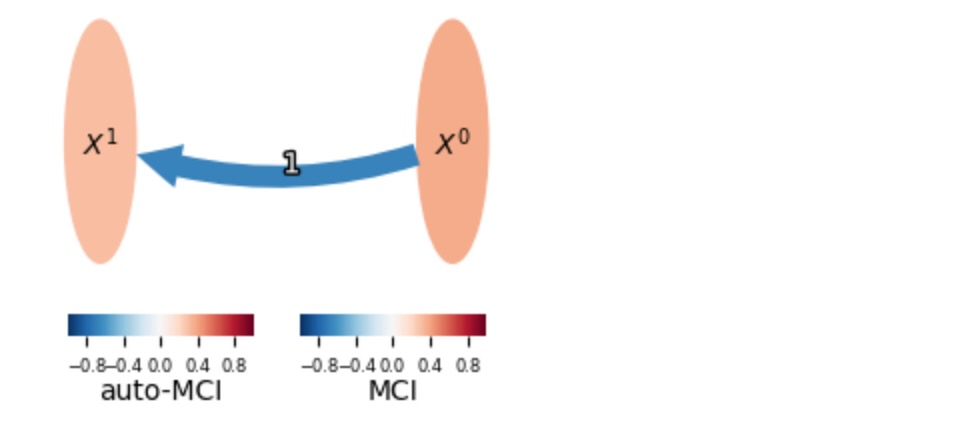
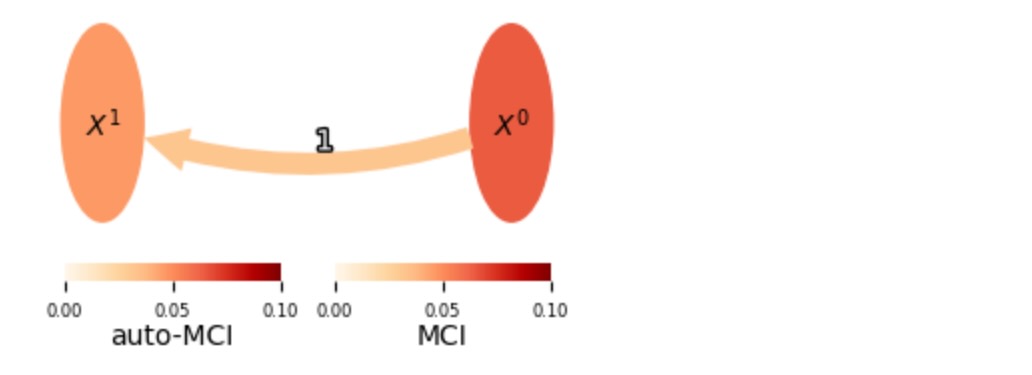
しかし、全体のサンプルのリンクの検出の失敗は、部分相関のためにだけ発生します。正と負の従属性は除外されます。下に見られるように、CMIknnの使用はリンクを回復します。CMIknnを速くするために、ここで私たちは、significance='fixed_thres'オプションを使います。そして、pc_alphaとalpha_levelは、任意の条件独立性テストで、 I* を閾値として解釈されます。条件独立性テストの詳細はチュートリアルを参照してください。
cmi_knn = CMIknn(significance='fixed_thres', mask_type=None)
fixed_thres = 0.01
pcmci = PCMCI(dataframe=dataframe, cond_ind_test=cmi_knn)
results = pcmci.run_pcmci(tau_max=2, pc_alpha=fixed_thres, alpha_level=fixed_thres)fig_ax = tp.plot_graph(val_matrix=results['val_matrix'],
node_aspect=20,
node_size=0.02,
figsize=(3,2),
vmin_edges=0.,
vmax_edges = 0.1,
edge_ticks=0.05,
cmap_edges='OrRd',
vmin_nodes=0.,
vmax_nodes= 0.1,
node_ticks=0.05,
cmap_nodes='OrRd',
graph=results['graph'], var_names=var_names)
fig_ax[0].tight_layout()