このノートブックは、TIGRAMITEのために多重データセットの機能を説明します。それは、PCMCIやPCMCI+のような因果探索メソッドや、また、時系列の多重データのCausalEffectクラスのツールを許容します。ここで、私たちは、PCMCI/PCMCI+の機能に焦点を当てます。手短に多重-PCMCIとしてこれを参照します。
概要
要約すると、多重-PCMCIは、二つの機能を実装します。それは標準のPCMCIから区別します。これらは、
- それは、単一の時系列を操作しませんが、むしろ、例えば、時系列の多重配列を収集します。条件独立性テストのサンプルは、全てのデータセットから生成されます。
- 条件独立性テストのサンプルを生成するために使われる時間ステップを規定します。この仕様は必要とされませんが、デフォルトのメソッド毎に、できる限り多くのサンプルを生成します。
実際にどのように、多重PCMCIが使われるかを見るために、次のセクションに進みます。多重PCMCIによって供給される新しい機能のPCMCIと多重PCMCIを区別することについて、もっと学習するためにここを読み進めてください。
(*) 単一の時系列は、典型的に多変量です。時系列の多重因子を持ちます。
詳細
標準のPCMCIアルゴリズムは単一の時系列を操作します。それはいわゆるデータはシェイプ(T,N)の配列です。ここで、Tは時間ステップ、Nは変数の数です(時系列の因子数)。アルゴリズムが、条件時系列Xt-r,⊥ Yt | Zt-τk,の統計テストを実行するとき、ここで、X,YとZは、N個の変数の任意の三つで、τi ≧ 0と τk ≧ 0 は、時間遅延、このテストのサンプルは、時系列データの異なる時間ステップから生成されます。これは、ステーショナリティーの仮定から適応されます。
もっと正確には、このテストのためのサンプルは、範囲s =2τmax, 2τmax + 1,…,T-1(最後の時間ステップがT-1のため、0から開始します)のs に対して、(Xs-τ, Ys, Zs-τk)になります。ここで、τmaxは、最大考慮時間遅延、それは、τiとτkが、τi ≦ τmax、τk ≦ τmaxに制限されることを意味しています。これは、s ≧ τmaxの制限に対応する最初のτmax時間ステップが、無視される必要があることを正当化します。なぜなら、(Xs-r,Ys,Zs-τk)内の小文字の識別は、負の値が許されます、こうして範囲外になります。強い制限s ≧ 2τmaxの理由は、PCMCIの設計に置かれます。その詳細はここでは重要ではありません。
実際は、しかし、ただの単一のアクセスでなく、同じ過程の対応する多重時系列へのアクセスになります。相違は、同じ過程の実現値のそれぞれが、シェイプ(T(m),N)の配列Mを持つでしょう。条件独立性テストでは、これらのMデータセットから選んだサンプルを結合し、基礎となる共有過程の単一の因果グラフを学習します。データセットは、上の小文字m, 0 ≦ m ≦ M-1、でインデックスされ、それは同じ時間の長さを必要としません。例えば、T(m)はmに依存します。
デフォルトで、基礎になる過程は、ステーショナリーになることが仮定されます。それは、データセットm1の時間ステップに対応するデータセットm0の時間ステップを規定する必要はありません。テストXt-τ ⊥ Yt | Zt-τkのためのサンプルは、こうして、0 ≦ m ≦ M - 1の時に、s=2τmax, 2 τmax + 1,…T(m)-1で、(Xs-τi(m),Ys(m), Zs-τk(m))になります。これは、多重PCMCIに実装された鍵となる機能です。(これは、上のリストの最初の重点項目)
多重PCMCIは、潜在的に非ステーショナリティーを考慮に入れた分析を実行するための、機能を含みます。それは、結合され、条件独立性テストに使用するデータセットの時間ステップを、注意深く規定する必要があります。(上のリストの2番目の重点項目)。これは、情報の二つの部分を要求します。
- 最初に、データセットm1の時間ステップに対応するデータセットm0の時間ステップを規定するために、時間上で個別のデータセットを整列させる必要があります。言い換えると、個別の時系列データセットは、共通の時間軸上で、整列させる必要があります。例えば、データセットは、正確な刺激を表面化する異なる被験者で計測した神経の活動で良いでしょう。その時、個別の被験者に与えられる刺激、時間ステップT(m)=t(m)を規定する必要があります。デフォルトでは、データセットは、時間ステップ0で整列させられます。これは、
time_offsetsキーワード引数によって修正されます。 - 2番目に、サンプルを生成するのに使う時間軸の時間ステップを規定する必要があります。前の例を続けると、刺激を与えた後、最初の1分に注意を制限するか、または、刺激を与えた後の最初と2番目の1分を分離して分析したいかもしれません。他の例では、環境の時系列は、夏と冬場の月を分けて分析するかもしれません。デフォルトでは、できる限り多くのサンプルを生成します。例えば、全ての時間ステップ、各時系列データセットの最初の時間ステップの2τmax以外が使われるかもしれません。これは、
reference_pointsキーワード引数で修正されます。
使用法
この例は、多重データ-PCMCIの実際の使用を説明します。それは五つの部分に分割されます。
- 基本とコマンドの使い方
- 事例
reference_pointsキーワード引数time_offsetsキーワード引数- さらに進んだコメント
1. 基本とコマンドの使い方
多重PCMCIは、現在のTIGRAMITEクラスPCMCIとDataFrameに実装されます。しかし、多重PCMCIクラスはPredictionクラスでは働かないことに注意してください。
多重PCMCIは、一つまたは、二つの様式のデータを予期します。
- シェイプ(M.T,N)の3D numpy配列、ここで、最初の次元は、個別のデータセットに対応し、2番目は時間ステップ、3番目は変数に対応します。これは全てのデータセットが同じ時間の長さと
time_offsets機能が、使えません。例えば、time_offsetsは、Noneに設定します。 - 時間の長さT(m),シェイプ(T(m),N)の2Dnumpy配列からなるdictデータは、エントリーを超えて変異しますが、変数の数Nは、全てのエントリーで同じである必要があります。
多重データ-PCMCIで使うDataFrameオブジェクトの初期化の方法に例:
## Option 1: Data is a 3D numpy array
# data = np.random.randn(8, 100, 5)
# dataframe = DataFrame(data, analysis_mode = 'multiple')
## Option 2: Data is a dictionary of 2D numpy arrays
# time_lengths = [100, 105, 92, 103, 90]
# data = {m: np.random.randn(T, 5) for m, T in enumerate(time_lengths)}
# dataframe = DataFrame(data, analysis_mode = 'multiple') ここで、鍵は、キーワード引数analysis_mode='multiple'とするanalysisの仕様です。それは、DataFrameクラスに、標準のPCMCIの代わりに、多重PCMCIを実行するために使うことを告げます。もし、規定しないならば、analysis_modeは、デフォルトでanalysis_mode='single'に設定されます。それは、標準のPCMCIに一致します。
analysis_mode='single'で、data引数は、シェイプ (T,N)の2D numpy配列、または、シェイプ(T,N)の2D numpy配列からなる単一エントリーのdictデータ、として、与えられることができます。
ここから、すべては、通常通り働きます。あなたは、PCMCIの代わりに、多重PCMCIを使うことをすでに規定しています。DataFrameオブジェクトを構築するときに、PCMCIオブジェクトを使う、または構築するときに、再度これを規定する必要なありません。したがって、あなたは、例えば、以下の例を実行して良いでしょう。
# from tigramite.independence_tests.parcorr import ParCorr
# pcmci = PCMCI(dataframe = dataframe, cond_ind_test = ParCorr())
# results = pcmci.run_pcmci(tau_max = 2, pc_alpha = 0.05)2. 事例
import numpy as np
np.random.seed(42)
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.data_processing import DataFrame
from tigramite.pcmci import PCMCI
import tigramite.plotting as tpデータ生成:説明する目的で、私たちは、人工的なデータを生成します。すなわち、いくつかの実現値、例えば、標準正規ノイズのある、一次の線形 VAR過程から多重のインスタンスです。
## Option 1: Data is 3D numpy array
M = 5 # number of datasets
T = 60 # number of time steps
N = 3 # number of variables
data = np.random.randn(M, T, N)
for t in range(1, T):
data[:, t, 0] += 0.7*data[:, t-1, 0]
data[:, t, 1] += 0.6*data[:, t-1, 1] + 0.6*data[:, t-1, 0]
data[:, t, 2] += 0.5*data[:, t-1, 2] - 0.6*data[:, t-1, 1]## Option 2: Data is dictionary of 2D numpy arrays
M = 5 # number of datasets
T = [40, 50, 60, 70, 80] # number of time steps for the individual datasets
N = 3 # number of variables
data = {i: np.random.randn(T[i], N) for i in range(M)}
for i in range(M):
for t in range(1, T[i]):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1] + 0.6*data[i][t-1, 0]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]DataFrameオブジェクトのインスタンス化: 上に説明したようにDataFrameオブジェクトを作ります。オプションのキーワード引数var_namesを使って変数名を設定することに注意してください。私たちはここで、下のもっと情報のあるグラフィカルな可視化のためにこれを選択します。
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']
dataframe = DataFrame(data, analysis_mode = 'multiple', var_names = var_names)時系列の図示:個別の時系列データセットを図示目するために、plot_timeseries()を使います。そして、引数selected_datasetによって必要なデータセットを規定します。
for member in dataframe.values.keys():
tp.plot_timeseries(selected_dataset = member, dataframe = dataframe)
plt.show()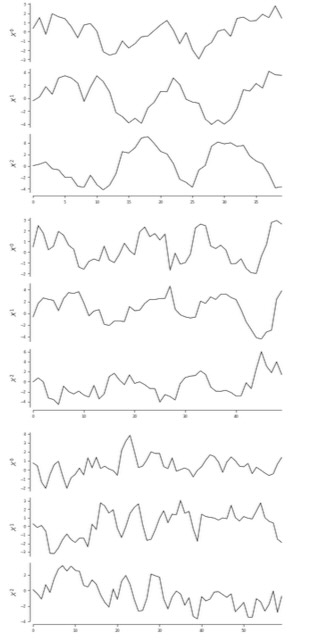
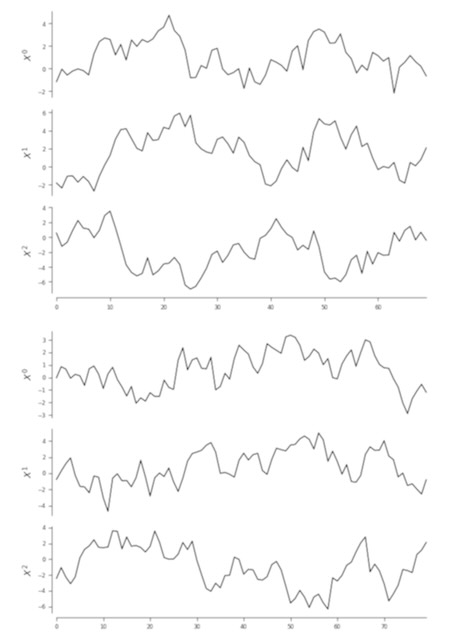
多重データPCMCIの実行:多重データPCMCIを実行するために、あなたが標準のPCMCIで行ったのと同じ方法で、PCMCIオブジェクトを生成し、適用します。標準のPCMCIよりむしろ多重データPCMCIに使うための情報は、DataFrameオブジェクトのインスタンス化をすでに規定してました。説明の目的で、私たちは、ここで、結果を図示します。あなたは、PCMCI+の代わりにPCMCIを走らせることもできます。
pcmci = PCMCI(dataframe = dataframe, cond_ind_test = ParCorr())
results = pcmci.run_pcmciplus(tau_max = 2, pc_alpha = 0.01)
tp.plot_graph(graph=results['graph'], val_matrix=results['val_matrix'], var_names=var_names)
plt.show()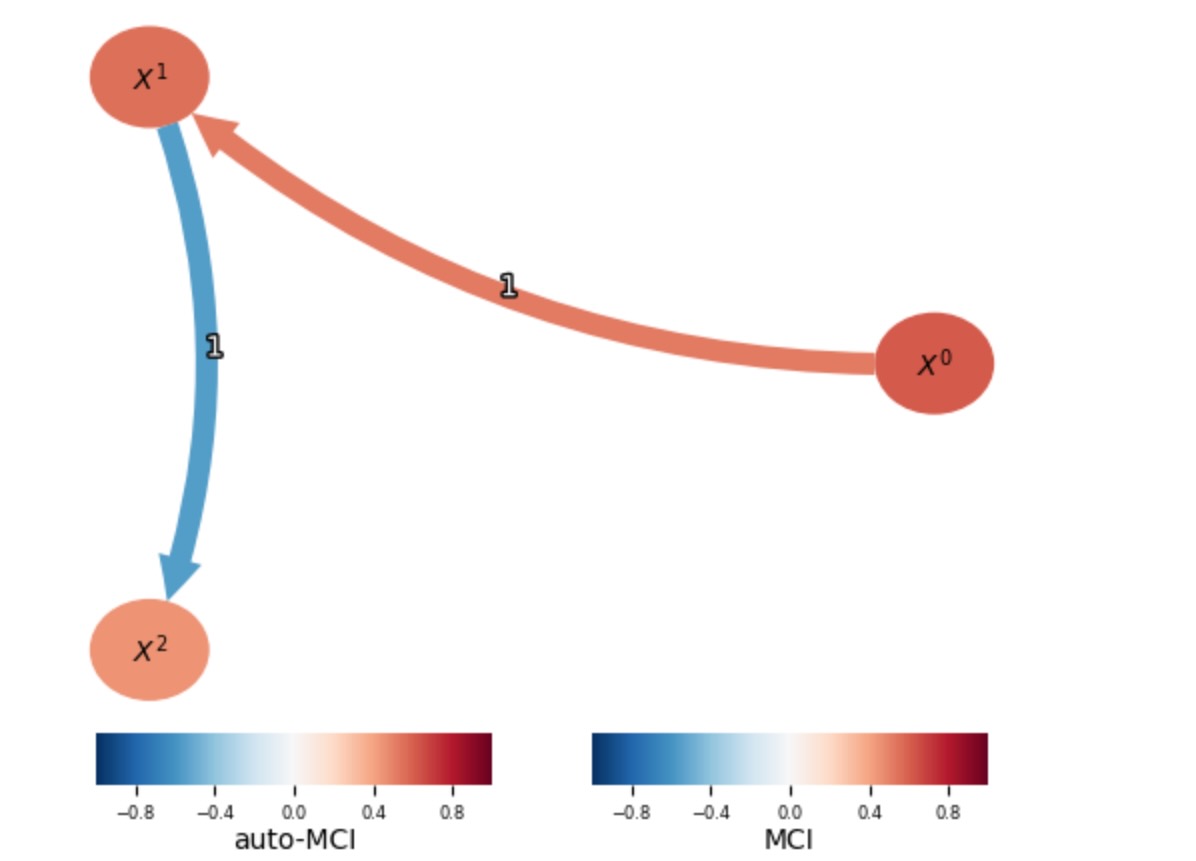
3. reference_pointsキーワード引数
サンプルの生成とまた条件独立性テストのために使う時間ステップの仕様は、DataFrameオブジェクトのインスタンス化で発生します。これは、オプションのキーワード引数reference_pointsによって実行されます。それは、以下のように進みます。詳しい事例は下を参照してください。私たちは、ここで、time_offsetsをNoneに仮定します。そうして、個別の時系列データセットは、0番目の時間ステップに揃えられます。
- 規定するために、最初の100時間ステップだけは、リスト
[0,1,..,98,99]または、同様にnumpyの配列np.array([0,1,…,98,99])reference_pointsキーワード引数に渡されて、考慮されます。 - 使用する単一の時間ステップt0のみ規定するために、リスト[t_0]、または、整数t_0に渡されます。
- もし、規定しないならば、
reference_pointsはデフォルトでNoneに設定します。これは、[0,1,…,T^{\text{max}} -1]に渡すことと同様です。ここで、Tmax = max 0 ≦ m ≦ M-1 T(m)は、もっとも長い時系列データセットの時間ステップ数です。こうして、できる限り多くのサンプルが取られます。 - 0より小さいまたは、Tmax -1より大きい全ての規定された時間ステップは、自動的に破棄されます。少なくとも一つの規定された時間ステップが、{0,1,…,Tmax -1}内にある必要があります。
- 渡されるリストは、インターバルの一致する必要なありません。例えば、あなたは、
[0,2,4,…]を渡すことによって、全ての2番目の時間ステップを使うことによって、規定しても構いません。 - 全てのケースで、最初のs ≧2τmax 時間ステップは、
PCMCI.run_pcmci()または、PCMCI.run_pcmciplus()が実行されたときに、自動的に破棄されます。
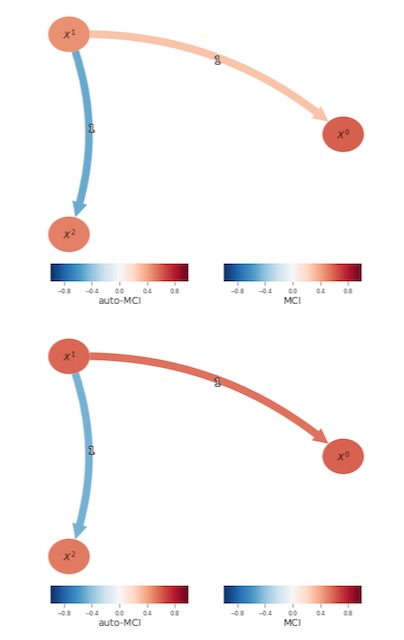
以下、私たちは、因果グラフが時系列の継続期間で変化する例について考慮します。特に、正確な因果リンクの強度の最初の弱さは、そのとき、その方向を変え、そして、再び強度を成長させます。これは、また、マスキングの機能によって、取り扱われますが、例では、reference_pointsキーワードの一つの使用ケースを説明するために扱います。:それは、考慮される時間ウィンドウを規定します。したがって、因果グラフがどのように、時間上で変化し、そして変化するかどうかを分析することを許容します。
T = [100, 120, 150, 200, 110, 180, 190, 77] # number of time steps of the individual datasets
M = len(T) # number of datasets
N = 3 # number of variables
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']
data = {i: np.random.randn(T[i], N) for i in range(M)}
for i in range(M):
for t in range(1, min(40, T[i])):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1] + 0.6*data[i][t-1, 0]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
for t in range(40, min(80, T[i])):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1] + 0.3*data[i][t-1, 0]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
for t in range(80, min(120, T[i])):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
for t in range(120, min(160, T[i])):
data[i][t, 0] += 0.7*data[i][t-1, 0] + 0.3*data[i][t-1, 1]
data[i][t, 1] += 0.6*data[i][t-1, 1]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
for t in range(160, min(200, T[i])):
data[i][t, 0] += 0.7*data[i][t-1, 0] + 0.6*data[i][t-1, 1]
data[i][t, 1] += 0.6*data[i][t-1, 1]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]def run_and_plot(dataframe, cond_ind_test):
# Create and run Multidata-PCMCIplus
pcmci = PCMCI(dataframe = dataframe, cond_ind_test = cond_ind_test)
results = pcmci.run_pcmciplus(tau_max = 2, pc_alpha = 0.01)
tp.plot_graph(graph=results['graph'], val_matrix=results['val_matrix'], var_names=var_names)
plt.show()# Run through the five regimes (which we here assume to be known)
for i in range(5):
# Define the respective time steps and accordingly create the DataFrame object
# by using the 'reference_points' keyword
reference_points = list(range(i*40, (i+1)*40))
dataframe = DataFrame(data,
analysis_mode = 'multiple',
reference_points = reference_points,
var_names = var_names
)
# Run Multidata-PCMCIplus and plot the results
run_and_plot(dataframe = dataframe, cond_ind_test = ParCorr())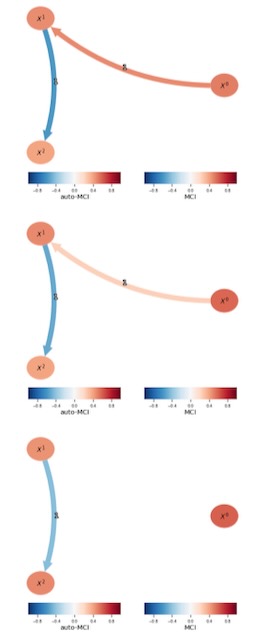
4. time_offsetsキーワード引数
共有する時間軸上の個別の時系列データセットの整列はまた、DataFrameオフジェクトのインスタンス化で発生します。これは、オプションキーワードtime_offsetsの方法によって、実行されます。それは以下のように働きます。詳しくは以下を参照してください。
time_offsetsの使用は、次を必要とします。最初に、analysis_mode='multiple'そして2番目に、data引数は、3Dのnumpy配列よりむしろdictionary(dict型)として与えられます。それ以外ではNoneが渡されます。それはまたデフォルト設定です。time_offsetsは、様式{key(m_0):time_offset(m_0), key(m_1):time_offset(m_1),…}のdictionary(dict型)を予期します。- このdictionaryのキーのセットは、
dataに渡すdicttoinaryのキーのセットを正確に承認する必要があります。 - その値は非負の数でなけれならず、少なくともその一つの数は、0に等しくなければなりません。
- 非ゼロの時間オフセット
time_offset(m_0)は、多くの時間ステップによって、共有する時間軸上で、時間上前に進む、データセットm0に一致してシフトします。 - 例えば、二つのデータセットm0とm1を考えます。
reserence_points=[10,11,12]とtime_offsets={m_0:0,m_1:3}とおきます。そのとき、m1は時間指数7,8,9に対応する点7,8,9を参照しますが、m0は、時間の指数10,11,12に対応する点10,11,12を参照します。
以下、私たちは、過程の下の因果グラフが、時間で変化する例を考慮します。特に、100番目の時間ステップの後、リンクの符号は反転します。最初のデータセットはこの過程の最初の110の時間ステップを実現します。そして、2番目のデータセットは、時間ステップ90で開始し、110に時間長を実現します。従って、最初のデータセットの90番目の時間の指標は、2番目のデータセットの0番目の時間指標に一致します。私たちは、過程のもとで最初と2番目の100時間ステップを分離して分析するために、time_offsetsとreference_pointsキーワード引数を組み合わせます。
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']
M = 2
N = 3
data = {i: np.random.randn(200, N) for i in range(M)}
for i in range(M):
for t in range(1, 100):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1] + 0.6*data[i][t-1, 0]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
for t in range(100, 200):
data[i][t, 0] += 0.7*data[i][t-1, 0]
data[i][t, 1] += 0.6*data[i][t-1, 1] - 0.6*data[i][t-1, 0]
data[i][t, 2] += 0.5*data[i][t-1, 2] - 0.6*data[i][t-1, 1]
data[0] = data[0][:110, :]
data[1] = data[1][90:, :]time_offsets = {0: 0, 1: 90}
# First 100 time steps
reference_points = list(range(100))
dataframe = DataFrame(data,
analysis_mode = 'multiple',
reference_points = reference_points,
time_offsets = time_offsets,
var_names = var_names)
run_and_plot(dataframe = dataframe, cond_ind_test = ParCorr())
# Second 100 time steps
reference_points = list(range(100, 200))
dataframe = DataFrame(data,
analysis_mode = 'multiple',
reference_points = reference_points,
time_offsets = time_offsets,
var_names = var_names)
run_and_plot(dataframe = dataframe, cond_ind_test = ParCorr())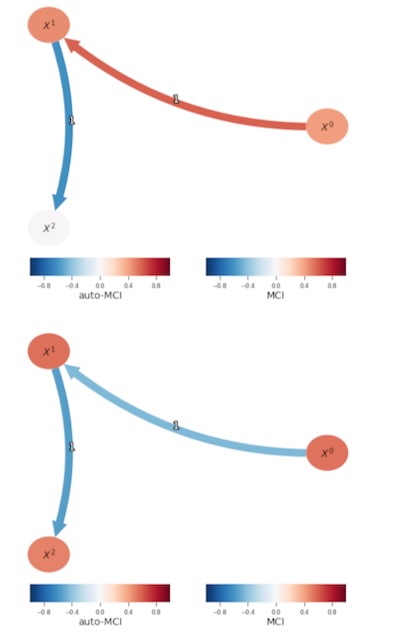
5. 更に進んだコメント
欠測値を取り使う機能は、標準のPCMCIと同様の方法で働き続けます。
マスキング機能もまた同様に、以下の性質で働きます。maskは、dataを同じ様式で与えなければなりません。例えば、もし、dataが、dictionaryによって規定されると、そのとき、maskは、同じ様式のdictionaryで規定されなければなりません。
欠測値とマスキングに関するもっと詳しい情報は、GitHub TIGRAMITEレポジトリの対応するチュートリアルを参照してください。
6. その他のTigramiteメソッドの統合
最初に言及したように、tigramiteの高度なモジュール設定は、あなたが新しい多重のデータセット、さらにまた、DataFrameクラスを基礎にしたtigramiteの他のメソッド、例えば、因果グラフを与えることで、因果の影響を推定するためにCausalEffectクラスの特徴を使うことができることを示しています。
欠測値とマスキングに関するもっと詳しい情報は、GitHub TIGRAMITEレポジトリの対応するチュートリアルを参照してください。
