ガウス混合モデルと異なり、(階層)回帰モデルは、独立した変数です。これらの変数は尤度関数に影響しますが、ランダム変数ではありません。ミニバッチを使う場合、それに注意すべきです。
%env PYTENSOR_FLAGS=device=cpu, floatX=float32, warn_float64=ignore
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
import pytensor.tensor as pt
import seaborn as sns
from scipy import stats
print(f"Running on PyMC v{pm.__version__}")env: PYTENSOR_FLAGS=device=cpu, floatX=float32, warn_float64=ignore Running on PyMC v5.0.1
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")try:
data = pd.read_csv(os.path.join("..", "data", "radon.csv"))
except FileNotFoundError:
data = pd.read_csv(pm.get_data("radon.csv"))
data| Unnamed: 0 | idnum | state | state2 | stfips | zip | region | typebldg | floor | room | ... | pcterr | adjwt | dupflag | zipflag | cntyfips | county | fips | Uppm | county_code | log_radon | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 5081.0 | MN | MN | 27.0 | 55735 | 5.0 | 1.0 | 1.0 | 3.0 | ... | 9.7 | 1146.499190 | 1.0 | 0.0 | 1.0 | AITKIN | 27001.0 | 0.502054 | 0 | 0.832909 |
| 1 | 1 | 5082.0 | MN | MN | 27.0 | 55748 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 14.5 | 471.366223 | 0.0 | 0.0 | 1.0 | AITKIN | 27001.0 | 0.502054 | 0 | 0.832909 |
| 2 | 2 | 5083.0 | MN | MN | 27.0 | 55748 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 9.6 | 433.316718 | 0.0 | 0.0 | 1.0 | AITKIN | 27001.0 | 0.502054 | 0 | 1.098612 |
| 3 | 3 | 5084.0 | MN | MN | 27.0 | 56469 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 24.3 | 461.623670 | 0.0 | 0.0 | 1.0 | AITKIN | 27001.0 | 0.502054 | 0 | 0.095310 |
| 4 | 4 | 5085.0 | MN | MN | 27.0 | 55011 | 3.0 | 1.0 | 0.0 | 4.0 | ... | 13.8 | 433.316718 | 0.0 | 0.0 | 3.0 | ANOKA | 27003.0 | 0.428565 | 1 | 1.163151 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 914 | 914 | 5995.0 | MN | MN | 27.0 | 55363 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 4.5 | 1146.499190 | 0.0 | 0.0 | 171.0 | WRIGHT | 27171.0 | 0.913909 | 83 | 1.871802 |
| 915 | 915 | 5996.0 | MN | MN | 27.0 | 55376 | 5.0 | 1.0 | 0.0 | 7.0 | ... | 8.3 | 1105.956867 | 0.0 | 0.0 | 171.0 | WRIGHT | 27171.0 | 0.913909 | 83 | 1.526056 |
| 916 | 916 | 5997.0 | MN | MN | 27.0 | 55376 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 5.2 | 1214.922779 | 0.0 | 0.0 | 171.0 | WRIGHT | 27171.0 | 0.913909 | 83 | 1.629241 |
| 917 | 917 | 5998.0 | MN | MN | 27.0 | 56297 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 9.6 | 1177.377355 | 0.0 | 0.0 | 173.0 | YELLOW MEDICINE | 27173.0 | 1.426590 | 84 | 1.335001 |
| 918 | 918 | 5999.0 | MN | MN | 27.0 | 56297 | 5.0 | 1.0 | 0.0 | 4.0 | ... | 8.0 | 1214.922779 | 0.0 | 0.0 | 173.0 | YELLOW MEDICINE | 27173.0 | 1.426590 | 84 | 1.098612 |
919 rows × 30 columns
county_idx = data["county_code"].values
floor_idx = data["floor"].values
log_radon_idx = data["log_radon"].values
coords = {"counties": data.county.unique()} ここで、log_randon_idx_tは独立した変数です。floor_idx_tとcounty_idx_tは独立変数を決定します。
log_radon_idx_t = pm.Minibatch(log_radon_idx, batch_size=100)
floor_idx_t = pm.Minibatch(floor_idx, batch_size=100)
county_idx_t = pm.Minibatch(county_idx, batch_size=100)with pm.Model(coords=coords) as hierarchical_model:
# Hyperpriors for group nodes
mu_a = pm.Normal("mu_alpha", mu=0.0, sigma=100**2)
sigma_a = pm.Uniform("sigma_alpha", lower=0, upper=100)
mu_b = pm.Normal("mu_beta", mu=0.0, sigma=100**2)
sigma_b = pm.Uniform("sigma_beta", lower=0, upper=100) 各州の区間、グループ平均mu_aの周辺に分布します。上記で私たちがmuとsdを固定値に設定します。すべてのaとbのために、共通のグループ分布をプラグインします。(それは私たちの例では、ユニークな州の数として同じ長さのベクターになります)
with hierarchical_model:
a = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="counties")
# Intercept for each county, distributed around group mean mu_a
b = pm.Normal("beta", mu=mu_b, sigma=sigma_b, dims="counties") radonレベルa[county_index]のモデル予測は、a[0,0,0,1,1,..]に変換されます。私たちはこのように、多重の州の住宅保有尺度を係数にリンクします。
with hierarchical_model:
radon_est = a[county_idx_t] + b[county_idx_t] * floor_idx_t最後に、私たちは、尤度を規定します。
with hierarchical_model:
# Model error
eps = pm.Uniform("eps", lower=0, upper=100)
# Data likelihood
radon_like = pm.Normal(
"radon_like", mu=radon_est, sigma=eps, observed=log_radon_idx_t, total_size=len(data)
) Random変数、randon_like、log_randon_idx_tに関連した、尤度項の観測値として示すために、ADVIへの関数で与えられます。
一方で、minibatchesは上の三つの変数を含む必要があります。
その後、ADVIをミニバッチで実行します。
with hierarchical_model:
approx = pm.fit(100_000, callbacks=[pm.callbacks.CheckParametersConvergence(tolerance=1e-4)])
idata_advi = approx.sample(500)
ELBOのトレースをチェックし、MCMCの結果と比較してください。
plt.plot(approx.hist);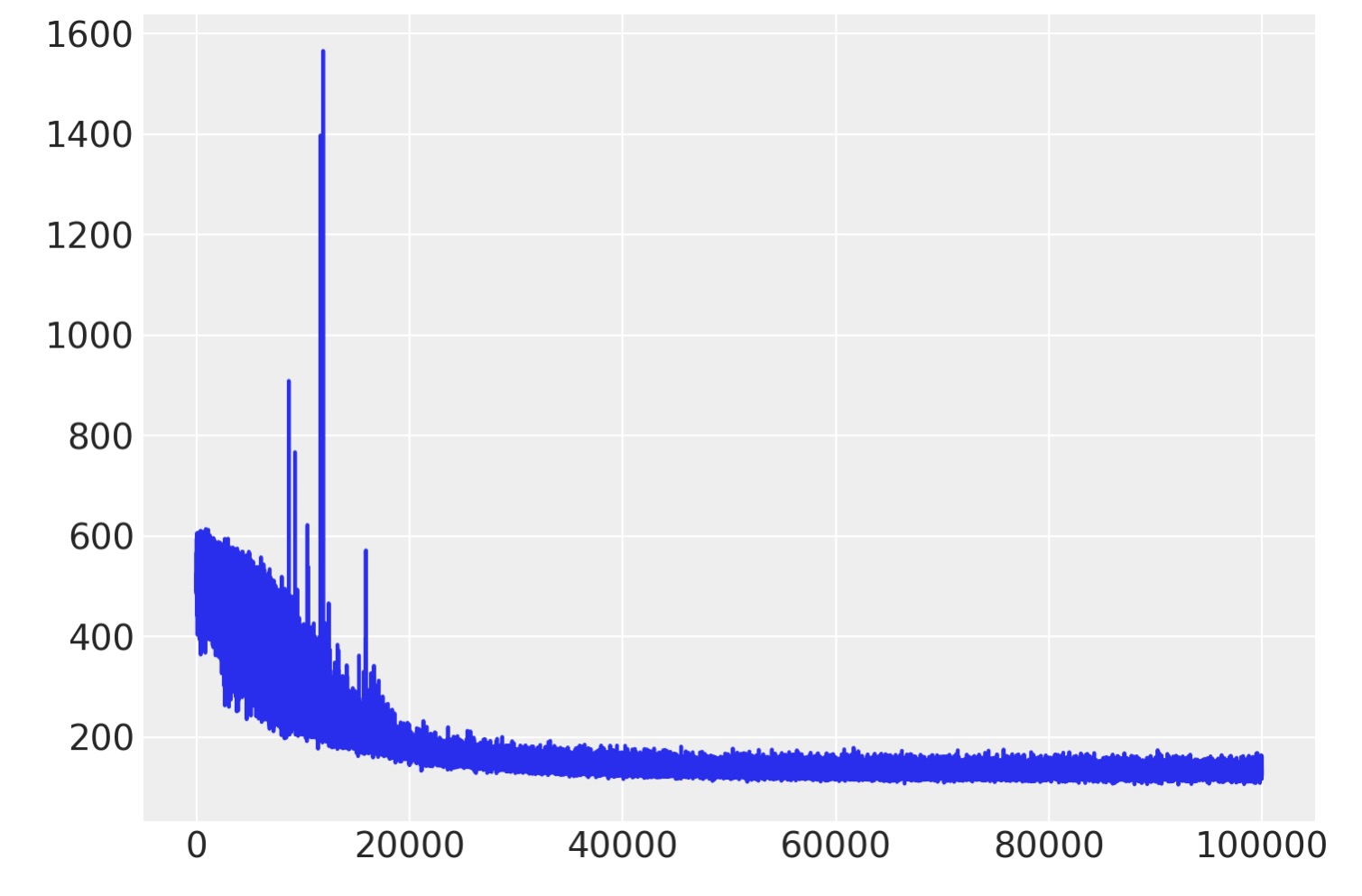
私たちは、平均領域の近似から共分散行列を抽出することができます。そして、NUTSアルゴリズムのために、スケーリング行列として使います。
scaling = approx.cov.eval()そしてまた、私たちは、サンプラーの開始ポイントとして使うためにサンプル(各チェインに一つ)を生成します。
n_chains = 4
sample = approx.sample(return_inferencedata=False, size=n_chains)
start_dict = list(sample[i] for i in range(n_chains))# Inference button (TM)!
with pm.Model(coords=coords):
mu_a = pm.Normal("mu_alpha", mu=0.0, sigma=100**2)
sigma_a = pm.Uniform("sigma_alpha", lower=0, upper=100)
mu_b = pm.Normal("mu_beta", mu=0.0, sigma=100**2)
sigma_b = pm.Uniform("sigma_beta", lower=0, upper=100)
a = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="counties")
b = pm.Normal("beta", mu=mu_b, sigma=sigma_b, dims="counties")
# Model error
eps = pm.Uniform("eps", lower=0, upper=100)
radon_est = a[county_idx] + b[county_idx] * floor_idx
radon_like = pm.Normal("radon_like", mu=radon_est, sigma=eps, observed=log_radon_idx)
# essentially, this is what init='advi' does
step = pm.NUTS(scaling=scaling, is_cov=True)
hierarchical_trace = pm.sample(draws=2000, step=step, chains=n_chains, initvals=start_dict)
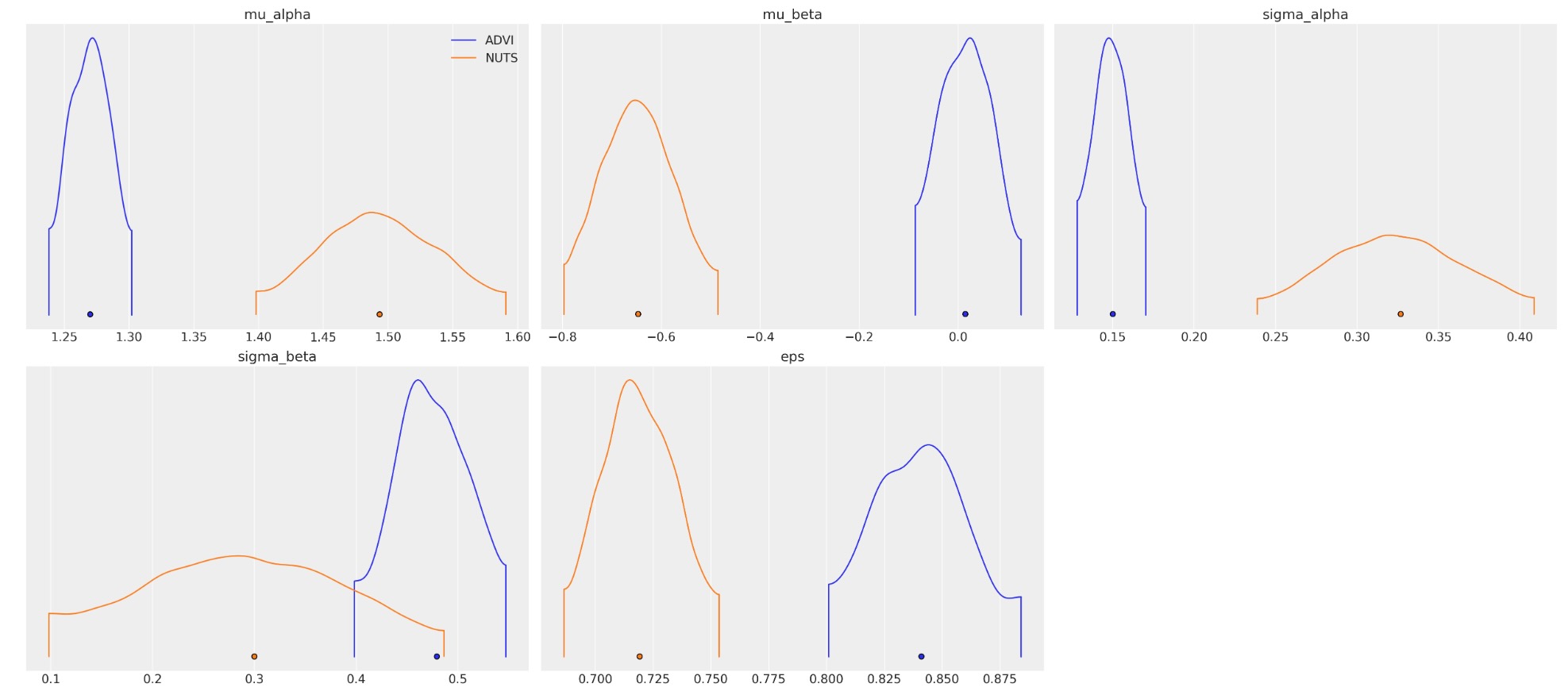
az.plot_density(
data=[idata_advi, hierarchical_trace],
var_names=["~alpha", "~beta"],
data_labels=["ADVI", "NUTS"],
);