切り捨て、または打ち切りデータのベイジアン回帰

このノートブックは、あなたの結果の変数が切り捨てか打ち切りされている時に、線形回帰を導く方法の例を提供します。

from copy import copy

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import xarray as xr

from numpy.random import default_rng
from scipy.stats import norm, truncnorm

%config InlineBackend.figure_format = 'retina'
rng = default_rng(12345)
az.style.use("arviz-darkgrid")

切り捨て(Truncation)と打ち切り(censoring)

　切り捨てと打ち切りによる削除は欠測データの例です。切り捨てと打ち切り削除は時に混同されます。そのため、何らかの定義を見てみましょう。

• 切り捨ては欠測データ問題の一種です。そこでは、あなたが簡単に任意のデータを認識できず、結果の変数が正確な境界のセットの外に落ちています。
• 打ち切りは、測定が正確な境界のセットで敏感である時に発生します。しかし、それらの境界の外側で破棄されるデータよりむしろ、境界を超えて測定する記録することにあります。

　いくらかのコードと図とともの、もっと進んで探索しましょう。最初に、私たちは、任意の真のスキャッターデータ(x,y)を生成します。ここでyは私たちの結果の変数、xは任意の予測変数です。

slope, intercept, σ, N = 1, 0, 2, 200
x = rng.uniform(-10, 10, N)
y = rng.normal(loc=slope * x + intercept, scale=σ)

　(x,y)のスキャッターデータのこの例では、私たちは、私たちの結果の変数が境界のセットの外側に落ちる任意のデータを単純にフィルター除外するものとして、切り捨て過程を説明することができます。

def truncate_y(x, y, bounds):
    keep = (y >= bounds[0]) & (y <= bounds[1])
    return (x[keep], y[keep])

　打ち切りでは、しかし、私たちは、yの値を、それらを超える境界と等しいものとして設定します。

def censor_y(x, y, bounds):
    cy = copy(y)
    cy[y <= bounds[0]] = bounds[0]
    cy[y >= bounds[1]] = bounds[1]
    return (x, cy)

　私たちの生成した(x,y)データ(実験値は現実の世界では見ることはありません)をもとにして、私たちは、切り捨てデータ(xt,yt)と打ち切りデータ(xc,yc)のための私たちの実際の観測データセットを生成することができます。

bounds = [-5, 5]
xt, yt = truncate_y(x, y, bounds)
xc, yc = censor_y(x, y, bounds)

　私たちは、この(グレイの)潜在データと下にある残りの切り捨てと打ち切りデータ(黒)を可視化できます。

fig, axes = plt.subplots(1, 2, figsize=(10, 5))

for ax in axes:
    ax.plot(x, y, ".", c=[0.7, 0.7, 0.7])
    ax.axhline(bounds[0], c="r", ls="--")
    ax.axhline(bounds[1], c="r", ls="--")
    ax.set(xlabel="x", ylabel="y")

axes[0].plot(xt, yt, ".", c=[0, 0, 0])
axes[0].set(title="Truncated data")

axes[1].plot(xc, yc, ".", c=[0, 0, 0])
axes[1].set(title="Censored data");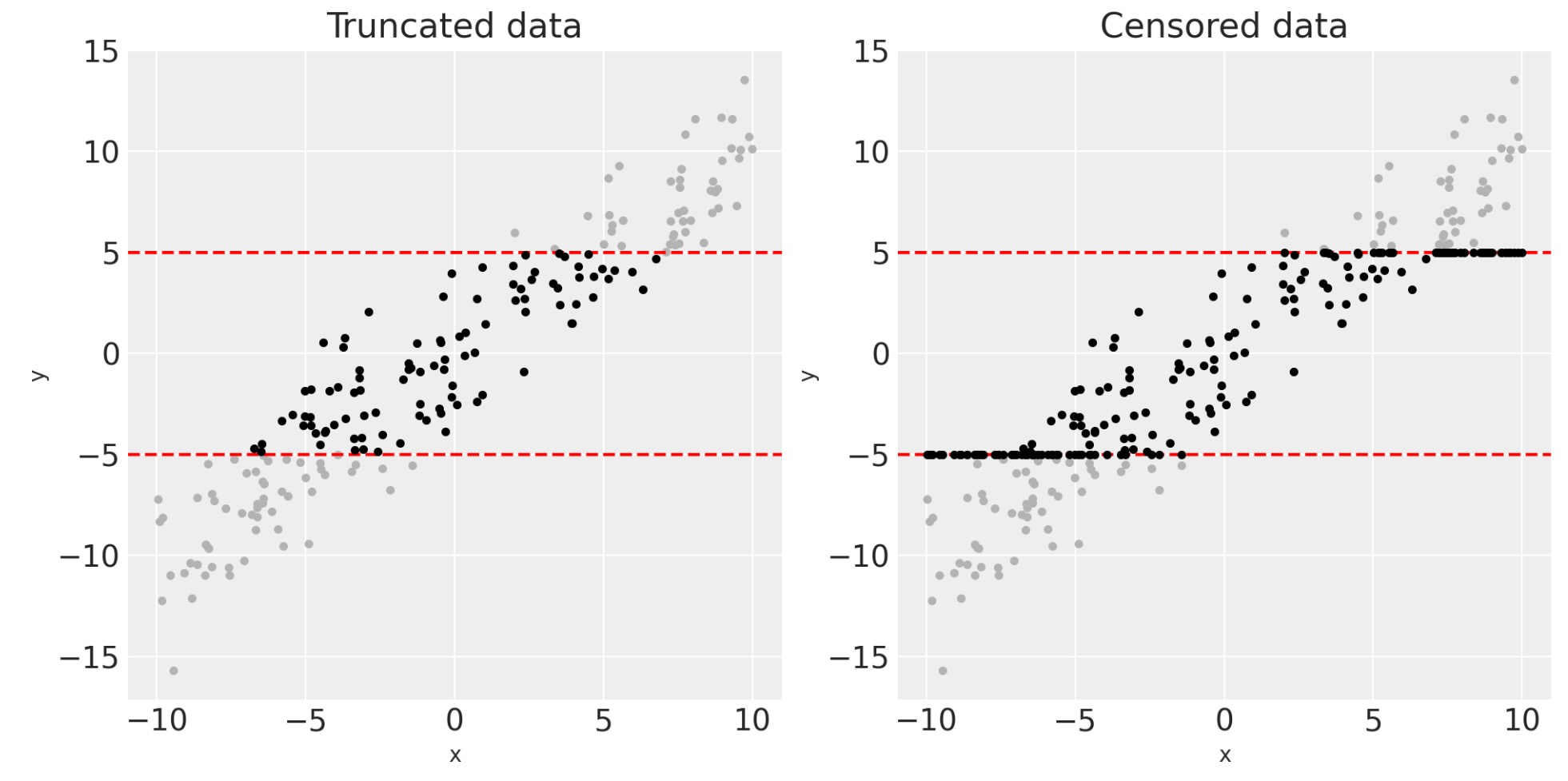

切り捨てと打ち切り回帰の問題を解決する

　もし、私たちが、切り捨て、または打ち切りデータのどちらかの規則的な線形回帰を実行したならば、傾きが低く見積もりがちになることが、直感的にわかるでしょう。切り捨て回帰と打ち切り回帰は、(aka Tobit回帰)は、これらの欠測データの問題を取り扱うために設計されました。そして望むべき回帰の結果は、切り捨てまたは打ち切りのよって生み出される隔たりから解き放たれた傾きになります。

　このセクションで、私たちは、問題の範囲を見るために、これらのデータセットでベイジアン線形回帰を実行します。私たちは、PyMCモデルで定義され、MCMCサンプリングを導き、MCMCサンプルイングデータとモデルを返す、関数定義によって開始します。

def linear_regression(x, y):
    with pm.Model() as model:
        slope = pm.Normal("slope", mu=0, sigma=1)
        intercept = pm.Normal("intercept", mu=0, sigma=1)
        σ = pm.HalfNormal("σ", sigma=1)
        pm.Normal("obs", mu=slope * x + intercept, sigma=σ, observed=y)

    return model

　そのため、私たちは、切り捨てと打ち切りデータを別々に実行できます。

trunc_linear_model = linear_regression(xt, yt)

with trunc_linear_model:
    trunc_linear_fit = pm.sample()

cens_linear_model = linear_regression(xc, yc)

with cens_linear_model:
    cens_linear_fit = pm.sample()

　傾きのパラメータを超えた事後分布を図示することによって、私たちは、傾きがかなり外れているか推定することを見ることができます。そのため、私たちが傾きの回帰を低く推定するのは本当です。

fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True)

az.plot_posterior(trunc_linear_fit, var_names=["slope"], ref_val=slope, ax=ax[0])
ax[0].set(title="Linear regression\n(truncated data)", xlabel="slope")

az.plot_posterior(cens_linear_fit, var_names=["slope"], ref_val=slope, ax=ax[1])
ax[1].set(title="Linear regression\n(censored data)", xlabel="slope");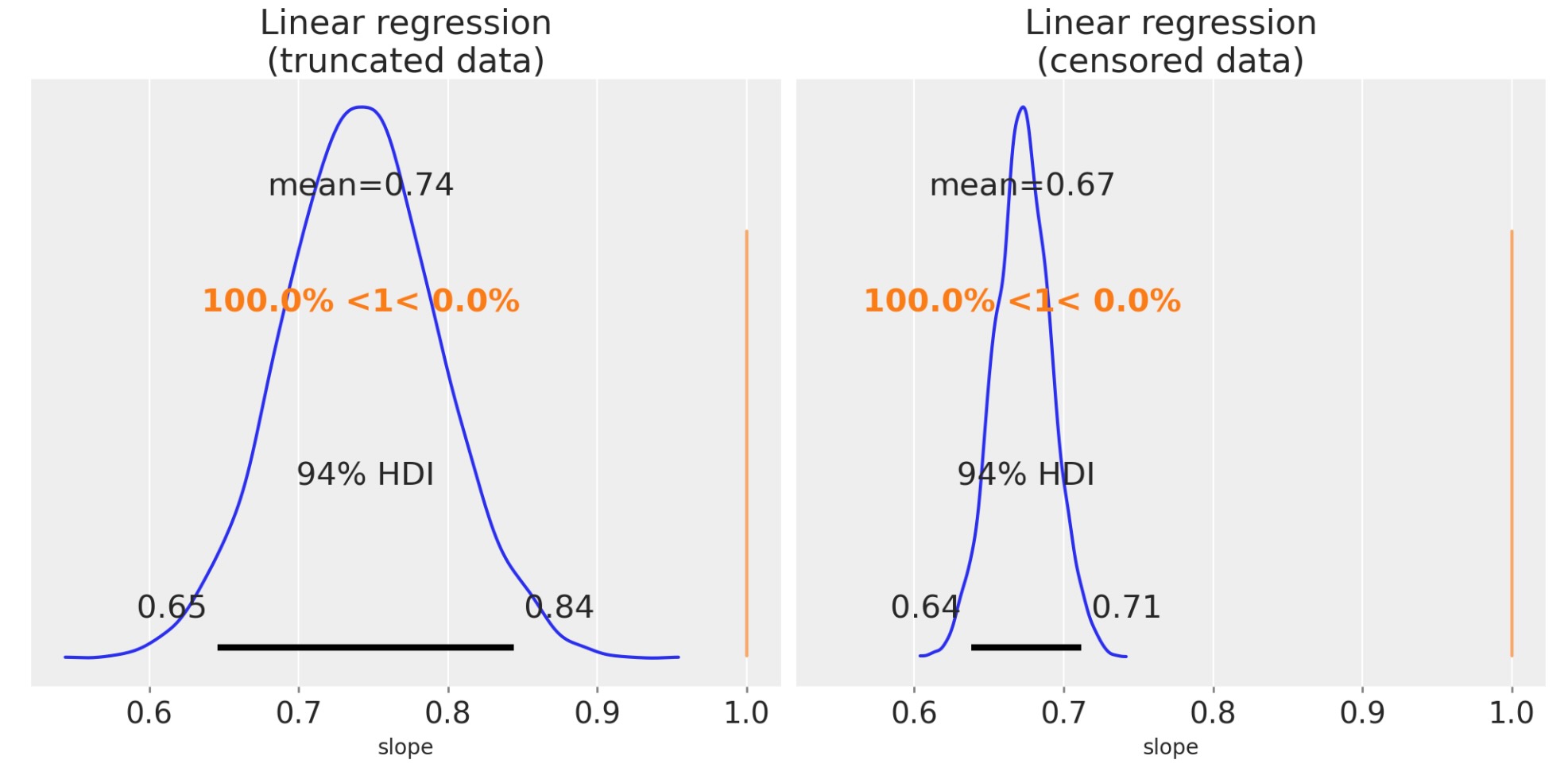

　問題の範囲を正しく理解するために、私たちは、データの間に適合する事後予測を可視化できます。

def pp_plot(x, y, fit, ax):
    # plot data
    ax.plot(x, y, "k.")
    # plot posterior predicted... samples from posterior
    xi = xr.DataArray(np.array([np.min(x), np.max(x)]), dims=["obs_id"])
    post = az.extract(fit)
    y_ppc = xi * post["slope"] + post["intercept"]
    ax.plot(xi, y_ppc, c="steelblue", alpha=0.01, rasterized=True)
    # plot true
    ax.plot(xi, slope * xi + intercept, "k", lw=3, label="True")
    # plot bounds
    ax.axhline(bounds[0], c="r", ls="--")
    ax.axhline(bounds[1], c="r", ls="--")
    ax.legend()
    ax.set(xlabel="x", ylabel="y")


fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True, sharey=True)

pp_plot(xt, yt, trunc_linear_fit, ax[0])
ax[0].set(title="Truncated data")

pp_plot(xc, yc, cens_linear_fit, ax[1])
ax[1].set(title="Censored data");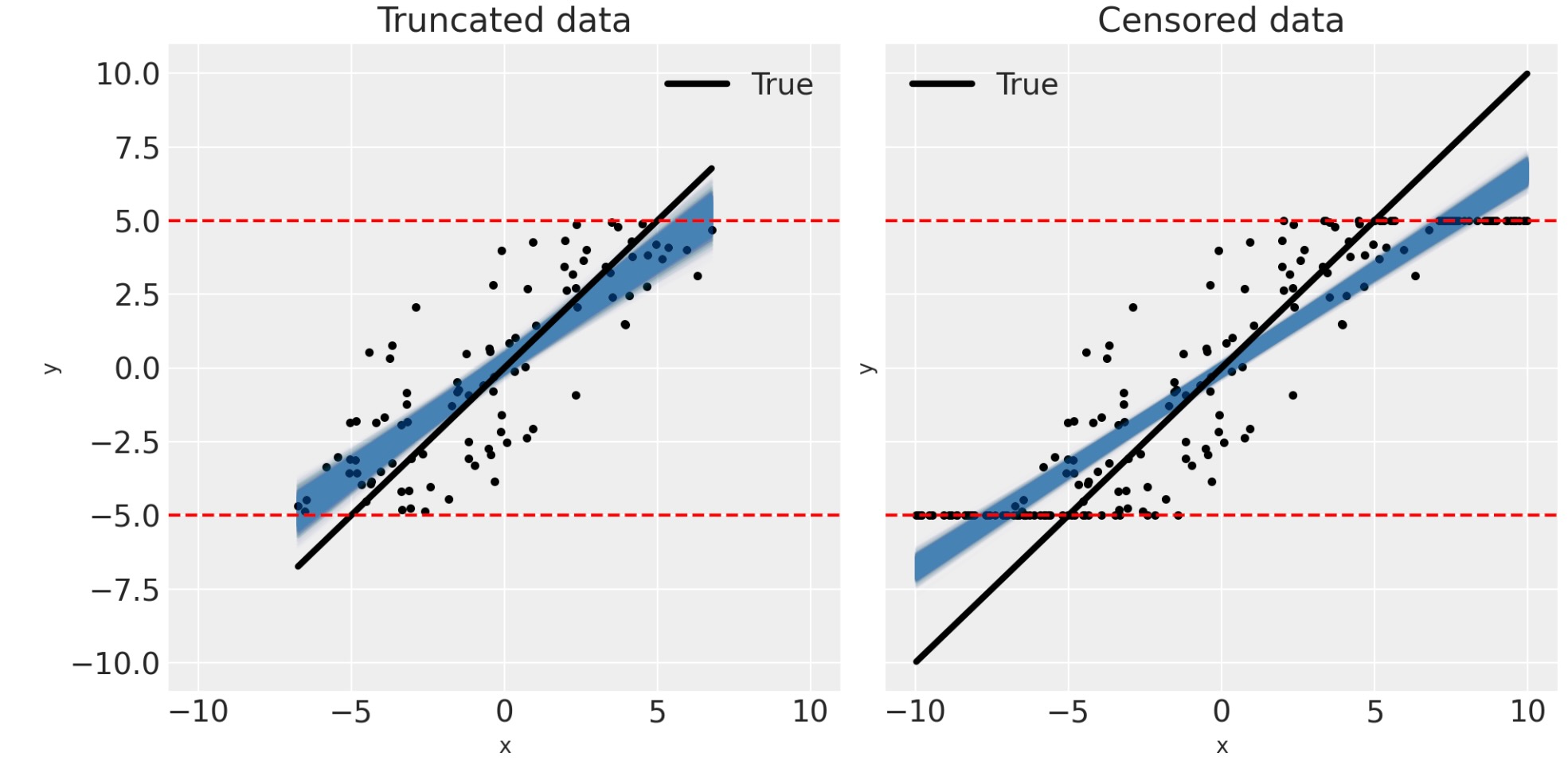

　これらの図を見ることによって、低い推定の隔たりの範囲に影響する因子が何か直感的に予測することができます。最初に、切り捨てと打ち切りの境界が、少数のデータポイントにだけ影響するように、とても広ければ、その時、低い推定の隔たりは減少します。ゼロ測定ノイズの制限で、切り捨てデータのために真の傾きを完全に回復させることができるでしょう。しかし、打ち切りのケースには、常に幾らかの隔たりがあります。それにもかかわらず、測定エラーがゼロに近いか、実際に無関係なように、境界が非常に広いのでなければ、切り捨て、または打ち切り回帰モデルを使うことが賢明です。

切り捨てと打ち切り回帰モデルの実装

　ここで、私たちは、回帰の傾きを低く推定する観点から、切り捨てと打ち切りデータの回帰を導く問題をみました。これは、解決するために設計された切り捨てと打ち切りの回帰モデルです。切り捨てと打ち切りの回帰の両方によって取られる一般的なアプローチは、データ生成過程で切り捨てと打ち切りの段階の事前知識を符号化することです。これはいろいろな方法で尤度関数を修正することによって実行されます。

切り捨て回帰モデル

　切り捨て回帰モデルは、実装するのは全く簡単です。正規尤度は正規として回帰傾きの中心になります。しかし、私たちは、境界で切り捨てられる正規分布を単に規定します。

def truncated_regression(x, y, bounds):
    with pm.Model() as model:
        slope = pm.Normal("slope", mu=0, sigma=1)
        intercept = pm.Normal("intercept", mu=0, sigma=1)
        σ = pm.HalfNormal("σ", sigma=1)
        normal_dist = pm.Normal.dist(mu=slope * x + intercept, sigma=σ)
        pm.Truncated("obs", normal_dist, lower=bounds[0], upper=bounds[1], observed=y)
    return model

　切り捨て回帰は、観測を生成する過程に関する私たちの知識を反映して尤度を更新することによって、隔たった問題を解決します。従って、私たちは、切り捨ての境界の外側の任意のデータを観測する機会はゼロです。そして、それで尤度はこれを反映します。私たちは、これを以下の図で可視化できます。正規分布に比較して、切り捨て正規の確率密度は、このケースで、切り捨て境界(y < -1)の外側でゼロです。

fig, ax = plt.subplots(figsize=(10, 3))
y = np.linspace(-4, 4, 1000)
ax.fill_between(y, norm.pdf(y, loc=0, scale=1), 0, alpha=0.2, ec="b", fc="b", label="Normal")
ax.fill_between(
    y,
    truncnorm.pdf(y, -1, float("inf"), loc=0, scale=1),
    0,
    alpha=0.2,
    ec="r",
    fc="r",
    label="Truncated Normal",
)
ax.set(xlabel="$y$", ylabel="probability")
ax.axvline(-1, c="k", ls="--")
ax.legend();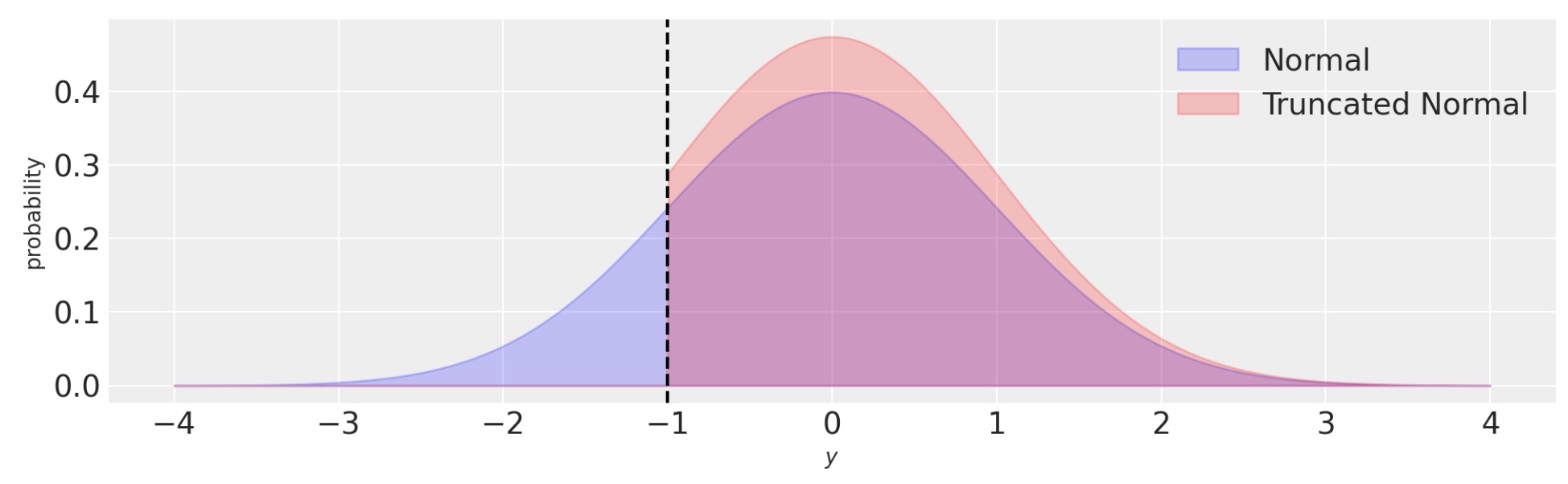

打ち切り回帰モデル

def censored_regression(x, y, bounds):
    with pm.Model() as model:
        slope = pm.Normal("slope", mu=0, sigma=1)
        intercept = pm.Normal("intercept", mu=0, sigma=1)
        σ = pm.HalfNormal("σ", sigma=1)
        y_latent = pm.Normal.dist(mu=slope * x + intercept, sigma=σ)
        obs = pm.Censored("obs", y_latent, lower=bounds[0], upper=bounds[1], observed=y)

    return model

　新しいpm.Censored分布に感謝します。それは、打ち切りデータのモデルを書くのに本当にまっすぐです。覚えておくべき一つのことは、打ち切りする潜在変数は、上のモデルのpm.Normal.distとして、.distメソッドで呼ばれる必要があります。

　舞台裏で、pm.Censoredは、次のことを理解するために尤度関数を調整します。

• 低い境界の確率は、ー♾️から低い境界までの分布関数の累積に等しい
• 上位の境界の確率は、上位の境界から♾️への分布関数の累積に等しい。

これは、下の図で、視覚的に示されます。技術的には境界の確率密度は、境界のbinの幅は正確にゼロであるため、無限です。

fig, ax = plt.subplots(figsize=(10, 3))

with pm.Model() as m:
    pm.Normal("y", 0, 2)

with pm.Model() as m_censored:
    pm.Censored("y", pm.Normal.dist(0, 2), lower=-1.0, upper=None)

logp_fn = m.compile_logp()
logp_censored_fn = m_censored.compile_logp()

xi = np.hstack((np.linspace(-6, -1.01), [-1.0], np.linspace(-0.99, 6)))

ax.plot(xi, [np.exp(logp_fn({"y": x})) for x in xi], label="uncensored")
ax.plot(xi, [np.exp(logp_censored_fn({"y": x})) for x in xi], label="censored", lw=8, alpha=0.6)
ax.axvline(-1, c="k", ls="--")
ax.legend()
ax.set(xlabel="$y$", ylabel="probability density", ylim=(-0.02, 0.4));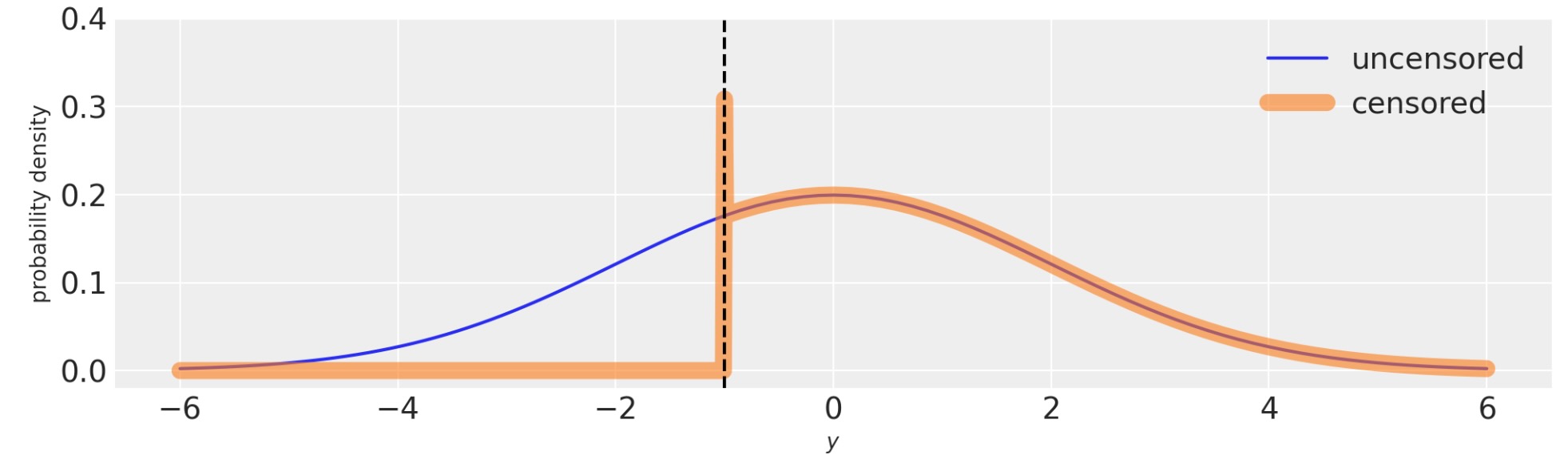

切り捨てと打ち切り回帰の実行

　ここで、私たちは、切り捨てデータの切り捨て回帰モデルのパラメータの推定を導くことができます。

truncated_model = truncated_regression(xt, yt, bounds)

with truncated_model:
    truncated_fit = pm.sample()

　そして、打ち切りデータの打ち切り回帰モデル

censored_model = censored_regression(xc, yc, bounds)

with censored_model:
    censored_fit = pm.sample(init="adapt_diag")

　私たちは、以前のように同じことができます。傾きの事後推定を可視化します。

fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True)

az.plot_posterior(truncated_fit, var_names=["slope"], ref_val=slope, ax=ax[0])
ax[0].set(title="Truncated regression\n(truncated data)", xlabel="slope")

az.plot_posterior(censored_fit, var_names=["slope"], ref_val=slope, ax=ax[1])
ax[1].set(title="Censored regression\n(censored data)", xlabel="slope");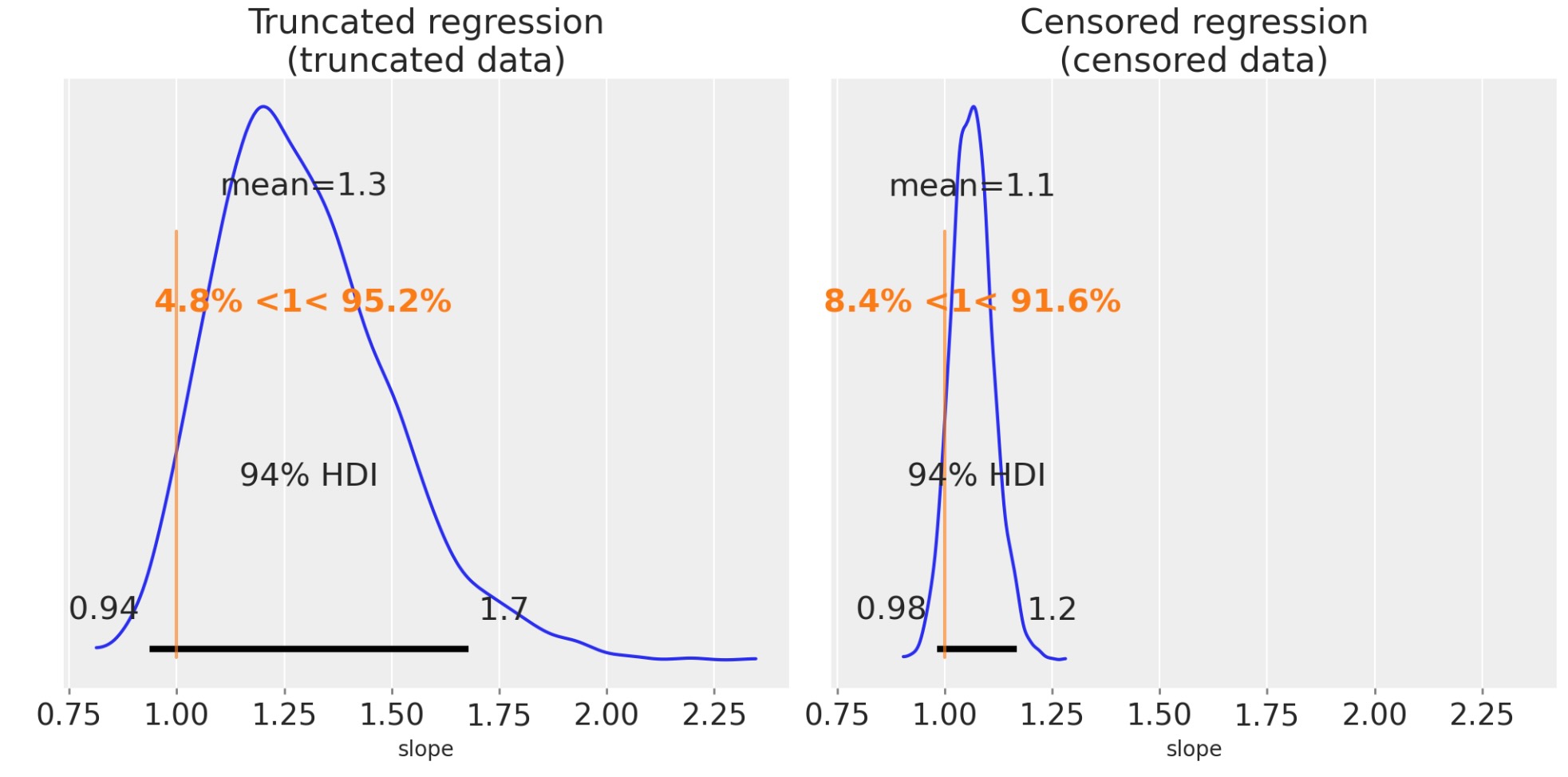

　これらは、ずっとよい推定になります。興味深いことに、私たちは、打ち切りデータが切り捨てデータよりももっと正確に推定していることがわかります。これは、必ずしも、必要なケースでなく、しかし、ここの直感は、xとyのデータが切り捨てで完全に破棄されますが、yデータだけが、打ち切りでは部分的に未知になります。

　私たちは、その時、もし実験が切り捨てか打ち切りデータを選択すると、切り捨てを超えて打ち切りを選択する方が良いことを予測できます。

　対応して、私たちは、事後予測図の視覚的な検査を通してモデルが適切であることを確認することができます。

fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True, sharey=True)

pp_plot(xt, yt, truncated_fit, ax[0])
ax[0].set(title="Truncated data")

pp_plot(xc, yc, censored_fit, ax[1])
ax[1].set(title="Censored data");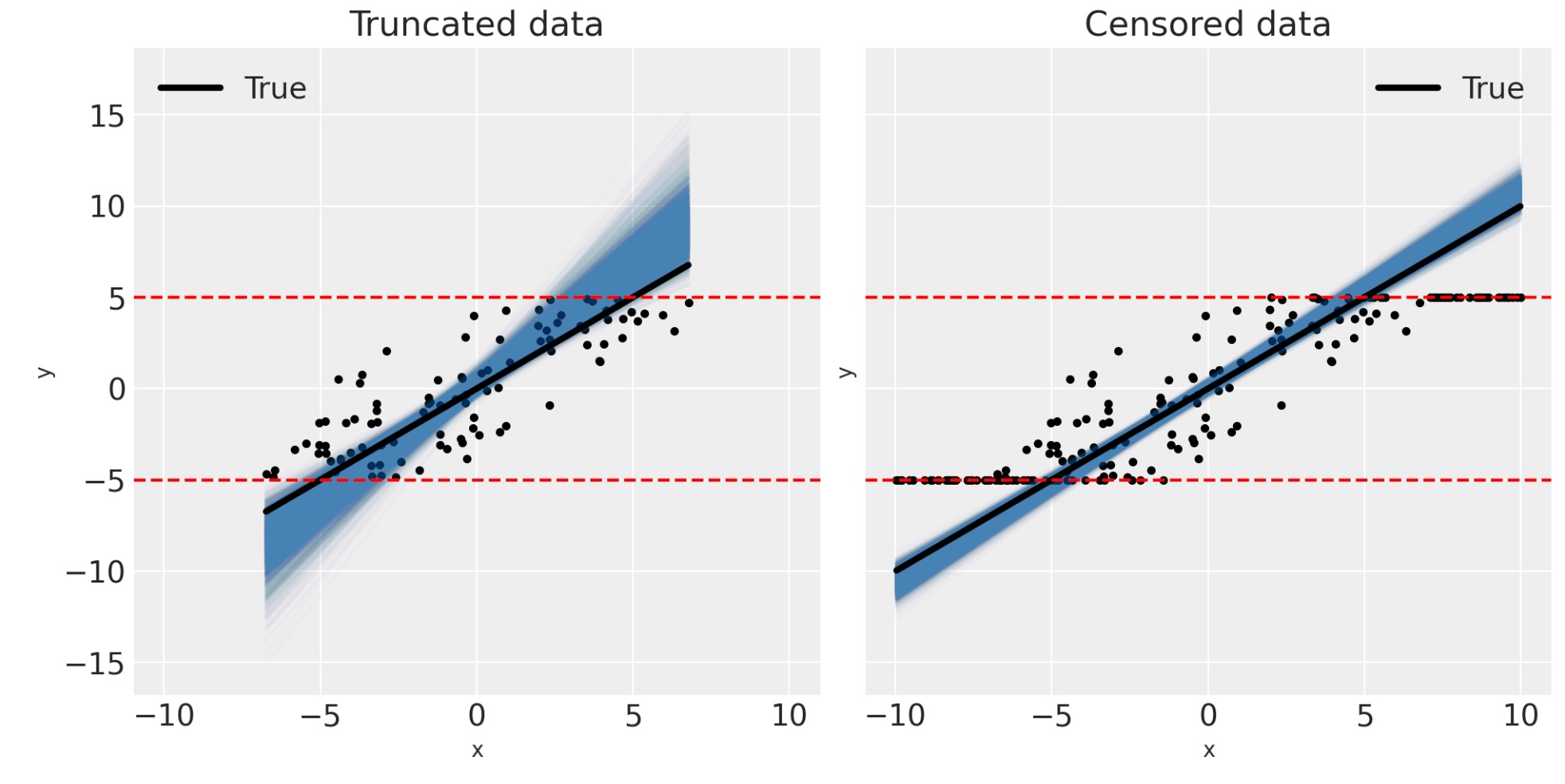

　これは、私たちの切り捨てと打ち切りデータとPyMCの切り捨てと打ち切り回帰モデル私たちのガイドを終わります。回帰の傾きの推定の隔たりの範囲は、上で議論した要因の数で変わりますが、望むべきは、これらの例が、回帰分析にデータ生成過程のあなたの知識を符号化することの重要性を、あなたを納得させることです。

さらに進んだトピック

　未知の潜在パラメータとして境界を取り扱うのは可能です。もし、正確にわからないことがあり、これらの境界を超えて事前に様式化できるならば、その時、境界が何かを推論することができます。これは、過剰なものとして説明されます、しかし、あなたのデータ分析の文脈に依存して、妥当な回帰推定を得るために、境界の推定の'十分に適切’なポイントを抽出するためには完全に十分でしょう。

　上で表した打ち切り回帰モデルは一つの特別なアプローチを取ります。そして、他にもあります。例えば、それは打ち切りデータの真の潜在yの値を超えて、事後の確信を推論するのに達しません。不当に、これら打ち切りしたyの値のせいにする打ち切り回帰モデルを構築することはできます。しかし、私たちは、imputationのトピックは、それ固有の処置が相応しいので、ここで取り扱いません。PyMC打ち切りデータモデル(ハイパーリンク)の例は、特に、不当に打ち切りデータのせいにするモデルの例(ハイパーリンク)で、このトピックをカバーします。

さらに進んだ資料

　このトピックを見た時、私は、もっとも多くの資料は、実際の実装より、数学的な由来に終点を当て、最大尤度推定アプローチに焦点を当てていることを発見しました。一つの良い簡潔な８０ページの数学の本は、Breenと他の著者による[] は、切り捨てと打ち切りを、他の欠測データシナリオ同様にカバーします。それは、Gelman et al[2013]とGelman et al[2020]によるBayesian Data Analysisは、このトピックに少数のページを割り当てています。