from copy import copy
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from numpy.random import default_rng%config InlineBackend.figure_format = 'retina'
rng = default_rng(1234)
az.style.use("arviz-darkgrid")このベイジアン生存分析のノートブックの例は、打ち切りデータの点に触れます。打ち切りは欠損データの問題の様式になります。それは正確な閾値より大きい観測値が、その閾値にクリップダウンするか、または、正確な閾値より小さい観測値はその閾値の上にクリップアップするか、その両方です。それは、打ち切りのインターバルに対応した右、左があります。このノートブックの例では、私たちは打ち切りのインターバルを考慮します。
打ち切りデータは多くのモデリングの問題を生じます。二つの共通の例は、
- 生存分析:生存時間に関する、正確な薬の処理の効果を研究するとき、すべての被験者が死亡するまで、延長するのは不可能です。学習の終了時に多くの患者に対して処置が管理された後、時間Tの時点で、まだ生存しているデータだけが集められます。:実際、彼らの生存時間は、Tよりも大きくなります。
- 打ち切りの状況:打ち切りは制限された範囲になります。そして上位と下位の制限は、単純に最も高いものともっとも低い値になって報告されます。例えば、多くの水銀体温計は、温度の狭い範囲だけを報告します。
これらのノートブックは、PyMC3の打ち切りデータの処理を二つの異なる方法で表現します。
- 打ち切り転嫁モデルは、パラメータとして打ち切りデータを表現し、すべての打ち切った値に対して、最もらしい値を作ります。このimputationmの結果、このモデルは、作った値の最もらしいセットを生成することができます。それは、打ち切られます。各打ち切りのデータは、ランダムな値として、紹介されます。
- imputeされない打ち切りモデルは、打ち切りデータが統合され、対数尤度を通過したときだけ説明されます。この方法は、もっと大きな量の打ち切りデータを、十分にもっと早く収束して処理します。
ベースラインを設定するために、私たちは、打ち切らないモデルと打ち切らないデータを比較します。
# Produce normally distributed samples
size = 500
true_mu = 13.0
true_sigma = 5.0
samples = rng.normal(true_mu, true_sigma, size)
# Set censoring limits
low = 3.0
high = 16.0
def censor(x, low, high):
x = copy(x)
x[x <= low] = low
x[x >= high] = high
return x
# Censor samples
censored = censor(samples, low, high)# Visualize uncensored and censored data
_, ax = plt.subplots(figsize=(10, 3))
edges = np.linspace(-5, 35, 30)
ax.hist(samples, bins=edges, density=True, histtype="stepfilled", alpha=0.2, label="Uncensored")
ax.hist(censored, bins=edges, density=True, histtype="stepfilled", alpha=0.2, label="Censored")
[ax.axvline(x=x, c="k", ls="--") for x in [low, high]]
ax.legend();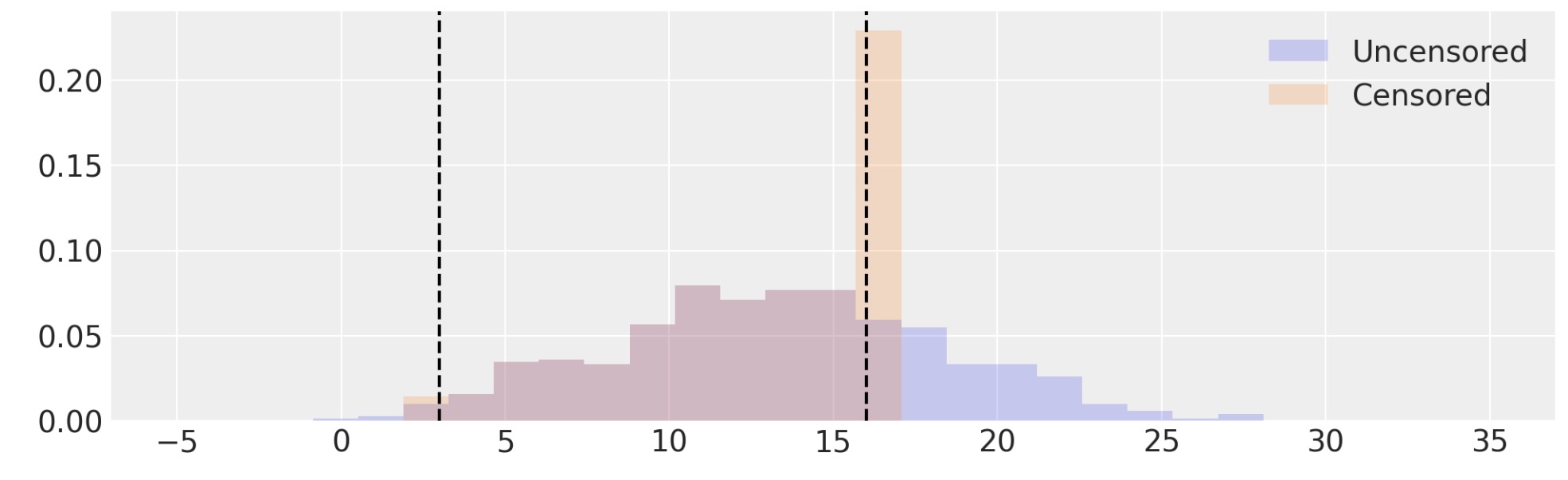
打ち切らないデータ
def uncensored_model(data):
with pm.Model() as model:
mu = pm.Normal("mu", mu=((high - low) / 2) + low, sigma=(high - low))
sigma = pm.HalfNormal("sigma", sigma=(high - low) / 2.0)
observed = pm.Normal("observed", mu=mu, sigma=sigma, observed=data)
return model私たちは、打ち切らないデータ上で打ち切らないモデルの実行を予測します。私たちは、平均と分散の妥当な推定を取得します。
uncensored_model_1 = uncensored_model(samples)
with uncensored_model_1:
idata = pm.sample()
az.plot_posterior(idata, ref_val=[true_mu, true_sigma], round_to=3);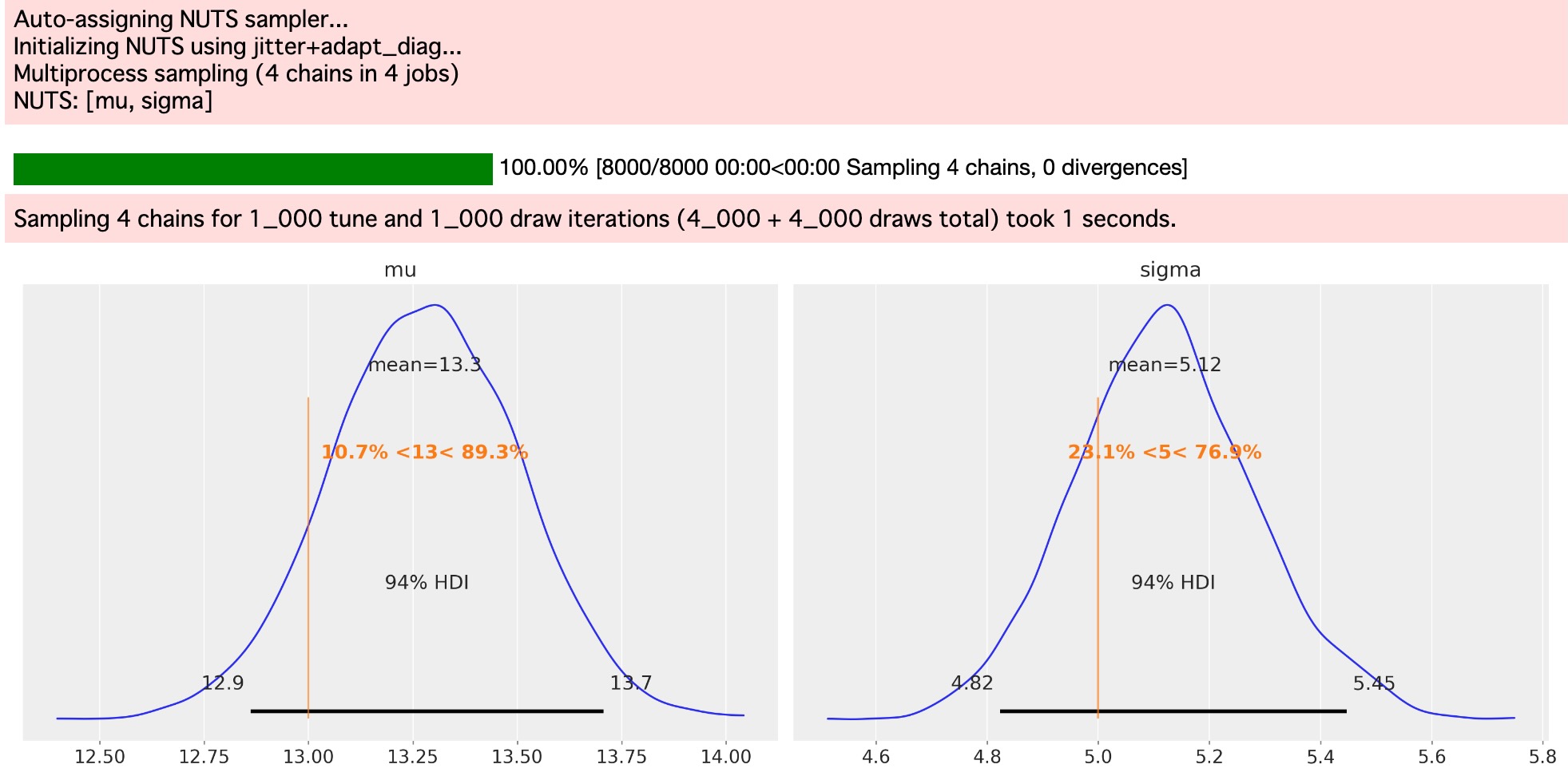
そして、それは正確に私たちが発見することです。
問題は、打ち切りデータのコンテキストです。私たちは、真の値にアクセスしません。もし私たちが、打ち切りデータにおいて、同じ打ち切らないデータを使うならば、私たちは、パラメータ推定が偏っていることを予期します。もし、私たちが、平均と分散の推定ポイントを計算するならば、そのとき私たちは、私たちが平均と分散を、この特別なデータセットと打ち切りの境界のために、弱く推定しがちであることがわかります。
print(f"mean={np.mean(censored):.2f}; std={np.std(censored):.2f}")mean=12.32; std=3.76uncensored_model_2 = uncensored_model(censored)
with uncensored_model_2:
idata = pm.sample()
az.plot_posterior(idata, ref_val=[true_mu, true_sigma], round_to=3);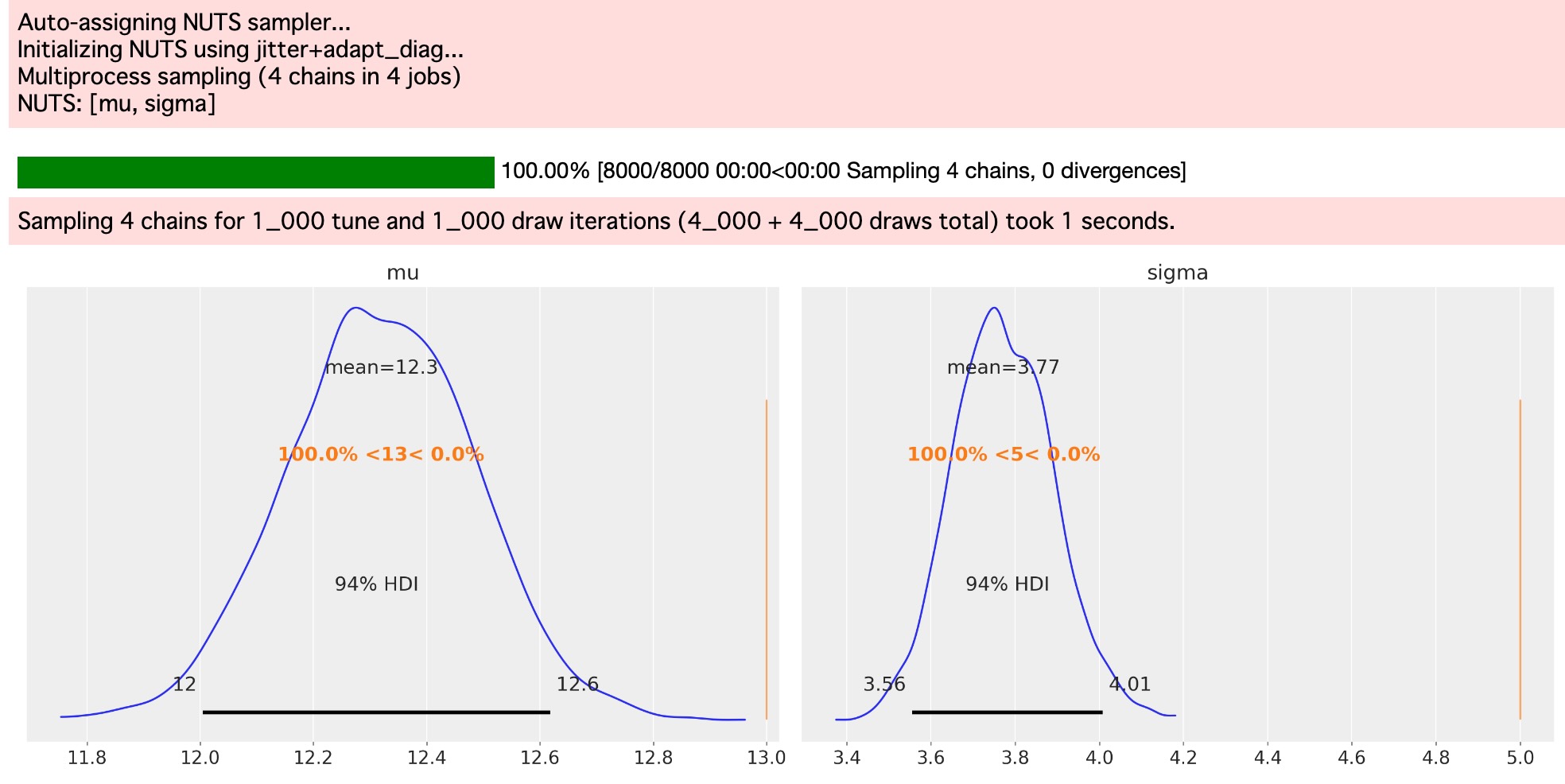
上の図は、これを確認します。
打ち切りデータモデル
下のモデルは、打ち切りデータを処理する二つのアプローチを示します。最初に、私たちは観測値を計測するために、少しデータの前処理を必要とします。それは、左または右の打ち切りデータです。私たちは、私たちが観測した打ち切らないデータを抽出します。
モデル1 ー打ち切りデータのimputed 打ち切りモデル
このモデルでは、私たちは打ち切らないデータとして、同じ分布から、打ち切りの値をimputeします。事後分布からのサンプリングは、可能な打ち切らないデータセットを生成します。
n_right_censored = sum(censored >= high)
n_left_censored = sum(censored <= low)
n_observed = len(censored) - n_right_censored - n_left_censored
uncensored = censored[(censored > low) & (censored < high)]
assert len(uncensored) == n_observedwith pm.Model() as imputed_censored_model:
mu = pm.Normal("mu", mu=((high - low) / 2) + low, sigma=(high - low))
sigma = pm.HalfNormal("sigma", sigma=(high - low) / 2.0)
right_censored = pm.Normal(
"right_censored",
mu,
sigma,
transform=pm.distributions.transforms.Interval(high, None),
shape=int(n_right_censored),
initval=np.full(n_right_censored, high + 1),
)
left_censored = pm.Normal(
"left_censored",
mu,
sigma,
transform=pm.distributions.transforms.Interval(None, low),
shape=int(n_left_censored),
initval=np.full(n_left_censored, low - 1),
)
observed = pm.Normal("observed", mu=mu, sigma=sigma, observed=uncensored, shape=int(n_observed))
idata = pm.sample()
az.plot_posterior(idata, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma], round_to=3);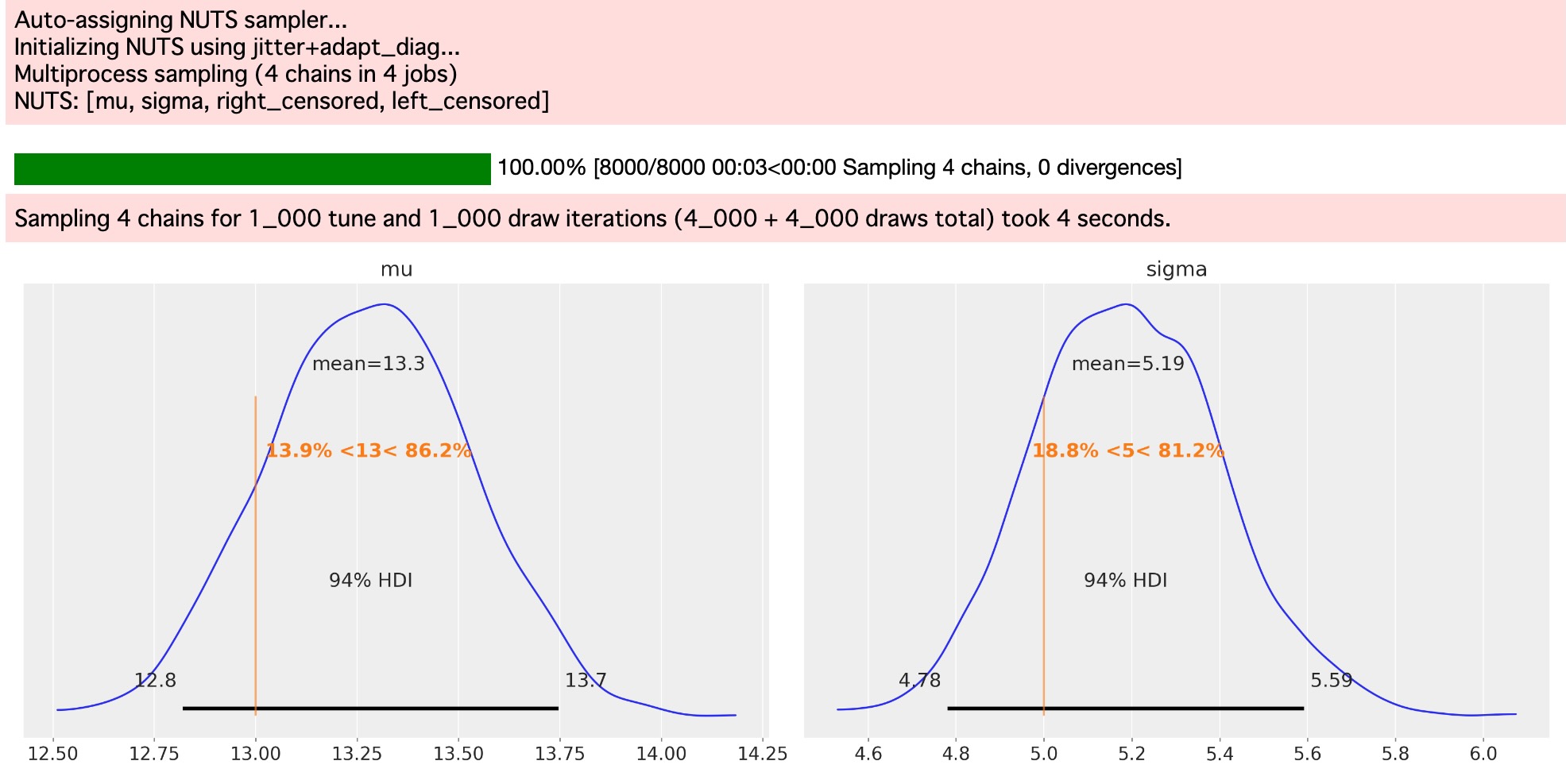
私たちは、隔たっている平均と分散の推定が(打ち切らないモデルで表現します)、大規模に削除されることがわかります。
モデル2ー打ち切りデータのimputeされない打ち切りモデル
ここで、私たちはpm.Censoredを利用することができます。
with pm.Model() as unimputed_censored_model:
mu = pm.Normal("mu", mu=0.0, sigma=(high - low) / 2.0)
sigma = pm.HalfNormal("sigma", sigma=(high - low) / 2.0)
y_latent = pm.Normal.dist(mu=mu, sigma=sigma)
obs = pm.Censored("obs", y_latent, lower=low, upper=high, observed=censored)サンプリング
with unimputed_censored_model:
idata = pm.sample()
az.plot_posterior(idata, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma], round_to=3);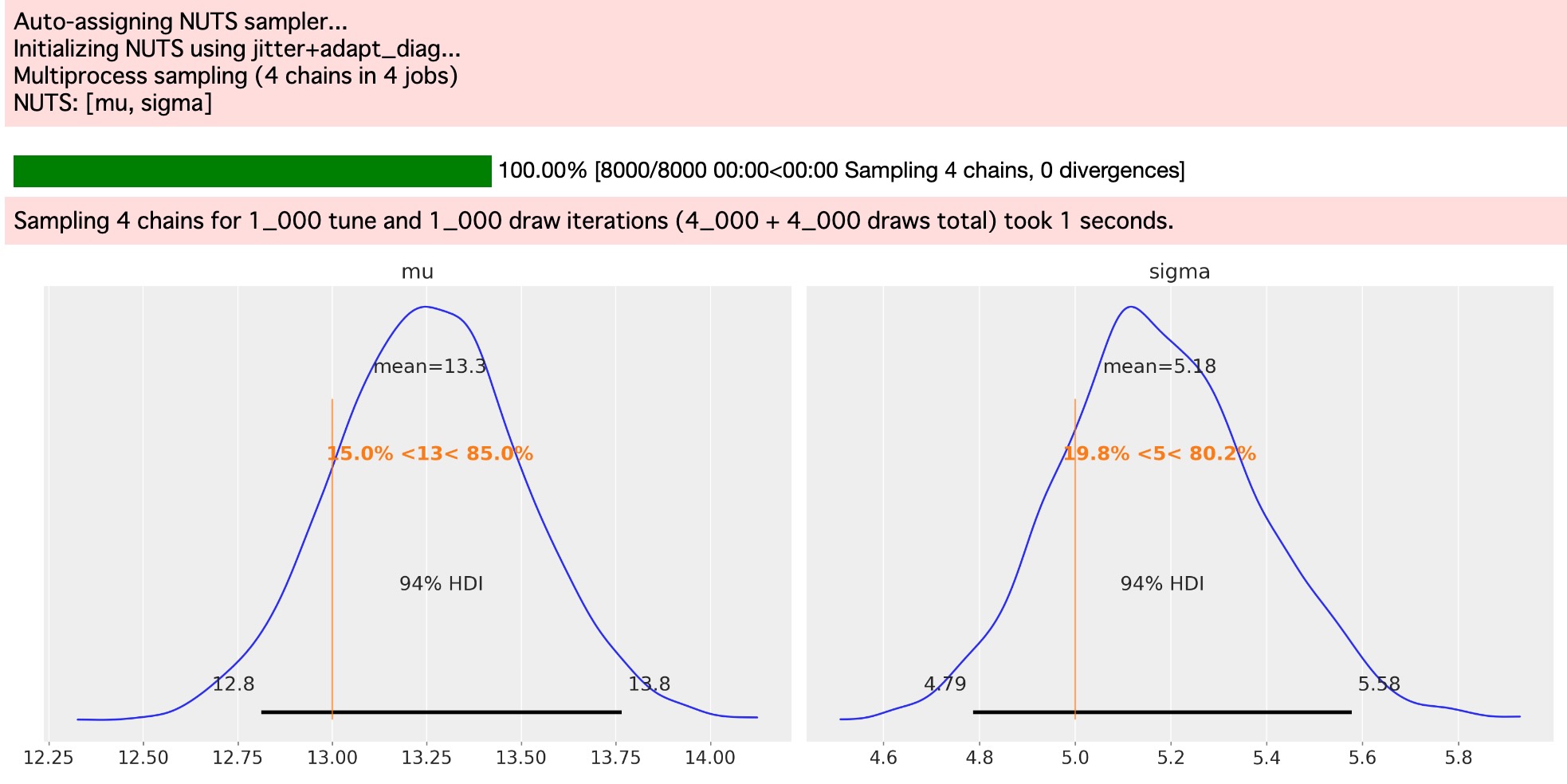
再度、平均と分散の推定の隔たりが大きく削除されます。
議論
私たちが両方のモデルが、打ち切らないモデルと同様に、分布を基礎にした平均と分散を取り込むために表現していることがわかります。追加で、imputeされたモデルは、打ち切った値のデータセットを生成することができます。(それらを生成するために、right_censoredとleft_censoredの事後分布からサンプルして)imputeされない打ち切りモデルは、より早く収束し、打ち切りデータをもっとよくスケールします。
製作者
- 著者:Luis Mario Domenzain 2017年 3月7日
- 更新:George Ho 2018年 7月14日
- 更新:Benjamin Vincent 2021年5月
- 更新:Benjamin Vincent PyMCv4 2022年5月