pyMCのインストール
pyMCはバージョン4がリリースされています。従来pyMC3と呼んでいたものは4.0を契機にpyMCと名称が変更されています。pyMC3はバックエンドがTheanoでしたが、リリース4はAesraに変更されました。AesraはTheanoのライブラリコードを再構築した新バージョンに伴う名称変更とのことです。
conda install -c conda-forge "pymc>=4"pyMC用に仮想環境を作成してインストールする場合。以下は、"pymc_env"という仮想環境を作成しています。
conda create -c conda-forge -n pymc_env "pymc>=4"
conda activate pymc_envJAXバックエンドを使ったサンプリングをイネーブルにする場合は、以下のパッケージをpipでインストールします。
pip install numpyroBlackJAXのサンプリングを使う場合は、以下のパッケージをインストールします。
pip install blackjaxAPI サンプルコード
ガウス混合モデル
あるリスクがマクロ経済変数のような共通経済因子群に依存し、その因子群が確率的にモデル化されていると仮定して、その因子群のデータの分布からなるリスクを推論するのに混合モデルを用いることもできます。
以下のガウス混合モデルは、いくつかのガウス分布(正規分布)からなる分布の標準偏差と平均を推定しています。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
from scipy.stats import norm
from xarray_einstats.stats import XrContinuousRV%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")まず、シミュレートした実現値を生成します。(各因子を所与のものとします)
k = 3 ndata = 500 centers = np.array([-5, 0, 5]) sds = np.array([0.5, 2.0, 0.75]) idx = rng.integers(0, k, ndata) x = rng.normal(loc=centers[idx], scale=sds[idx], size=ndata) plt.hist(x, 40);
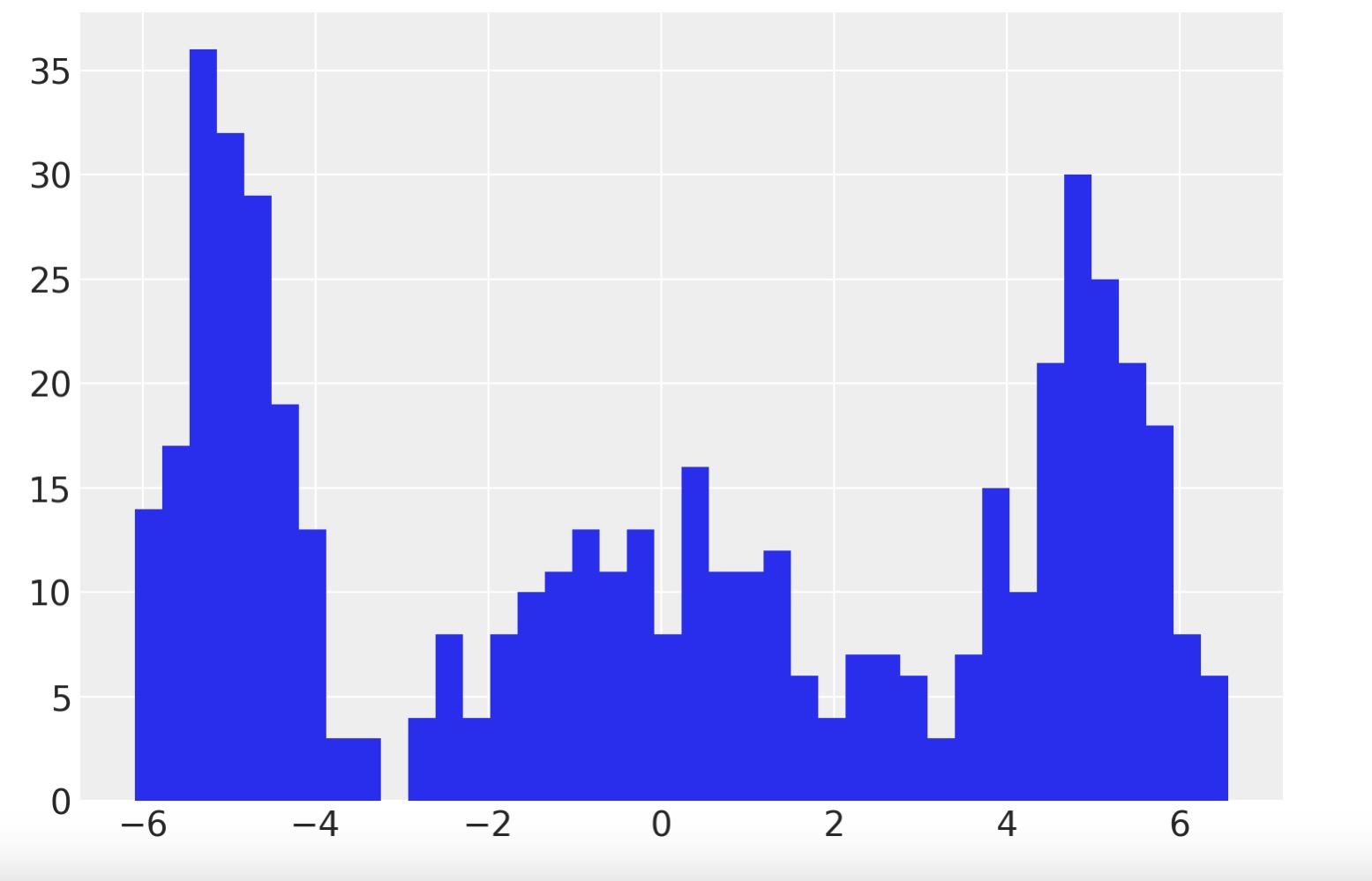
この三つのクラスターに関して平均値と偏差を求めます。pyMCモデルでは、pmNormalMixture分布を用いて簡単にガウス混合分布モデルが作れます。
with pm.Model(coords={"cluster": range(k)}) as model:
μ = pm.Normal(
"μ",
mu=0,
sigma=5,
transform=pm.distributions.transforms.univariate_ordered,
initval=[-4, 0, 4],
dims="cluster",
)
σ = pm.HalfNormal("σ", sigma=1, dims="cluster")
weights = pm.Dirichlet("w", np.ones(k), dims="cluster")
pm.NormalMixture("x", w=weights, mu=μ, sigma=σ, observed=x)
pm.model_to_graphviz(model)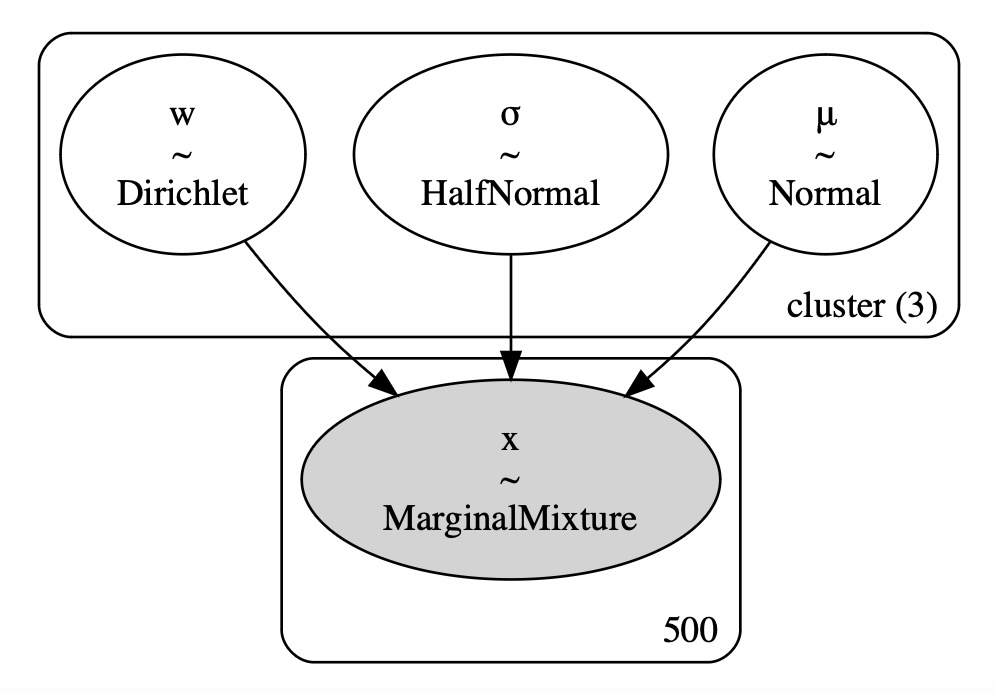
with model:
idata = pm.sample()
MCMCチェインのトレースをプロットします。
az.plot_trace(idata, var_names=["μ", "σ"], lines=[("μ", {}, [centers]), ("σ", {}, [sds])])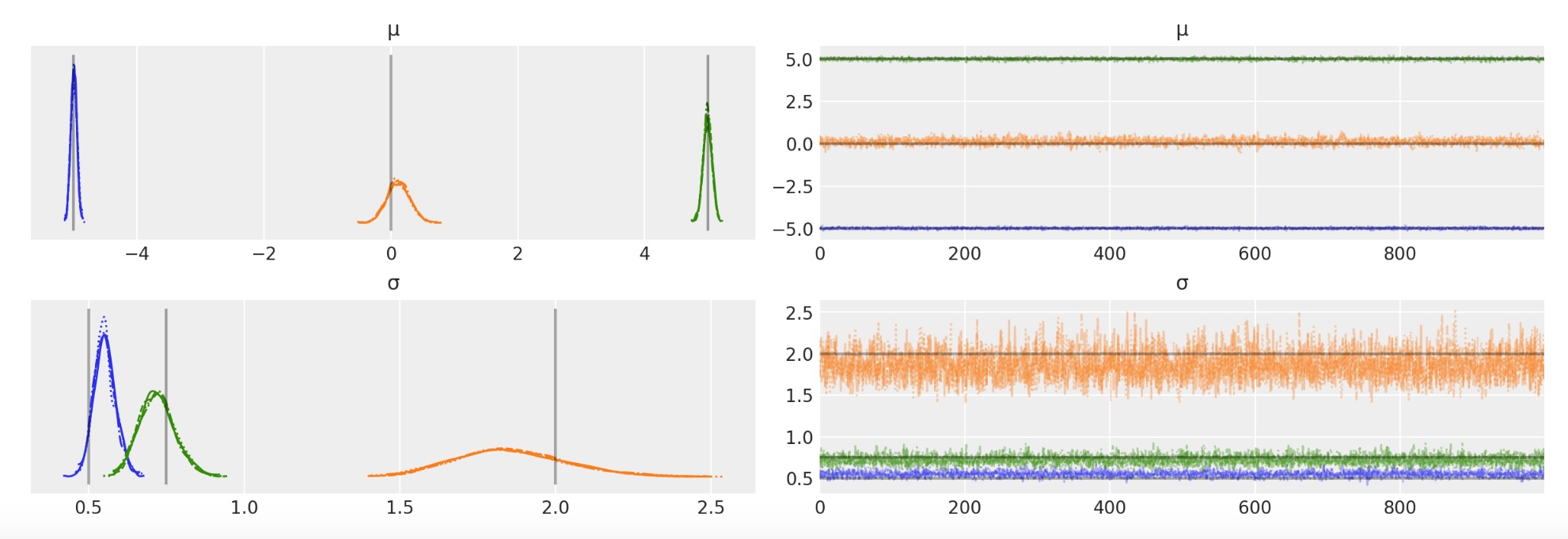
事後平均を元に確率密度関数を計算します。
xi = np.linspace(-7, 7, 500)
post = idata.posterior
pdf_components = XrContinuousRV(norm, post["μ"], post["σ"]).pdf(xi) * post["w"]
pdf = pdf_components.sum("cluster")
fig, ax = plt.subplots(3, 1, figsize=(7, 8), sharex=True)
# empirical histogram
ax[0].hist(x, 50)
ax[0].set(title="Data", xlabel="x", ylabel="Frequency")
# pdf
pdf_components.mean(dim=["chain", "draw"]).sum("cluster").plot.line(ax=ax[1])
ax[1].set(title="PDF", xlabel="x", ylabel="Probability\ndensity")
# plot group membership probabilities
(pdf_components / pdf).mean(dim=["chain", "draw"]).plot.line(hue="cluster", ax=ax[2])
ax[2].set(title="Group membership", xlabel="x", ylabel="Probability");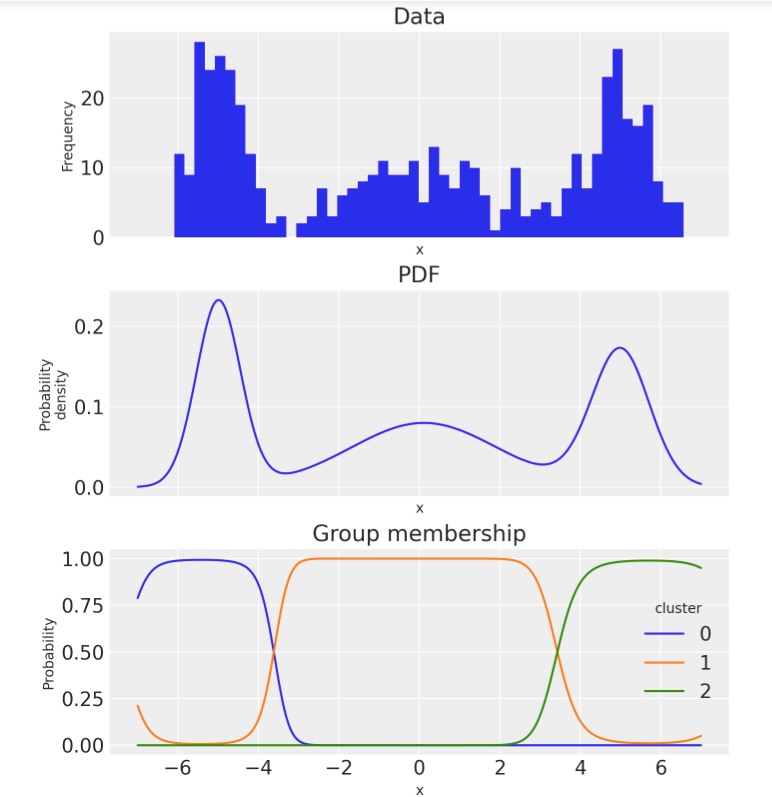
製作者
製作:Abe Flaxman
更新:Thomas Wiecki.
更新:Benjamin T.Vincent 2022 4月 pm.NormalMixtureを使用
更新: Benjamin T.Vincent 2023 2月 pyMC v5