離散分布
| 離散分布 |
| pymc.Bernoulli |
| pymc.BetaBinomial |
| pymc.Binomial |
| pymc.Categorical |
| pymc.DiracDelta |
| pymc.DiscreteUniform |
| pymc.DiscreteWeibull |
| pymc.Geometric |
| pymc.HyperGeometric |
| pymc.NagativeBinomial |
| pymc.OrderedLogistic |
| pymc.OrderedProbit |
| pymc.Poisson |
| pymc.ZeroInflatedBinomial |
| pymc.ZeroInflatedNegativeBinomial |
| pymc.ZeroInflatedPoisson |
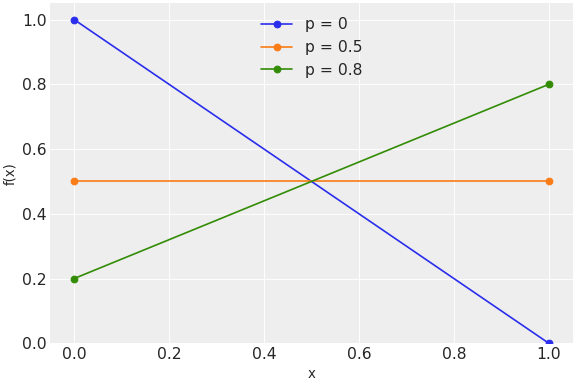
pymc.Bernoulli
ベルヌーイ対数尤度
class pymc.Bernoulli(name, *args, **kwargs)
| 変数 | | |
| p | 浮動小数点のtensor_like | 確率 0 < p < 1 |
| logit_p | 浮動小数点のtensor_like | 代替確率 |
| メソッド | |
| Bernoulli.__init__(*args,**kwargs) | |
| Bernoulli.dist([p,logit_p]) | c/s分布に一致したテンソル変数を生成する。 |
| Bernoulli.logcdf(p) | |
| Bernoulli.logp(p) | |
| Bernoulli.moment(size,p) | |
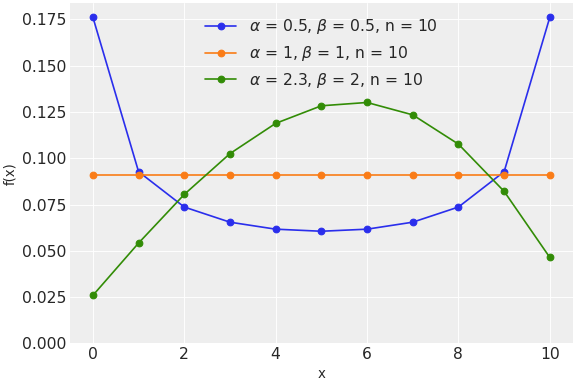
pymc.BetaBinomial
ベータ二項対数分布
class pymc.BetaBinomial(name, *args, **kwargs)
| 変数 | | |
| n | 浮動小数点のtensor_like | ベルヌーイトライアル数, n > 0 |
| alpha | 浮動小数点のtensor_like | alpha > 0 |
| beta | 浮動小数点のtensor_like | beta > 0 |
| メソッド | |
| BetaBinomial.__init__(*args,**kwargs) | |
| BetaBinomial.dist(alpha,beta,n,*args,...) | c/s分布に一致したテンソル変数を生成する。 |
| BetaBinomial.logcdf(n,alpha,beta) | |
| BetaBinomial.logp(n,alpha,beta) | |
| BetaBinomial.moment(size,n,alpha,beta) | |
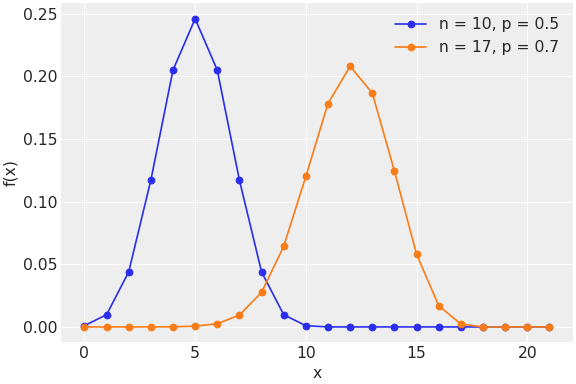
pymc.Binomial
二項対数尤度
class pymc.Binomial(name, *args, **kwargs)
| 変数 | | |
| n | 浮動小数点のtensor_like | ベルヌーイトライアル数, n >= 0 |
| p | 浮動小数点のtensor_like | 各トライアルの成功確率 0 < p < 1 |
| logit_p | 浮動小数点のtensor_like | 代替確率オッズ |
| メソッド | |
| Binomial.__init__(*args,**kwargs) | |
| Binomial.dist(n[,p,logit_p]) | c/s分布に一致したテンソル変数を生成する。 |
| Binomial.logcdf(n,p) | |
| Binomial.logp(n,p) | |
| Binomial.moment(size,n,p) | |
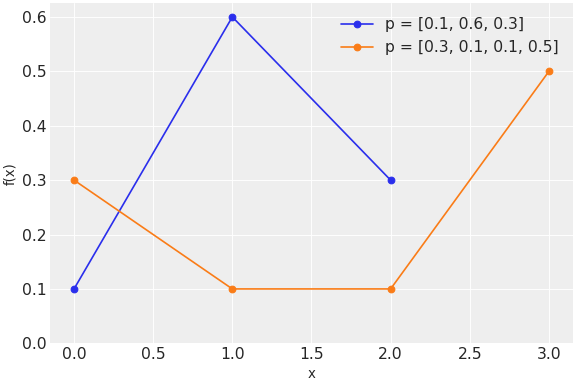
pymc.Categorical
カテゴリカル対数尤度
class pymc.Categorical(name, *args, **kwargs)
| 変数 | | |
| p | 浮動小数点のtensor_like | 0 < p、各要素の合計が1 |
| logit_p | 浮動小数点のtensor_like | 代替確率オッズ |
| メソッド | |
| Categorical.__init__(*args,**kwargs) | |
| Categorical.dist([p,logit_p]) | c/s分布に一致したテンソル変数を生成する。 |
| Categorical.logp(p) | |
| Categorical.moment(size,p) | |
pymc.DiracDelta
ディラックデルタ対数尤度
class pymc.DiracDelta(name, *args, **kwargs)
| 変数 | | |
| c | 浮動小数点または整数のtensor_like | 0 < p、各要素の合計が1 |
| メソッド | |
| DiracDelta.__init__(*args,**kwargs) | |
| DiracDelta.dist(c,*args,**kargs) | c/s分布に一致したテンソル変数を生成する。 |
| DiracDelta.logcdf(c) | |
| DiracDelta.logp(c) | |
| DiracDelta.moment(size,c) | |
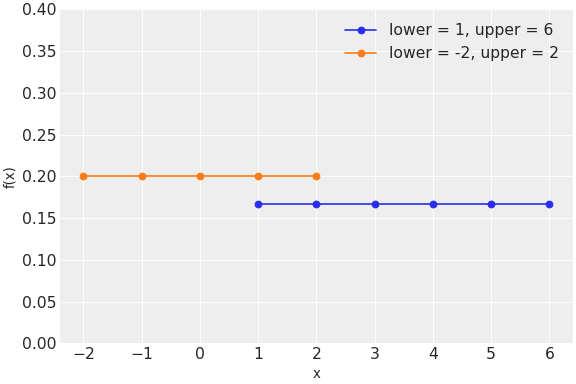
pymc.DiscreteUniform
離散一様分布
class pymc.DiscreteUniform(name, *args, **kwargs)
| 変数 | | |
| lower | 浮動小数点のtensor_like | 下限 |
| upper | 浮動小数点のtensor_like | 上限 |
| メソッド | |
| DiscreteUniform.__init__(*args,**kwargs) | |
| DiscreteUniform.dist(lower,upper,*args) | c/s分布に一致したテンソル変数を生成する。 |
| DiscreteUniform.icdf(lower,upper) | |
| DiscreteUniform.logcdf(lower,upper) | |
| DiscreteUniform.logp(lower,upper) | |
| DiscreteUniform.moment(size,lower,upper) | |
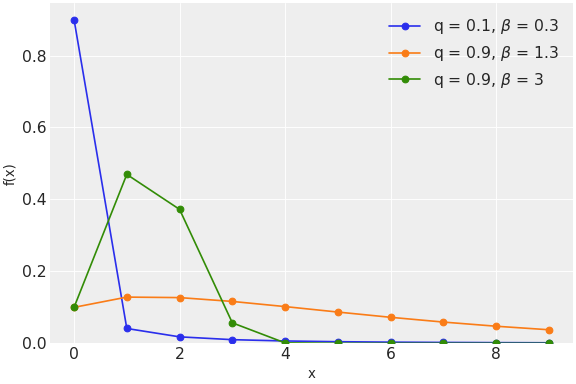
pymc.DiscreteWeibull
離散ワイブル対数尤度
class pymc.DiscreteWeibull(name, *args, **kwargs)
| 変数 | | |
| q | 浮動小数点のtensor_like | シェイプパラメータ 0 < p <1 |
| beta | 浮動小数点のtensor_like | シェイプパラメータ beta > 0 |
| メソッド | |
| DiscreteWeibull.__init__(*args,**kwargs) | |
| DiscreteWeibull.dist(q,beta,*args,**kwargs) | c/s分布に一致したテンソル変数を生成する。 |
| DiscreteWeibull.logcdf(q,beta) | |
| DiscreteWeibull.logp(q,beta) | |
| DiscreteWeibull.moment(size,q,beta) | |
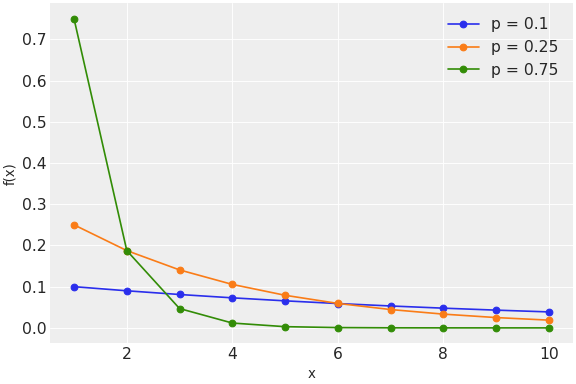
pymc.Geometric
ジオメトリック対数尤度
class pymc.Geometric(name, *args, **kwargs)
| 変数 | | |
| p | 浮動小数点のtensor_like | 個別トライアルの成功確率 0 < p <=1 |
| メソッド | |
| Geometric.__init__(*args,**kwargs) | |
| Geometric.dist(p,*args,**kwargs) | c/s分布に一致したテンソル変数を生成する。 |
| Geometric.icdf(p) | |
| Geometric.logcdf(p) | |
| Geometric.logp(p) | |
| Geometric.moment(size,p) | |
pymc.HyperGeometric
離散ハイパージオメトリック分布
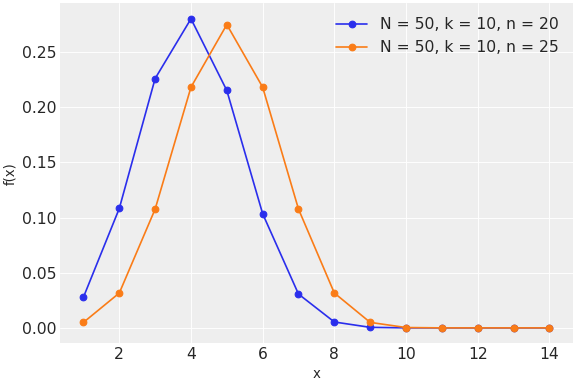
class pymc.HyperGeometric(name, *args, **kwargs)
| 変数 | | |
| N | 浮動小数点または整数のtensor_like | populationの合計サイズ |
| k | 浮動小数点または整数のtensor_like | 個別の成功数 0 <= k <= N |
| n | 浮動小数点または整数のtensor_like | 出力サンプル数 0<= n <= N |
| メソッド | |
| HyperGeometric.__init__(*args,**kwargs) | |
| HyperGeometric.dist(N,k,n,*args,**kwargs) | c/s分布に一致したテンソル変数を生成する。 |
| HyperGeometric.logcdf(good,bad,n) | |
| HyperGeometric.logp(good,bad,n) | |
| HyperGeometric.moment(size,good,bad,n) | |
pymc.NeativeBinomial
逆二項対数分布
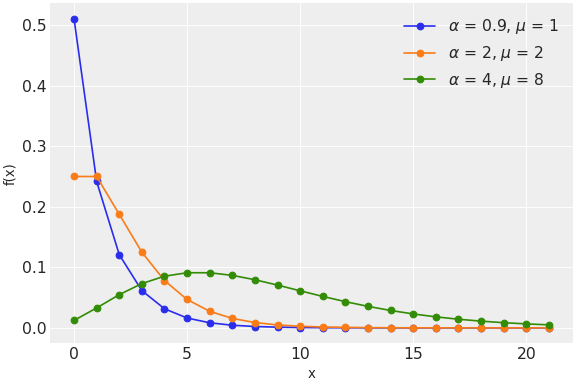
class pymc.NegativeBinomial(name, *args, **kwargs)
| 変数 | | |
| alpha | 浮動小数点のtensor_like | ガンマ分布、シェイプパラメータ alpha > 0 |
| mu | 浮動小数点のtensor_like | ガンマ分布 平均 mu > 0 |
| p | 浮動小数点のtensor_like | 各トライアルの成功確率 0 < p <1 |
| n | 浮動小数点のtensor_like | 目標成功トライアル数 |
| メソッド | |
| NegativeBinomial.__init__(*args,**kwargs) | |
| NegativeBinomial.dist([mu,alpha,p,n]) | c/s分布に一致したテンソル変数を生成する。 |
| NegativeBinomial.get_n_p([mu,alpha,p,n]) | |
| NegativeBinomial.logcdf(n,p) | |
| NegativeBinomial.logp(n,p) | |
| NegativeBinomial.moment(size,n,p) | |
pymc.OrderedLogistic
順序ロジスティック分布のためのラッパークラス
class pymc.OrderedLogistic(name, *args, compute_p=True, **kwargs)
| 変数 | | |
| eta | 浮動小数点のtensor_like | 予測 |
| cutpoints | 浮動小数点のtensor_like | カットポイント長さ K-1の配列 |
| compute_p | 真偽値、 | デフォルト値 真 |
(使用例)
# Generate data for a simple 1 dimensional example problem
n1_c = 300; n2_c = 300; n3_c = 300
cluster1 = np.random.randn(n1_c) + -1
cluster2 = np.random.randn(n2_c) + 0
cluster3 = np.random.randn(n3_c) + 2
x = np.concatenate((cluster1, cluster2, cluster3))
y = np.concatenate((1*np.ones(n1_c),
2*np.ones(n2_c),
3*np.ones(n3_c))) - 1
# Ordered logistic regression
with pm.Model() as model:
cutpoints = pm.Normal("cutpoints", mu=[-1,1], sigma=10, shape=2,
transform=pm.distributions.transforms.univariate_ordered)
y_ = pm.OrderedLogistic("y", cutpoints=cutpoints, eta=x, observed=y)
idata = pm.sample()
# Plot the results
plt.hist(cluster1, 30, alpha=0.5);
plt.hist(cluster2, 30, alpha=0.5);
plt.hist(cluster3, 30, alpha=0.5);
posterior = idata.posterior.stack(sample=("chain", "draw"))
plt.hist(posterior["cutpoints"][0], 80, alpha=0.2, color='k');
plt.hist(posterior["cutpoints"][1], 80, alpha=0.2, color='k');
| メソッド | |
| OrderedLogistic.__init__(*args,**kwargs) | |
| OrderedLogistic.dist(*args,**kwargs) | |
pymc.OrderedProbit
順序プロビット分布のためのラッパークラス
class pymc.OrderedProbit(name, *args, compute_p=True, **kwargs)
| 変数 | | |
| eta | 浮動小数点のtensor_like | 予測 |
| cutpoints | 浮動小数点のtensor_like | カットポイント長さ K-1の配列 |
| sigma | 浮動小数点のtensor_like | probit関数の標準偏差 |
| compute_p | 真偽値、 | デフォルト値 真 |
| メソッド | |
| OrderedProbit.__init__(*args,**kwargs) | |
| OrderedProbit.dist(*args,**kwargs) | |
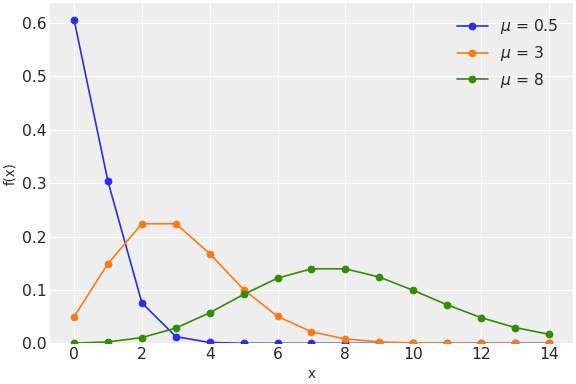
pymc.Poisson
ポワソン対数尤度
class pymc.Poisson(name, *args, **kwargs
| 変数 | | |
| mu | 浮動小数点のtensor_like | 与えられたインターバルでの予測発生回数 |
| メソッド | |
| NegativeBinomial.__init__(*args,**kwargs) | |
| NegativeBinomial.dist(mu,*args,**kwargs) | c/s分布に一致したテンソル変数を生成する。 |
| NegativeBinomial.logcdf(mu) | |
| NegativeBinomial.logp(mu) | |
| NegativeBinomial.moment(size,mu) | |
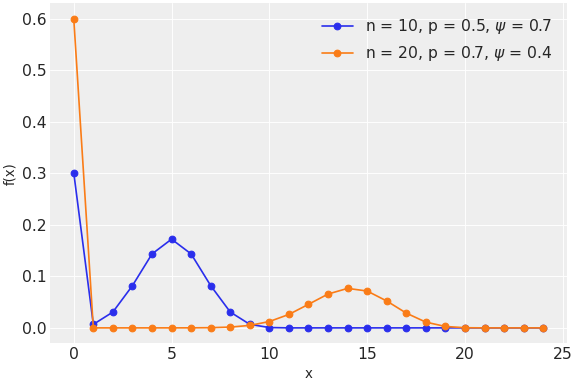
pymc.ZeroInflatedBinomial
ゼロ過剰二項分布
class pymc.ZeroInflatedBinomial(name, psi, n, p, **kwargs)
| 変数 | | |
| pai | 浮動小数点または整数のtensor_like | 与えられたインターバルでの予測発生回数 |
| n | 浮動小数点または整数のtensor_like | ベルヌーイトライアル数 (n >= 0) |
| p | 浮動小数点または整数のtensor_like | 各トライアルの成功確率 |
| メソッド | |
| ZeroInflatedBinomial.__init__(*args,**kwargs) | |
| ZeroInflatedBinomial.dist(psi,n,p,**kwargs) | |
pymc.ZeroInflatedNegativeBinomial
ゼロ過剰 逆二項分布対数尤度
class pymc.ZeroInflatedNegativeBinomial(name, psi, mu=None, alpha=None, p=None, n=None, **kwargs)
| 変数 | | |
| psi | 浮動小数点のtensor_like | 逆二項変数の予測proportion |
| mu | 浮動小数点のtensor_like | ポワソン分布パラメータ (mu >= 0) |
| alpha | 浮動小数点のtensor_like | ガンマ分布パラメータ (alpha > 0) |
| p | 浮動小数点のtensor_like | 各トライアルの成功確率 (0 < p < 1) |
| n | 浮動小数点のtensor_like | 目標成功トライアル数 (n > 0) |
| メソッド | |
| ZeroInflatedNegativeBinomial.__init__(*args,**kwargs) | |
| ZeroInflatedNegativeBinomial.dist(psi[,mu,,...]) | |
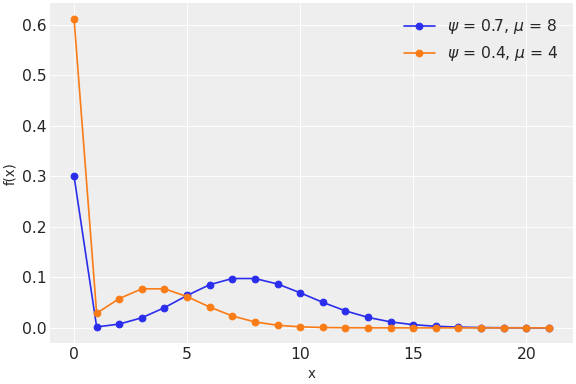
pymc.ZeroInflatedPoisson
ゼロ過剰ポワソン対数尤度
class pymc.ZeroInflatedPoisson(name, psi, mu, **kwargs)
| 変数 | | |
| psi | 浮動小数点のtensor_like | ポワソン変数の予測proportion |
| mu | 浮動小数点のtensor_like | 与えられたインターバルでの発生数 (mu >= 0) |
| メソッド | |
| ZeroInflatedPoisson.__init__(*args,**kwargs) | |
| ZeroInflatedPoisson.dist(psi,mu,**kwargs) | |