このノートブックでは、pymc-bartの論文[Quiroga et al.,2022(注2)]の4.1章に記述されているBARTを使った不均一分散性のモデル化を示します。私たちは、Rパッケージ datarium[Kassambara,2019(注1)]で提供されるマーケティングのデータセットを使います。この考えは、マーケティングチャンネルが予算の関数として売り上げへの貢献をモデル化することです。
(注1)
Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, and Osvaldo A Martin. Bayesian additive regression trees for probabilistic programming. 2022.
(注2)
Alboukadel Kassambara. datarium: Data Bank for Statistical Analysis and Visualization. 2019. R package version 0.1.0.
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb%config InlineBackend.figure_format = "retina"
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [10, 6]
rng = np.random.default_rng(42)注意: BARTは 3.7<= pythonバージョン <3.11 で動作します。
python38環境にgraphvizがインストールされていなければ、以下のコマンドでgraphvizをインストーしてください。
(base) conda activate python38
(python38) conda install -c conda-forge python-graphvizpython38環境の構築は以下の記事も参考にしてください。
データの読み込み
try:
df = pd.read_csv(os.path.join("..", "data", "marketing.csv"), sep=";", decimal=",")
except FileNotFoundError:
df = pd.read_csv(pm.get_data("marketing.csv"), sep=";", decimal=",")
n_obs = df.shape[0]
df.head()| youtube | newspaper | sales | ||
|---|---|---|---|---|
| 0 | 276.12 | 45.36 | 83.04 | 26.52 |
| 1 | 53.40 | 47.16 | 54.12 | 12.48 |
| 2 | 20.64 | 55.08 | 83.16 | 11.16 |
| 3 | 181.80 | 49.56 | 70.20 | 22.20 |
| 4 | 216.96 | 12.96 | 70.08 | 15.48 |
EDA
データを観察することから始めます。Youtubeに焦点を当てます。
fig, ax = plt.subplots()
ax.plot(df["youtube"], df["sales"], "o", c="C0")
ax.set(title="Sales as a function of Youtube budget", xlabel="budget", ylabel="sales");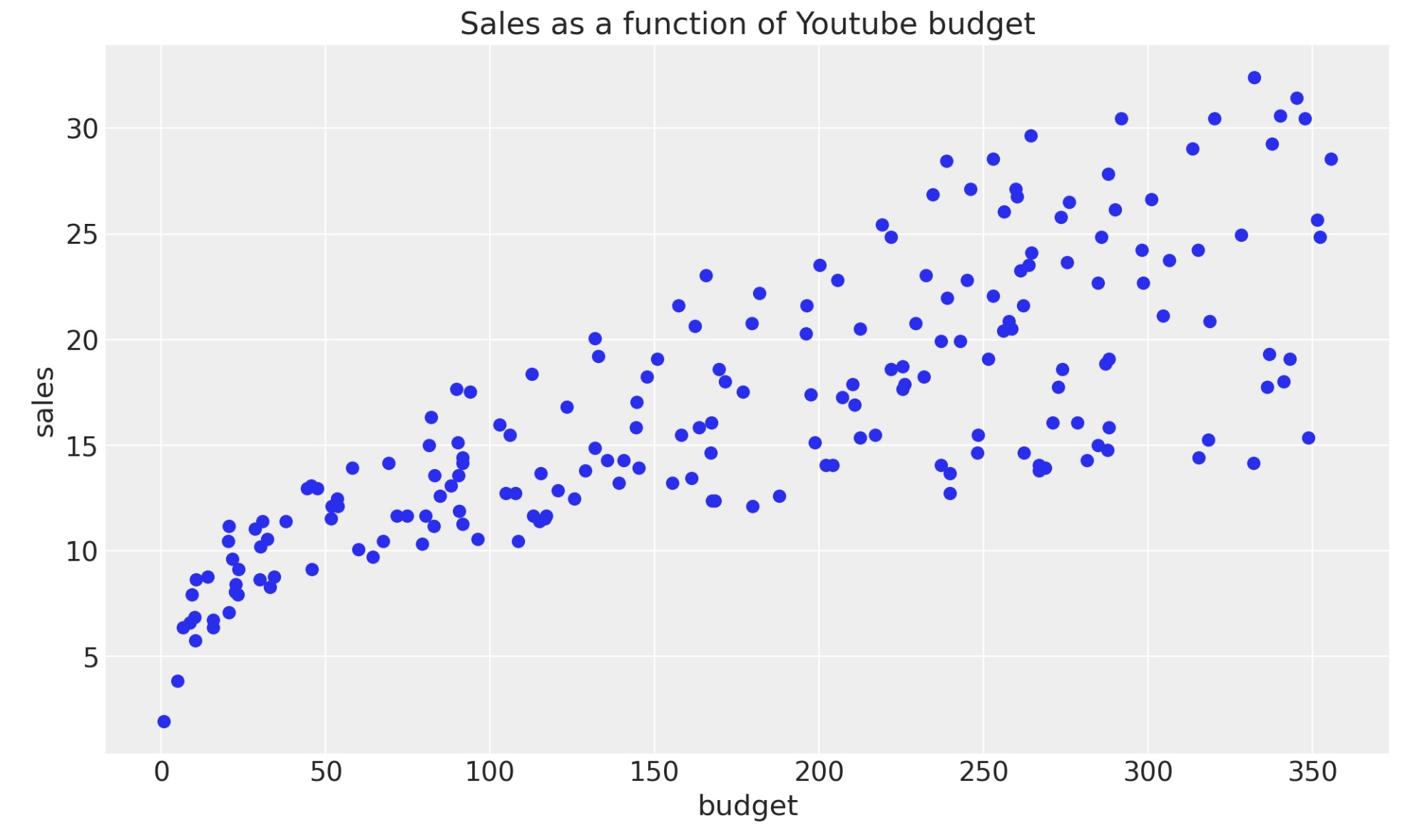
平均と分散の両方が予算の関数として増加することは明らかに見て取れます。一つの可能性は、それらの関数、例えば二乗平均や対数、の明白なパラメータ化を、手動で選択することです。しかし、この例では、BARTを使ったデータからそれらの関数を学習していきます。
モデルの仕様
モデル化のデータの準備を進めます。budgetを予測変数、salesをレスポンスとして使います。
X = df["youtube"].to_numpy().reshape(-1, 1)
Y = df["sales"].to_numpy()次に、モデルを規定します。平均と分散の両方でモデルをベクター化することができる、ただ一つのBART分布を必要とすることに注意します。私たちは売り上げが正になることを予期するため尤度としてガンマ分布を使います。
with pm.Model() as model_marketing_full:
w = pmb.BART("w", X=X, Y=np.log(Y), m=200, shape=(2, n_obs))
y = pm.Gamma("y", mu=pm.math.exp(w[0]), sigma=pm.math.exp(w[1]), observed=Y)
pm.model_to_graphviz(model=model_marketing_full)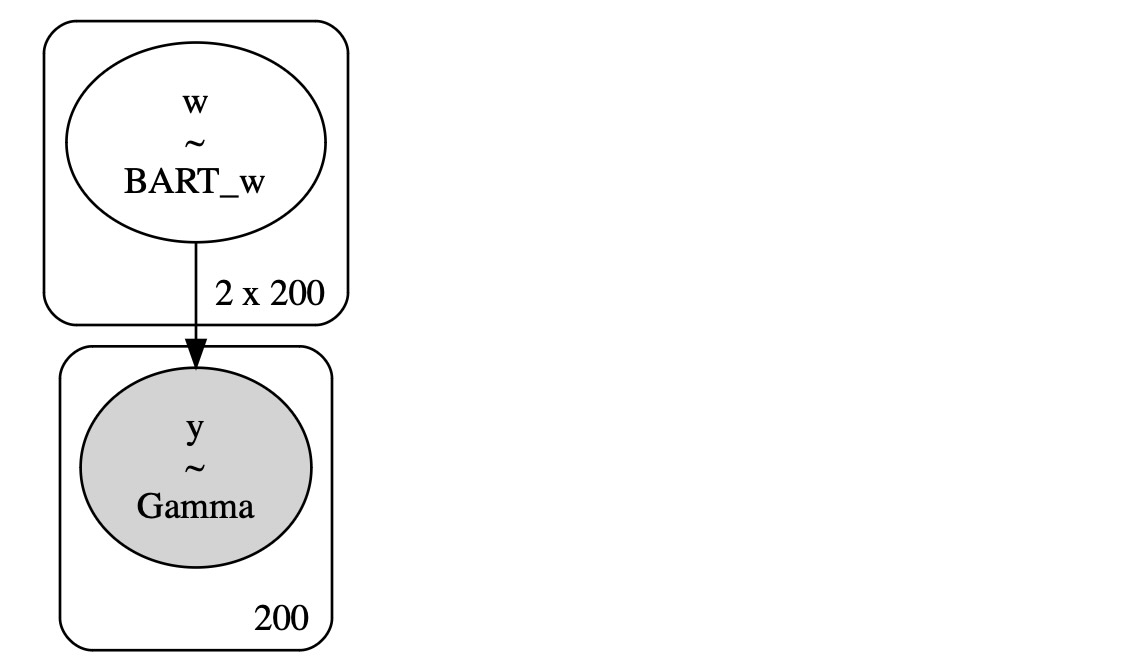
ここで、モデルを適合します。
with model_marketing_full:
idata_marketing_full = pm.sample(random_seed=rng)
posterior_predictive_marketing_full = pm.sample_posterior_predictive(
trace=idata_marketing_full, random_seed=rng
)
結果
ここで、平均と尤度の事後予測分布を視覚化できます。
posterior_mean = idata_marketing_full.posterior["w"].mean(dim=("chain", "draw"))[0]
w_hdi = az.hdi(ary=idata_marketing_full, group="posterior", var_names=["w"])
pps = az.extract(
posterior_predictive_marketing_full, group="posterior_predictive", var_names=["y"]
).Tidx = np.argsort(X[:, 0])
fig, ax = plt.subplots()
az.plot_hdi(x=X[:, 0], y=pps, ax=ax, fill_kwargs={"alpha": 0.3, "label": r"Likelihood $94\%$ HDI"})
az.plot_hdi(
x=X[:, 0],
hdi_data=np.exp(w_hdi["w"].sel(w_dim_0=0)),
ax=ax,
fill_kwargs={"alpha": 0.6, "label": r"Mean $94\%$ HDI"},
)
ax.plot(X[:, 0][idx], np.exp(posterior_mean[idx]), c="black", lw=3, label="Posterior Mean")
ax.plot(df["youtube"], df["sales"], "o", c="C0", label="Raw Data")
ax.legend(loc="upper left")
ax.set(
title="Sales as a function of Youtube budget - Posterior Predictive",
xlabel="budget",
ylabel="sales",
);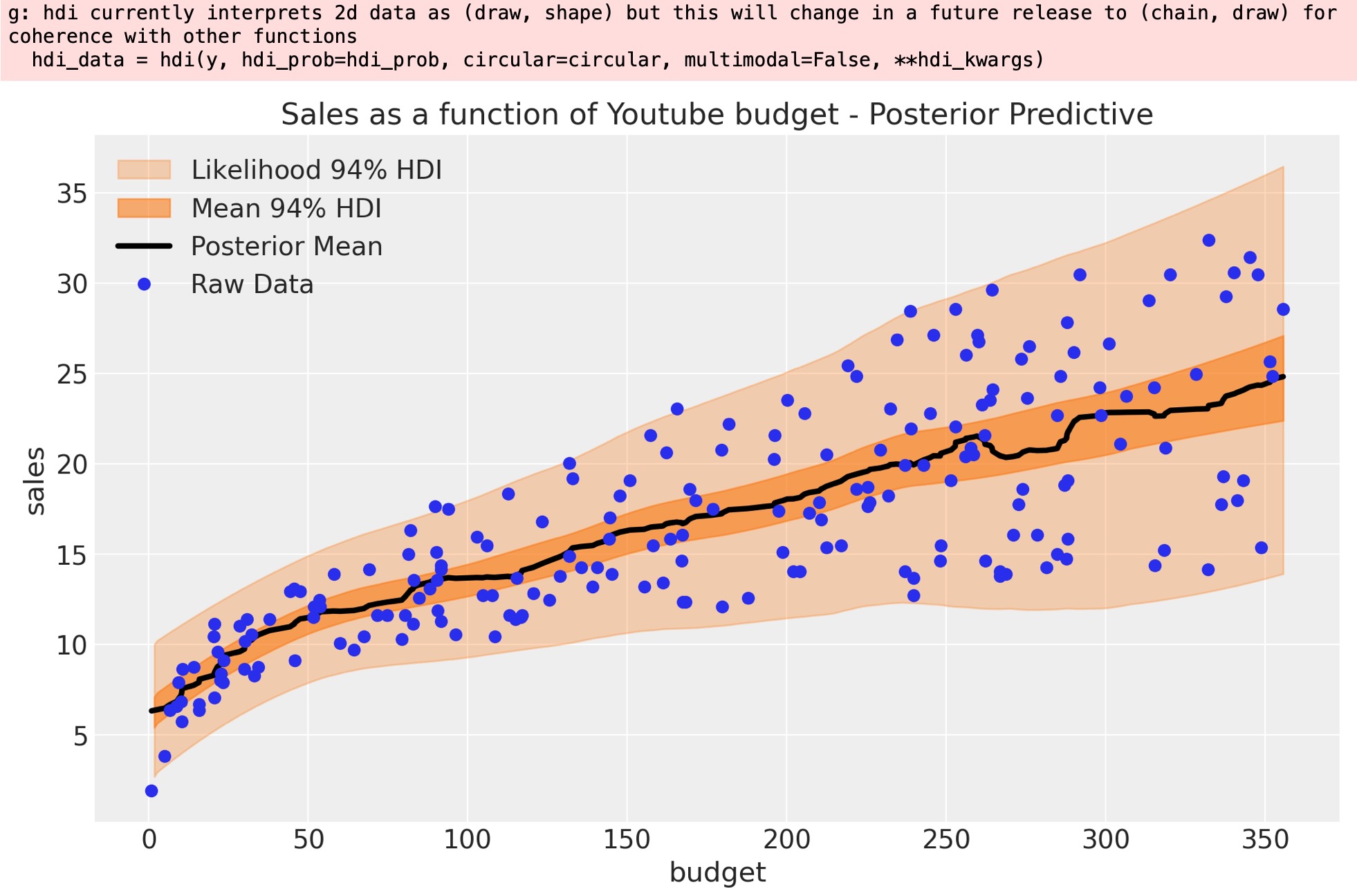
適合はうまく行ってます。平均と分散が、予算の関数として増加していることがわかります。
製作者
著者:Juan Orduz 2022年2月
更新:Osvaldo Martin 2023年3月
参考資料
- Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, and Osvaldo A Martin. Bayesian additive regression trees for probabilistic programming. 2022
- Alboukadel Kassambara. datarium: Data Bank for Statistical Analysis and Visualization. 2019. R package version 0.1.0.