BARTと分位点回帰

from pathlib import Path

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb

from scipy import stats

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.3.1

%config InlineBackend.figure_format = "retina"
RANDOM_SEED = 5781
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

　通常、回帰を行うとき、何らかの分布の条件付き平均をモデル化します。共通のケースは、折り返さない連続した正規分布、計数データに対するポワソン分布です。

　分位点回帰は、代わりにレスポンス変数の条件付き分位数を見積もります。仮に分位数が0.5であるときにその中間値を見積もります。これは、ロバスト回帰の実行する方法として役立ちます。同じやり方で、正規分布の代わりにステューデントT分布を使います。しかし、いくつかの問題のために、私たちは、実際に、平均から離れた反応の振る舞いに注意します。例えば、医療研究ではパソロジーや潜在的健康リスクが、例えば、オーバーウェイトとアンダーウェイトのような、高い、または低い分位点で発生します。エコロジーのような任意の他の分野で、分位点回帰は、変数間の複雑な相互作用の存在のために適合させます。相互の変数の結果は、変数の相違する範囲で異なります。

非対称ラプラス分布

　最初に、分位点回帰のためのベイジアンモデルの書き方、または分位点回帰の尤度として使う分布について考えるのは奇妙なことです。しかし、答えは全く簡単に明らかになります。私たちは、非対称なラプラス分布を使う必要があります。この分布は、平均を操作する単一のパラメータを持ち、もう一つはスケール、3番目の変数は非対称性を操作します。この非対称なパラメータについて少なくとも二つの代替的なパラメータ化があります。kの項は０から無限大までのパラメータで、q項は０と１の間の数値です。この潜在的なパラメータ化は、利率の分位点として直接解釈できる分位点回帰にとってもっと直感的です。

　次のセルで、非対称ラプラスファミリーから３の分布のpdf（Probability Density Function:確率密度関数）を計算します。

x = np.linspace(-6, 6, 2000)
for q, m in zip([0.2, 0.5, 0.8], [0, 0, -1]):
    κ = (q / (1 - q)) ** 0.5
    plt.plot(x, stats.laplace_asymmetric(κ, m, 1).pdf(x), label=f"q={q:}, μ={m}, σ=1")
plt.yticks([])
plt.legend();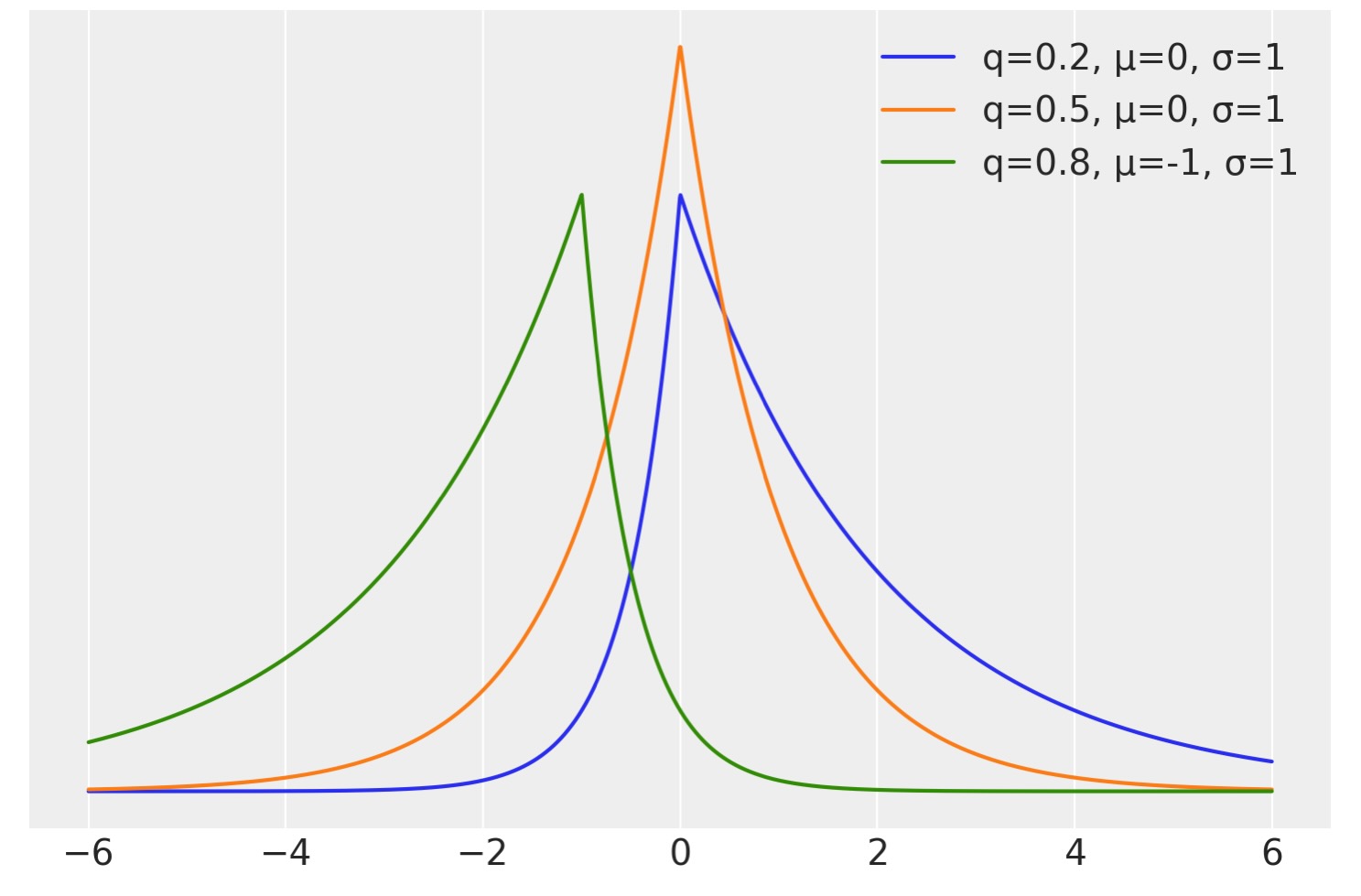

　彼らの年齢の関数として、”Body Mass Index for Dutch kids and young mem”(オランダの少年と若い男性の体重指標)をモデルの簡単なデータセットに使います。

try:
    bmi = pd.read_csv(Path("..", "data", "bmi.csv"))
except FileNotFoundError:
    bmi = pd.read_csv(pm.get_data("bmi.csv"))

bmi.plot(x="age", y="bmi", kind="scatter");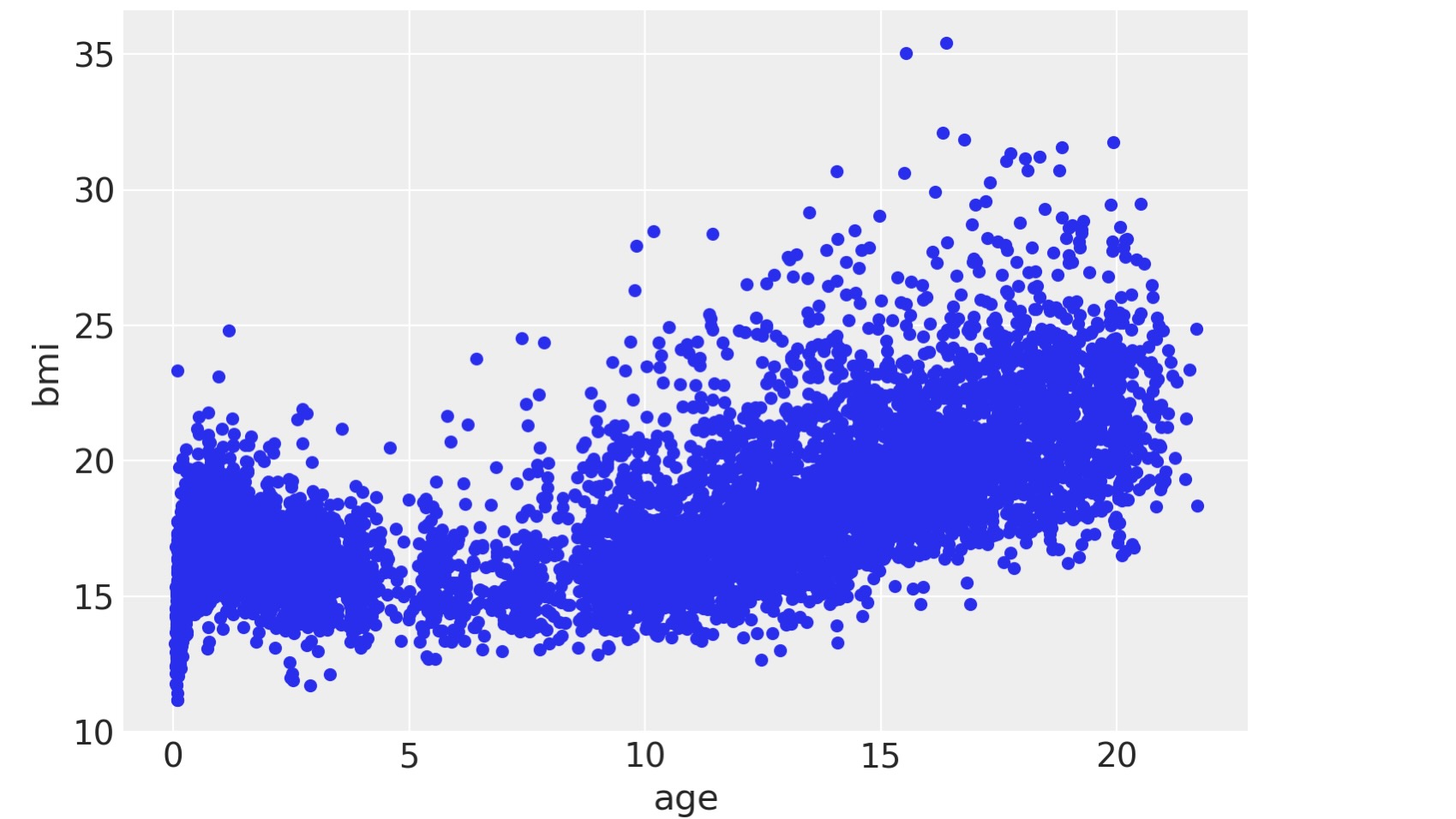

　BMIと年齢間の関係の前の図から、線形からは遠いことがわかります。そしてこのためにBARTを使います。

　0.1,0.5,そして0.9の三つの分位点のモデルにします。私たちは、非対称ラプラス分布のqをたったひとつの異なる値にして、三つに分離したモデルに適合させることで計算することができます。あるいは、y_stackとして観測値をスタックし、単一のモデルに適合することができます。

y = bmi.bmi.values
X = bmi.age.values[:, None]


y_stack = np.stack([bmi.bmi.values] * 3)
quantiles = np.array([[0.1, 0.5, 0.9]]).T
quantiles

array([[0.1],
       [0.5],
       [0.9]])

with pm.Model() as model:
    μ = pmb.BART("μ", X, y, shape=(3, 7294))
    σ = pm.HalfNormal("σ", 5)
    obs = pm.AsymmetricLaplace("obs", mu=μ, b=σ, q=quantiles, observed=y_stack)

    idata = pm.sample(compute_convergence_checks=False)

　次の図で、三つの適合した曲線の結果を見ることができます。目立つ一つの特徴は、中間線と他の二つの線の間の距離が同じではなく、ギャップがあることです。同じパターンに沿った曲線の形状もまた、正確に同じではありません。

plt.plot(bmi.age, bmi.bmi, ".", color="0.5")
for idx, q in enumerate(quantiles[:, 0]):
    plt.plot(
        bmi.age,
        idata.posterior["μ"].mean(("chain", "draw")).sel(μ_dim_0=idx),
        label=f"q={q:}",
        lw=3,
    )

plt.legend();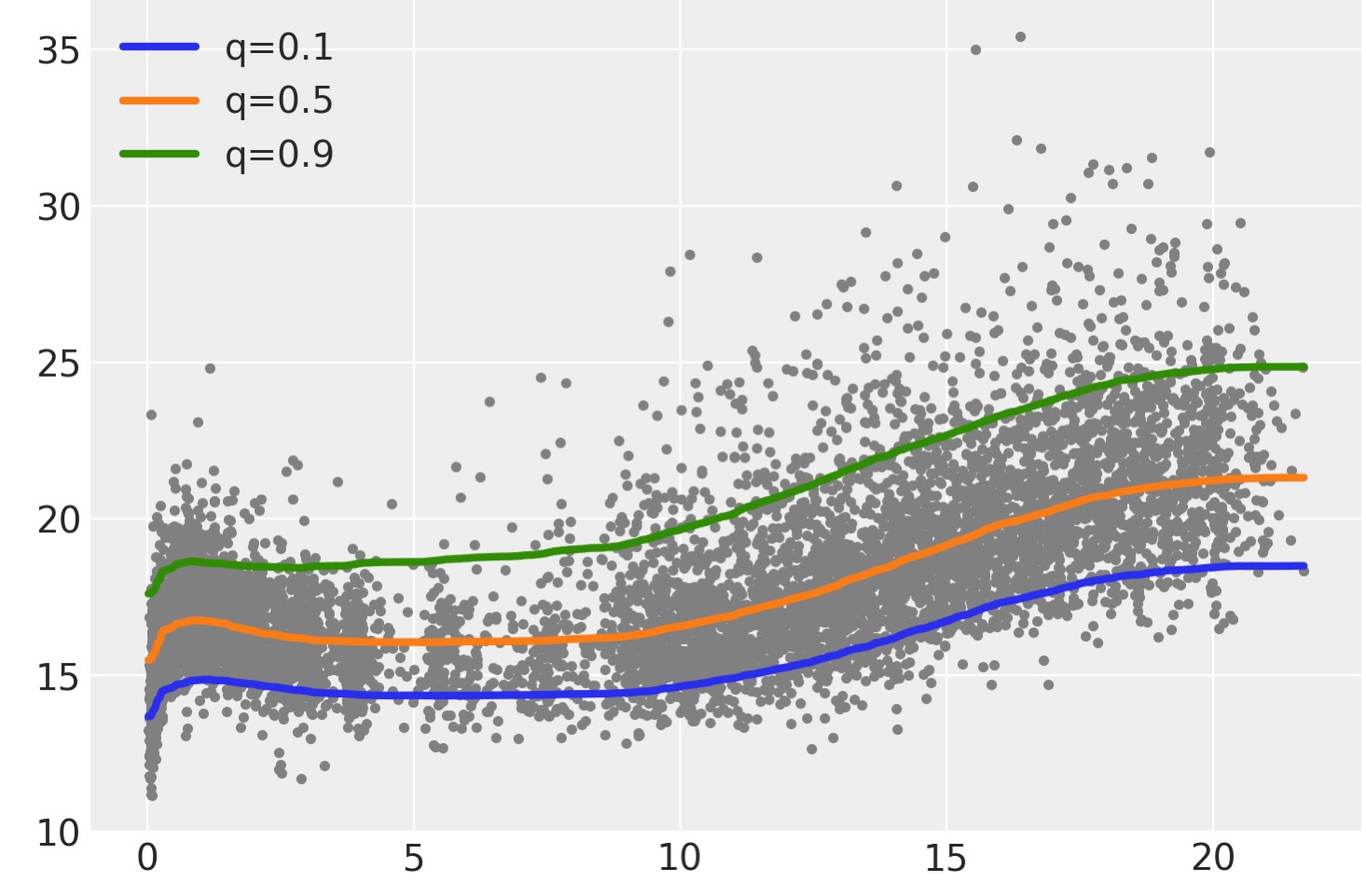

これらの要点のより良い理解のために、正規尤度のBART回帰を計算し、そして、それらの適合から同じ三つの分位点を計算しましょう。

y = bmi.bmi.values
x = bmi.age.values[:, None]
with pm.Model() as model:
    μ = pmb.BART("μ", x, y)
    σ = pm.HalfNormal("σ", 5)
    obs = pm.Normal("obs", mu=μ, sigma=σ, observed=y)

    idata_g = pm.sample(compute_convergence_checks=False)
    idata_g.extend(pm.sample_posterior_predictive(idata_g))

idata_g_mean_quantiles = idata_g.posterior_predictive["obs"].quantile(
    quantiles[:, 0], ("chain", "draw")
)

plt.plot(bmi.age, bmi.bmi, ".", color="0.5")
for q in quantiles[:, 0]:
    plt.plot(bmi.age.values, idata_g_mean_quantiles.sel(quantile=q), label=f"q={q:}")

plt.legend()
plt.xlabel("Age")
plt.ylabel("BMI");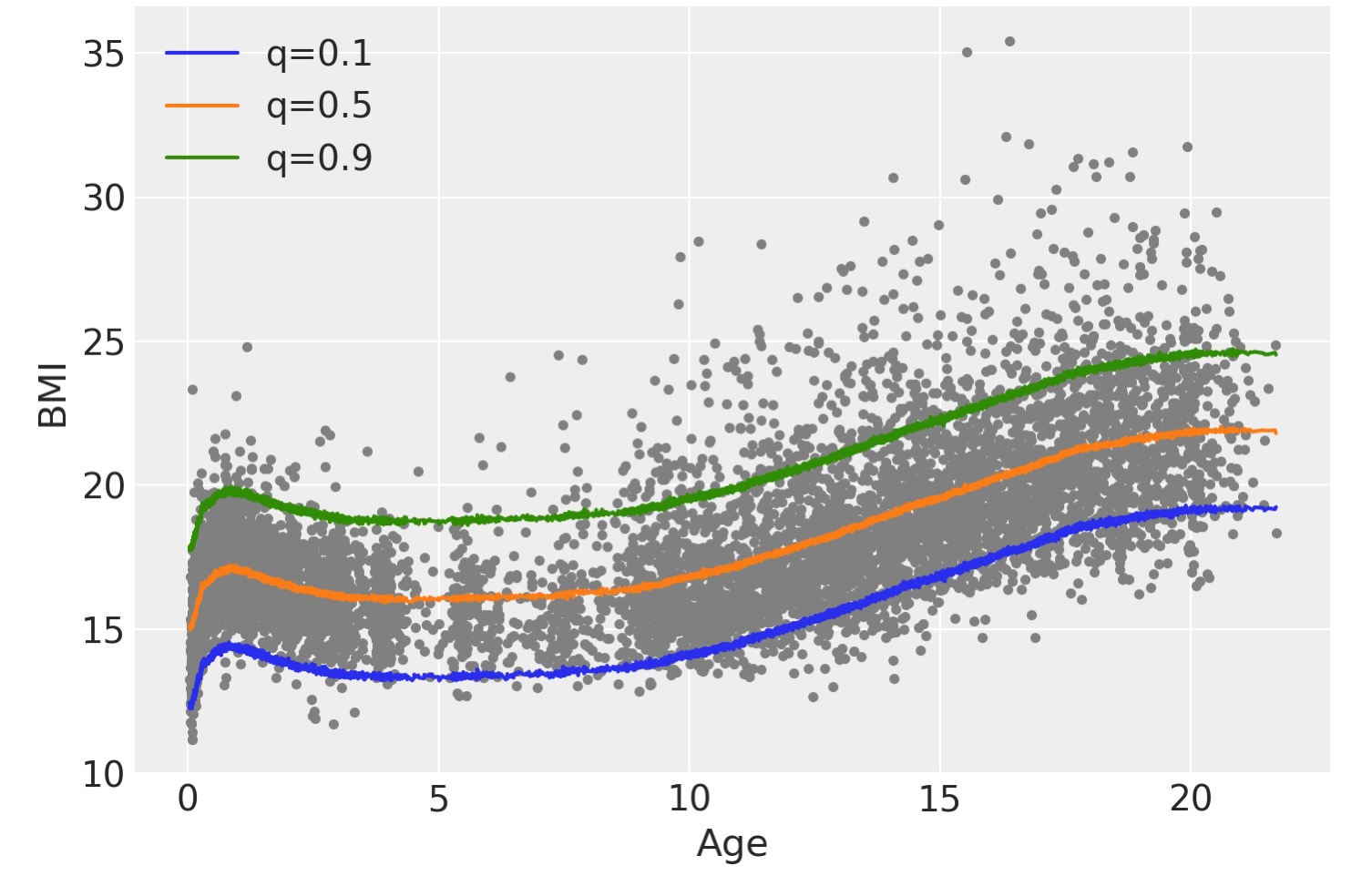

　正規尤度を使うときに、そして、分位点を計算した適合から、分位点 q=0.1とq=0.9は、1=0.5に対して対称です。曲線の形状もまた、特にちょうど上下にずらしたように同じです。追加すると、ガウスファミリーの変数が常に同じ状態にあるのに対して、非対称ラプラスファミリーは、年齢が増加するとBMIの変数も増加することを説明するのを認めます。