変分推論:ベイジアン・ニューラル・ネットワーク

機械学習の現在のトレンド

　確率プログラミング、機械学習、ビッグデータは、機械学習のもっとも大きなトピックです。確率プログラミングの中では、多くのイノベーションは変分推論を使ってスケールを問題にすることに焦点を当てます。この例では、私は、簡単なベイジアンニューラルネットワークに適合するために、PyMCの変分推論を使う方法を示します。私はまた、未来の研究を探検するために非常に興味深い道を開くことができる　確率プログラミングと機械学習をどのように橋渡しするか議論します。

確率プログラミング

　確率プログラミングはカスタム確率モデルの柔軟な作成を許容します。そして、データから学習することと推論が主要な懸案になります。アプローチはベイジアンアプローチを継承します。そのため、私たちは、モデルの制限と情報の提供のために事前分布を規定し、そして事後分布の様式の不確実性の推定を得ます。MCMCサンプリングアルゴリズムを使うことで、私たちは、非常に柔軟な推定のこれらのモデルに、この事後分布からサンプルを出力することができます。PyMC, NumPyro, とStanは、これらのモデルを構築して推定するための現在の最新のツールです。一つの主要なサンプリングの欠点は、しかしながら、それがしばしば、特に高次のモデルと大きなデータセットに対して、遅いことです。それが、近年、多くの推論アルゴリズムが開発されてきた理由です。そのほとんどはMCMC同様に柔軟で、もっと高速です。事後分布からサンプルを出力する代わりに、これらのアルゴリズムは代わりに分布（例えば正規分布）をサンプリングの問題と最適化の問題を調整した事後分布に適合させます。自動微分変分推論[Kucukelbir et al., 2015(参考文献)]は、いくつかのプログラミングパッケージ、PyMC, NumPyro,とStanに実装されています。

　残念なことに、分類や（非線形）回帰のような伝統的なML問題になるとき、確率プログラミングはしばしば、アンサンブル・ラーニング(例えば、ランダムフォレスト、グラジェントブーステッド回帰ツリー)のようなもっと良いアルゴリズム的なアプローチの下につきます。

深層学習

　今は第三のルネッサンスの中です。ニューラルネットワークは、ほとんどどのような対象の認識のベンチマークでも優位性を持つことによって、Atariのゲームを蹴飛ばし[Mnih et al.,2013(参考文献)]、碁の世界チャンピオンLee Sedolを負かすことで[D.Silver, 2016(参考文献)]、繰り返しヘッドラインになってきました。統計的な点からニューラルネットワークは非線形関数の近似と学習の表現で非常に高品質です。分類でもっともよく知られていますが、それらは、オートエンコーダ[KingmaとWelling, 2014(参考文献)]付きの教師なし学習、そしてすべてのその他の興味深い方法(例えば、リカレント・ニューラルネットワーク、または多重な形態の分布へのMDNs)、に拡張されました。なぜそれほどうまくいくのでしょう？統計的な性質はまだ完全に理解されていないので、本当に誰もわかっていません。

　深層学習の革命の大部分は、それらの非常に複雑なモデルの訓練する能力です。これはいくつかの柱に基づきます。

• スピード：もっと高速な処理を許すGPUの促進
• ソフトウエア：PyTorchやTensorFlowのようなフレームワークは、抽象モデルを柔軟に作成することを許します。それはCPU ,GPU 向けにコンパイルされ、最適化されます。
• 学習アルゴリズム：データのサブセットを訓練すること-確率的に勾配下降ーはこれらのモデルを大量のデータで訓練することを許容します。ドロップアウトのような技術は、過学習を避けます。
• アーキテクチャ：多くのイノベーションは、畳み込みニューラルネットのような入力層、またはMDNsのような出力層の変化からなります。

深層学習と確率プログラミングの橋渡し

　一方の手に、私たちは確率プログラミングを持ちます、それは、私たちのデータに洞察を得るために、非常に原理的なよく知られている方法で、モデルに焦点を当てむしろ小さなモデルを構築します。もう一方の手に、深層学習を持っています。それは予測において驚くほど高度に複雑なモデルと大量に訓練するために多くの経験を使います。私たちはこのように、機械学習の新しいイノベーションを解き放つことを期待してこれら二つのアプローチを結びつけることができる交点にいます。さらなる動機づけには、Dustin Tranのブログ投稿も参照してください。

　これは、確率プログラミングをもっと広い領域の興味深い問題に適用しますが、私は、深層学習のイノベーションに対する偉大な見込みの掌握に、これが橋渡しすると信じています。いくつかの考えは、

• 予測の不確実性：私たちは以下で見るように、ベイジアンニューラルネットワークは、その予測の不確実性について私たちに情報を与えます。私は、不確実性が機械学習を正しく理解する概念であると考えています。それが現実世界への応用で重要なのは明白です。しかし、訓練においても役に立ちます。例えば、私たちはサンプルでモデルの特徴を訓練します。それはもっとも不確実です。
• 表現の不確実性：私たちは、学習したネットワークの表現の安定性についての情報を与える重みの不確実な推定を得ます。
• 事前分布の規制：重みはしばしば、オーバーフィットを避けるための L2ー規制です。これはとても本質的に、重みの係数としてガウス事前分布になります。私たちは、しかし、不足状況(これはL1-ノルムを使うことと同様です)を強制するためのスパイク・アンド・スラブのような、その他のすべての事前分布が想像できます。
• 事前分布に影響を与える学習の伝送：もし私たちが、認識しているデータセットで新しいオブジェクトのネットワークを訓練したいのであれば、GoogLeNet[Szegedy et al, 2014(参考文献)]のような、その他の事前に訓練されたネットワークから回収した重みの周りの中心に影響のある事前分布を置くことによって学習をブートストラップできます。　
• 階層化ニューラルネットワーク：確率プログラミングの非常に強力なアプローチは、階層モデリングです。それは全体の集団のサブグループで学習されたことを蓄えておくことを許します(PyMCの階層線形回帰を参照してください。)。階層データセットでニューラルネットワークを適用することは、私たちは、サブグループに特化した個別のニューラルネットを訓練できます。それはまだ全体の集団の表現に関して影響を持っています。例えば、自動車の写真から車の車種を分類する訓練をしたネットワークを想像してください。私たちは、階層化ニューラルネットワークを訓練できます。そこでサブニューラルネットワークは、単一の工業製品だけから、モデルがかけ離れていることをわかるために訓練されます。正確な工業製品からすべての自動車にある直感的知識は、正確な類似性を共有します。そのため、ブランドを特定する個別のネットワークを訓練するのが賢明です。しかし、個別のネットワークが高次の層に接続されているために、それらは、またすべてのブランドに役立つ特徴に関するその他の特別なサブネットワークの情報を共有しています。興味深いことに、ネットワークの異なる層は階層の色々なレベルによって影響されます。ー例えば、視覚的な線を抽出する早い層は、高次の表現は異なりますが、すべてのサブネットワークに識別されます。階層モデルはデータから全てを学習します。
• その他のハイブリッドアーキテクチャ：私たちは、自由にすべての種類のネットワークを構築することができます。例えば、ベイジアン・ノンパラメトリックは、隠れ層の形とサイズを、訓練中に把握する問題に対して最適なスケールのネットワークアーキテクチャに、柔軟に適合するのに使うことができます。現在、これは高価なハイパーパラメータの最適化と多くの種類の知識が要求されます。

PyMCのベイジアン・ニューラル・ネットワーク

データの生成

　最初に、任意のtoyデータを生成しましょう。線形に分離されない単純な2値分類のです。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
import pytensor.tensor as pt
import seaborn as sns

from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import scale

%config InlineBackend.figure_format = 'retina'
floatX = pytensor.config.floatX
RANDOM_SEED = 9927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
X = X.astype(floatX)
Y = Y.astype(floatX)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)

fig, ax = plt.subplots()
ax.scatter(X[Y == 0, 0], X[Y == 0, 1], color="C0", label="Class 0")
ax.scatter(X[Y == 1, 0], X[Y == 1, 1], color="C1", label="Class 1")
sns.despine()
ax.legend()
ax.set(xlabel="X", ylabel="Y", title="Toy binary classification data set");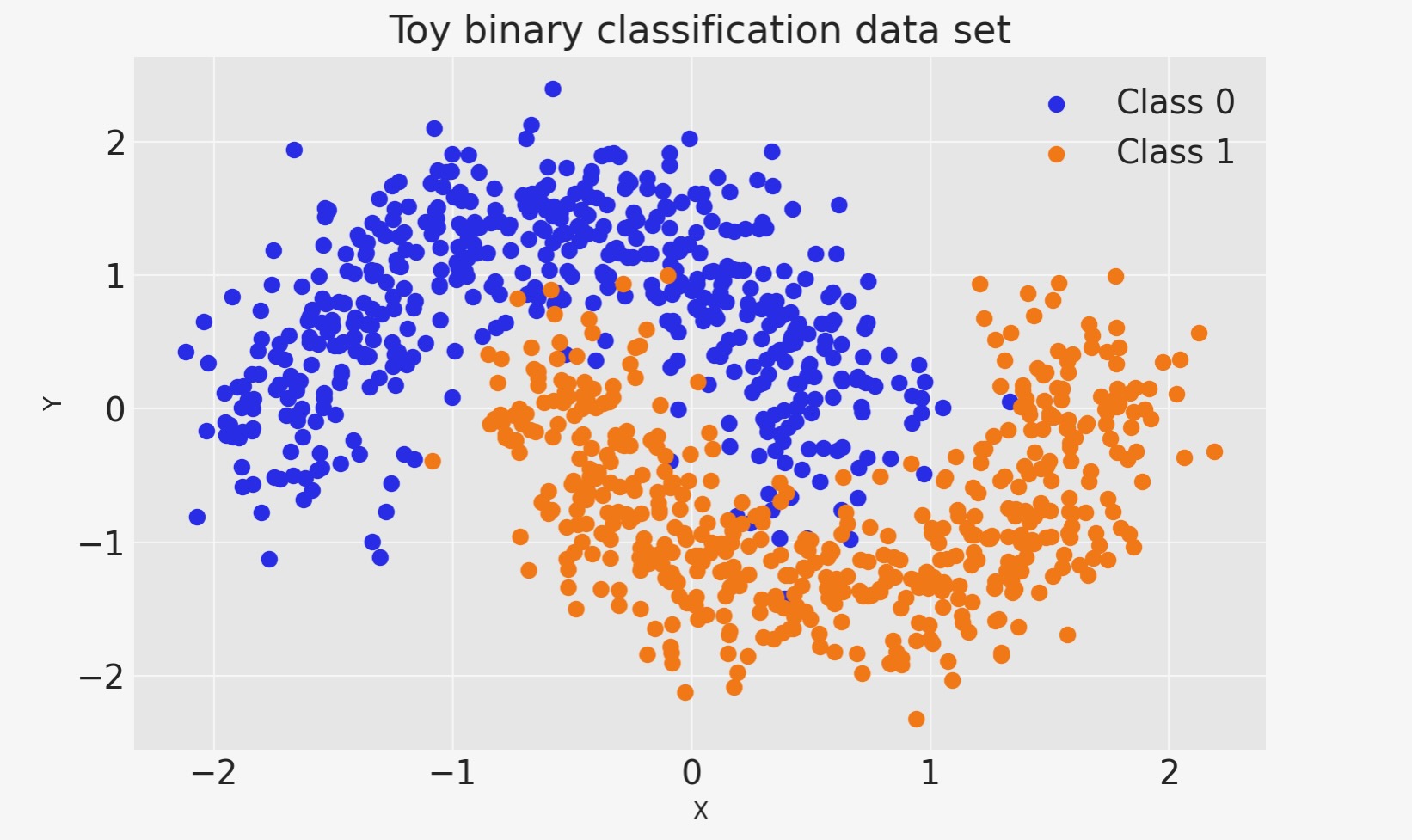

モデル仕様

　ニューラルネットワークは全く単純です。基本ユニットは、ロジスティック回帰以上はないパーセプトロンです。私たちは、これらの多くを並列に使います。その後、隠れ層を得るまでそれをスタックします。ここで、私たちは各層５ニューロンの二つの隠れ層を使います。それはこうした単純な問題には充分です。

def construct_nn(ann_input, ann_output):
    n_hidden = 5

    # Initialize random weights between each layer
    init_1 = rng.standard_normal(size=(X_train.shape[1], n_hidden)).astype(floatX)
    init_2 = rng.standard_normal(size=(n_hidden, n_hidden)).astype(floatX)
    init_out = rng.standard_normal(size=n_hidden).astype(floatX)

    coords = {
        "hidden_layer_1": np.arange(n_hidden),
        "hidden_layer_2": np.arange(n_hidden),
        "train_cols": np.arange(X_train.shape[1]),
        # "obs_id": np.arange(X_train.shape[0]),
    }
    with pm.Model(coords=coords) as neural_network:
        ann_input = pm.Data("ann_input", X_train, mutable=True, dims=("obs_id", "train_cols"))
        ann_output = pm.Data("ann_output", Y_train, mutable=True, dims="obs_id")

        # Weights from input to hidden layer
        weights_in_1 = pm.Normal(
            "w_in_1", 0, sigma=1, initval=init_1, dims=("train_cols", "hidden_layer_1")
        )

        # Weights from 1st to 2nd layer
        weights_1_2 = pm.Normal(
            "w_1_2", 0, sigma=1, initval=init_2, dims=("hidden_layer_1", "hidden_layer_2")
        )

        # Weights from hidden layer to output
        weights_2_out = pm.Normal("w_2_out", 0, sigma=1, initval=init_out, dims="hidden_layer_2")

        # Build neural-network using tanh activation function
        act_1 = pm.math.tanh(pm.math.dot(ann_input, weights_in_1))
        act_2 = pm.math.tanh(pm.math.dot(act_1, weights_1_2))
        act_out = pm.math.sigmoid(pm.math.dot(act_2, weights_2_out))

        # Binary classification -> Bernoulli likelihood
        out = pm.Bernoulli(
            "out",
            act_out,
            observed=ann_output,
            total_size=Y_train.shape[0],  # IMPORTANT for minibatches
            dims="obs_id",
        )
    return neural_network


neural_network = construct_nn(X_train, Y_train)

　それほど悪くないです。Normal事前分布は、重みを規制するのに役立ちます。通常、定数bを入力に追加しますが、コードを綺麗に維持するためにあえて除外します。

変分推論：スケーリングモデルの複雑性

　私たちは、ここでpymc.NUTSのようなMCMCサンプラーを走らせます。それは、このケースではかなりよく働きます。しかし、既に言及したように、これは、モデルをもっと層のある深いアーキテクチャに拡張すると、非常に遅くなります。

　その代わりに、私たちはpymc.ADVI 変分推論アルゴリズムを使います。これは、より高速で、より良いスケールになります。これは、平均場近似です。そのため私たちは事後分布の相関を無視します。

%%time

with neural_network:
    approx = pm.fit(n=30_000)

　目的関数を図示すると、最適化の繰り返しは適合を改善することがわかります。

plt.plot(approx.hist, alpha=0.3)
plt.ylabel("ELBO")
plt.xlabel("iteration");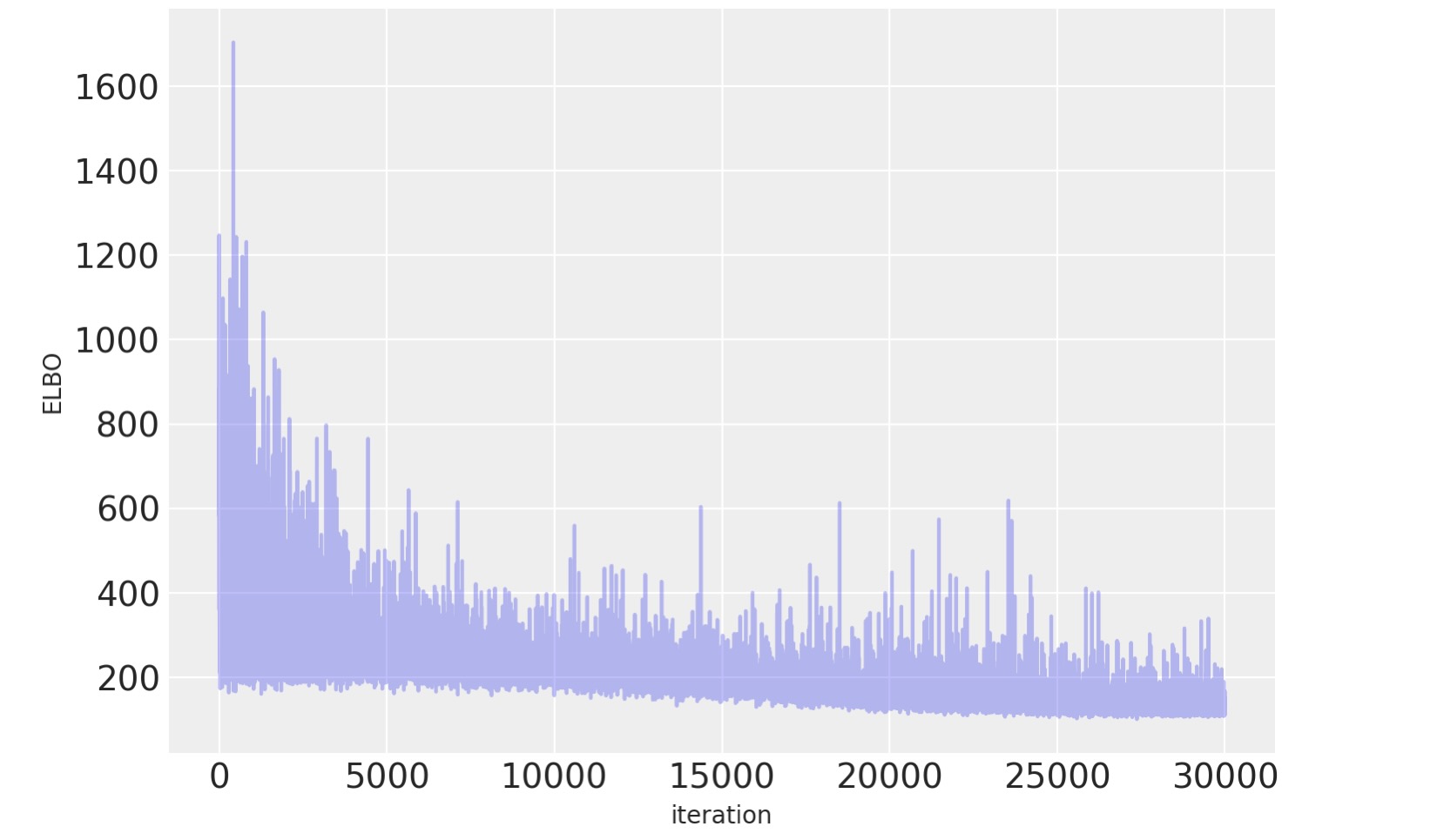

trace = approx.sample(draws=5000)

　ここで、モデルを訓練します。事後予測チェックを使って拒むセットを予測しましょう。私たちは、事後分布(変分推定からサンプルされた)から新しいデータ(このケースでは分類予測)を生成するために、sample_posterior_predictive()を使うことができます。

with neural_network:
    pm.set_data(new_data={"ann_input": X_test})
    ppc = pm.sample_posterior_predictive(trace)
    trace.extend(ppc)

　私たちは、class1の根底にある確率を推定するために、各観測値の予測を平均できます。

pred = ppc.posterior_predictive["out"].mean(("chain", "draw")) > 0.5

fig, ax = plt.subplots()
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1")
sns.despine()
ax.set(title="Predicted labels in testing set", xlabel="X", ylabel="Y");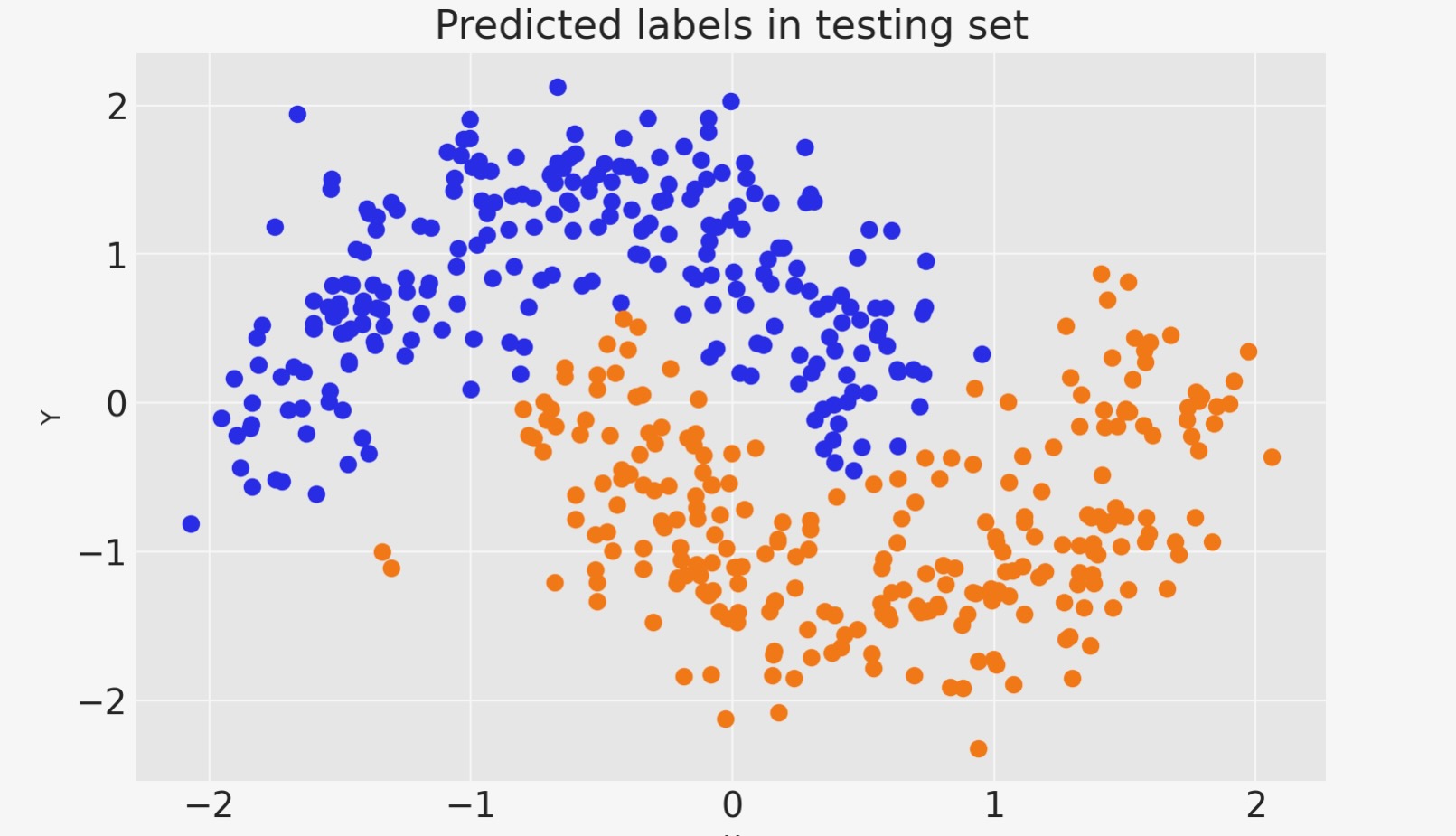

print(f"Accuracy = {(Y_test == pred.values).mean() * 100}%")

Accuracy = 95.6%

私たちのニューラルネットワークがよくやりました。

分類が学んだことを見てみましょう

　このために、私たちは、入力空間全体をおおう格子のクラス確率予測を評価します。

grid = pm.floatX(np.mgrid[-3:3:100j, -3:3:100j])
grid_2d = grid.reshape(2, -1).T
dummy_out = np.ones(grid.shape[1], dtype=np.int8)

with neural_network:
    pm.set_data(new_data={"ann_input": grid_2d, "ann_output": dummy_out})
    ppc = pm.sample_posterior_predictive(trace)

y_pred = ppc.posterior_predictive["out"]

確率の様相

cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(
    grid[0], grid[1], y_pred.mean(("chain", "draw")).values.reshape(100, 100), cmap=cmap
)
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1")
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel="X", ylabel="Y")
cbar.ax.set_ylabel("Posterior predictive mean probability of class label = 0");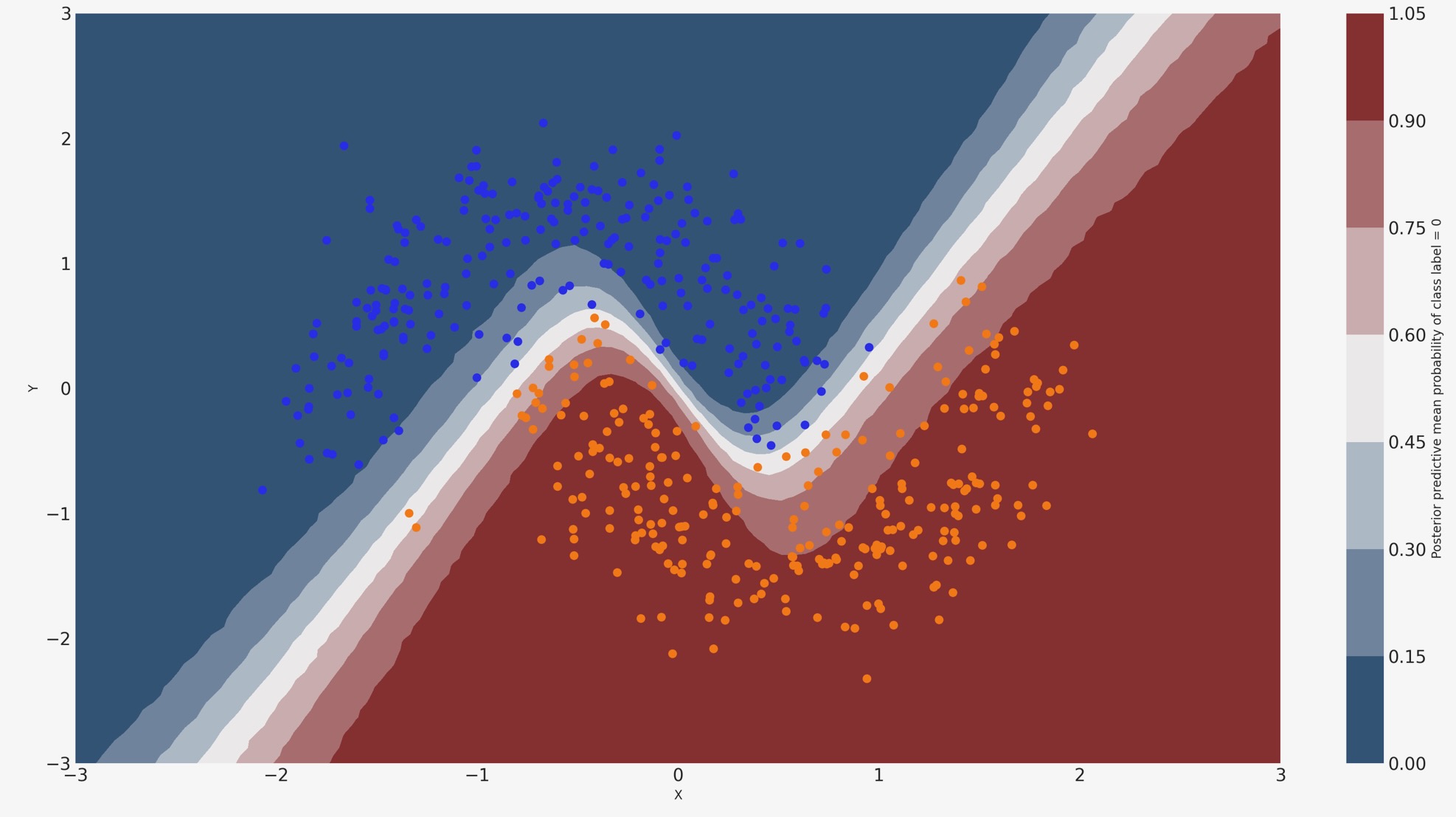

予測値の不確実性

　私たちは、上のノンベイジアンニューラルネットワークのすべてを処理したことに注意して下さい。各クラスラベルの事後予測の平均は、最大尤度予測値と一致しています。しかし、私たちは、予測の不確実性を理解するために事後予測の標準偏差を見ることができます。ここに示します。

cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(
    grid[0], grid[1], y_pred.squeeze().values.std(axis=0).reshape(100, 100), cmap=cmap
)
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1")
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel="X", ylabel="Y")
cbar.ax.set_ylabel("Uncertainty (posterior predictive standard deviation)");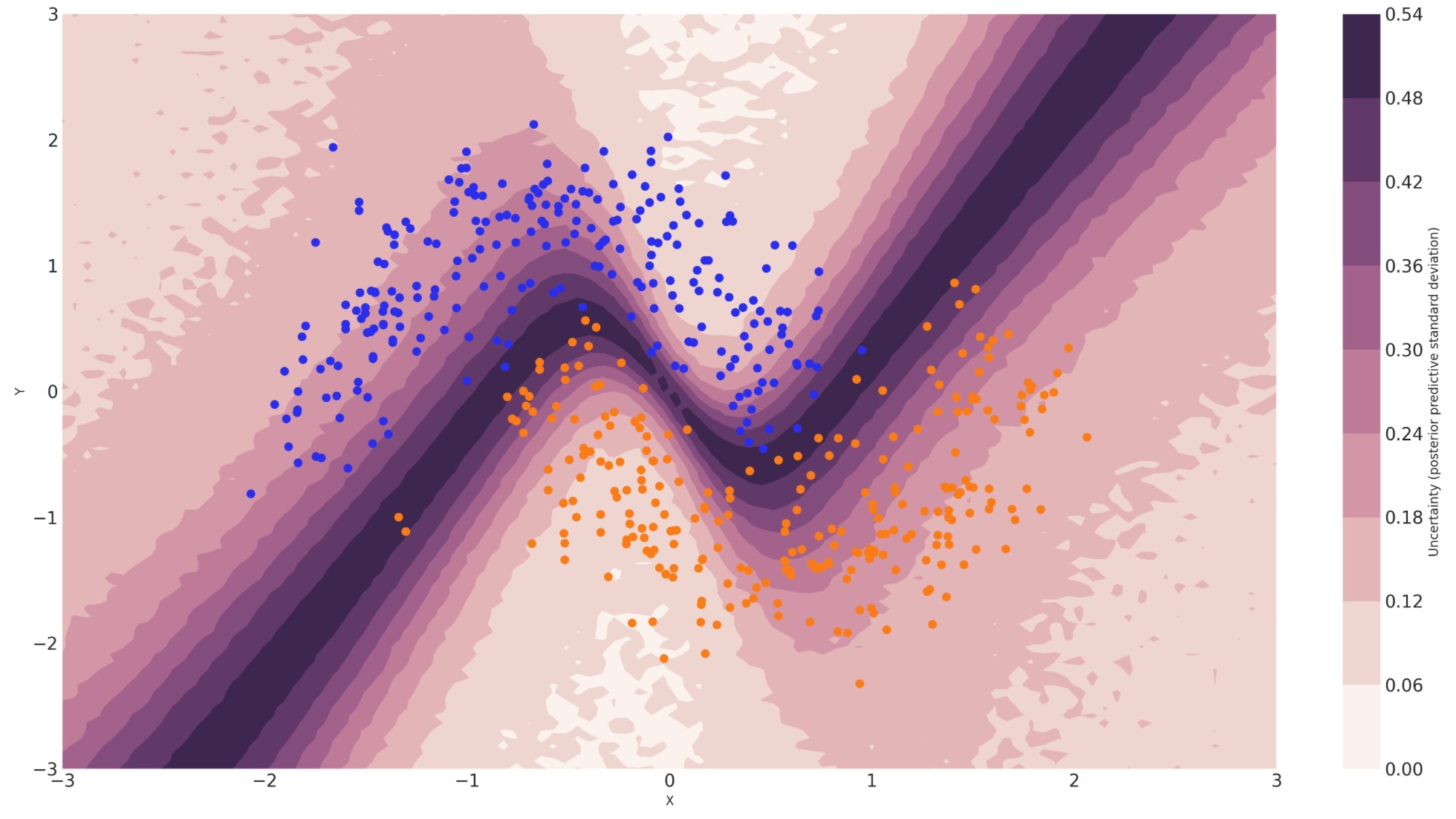

　私たちは、決定境界にとても密接しているのを見ることができます。どのラベルを予測するかの私たちの不確実性は、もっとも高くなります。あなたは、不確実性に関連した予測がヘルスケアのような多くの応用に対して重大な性質であることが想像できます。正確さをもっと最大化するために、私たちは、第一に高い不確実な領域からサンプルしモデルを訓練したいかもしれません。

ミニバッチADVI

　そこまで、私たちは、一旦すべてのデータでモデルを訓練しました。明白に、これはImageNetのようにスケールしません。さらには、データのミニバッチの訓練は(確率的勾配下降)局所的な最小を避け、より速い収束に導くことができます。

　幸いにも、ADVIはミニバッチで同様に走らせることができます。いくつかの設定が必要です。

minibatch_x = pm.Minibatch(X_train, batch_size=50)
minibatch_y = pm.Minibatch(Y_train, batch_size=50)
neural_network_minibatch = construct_nn(minibatch_x, minibatch_y)
with neural_network_minibatch:
    approx = pm.fit(40000, method=pm.ADVI())

plt.plot(approx.hist)
plt.ylabel("ELBO")
plt.xlabel("iteration");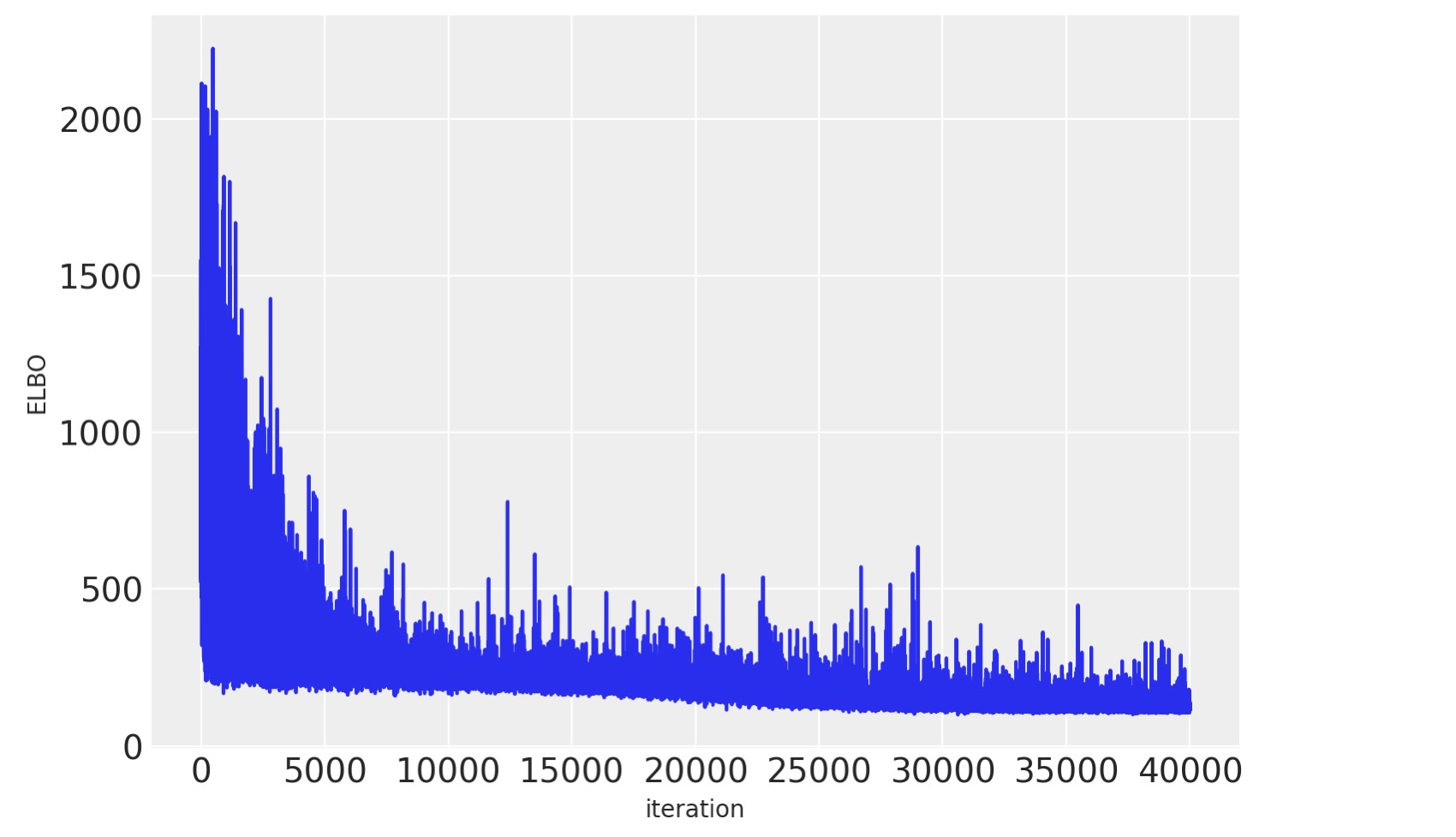

　あなたがわかるように、ミニバッチADVIの実行時間は非常に低くなります。収束も早くなるようです。

　楽しみなことに、私たちはトレースを見ることができます。ポイントは、私たちはまたニューラルネットワークの重みの不確実性を取得することです。

az.plot_trace(trace);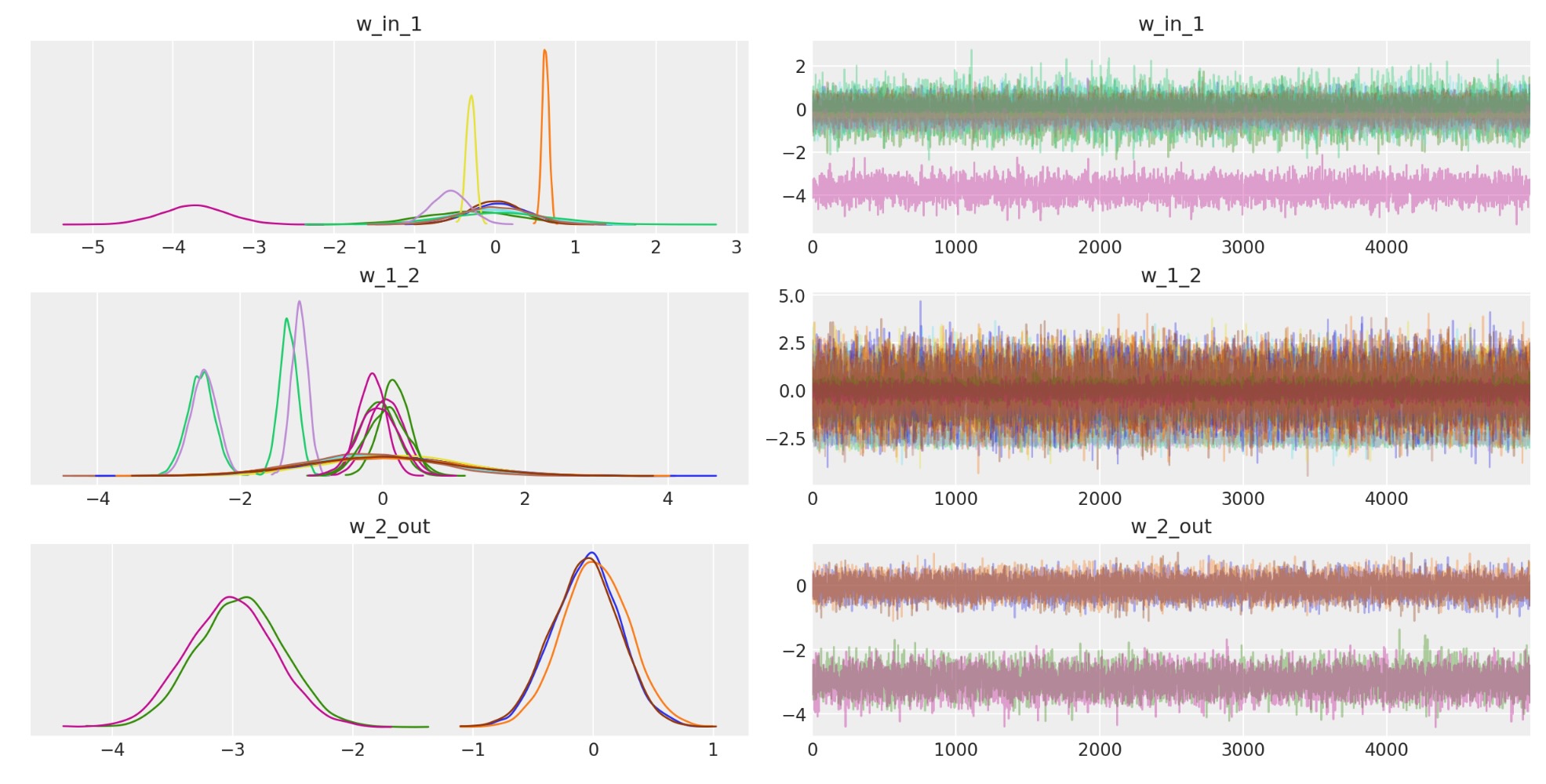

　あなたは、上記ネットワークが本当に深くないと主張するかもしれません。しかし、私たちは、もっと難解なデータセットを訓練するためにそれを畳み込むことを含んだ、より多くの層を持つよう簡単に拡張できます。