差分の差分法

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

イントロダクション

　このノートブックは因果推論に関する差分の差分法アプローチの簡易な概要です。pyMCを使って、ベイズネットワーク下でこの種の分析の進め方について動作例を示します。高い水準でこのアプローチの概要をこのノートブックが提供しますが、因果推論に関して二つの優れたテキストブックを調べることを推薦します。"The Effect" と　"Causal Inference: The Mixtape" は両方、差分の差分法に関する章を割いています。

　差分の差分法は因果推論に取り組む良いアプローチです。もし、

処置や介入の原因の影響(causal impact)を知りたいならば
事前と事後の処置を計測するならば
処置と対照グループの取り扱いの両方
処置をランダム割り当てない、これは、擬似的な実験（quasi-experimental）を設定する場合、

　それ以外では、あなたが使える適したより良いやり方のアプローチがあります。

　処置の原因の影響を予測するために必要としているのは、観測事実に逆らう思考(counterfactual thinking(注）)を伴うことを記します。これは、”もし処置が施されなかったら、処置したグループの処置後の結果はどうなったか？”を問いますが、私たちはこれを観測できないことが理由です。

例

　古典的な例では、CardとKrugerによる研究があります。この研究は、ファーストフードセクターの雇用における最低賃金の増加の影響を実験しました。これは擬似的な実験を設定します。なぜなら、介入はランダムに異なる地域ユニットに適用しないからです。介入は1992年4月のニュージャージーに適用します。もし、ニュージャージーだけの介入の事前と事後の雇用率を計測するならば、時間経過で変化する除外された変数(例えば季節効果)のために、制御を失敗します。これは、雇用率の変化に関する代替の因果の説明を与えます。しかし、抑制する州（ペンシルバニア）を選択することによって、これが、ペンシルバニアの雇用の変化がcounterfactual　ーニュージャージーで介入がなければ、何が起こっていたか？　ー　に一致することを予測できるようにします。

因果DAG

　差分の差分法のための因果DAGを以下に与えます。それは、

観測の処置の状態は、因果的にグループと時間に影響されます。処置とグループは異なることを注記します。グループは実験または抑制のどちらか一方、しかし、実験グループは、介入時以後に処置されただけで、従って、処置の状態は、グループと時間の両方に依存します。
計測の結果は時間、グループ、処置によって、因果的に影響されます。
追加の因果の影響は考慮しません。

　私たちは、第一に結果としての、どのように時間経過上でこれが変化したのか、処置の効果に興味があります。もし処置、時間、処置グループ(対照グループは含まない)の結果だけに焦点を当てるならば、結果の変化を時間上で処置グループに発生する任意の数の他の因子よりむしろ、処置のせいにすることができません。他の言い方をすれば、これは、処置が時間によって完全に決定されます。それで、処置や時間によって原因づけられるものとして計測しまする結果の事前と事後の変化の違いを明らかにする方法がありません。

　しかし、対照グループを追加することで、対照グループの時間の変化と処置グループの時間変化を比較することができます。差分の差分法アプローチの鍵となる仮定の一つは、並列トレンド仮定ですーそれは両方のグループが、時間経過において同様の変化することです。別の言い方をすると、もし、対照グループと処置グループが時間経過で同様に変化するならば、時間経過上でグループの差分の差分法が処置に基づくものだと公平に納得させることができます。

差分の差分法モデルを定義

　注記：私は、あなたが他のリソースで見つけるかもしれないモデルと比較して少し違ったモデルを定義します。これは、このノートブックの後の方でcounterfactual 推論をやりやすくして、そして、連続時間のトレンドの仮定を強調するためです。

　最初に、結果の予測値を計算するためのPython関数を定義します。

def outcome(t, control_intercept, treat_intercept_delta, trend, Δ, group, treated):
    return control_intercept + (treat_intercept_delta * group) + (t * trend) + (Δ * treated * group)

　しかし、この数学式を厳密にみてみます。i番目の観測の予期値は、μiは以下で定義されます。

　　　μ_i = β_c + (β_Δ　. group_i ) + (trend . t_i ) + ( Δ . treated_i . group_i )

ここで、以下のパラメータがあります。

βcは操作グループの切片です
βΔは操作グループの切片から途中で区切られたれた処置グループの屈折です。
Δは処置の因果の影響(causal impact)です
トレンドは傾きで、モデルのコアの仮定は、傾きが両グループで一致していることです。

そして以下の観測データ：

t_i は時間、介入の事前計測時間はt=0,介入の事後計測時間はt=1となるように、扱いやすく調整します。
group_iは抑制(g=0)と処置グループ(g=1)のためのダミー変数です。
treated_iは、処置ずみ、未処置のバイナリ変数です。そしてこれは、時間とグループの関数です。 treated = f(t_i, grouo_i)

　私たちは、この潜在的な点を規定することができます。処置は、上のDAGを見ること、この関数を定義するためのPython関数を書くことで、時間とグループによる因果上の影響を受けます。

def is_treated(t, intervention_time, group):
    return (t > intervention_time) * group

差分の差分法モデルの可視化

　頻繁に、百聞は一見にしかずというように、もし、上の解説が混乱するならば、以下の図から何らかのより視覚的な直感を得た後で、再度読むことを勧めます。

# true parameters
control_intercept = 1
treat_intercept_delta = 0.25
trend = 1
Δ = 0.5
intervention_time = 0.5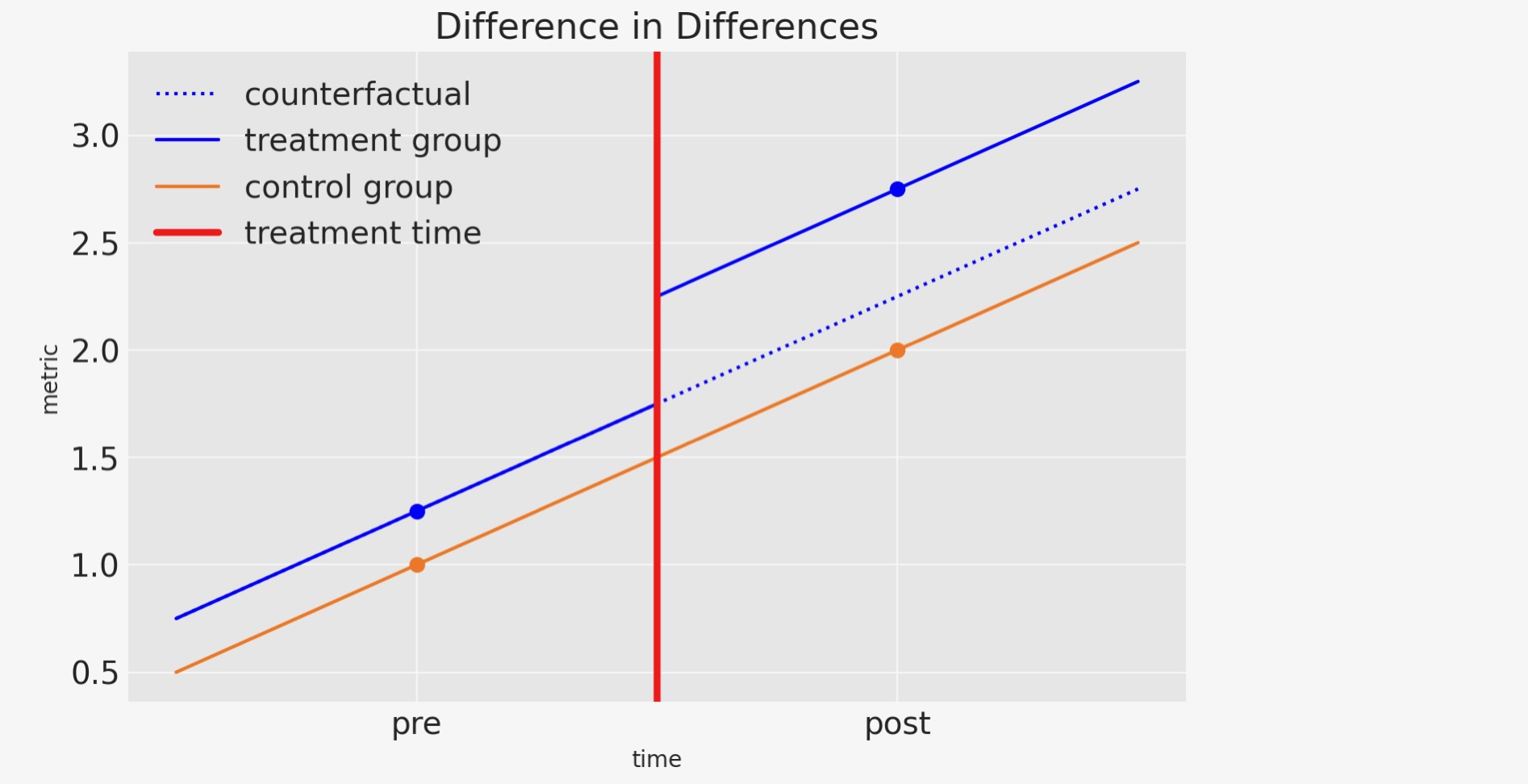

コードを表示

fig, ax = plt.subplots()
ti = np.linspace(-0.5, 1.5, 1000)
ax.plot(
    ti,
    outcome(
        ti,
        control_intercept,
        treat_intercept_delta,
        trend,
        Δ=0,
        group=1,
        treated=is_treated(ti, intervention_time, group=1),
    ),
    color="blue",
    label="counterfactual",
    ls=":",
)
ax.plot(
    ti,
    outcome(
        ti,
        control_intercept,
        treat_intercept_delta,
        trend,
        Δ,
        group=1,
        treated=is_treated(ti, intervention_time, group=1),
    ),
    color="blue",
    label="treatment group",
)
ax.plot(
    ti,
    outcome(
        ti,
        control_intercept,
        treat_intercept_delta,
        trend,
        Δ,
        group=0,
        treated=is_treated(ti, intervention_time, group=0),
    ),
    color="C1",
    label="control group",
)
ax.axvline(x=intervention_time, ls="-", color="r", label="treatment time", lw=3)
t = np.array([0, 1])
ax.plot(
    t,
    outcome(
        t,
        control_intercept,
        treat_intercept_delta,
        trend,
        Δ,
        group=1,
        treated=is_treated(t, intervention_time, group=1),
    ),
    "o",
    color="blue",
)
ax.plot(
    t,
    outcome(
        t,
        control_intercept,
        treat_intercept_delta,
        trend,
        Δ=0,
        group=0,
        treated=is_treated(t, intervention_time, group=0),
    ),
    "o",
    color="C1",
)
ax.set(
    xlabel="time",
    ylabel="metric",
    xticks=t,
    xticklabels=["pre", "post"],
    title="Difference in Differences",
)
ax.legend();

この図を見ることにより差分の差分法の直感をまとめることができます。

処置と対照グループは同様のやり方で時間軸上、発展していくことを仮定します。
処置の事前と事後から対照グループの傾きを簡単に見積もることができます。
私たちは、counterfactual思考に従事することができます。そして、”もし、処置しなかったならば、処置グループの事後処置の結果はどうなっていたか？”を問うことができます。

　もし、私たちが、この質問とこのCounterfactual量の推定に応えることができるなら、私たちは"処置の因果の効果(causal impact)はどれくらいか？"と問うことができます。そして、観測事後処置とCounterfactual量に逆らった処置グループの結果を比較することで、この質問に応えることができます。

　私たちは、これを視覚と他の方法の状態について考えることができます。対照グループの事前と事後の相違を見ることによって、抑制と処置グループの事前と事後の相違の任意の相違を、処置の因果の結果のせいにすることができます。そして、それが、差分の差分法と呼ばれる方法です。

合成データセットの生成

df = pd.DataFrame(
    {
        "group": [0, 0, 1, 1] * 10,
        "t": [0.0, 1.0, 0.0, 1.0] * 10,
        "unit": np.concatenate([[i] * 2 for i in range(20)]),
    }
)

df["treated"] = is_treated(df["t"], intervention_time, df["group"])

df["y"] = outcome(
    df["t"],
    control_intercept,
    treat_intercept_delta,
    trend,
    Δ,
    df["group"],
    df["treated"],
)
df["y"] += rng.normal(0, 0.1, df.shape[0])
df.head()

	group	t	unit	treated	y
0	0	0.0	0	0	0.977736
1	0	1.0	0	0	2.132566
2	1	0.0	1	0	1.192903
3	1	1.0	1	1	2.816825
4	0	0.0	2	0	1.114538

　時間単位で二つの点のパネルデータを見ます。事前(t=0)と(t=1)介入計測時間

sns.lineplot(df, x="t", y="y", hue="group", units="unit", estimator=None)
sns.scatterplot(df, x="t", y="y", hue="group");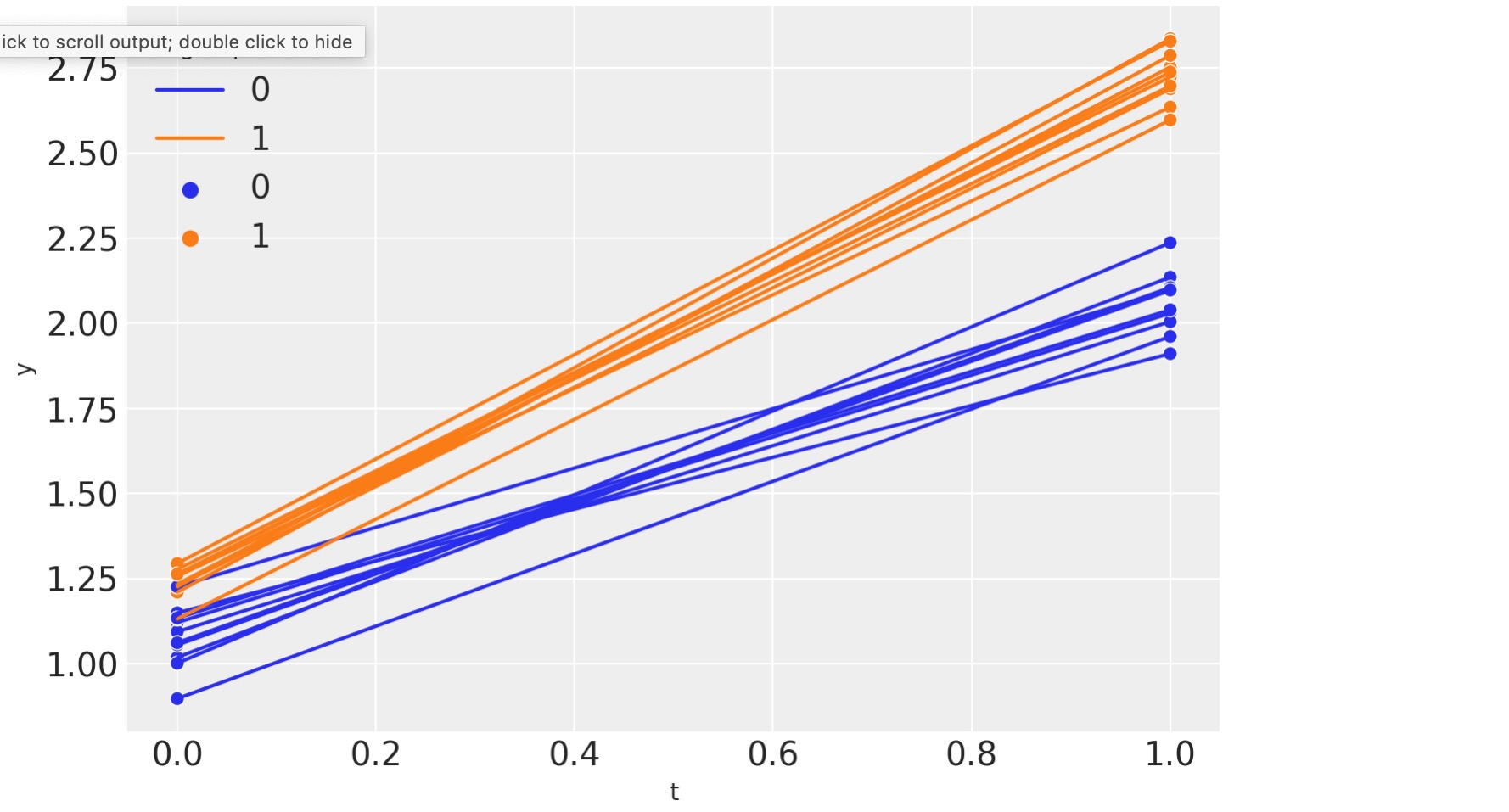

　もし必要ならば、このように差分の差分法の予測点を計算することができます。

diff_control = (
    df.loc[(df["t"] == 1) & (df["group"] == 0)]["y"].mean()
    - df.loc[(df["t"] == 0) & (df["group"] == 0)]["y"].mean()
)
print(f"Pre/post difference in control group = {diff_control:.2f}")

diff_treat = (
    df.loc[(df["t"] == 1) & (df["group"] == 1)]["y"].mean()
    - df.loc[(df["t"] == 0) & (df["group"] == 1)]["y"].mean()
)

print(f"Pre/post difference in treatment group = {diff_treat:.2f}")

diff_in_diff = diff_treat - diff_control
print(f"Difference in differences = {diff_in_diff:.2f}")

Pre/post difference in control group = 0.99
Pre/post difference in treatment group = 1.49
Difference in differences = 0.50

　しかし、私たちはベイジアンなので、ベイズをやりましょう。

ベイジアン差分の差分法

PyMCモデル

　既によくPyMCに精通していれば、このモデルがかなり簡単であるとわかるでしょう。私たちは少数の成分を持ちます。

データノードを定義します。これは付加的なものですが、事後予測チェックとcounterfactual予測で実行した時に後で有用です。
事前定義
上で既に定義したoutcome結果関数を使ってモデルの予測を評価します。
正規尤度分布を定義

with pm.Model() as model:
    # data
    t = pm.MutableData("t", df["t"].values, dims="obs_idx")
    treated = pm.MutableData("treated", df["treated"].values, dims="obs_idx")
    group = pm.MutableData("group", df["group"].values, dims="obs_idx")
    # priors
    _control_intercept = pm.Normal("control_intercept", 0, 5)
    _treat_intercept_delta = pm.Normal("treat_intercept_delta", 0, 1)
    _trend = pm.Normal("trend", 0, 5)
    _Δ = pm.Normal("Δ", 0, 1)
    sigma = pm.HalfNormal("sigma", 1)
    # expectation
    mu = pm.Deterministic(
        "mu",
        outcome(t, _control_intercept, _treat_intercept_delta, _trend, _Δ, group, treated),
        dims="obs_idx",
    )
    # likelihood
    pm.Normal("obs", mu, sigma, observed=df["y"].values, dims="obs_idx")

pm.model_to_graphviz(model)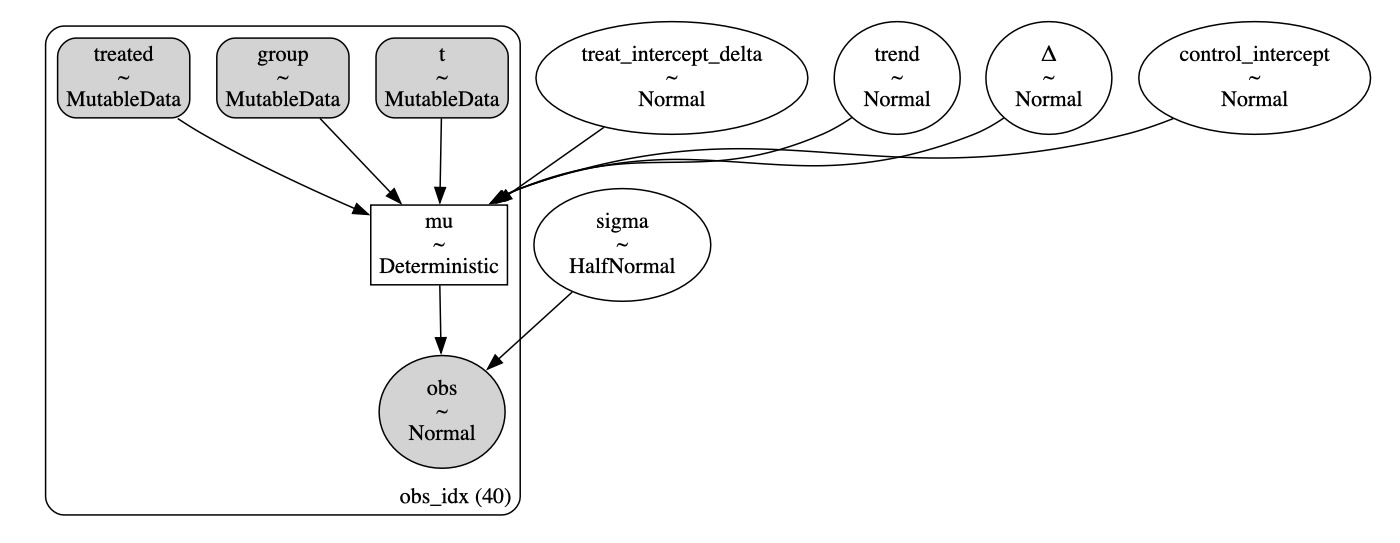

推論

with model:
    idata = pm.sample()

az.plot_trace(idata, var_names="~mu");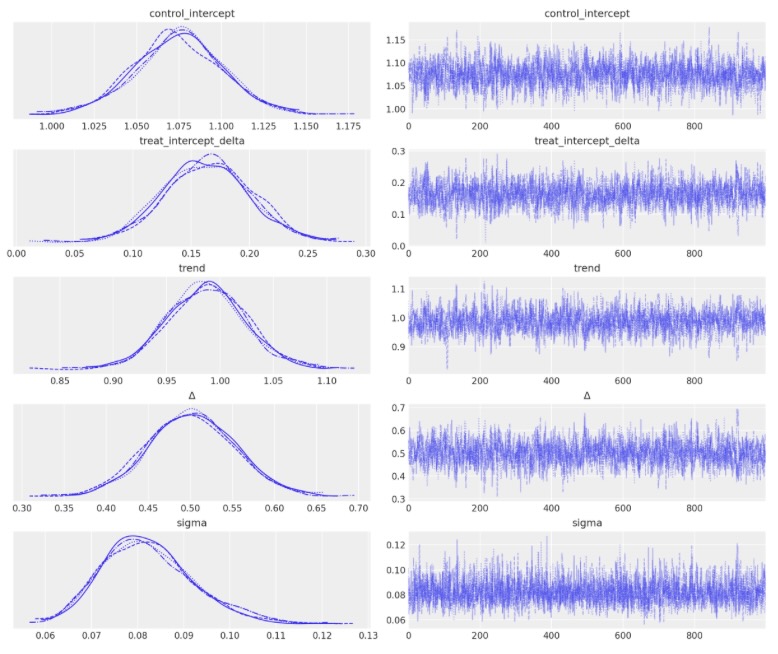

事後予測

注記：技術的に、μのために'前進する予測'を行います。これは、その入力の決定関数なので、もし、予測した観測値を生成するならば、事後予測は、より適当なレベルになります。それらは、私たちがデータを特徴づけた正規尤度を基礎にした確率になります。それにもかかわらず、このセクションは私たちがベイジアンワークフローに従う事実を強調するために事後予測と呼ばれます。

# pushforward predictions for control group
with model:
    group_control = [0] * len(ti)  # must be integers
    treated = [0] * len(ti)  # must be integers
    pm.set_data({"t": ti, "group": group_control, "treated": treated})
    ppc_control = pm.sample_posterior_predictive(idata, var_names=["mu"])

# pushforward predictions for treatment group
with model:
    group = [1] * len(ti)  # must be integers
    pm.set_data(
        {
            "t": ti,
            "group": group,
            "treated": is_treated(ti, intervention_time, group),
        }
    )
    ppc_treatment = pm.sample_posterior_predictive(idata, var_names=["mu"])

# counterfactual: what do we predict of the treatment group (after the intervention) if
# they had _not_ been treated?
t_counterfactual = np.linspace(intervention_time, 1.5, 100)
with model:
    group = [1] * len(t_counterfactual)  # must be integers
    pm.set_data(
        {
            "t": t_counterfactual,
            "group": group,
            "treated": [0] * len(t_counterfactual),  # THIS IS OUR COUNTERFACTUAL
        }
    )
    ppc_counterfactual = pm.sample_posterior_predictive(idata, var_names=["mu"])

包み込む

コードを表示

ax = sns.scatterplot(df, x="t", y="y", hue="group")

az.plot_hdi(
    ti,
    ppc_control.posterior_predictive["mu"],
    smooth=False,
    ax=ax,
    color="blue",
    fill_kwargs={"label": "control HDI"},
)
az.plot_hdi(
    ti,
    ppc_treatment.posterior_predictive["mu"],
    smooth=False,
    ax=ax,
    color="C1",
    fill_kwargs={"label": "treatment HDI"},
)
az.plot_hdi(
    t_counterfactual,
    ppc_counterfactual.posterior_predictive["mu"],
    smooth=False,
    ax=ax,
    color="C2",
    fill_kwargs={"label": "counterfactual"},
)
ax.axvline(x=intervention_time, ls="-", color="r", label="treatment time", lw=3)
ax.set(
    xlabel="time",
    ylabel="metric",
    xticks=[0, 1],
    xticklabels=["pre", "post"],
    title="Difference in Differences",
)
ax.legend();

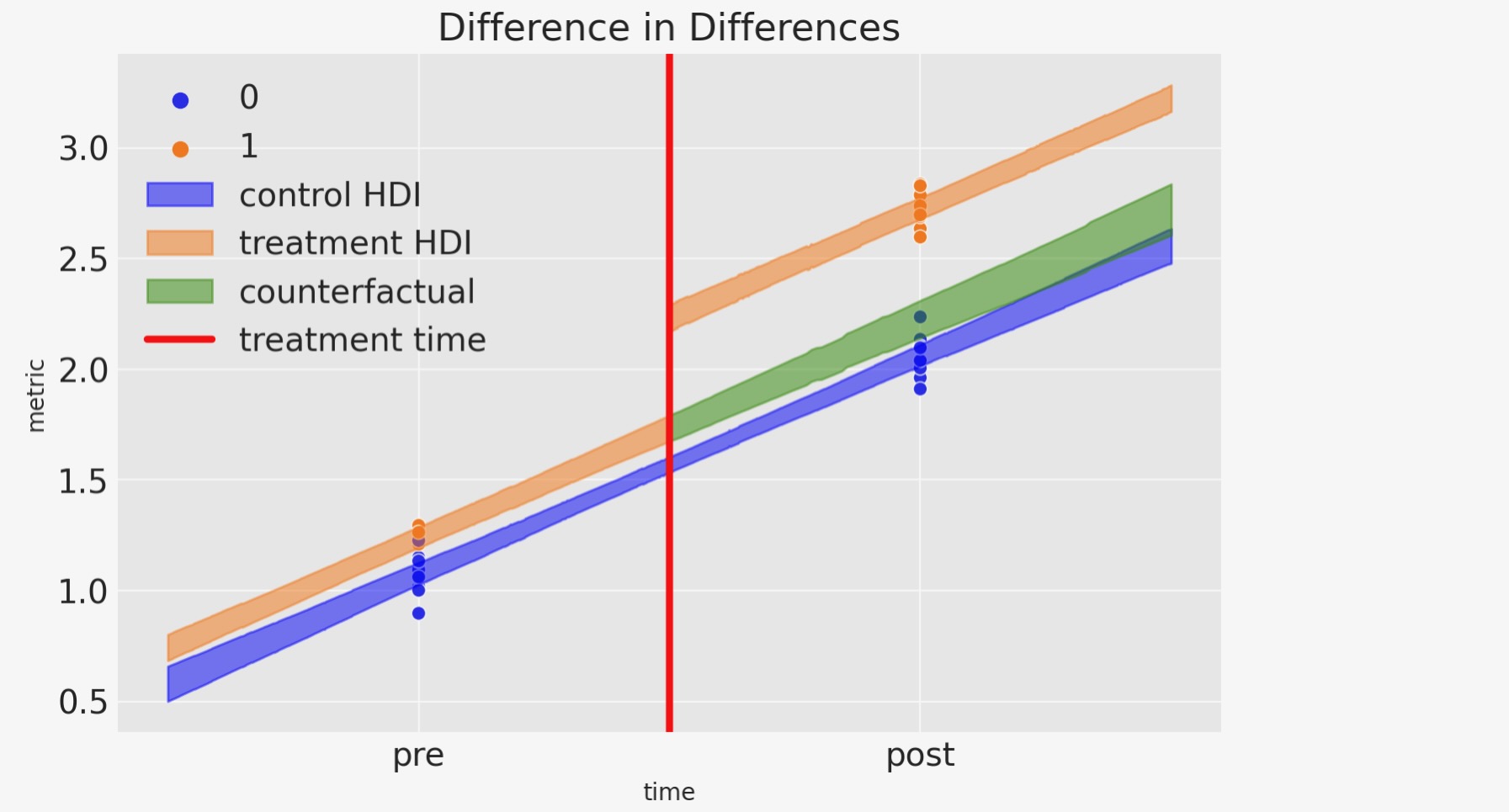
これは、とても良い図です。しかし、ここで進めていく極めて少数のことがあります。それでは続けましょう。

青い共有領域は、対照グループの予測領域のための信頼区間を提供します。
オレンジの共有領域は処置グループのために同様の領域を提供します。私たちは、いかにして、介入の後で結果が急速にジャンプするか見ることができます。
緑の共有領域はかなり真新しい、良いものです。”処置グループが処置されなかったら、何を予期するか”のCounerfactual予測を提供します。定義より、介入時の後は処置しない処置グループの項目の任意の観測値を作りません。それにもかかわらず、ノートブックの先頭、ベイジアン予測法の概要で記述したモデルでは、私たちは、"what if"疑問に、動機づけることができます。
このCounterfactual予測と観測値(処置条件の事後処置)の相違は、私たちが予測した因果上の効果を提供します。事後分布についてもっと詳しく見ていきましょう。

ax = az.plot_posterior(idata.posterior["Δ"], ref_val=Δ, figsize=(10, 3))
ax.set(title=r"Posterior distribution of causal impact of treatment, $\Delta$");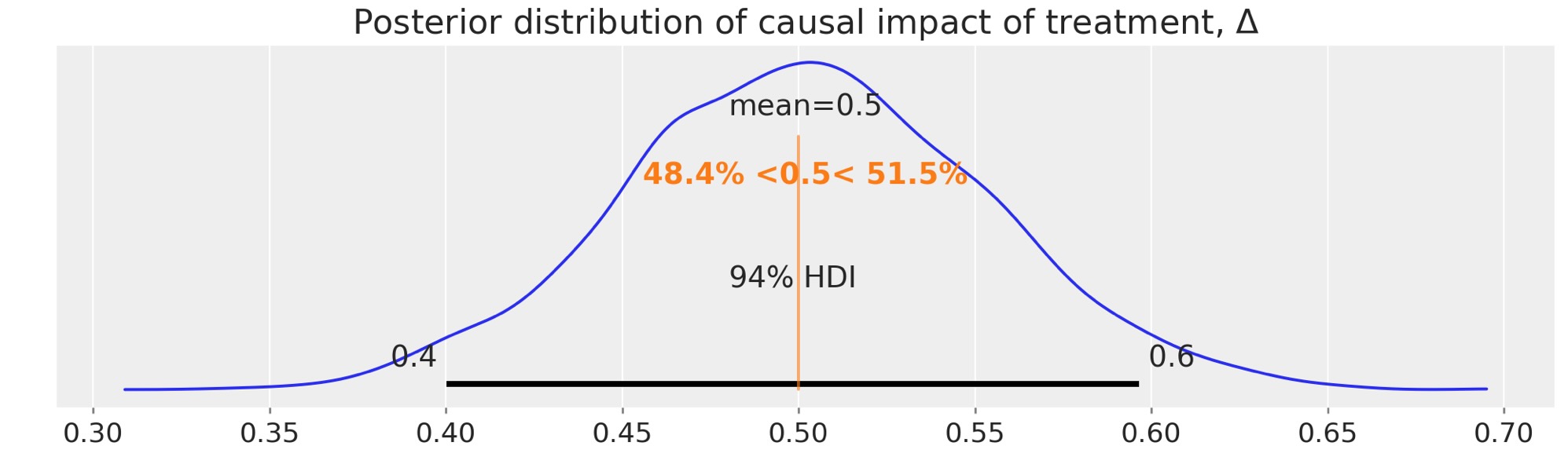

　結果を得ました。差分の差分法アプローチを用いた予測した因果の効果を超えて完全な事後分布を得ました。

結果

　もちろん、差分の差分法アプローチを使った実際の応用へアプローチするとき、もっと多くの調査が必要とされます。読者は、上のイントロダクションでリストしたテキストブックと重要な文脈の議題を詳細に覆う有用なレビュー論文を調べることを強く推奨されます。追加で、Bertrand et al[2004]は、それらが強調する任意の問題への提案した解決法と同様の懐疑的な視点のアプローチをとっています。

参考資料

Nick Huntington-Klein. The effect: An introduction to research design and causality. Chapman and Hall/CRC, 2021.
Scott Cunningham. Causal inference: The Mixtape. Yale University Press, 2021.
David Card and Alan B Krueger. Minimum wages and employment: a case study of the fast food industry in new jersey and pennsylvania. 1993.
Coady Wing, Kosali Simon, and Ricardo A Bello-Gomez. Designing difference in difference studies: best practices for public health policy research. Annu Rev Public Health, 39(1):453–469, 2018.
Marianne Bertrand, Esther Duflo, and Sendhil Mullainathan. How much should we trust differences-in-differences estimates? The Quarterly journal of economics, 119(1):249–275, 2004.

製作者

著者：Benjamin T. Vincent 2022年 9月

更新：Benjamin T. Vincent 2023年 2月　PyMC v5