ディリクレ過程
ディリクレ過程は分布の空間を覆う柔軟な確率分布です。もっとも一般的には、空間Ω の確率分布P、は一つの測度であり、全体の空間(P(Ω)=1)の一つの測度で割り当てられます。ディリクレ過程 P〜DP(α, P0)は、Ωのすべての有限の分離した境界、S1,…,Snの性質を持つ測度です。
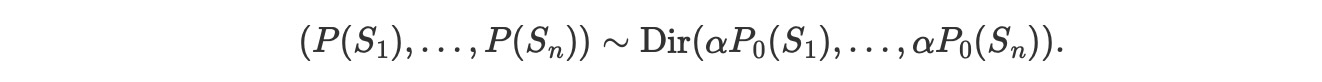
ここで、P0は、Ω空間の基礎確率測度です。正確さのパラメータα >0は、ディリクレ過程からのサンプルがどのくらい基礎測度 P0に近いかを操作します。α ->♾️なので、ディリクレ過程からのサンプルは、基礎測度 P0にアプローチします。
ディリクレ過程は、MCMCシミュレーションするのに全く適したいくつかの性質を持っています。
- ディリクレ過程からiid観測値, w1,w2,…,wnで与えられる事後分布は、またディリクレ過程P〜DP(α,P0)になります。
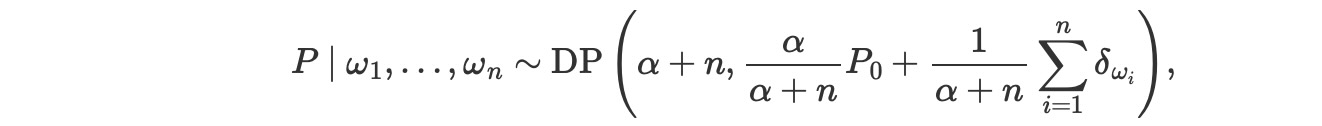
ここで、δは、ディラックのデルタ尺度です。
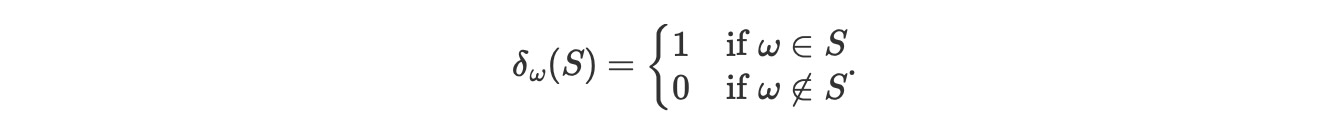
2. 新しい観測値による事後予測分布は、基礎尺度と観測値の間の中間物です。
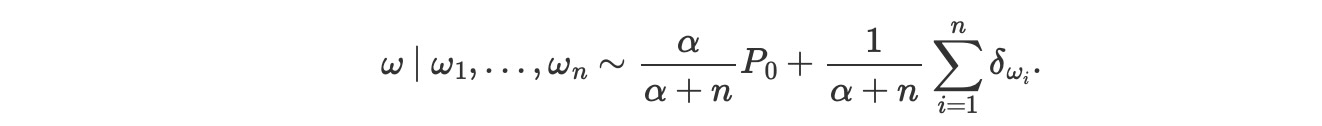
私たちは、事前分布の正確さαが、事前のサンプルサイズとして、本質的に解釈できることがわかります。この事後予測分布はまた、それ自身をギッブスサンプリングします。
3. ディリクレ過程からのサンプルP〜DP(α,P0)は、確率1から分離したものです。それは、Ωの要素w1,w2…,wnと、重みμ1,…μn Σμi = 1があります。
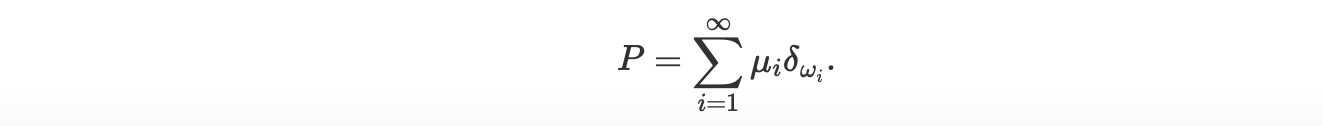
4. "stick-breaking過程"は、単純にサンプルされる上の重さμiとサンプルwiに明白な構造を与えます。仮に、β1,β2,…,Beta(1, α)ならば、μi = βi Πj=1 i-1(1 - βj). この表現とstick breakingの間の関係は、以下のように説明されます。
- 長さ1のstickから開始します。
- stickを二つに分離します。最初の量は、μ1=β1 そして、2番目の量は、1ーμ1
- 2番目の部分をさらに二つに分離します。最初の量は、β2,そして2番目の量は1 - β2, stickの最初の部分の長さは、β2(1 - β1); 2番目の部分の長さは、 (1 - β 1)(1 - β2).
- この方法で以前の分離から2番目の部分の分離を永遠に続けます。仮に、w1,w2,…〜P0 ,ならば
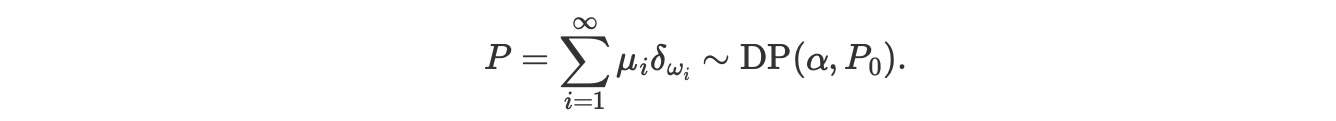
[さらに進んだ見解へは]http://mlg.eng.cam.ac.uk/tutorials/07/ywt.pdf) そして、ディリクレ過程その他の趣への簡易イントロダクションとその応用を参照してください。
私たちは、Pythonでディリクレ過程から簡易にサンプルするために、上のstick-breaking過程を使うことができます。この例では、α=2、 基本分布はN(0,1)です。
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import scipy as sp
import seaborn as sns
import xarray as xr%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")N = 20
K = 30
alpha = 2.0
P0 = sp.stats.norm私たちはstick-breaking 過程からサンプルを出力し、図示します。
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
x_plot = xr.DataArray(np.linspace(-3, 3, 200), dims=["plot"])
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
ax.set_title(rf"$\alpha = {alpha}$")
ax.legend(loc=2);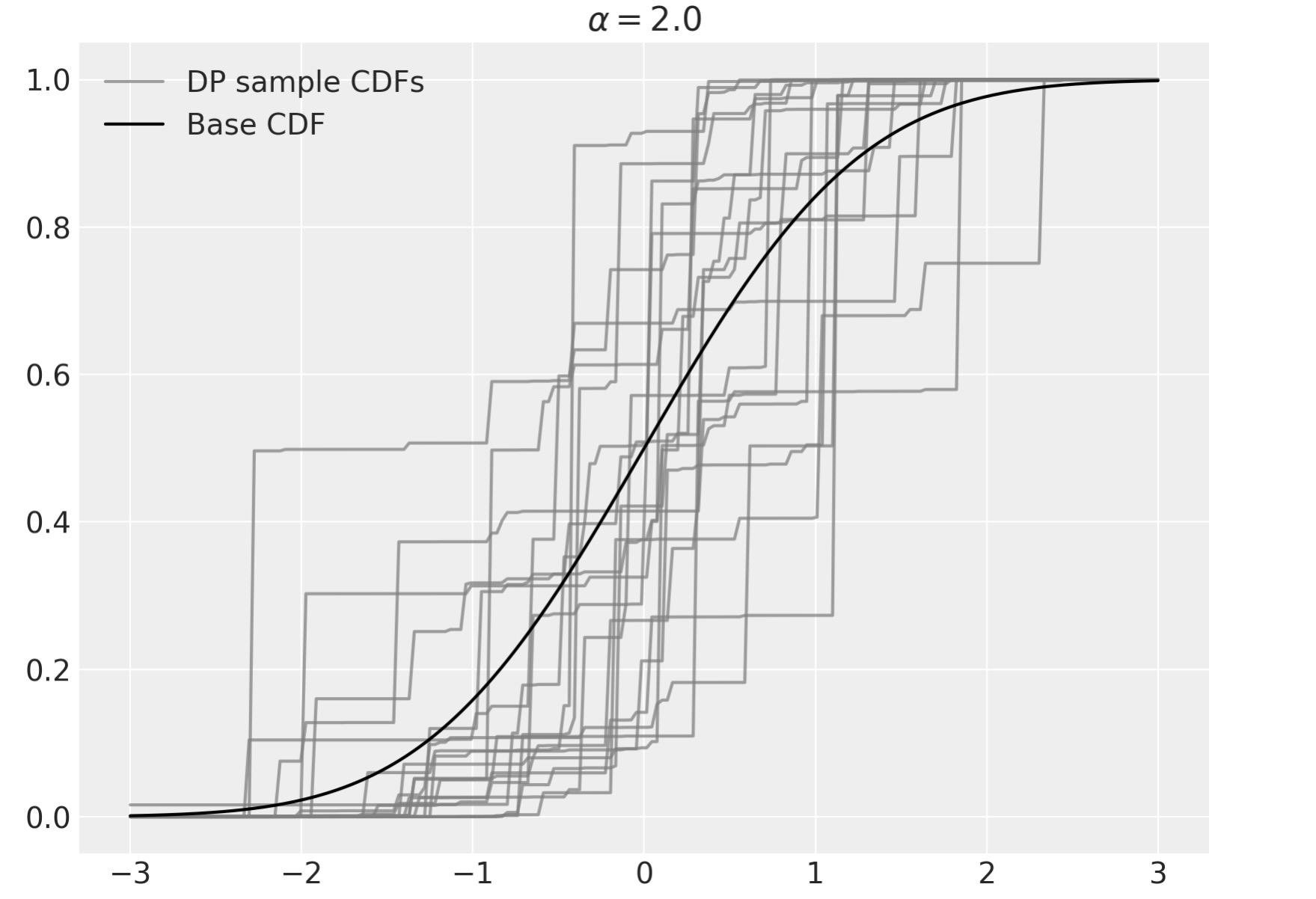
上の状態で、α-> ♾️、ディリクレ過程からのサンプルは、基本分布に収束します。
fig, (l_ax, r_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(16, 6))
K = 50
alpha = 10.0
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)
l_ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
l_ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
l_ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
l_ax.set_title(rf"$\alpha = {alpha}$")
l_ax.legend(loc=2)
K = 200
alpha = 50.0
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)
r_ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
r_ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
r_ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
r_ax.set_title(rf"$\alpha = {alpha}$")
r_ax.legend(loc=2);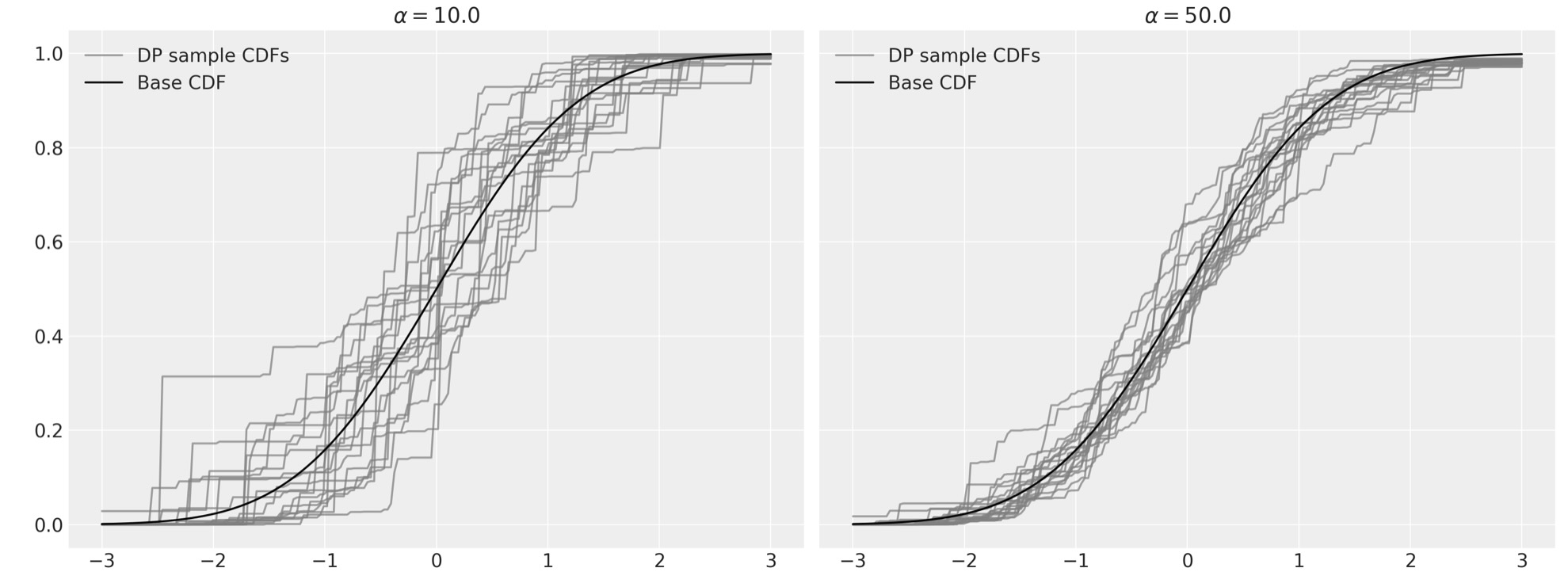
ディリクレ過程混合
密度推定のタスクのために、ディリクレ過程からのサンプルの分離は、相当不利になります。この問題は密度推定のためにディリクレ過程混合を使うことによって、間接的な他のレベルで解決できます。ディリクレ過程混合は、パラメトリックファミリーF={fθ|θ…}から、成分密度を使います。そして、混合重みをディリクレ過程として表します。もし、P0がパラメータ空間θの確率測度ならば、ディリクレ過程混合は、階層モデルになります。
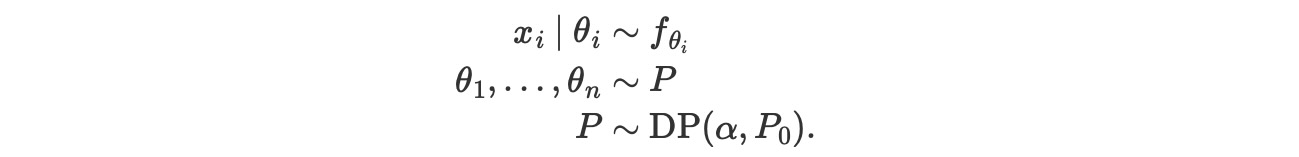
このモデルを説明するために、私たちは、α=2のディリクレ過程混合から出力をシミュレートします。
θ〜N(0,1), x|θ〜N(θ,(0.3)2)
N = 5
K = 30
alpha = 2
P0 = sp.stats.norm
f = lambda x, theta: sp.stats.norm.pdf(x, theta, 0.3)
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
theta = P0.rvs(size=(N, K))
dpm_pdf_components = f(x_plot, theta[..., np.newaxis])
dpm_pdfs = (w[..., np.newaxis] * dpm_pdf_components).sum(axis=1)
fig, ax = plt.subplots(figsize=(8, 6)) ax.plot(x_plot, dpm_pdfs.T, c="gray") ax.set_yticklabels([]);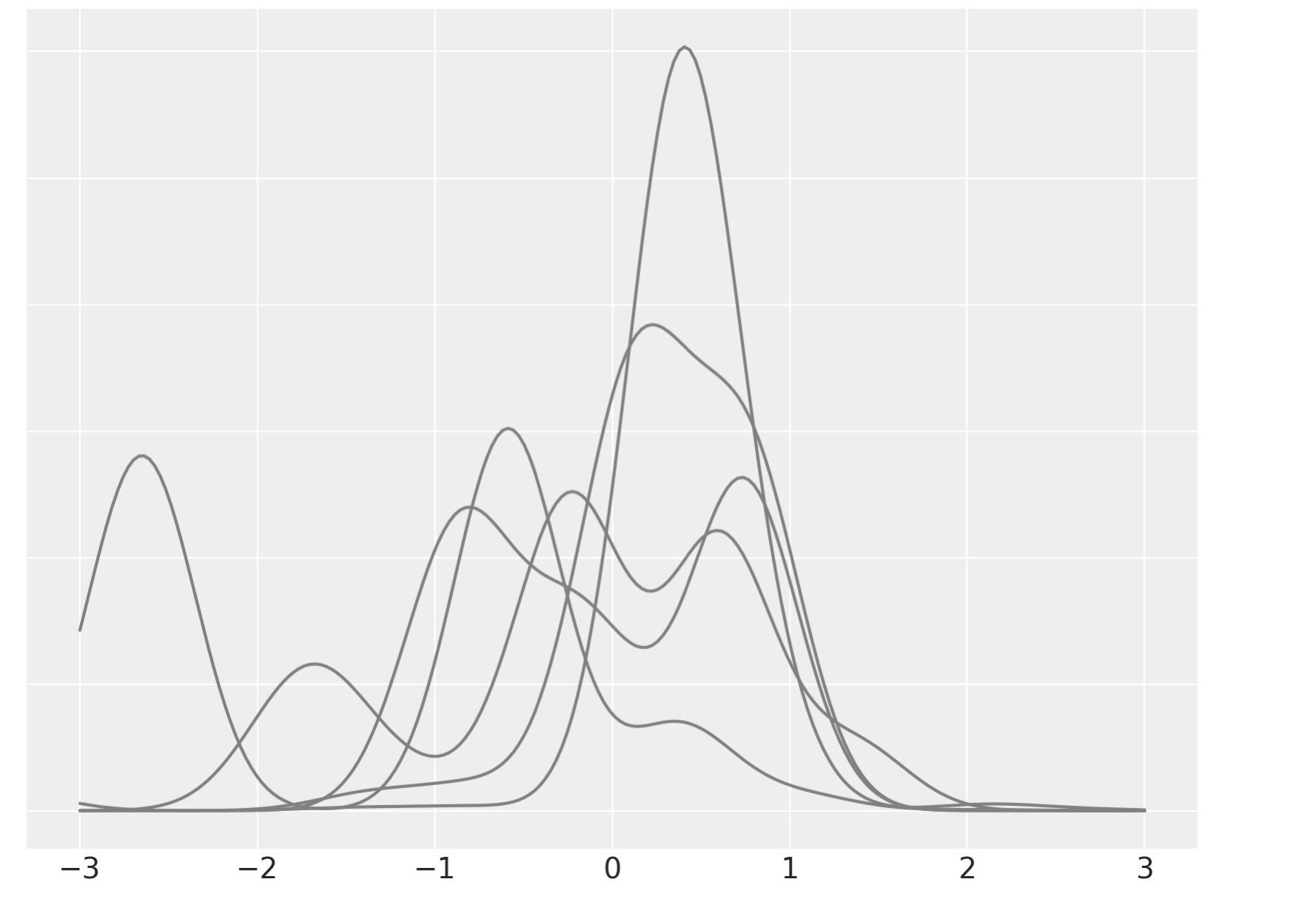
私たちはここで、単独の混合に焦点を当てます。そして、それを個別の混合成分に分離します。
fig, ax = plt.subplots(figsize=(8, 6))
ix = 1
ax.plot(x_plot, dpm_pdfs[ix], c="k", label="Density")
ax.plot(
x_plot,
(w[..., np.newaxis] * dpm_pdf_components)[ix, 0],
"--",
c="k",
label="Mixture components (weighted)",
)
ax.plot(x_plot, (w[..., np.newaxis] * dpm_pdf_components)[ix].T, "--", c="k")
ax.set_yticklabels([])
ax.legend(loc=1);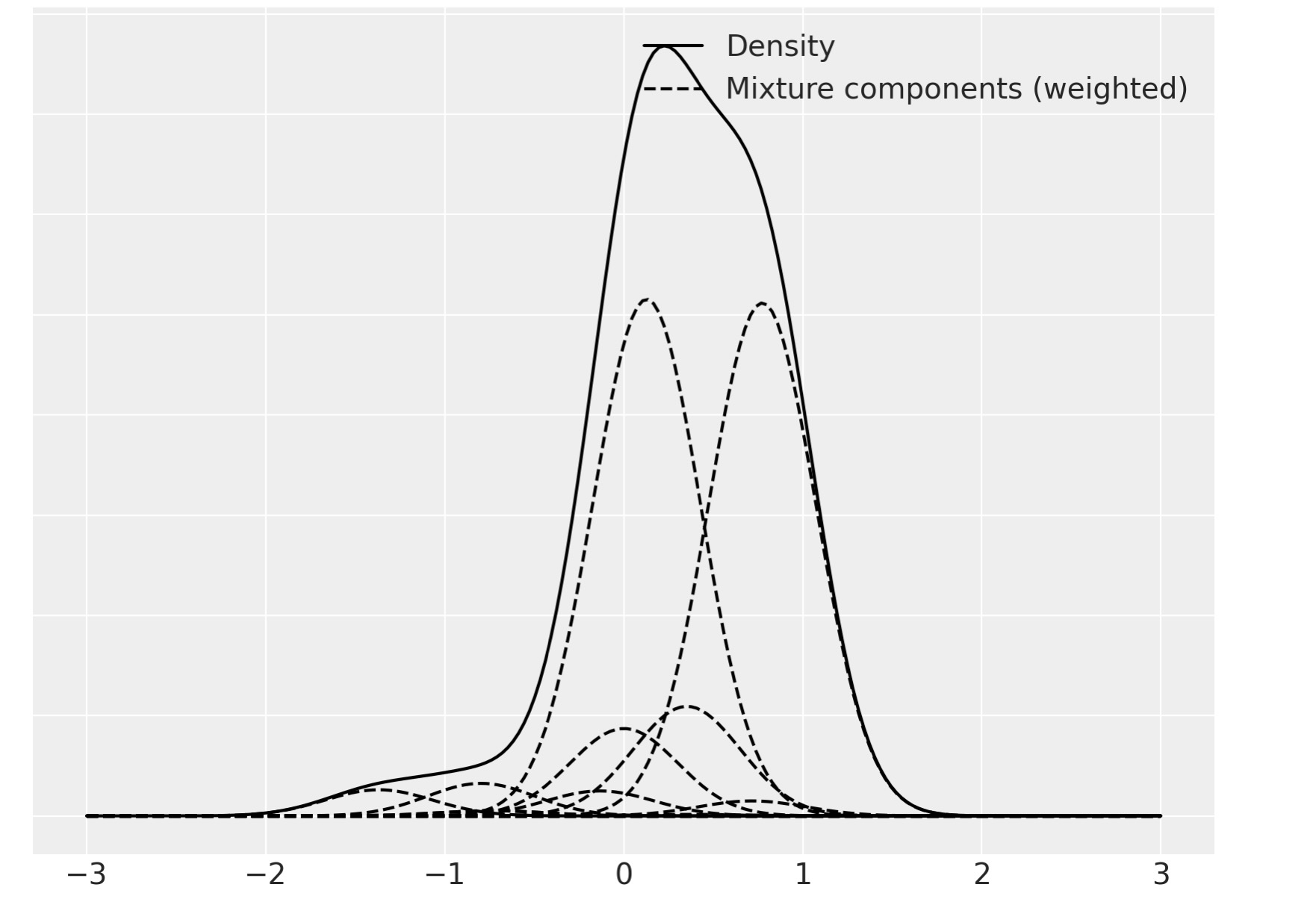
これらの確率過程からのサンプリングは楽しみです。しかし、これらの考えは、私たちがデータにそれを適合するときに、本当に役立つことになります。サンプルの分離とディリクレ過程のstick-breaking表現は、それら自身を事後分布のマルコフチェイン・モンテカルロのシミュレーションに与えます。私たちはこれをPyMCを使ってこのサンプリングを実行します。
私たちの最初の例は、イエローストーン国立公園のOld Faithful間欠泉の噴水の間隔、待機時間の密度を推定するのにディリクレ過程を使います。
try:
old_faithful_df = pd.read_csv(os.path.join("..", "data", "old_faithful.csv"))
except FileNotFoundError:
old_faithful_df = pd.read_csv(pm.get_data("old_faithful.csv"))事前分布の規定で便利なように、私たちは、噴水の間の待機時間を標準化します。
old_faithful_df["std_waiting"] = (
old_faithful_df.waiting - old_faithful_df.waiting.mean()
) / old_faithful_df.waiting.std()old_faithful_df.head()| eruptions | waiting | std_waiting | |
|---|---|---|---|
| 0 | 3.600 | 79 | 0.596025 |
| 1 | 1.800 | 54 | -1.242890 |
| 2 | 3.333 | 74 | 0.228242 |
| 3 | 2.283 | 62 | -0.654437 |
| 4 | 4.533 | 85 | 1.037364 |
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting, bins=n_bins, color="C0", lw=0, alpha=0.5)
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_ylabel("Number of eruptions");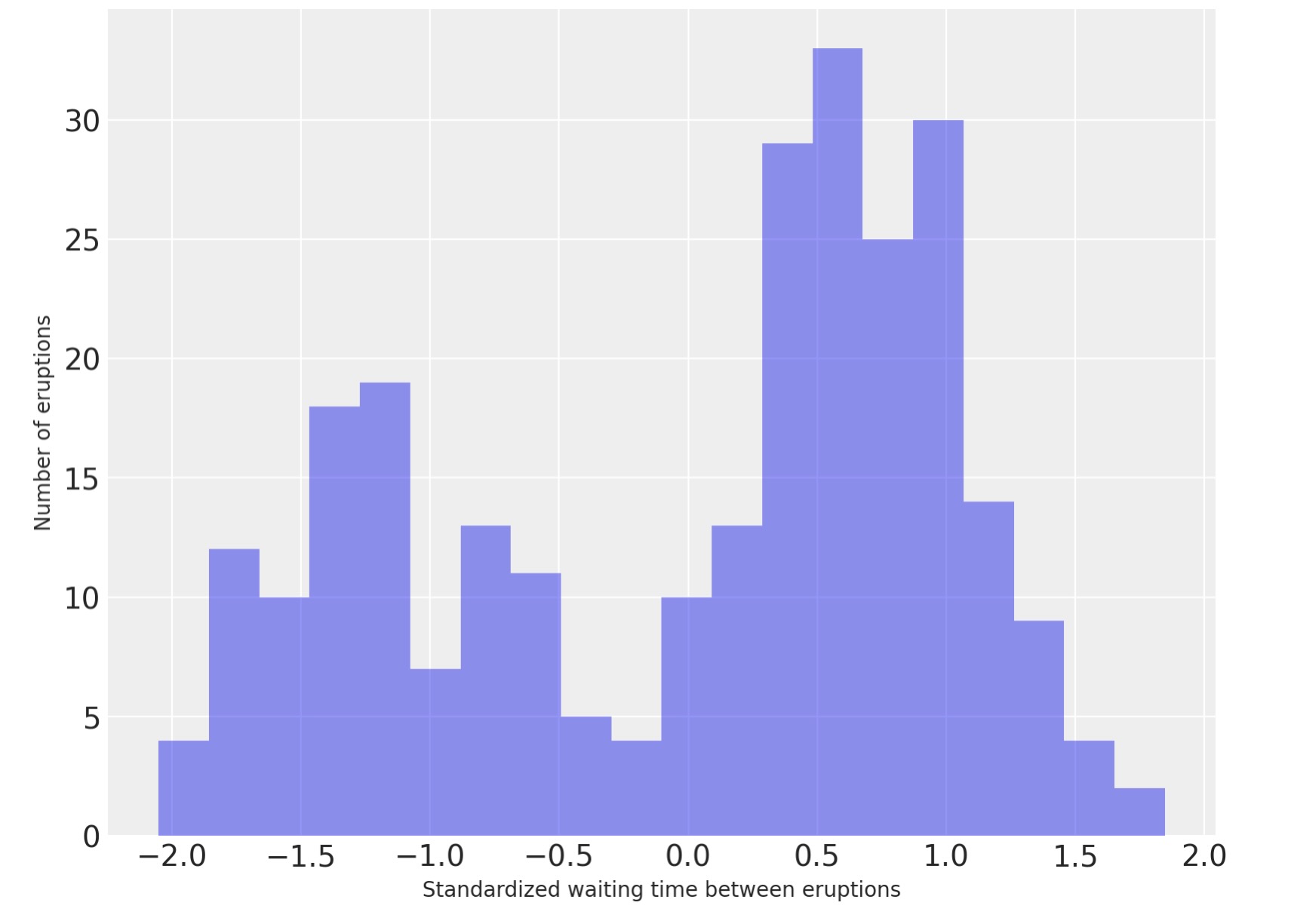
洞察の鋭い読者は私たちは、その定義によって示されているように、stick-breaking過程を永遠に続けていくのではなく、しかしむしろ、有限の数の分離後、この過程を切り詰めることに気づくでしょう。明白に、ディリクレ過程を計算するとき、メモリ内での重さとそのポイントの量を有限の数だけをストアする必要があります。この制限は、ひどく骨が折れるものではありません。観測数は有限なので、わずかでない塊で混合に提供する混合成分の数は、サンプル数よりもゆっくりと成長します。この直感は、無視できない塊を混合に提供する成分の数が、αlogNに達することを示すために形式化できます。ここでNはサンプルサイズです。
ディリクレ過程のために色々なcleverなギッブスサンプリングがあります。それは、成分は必要なだけ成長してストアされます。確率的な記憶は、有限な多くの成分をメモリにストアするだけの間、ディリクレ過程をシミュレーションするための別のパワフルな技術です。この紹介例では、私たちは、成分を固定数 K の後でストアされるディリクレ過程成分を簡単に切り詰める かなり洗練さの低いアプローチを取ります。そして、きりつめのための適合を供給します。K>5α+2は、混合の重み(Σi=1 K wi > 0.99)のほとんど全てを取り込むために、もっともありそうな充分さを表しています。実際は、私たちは、わずかでない塊で混合に提供する成分の数をチェックすることによって、ディリクレ過程への切り詰めた近似の妥当さを検証できます。仮に、私たちのシミュレーションで、すべての成分がわずかでない塊を混合に提供するならば、私たちは、ディリクレ過程をとても早く切り詰めます。
私たちの(切り詰めた)標準化された待機時間のディリクレ過程混合モデルは、
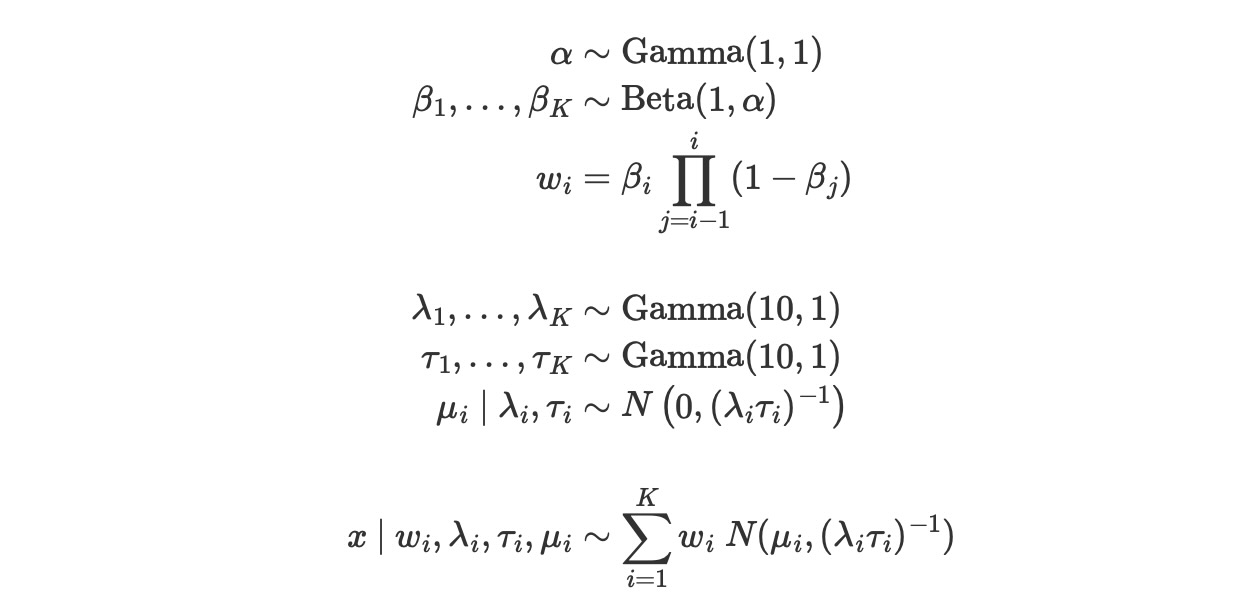
αを固定する代わりに、私たちの以前のシミュレーションにあるように、私たちは、αの事前分布を規定し、その後、観測値からその事後分布を学習して良いことに注意してください。
私たちはここで、このモデルをPyMCを使って構築します。
N = old_faithful_df.shape[0]
K = 30def stick_breaking(beta):
portion_remaining = pt.concatenate([[1], pt.extra_ops.cumprod(1 - beta)[:-1]])
return beta * portion_remainingwith pm.Model(coords={"component": np.arange(K), "obs_id": np.arange(N)}) as model:
alpha = pm.Gamma("alpha", 1.0, 1.0)
beta = pm.Beta("beta", 1.0, alpha, dims="component")
w = pm.Deterministic("w", stick_breaking(beta), dims="component")
tau = pm.Gamma("tau", 1.0, 1.0, dims="component")
lambda_ = pm.Gamma("lambda_", 10.0, 1.0, dims="component")
mu = pm.Normal("mu", 0, tau=lambda_ * tau, dims="component")
obs = pm.NormalMixture(
"obs", w, mu, tau=lambda_ * tau, observed=old_faithful_df.std_waiting.values, dims="obs_id"
)私たちは、ADVIで初期化したNUTSを使って、モデルから1000回サンプルします。
with model:
trace = pm.sample(
tune=2500,
init="advi",
target_accept=0.975,
random_seed=RANDOM_SEED,
)
αの事後分布は0.25と1の間で高く集中しています。
az.plot_trace(trace, var_names=["alpha"]);
切り詰めが、私たちの結果に隔たっていないことを検証するために、各成分の事後予測混合重みを図示します。
fig, ax = plt.subplots(figsize=(8, 6))
plot_w = np.arange(K) + 1
ax.bar(plot_w - 0.5, trace.posterior["w"].mean(("chain", "draw")), width=1.0, lw=0)
ax.set_xlim(0.5, K)
ax.set_xlabel("Component")
ax.set_ylabel("Posterior expected mixture weight");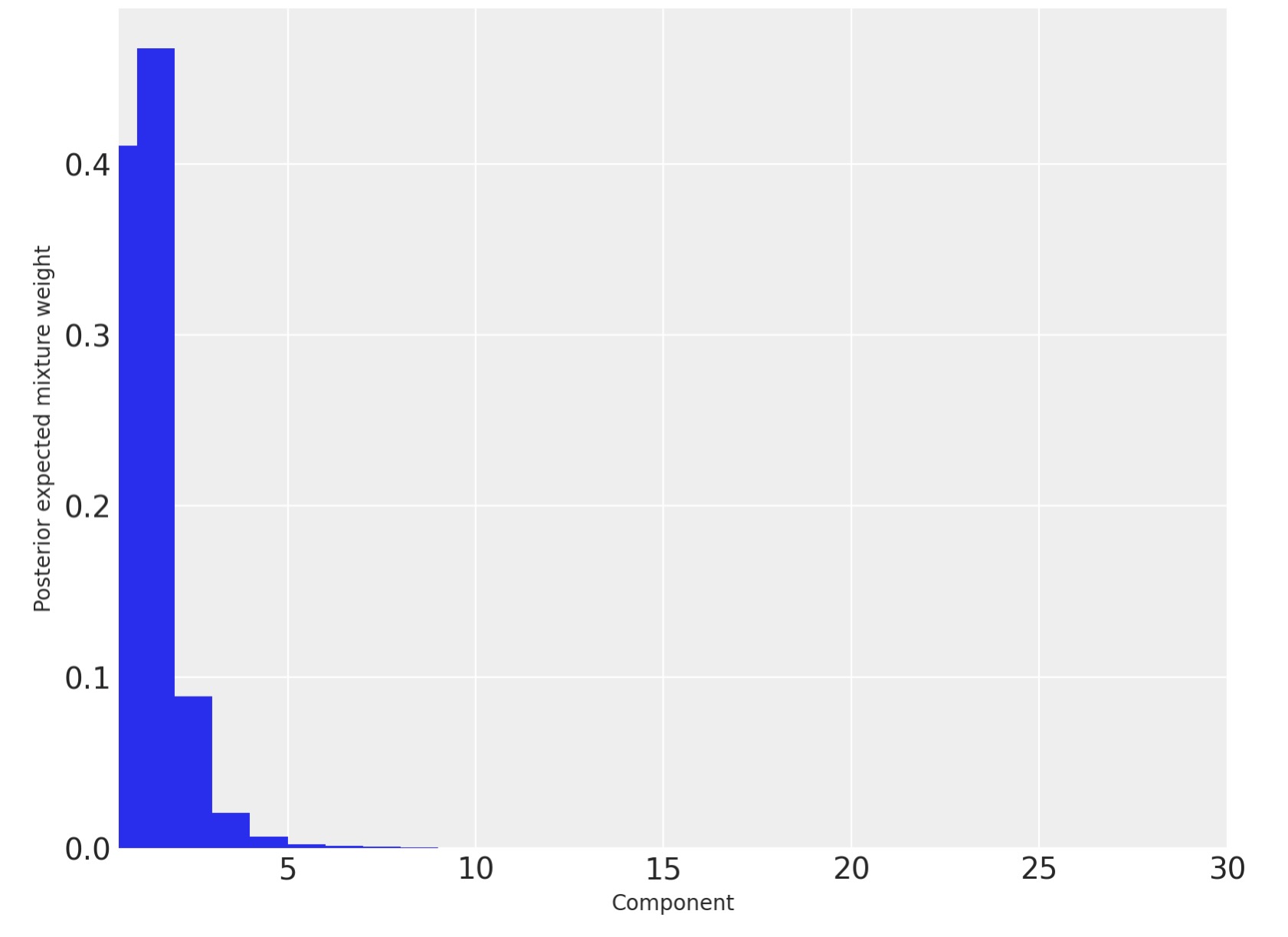
私たちは、三つの成分だけが事後予測重みを評価できることがわかります。そのため、ディリクレ過程をを13成分で切り詰めることは私たちの推定にはっきりとわかるほどの影響がないことを私たちは断定します。
私たちは、ここで、事後密度推定を計算し図示します。
post_pdf_contribs = xr.apply_ufunc(
sp.stats.norm.pdf,
x_plot,
trace.posterior["mu"],
1.0 / np.sqrt(trace.posterior["lambda_"] * trace.posterior["tau"]),
)
post_pdfs = (trace.posterior["w"] * post_pdf_contribs).sum(dim=("component"))
post_pdf_quantiles = post_pdfs.quantile([0.1, 0.9], dim=("chain", "draw"))fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting.values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.5)
ax.fill_between(
x_plot,
post_pdf_quantiles.sel(quantile=0.1),
post_pdf_quantiles.sel(quantile=0.9),
color="gray",
alpha=0.45,
)
ax.plot(x_plot, post_pdfs.sel(chain=0, draw=0), c="gray", label="Posterior sample densities")
ax.plot(
x_plot,
az.extract(post_pdfs, var_names="x", num_samples=100),
c="gray",
)
ax.plot(x_plot, post_pdfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_yticklabels([])
ax.set_ylabel("Density")
ax.legend(loc=2);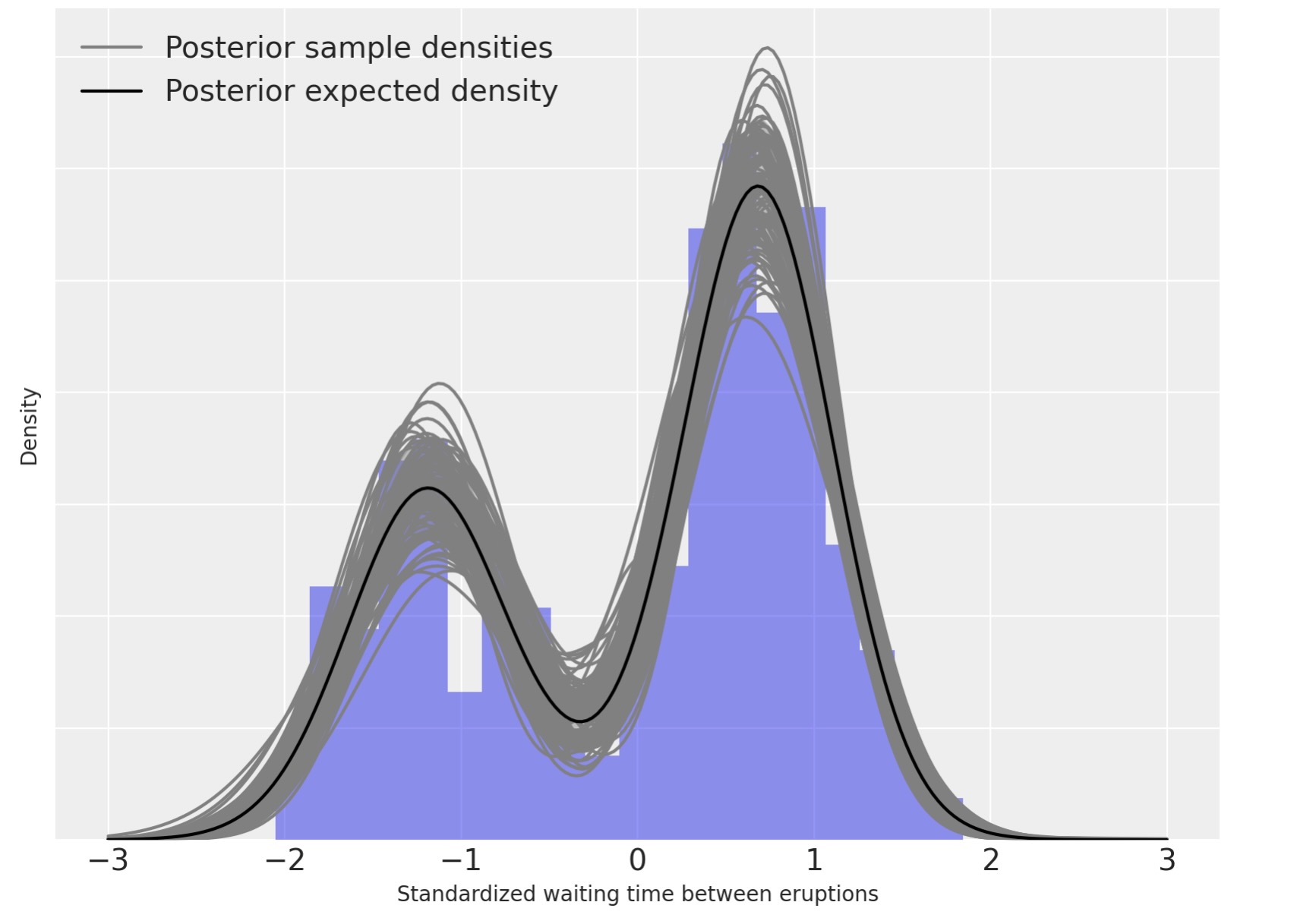
上のように、私たちは、この密度推定をその混合成分に分解できます。
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting.values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.5)
ax.plot(x_plot, post_pdfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.plot(
x_plot,
(trace.posterior["w"] * post_pdf_contribs).mean(dim=("chain", "draw")).sel(component=0),
"--",
c="k",
label="Posterior expected mixture\ncomponents\n(weighted)",
)
ax.plot(
x_plot,
(trace.posterior["w"] * post_pdf_contribs).mean(dim=("chain", "draw")).T,
"--",
c="k",
)
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_yticklabels([])
ax.set_ylabel("Density")
ax.legend(loc=2);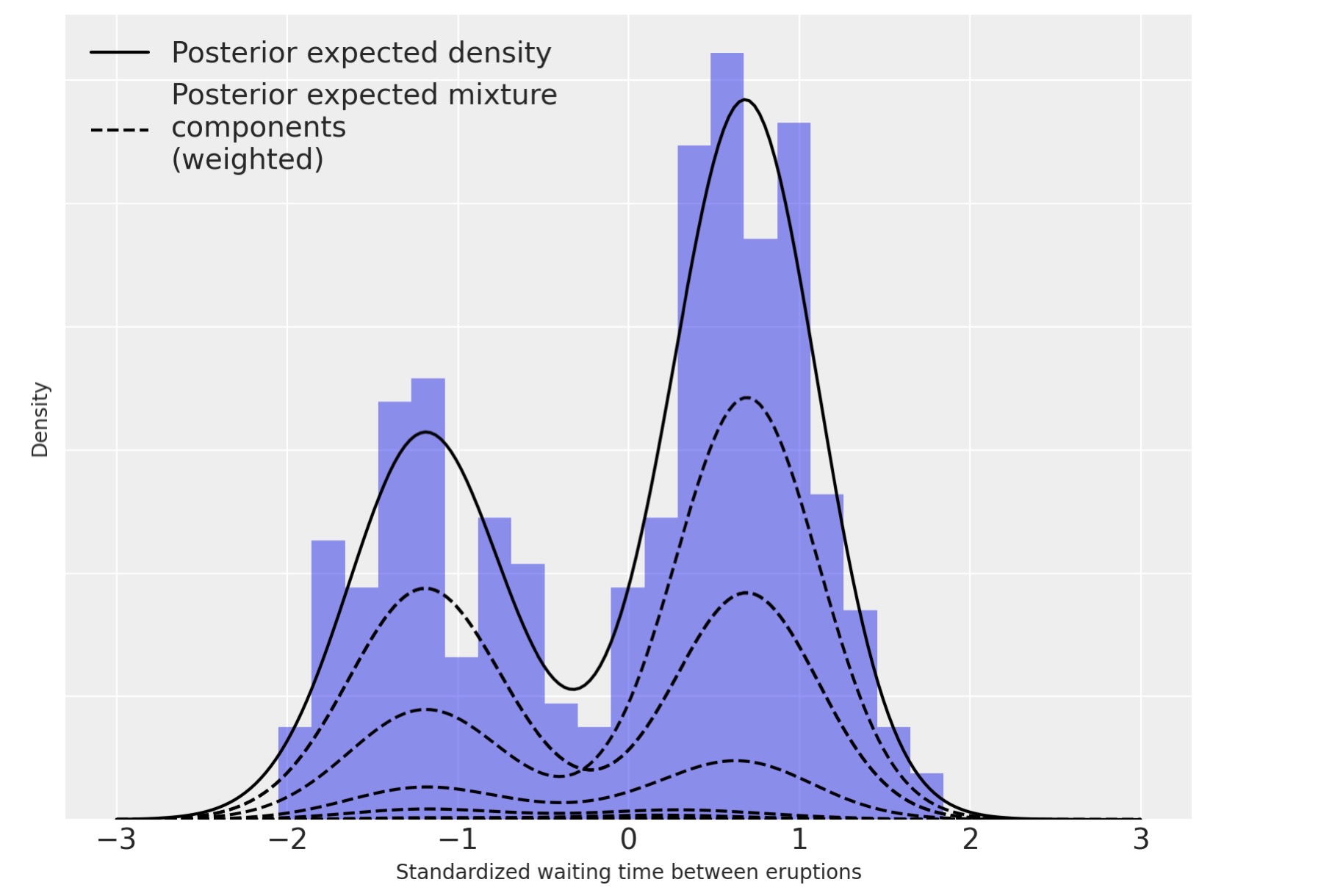
ディリクレ過程混合モデルは、パラメトリック成分分布{fθ| fθ ⊆ θ}のファミリーの間では、信じられない程、柔軟です。私たちは、この柔軟性を年間の日照時間密度を推定するため、下のポワソン成分分布を使うことによって説明します。このデータセットは企画され、ダウンロードできます。
kwargs = dict(sep=";", names=["time", "sunspot.year"], usecols=[0, 1])
try:
sunspot_df = pd.read_csv(os.path.join("..", "data", "sunspot.csv"), **kwargs)
except FileNotFoundError:
sunspot_df = pd.read_csv(pm.get_data("sunspot.csv"), **kwargs)sunspot_df.head()| time | sunspot.year | |
|---|---|---|
| 0 | 1700.5 | 8.3 |
| 1 | 1701.5 | 18.3 |
| 2 | 1702.5 | 26.7 |
| 3 | 1703.5 | 38.3 |
| 4 | 1704.5 | 60.0 |
この例では、モデルは、
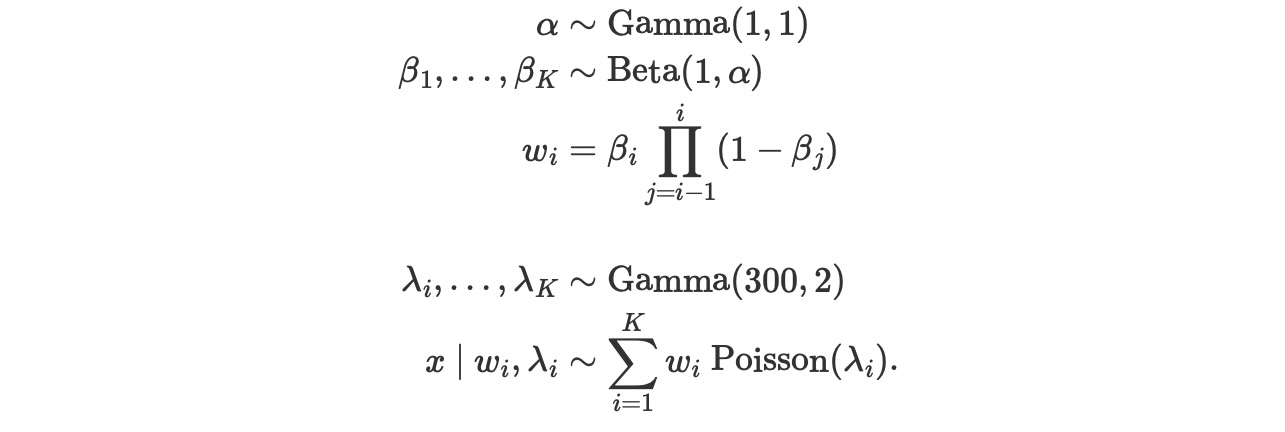
K = 50
N = sunspot_df.shape[0]with pm.Model(coords={"component": np.arange(K), "obs_id": np.arange(N)}) as model:
alpha = pm.Gamma("alpha", 1.0, 1.0)
beta = pm.Beta("beta", 1, alpha, dims="component")
w = pm.Deterministic("w", stick_breaking(beta), dims="component")
# Gamma is conjugate prior to Poisson
lambda_ = pm.Gamma("lambda_", 300.0, 2.0, dims="component")
obs = pm.Mixture(
"obs", w, pm.Poisson.dist(lambda_), observed=sunspot_df["sunspot.year"], dims="obs_id"
)with model:
trace = pm.sample(
tune=5000,
init="advi",
target_accept=0.95,
random_seed=RANDOM_SEED,
)
日照モデルでは、αの事後分布は、0.6から1.2の間に集中します。OldFaithful待機時間モデルに対するものより多くの成分を無視できないほどの量を混合へ提供することを、私たちが予期していることを示しています。
az.plot_trace(trace, var_names=["alpha"]);
実際は、私たちは10と15の間に混合成分がはっきりわかるほどの事後予測重みを持つことがわかります。
fig, ax = plt.subplots(figsize=(8, 6))
plot_w = np.arange(K) + 1
ax.bar(plot_w - 0.5, trace.posterior["w"].mean(("chain", "draw")), width=1.0, lw=0)
ax.set_xlim(0.5, K)
ax.set_xlabel("Component")
ax.set_ylabel("Posterior expected mixture weight");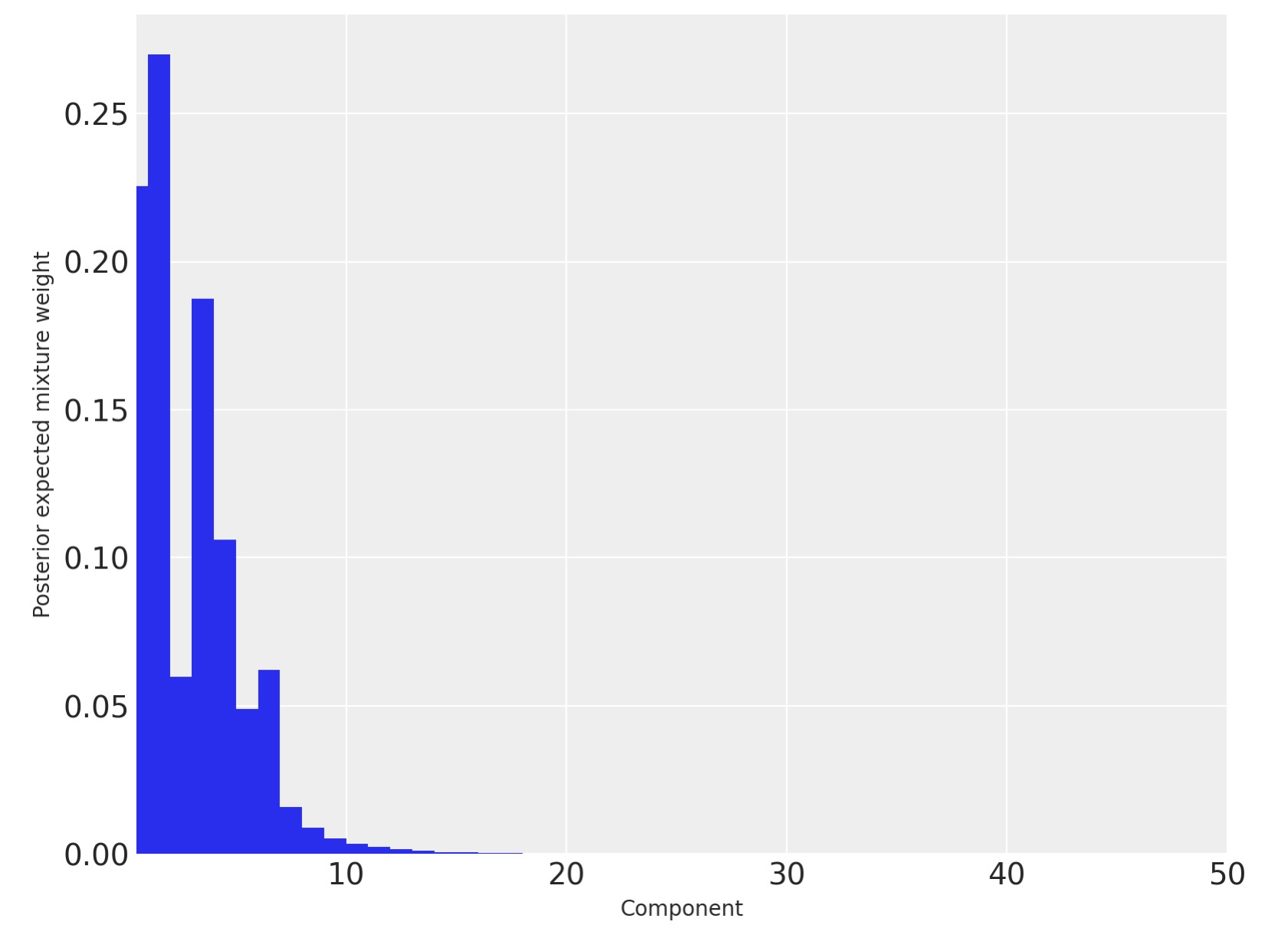
私たちはここで、適合した密度推定を計算し図示します。
x_plot = xr.DataArray(np.arange(250), dims=["plot"])
post_pmf_contribs = xr.apply_ufunc(sp.stats.poisson.pmf, x_plot, trace.posterior["lambda_"])
post_pmfs = (trace.posterior["w"] * post_pmf_contribs).sum(dim=("component"))
post_pmf_quantiles = post_pmfs.quantile([0.025, 0.975], dim=("chain", "draw"))fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(sunspot_df["sunspot.year"].values, bins=40, density=True, lw=0, alpha=0.75)
ax.fill_between(
x_plot,
post_pmf_quantiles.sel(quantile=0.025),
post_pmf_quantiles.sel(quantile=0.975),
color="gray",
alpha=0.45,
)
ax.plot(x_plot, post_pmfs.sel(chain=0, draw=0), c="gray", label="Posterior sample densities")
ax.plot(
x_plot,
az.extract(post_pmfs, var_names="x", num_samples=100),
c="gray",
)
ax.plot(x_plot, post_pmfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.set_xlabel("Yearly sunspot count")
ax.set_yticklabels([])
ax.legend(loc=1);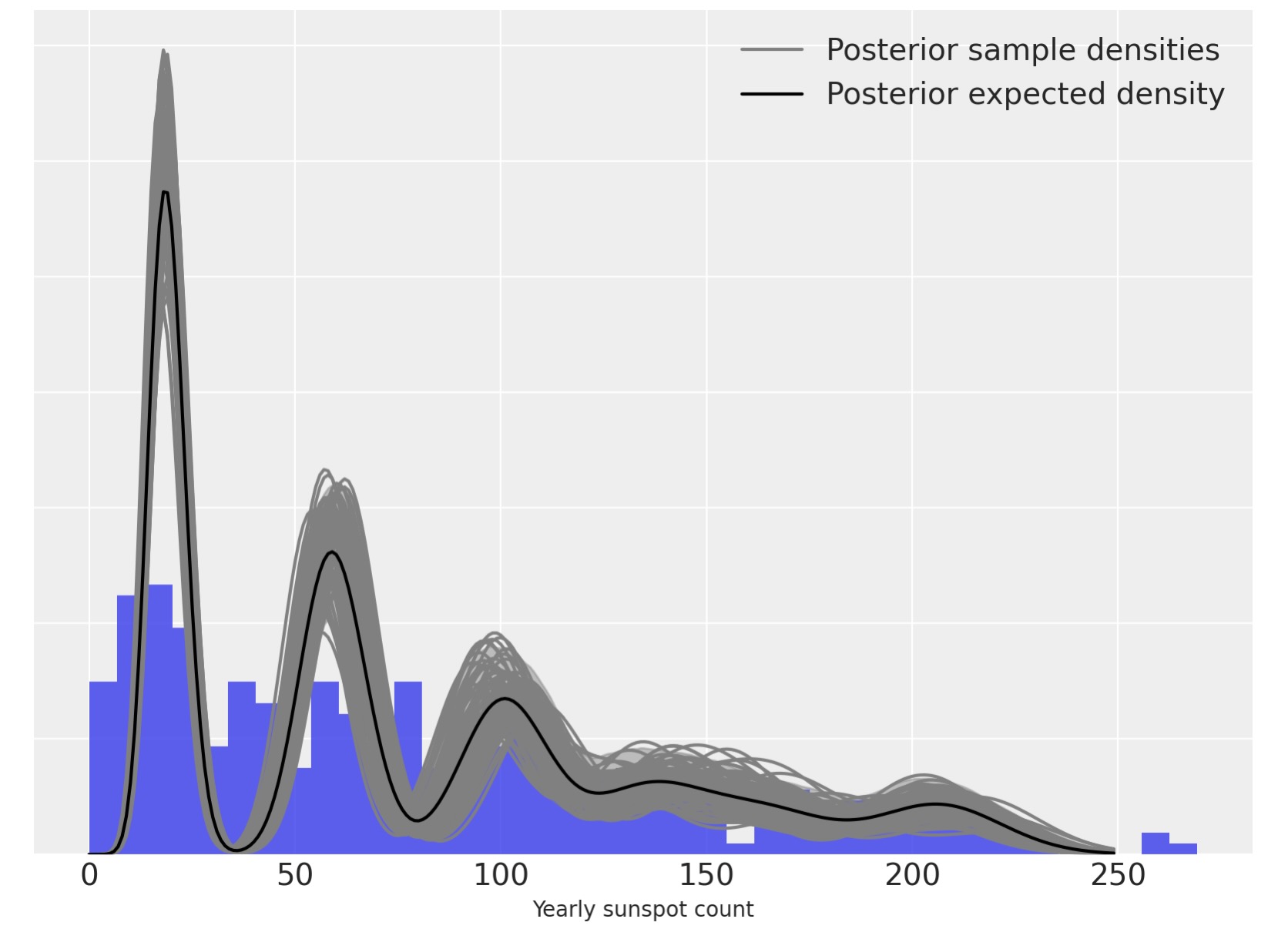
再び、私たちは、事後予測密度を重み付けした混合密度へ分解できます。
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 40
ax.hist(sunspot_df["sunspot.year"].values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.75)
ax.plot(x_plot, post_pmfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.plot(
x_plot,
(trace.posterior["w"] * post_pmf_contribs).mean(dim=("chain", "draw")).sel(component=0),
"--",
c="k",
label="Posterior expected mixture\ncomponents\n(weighted)",
)
ax.plot(
x_plot,
(trace.posterior["w"] * post_pmf_contribs).mean(dim=("chain", "draw")).T,
"--",
c="k",
)
ax.set_xlabel("Yearly sunspot count")
ax.set_yticklabels([])
ax.legend(loc=1);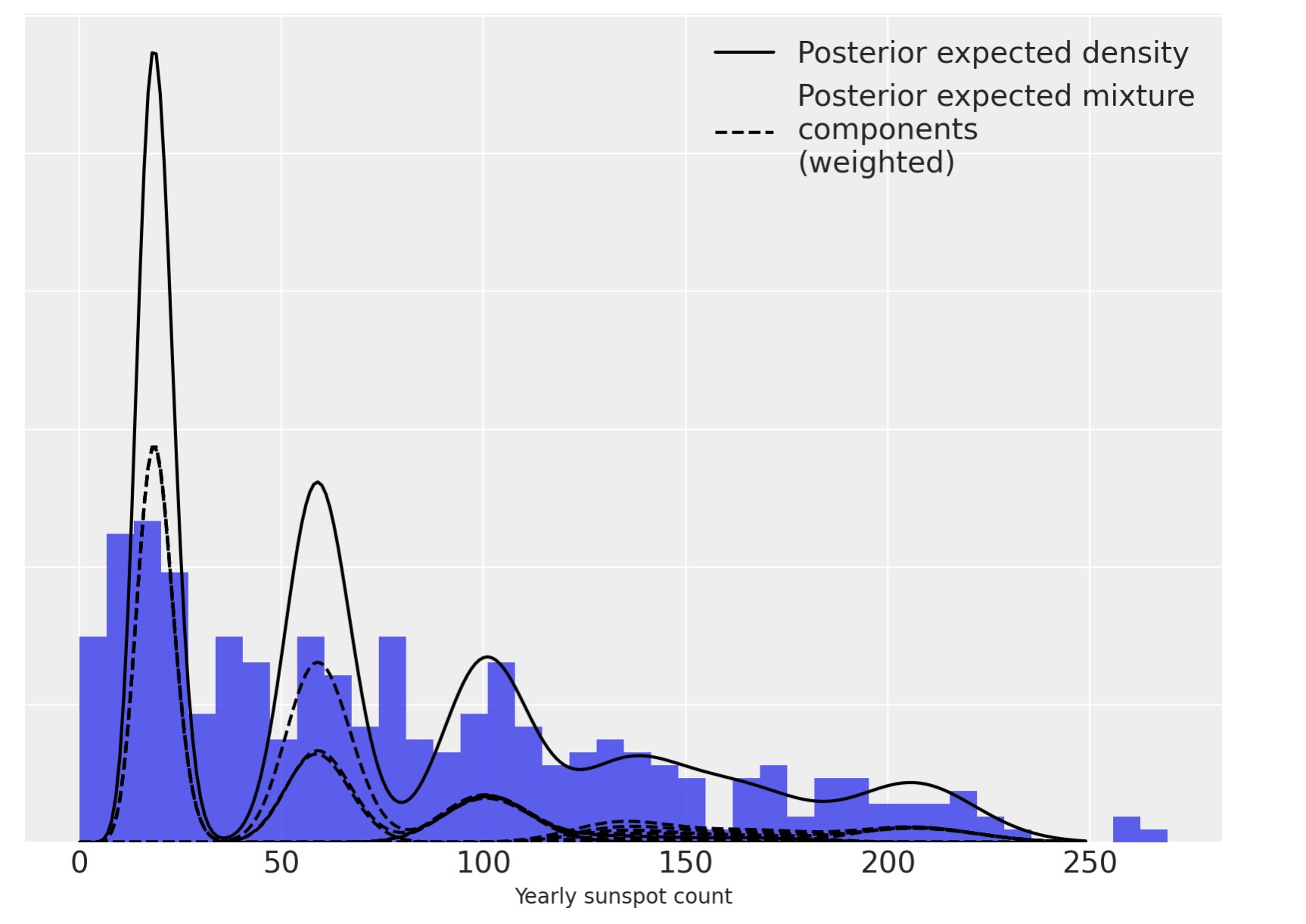
製作者
著作:Austin Rochford 彼のブログ投稿から
更新:Abhipsha Das 2021年 8月
更新:Benjamin T. Vincent 2023年 2月 PyMC v5 az.extractを使用