回帰不連続設計分析

　半実験は、実験的な介入と量的な測定を含みます。しかし、半実験は、テストまたは、照合グループののためのユニット(例えば、細胞、人々、企業、学校、状態)のランダムな割り当ては含みません。このランダムな割り当てを伝えるための能力のなさは、観察基準とテストグループの間で、何らかの相違があることが、介入のためであり誤りを生む因子のためではないということを示すことが困難なものとして因果を主張する問題をもたらします。

　回帰の不連続な設計( regression discontinuity design:RDD)は、半実験の設計の特別な様式です。それは照合グループとテストグループからなり、条件のためのユニットの割り当ては、ランダムではなく、基準の閾値を元に選択されます。

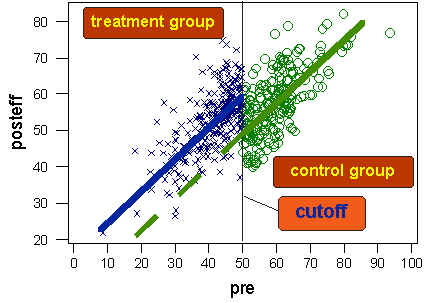
　回帰不連続設計の図です。緑の点線は処置をしなかった場合のテストグループの事後テストの推定を示しています。イメージは以下のサイトのものです。 https://conjointly.com/kb/regression-discontinuity-design/.

　非常に低いスコアのユニットは、非常に高いスコアのユニットより何らかの次元で、体系的に異なる傾向があります。例えば、もし、私たちが、最も高いアーカイブの学生と最も低いアーカイブの学生を見た場合、全ての尤度に置いて、誤りを生む変数があります。高いスコアの学生は、最も低いスコアの学生よりももっと特権的な背景からくるものを持っている傾向があります。

　私たちは、追加の指導をスコアの最も低いスコアの半分の生徒に与えると、その後、私たちはテストと照合グループの間で、特権に関して何らかの測度の大きな相違を持つことを、簡単に想像することができます。最初の印象では、これは、不連続な設計の役に立たない回帰を作るように見えます。ランダムな割り当ての全体のポイントは、照合とテストグループの間で、体系的に隔たって減少するか削除されます。しかし、閾値を使うことで、グループ間の誤りを生む変数の相違を最大化させるようです。チグハグなことをしているのではありません。

　鍵になる点は、しかし、学生のスコアの閾値からちょうど上と下は、彼らの特権の体系的に相違する傾向がかなり小さくなります。そして、もし、私たちが、閾値のちょうど上としたでそれらのテスト後のスコアが不連続になっている意味のある証拠を見つけるならば、その時、(閾値の基準によって適用される)介入、が因果的な反応だったことは、相当もっともらしいことになります。

不連続設計のシャープと曖昧な回帰

　回帰の不連続設計は二つのカテゴリーに分離することに注意してください。このノートブックは、シャープ不連続回帰設計に焦点を当てます。しかし、シャープとファジィな変異を理解するのは重要です。

• シャープ：ここで、照合または処置グループの割り当ては、純粋に閾値に支配されます。どのユニットがどのグループに属するか不確実性はありません。
• ファジィ：ある状況では、閾値を元にした照合と処置の間のはっきりした境界は、なくても良いでしょう。代替的に、研究される実際のユニットの側で準拠はありません。例えば、患者は、必ずしも、薬を摂るように完全に人の要求を受ける必要はありません。そのため、テストグループに割り当てられた患者の何らかの未知の促進が、人の要求を受け入れないため、実際には照合グループなるかもしれません。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

RANDOM_SEED = 123
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
%config InlineBackend.figure_format = 'retina'

シミュレート用データの生成

　ここで、私たちは、わずかな/ゼロ　計測のノイズがあることを仮定することに注意してください。しかし、テスト前からテスト後へ、真の値がいくらか変動します。テストの前と後の結果でノイズの測定を説明することができます。しかし、このノートブックでは、取り扱いません。

# define true parameters
threshold = 0.0
treatment_effect = 0.7
N = 1000
sd = 0.3  # represents change between pre and post test with zero measurement error

# No measurement error, but random change from pre to post
df = (
    pd.DataFrame.from_dict({"x": rng.normal(size=N)})
    .assign(treated=lambda x: x.x < threshold)
    .assign(y=lambda x: x.x + rng.normal(loc=0, scale=sd, size=N) + treatment_effect * x.treated)
)

df

1000 rows × 3 columns

def plot_data(df):
    fig, ax = plt.subplots(figsize=(12, 7))
    ax.plot(df.x[~df.treated], df.y[~df.treated], "o", alpha=0.3, label="untreated")
    ax.plot(df.x[df.treated], df.y[df.treated], "o", alpha=0.3, label="treated")
    ax.axvline(x=threshold, color="k", ls="--", lw=3, label="treatment threshold")
    ax.set(xlabel=r"observed $x$ (pre-test)", ylabel=r"observed $y$ (post-test)")
    ax.legend()
    return ax


plot_data(df);

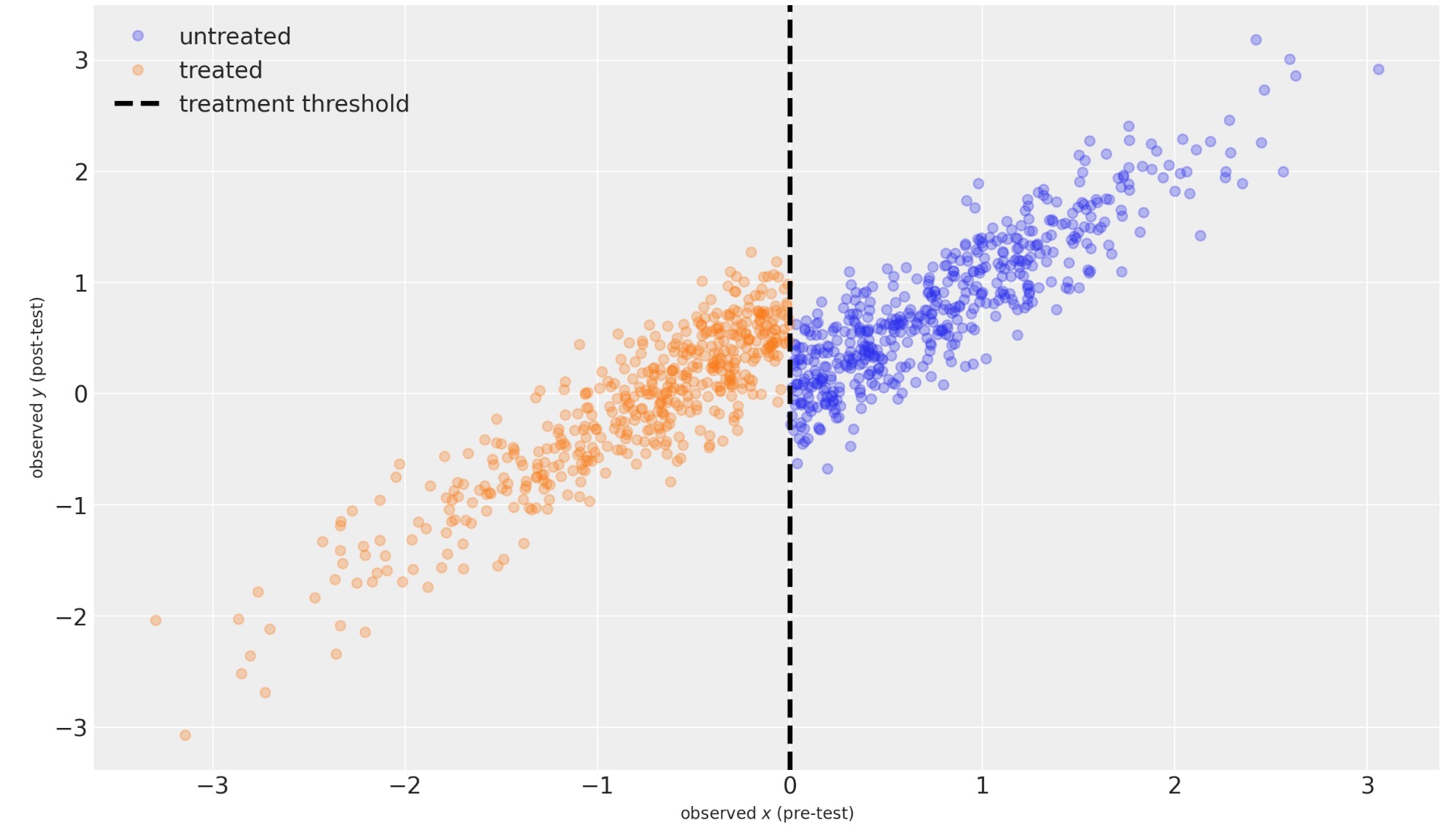
シャープ回帰不連続モデル

　私たちは、ベイジアン回帰不連続モデルを定義できます。

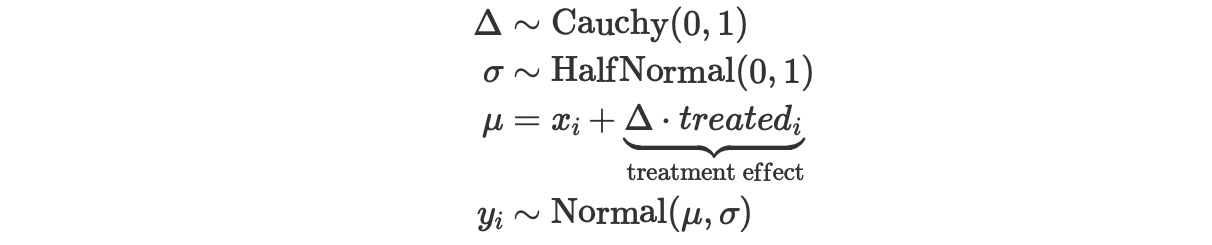
ここで、

• Δは不連続のサイズ
• σは、事前、事後のテストのスコアの変化の標準偏差
• xiとyiは、ユニットiの事前、事後テスト計測で観測されます
• treatedは、観測のための指示変数(０が照合グループ、1がテストグループ)

注記：

• 私たちは、測定エラーがないという簡単な仮定を置きます。
• ここで、私たちは、事前テストと事後テストの両方で同じ測定（例えば、温度、教育の達成度、）を使うという状況で、私たちを制限します。そのため、処置しない事後テストの測定は、y〜Normal(μ = x,σ)としてモデルにできます。
• 事前と事後のテストの測定器具が識別されないケースは、その後、私たちが、事前と事後のテスト測定の間で'交換レート'を取りこむために傾きと切片のパラメータにμを置きます。
• 私たちはユニットが処置されているかどうか、正確に観測することを仮定します。

with pm.Model() as model:
    x = pm.MutableData("x", df.x, dims="obs_id")
    treated = pm.MutableData("treated", df.treated, dims="obs_id")
    sigma = pm.HalfNormal("sigma", 1)
    delta = pm.Cauchy("effect", alpha=0, beta=1)
    mu = pm.Deterministic("mu", x + (delta * treated), dims="obs_id")
    pm.Normal("y", mu=mu, sigma=sigma, observed=df.y, dims="obs_id")

pm.model_to_graphviz(model)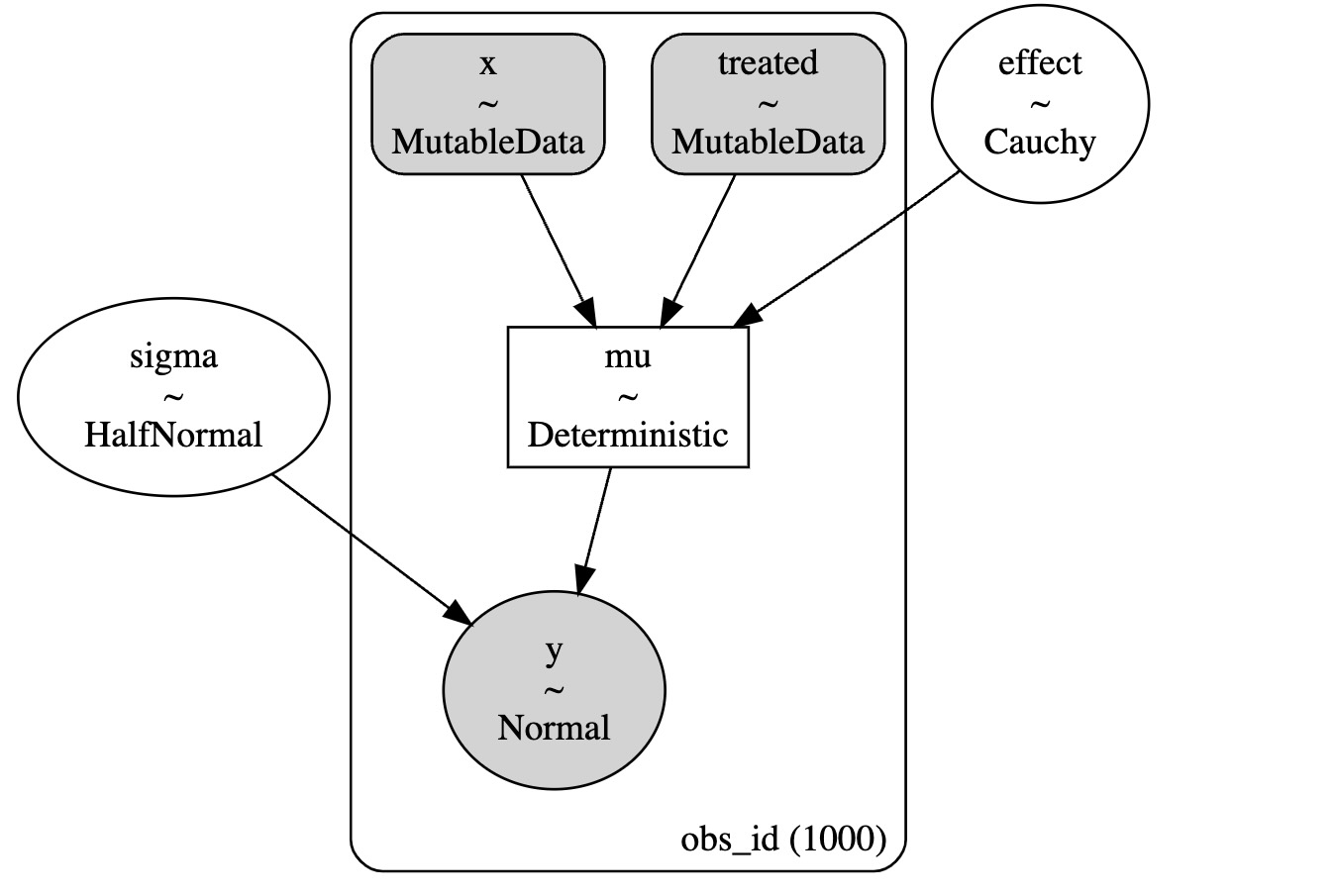

推論

with model:
    idata = pm.sample(random_seed=RANDOM_SEED)

　私たちは、警告なしでサンプリングできました。問題なくMCMCのトレースを表示します。

az.plot_trace(idata, var_names=["effect", "sigma"]);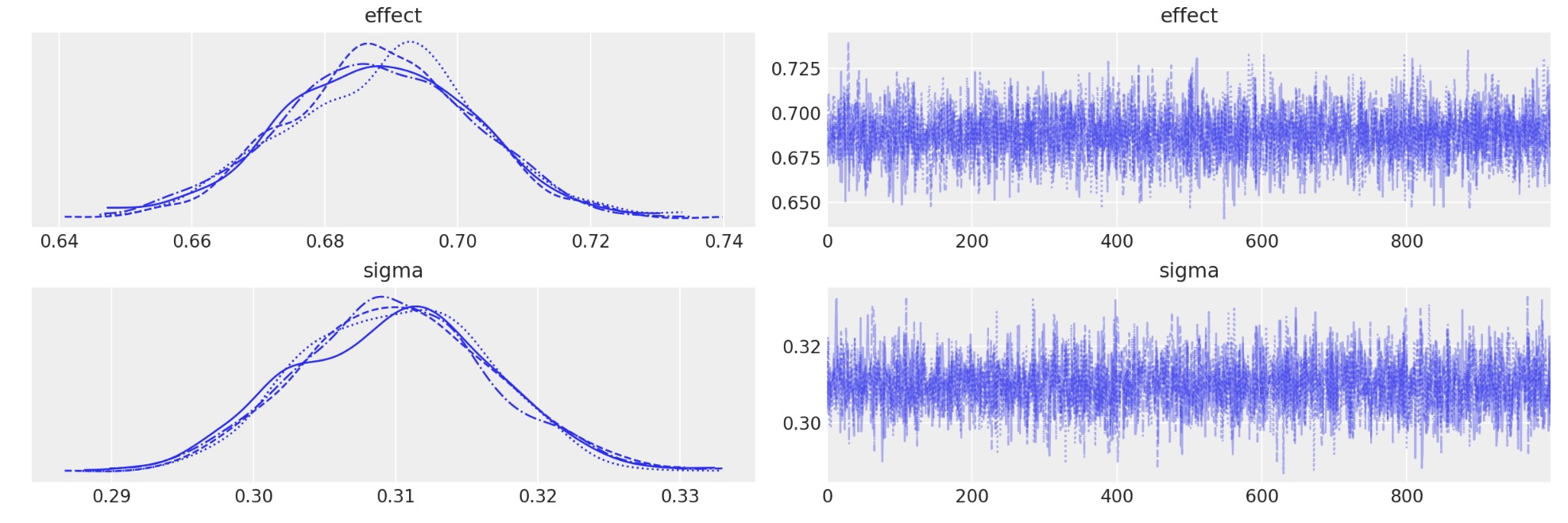

　私たちは、真の不連続な量(左）と、事前と事後のテスト間のユニットの変化の標準偏差（右）を正確に回復することができることがわかります。

az.plot_posterior(
    idata, var_names=["effect", "sigma"], ref_val=[treatment_effect, sd], hdi_prob=0.95
);

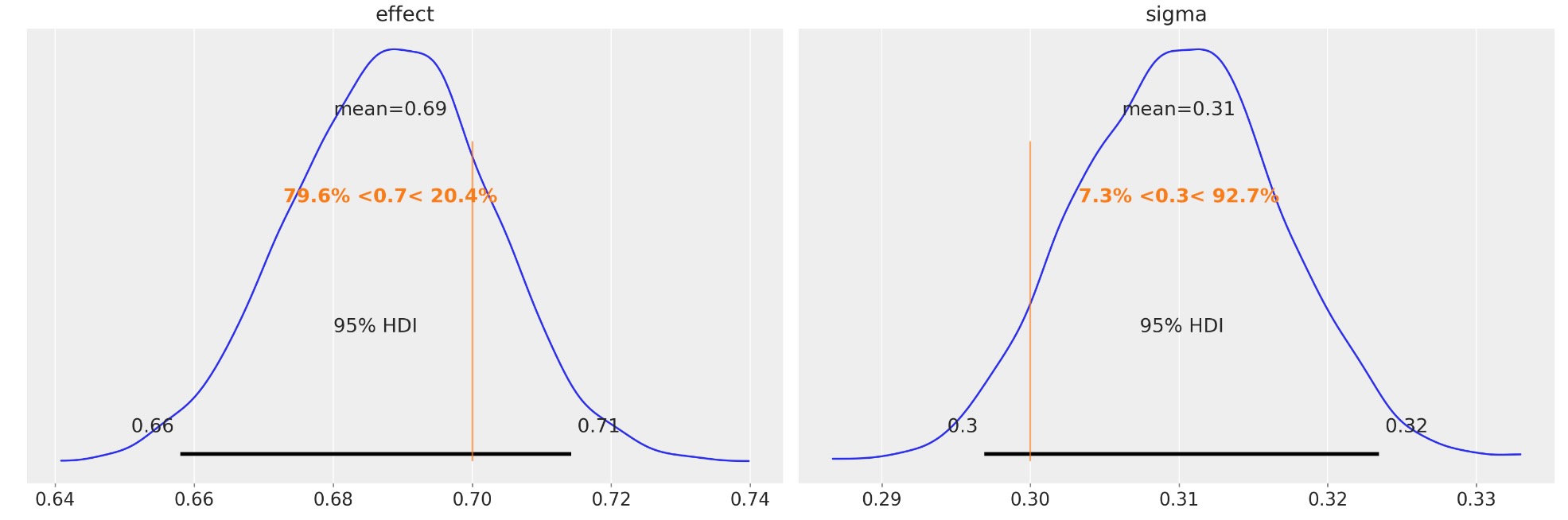
　最も重要なことは、事後のeffectパラメータです。私たちは、（95%の信頼区間で）結果の強さ、または結果の有無(例えば、ベイズ因子またはROPE)について判断する基礎に使うことができます。

Counterfactual質問

　私たちは、もし、以下ならば、何を予期するかを尋ねるために、事後予測を使うことができます。

• 処置されたユニットはなかった。(青い影の領域、非常に細い)
• 全てのユニットが処置された（オレンジの影の領域）

技術ノート：様式としては、私たちはyの事後予測を実行します。異なる乱数の種で何度もpm.sample_posterior_predictiveを実行することは、毎回、新しい、異なるyの結果を得ます。しかし、これは、muのためのケース(私たちは、正式な事後予測を行っていません)ではありません。これは、muが決定関数(mu = x + delta*treated)のためです。そのため、すでに観測したdeltaの事後サンプルのために、muの値は、xとtreatedデータの値によって完全に決定されます。

# MODEL EXPECTATION WITHOUT TREATMENT ------------------------------------
# probe data
_x = np.linspace(np.min(df.x), np.max(df.x), 500)
_treated = np.zeros(_x.shape)

# posterior prediction (see technical note above)
with model:
    pm.set_data({"x": _x, "treated": _treated})
    ppc = pm.sample_posterior_predictive(idata, var_names=["mu", "y"])

# plotting
ax = plot_data(df)
az.plot_hdi(
    _x,
    ppc.posterior_predictive["mu"],
    color="C0",
    hdi_prob=0.95,
    ax=ax,
    fill_kwargs={"label": r"$\mu$ untreated"},
)

# MODEL EXPECTATION WITH TREATMENT ---------------------------------------
# probe data
_x = np.linspace(np.min(df.x), np.max(df.x), 500)
_treated = np.ones(_x.shape)

# posterior prediction (see technical note above)
with model:
    pm.set_data({"x": _x, "treated": _treated})
    ppc = pm.sample_posterior_predictive(idata, var_names=["mu", "y"])

# plotting
az.plot_hdi(
    _x,
    ppc.posterior_predictive["mu"],
    color="C1",
    hdi_prob=0.95,
    ax=ax,
    fill_kwargs={"label": r"$\mu$ treated"},
)
ax.legend()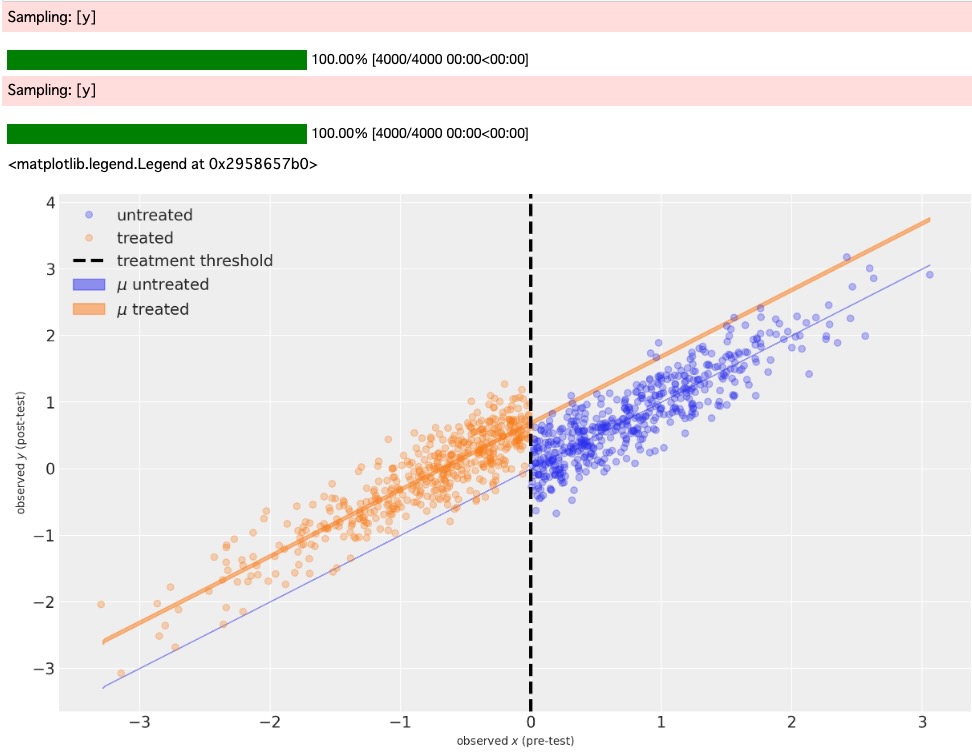

　青の影の領域は、処置のないケースでの、事前テスト測定する可能な範囲のための、事後テスト測定の推定値の９５％信頼領域を表示しています。これは、この特別なモデルでは、μ = x を仮定しているのため、実際、無限に細くなります。

　オレンジの影の部分は、処置を実施したケースで、事前テストの測定の可能な範囲のために、事後テスト測定の推定値の95%信頼領域を表示しています。

　両方は、counterfactual推論の例として、実際に非常に興味があります。私たちは、閾値以下で処置していない、どのようなユニットも観測していません。閾値以上で処置したユニットも観測していません。しかし、私たちのモデルの仮定は、現実の良い説明です。私たちは、counterfactual質問を尋ねることができます。"閾値より上のユニットが処置されていたらどうだったか？”　そして　”閾値より下のユニットが処置されていればどうなるか？”

結論

　このノートブックでは、私たちは、単に回帰不連続設計からデータを分析する方法の表面に触れたに過ぎません。間違いなく、私たちは、私たちが、因果の宣言ができるアプローチの核心の性質に焦点に注力できるように、最も簡単な可能なケースに私たちの焦点を制限しました。