実験に基づく近似の概要

　ほとんどのモデルで、私たちは、NUTSやメトロポリスのようなMCMCアルゴリズムのサンプリングを使います。PyMCでは私たちは、MCMCのトレースをストアし、その後、それらを使って分析を実行します。PyMCは変分推論サブモジュールのために、同様の概念があります。このタイプの近似は、粒子をSVGDサンプラーのためにストアします。独立したSVGD粒子とMCMCサンプルの間に相違はありません。実験上は、MCMCサンプリング出力と　apply_replacementsやsample_nodeのような、完全に本格的なVI ユーティリティの間の橋渡しとして動作します。インターフェイスを記述するために、variational_api_quickstart(TBD)を参照してください。ここで私たちは、Empiricalに焦点を当てます。そして、Empirical近似への規定事項の概要を与えます。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
import seaborn as sns

from pandas import DataFrame

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.0.1

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
np.random.seed(42)

多重様式密度

　最初にNUTSトレースを得たところから、variational_api_quickstartからの問題を思い出しましょう。

w = pm.floatX([0.2, 0.8])
mu = pm.floatX([-0.3, 0.5])
sd = pm.floatX([0.1, 0.1])

with pm.Model() as model:
    x = pm.NormalMixture("x", w=w, mu=mu, sigma=sd)
    trace = pm.sample(50_000, return_inferencedata=False)

with model:
    idata = pm.to_inference_data(trace)
az.plot_trace(idata);

　よくできました。最初のトレースでEmpirical近似を生成できます。

print(pm.Empirical.__doc__)

**Single Group Full Rank Approximation**

    Builds Approximation instance from a given trace,
    it has the same interface as variational approximation

with model:
    approx = pm.Empirical(trace)

approx

<pymc.variational.approximations.Empirical at 0x134f51510>

　このタイプの近似は、それ自身をサンプルのための基礎になるストレージを持ちます。それはpytensor.sharedです。

approx.histogram

histogram

approx.histogram.get_value()[:10]

array([[0.41748522],
       [0.43779916],
       [0.31987749],
       [0.33221794],
       [0.43584405],
       [0.43584405],
       [0.47041292],
       [0.44583318],
       [0.47309763],
       [0.47309763]])

approx.histogram.get_value().shape

(200000, 1)

　それは、実際に、あなたが前にトレースしたサンプル数と同数になります。私たちの特別なケースでは、それは50kです。他になすべきことは、あなたが一つ以上の多重トレースを行うならば、一度により多くのサンプルを得ることになります。私たちはEmpirical生成のためにすべてのトレースを一次元化します。
　このヒストグラムは私ちがどのくらいのサンプルをストアしているか示します。構造はかなり単純です。(n_samples,n_dim)　これらの変数の命令は、クラス内部でストアされます。ほとんどのケースで、エンドユーザーには必要ありません。

approx.ordering

OrderedDict([('x', ('x', slice(0, 1, None), (), dtype('float64')))])

　事後分布からのサンプリングは、一様に交換して実行します。approx.sample(1000)を呼び出してください。そして、あなたは再度トレースを取得しますが、秩序は、決定されていません。approx.sample()で基盤を再構築する方法は現在のところありません。

new_trace = approx.sample(50000)

　サンプリング関数がコンパイルされた後、サンプリングは本当に高速になります。

az.plot_trace(new_trace);

　あなたは、もはや何の秩序もないことがわかりますが、再構築の密度は同一です。

２次の密度

mu = pm.floatX([0.0, 0.0])
cov = pm.floatX([[1, 0.5], [0.5, 1.0]])
with pm.Model() as model:
    pm.MvNormal("x", mu=mu, cov=cov, shape=2)
    trace = pm.sample(1000, return_inferencedata=False)
    idata = pm.to_inference_data(trace)

with model:
    approx = pm.Empirical(trace)

az.plot_trace(approx.sample(10000));

kdeViz_df = DataFrame(
    data=approx.sample(1000).posterior["x"].squeeze(),
    columns=["First Dimension", "Second Dimension"],
)

sns.kdeplot(data=kdeViz_df, x="First Dimension", y="Second Dimension")
plt.show()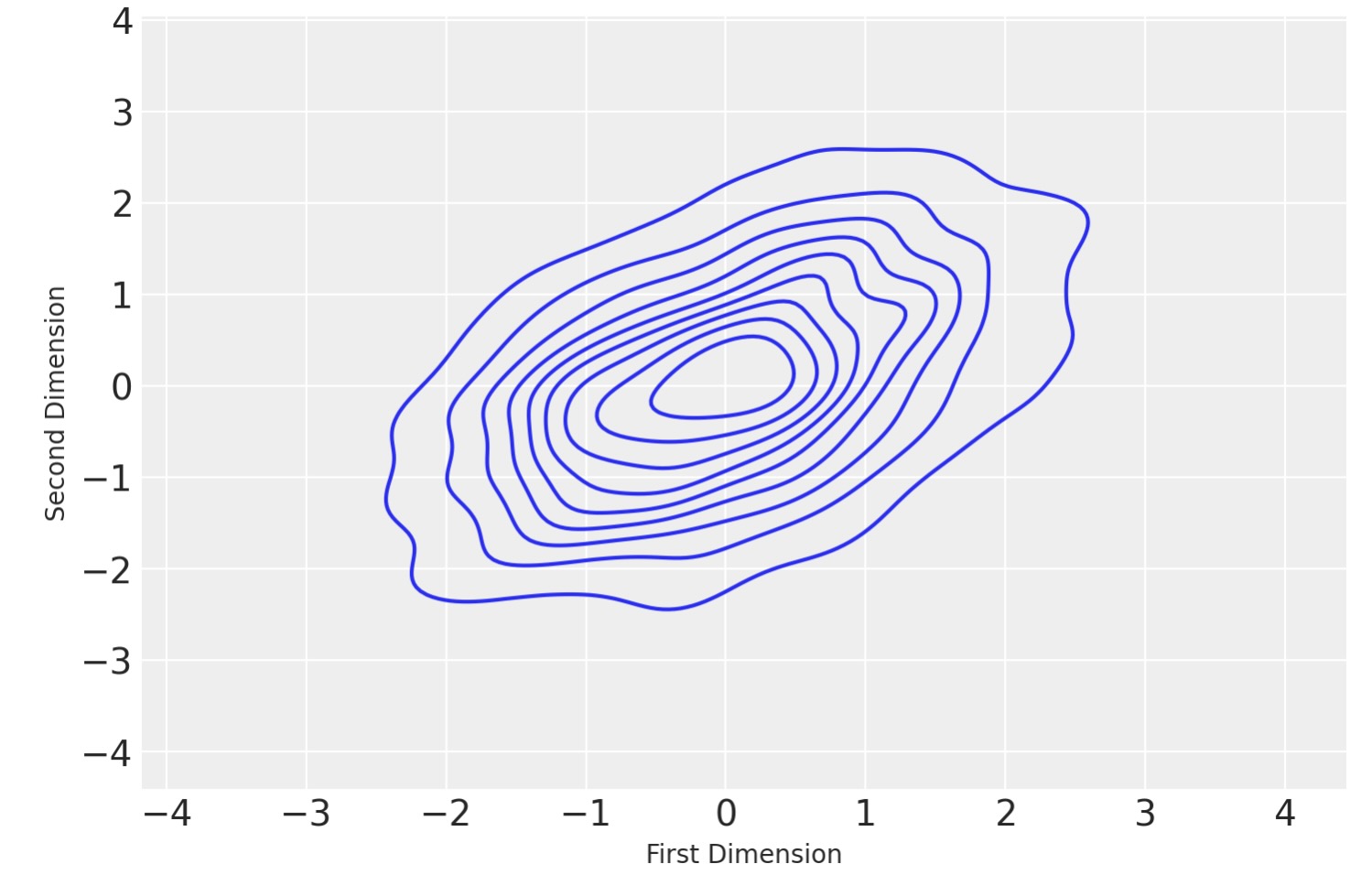

　前に、trace_cov関数がありました。

with model:
    print(pm.trace_cov(trace))

[[0.95108725 0.47666724]
 [0.47666724 0.97388498]]

　ここで、私たちは、Empiricalを使用して同じ共分散を推定することができます。

print(approx.cov)

Elemwise{true_div,no_inplace}.0

　それは、私たちが評価する必要なあるテンソルオブジェクトです。

print(approx.cov.eval())

[[0.95084948 0.47654807]
 [0.47654807 0.97364151]]

　推定は非常に近く、精度のエラーのせいで異なります。私たちは、同じ方法で平均を取得できます。

print(approx.mean.eval())

[0.02427368 0.03659135]