import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
from scipy import statsRANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")このノートブックでは、ここのデータが、ポワソン分布ではなく負の二項分布であることを除いて、Jonathan SedarによるGLMポワソン回帰の例に緊密に従います。(それはIan Osvaldによるプロジェクトで次々に印象づけられました)
負の二項回帰は、分散が平均より高いデータを計数するモデルを使います。負の二項分布は、ポワソン分布について考えます。そのレートパラメータはガンマ分布です。その結果、レートパラメータは、分散が増加することを説明するために調整することができます。
データ生成
ポワソン回帰例では、私たちは、くしゃみは任意のベースラインのレートで発生することを仮定しました。アルコールの消費、抗ヒスタミン剤の未摂取、またはその両方、その頻度の増加です。
ポワソンデータ
最初に、ポアソン回帰例から任意のポアソン分布データを見ていきましょう。
# Mean Poisson values
theta_noalcohol_meds = 1 # no alcohol, took an antihist
theta_alcohol_meds = 3 # alcohol, took an antihist
theta_noalcohol_nomeds = 6 # no alcohol, no antihist
theta_alcohol_nomeds = 36 # alcohol, no antihist
# Create samples
q = 1000
df_pois = pd.DataFrame(
{
"nsneeze": np.concatenate(
(
rng.poisson(theta_noalcohol_meds, q),
rng.poisson(theta_alcohol_meds, q),
rng.poisson(theta_noalcohol_nomeds, q),
rng.poisson(theta_alcohol_nomeds, q),
)
),
"alcohol": np.concatenate(
(
np.repeat(False, q),
np.repeat(True, q),
np.repeat(False, q),
np.repeat(True, q),
)
),
"nomeds": np.concatenate(
(
np.repeat(False, q),
np.repeat(False, q),
np.repeat(True, q),
np.repeat(True, q),
)
),
}
)df_pois.groupby(["nomeds", "alcohol"])["nsneeze"].agg(["mean", "var"])| mean | var | ||
|---|---|---|---|
| nomeds | alcohol | ||
| False | False | 1.047 | 1.127919 |
| True | 2.986 | 2.960765 | |
| True | False | 5.981 | 6.218858 |
| True | 35.929 | 36.064023 |
ポワソン分布のランダム変数の平均と分散は等しいので、サンプルの平均と分散はとても近接しています。
負の二項データ
ここで、データセットの各サブジェクトが風邪をひいていることを考えます。それらのくしゃみの分散は増加します。(1日に70回以上のくしゃみをするのに、信じられないほど少ない理由)もし、くしゃみの数の平均が同じで、分散が増加するならば、データは負の二項分布に従うかもしれません。
# Gamma shape parameter
alpha = 10
def get_nb_vals(mu, alpha, size):
"""Generate negative binomially distributed samples by
drawing a sample from a gamma distribution with mean `mu` and
shape parameter `alpha', then drawing from a Poisson
distribution whose rate parameter is given by the sampled
gamma variable.
"""
g = stats.gamma.rvs(alpha, scale=mu / alpha, size=size)
return stats.poisson.rvs(g)
# Create samples
n = 1000
df = pd.DataFrame(
{
"nsneeze": np.concatenate(
(
get_nb_vals(theta_noalcohol_meds, alpha, n),
get_nb_vals(theta_alcohol_meds, alpha, n),
get_nb_vals(theta_noalcohol_nomeds, alpha, n),
get_nb_vals(theta_alcohol_nomeds, alpha, n),
)
),
"alcohol": np.concatenate(
(
np.repeat(False, n),
np.repeat(True, n),
np.repeat(False, n),
np.repeat(True, n),
)
),
"nomeds": np.concatenate(
(
np.repeat(False, n),
np.repeat(False, n),
np.repeat(True, n),
np.repeat(True, n),
)
),
}
)
df| nsneeze | alcohol | nomeds | |
|---|---|---|---|
| 0 | 1 | False | False |
| 1 | 0 | False | False |
| 2 | 1 | False | False |
| 3 | 0 | False | False |
| 4 | 1 | False | False |
| ... | ... | ... | ... |
| 3995 | 29 | True | True |
| 3996 | 21 | True | True |
| 3997 | 28 | True | True |
| 3998 | 19 | True | True |
| 3999 | 19 | True | True |
4000 rows × 3 columns
df.groupby(["nomeds", "alcohol"])["nsneeze"].agg(["mean", "var"])| mean | var | ||
|---|---|---|---|
| nomeds | alcohol | ||
| False | False | 0.945 | 0.956932 |
| True | 3.051 | 3.752151 | |
| True | False | 5.834 | 9.065510 |
| True | 35.639 | 158.076756 |
ポワソン回帰の例のように、飲酒と/または抗ヒスタミン剤を摂取しないことは、くしゃみのレートを異なる段階に増加させます。この例と違い、アルコールとnemeds、nsneezeの分散の各組み合わせは、平均より高くなります。これは、ポワソン分布の平均と分散が等しいために、ポワソン分布は、データに貧弱に適合するであろうことを示唆しています。
データの可視化
g = sns.catplot(x="nsneeze", row="nomeds", col="alcohol", data=df, kind="count", aspect=1.5)
# Make x-axis ticklabels less crowded
ax = g.axes[1, 0]
labels = range(len(ax.get_xticklabels(which="both")))
ax.set_xticks(labels[::5])
ax.set_xticklabels(labels[::5]);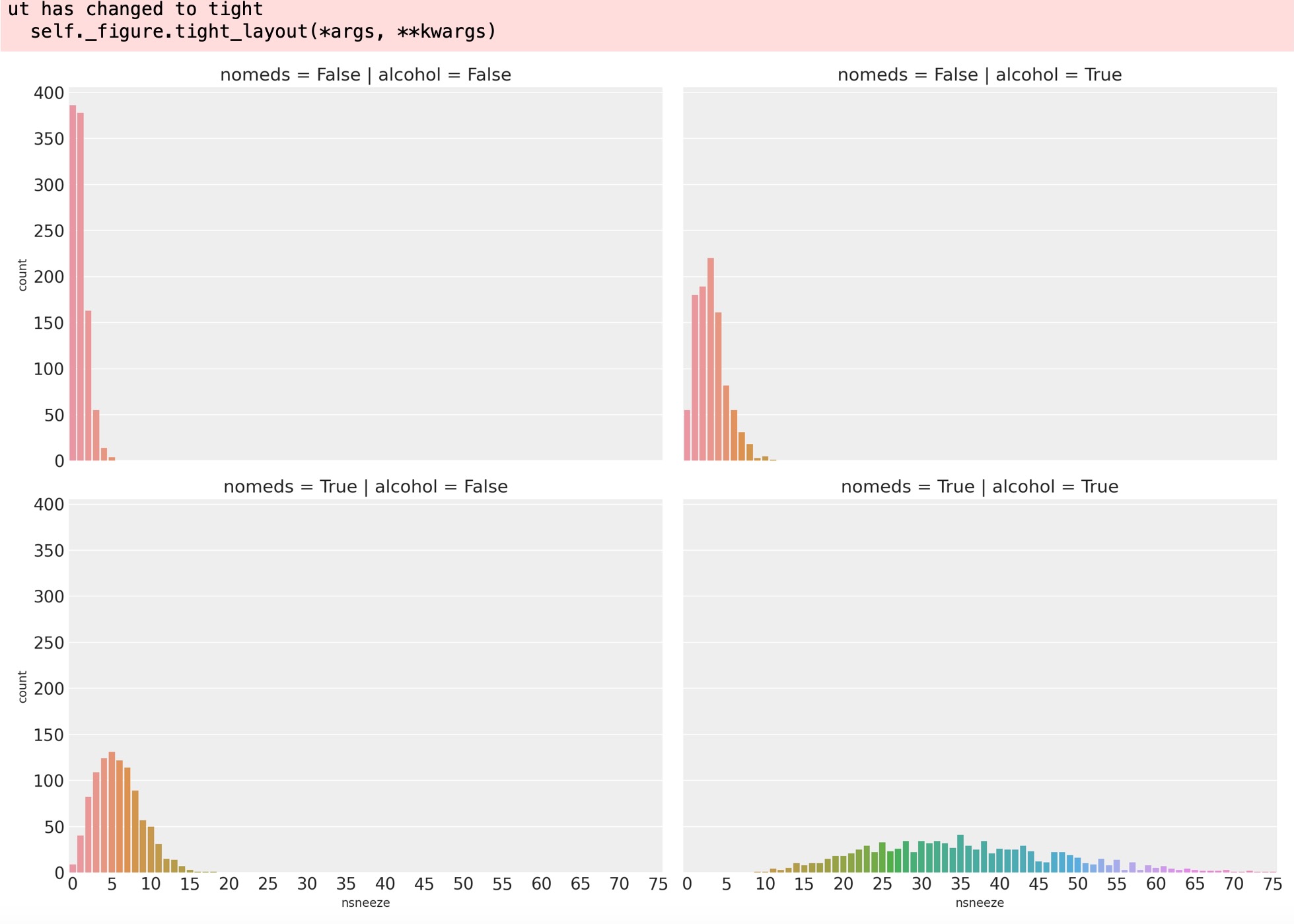
負の二項回帰
GLMモデルの生成
COORDS = {"regressor": ["nomeds", "alcohol", "nomeds:alcohol"], "obs_idx": df.index}
with pm.Model(coords=COORDS) as m_sneeze_inter:
a = pm.Normal("intercept", mu=0, sigma=5)
b = pm.Normal("slopes", mu=0, sigma=1, dims="regressor")
alpha = pm.Exponential("alpha", 0.5)
M = pm.ConstantData("nomeds", df.nomeds.to_numpy(), dims="obs_idx")
A = pm.ConstantData("alcohol", df.alcohol.to_numpy(), dims="obs_idx")
S = pm.ConstantData("nsneeze", df.nsneeze.to_numpy(), dims="obs_idx")
λ = pm.math.exp(a + b[0] * M + b[1] * A + b[2] * M * A)
y = pm.NegativeBinomial("y", mu=λ, alpha=alpha, observed=S, dims="obs_idx")
idata = pm.sample()
結果の表示
az.plot_trace(idata, compact=False);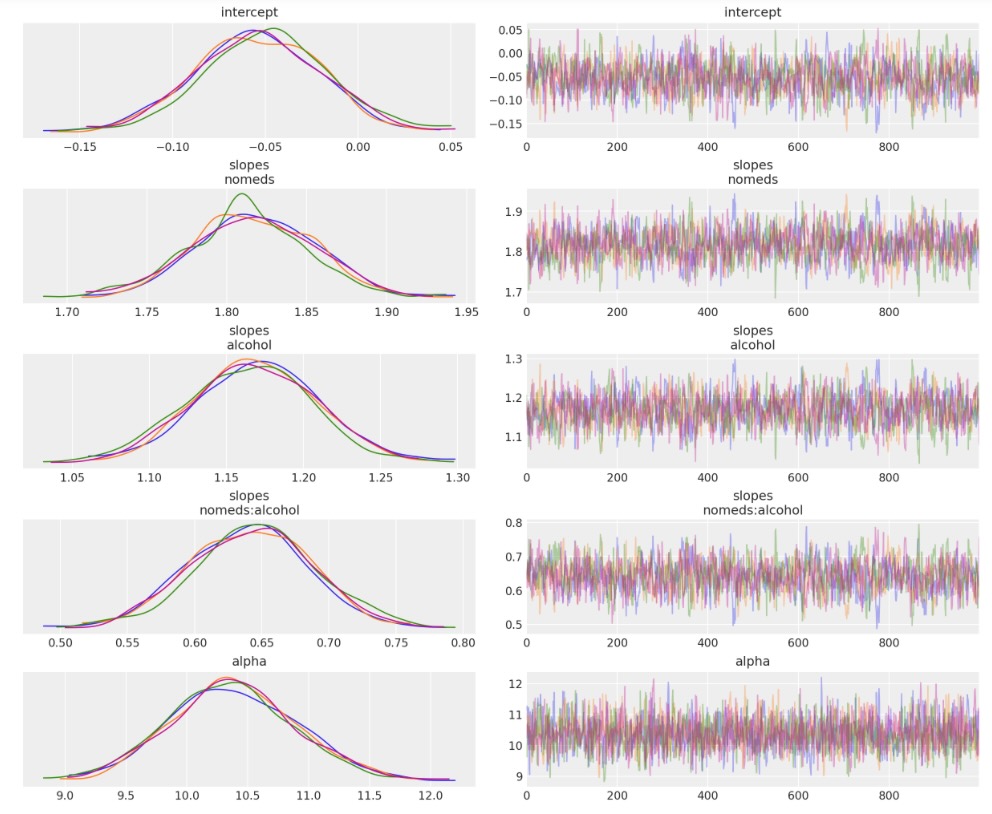
# Transform coefficients to recover parameter values
az.summary(np.exp(idata.posterior), kind="stats", var_names=["intercept", "slopes"])| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| intercept | 0.949 | 0.032 | 0.889 | 1.010 |
| slopes[nomeds] | 6.154 | 0.235 | 5.737 | 6.613 |
| slopes[alcohol] | 3.218 | 0.130 | 2.968 | 3.457 |
| slopes[nomeds:alcohol] | 1.902 | 0.086 | 1.743 | 2.066 |
az.summary(idata.posterior, kind="stats", var_names="alpha")| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| alpha | 10.38 | 0.52 | 9.447 | 11.395 |
平均の値は、私たちがデータを生成したときに規定した値に近接しています。
- データレートは一定で1
- 飲酒はベースレートの3倍
- 抗ヒスタミン剤の未摂取は、ベースレートの6倍増加
- 飲酒と抗ヒスタミン剤の未接種の両方はレートを倍にし、それは、それらのレートが独立していれば、予期されるのものです。もしそれらが独立していれば、その時両方のケースでは、ベースレートの3x6=18倍になりますが、代わりに、ベースレートは、3x6x2=36倍に増加します。
最後に、nsneeze_alphaの平均は、実際の値10と全く近接しています。
より詳しくはbambiの負の二項例を参照してください。
製作者
著者:Ian Ozsvald
更新:Abhipsha Das 2021年 8月
更新:Benjamin Vincent 2022年 6月 PyMC4