GLM: ロバスト線形回帰

このチュートリアルは、ベイジアン一般化線形回帰(GLMs)の３部構成の2番目です。初稿は、Thomas Wieckiのブログによります。

1. 線形回帰
2. ロバスト線形回帰
3. 階層線形回帰

このブログの投稿では、以下のことを記します。

• どのように少数の外れ値が線形回帰の適合に大きな影響を与えることができるか
• 正規尤度をステューデントTの分布に取り替えることで、ロバスト線形回帰をもたらすことができるか

線形回帰チュートリアルでは、私は、回帰線からくる平均と正規分布の尤度を最大化するのと同じように、どのように回帰線の二乗距離を最小にするか記述しました。この最後の確率式は、ベイジアン線形回帰モデルを簡単に定式化します。

これは、シミュレートしたデータ上で素晴らしく働きます。シミュレートしたデータの問題は、それがシミュレートされていることです。現実の世界においては、もっと乱雑で、正規のような仮定は、少数の外れ値で簡単に乱されます。

もし、私たちが最後の投稿からのシミュレートしたデータに、任意の外れ値を追加して、何が起きるか見てみましょう。

最初にモジュールをインポートします。

%matplotlib inline

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
import pytensor.tensor as pt
import xarray as xr

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

任意のデータを生成し、任意の外れ値を追加します。

size = 100
true_intercept = 1
true_slope = 2

x = np.linspace(0, 1, size)
# y = a + b*x
true_regression_line = true_intercept + true_slope * x
# add noise
y = true_regression_line + rng.normal(scale=0.5, size=size)

# Add outliers
x_out = np.append(x, [0.1, 0.15, 0.2])
y_out = np.append(y, [8, 6, 9])

data = pd.DataFrame(dict(x=x_out, y=y_out))

データを真の回帰線を一緒に図示します。(左上の角の3点が、私たちが追加した外れ値です)

fig = plt.figure(figsize=(7, 5))
ax = fig.add_subplot(111, xlabel="x", ylabel="y", title="Generated data and underlying model")
ax.plot(x_out, y_out, "x", label="sampled data")
ax.plot(x, true_regression_line, label="true regression line", lw=2.0)
plt.legend(loc=0);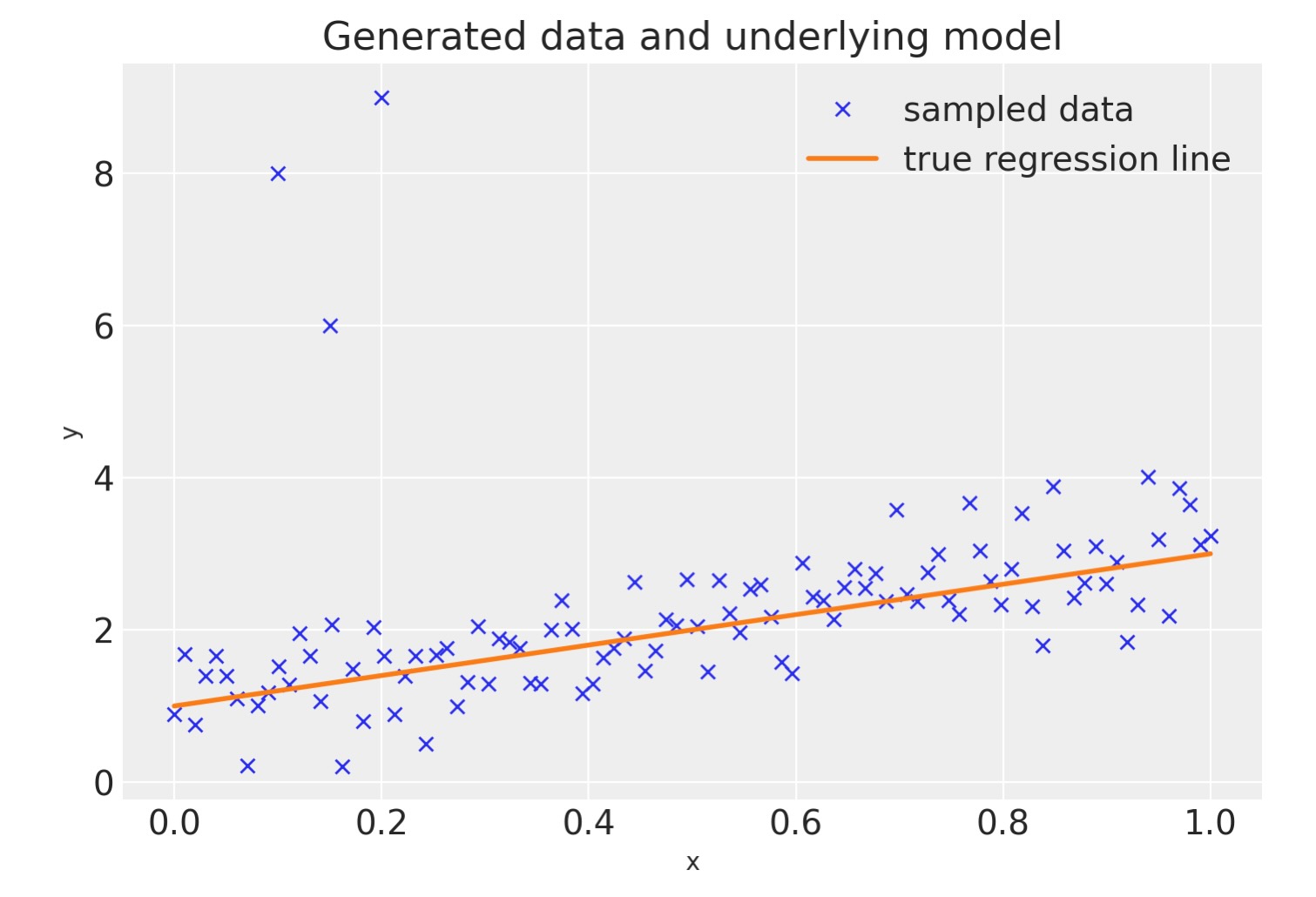

ロバスト回帰

正規尤度

正規尤度の回帰モデルで適合されたベイジアン線形回帰モデルで予測したら、何が起こるか見てみましょう。
均衡モデルがコードを一行使って構築できるように、バンビライブラリは、簡単に使えます。バンビを用いたこれと同じノートブックのバージョンが、Bambiのドキュメントで利用できます。

with pm.Model() as model:
    xdata = pm.ConstantData("x", x_out, dims="obs_id")

    # define priors
    intercept = pm.Normal("intercept", mu=0, sigma=1)
    slope = pm.Normal("slope", mu=0, sigma=1)
    sigma = pm.HalfCauchy("sigma", beta=10)

    mu = pm.Deterministic("mu", intercept + slope * xdata, dims="obs_id")

    # define likelihood
    likelihood = pm.Normal("y", mu=mu, sigma=sigma, observed=y_out, dims="obs_id")

    # inference
    trace = pm.sample(tune=2000)

適合の評価のために、以下のコードは、事後分布から回帰パラメータを得ることによって事後予測線形線を計算します。そして、それら20の回帰線を図示します。

post = az.extract(trace, num_samples=20)
x_plot = xr.DataArray(np.linspace(x_out.min(), x_out.max(), 100), dims="plot_id")
lines = post["intercept"] + post["slope"] * x_plot

plt.scatter(x_out, y_out, label="data")
plt.plot(x_plot, lines.transpose(), alpha=0.4, color="C1")
plt.plot(x, true_regression_line, label="True regression line", lw=3.0, c="C2")
plt.legend(loc=0)
plt.title("Posterior predictive for normal likelihood");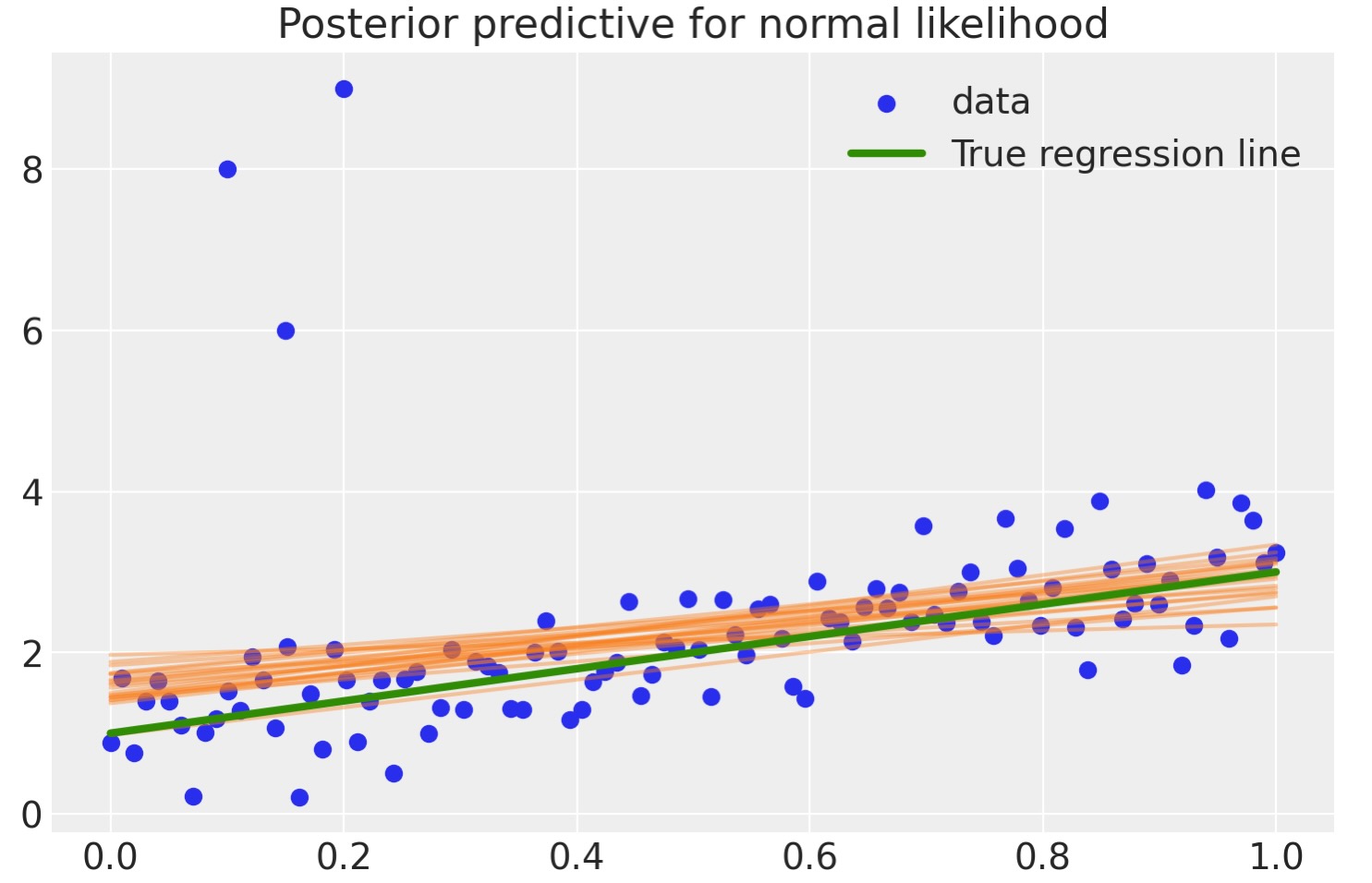

見てわかるように、適合は全く歪んでいます。異なる事後予測線形線の広い範囲によって示されるように私たちの予測は、かなり大きな不確実性を持っています。なぜこうなったのか？理由は、正規分布がテイル領域で量を持たないため、結果として外れ値が強力に適合に影響しています。

頻度主義ではロバスト回帰を予期します。適合を評価するのに二乗距離の計測を使いません。

しかし、ベイジアンはどうするか？問題は、正規分布の正しいテイルにあるため、私たちは、私たちのデータが正規分布ではないこと、代わりに次に見るようにヘビィテイルを持つステユーデントT分布による分布であることを、代わりに仮定できます。

それらを探して取得するために二つの分布を見てみましょう。

normal_dist = pm.Normal.dist(mu=0, sigma=1)
t_dist = pm.StudentT.dist(mu=0, lam=1, nu=1)
x_eval = np.linspace(-8, 8, 300)
plt.plot(x_eval, pm.math.exp(pm.logp(normal_dist, x_eval)).eval(), label="Normal", lw=2.0)
plt.plot(x_eval, pm.math.exp(pm.logp(t_dist, x_eval)).eval(), label="Student T", lw=2.0)
plt.xlabel("x")
plt.ylabel("Probability density")
plt.legend();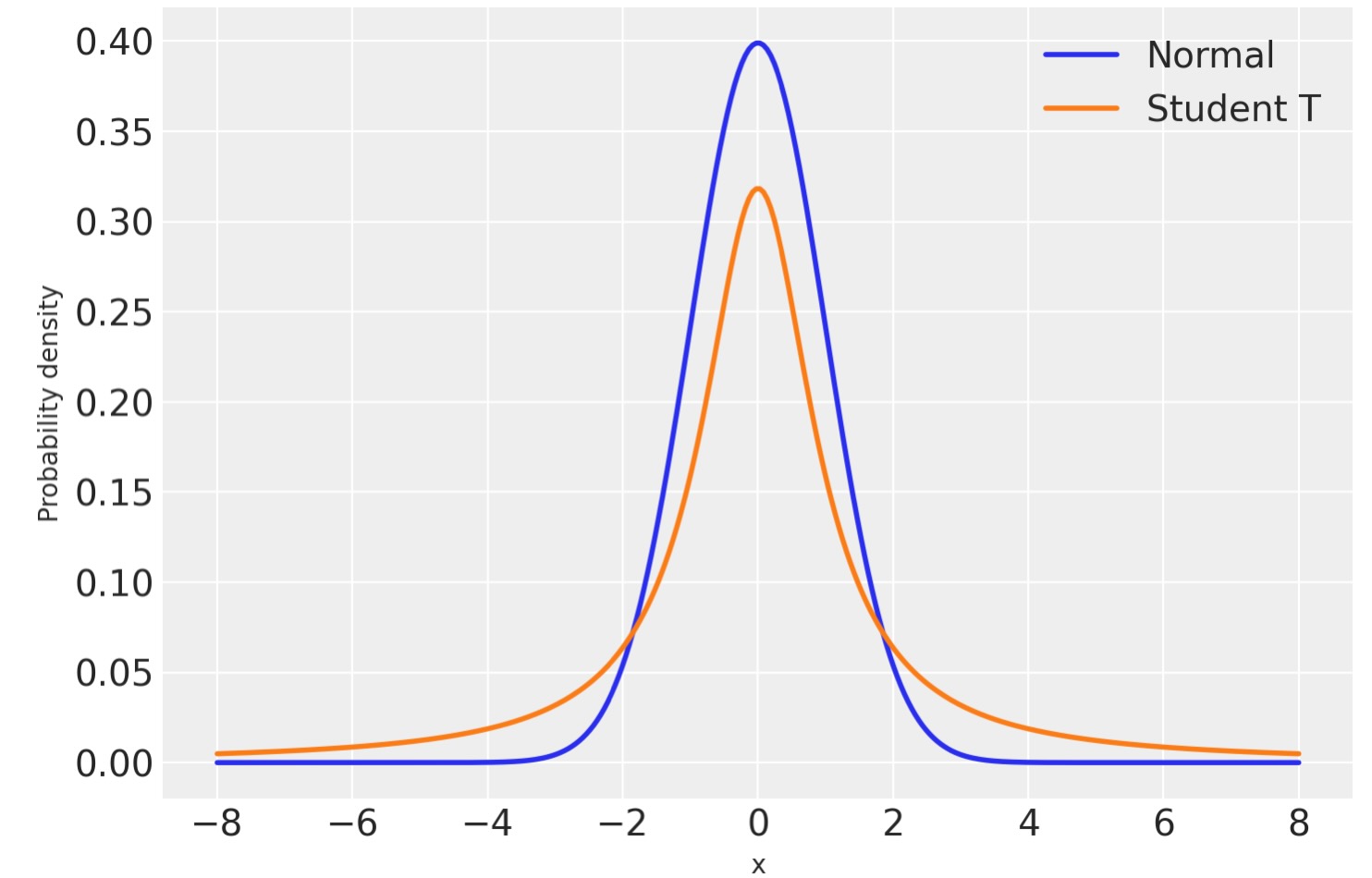

見てわかるように、平均から離れている値の確率は、正規分布の配位よりT分布の配位の方がより適合します。

以下は、正規分布に対して、自由度ν=3のステユーデントT分布に従う尤度の項を持つPyMCモデルです。

with pm.Model() as robust_model:
    xdata = pm.ConstantData("x", x_out, dims="obs_id")

    # define priors
    intercept = pm.Normal("intercept", mu=0, sigma=1)
    slope = pm.Normal("slope", mu=0, sigma=1)
    sigma = pm.HalfCauchy("sigma", beta=10)

    mu = pm.Deterministic("mu", intercept + slope * xdata, dims="obs_id")

    # define likelihood
    likelihood = pm.StudentT("y", mu=mu, sigma=sigma, nu=3, observed=y_out, dims="obs_id")

    # inference
    robust_trace = pm.sample(tune=4000)

robust_post = az.extract(robust_trace, num_samples=20)
x_plot = xr.DataArray(np.linspace(x_out.min(), x_out.max(), 100), dims="plot_id")
robust_lines = robust_post["intercept"] + robust_post["slope"] * x_plot

plt.scatter(x_out, y_out, label="data")
plt.plot(x_plot, robust_lines.transpose(), alpha=0.4, color="C1")
plt.plot(x, true_regression_line, label="True regression line", lw=3.0, c="C2")
plt.legend(loc=0)
plt.title("Posterior predictive for Student-T likelihood")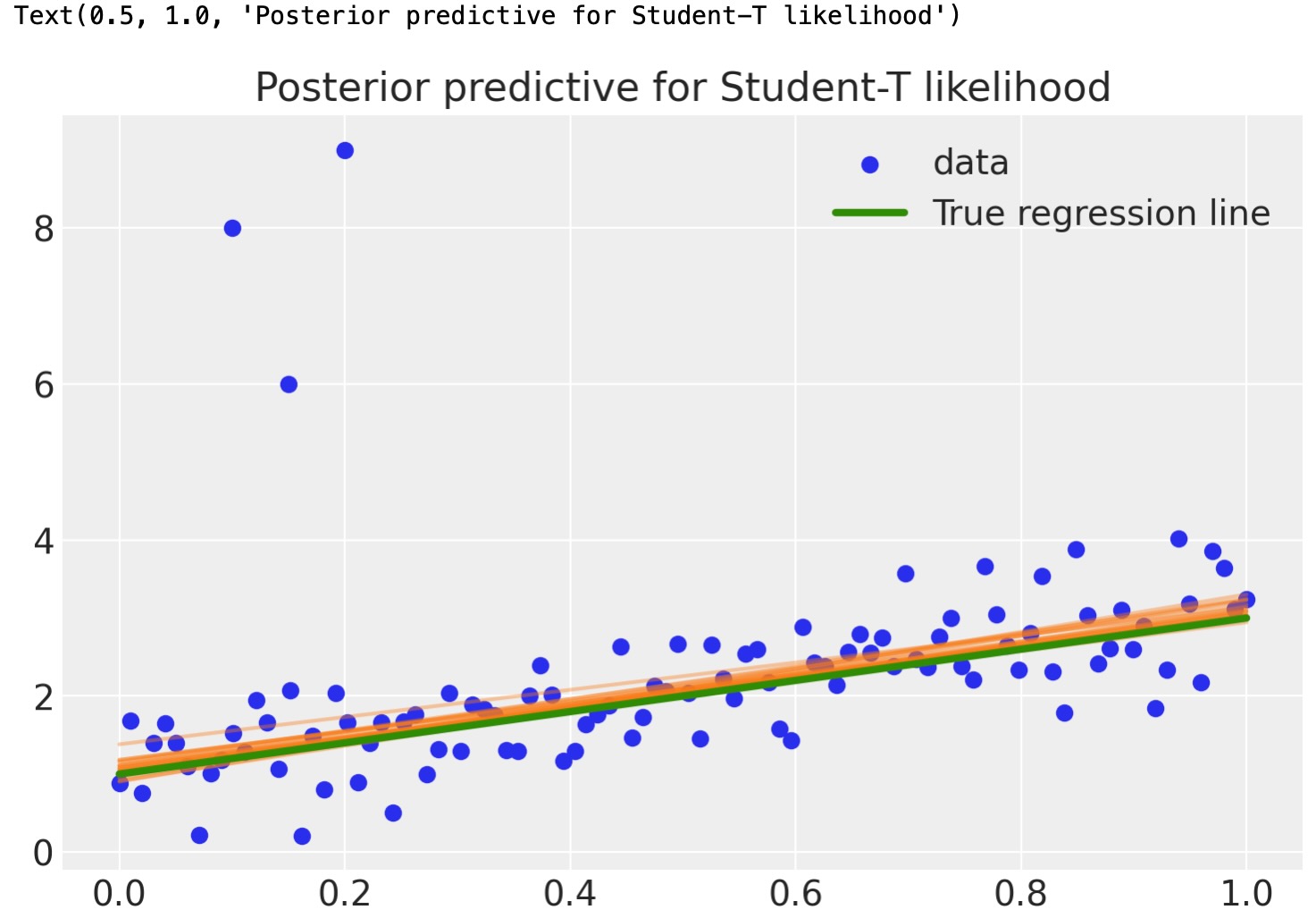

かなり良くなりました。外れ値はついに私たちの予測への影響はほとんどありません。　なぜなら私たちの尤度関数は、外れ値が正規分布下より正確であることを仮定します。

結果

• 正規分布からステューデントT分布へ尤度を変更することによって、それはテイルに多くの量もちます-私たちは、ロバスト回帰を実行することができます。