pyMCを使った Hogg 2010 信号とノイズの方法を用いた外れ値検知のロバスト回帰
モデル化の概念
- このモデルは二つの尤度を組み合わせたものとしてカスタム尤度の関数を使います。一つは、主要なデータ生成関数(私たちが注意する線形モデル)、もう一つは外れ値です。
- モデルは主流から外れません。そして、このように各データポイントのために外れ値を分類します。
- データセットは微小でこのノートブック専用です。xとy両方にエラーを含みます。しかし、ここではyのエラーだけ処理します。
補完的アプローチ
- これは、一般化線形モデル/GLM-ロバストの例で記述したように、スチューデントーTのロバスト回帰への補完的なアプローチです。そしてこのアプローチもまた比較されます。
- 簡易なツイッターによるやりとりの後、解説された、Dan FMによる要点も参照してください。彼の"Hogg解決"モデルは同じ構造のモデルを使用します。そして、懸命にも外れ値クラスを超えて主流から外れ無いだけでなく、pm.Deteministic(本当に有用な関数です)を使用してサンプリングする間もまた主流を外れることはありません。
- 尤度の評価は、本質的に”データ分析レシピ:モデルのデータへの適合”- Hogg [2010] のeqn17の複写です。
- モデルはJake VanderplasとBrigitta SipoczのAstroMLブックの実装[Zeijiko Ivezic et al, 2014, Vanderplas et al, 2012] から明確に適用されます。
設定
インストレーションノート
実装されたノートブックの環境と依存性の完全な詳細はオリジナルプロジェクトのREADMEを参照してください。このノートブックが実行する環境のまとめた結果は、Watermark項で利用できます。
注意
このノートブックはライブラリを使います、それはpyMCに依存していません。そしてこのノートブックで走らせるために、特別にインストールする必要があります。
%matplotlib inline
%config InlineBackend.figure_format = 'retina'インポート
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
from matplotlib.lines import Line2D
from scipy import statsaz.style.use("arviz-darkgrid")データ読み込み
下記URLで利用できるHogg 2010のデータを使います。
https://github.com/astroML/astroML/blob/master/astroML/datasets/hogg2010test.py
以下にハードコピーを記します。便利に使えるように非常に小さなデータセットになっています。
# cut & pasted directly from the fetch_hogg2010test() function
# identical to the original dataset as hardcoded in the Hogg 2010 paper
dfhogg = pd.DataFrame(
np.array(
[
[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56],
]
),
columns=["id", "x", "y", "sigma_y", "sigma_x", "rho_xy"],
)
dfhogg["id"] = dfhogg["id"].apply(lambda x: "p{}".format(int(x)))
dfhogg.set_index("id", inplace=True)
dfhogg.head()| x | y | sigma_y | sigma_x | rho_xy | |
|---|---|---|---|---|---|
| id | |||||
| p1 | 201.0 | 592.0 | 61.0 | 9.0 | -0.84 |
| p2 | 244.0 | 401.0 | 25.0 | 4.0 | 0.31 |
| p3 | 47.0 | 583.0 | 38.0 | 11.0 | 0.64 |
| p4 | 287.0 | 402.0 | 15.0 | 7.0 | -0.27 |
| p5 | 203.0 | 495.0 | 21.0 | 5.0 | -0.33 |
1. 基本EDA
探索データ分析
ノート:
- これはとても基本的なことです。そのため私たちは簡単にpymc部を取得できます。
- データセットはx、y両方にエラーを含みますが、ここではyのエラーだけを処理します。
- より詳細は、Hogg et al 2010を参照してください。
with plt.rc_context({"figure.constrained_layout.use": False}):
gd = sns.jointplot(
x="x",
y="y",
data=dfhogg,
kind="scatter",
height=6,
marginal_kws={"bins": 12, "kde": True, "kde_kws": {"cut": 1}},
joint_kws={"edgecolor": "w", "linewidth": 1.2, "s": 80},
)
_ = gd.ax_joint.errorbar(
"x", "y", "sigma_y", "sigma_x", fmt="none", ecolor="#4878d0", data=dfhogg, zorder=10
)
for idx, r in dfhogg.iterrows():
_ = gd.ax_joint.annotate(
text=idx,
xy=(r["x"], r["y"]),
xycoords="data",
xytext=(10, 10),
textcoords="offset points",
color="#999999",
zorder=1,
)
_ = gd.fig.suptitle(
(
"Original datapoints in Hogg 2010 dataset\n"
+ "showing marginal distributions and errors sigma_x, sigma_y"
),
y=1.05,
);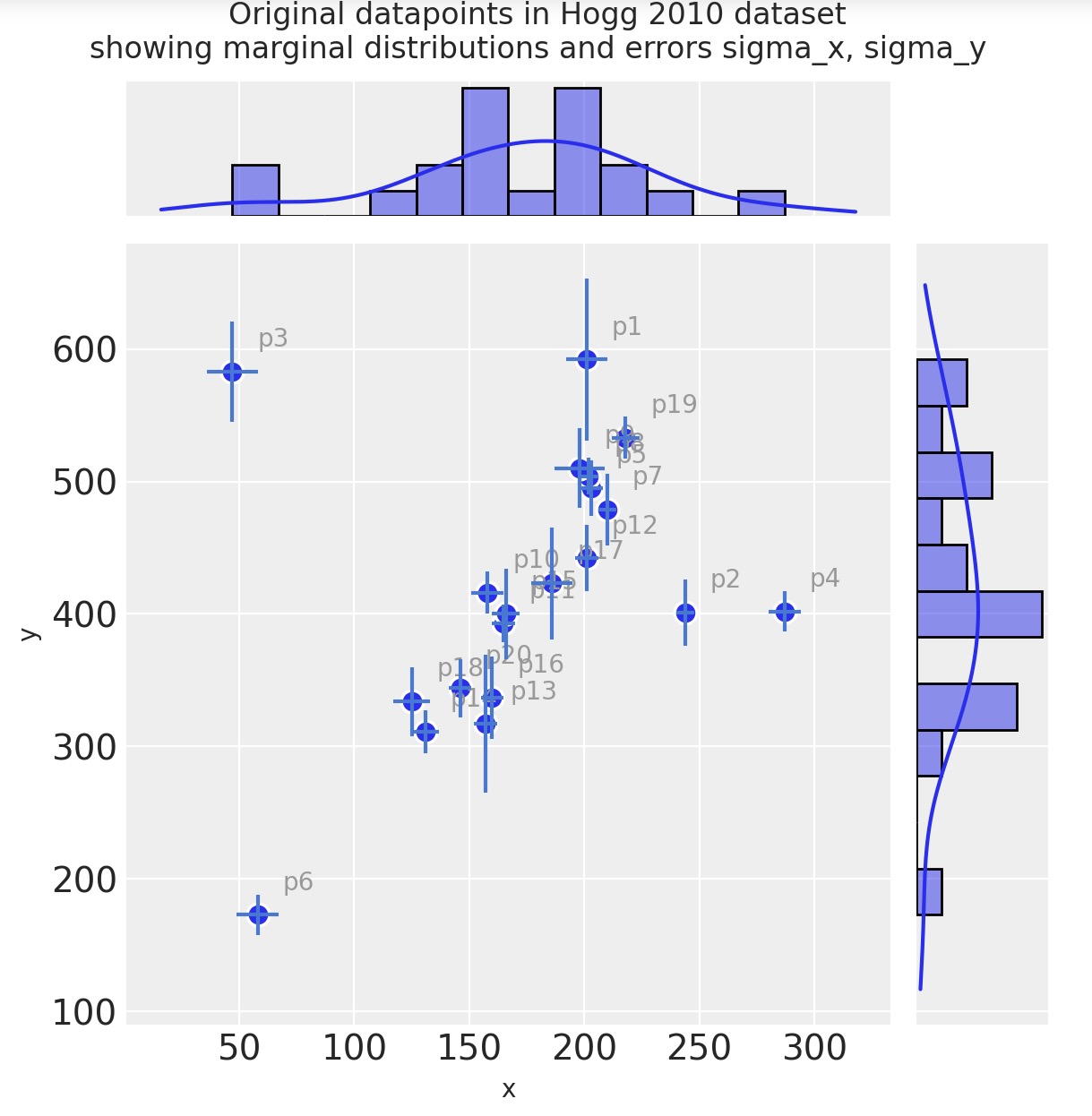
観測
- 目視で判断しただけでも、観測値のほとんどが、正のグラジェント直線の周りにあることがわかります。
- そのような直線から少数のデータポイントが外れ値であることが見えます。
- (xとyの独立した)エラーの尺度は、観測を横切って変異します。
2. 基本特徴エンジニアリング
2.1 変換とデータセットの正規化
入力値を線形モデルに正規化する共通の練習です。なぜなら、これは、同じ範囲に係数を置くように導き、Gelman[2008] がノートしたように、より直接的に比較できます。
そのため、以下、上記のGelmanの論文にあるように、ここで、標準偏差を2で除算します。
- モデルはとても簡単なので、scikit-learnの FunctionTransfermerを使うよりむしろ、直接正規化します。
- rho_xyを今回は無視します。
特徴yの出力のスケーリングとsigma_y:エラーの測定に関する 追加ノート
- これは慣例的ではありません。通常、特徴の出力はスケーリングしません。
- しかし、Hoggモデルでは、正規の慣例の二つの部分の尤度関数に適合させます。その尤度関数は、許容される外れ値をそれ自身の正規分布に適合させることによって、大域的に対数損失の最小化を促進させます。この外れ値の分布は、sigma_yからのオフセットsigma_y_outとして置いた、標準偏差を使って規定します。
- このオフセット値は、yの標準偏差として、同じスケールで再配置するために、sgma_yを要求する結果です。
正規化(平均値を中央に標準偏差を2分割)
dfhoggs = (dfhogg[["x", "y"]] - dfhogg[["x", "y"]].mean(0)) / (2 * dfhogg[["x", "y"]].std(0))
dfhoggs["sigma_x"] = dfhogg["sigma_x"] / (2 * dfhogg["x"].std())
dfhoggs["sigma_y"] = dfhogg["sigma_y"] / (2 * dfhogg["y"].std())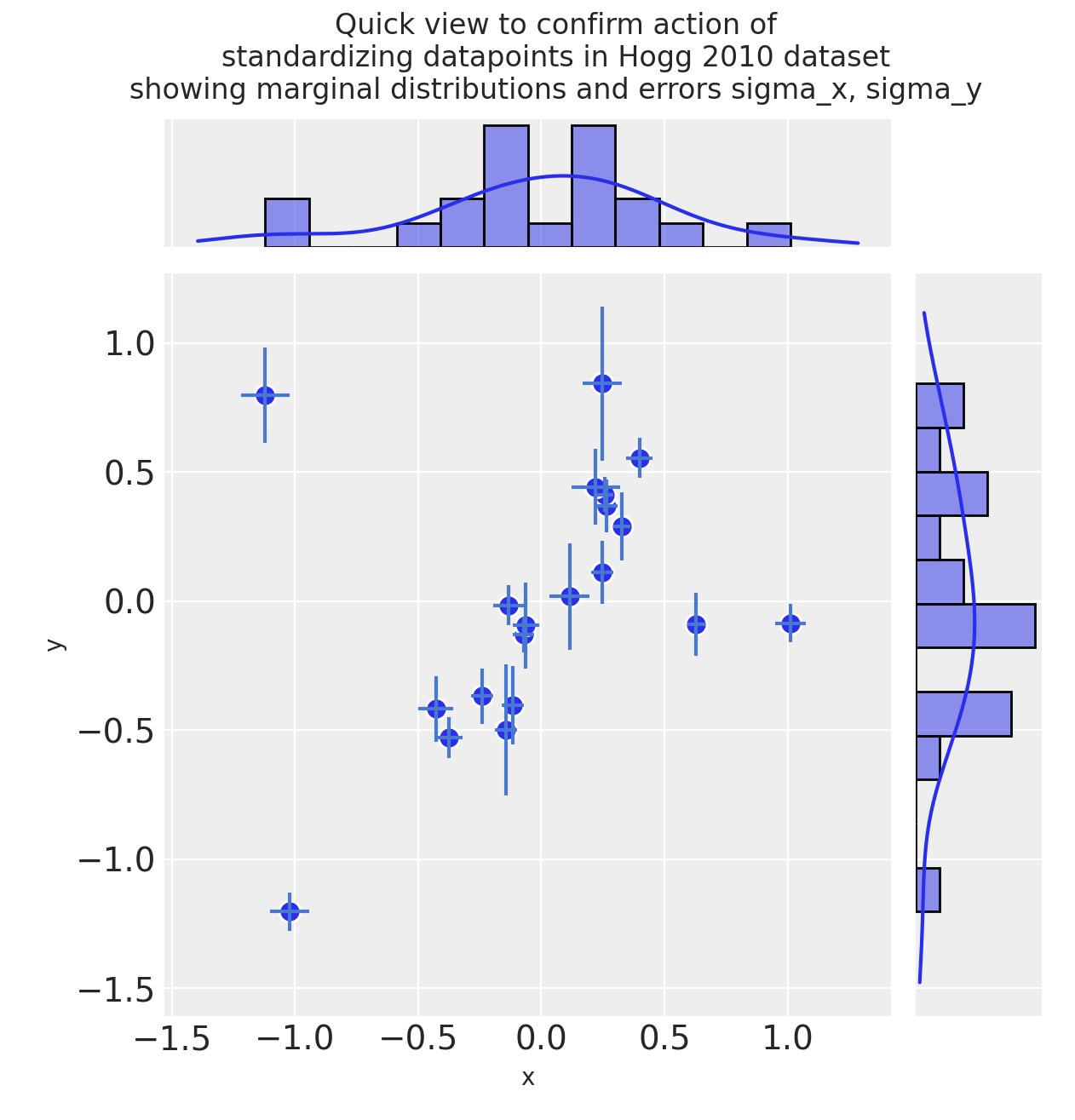
3. 外れ値を訂正しない簡易線形モデル
3.1 モデルの規定
先に進める前に、正規尤度関数による簡単な線形モデルへの適合をデモします。事前分布は正規分布です。そのため、リッジ回帰のOLSのように振る舞います。
ノート:データセットは、sigma_xとrho_xyを含みます。しかし、私たちは、sigma_yを使うことだけを選択します。

ここで
- ここで、β = {1, β j⊆Xj} <- Xjの線形係数、このケースでは、1+x
- σ = エラー項 このケースでは unplooled σ 各データポイントの測定エラー sigma_y
coords = {"coefs": ["intercept", "slope"], "datapoint_id": dfhoggs.index}
with pm.Model(coords=coords) as mdl_ols:
# Define weakly informative Normal priors to give Ridge regression
beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")
# Define linear model
y_est = beta[0] + beta[1] * dfhoggs["x"]
# Define Normal likelihood
pm.Normal("y", mu=y_est, sigma=dfhoggs["sigma_y"], observed=dfhoggs["y"], dims="datapoint_id")
pm.model_to_graphviz(mdl_ols)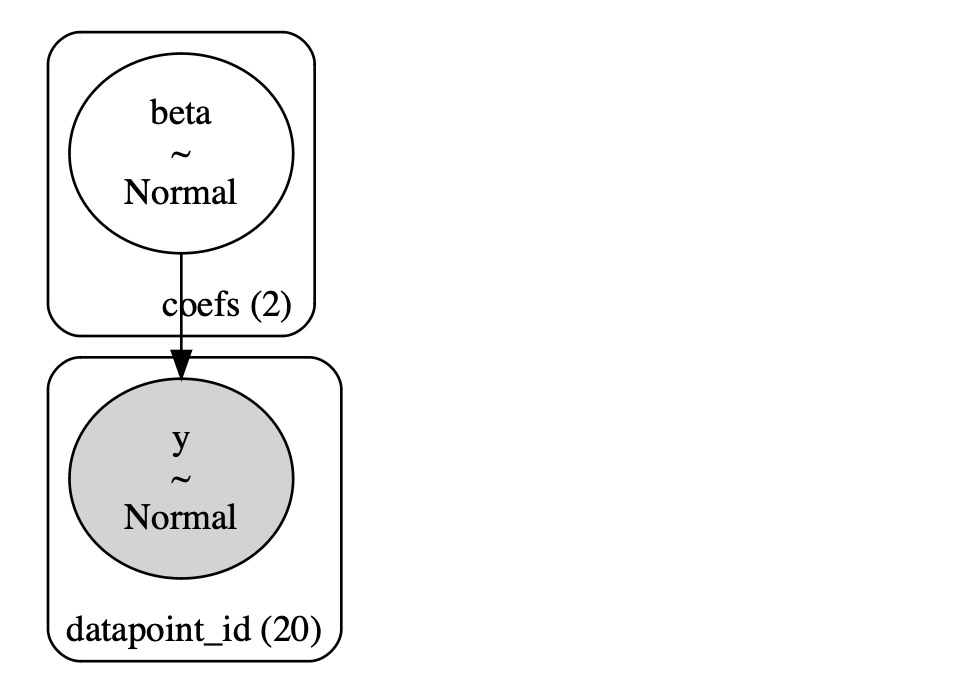
3.2 モデルの適合
私たちはここで、事前予測チェックのために意図的にステップを外します。
3.2.1 事後サンプル
with mdl_ols:
trc_ols = pm.sample(
tune=5000,
draws=500,
chains=4,
cores=4,
init="advi+adapt_diag",
n_init=50000,
)
3.2.2 診断図
ノート:OLS適合と最終比較図のデータポイントを比較します。
トレース図
_ = az.plot_trace(trc_ols, compact=False)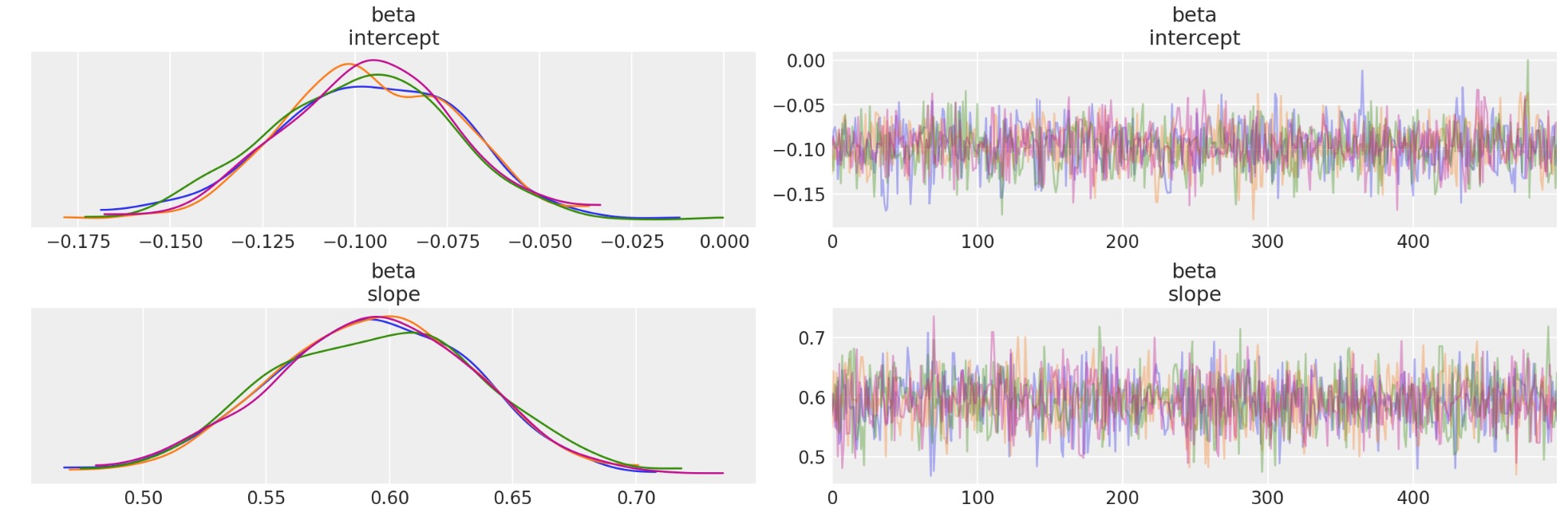
事後接合分布を図示します。2Dの接合分布として簡単に図示することができます。
marginal_kwargs = {"kind": "kde", "rug": True, "color": "C0"}
ax = az.plot_pair(
trc_ols,
var_names="beta",
marginals=True,
kind=["scatter", "kde"],
scatter_kwargs={"color": "C0", "alpha": 0.4},
marginal_kwargs=marginal_kwargs,
)
fig = ax[0, 0].get_figure()
fig.suptitle("Posterior joint distribution (mdl_ols)", y=1.02);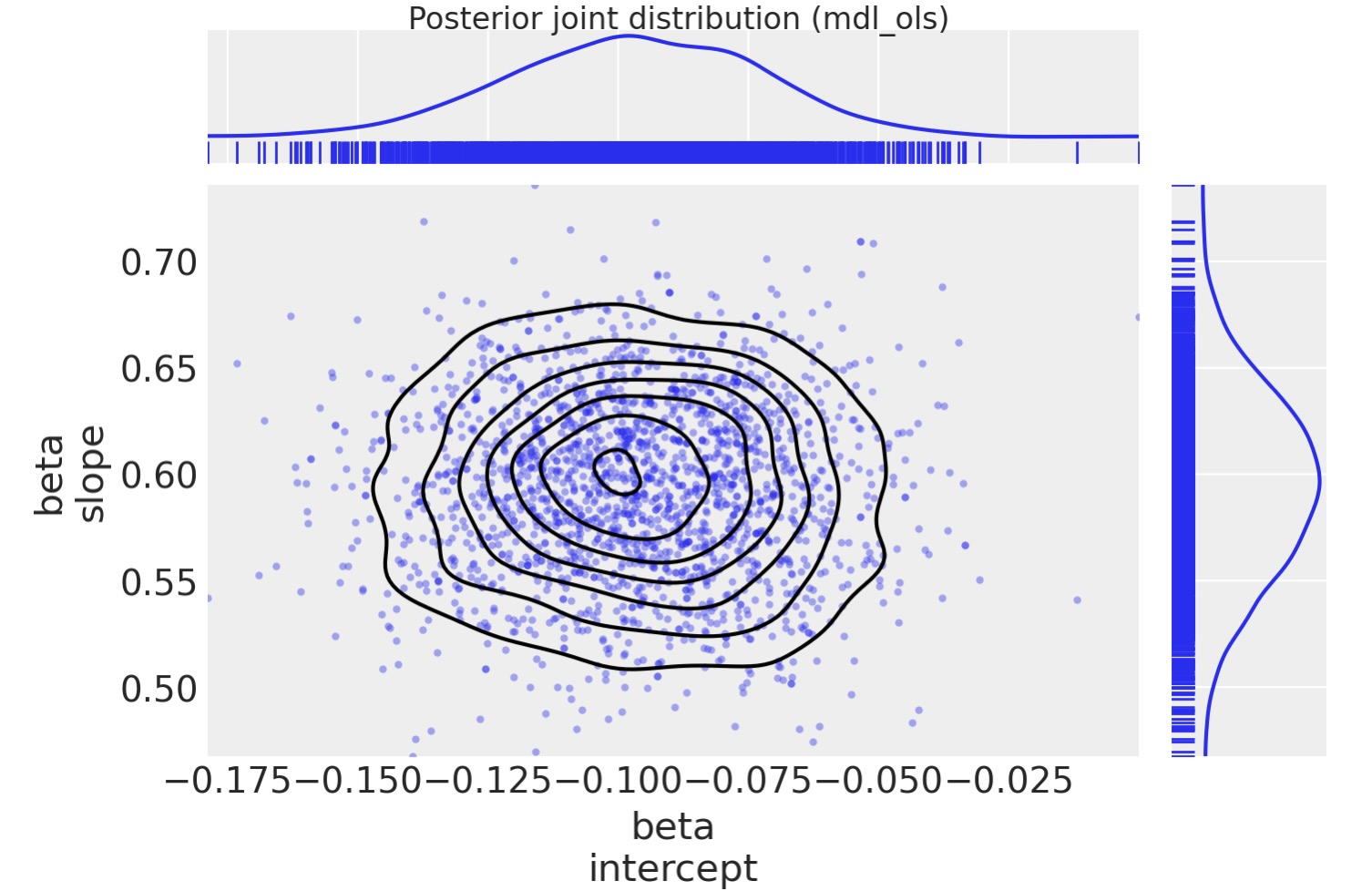
4.ロバスト ステユーデントT 尤度の簡易線形モデル
PyMC3ドキュメントにあるThomas Wieckiのノートブックの例にあるステユーデントTを基礎とした方法と直接比較するために、この簡潔なセクションを追加します。
尤度のために、正規分布を使う代わりに厚いテイルを持つステユーデントTを使います。理論では、これは、尤度の予測において外れ値に微小な影響を持つことを許容します。この方法は内部、外れ値フラグの出力しません。しかし、以下の信号とノイズモデルより簡単に高速に実行可能です。そのため、比較的に役立ちます。
4.1 モデルの規定
この変更では、尤度が外れ値に対し、より強くになることを許容します。(厚いテイルを持ちます)

ここで
- β = {1, β j⊆Xj} <- Xjの線形係数、このケースでは、1+x
- σ = エラー項 このケースでは unplooled σ 各データポイントの測定エラー sigma_y
- ν = 自由度 <- 厚いテイルのpdfを許容し、外れ値のデータポイントからの影響を少なくします。
ノート:データセットはsigma_y とrho_xyが利用できます。しかし、この例題ではsigma_yを使うことだけを選択します。
with pm.Model(coords=coords) as mdl_studentt:
# define weakly informative Normal priors to give Ridge regression
beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")
# define linear model
y_est = beta[0] + beta[1] * dfhoggs["x"]
# define prior for StudentT degrees of freedom
# InverseGamma has nice properties:
# it's continuous and has support x ∈ (0, inf)
nu = pm.InverseGamma("nu", alpha=1, beta=1)
# define Student T likelihood
pm.StudentT(
"y", mu=y_est, sigma=dfhoggs["sigma_y"], nu=nu, observed=dfhoggs["y"], dims="datapoint_id"
)
pm.model_to_graphviz(mdl_studentt)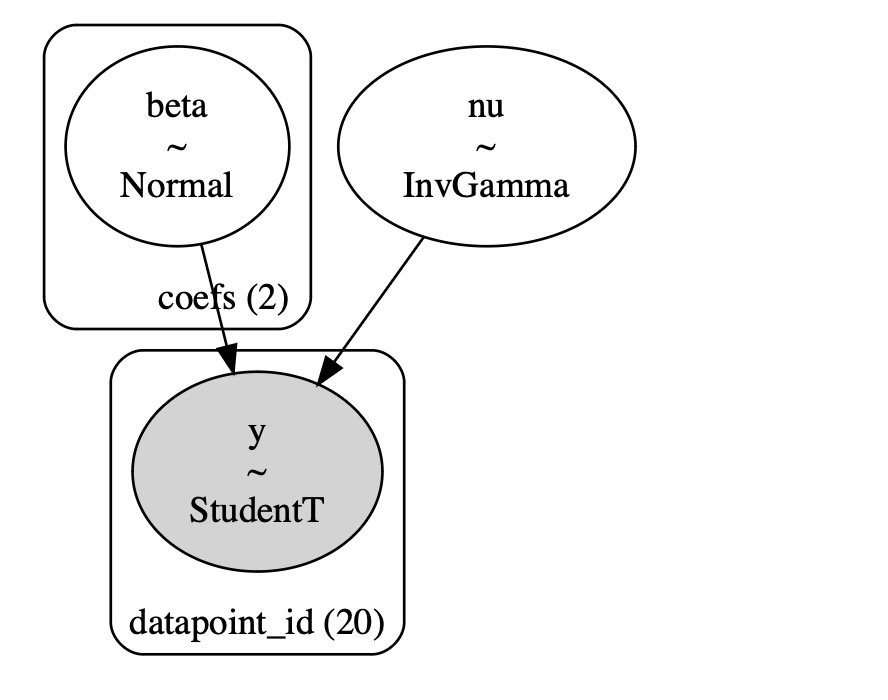
4.2 モデルの適合
4.2.1 事後サンプル
with mdl_studentt:
trc_studentt = pm.sample(
tune=5000,
draws=500,
chains=4,
cores=4,
init="advi+adapt_diag",
n_init=50000,
)
4.2.2 診断図
ノート:スチューデントTの適合を図示します。そして、最終の比較図とデータポイントを比較します。
トレース図
_ = az.plot_trace(trc_studentt, compact=False);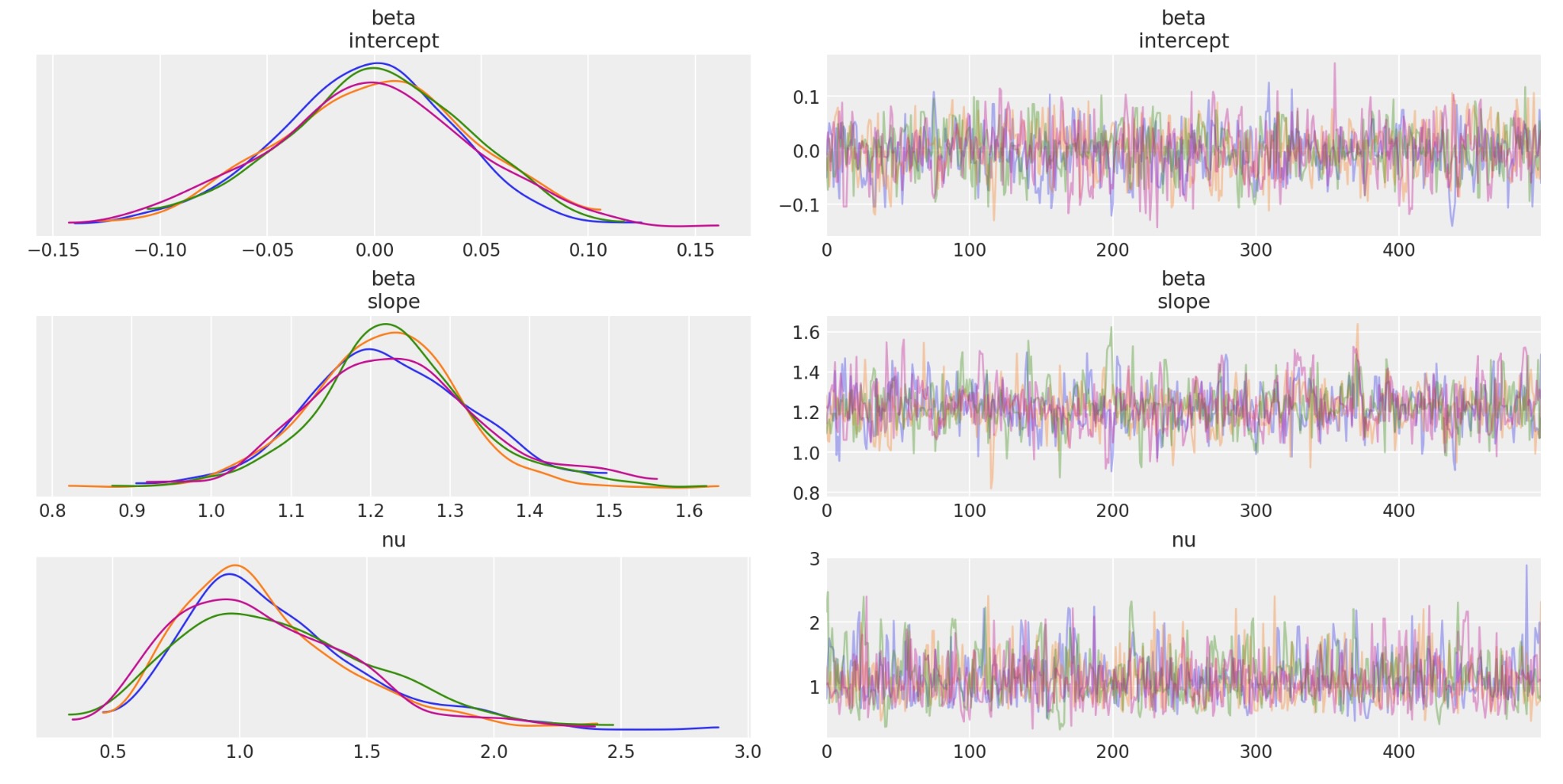
事後適合分布を図示します。
marginal_kwargs["color"] = "C1"
ax = az.plot_pair(
trc_studentt,
var_names="beta",
kind=["scatter", "kde"],
divergences=True,
marginals=True,
marginal_kwargs=marginal_kwargs,
scatter_kwargs={"color": "C1", "alpha": 0.4},
)
ax[0, 0].get_figure().suptitle("Posterior joint distribution (mdl_studentt)");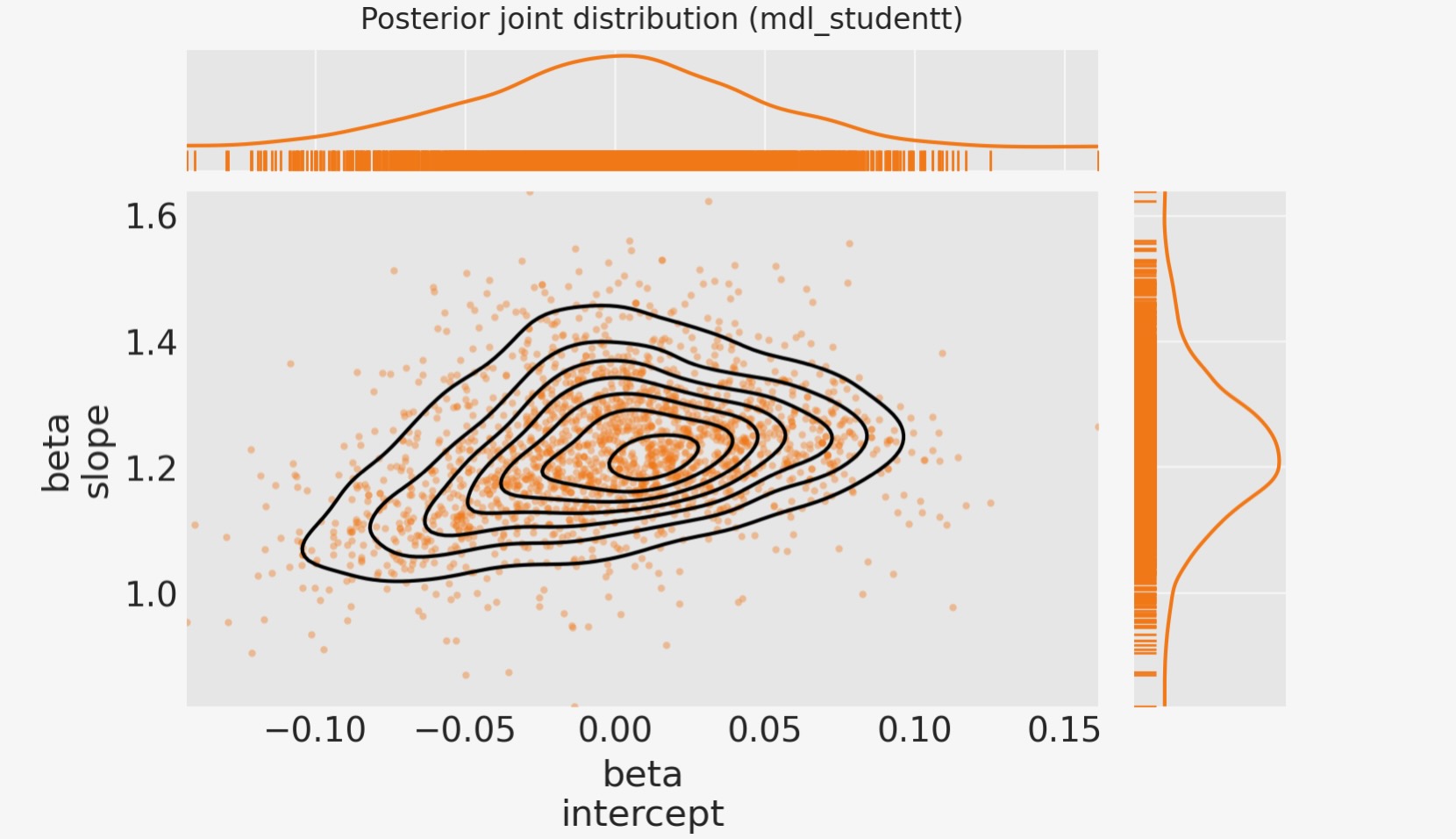
4.2.3 事後接合分布のOLSからステユーデントTへの遷移図
marginal_kwargs["rug"] = False
marginal_kwargs["color"] = "C0"
ax = az.plot_pair(
trc_ols,
var_names="beta",
kind=["scatter", "kde"],
divergences=True,
figsize=[12, 12],
marginals=True,
marginal_kwargs=marginal_kwargs,
scatter_kwargs={"color": "C0", "alpha": 0.4},
kde_kwargs={"contour_kwargs": {"colors": "C0"}},
)
marginal_kwargs["color"] = "C1"
az.plot_pair(
trc_studentt,
var_names="beta",
kind=["scatter", "kde"],
divergences=True,
marginals=True,
marginal_kwargs=marginal_kwargs,
scatter_kwargs={"color": "C1", "alpha": 0.4},
kde_kwargs={"contour_kwargs": {"colors": "C1"}},
ax=ax,
)
ax[0, 0].get_figure().suptitle(
"Posterior joint distributions\n(showing general movement from OLS to StudentT)"
);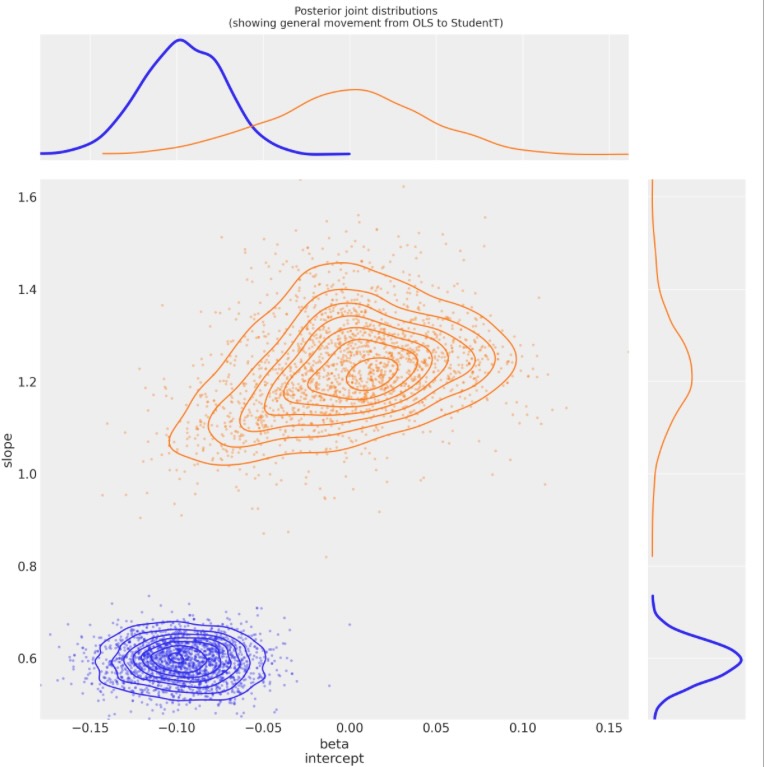
観測
- 両方のβパラメータはOLS回帰より大きい変異が見られます。
- これは、νが nu~1の値に収束するように見えるためです。ファットテイルな尤度は薄いテイルよりもよく適合することを示しています。
- パラメータβ(切片)はより一層ゼロに近づきます。興味深いことに、理論的な関係であるy ~ f(x)がオフセットを持たないならば、この中央の平均のデータセットのために、切片は実際0になります。それはOLSモデルの外れ値により、もっと簡単にそうなります。
- βパラメータ1(傾き)はおそらくよりいっそう理論的に関数f(x)に近づきます。
5.際立った外れ値へのカスタム尤度による線形モデル
(Hogg 2010)の論文と、モデル化の技術についてより完全な情報があるJake Vanderplasのコードを読んでください。
一般的な考えは、どちらか一方により記述できるデータポイントからなる混合モデルを作ることです。
- 提案する(線形)モデルは(データポイントは内部)
- 2番目のモデル、これも利便性のため線形モデルで提案しますが、異なる平均値と分散を持っています。(このデータポイントは外れ値です)
5.1 モデルの規定
尤度は、二つの尤度を混合して評価します。一つは内部、もう一つは外れ値です。ベルヌーイ分布は、N個のデータポイントを内部か外れ値のグループのどちらか一方に、ランダムに振り分けます。そして、いつものようにロバストモデルパラメータと内部、外れ値フラグを推量できるようにモデルをサンプルします。
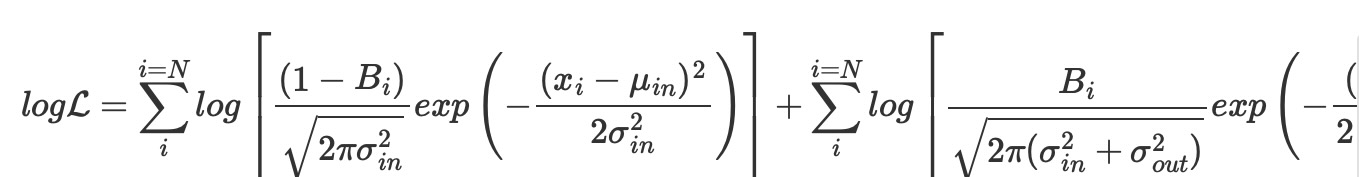
ここで
- Bi はベルヌーイ分布 Bi ⊆{0(inlier), 1(outlier)}
- μin = βT xi 他の観測値の前、β = {1, β j⊆Xj} <- Xj の線型係数、このケースでは 1 + x
- σin = ノイズ項 <- このケースでは、unpooled σi 各データポイントのエラー sigma_y を測定します。
- μout <- 外れ値のためのランダムpooled 変数
- σout = 追加のノイズ項 <- 外れ値のためのランダムなunpooled 変数
このノートブックは、尤度を作るためにlogpを合体させたPotential()クラスを使います。そして、ここでベルヌーイ切替変数、特徴を観測せずにモデルを構築します。
Potentialの使い方には記しません。Potentialの使い方の詳細に関して参照する価値のある他の資料が利用できます。
- Junpenglaoの尤度のプレゼンテーション PyData ベルリン 2018
- 論文・講義と相互確認の例
- CamDPの確率プログラミングと 'Bayesian methods for Hackers' 5章 損失関数,例:正しい価格によるショーケースの最適化。
- 他の使用例、左のサイドバーにあるpymc3.Potentialタグを探してください。(原文はpymcのサイトに記載)
with pm.Model(coords=coords) as mdl_hogg:
# state input data as Theano shared vars
tsv_x = pm.ConstantData("tsv_x", dfhoggs["x"], dims="datapoint_id")
tsv_y = pm.ConstantData("tsv_y", dfhoggs["y"], dims="datapoint_id")
tsv_sigma_y = pm.ConstantData("tsv_sigma_y", dfhoggs["sigma_y"], dims="datapoint_id")
# weakly informative Normal priors (L2 ridge reg) for inliers
beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")
# linear model for mean for inliers
y_est_in = beta[0] + beta[1] * tsv_x # dims="obs_id"
# very weakly informative mean for all outliers
y_est_out = pm.Normal("y_est_out", mu=0, sigma=10, initval=pm.floatX(0.0))
# very weakly informative prior for additional variance for outliers
sigma_y_out = pm.HalfNormal("sigma_y_out", sigma=10, initval=pm.floatX(1.0))
# create in/outlier distributions to get a logp evaluated on the observed y
# this is not strictly a pymc3 likelihood, but behaves like one when we
# evaluate it within a Potential (which is minimised)
inlier_logp = pm.logp(pm.Normal.dist(mu=y_est_in, sigma=tsv_sigma_y), tsv_y)
outlier_logp = pm.logp(pm.Normal.dist(mu=y_est_out, sigma=tsv_sigma_y + sigma_y_out), tsv_y)
# frac_outliers only needs to span [0, .5]
# testval for is_outlier initialised in order to create class asymmetry
frac_outliers = pm.Uniform("frac_outliers", lower=0.0, upper=0.5)
is_outlier = pm.Bernoulli(
"is_outlier",
p=frac_outliers,
initval=(np.random.rand(tsv_x.eval().shape[0]) < 0.4) * 1,
dims="datapoint_id",
)
# non-sampled Potential evaluates the Normal.dist.logp's
potential = pm.Potential(
"obs",
((1 - is_outlier) * inlier_logp).sum() + (is_outlier * outlier_logp).sum(),
)5.2 モデルを適合する
5.2.1 事後サンプル
pm.sampleは便利に自動的に、サンプリング過程を合体して生成します。
- 微分サンプラーを使ってベルヌーイ変数()をサンプル
- 連続サンプラーを使って連続変数をサンプル
詳しいノート:
- これは、ADVIで初期化できないことを意味します。そのため、jitter+ adapt_diagを使って初期化します。
- 特別ばステッパーにkwargsを渡すために、ステッパの小文字名をdict形式のデータ型で包み込みます。e.g nuts={'target_accept':0.85}
with mdl_hogg:
trc_hogg = pm.sample(
tune=10000,
draws=500,
chains=4,
cores=4,
init="jitter+adapt_diag",
nuts={"target_accept": 0.99},
)
5.2.2 診断図
このモデルの適合を図示し、最終的な比較図でデータポイントを比較します。
rvs = ["beta", "y_est_out", "sigma_y_out", "frac_outliers"]
_ = az.plot_trace(trc_hogg, var_names=rvs, compact=False);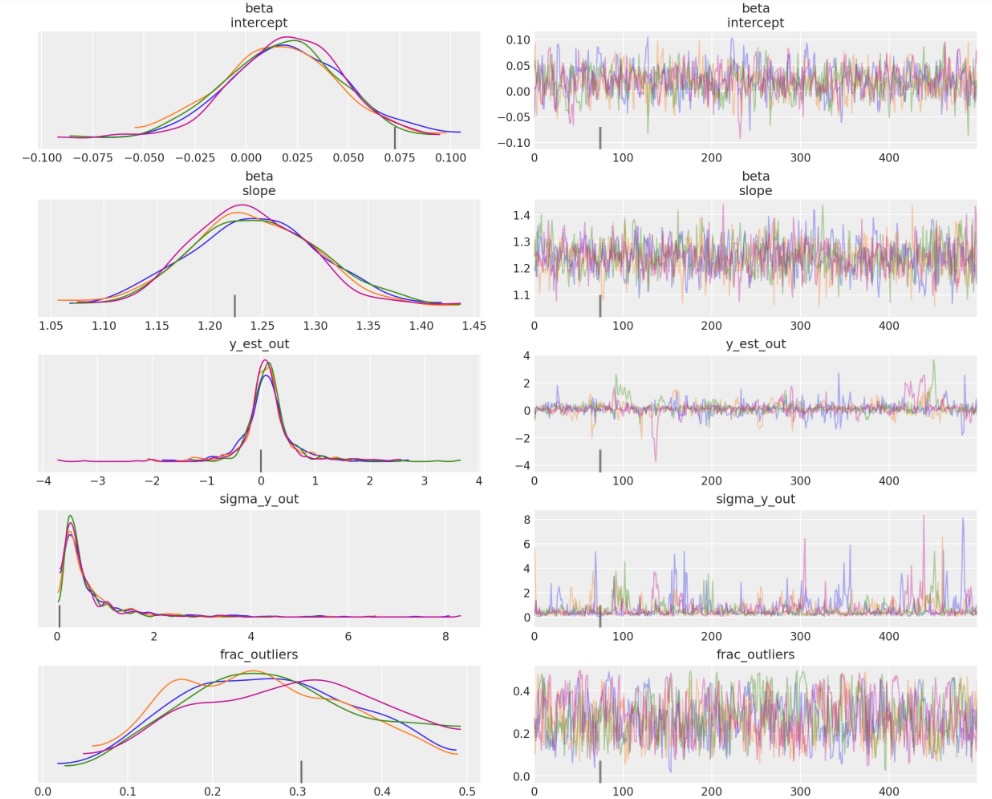
観測
- デフォルトでtarget_accept=0.8 多くの発散があります。これは、特に安定したモデルでは無いことを示しています。
- しかし、target_accept=0.9では(5000から10000にtuneを増加した)、トレースは少数の発散を見せています。それは多少良い振る舞いに見えます。
- 観測値(inlier)モデルのベータパラメータ、外れ値モデルのy_est_outパラメータにとって、(平均は)適当な集まりに見えます。
- 外れ値モデルのパラメータy_sigma_out(追加のpoolした変数)のためのトレースは、時に少し乱れます。
- frac_outliersはとても分散されていて興味深いです。これは全く平坦な分布です。他の観測値と外れ値の状態が問題となる少数のデータポイントがあることが提案されています。
- 実際にThomasが彼のv2.0のノートブックに記しているように、私たちは、はっきりと潜在ラベルを二者択一のとしてモデル化しているため、サンプラーは問題を抱えます。-このモデルを境界混合モデルに書き換える方が良いでしょう。
簡単なトレースの結果 inc rhat
az.summary(trc_hogg, var_names=rvs)| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta[intercept] | 0.019 | 0.028 | -0.033 | 0.074 | 0.001 | 0.001 | 978.0 | 1049.0 | 1.00 |
| beta[slope] | 1.241 | 0.060 | 1.125 | 1.347 | 0.002 | 0.001 | 1241.0 | 1177.0 | 1.00 |
| y_est_out | 0.130 | 0.485 | -0.712 | 1.110 | 0.025 | 0.018 | 541.0 | 279.0 | 1.01 |
| sigma_y_out | 0.651 | 0.766 | 0.056 | 1.835 | 0.038 | 0.027 | 483.0 | 611.0 | 1.01 |
| frac_outliers | 0.272 | 0.104 | 0.099 | 0.465 | 0.005 | 0.003 | 519.0 | 746.0 | 1.01 |
事後接合分布を図示します。
(これは、トレース上にたくさん集まっている、特にこのケースの診断において有用です。:モデルの仕様は奇妙な振る舞いに導きます)
marginal_kwargs["color"] = "C2"
marginal_kwargs["rug"] = True
x = az.plot_pair(
data=trc_hogg,
var_names="beta",
kind=["kde", "scatter"],
divergences=True,
marginals=True,
marginal_kwargs=marginal_kwargs,
scatter_kwargs={"color": "C2"},
)
ax[0, 0].get_figure().suptitle("Posterior joint distribution (mdl_hogg)");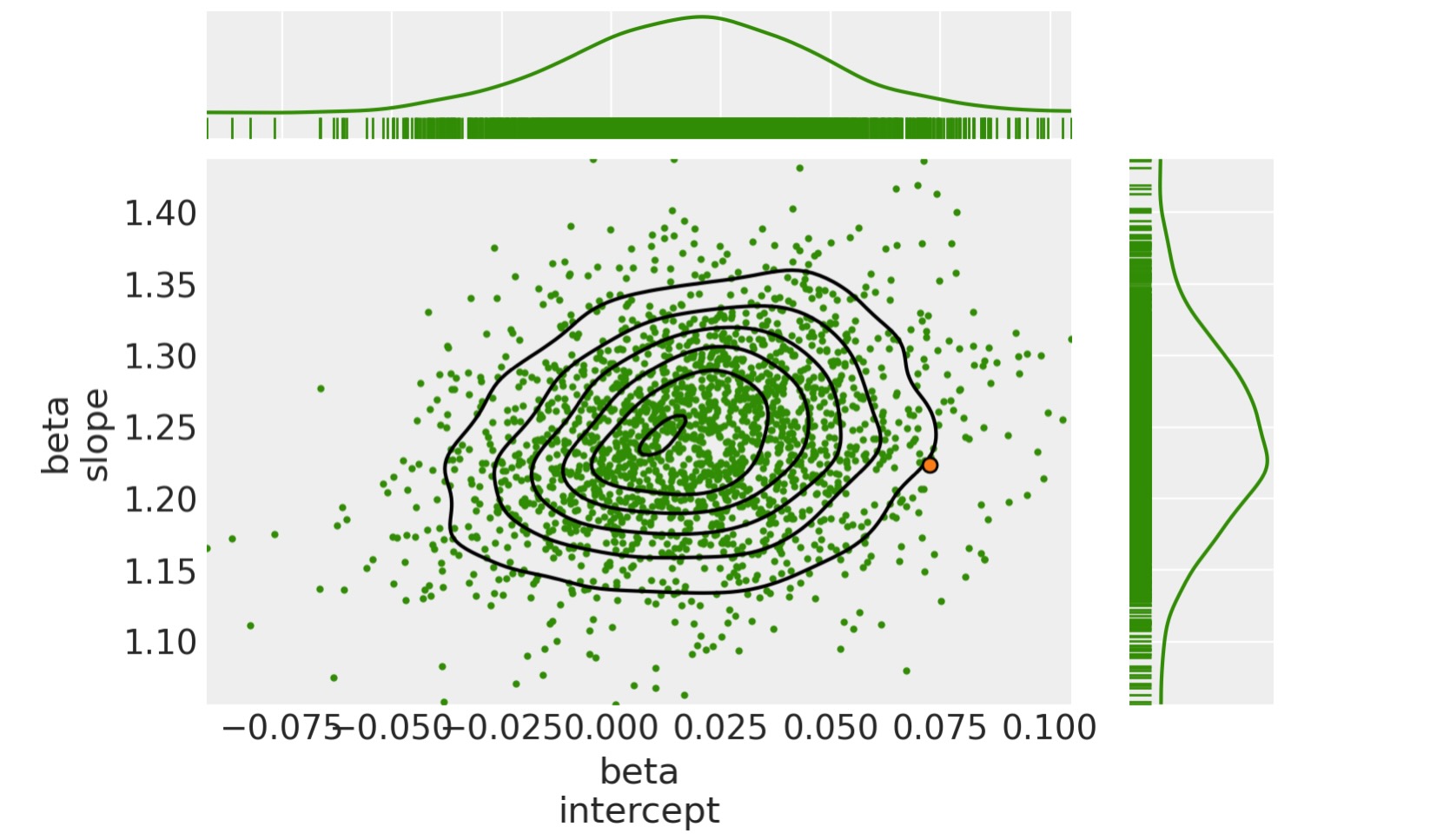
5.2.3 OLSからステユーデントT Hoggへの事後接合分布の遷移図
kde_kwargs = {"contour_kwargs": {"colors": "C0", "zorder": 4}, "contourf_kwargs": {"alpha": 0}}
marginal_kwargs["rug"] = False
marginal_kwargs["color"] = "C0"
ax = az.plot_pair(
trc_ols,
var_names="beta",
kind="kde",
divergences=True,
marginals=True,
marginal_kwargs={"color": "C0"},
kde_kwargs=kde_kwargs,
figsize=(8, 8),
)
marginal_kwargs["color"] = "C1"
kde_kwargs["contour_kwargs"]["colors"] = "C1"
az.plot_pair(
trc_studentt,
var_names="beta",
kind="kde",
divergences=True,
marginals=True,
marginal_kwargs=marginal_kwargs,
kde_kwargs=kde_kwargs,
ax=ax,
)
marginal_kwargs["color"] = "C2"
kde_kwargs["contour_kwargs"]["colors"] = "C2"
az.plot_pair(
data=trc_hogg,
var_names="beta",
kind="kde",
divergences=True,
marginals=True,
marginal_kwargs=marginal_kwargs,
kde_kwargs=kde_kwargs,
ax=ax,
show=True,
)
ax[0, 0].get_figure().suptitle(
"Posterior joint distributions" + "\nOLS, StudentT, and Hogg (inliers)"
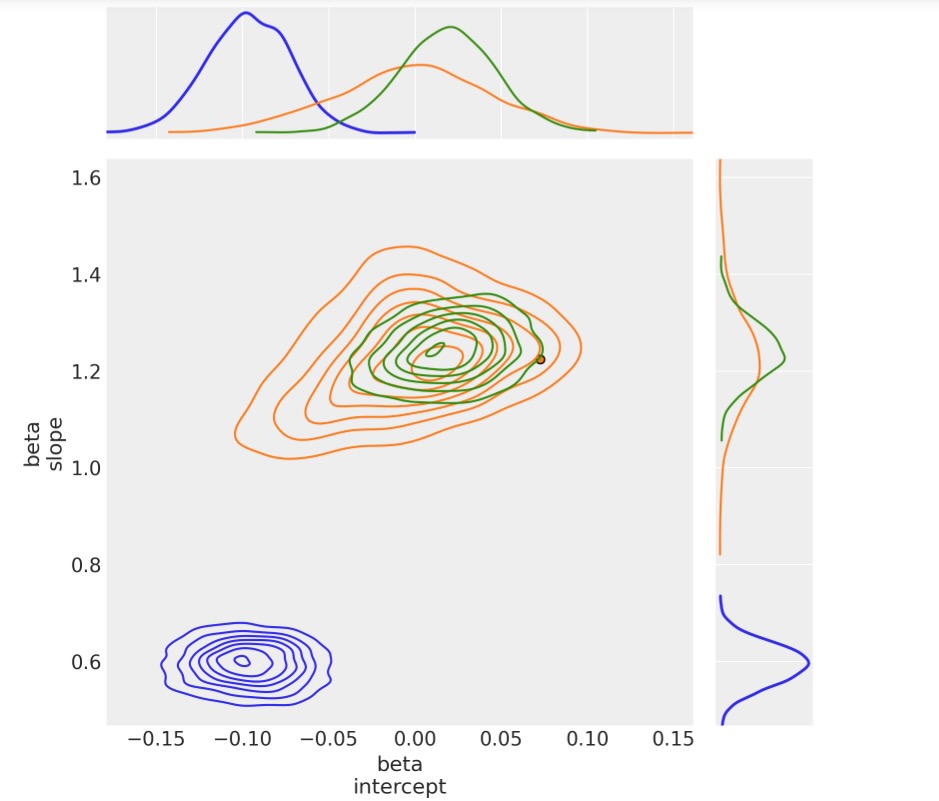
);
観測
- hogg_inlierとstudentモデルはb0_interceptとb1_slopeが同じ範囲に集まります。hogg_outlierモデルはstudentモデルの厚いテイルと同じ働きを実行するかもしれないことをしましています。:それは、対数確率がデータポイントの主要な線形分布からより大きく離れることを許容します。
- 予期する通り、(正規なので)hogg_inlierの事後は薄いテイルになり、より大きい確率で中央の値に集中します。
- hogg_inlierモデルはまた、b0_interceptのolsとstudentモデル遠く離れて見えます。外れ値は特別な次元で本当に歪めて提案されます。
5.3 外れ値の宣言
5.3.1 他の観測値と外れ値予測の範囲の図示
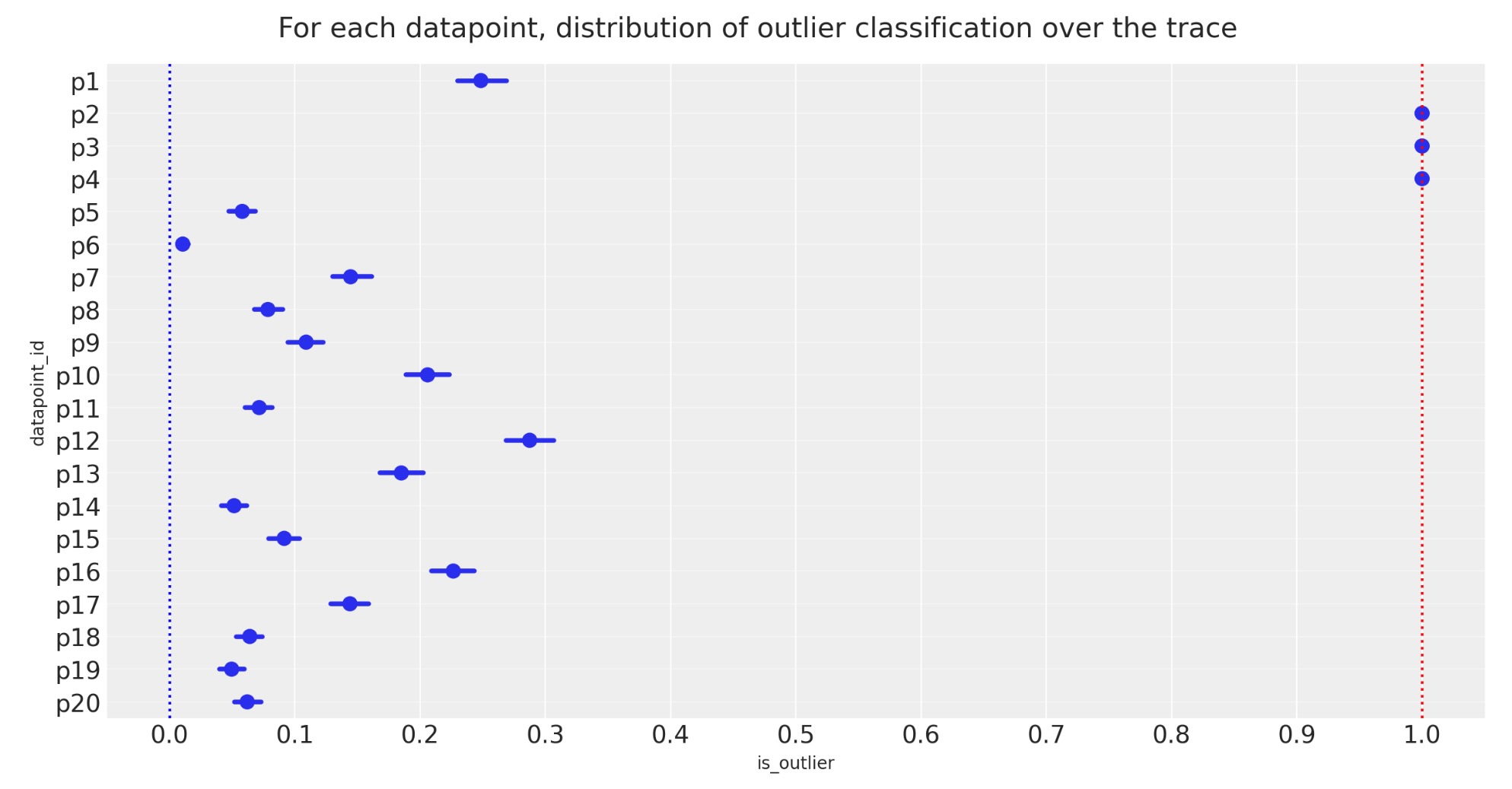
トレースの各ステップで各データポイントは、観測値か外れ値かどちらか一方になります。私たちは、データポイントが一つの状態にあるか又は別の状態にある時間が、異なって経過することを望んでいます。そのため、20データポイントのそれぞれについて簡単な状態数をみていきましょう。
dfm_outlier_results = trc_hogg.posterior.is_outlier.to_dataframe().reset_index()
with plt.rc_context({"figure.constrained_layout.use": False}):
gd = sns.catplot(
y="datapoint_id",
x="is_outlier",
data=dfm_outlier_results,
kind="point",
join=False,
height=6,
aspect=2,
)
_ = gd.fig.axes[0].set(xlim=(-0.05, 1.05), xticks=np.arange(0, 1.1, 0.1))
_ = gd.fig.axes[0].axvline(x=0, color="b", linestyle=":")
_ = gd.fig.axes[0].axvline(x=1, color="r", linestyle=":")
_ = gd.fig.axes[0].yaxis.grid(True, linestyle="-", which="major", color="w", alpha=0.4)
_ = gd.fig.suptitle(
("For each datapoint, distribution of outlier classification " + "over the trace"),
y=1.04,
fontsize=16,
)
観測
- 上の図は、パーセンテージで説明される、各データポイントが外れ値として印をつけられるトレースのサンプルの割合を示しています。
- 三つの点が[p2,p3,p4] 95%を超えて外れ値として時間を過ごしています。
- frac_outliers ~ 0.27の事後の値の平均は、20データポイントのうち、およそ5または6一致します。:仮にそれらが外れ値に向かって学習しているならば、データポイント[p1,p12,p16]を見ることで調査するかもしれ無いことを記します。
私たちが選択した95%の切り離しは、気まぐれで問題があります。しかし、今回はそれが望ましいので、これらの3を外れ値として申告します。そして、ポイントの平均を0.68より上に設定している少し異なった方法で申告したJake Vanderplsの外れ値と比較して、どのように見えるか、見てください。
5.3.2 外れ値の宣言
ノート
- 私は、その値が1である5から100までのパーセントで、5%切り離した値を==1をもつデータポイントを外れ値として宣言します。
- 外れ値のランキングを目的に進めて、代替として大きな値を切り離して試して見てください。
cutoff = 0.05
dfhoggs["classed_as_outlier"] = (
trc_hogg.posterior["is_outlier"].quantile(cutoff, dim=("chain", "draw")) == 1
)
dfhoggs["classed_as_outlier"].value_counts()False 17
True 3
Name: classed_as_outlier, dtype: int64調査するポイントのためのフラグもまた追加します。最後の図で注釈するためにこれを使います。
dfhoggs["annotate_for_investigation"] = (
trc_hogg.posterior["is_outlier"].quantile(0.75, dim=("chain", "draw")) == 1
)
dfhoggs["annotate_for_investigation"].value_counts()False 16
True 4
Name: annotate_for_investigation, dtype: int645.4 OLS、ステユーデント、Hoggの信号とノイズの事後予測図
import xarray as xr
x = xr.DataArray(np.linspace(-3, 3, 10), dims="plot_dim")
# evaluate outlier posterior distribution for plotting
trc_hogg.posterior["outlier_mean"] = trc_hogg.posterior["y_est_out"].broadcast_like(x)
# evaluate model (inlier) posterior distributions for all 3 models
lm = lambda beta, x: beta.sel(coefs="intercept") + beta.sel(coefs="slope") * x
trc_ols.posterior["y_mean"] = lm(trc_ols.posterior["beta"], x)
trc_studentt.posterior["y_mean"] = lm(trc_studentt.posterior["beta"], x)
trc_hogg.posterior["y_mean"] = lm(trc_hogg.posterior["beta"], x)with plt.rc_context({"figure.constrained_layout.use": False}):
gd = sns.FacetGrid(
dfhoggs,
height=7,
hue="classed_as_outlier",
hue_order=[True, False],
palette="Set1",
legend_out=False,
)
# plot hogg outlier posterior distribution
outlier_mean = az.extract(trc_hogg, var_names="outlier_mean", num_samples=400)
gd.ax.plot(x, outlier_mean, color="C3", linewidth=0.5, alpha=0.2, zorder=1)
# plot the 3 model (inlier) posterior distributions
y_mean = az.extract(trc_ols, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C0", linewidth=0.5, alpha=0.2, zorder=2)
y_mean = az.extract(trc_studentt, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C1", linewidth=0.5, alpha=0.2, zorder=3)
y_mean = az.extract(trc_hogg, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C2", linewidth=0.5, alpha=0.2, zorder=4)
# add legend for regression lines plotted above
line_legend = plt.legend(
[
Line2D([0], [0], color="C3"),
Line2D([0], [0], color="C2"),
Line2D([0], [0], color="C1"),
Line2D([0], [0], color="C0"),
],
["Hogg Inlier", "Hogg Outlier", "Student-T", "OLS"],
loc="lower right",
title="Posterior Predictive",
)
gd.ax.add_artist(line_legend)
# plot points
_ = gd.map(
plt.errorbar,
"x",
"y",
"sigma_y",
"sigma_x",
marker="o",
ls="",
markeredgecolor="w",
markersize=10,
zorder=5,
).add_legend()
gd.ax.legend(loc="upper left", title="Outlier Classification")
# annotate the potential outliers
for idx, r in dfhoggs.loc[dfhoggs["annotate_for_investigation"]].iterrows():
_ = gd.ax.annotate(
text=idx,
xy=(r["x"], r["y"]),
xycoords="data",
xytext=(7, 7),
textcoords="offset points",
color="k",
zorder=4,
)
## create xlims ylims for plotting
x_ptp = np.ptp(dfhoggs["x"].values) / 3.3
y_ptp = np.ptp(dfhoggs["y"].values) / 3.3
xlims = (dfhoggs["x"].min() - x_ptp, dfhoggs["x"].max() + x_ptp)
ylims = (dfhoggs["y"].min() - y_ptp, dfhoggs["y"].max() + y_ptp)
gd.ax.set(ylim=ylims, xlim=xlims)
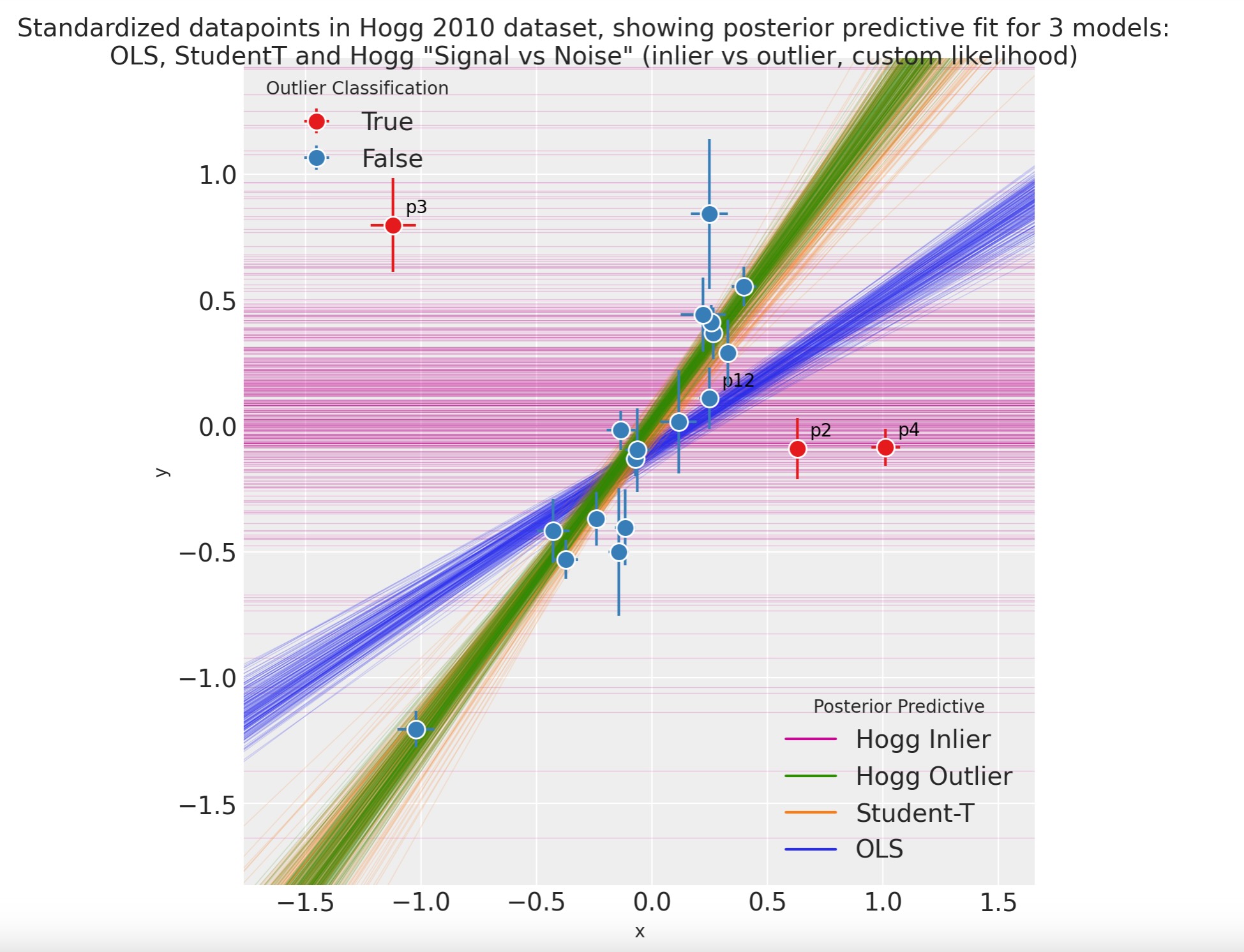
gd.fig.suptitle(
(
"Standardized datapoints in Hogg 2010 dataset, showing "
"posterior predictive fit for 3 models:\nOLS, StudentT and Hogg "
'"Signal vs Noise" (inlier vs outlier, custom likelihood)'
),
y=1.04,
fontsize=14,
);
観測
事後予測適合
- OLSモデルは緑色で示し、予測のように、データポイントに多数にうまく適合しているように見えません。外れ値によって歪められています。
- ステユーデントTは、オレンジ色で示されます。データポイントの主要な軸に非常にうまく適合し、外れ値を無視しています。
- Hoggの信号とノイズモデルは、二つの部分が示されます。
- 青は観測値で、データポイントの主要な座標にうまく適合し、外れ値を見ししています。
- 赤は外れ値で、非常に大きな分散と、青の観測値モデルより大きな対数確率をもつ外れ値を振り分けられています。
私たちは、Hoggの信号とノイズモデルが、データポイントを外れ値とみなす特別な予測で分離しているのがわかります。
- 青色の17の観測値データポイント、
- 赤色の3の外れ値のデータポイント
- 簡単な視覚の洞察から、Jake Vanderplasが発見して認めたように、分類は適切のようです。
- これらの赤と視覚上の検査を補助するために最も中心から離れた観測値を注釈します。
総合
- Hoggの信号とノイズは約束通り、振る舞います。ロバスト回帰の予測に分岐し、観測値と外れ値に明確にラベル分けします。しかし
- Hoggの信号とノイズは全く複雑です。回帰は頑丈のようですが、トレース図は多くの発散を履いており、モデルは潜在的に不安定です。
- 単純に、観測値・外れ値のラベル付なしにロバスト回帰が欲しいならば、簡単なモデル、素早いサンプリング、とても似通った予測を提案するステューデントTモデルは、良い妥協案になります。
参照資料
- David W. Hogg, Jo Bovy, and Dustin Lang. Data analysis recipes: fitting a model to data. 2010
- Željko Ivezić, Andrew J. Connolly, Jacob T. VanderPlas, and Alexander Gray. Statistics, Data Mining, and Machine Learning in Astronomy: A Practical Python Guide for the Analysis of Survey Data. Princeton University Press, 2014. ISBN 9781400848911.
- J.T. Vanderplas, A.J. Connolly, Ž. Ivezić, and A. Gray. Introduction to astroml: machine learning for astrophysics. In Conference on Intelligent Data Understanding (CIDU), 47–54. oct. 2012.
- Andrew Gelman. Scaling regression inputs by dividing by two standard deviations. Statistics in medicine, 27(15):2865–2873, 2008.
製作者
著者:Jon Sedar 2015年12月 原文の投稿はjonsedar/pymc3_examples
更新:Thomas Wieki 2018年7月 pm.Normal.dist().logp() , pm.Potential()を使用した外れ値モデル
更新:Jon Sedar 2019年11月 ステューデントTモデルの nu をより効果的に使用
更新:Jon Sedar 2020年5月 pymc=3.8, arviz=0.7
更新:Raul Maldonado 2021年4月 arviz.InferenceDataオブジェクト pymc=3.11, arviz=0.11.0
更新:Raul Maldonado 2021年5月 視覚化の更新 pymc=3.11, arviz=0.11.0
更新:Oriol Abril 2021年11月
更新: Benjamin Vincent 2023年2月 pyMC v5 az.extractを使用