pyMC ベイズ・確率プログラミング

多変量正規モデルのためのLKJコレスキー共分散事前分布

　逆ウィッシャート分布は、多変量正規分布の共分散行列と共役の事前分布です。それは、現代のベイジアン計算メソッドとしては、あまり適しているわけではありません。この理由で、LKJ事前分布は多変量正規分布の共分散行列をモデル化する時に推薦されます。

　LKJ分布と共分散のモデル化を説明するために、私たちは、最初に二次元の正規分布サンプルデータセットを生成します。

%env MKL_THREADING_LAYER=GNU
import arviz as az
import numpy as np
import pymc as pm
import seaborn as sns

from matplotlib import pyplot as plt
from matplotlib.lines import Line2D
from matplotlib.patches import Ellipse

print(f"Running on PyMC v{pm.__version__}")
env: MKL_THREADING_LAYER=GNU
Running on PyMC v5.0.1
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
N = 10000

mu_actual = np.array([1.0, -2.0])
sigmas_actual = np.array([0.7, 1.5])
Rho_actual = np.matrix([[1.0, -0.4], [-0.4, 1.0]])

Sigma_actual = np.diag(sigmas_actual) * Rho_actual * np.diag(sigmas_actual)

x = rng.multivariate_normal(mu_actual, Sigma_actual, size=N)
Sigma_actual
matrix([[ 0.49, -0.42],
        [-0.42,  2.25]])
var, U = np.linalg.eig(Sigma_actual)
angle = 180.0 / np.pi * np.arccos(np.abs(U[0, 0]))

fig, ax = plt.subplots(figsize=(8, 6))

e = Ellipse(mu_actual, 2 * np.sqrt(5.991 * var[0]), 2 * np.sqrt(5.991 * var[1]), angle=angle)
e.set_alpha(0.5)
e.set_facecolor("C0")
e.set_zorder(10)
ax.add_artist(e)

ax.scatter(x[:, 0], x[:, 1], c="k", alpha=0.05, zorder=11)
ax.set_xlabel("y")
ax.set_ylabel("z")

rect = plt.Rectangle((0, 0), 1, 1, fc="C0", alpha=0.5)
ax.legend([rect], ["95% density region"], loc=2);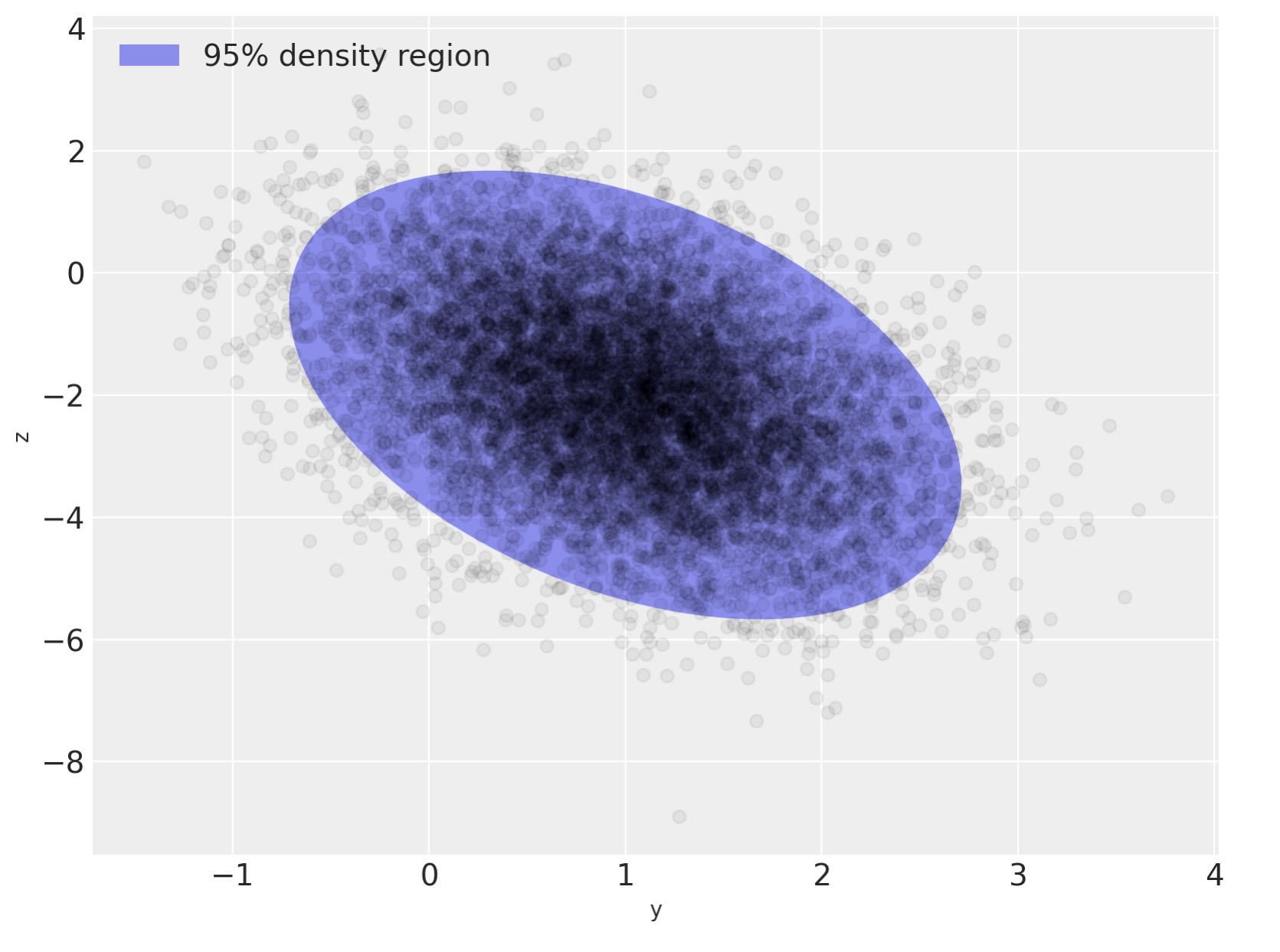

　多変量正規モデルのためにサンプリングした分布は、x〜N(μ, Σ), ここで、Σは、サンプリング分布の共分散行列、Σ= Cov(xi,xj).この分布の密度は、

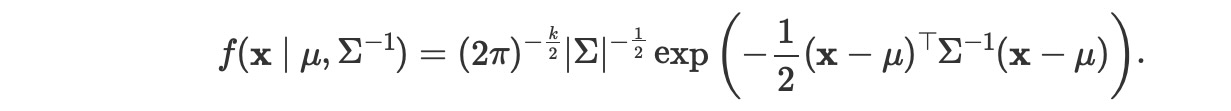
　LKJ分布は相関行列、C = Corr(xi,xj)、の事前分布を提供します。それは、共分散行列Σの事前分布を導く、各成分の標準偏差の事前分布を組み合わせたものです。逆Σは数値的に不安定で非効率なので、ΣのCholesky分解を使うことで計算優位性を持ちます。Σ= LLT, ここでLは、下三角行列。この分解は、後方置換を使って、(x-μ)T Σ-1 (x-μ)項の計算を許容します。それは、直接逆行列をとるより、もっと数値的に安定し、効果的です。

　PyMCは、LKJCholeskyCov分布を経由した共分散行列のCholesky分解のためにLKJ事前分布をサポートします。この分布は、パラメータnとsd_distをもち、それは、観測値xの次元であり、そして、成分標準偏差のPYMC分布です。それはまたハイパーパラメータetaをもち、xの成分間の相関の量を操作します。LKJ分布は密度f ( C | η ) ∝ | C |η-1,を持ちます、そして、η＝１は相関行列の一様分布に導きます。η→♾️の時に、成分間の相関の大きさは減少していきます。

　この例では、私たちは、Exponential(1.0)の事前分布の標準偏差をモデルにし、相関行列を、C〜LKJ(η＝２）とします。

with pm.Model() as m:
    packed_L = pm.LKJCholeskyCov(
        "packed_L", n=2, eta=2.0, sd_dist=pm.Exponential.dist(1.0, shape=2), compute_corr=False
    )

　Σのコレスキー分解は、下三角なので、LKJCholeskyCovは、対角と準対角のエントリーだけを効率的にストアします。

packed_L.eval()
array([ 0.07501226, -0.00520305,  0.26411501])

　私たちは、このベクターを、下三角の三角行列Lに変換するのに、expand_packed_trianglerを使います。その行列は、コレスキー分解,Σ = LL T

with m:
    L = pm.expand_packed_triangular(2, packed_L)
    Sigma = L.dot(L.T)

L.eval().shape
(2, 2)

　しばしば、しかしながら、コレスキー共分散行列の事後分布ではなく、相関行列と標準偏差の事後分布に関心を持つことでしょう。なぜでしょう。相関と標準偏差は、解釈するのが簡単です。そしてしばしば、モデルの科学的な意味を持ちます。PyMCv4では、compute_corr引数は、デフォルトでTrueに設定されます。それは、コレスキー分解、相関行列、標準偏差からなるtupleを返します。

coords = {"axis": ["y", "z"], "axis_bis": ["y", "z"], "obs_id": np.arange(N)}
with pm.Model(coords=coords) as model:
    chol, corr, stds = pm.LKJCholeskyCov(
        "chol", n=2, eta=2.0, sd_dist=pm.Exponential.dist(1.0, shape=2)
    )
    cov = pm.Deterministic("cov", chol.dot(chol.T), dims=("axis", "axis_bis"))

注　pm.Modelの引数

オリジナルは、PyMC v４で実装しているため、pm.Model()の引数にrng_seeder=RANDOM_SEED を指定していますが、

pm.Model(coords=coords, rng_seeder=RANDOM_SEED)

ここでは、pyMC v5 用に上記引数を外しています。

　私たちのモデルを計算するために、私たちは、独立で、弱く調整した事前分布　N(0,1.5) μをおきます。

with model:
    mu = pm.Normal("mu", 0.0, sigma=1.5, dims="axis")
    obs = pm.MvNormal("obs", mu, chol=chol, observed=x, dims=("obs_id", "axis"))

　私たちは、このモデルからNUTSを使ってサンプルします。そして結果を出力するためにトレースをArvizに渡します。

with model:
    trace = pm.sample(
        idata_kwargs={"dims": {"chol_stds": ["axis"], "chol_corr": ["axis", "axis_bis"]}},
    )
az.summary(trace, var_names="~chol", round_to=2)

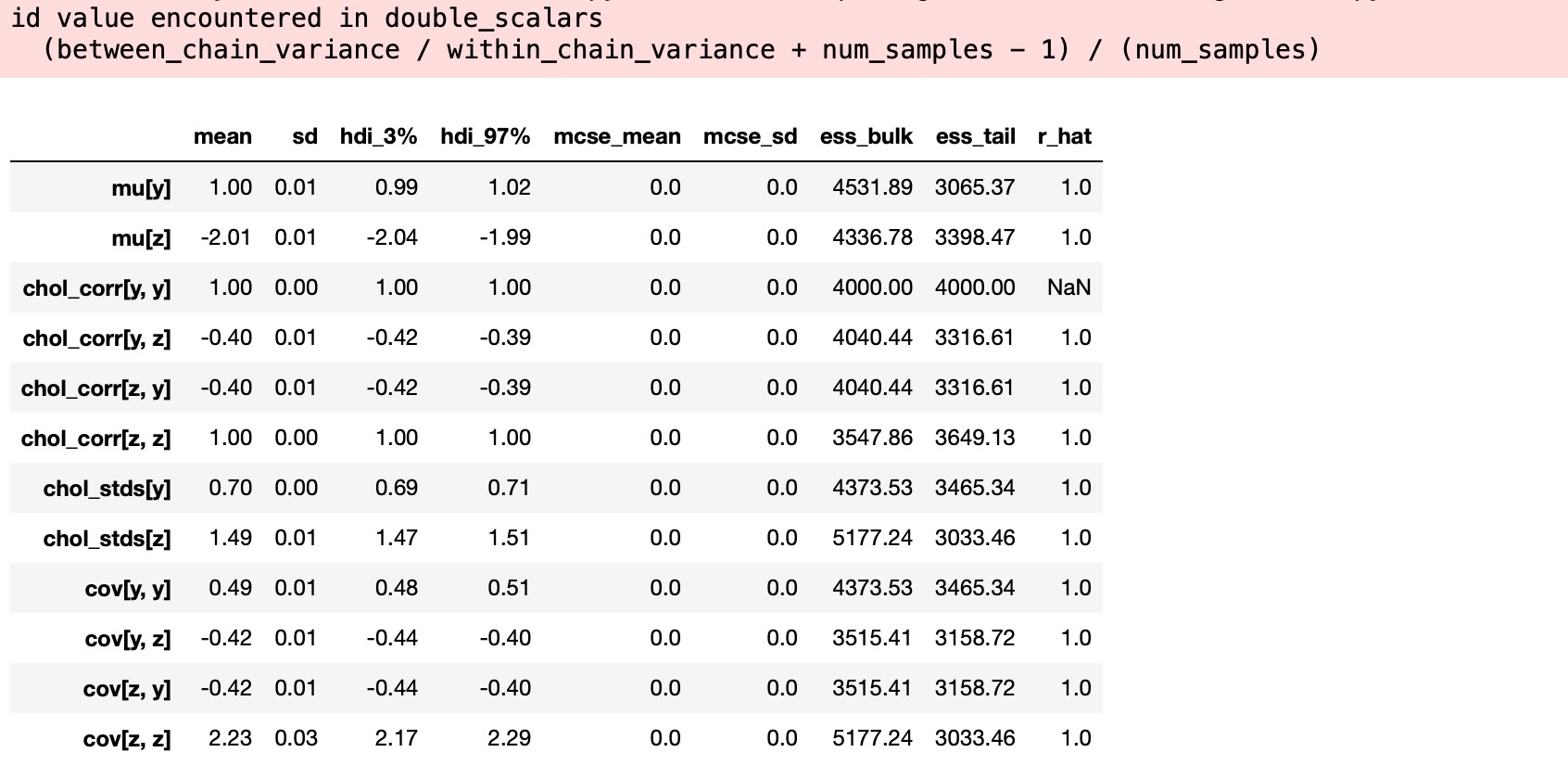
　サンプリングはうまくいきました。発散はなく、良いt-hatです。（相関行列の対角の要素を除いて、しかし、危惧することはありません。なぜなら、それらは、各チェインの各サンプルは１に等しくなります。そして、定数値の分散は定義されていません。もし、対角要素の一つが、定義されたr_hatを持つならば、それは、わずかな数値エラーのためである可能性が高いのです）

　あなたは、サンプラーが真の平均、相関、標準偏差を回復するのを見ることができます。しばしば、それはグラフから明確です。

az.plot_trace(
    trace,
    var_names="chol_corr",
    coords={"axis": "y", "axis_bis": "z"},
    lines=[("chol_corr", {}, Rho_actual[0, 1])],
);
az.plot_trace(
    trace,
    var_names=["~chol", "~chol_corr"],
    compact=True,
    lines=[
        ("mu", {}, mu_actual),
        ("cov", {}, Sigma_actual),
        ("chol_stds", {}, sigmas_actual),
    ],
);

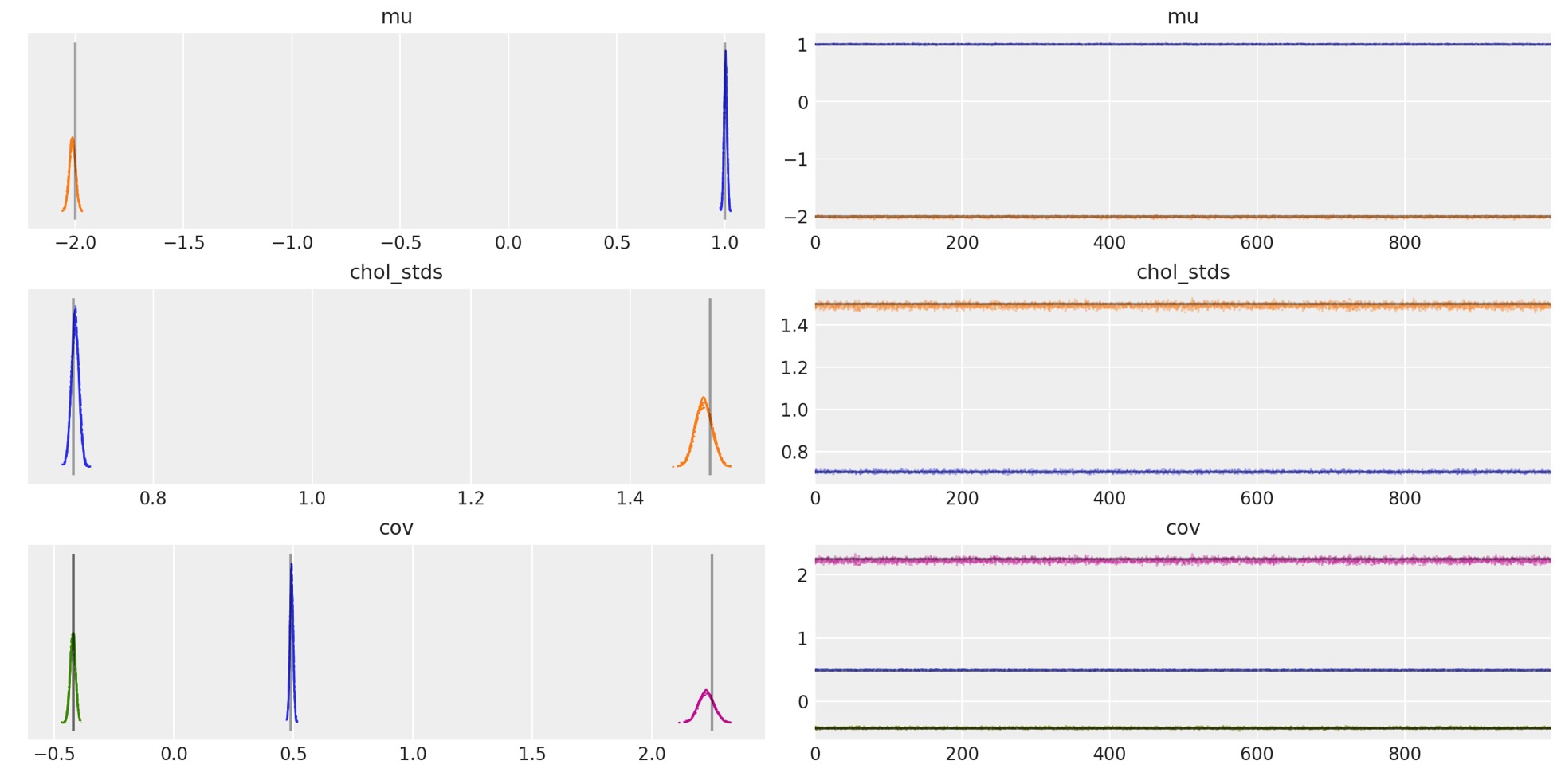
　事後分布の予測値は、各成分の真の値に非常に近接しています。どれくらい正確に近接しているか？μとΣのために、近さのパーセンテージを計算しましょう。

mu_post = trace.posterior["mu"].mean(("chain", "draw")).values
(1 - mu_post / mu_actual).round(2)
array([-0.  , -0.01])
Sigma_post = trace.posterior["cov"].mean(("chain", "draw")).values
(1 - Sigma_post / Sigma_actual).round(2)
array([[-0.01, -0.  ],
       [-0.  ,  0.01]])

　それで、事後分布の平均は、μとΣの真の値の３％内です。
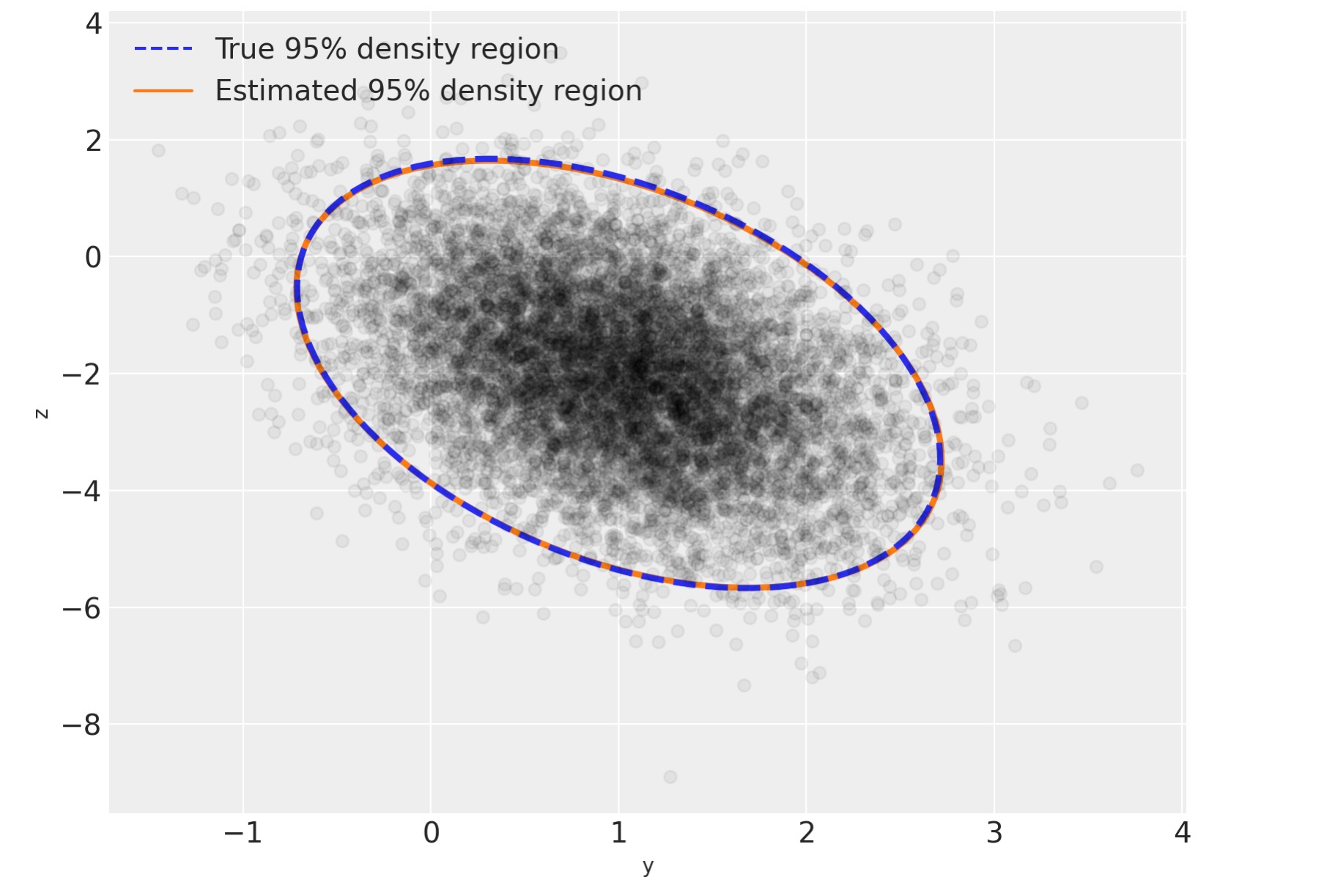
　ここで、私たちが最初に実行した図を複製しましよう。しかし、真の分布の最上位に事後分布を上書きします。 - あなたは、それが両者の間で素晴らしい視覚的な一致があることがわかるでしょう。

var_post, U_post = np.linalg.eig(Sigma_post)
angle_post = 180.0 / np.pi * np.arccos(np.abs(U_post[0, 0]))

fig, ax = plt.subplots(figsize=(8, 6))

e = Ellipse(
    mu_actual,
    2 * np.sqrt(5.991 * var[0]),
    2 * np.sqrt(5.991 * var[1]),
    angle=angle,
    linewidth=3,
    linestyle="dashed",
)
e.set_edgecolor("C0")
e.set_zorder(11)
e.set_fill(False)
ax.add_artist(e)

e_post = Ellipse(
    mu_post,
    2 * np.sqrt(5.991 * var_post[0]),
    2 * np.sqrt(5.991 * var_post[1]),
    angle=angle_post,
    linewidth=3,
)
e_post.set_edgecolor("C1")
e_post.set_zorder(10)
e_post.set_fill(False)
ax.add_artist(e_post)

ax.scatter(x[:, 0], x[:, 1], c="k", alpha=0.05, zorder=11)
ax.set_xlabel("y")
ax.set_ylabel("z")

line = Line2D([], [], color="C0", linestyle="dashed", label="True 95% density region")
line_post = Line2D([], [], color="C1", label="Estimated 95% density region")
ax.legend(
    handles=[line, line_post],
    loc=2,
);

-pyMC, ベイズ・確率プログラミング
-,