import arviz as az
import numpy as np
import pymc as pm
from matplotlib import pyplot as plt
from matplotlib.ticker import FormatStrFormatter
from scipy.special import betaln
from scipy.stats import beta
print(f"Running on PyMC v{pm.__version__}")Running on PyMC v5.0.1az.style.use("arviz-darkgrid")モデルを比較するためのベイズの方法は、各モデルで周辺尤度 p(y|Mk) を計算することです。言い換えると、Mkモデルで与えられる観測データの確率です。この量、周辺尤度は、ベイズ理論で正規化した定数です。ベイズ理論を書くことができれば、私たちはこれを見ることができます。そしてすべての推論がモデルと独立している事実を明らかにしているのがわかります。
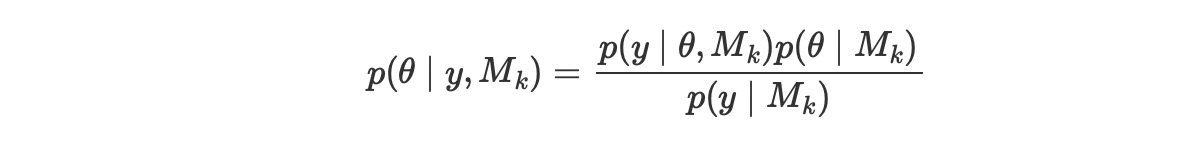
ここで、
- y はデータ
- θはパラメータ
- Mk Kモデルの中の一つのモデル
通常、推論を実行するとき、私たちは、この正規化した定数を計算する必要はありません。演習では、私たちはしばしば、定数因子で事後分布を計算します。それは、
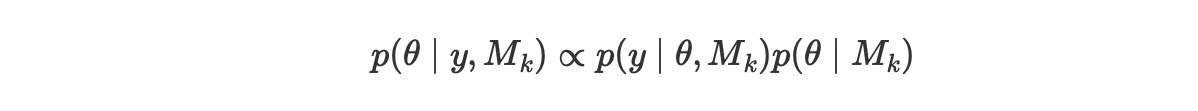
しかし、モデルの比較のために、周辺尤度のモデル平均は、重要な量です。これらのタスクを実行する方法だけでなく、あなたは、モデルの平均を読むことができ、ここ(ハイパーリンク)やその他で使っている代替的な方法でモデルを選択できます。実際、これらの代替的な方法は、周辺尤度を使うことと比較して良い選択ではありません。
ベイジアンモデルの選択
もし、私たちの主要な目的が、たった一つのモデル、モデルのセットから最高のモデル、を選択することであれば、最も大きいp(y|Mk)を持つ一つを選択することができます。もし、すべてのモデルが同じ事前確率を持っていることを仮定していれば、これは全体的にうまくいきます。そうでなければ、私たちは、すべてのモデルは、等しい事前分布でないことを説明する必要があります。そして以下を計算する必要があります。
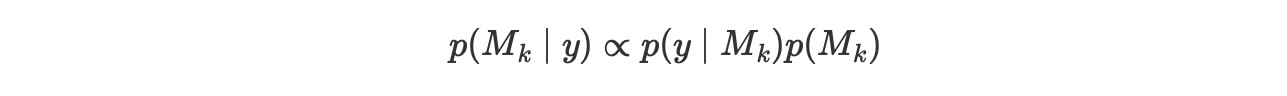
時に、主要な目的が、単一のモデルを維持するのでなく、あるものはもっと良くて、どのくらい良いのかを決定するために代わりにモデルを比較します。これは、ベイズ因子を使ってアーカイブすることができます。
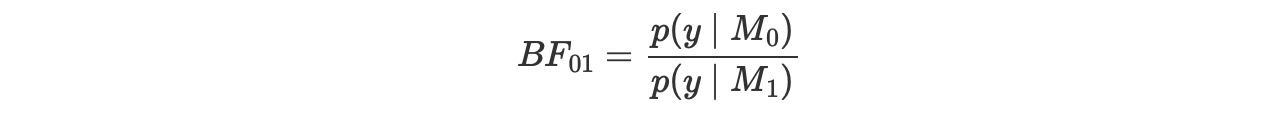
それは、二つのモデルの周辺尤度間の割合です。大きいBFが数値上、より良いモデルになります。BFの解釈を優しくするために、Harold Jeffreysは提案したベイズ因子の解釈のスケール、サポートのレベル、拡張にレベルを提案しています。これは、数値を言葉に置き換えた方法です。
- 1-3:anecodal
- 3-10:moderate
- 10-30:strong
- 30-100:very strong
- > 100:extreme
以下の数値を得た場合は、モデルには分母でサポートしていることに注意してください。これらのケースでもテーブルは利用できます。もちろん、あなたは、上のテーブルの値を、逆にすることができます。またはBFの値を逆にすることもできます。
これらのルールが利便性のためのであること、もっともよい簡単なガイドを覚えておくのはとても重要です。結果は、常に私たちの問題との文脈の中に置かれます。もしそれらが私たちの結果に同意するならば、それらによって他のものが評価できるように、十分な詳細さと伴奏すべきです。証拠は、素粒子物理や裁判とは異なり、数百人の死者を予防するために街から避難するのを、宣言するために必要です。
ベイジアンモデル平均
候補となっているモデルから一つのモデルを選択する代わりに、モデル平均は、候補のモデルの平均することによって一つのメタモデルを得ることです。これのベイジアンバージョンは、各モデルを周辺事後確率によって、重みづけします。
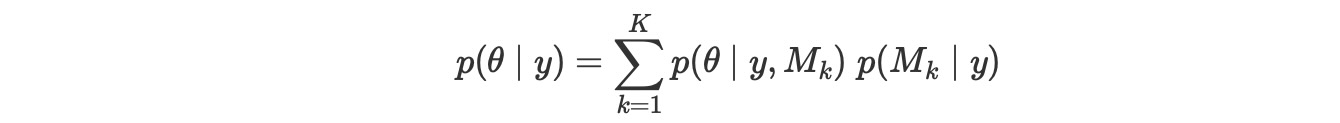
これは、もし、事前分布が正しく、正しいモデルが、私たちのセットのMkモデルの中の一つであれば、平均モデルは最適な方法です。そうでなければ、バイジアンモデル平均はasumptotically 比較できるモデルから、一つの単一のモデルを選択します。それはKullback-Leibier divergenceに密接しています。
この例(ハイパーリンク)を平均モデルを実行する代替的な方法としてチェックしてください。
いくつかの備考
ここで、私たちは、周辺尤度についていくつかの鍵となる事実を簡単に論じます。
- 良い点(good)
- オッカムの刃(Occam Razor)を含みます。より多くのパラメータをもつモデルは、少ないパラメータのモデルより不当な扱いを受けます。直感的な理由は、大きい数のパラメータは、尤度を反映してより幅広い事前分布になります。
- 悪い点(bad)
- 周辺尤度を計算することは、一般的に、困難な仕事です。高次のパラメータ空間をを超えて高い変位のある関数を積分するためです。一般的に、この積分は、多少洗練された方法を使って数値的に解決される必要があります。
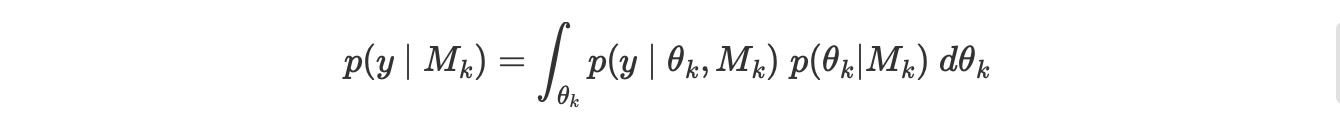
- ひどい点(ugly)
- 周辺尤度は、各モデルp(θk|Mk)のパラメータのために特定の事前分布に敏感に依存します。
goodとuglyが関係していることに注意してください。モデルを比較して周辺尤度を使うことは、良いアイデアですが、複雑なモデルの不当な扱いは、すでに含まれており、同時に、事前分布の変更は周辺尤度の計算に影響を与えます。最初に、これは少し馬鹿げて聞こえます。私たちはすでに事前分布が計算に影響することがわかっています。(さもなくば簡単にそれらを避けることができます)しかし、ここのポイントは、敏感さです。私たちは、れが、θの推論を多少同じに維持する。しかし、周辺尤度の値に大きな影響を与えることができる 事前分布の変更について論議してきました。
ベイズ因子の計算
周辺尤度は一般的に、いくつかの制限されたモデルを除いて、閉じた様式で利用できる。この理由のために、多くの方法は、周辺尤度を計算するために考案され、そしてベイズ因子が考案されてきました。これらのいくつかの方法は、とても簡単で、練習ではとても悪くは機能するほどnaiv(ハイパーリンク)です。最もよく使う方法は、統計的な仕組みの分野で提案されてきました。このつながりは、周辺尤度が分離関数(partition function)として知られる統計物理学の主要な量に相似しています。順番にもう一つのとても重要な量である自由エネルギーと密接に関係しています。統計の仕組みとベイジアン推論の間の繋がりの多くは、ここにまとめています。
階層モデルを使う
ベイズ因子の計算は階層モデルとして枠に嵌められる。高レベルパラメータは、各モデルに対応するインデックス、分類された分布からサンプルされます。言い換えると、私たちは同時に二つの競り合ったモデルの推論を実行します。そして、私たちは、モデル間でジャンプする差分dummy変数ををつかいます。各モデルで何回サンプリングを実施するかはp(Mk|y)に比例します。
この方法でベイズ因子を計算するときのいくつかの共通の問題は、あるモデルが定義により他のモデルより良ければ、他のモデルよりもそれでサンプリング時間をより多く使います。これは、可能性の低いモデルのサンプリング不足のために不正確さを導きます。他の問題は、パラメータの値が、パラメータがそのモデルへの適合に使われない時でさえ、更新されることです。それは、モデル0が選ばれた時に、モデル1のパラメータが更新され、しかし、それらはデータを説明するのに使われないため、そrらは事前分布によって制限されるだけになります。もし、事前分布が無駄すぎるならば、モデル1を選択した時に、パラメータの値が以前に受け付けられた値から遠すぎることが可能になります。それゆえステップが拒絶されます。そうしてサンプリングは問題を抱えて終了します。
私たちがこれらの問題を見つけるケースでは、私たちのモデルにふたつの変更を実装することによってサンプリングを解決することを試みます。
- 理想的には、それらが等しく訪問されるなら、私たちは両方のモデルでもっと良いサンプリングを取得で来ます。そして、私たちは、より好ましくないモデルを好ましくし、好ましくないものをもっとも好ましい一つにするためのそうした方法で各モデルに事前分布を適合することができます。これは、計算に事前分布を含まなければならないために、ベイズ因子の計算には影響しません。
- Krushkeとその他の人々が提案するように、偽りの事前分布を使います。このアイデアを簡単です。もし、それらの属するモデルが選択されていない時に、パラメータが無制限にドリフトするならば、一つの解決策は、しかし、それが使われていない時だけ、人工的にそれらを制限することを試みることです。あなたは、Kruschkeの本(注)とPythonへの移植で使用されたモデルで偽りの事前分布を使っている例を見つけることができます。
周辺尤度の計算のこのアプローチについて、もっと詳しく学習したければ、Doing Bayesian Data Analysisの12章を参照してください。この章は、古典的な仮説テストへの代替ベイズとしてベイズ因子の使い方を議論しています。
(注) Doing Bayesian Data Analysis. John K. Kruschke
邦訳は”ベイズ統計モデリング” R,JAGS,Stanによるチュートリアル
サンプルプログラムはRで書かれています。
分析
ベータ二項モデル(AKA コイン投げモデル)のような任意のモデルに対して、私たちは、分析的に周辺尤度を計算することができます。もし私たちがこのモデルを記述するならば、
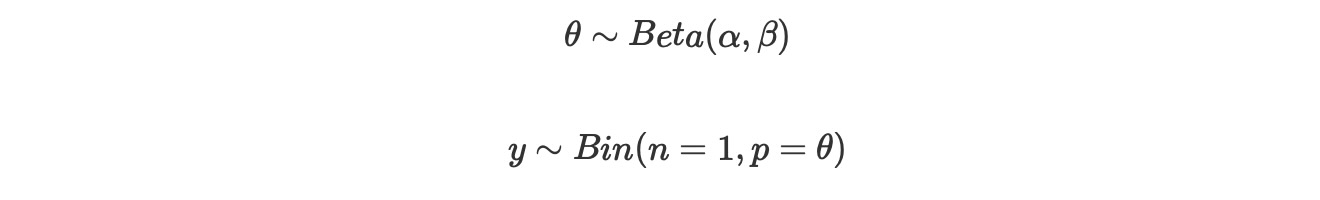
周辺尤度は、
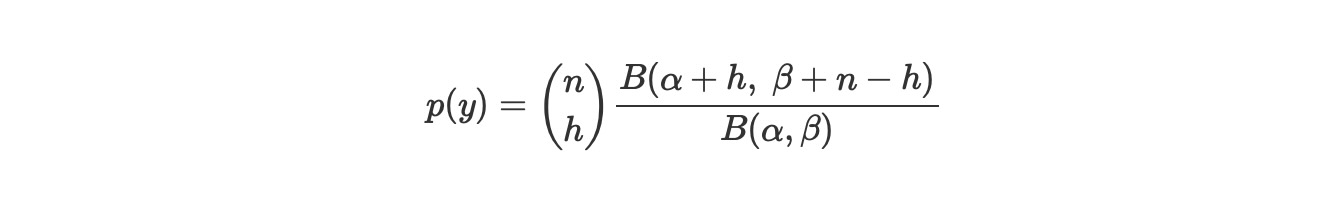
ここで、
- Bはベータ関数、ベータ分布と混乱しないように
- nはトライアル回数
- hは成功数
私たちは、ふたつのモデル下で周辺尤度の相対的な値について注意すれば良いので、私たちは、二項係数(nh)を除外することができます、こうして、私たちは次のように書けます。
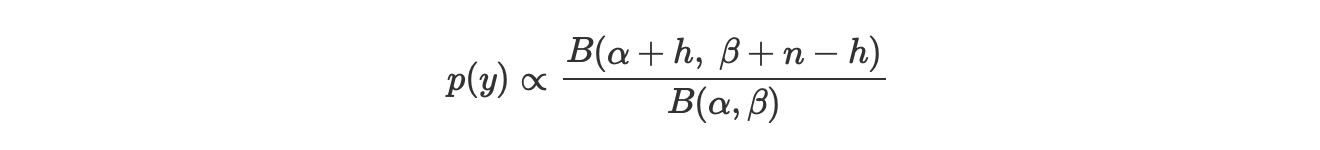
この式は、以下のセルでコード化されます。しかし歪曲して。私たちはbeta関数の代わりにbetaln関数を使います。これは、アンダーフローを防ぐための措置です。
def beta_binom(prior, y):
"""
Compute the marginal likelihood, analytically, for a beta-binomial model.
prior : tuple
tuple of alpha and beta parameter for the prior (beta distribution)
y : array
array with "1" and "0" corresponding to the success and fails respectively
"""
alpha, beta = prior
h = np.sum(y)
n = len(y)
p_y = np.exp(betaln(alpha + h, beta + n - h) - betaln(alpha, beta))
return p_y私たちのこの例のデータは、100回のコイン投げで構成されます。観測された"表"と”裏”は同数です。私たちはふたつのモデル、一つは一様分布、一つはθ=0,5の周辺にもっと集中した事前分布を比較します。
y = np.repeat([1, 0], [50, 50]) # 50 "heads" and 50 "tails"
priors = ((1, 1), (30, 30))for a, b in priors:
distri = beta(a, b)
x = np.linspace(0, 1, 300)
x_pdf = distri.pdf(x)
plt.plot(x, x_pdf, label=rf"$\alpha$ = {a:d}, $\beta$ = {b:d}")
plt.yticks([])
plt.xlabel("$\\theta$")
plt.legend()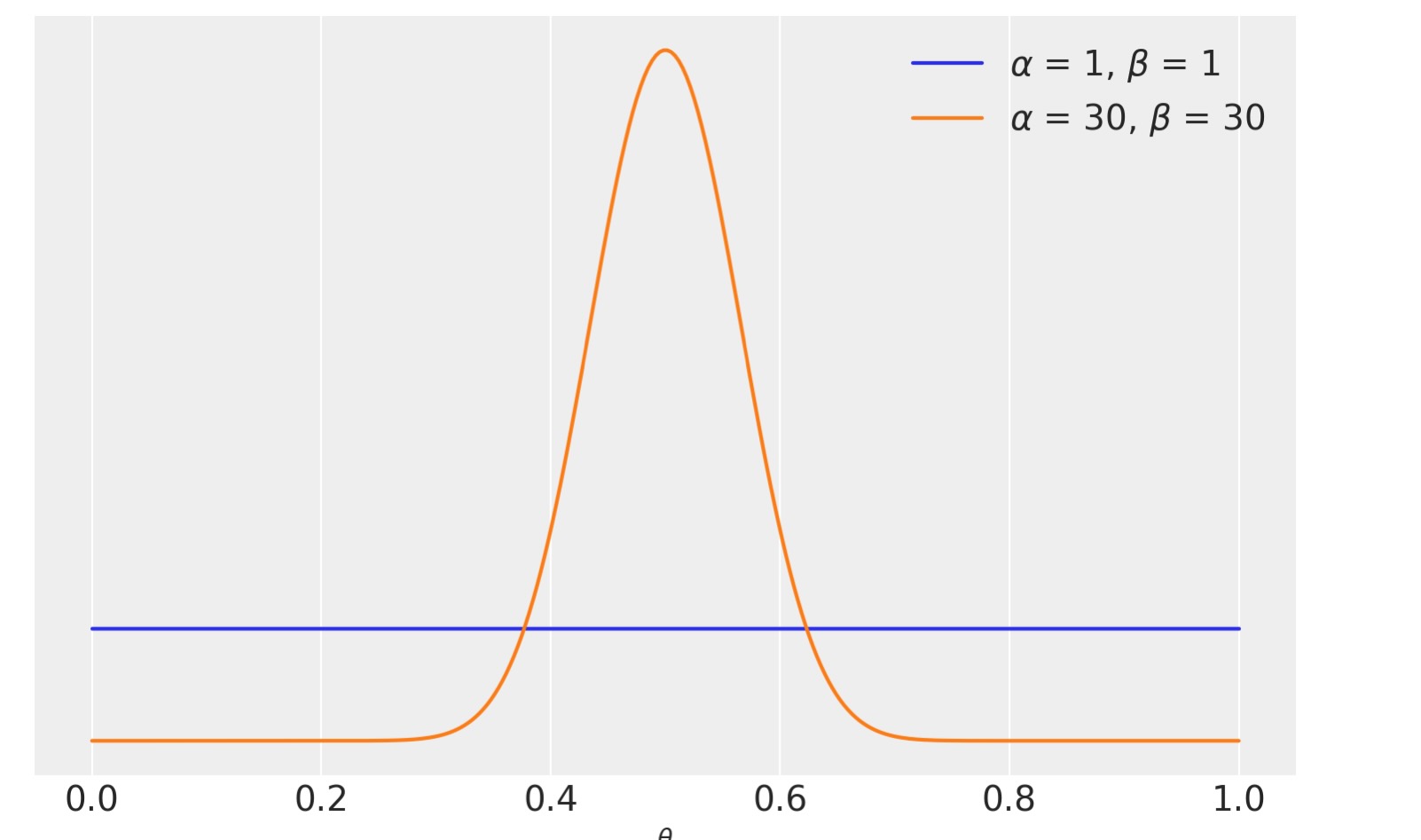
以下のセルはベイズ因子を返します。
BF = beta_binom(priors[1], y) / beta_binom(priors[0], y)
print(round(BF))5私たちは、beta(1,1)をもっと拡張したモデルより、5倍以上サポートするもっと集中した事前分布beta(30,30)のモデルを見ます。正確な数値に比べると、もっとも好ましいモデルの事前分布が、シータの値は0.5の周りで一定で、θ=0.5の周辺に集中し、データyは等しい数の表と裏を持っているので、これは、驚くべきことではありません。
連続モンテカルロ
連続モンテカルロサンプラーは、事前分布から事後分布への成功した強化したシーケンスの系列による基本的な進行の方法です。この過程の生産の良さは、周辺尤度の見積もりを得ることができるということです。実際、いくつかの理由で、戻り値は、対数周辺尤度になります。(アンダーフローを避けるのに役立ちます)
models = []
idatas = []
for alpha, beta in priors:
with pm.Model() as model:
a = pm.Beta("a", alpha, beta)
yl = pm.Bernoulli("yl", a, observed=y)
idata = pm.sample_smc(random_seed=42,progressbar=False)
models.append(model)
idatas.append(idata)


BF_smc = np.exp(
idatas[1].sample_stats["log_marginal_likelihood"].mean()
- idatas[0].sample_stats["log_marginal_likelihood"].mean()
)
np.round(BF_smc).item()5.0前のセルから見ることができるように、SMCは本質的に、分析的な計算と同じ答えを与えます。
注意:上のセルでは、対数スケールにしているため、異なる値を計算し、同じ理由で、結果を返す前にexpを取っています。最後に、私たちが平均を計算する理由は、チェインごとに周辺尤度の対数の値を取得しているためです。
(対数)周辺尤度をSMCを使って計算する利点は、密接な様式の式はもはや必要ないものとして、モデルのより幅広い範囲で、それを使うことができます。この柔軟性に私たちが払うコストは、もっと高価な計算になります。SMCは(PyMCで実装された独立したメトロポリスカーネルによる)、NUTSのような勾配を基礎としたサンプラーほど、堅牢でも効果的でもありません。問題の次元が事後のもっと正確な予測を増加させ、周辺尤度が大きい数値の出力(draws)を要求するので、順位の図示は、SMCのサンプリングの診断に役立つことができます。
ベイズ因子と推論
そこまで、私たちは、どのモデルがデータを説明するのに、よりよく見えるか判断するためにベイズ因子を使います。そして、他のものより5倍良いモデルの一つを取得します。
しかし、事後についてはどうでしょう。私たちは、それらのモデルから取得しますか?それらはどのように異なりますか?
az.summary(idatas[0], var_names="a", kind="stats").round(2)| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| a | 0.5 | 0.05 | 0.4 | 0.59 |
az.summary(idatas[1], var_names="a", kind="stats").round(2)| mean | sd | hdi_3% | hdi_97% | |
|---|---|---|---|---|
| a | 0.5 | 0.04 | 0.42 | 0.57 |
私たちは、結果がかなり似通っていることを図示します。このモデルがより広い事前分布を持っていることから予期されるように、私たちはθのために同じ平均値と、model_0のためにわずかに広い事後分布を持っています。私たちはまた、それらがどのくらい似ているかを見るために、事後予測分布をチャックすることができます。
ppc_0 = pm.sample_posterior_predictive(idatas[0], model=models[0]).posterior_predictive
ppc_1 = pm.sample_posterior_predictive(idatas[1], model=models[1]).posterior_predictive
_, ax = plt.subplots(figsize=(9, 6))
bins = np.linspace(0.2, 0.8, 8)
ax = az.plot_dist(
ppc_0["yl"].mean("yl_dim_2"),
label="model_0",
kind="hist",
hist_kwargs={"alpha": 0.5, "bins": bins},
)
ax = az.plot_dist(
ppc_1["yl"].mean("yl_dim_2"),
label="model_1",
color="C1",
kind="hist",
hist_kwargs={"alpha": 0.5, "bins": bins},
ax=ax,
)
ax.legend()
ax.set_xlabel("$\\theta$")
ax.xaxis.set_major_formatter(FormatStrFormatter("%0.1f"))
ax.set_yticks([]);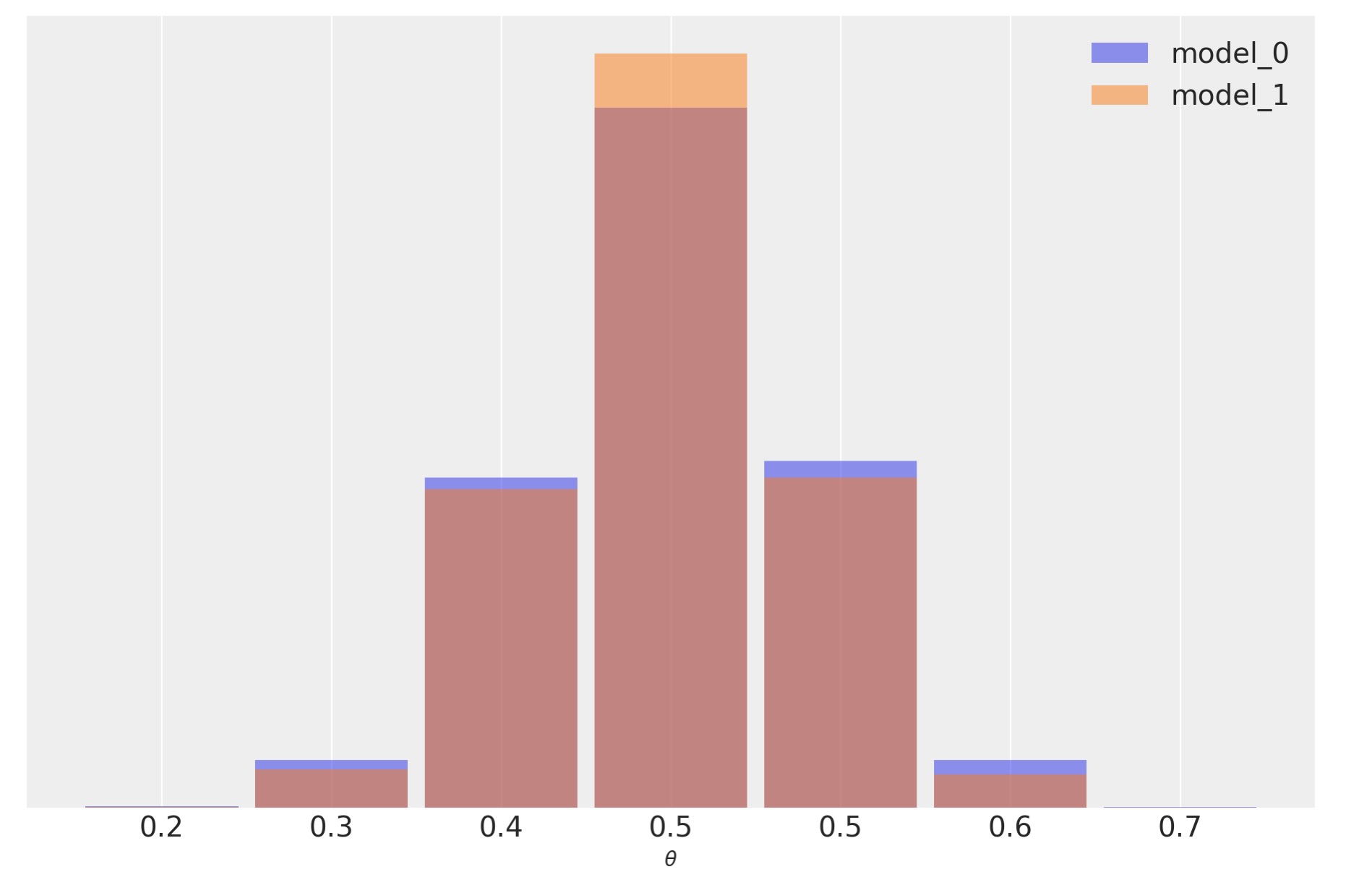
この例では、観測データyは、model_0(それは全ての可能なθの周りに同じ確率を割り当てられています)より、model_1(なぜなら事前分布が正しいθの値の周囲で集中しています)に対してもっと一定です。そして、この相違は、ベイズ因子によって取り込まれます。私たちは、全体で、パラメータの推定に無関係かもしれない事前分布の詳細を含んでいる、どのモデルがもっと良いかを、ベイズ因子が測定していると言えます。実際にこの例では、異なるベイズ因子の、二つの異なるモデルを持ち、しかし、それにもかかわらず、非常によく似た予測を得ることこが可能であることを、私たちは見ることができます。その理由は、非常に似た事後を誘発するポイントまで、データが事前分布の影響を減少するのに十分な情報を持っているためです。予測は事後から計算されるので、私たちはまた、非常ににた予測を取得します。モデルを比較するときに私たちが注意するもっともなシナリオは、モデルの予測の正確さです。もしふたつのモデルが同様の予測の正確さを持っていれば、両方のモデルは同じようなものとして考えます。予測の正確さを見積もるために、私たちはPSIS-LOO-CV(az.loo)mWAIC(az.waic),またはcross-valifdationのようなツールを使うことができます。
Savage-Dickey 密度率
前の例では、私たちは、ふたつの二項モデルを比較します。しかし、時に、私たちが必要とするものは、H0とそれに反するもう一つのH_1の帰無仮説の比較です。例えば、これはコインのバイアス?という問いに応えるとき、私たちはθの値を0.5を、私たちはθを変化するものとして、モデルの結果に対して比較します。null-モデルのこの種の比較は、代替の中にネストされ、nullは私たちが構築したモデルの特別な値を意味します。これらのケースでベイズ因子を計算することは、とても簡単で、どのような特別な方法も必要としません。なぜなら、数学が便利に働いて、私たちは、他の代替的なモデル下で、null-値で評価された事後と事前分布を単に比較する必要があります。私たちは、以下の式からそれが正しいことがわかります。
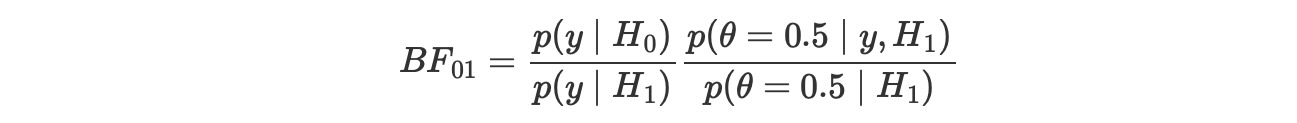
それは、H_0がH_1の特別なケースであるときに保持されます。
PyMCとArvizで処理しましょう。私たちは、単に、モデルのために事後分布と事前分布を取得する必要があるだけです。事前分布に、私たちが前に見た一様分布とベータ二項分布を試みましょう。
with pm.Model() as model_uni:
a = pm.Beta("a", 1, 1)
yl = pm.Bernoulli("yl", a, observed=y)
idata_uni = pm.sample(2000, random_seed=42)
idata_uni.extend(pm.sample_prior_predictive(8000))
そして、ここでArviZのaz.plot_bf関数
az.plot_bf(idata_uni, var_name="a", ref_val=0.5);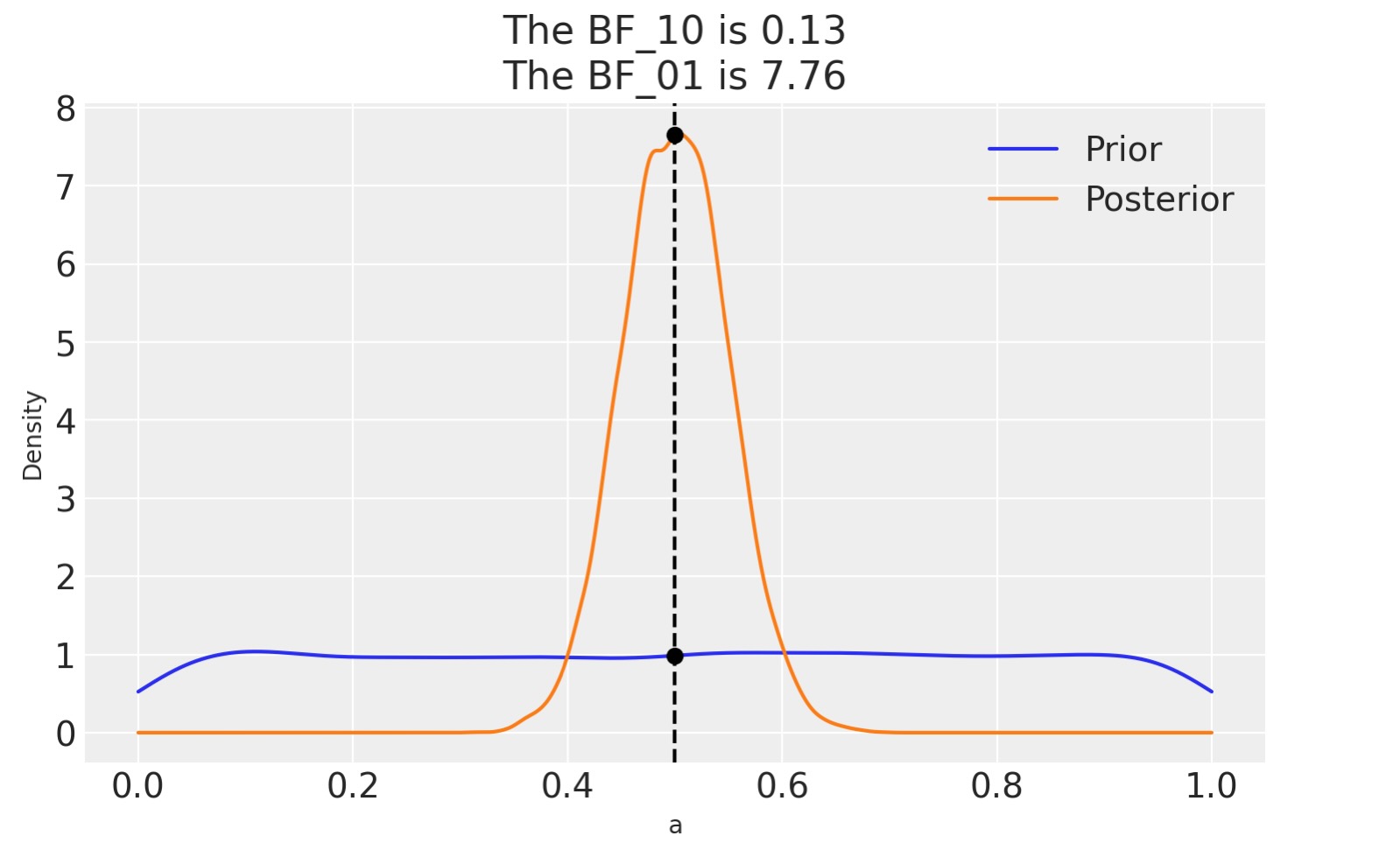
図は事前分布(青)に一つ、事後分布(オレンジ)に一つのKDEを示しています。ふたつの黒い点は、私たちが、評価しているふたつの分布を0.5として示しています。私たちはmベイズ因子を人気のあるBF_01 :~8をベイズ因子と見ることができます, それは、nullの人気のある適当な証拠として解釈することができます。(前に議論したJeffreyのスケールを見てください)
私たちがすでに議論したように、ベイズ因子は、全体として、どのモデルがデータをよりよく説明するかを測定しています。そして、もし事前分布が事後分布の計算に相対的に影響が低い時であっても、これは事前分布を含みます。私たちはnullに対する2番目のモデルで比較した時にこの事前分布の影響を見ることができます。
もし代わりに私たちのモデルが事前分布beta(30,30)のベータ二項分布だった場合、BF_01は、より低くなります(Jeffreyのスケール 個人の見解による証拠)。これは、モデル下でθ=0.5の値は、一様分布の事前分布より、もっと相応しいものです。そしてこうして、事前分布と事後分布は、もっとよく似てきます。すなわち、データを集めた後で、事後分布が0.5の周りに集中するのを見ることは、驚くべきことではありません。
私たち自身で見るためにそれを計算しましょう。
with pm.Model() as model_conc:
a = pm.Beta("a", 30, 30)
yl = pm.Bernoulli("yl", a, observed=y)
idata_conc = pm.sample(2000, random_seed=42)
idata_conc.extend(pm.sample_prior_predictive(8000))
az.plot_bf(idata_conc, var_name="a", ref_val=0.5);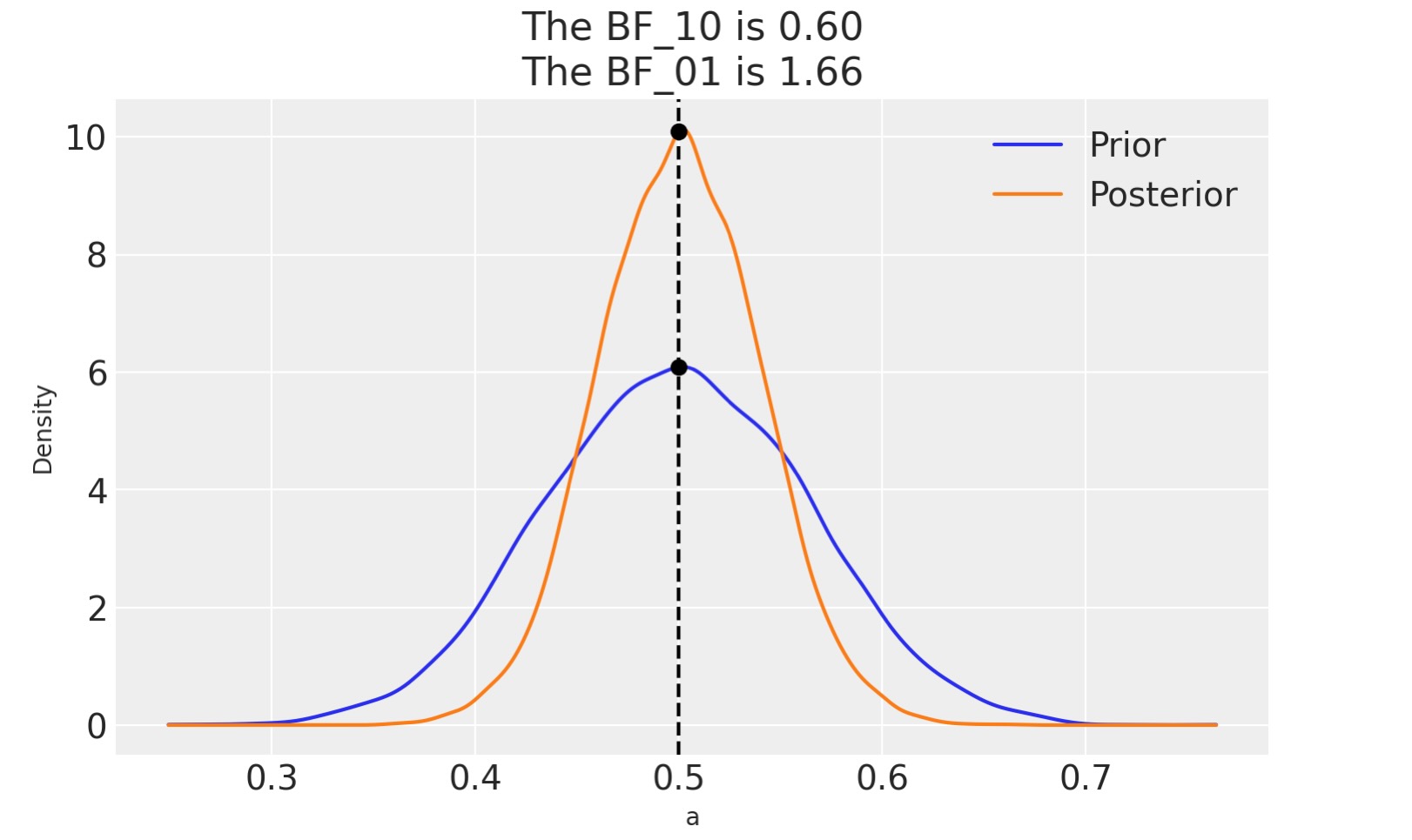
製作者
著者:Osvaldo Martin 2017年 9月
更新:Osvaldo Martin 2018年 8月
更新:Osvalso Martin 2022年 5月
更新:Osvaldo Martin 2022年 11月
更新:Reshama Shaikh 2023年 1月 PyMC v5
参考文献
- James M. Dickey and B. P. Lientz. The Weighted Likelihood Ratio, Sharp Hypotheses about Chances, the Order of a Markov Chain. The Annals of Mathematical Statistics, 41(1):214 – 226, 1970.
- Eric-Jan Wagenmakers, Tom Lodewyckx, Himanshu Kuriyal, and Raoul Grasman. Bayesian hypothesis testing for psychologists: a tutorial on the savage–dickey method. Cognitive Psychology, 60(3):158–189, 2010.