平均と共分散関数

%matplotlib inline

import arviz as az
import matplotlib.cm as cmap
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
import pytensor.tensor as pt
import scipy.stats as stats

RANDOM_SEED = 8927

rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = (10, 4)

　大きなセットの平均と共分散関数が、PyMCで利用できます。カスタムの平均と共分散関数を定義するのは相対的に簡単です。PyMCはPyTensorを使っているので、勾配はユーザーが定義する必要なありません。

平均関数

　以下の平均関数がPyMCで利用できます。

pymc.gp.mean.Zero
pymc.gp.mean.Constant
pymc.gp.mean.Linear

　全て同じ使い方に従います。最初に、平均関数を規定します。その後、任意の入力で評価できます。最初の二つの平均関数は、とても簡単です。入力に関わらず、gp.mean.Zeroは、入力値と同じ長さのゼロベクターを返します。

ゼロ

zero_func = pm.gp.mean.Zero()

X = np.linspace(0, 1, 5)[:, None]
print(zero_func(X).eval())

[0. 0. 0. 0. 0.]

PyMCの全てのGP実装のデフォルトの平均関数は、Zeroです。

定数

　gp.mean.Constantは、与えられた値のベクターを返します。

const_func = pm.gp.mean.Constant(25.2)

print(const_func(X).eval())

[25.2 25.2 25.2 25.2 25.2]

　シェイプが受信する入力に一致する限り、gp.mean.Constantは、PyMCランダム変数のベクターまたは、PyTensorのテンソルを受け入れます。

const_func_vec = pm.gp.mean.Constant(pt.ones(5))

print(const_func_vec(X).eval())

[1. 1. 1. 1. 1.]

線形

　gp.mean.Linearは、係数の行列とインターセプトのベクターを入力として受け取ります。

beta = rng.normal(size=3)
b = 0.0

lin_func = pm.gp.mean.Linear(coeffs=beta, intercept=b)

X = rng.normal(size=(5, 3))
print(lin_func(X).eval())

[ 1.03424803 -2.25903687  0.78030931  0.9880038  -3.45565466]

カスタム平均関数の定義

　カスタム平均関数を定義するために、サブクラス、gp.mean.Meanと、__call__と__init__メソッドを提供します。例えば、Constant平均関数のコードは、

import theano.tensor as tt

class Constant(pm.gp.mean.Mean):
    
    def __init__(self, c=0):
        Mean.__init__(self)
        self.c = c 

    def __call__(self, X): 
        return tt.alloc(1.0, X.shape[0]) * self.c

NumPyの代わりにPyTensorを使用する必要があることを覚えておいてください。

共分散関数

　PyMCは、もっと大きなビルトイン共分散関数(built-in covariance function)の体系を含んでいます。以下は、共分散関数によって与えられるGP事前分布から出力される関数を示しています。そしてどのように構成共分散関数が、まっすぐなやり方でPythonの操作を構築することができるか示します。私たちのゴールは、APIが、できるかぎり緊密にカーネル代数(RasmussenとWilliams[2006]のCh.4を参照)に従うことです。主要なドキュメントのPyMCの使用に関する概要を参照してください。

２次の指数

lengthscale = 0.2
eta = 2.0
cov = eta**2 * pm.gp.cov.ExpQuad(1, lengthscale)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(
        pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=K.shape[0]), draws=3, random_seed=rng
    ).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");

二次元(それ以上)の入力

両方の次元がアクティブ

高次の入力のカーネルを定義するのは簡単です。ls(lengthscale)パラメータは長さ２の配列であることを注記します。PyMCランダム変数のリストは、自動関連決定(ARD)を使うことができます。

x1 = np.linspace(0, 1, 10)
x2 = np.arange(1, 4)
# Cartesian product
X2 = np.dstack(np.meshgrid(x1, x2)).reshape(-1, 2)

ls = np.array([0.2, 1.0])
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls)

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);

一つの次元がアクティブ

ls = 0.2
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls, active_dims=[0])

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);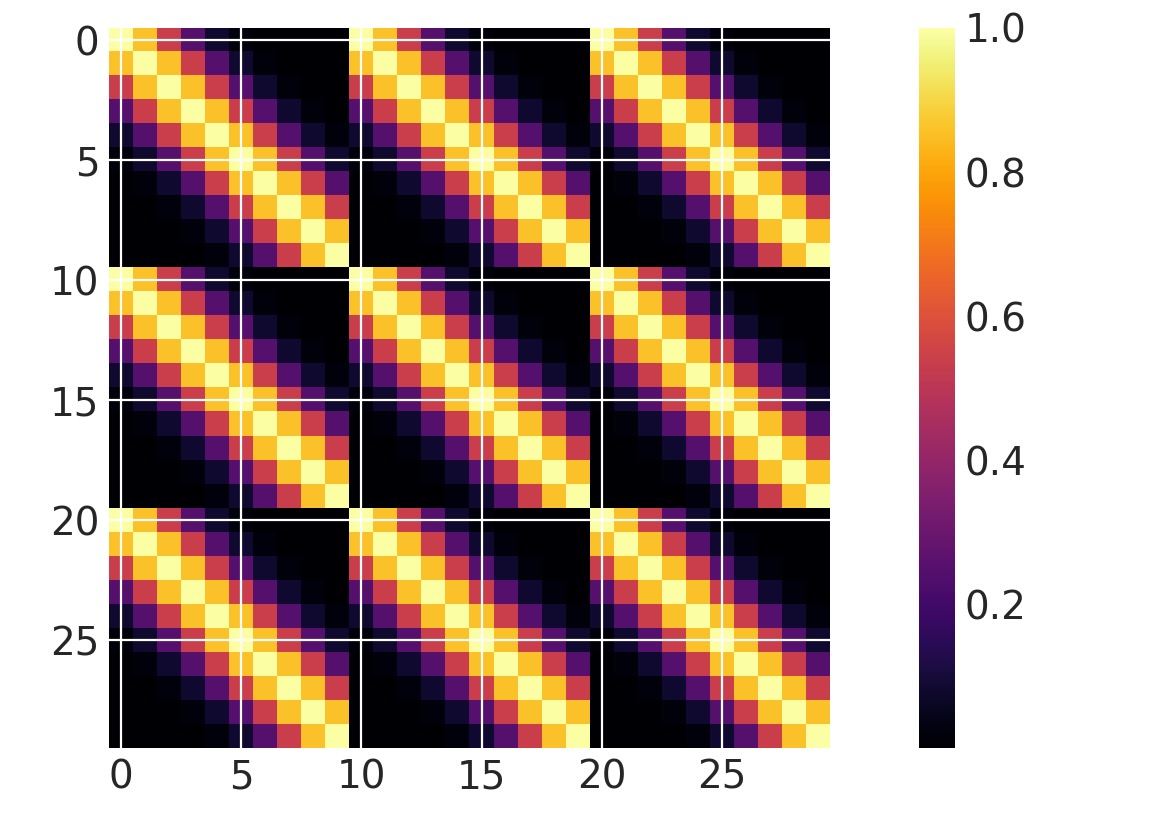

異なる次元での共分散の乗算

　これは、各次元で分離したlengthscaleパラメータとともに、二次元のExQuadを使う等式であることに注意してください。

ls1 = 0.2
ls2 = 1.0
cov1 = pm.gp.cov.ExpQuad(2, ls1, active_dims=[0])
cov2 = pm.gp.cov.ExpQuad(2, ls2, active_dims=[1])
cov = cov1 * cov2

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);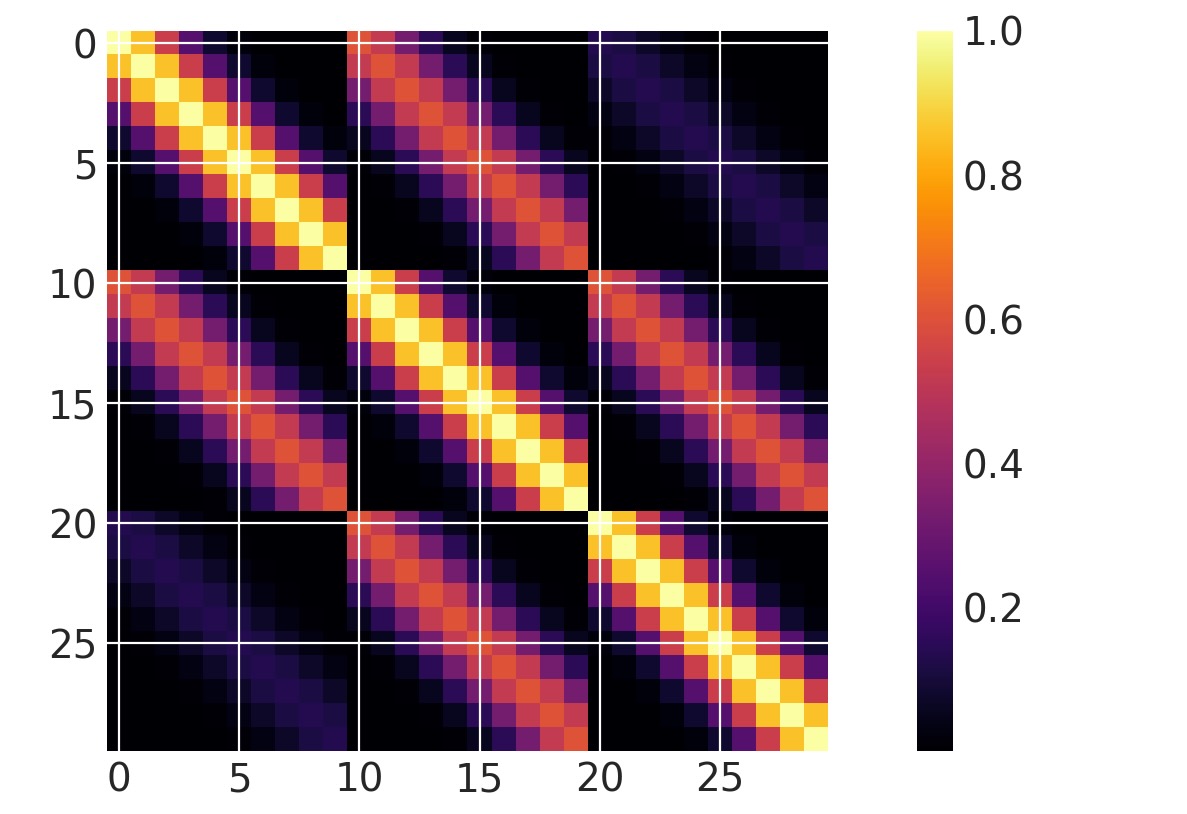

ホワイトノイズ

sigma = 2.0
cov = pm.gp.cov.WhiteNoise(sigma)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");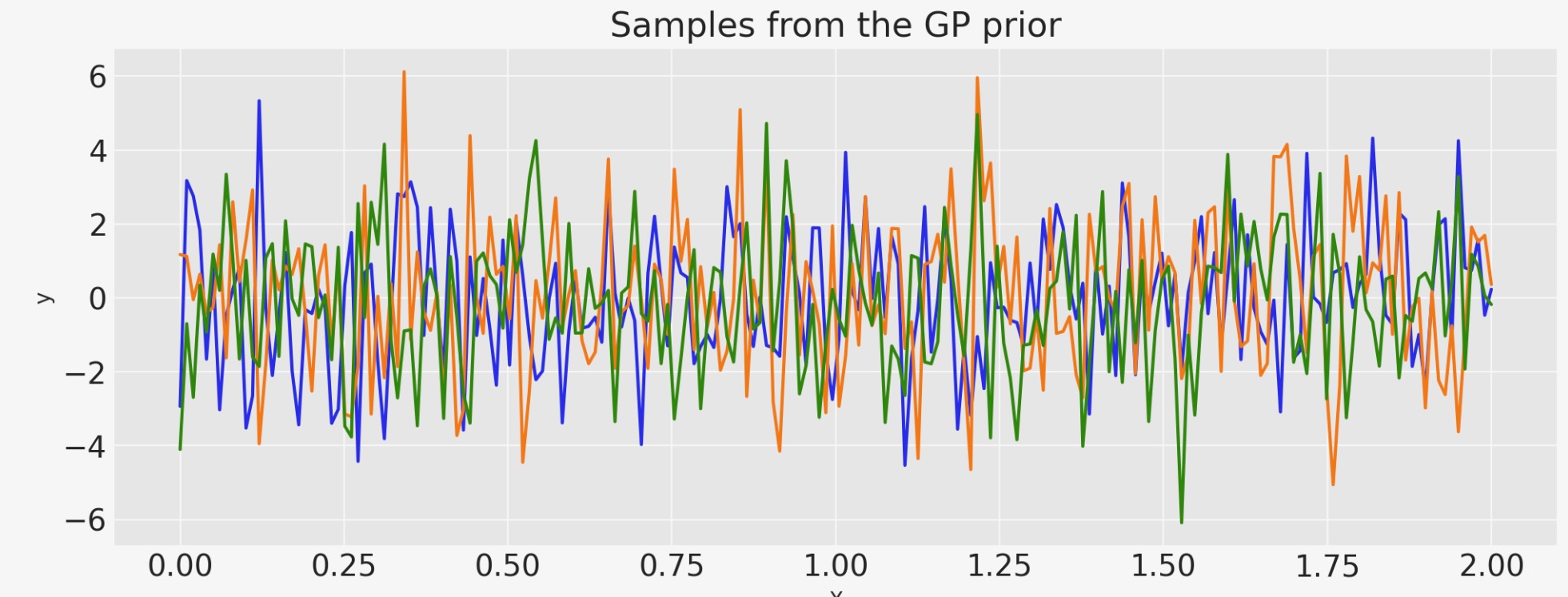

定数

　　　　　　　k(x,x') = c

c = 2.0
cov = pm.gp.cov.Constant(c)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");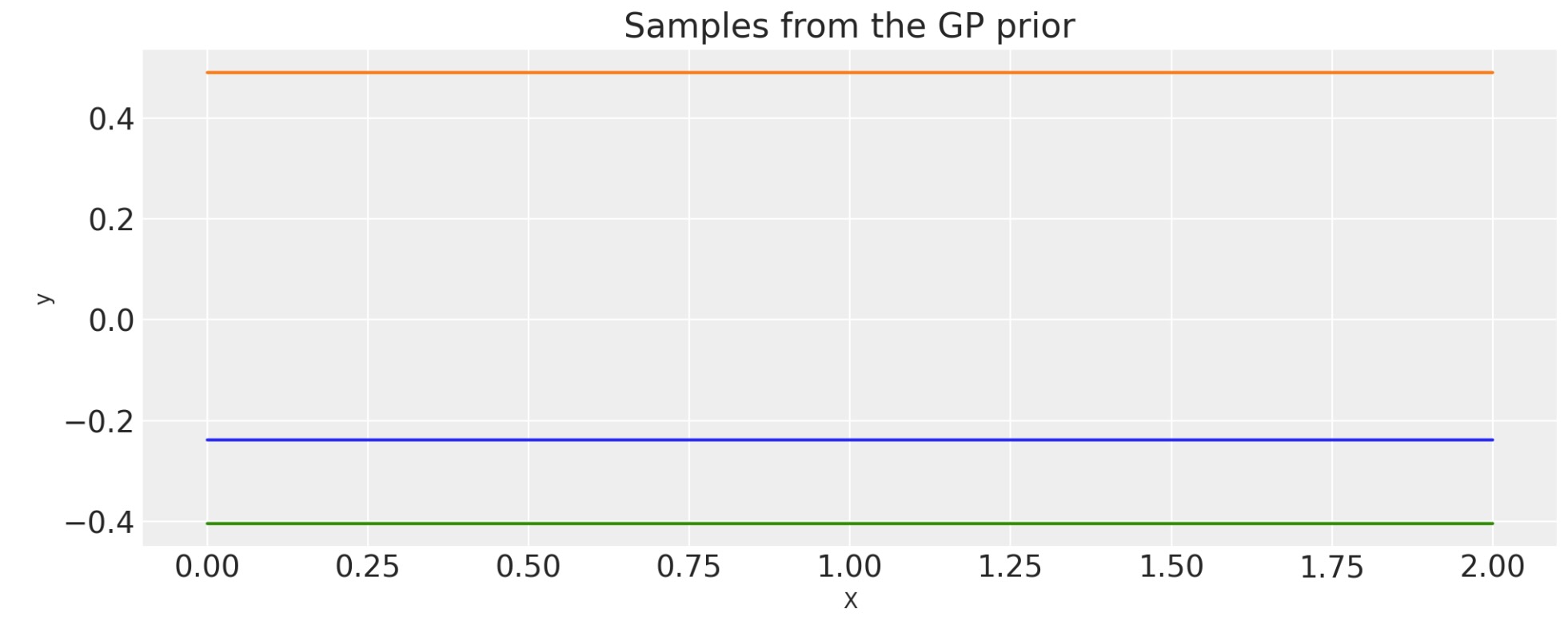

２次有理

alpha = 0.1
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.RatQuad(1, ls, alpha)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");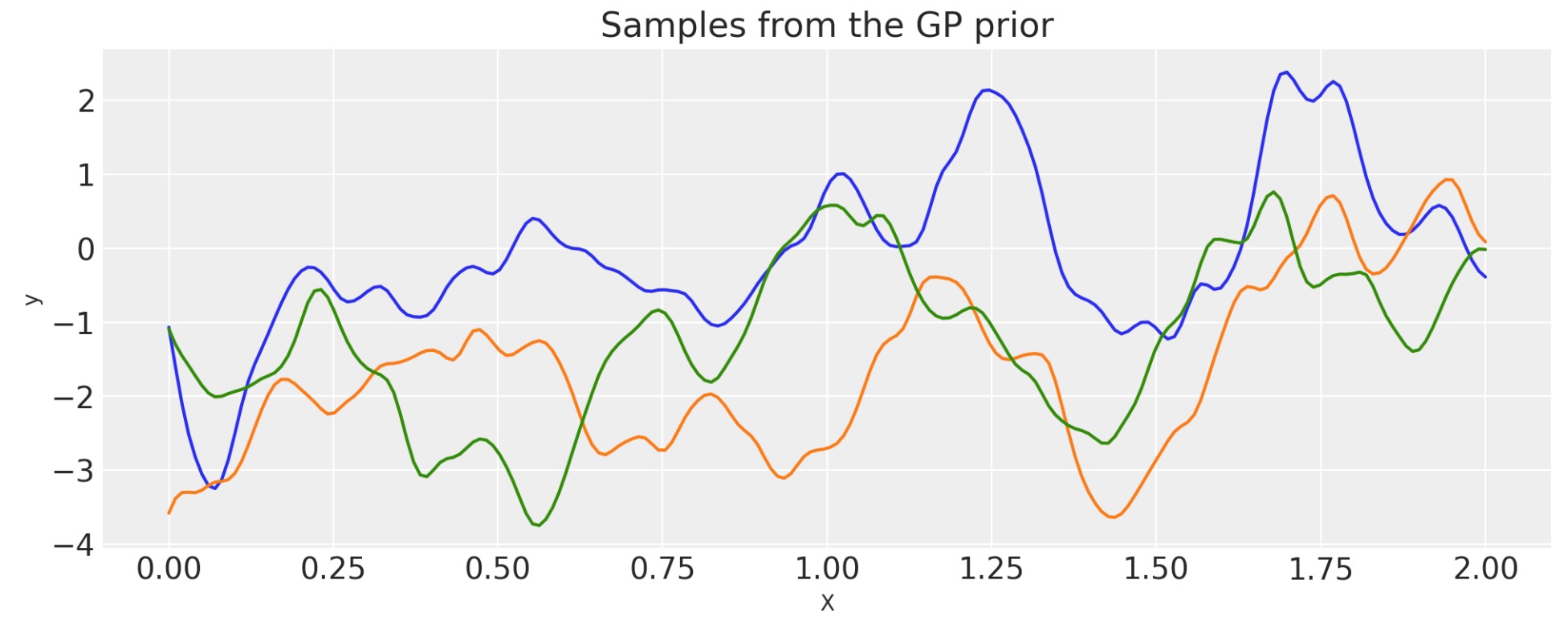

指数

inverse_lengthscale = 5
cov = pm.gp.cov.Exponential(1, ls_inv=inverse_lengthscale)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");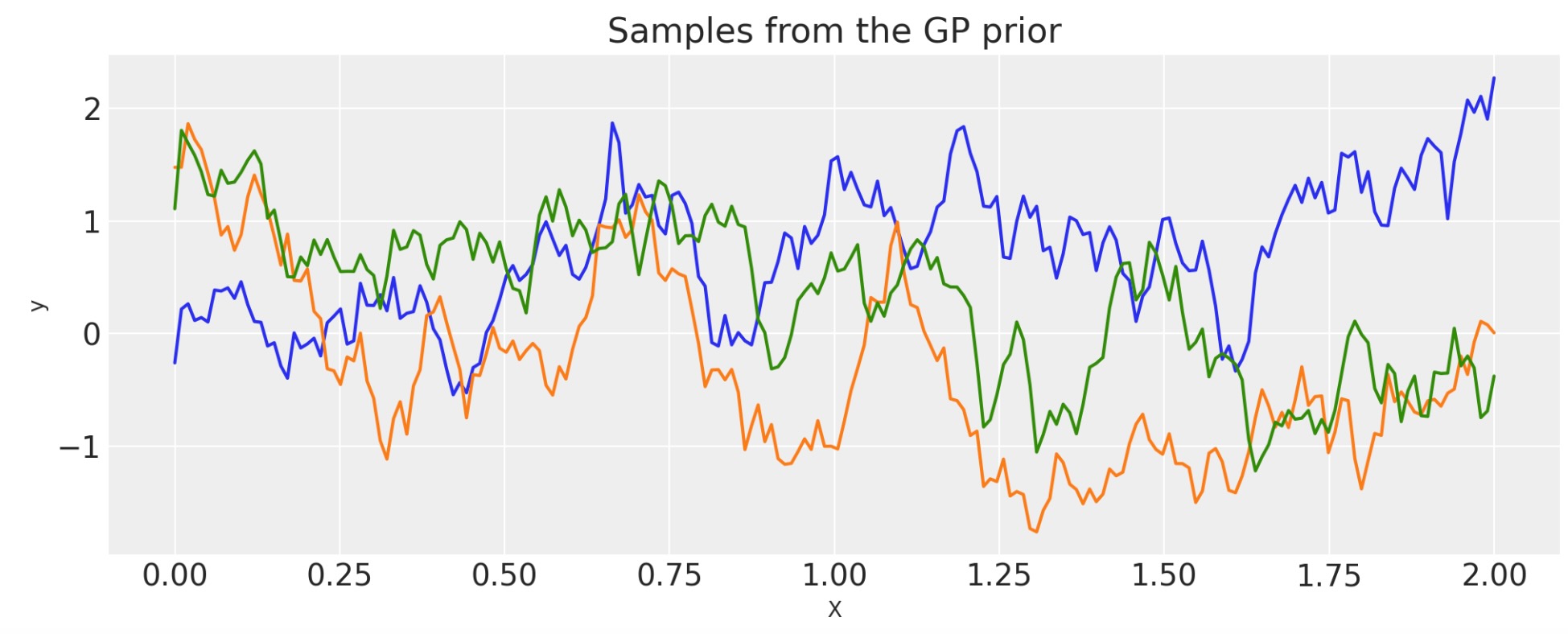

Matern 5/2

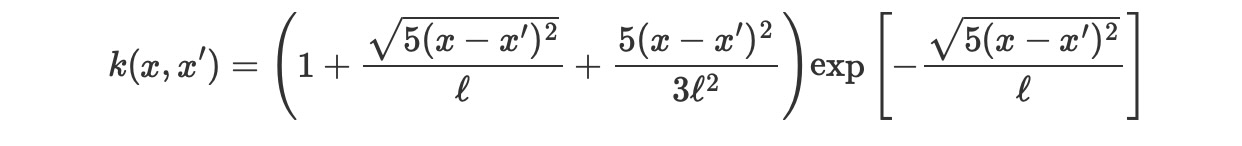
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern52(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");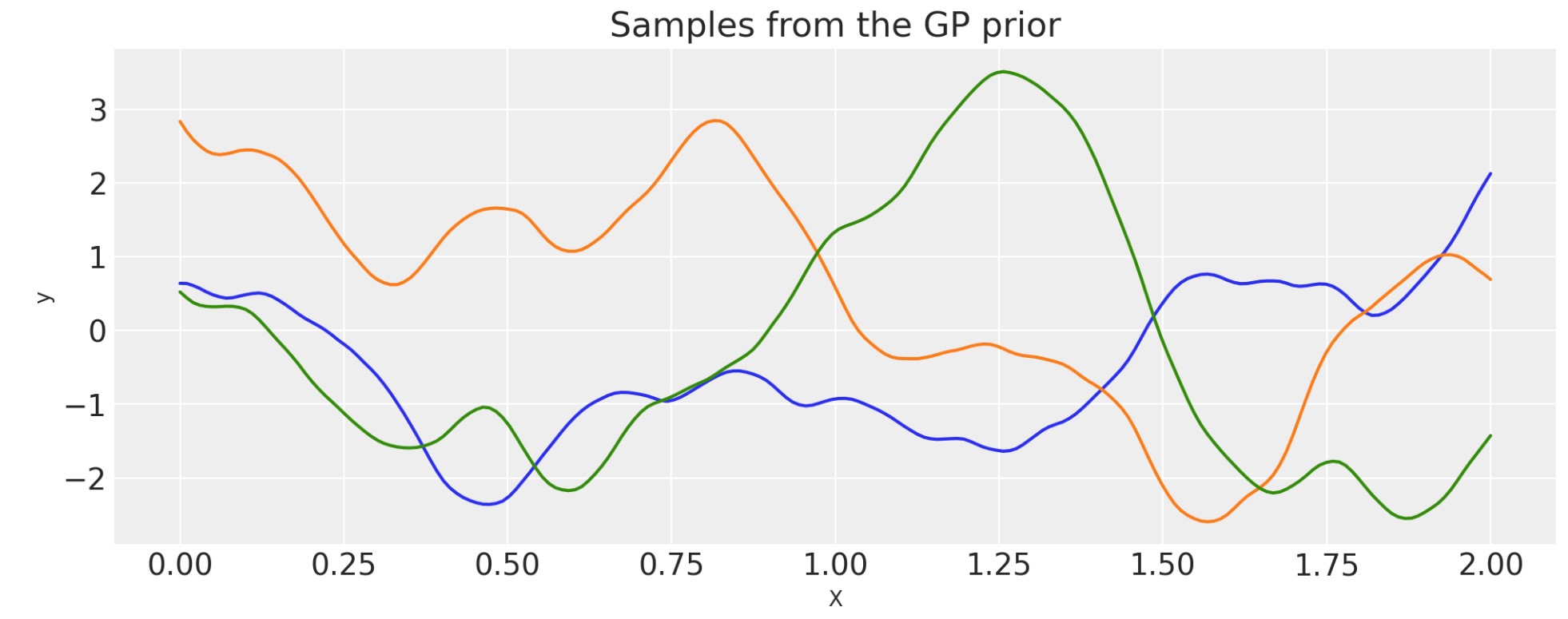

Matern 3/2

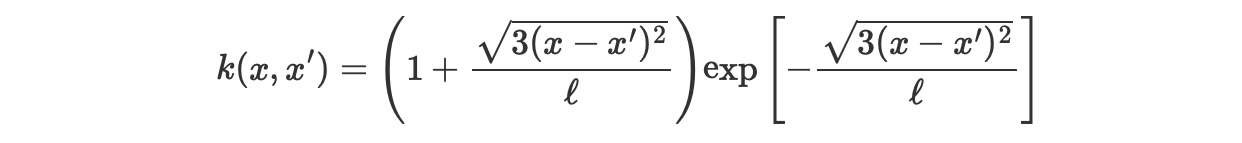
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern32(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");

Matern 1/2

ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern12(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");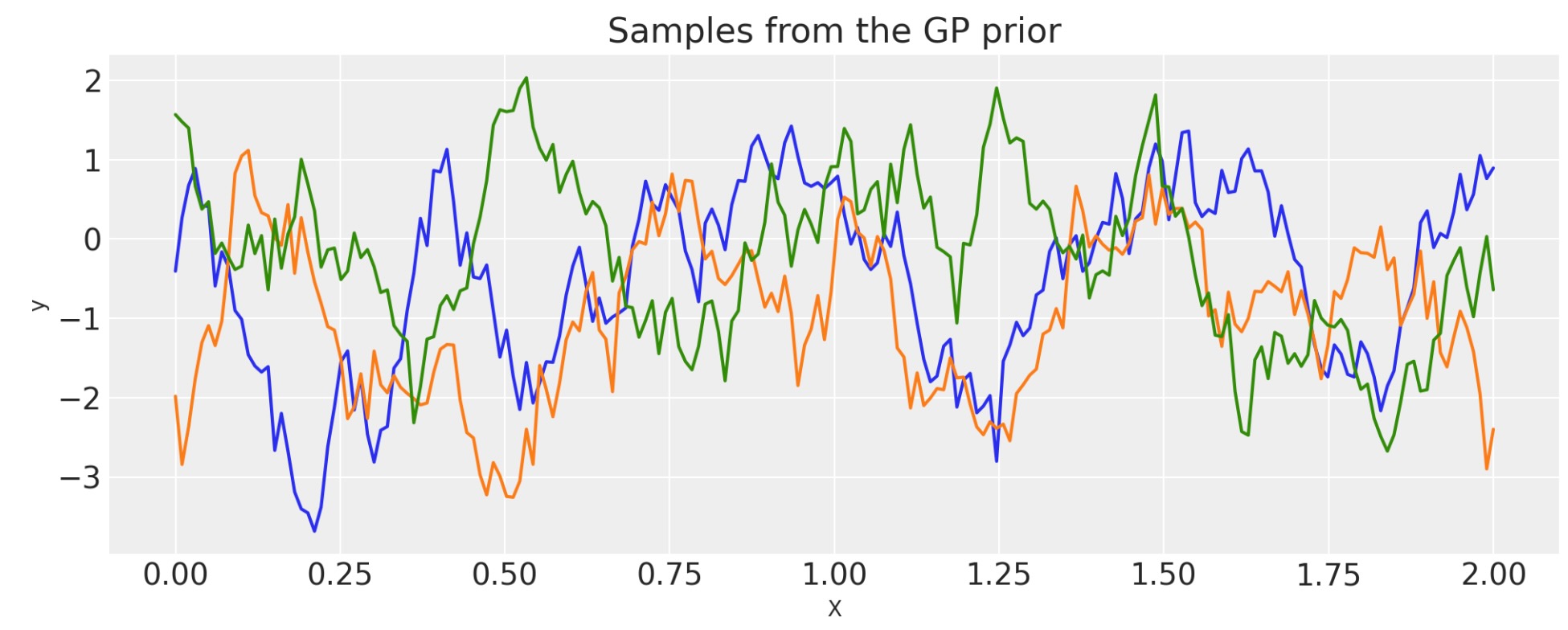

コサイン

period = 0.5
cov = pm.gp.cov.Cosine(1, period)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-4)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");

線形

　　　　　　　k(x,x') = (x - c )(x' - c)

c = 1.0
tau = 2.0
cov = tau * pm.gp.cov.Linear(1, c)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");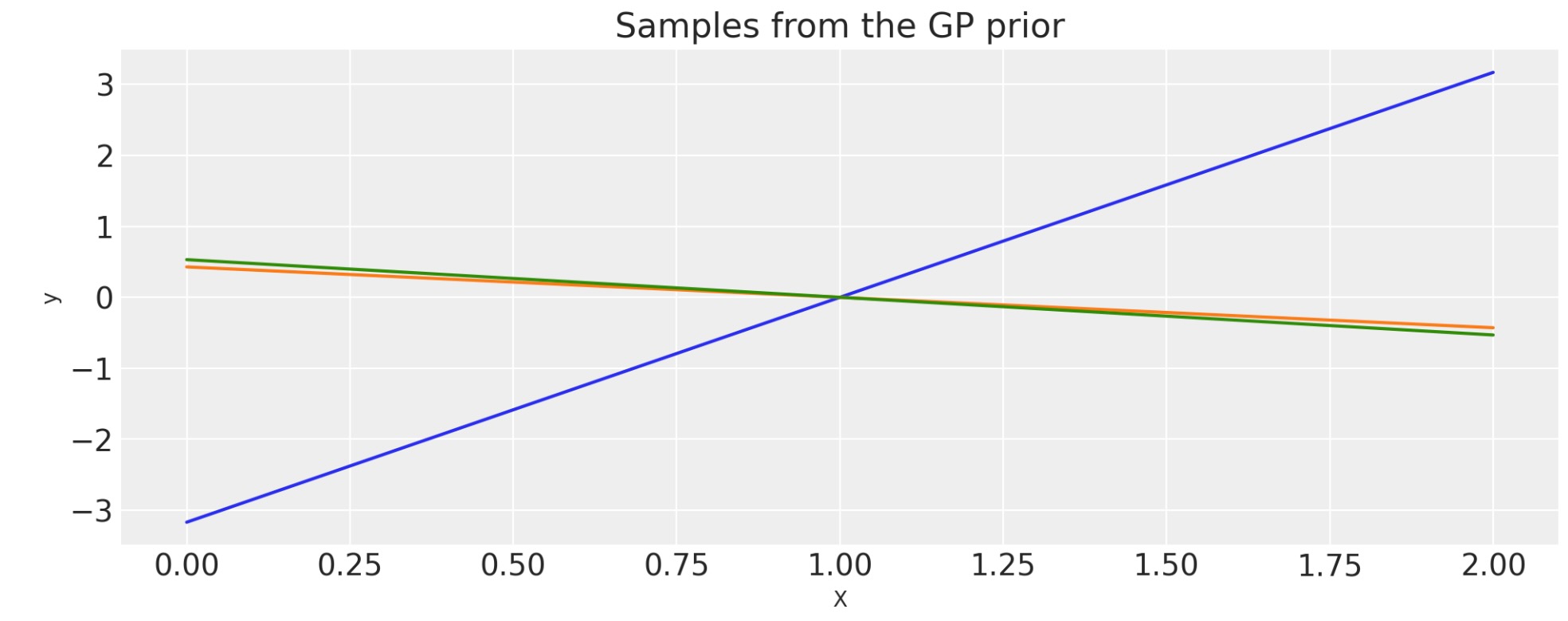

多項式

　　　　　　　k(x,x') = [ (x - c)(x' - c) + offset] ^d

c = 1.0
d = 3
offset = 1.0
tau = 0.1
cov = tau * pm.gp.cov.Polynomial(1, c=c, d=d, offset=offset)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");

事前計算ずみの共分散行列の多重化

　共分散関数covは、シェイプが適当であれば、numpy行列、K_cos,を乗算します。

# first evaluate a covariance function into a matrix
period = 0.2
cov_cos = pm.gp.cov.Cosine(1, period)
K_cos = cov_cos(X).eval()

# now multiply it with a covariance *function*
cov = pm.gp.cov.Matern32(1, 0.5) * K_cos

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");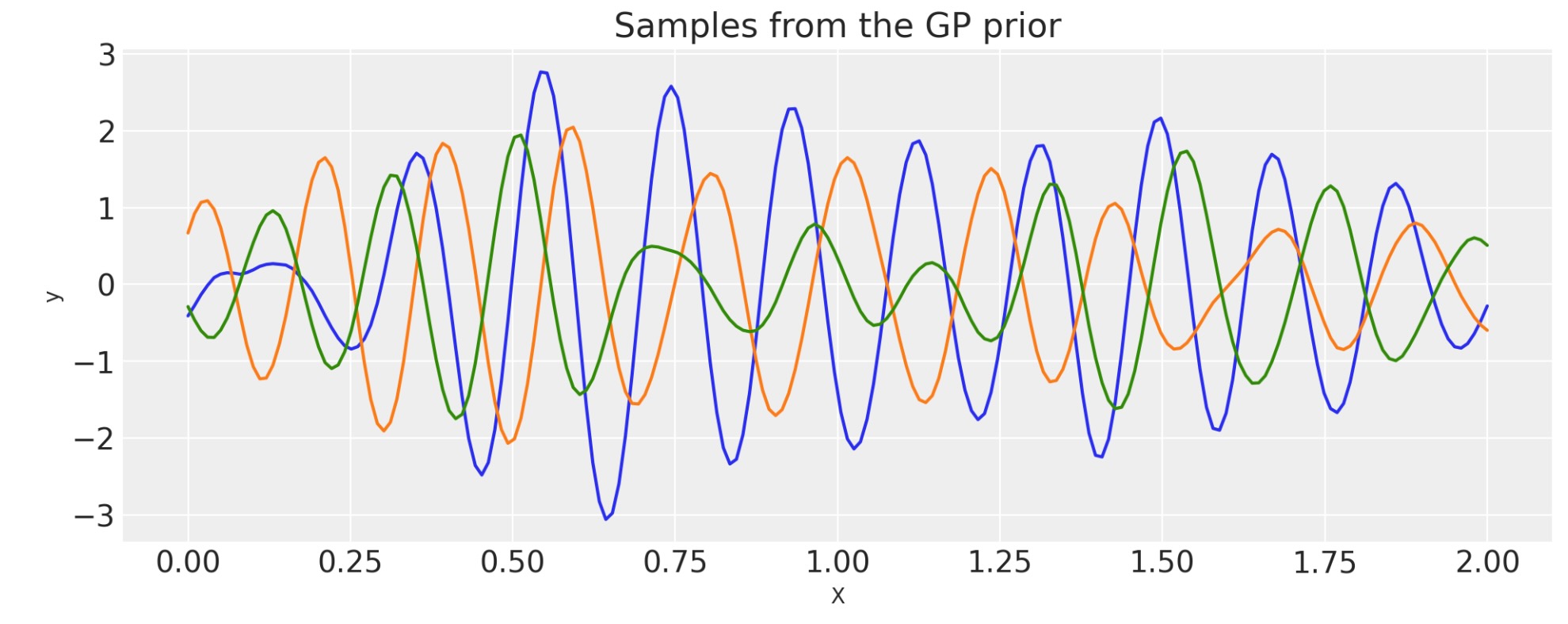

入力への恣意的なワープ関数の適用

　もし、k(x,x')が、正しい共分散関数であれば、その時それは、k(w(x),w(x'))
ワープ関数の最初の引数は、入力Xでなければなりません。残りの引数は乱数を含む、何か別のものです。

def warp_func(x, a, b, c):
    return 1.0 + x + (a * pt.tanh(b * (x - c)))


a = 1.0
b = 5.0
c = 1.0

cov_exp = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.WarpedInput(1, warp_func=warp_func, args=(a, b, c), cov_func=cov_exp)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 400)[:, None]
wf = warp_func(X.flatten(), a, b, c).eval()

plt.plot(X, wf)
plt.xlabel("X")
plt.ylabel("warp_func(X)")
plt.title("The warping function used")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");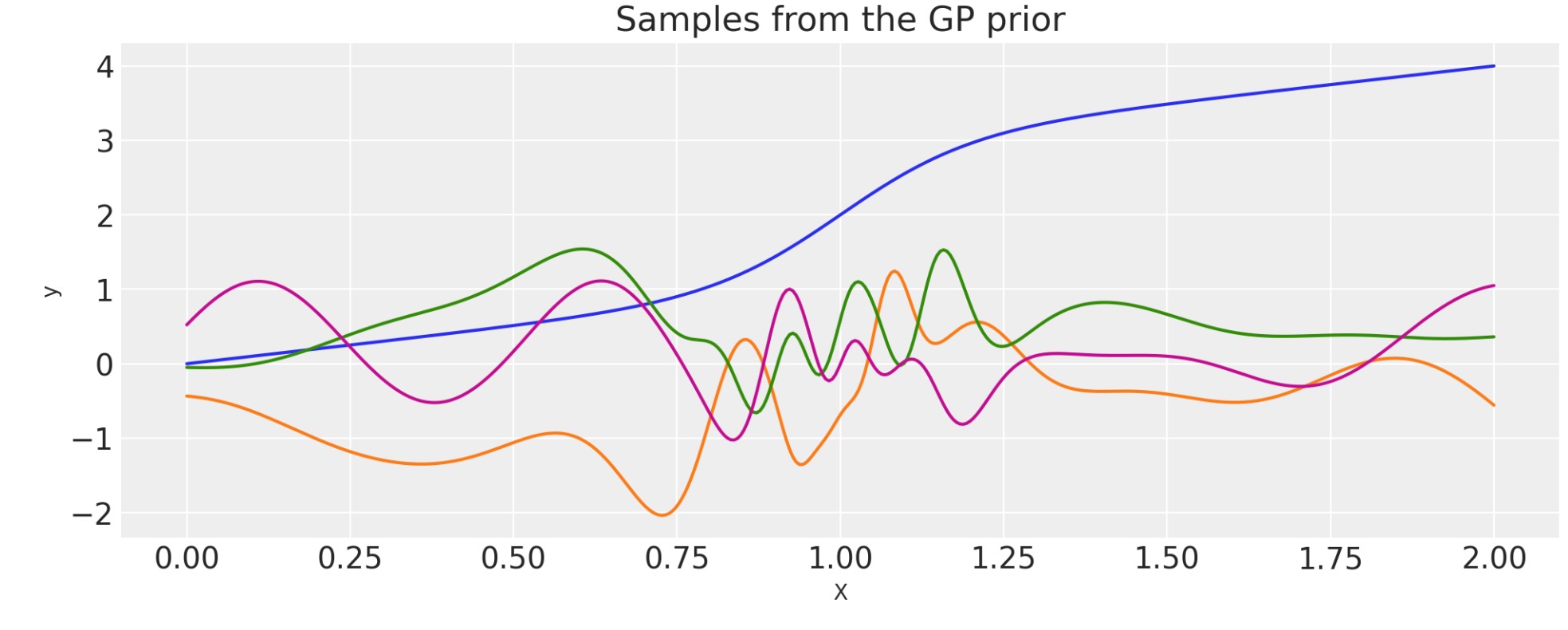

WarpedInputを使ったPeriodicの構築

　WarpedInputカーネルは、Periodic共分散を生成することができます。共分散モデル関数は、周期的ですが、正確な正弦波ではありません(Cosineカーネルのような）
周期カーネルは次で与えられます。

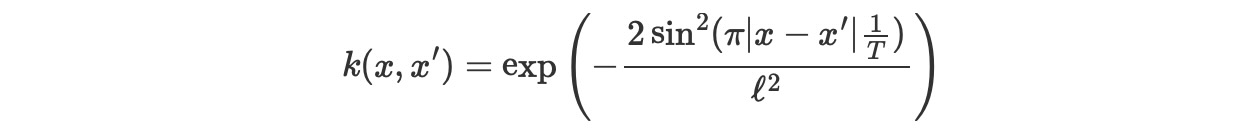
　Tは、周期で、lはlengthscaleです。関数u(x)=(sin(2πx(1/T)),cos(2πx(1/T)))によるExpQuadカーネルの入力をワープすることによって、生成することができます。
　このページの先頭で定義された入力xは、２秒です。私たちは、0.5の周期を使います。それは、このGP事前分布から出力される関数が２秒間で４回繰り返されることを意味します。

def mapping(x, T):
    c = 2.0 * np.pi * (1.0 / T)
    u = pt.concatenate((pt.sin(c * x), pt.cos(c * x)), 1)
    return u


T = 0.6
ls = 0.4
# note that the input of the covariance function taking
#    the inputs is 2 dimensional
cov_exp = pm.gp.cov.ExpQuad(2, ls)
cov = pm.gp.cov.WarpedInput(1, cov_func=cov_exp, warp_func=mapping, args=(T,))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");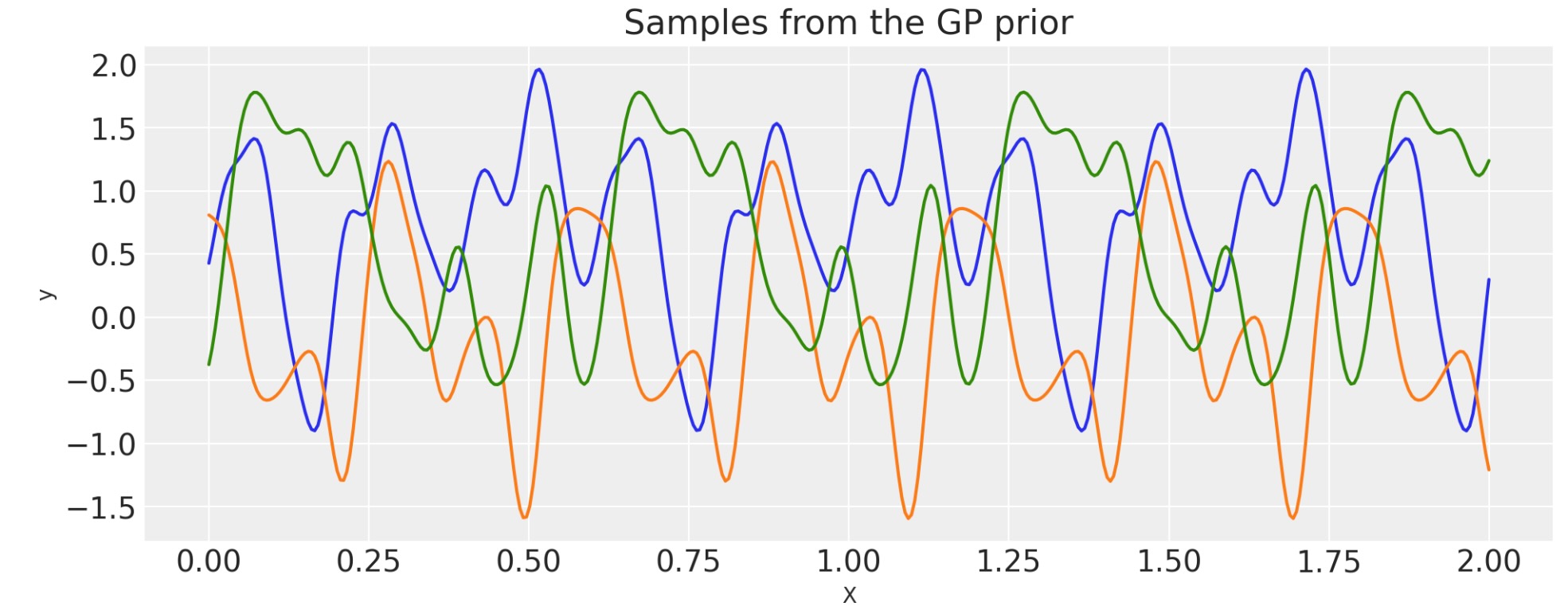

周期

　毎回、この方法で周期共分散を構築する必要はありません。もっと効果的な、この共分散関数の実装はビルトインされています。

period = 0.6
ls = 0.4
cov = pm.gp.cov.Periodic(1, period=period, ls=ls)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");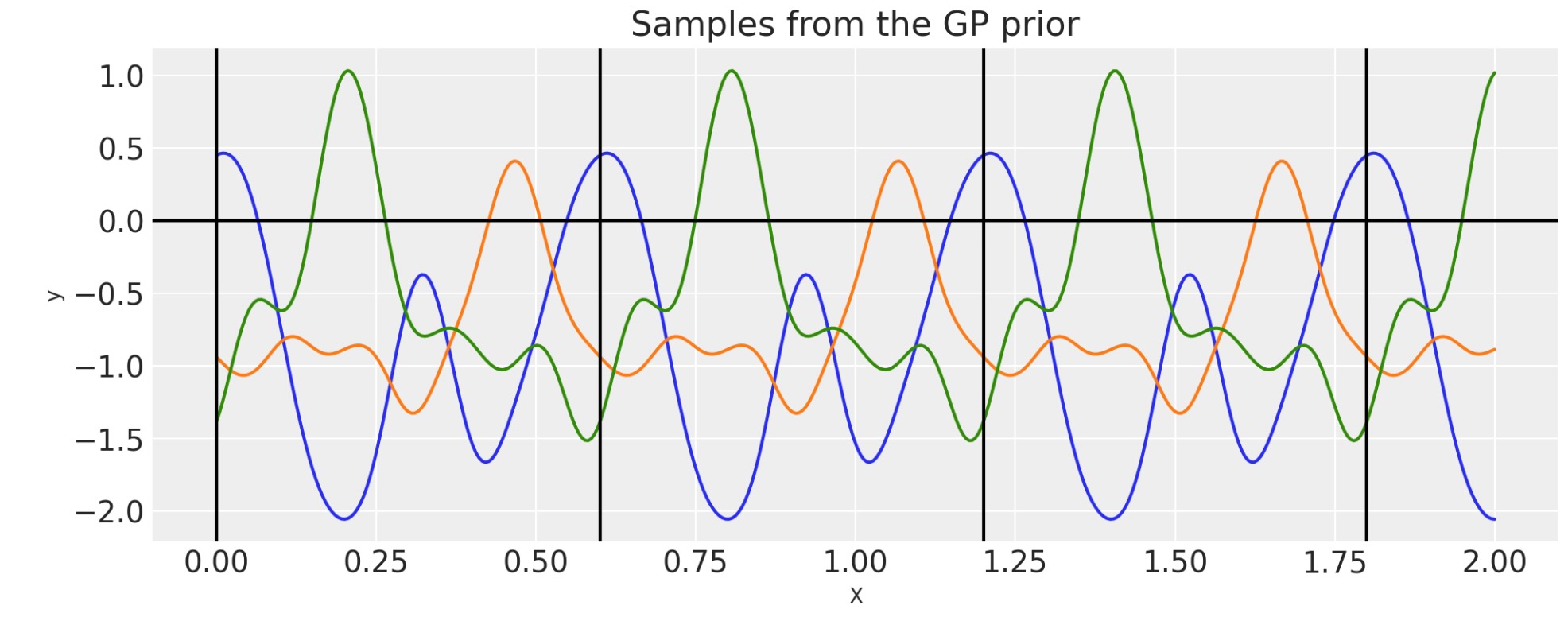

循環

循環カーネルは、Periodicと似ていますが、追加の抑制パラメータτを持っています。
PadonouとRoustant[2015],Weinland関数は、問題を解決するのに使います。そして、循環ドメイン(それだけでなく)内で、ポジティブな決定カーネルを確認します。

　ここで、cは、tの最大値で、τ ≧ 4 の任意の正の値
　サークルの測地線の距離に対するカーネルは、以下のようになります。

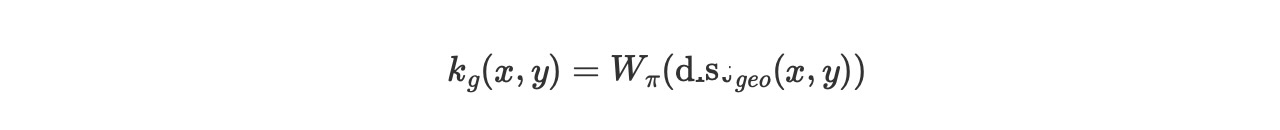
　簡潔には、あなたは以下のことを考えることができます。

tは時間、0から24まで進み、０に戻る
cはタイムスタンプの間の最大値、ここでは12になります
τは、相関の長さを制御、大きなτは、スムースさに乏しい関数を導きます。

period = 0.6
tau = 4
cov = pm.gp.cov.Circular(1, period=period, tau=tau)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");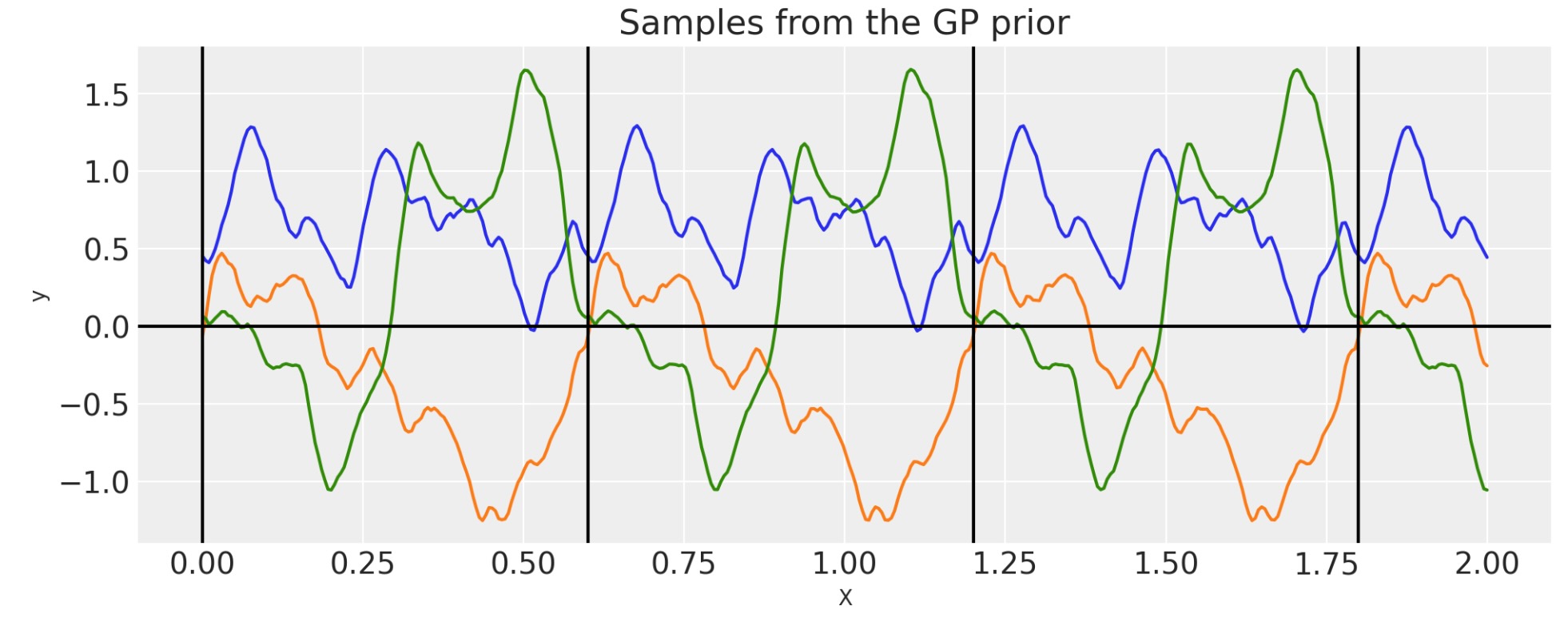

私たちは、τの効果を見ることができます。それは、もっとスムースではないパターンを追加します。

period = 0.6
tau = 40
cov = pm.gp.cov.Circular(1, period=period, tau=tau)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");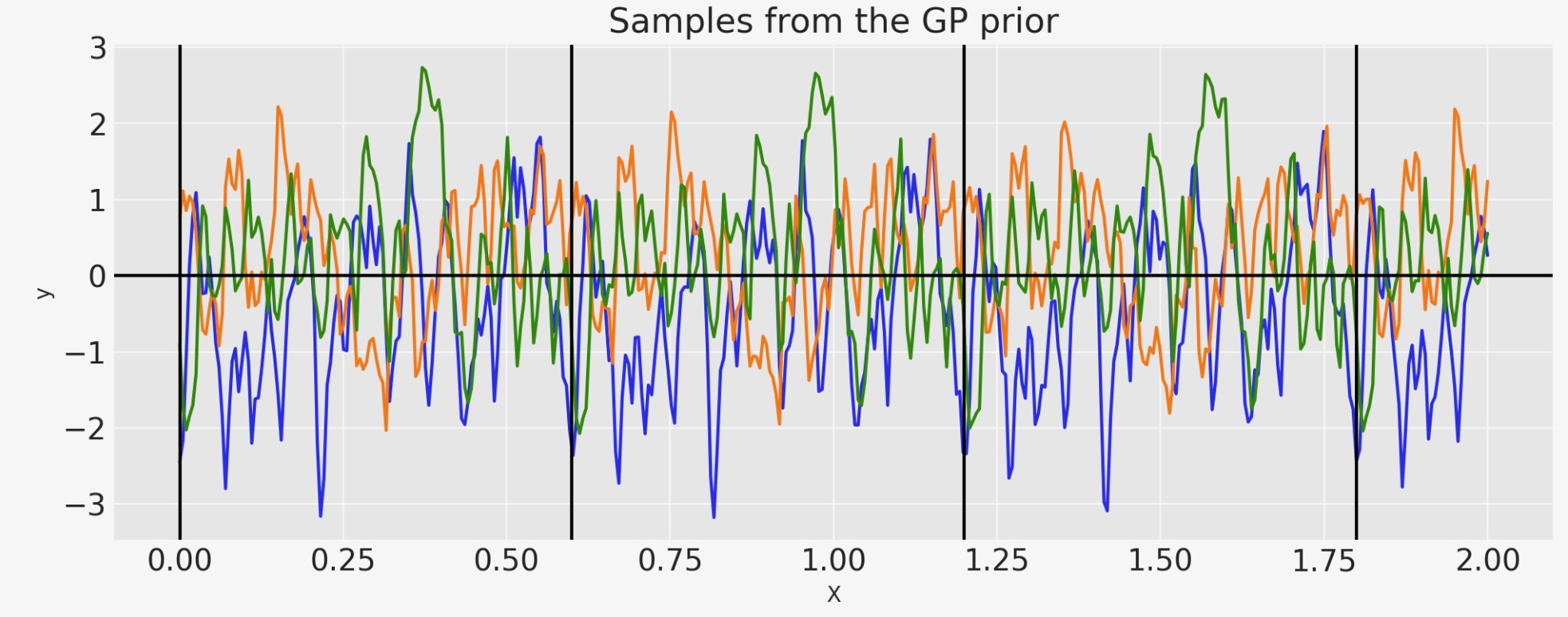

ギッブス

　ギッブス共分散関数は、ポジティブに定義したワープ関数にlengthscaleを適用します。WarpedInputと同様に、lengthscaleワープ関数は、固定かまたはランダムな変数のどちらかをパラメータに規定できます。

def tanh_func(x, ls1, ls2, w, x0):
    """
    ls1: left saturation value
    ls2: right saturation value
    w:   transition width
    x0:  transition location.
    """
    return (ls1 + ls2) / 2.0 - (ls1 - ls2) / 2.0 * pt.tanh((x - x0) / w)


ls1 = 0.05
ls2 = 0.6
w = 0.3
x0 = 1.0
cov = pm.gp.cov.Gibbs(1, tanh_func, args=(ls1, ls2, w, x0))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

wf = tanh_func(X, ls1, ls2, w, x0).eval()
plt.plot(X, wf)
plt.ylabel("lengthscale")
plt.xlabel("X")
plt.title("Lengthscale as a function of X")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");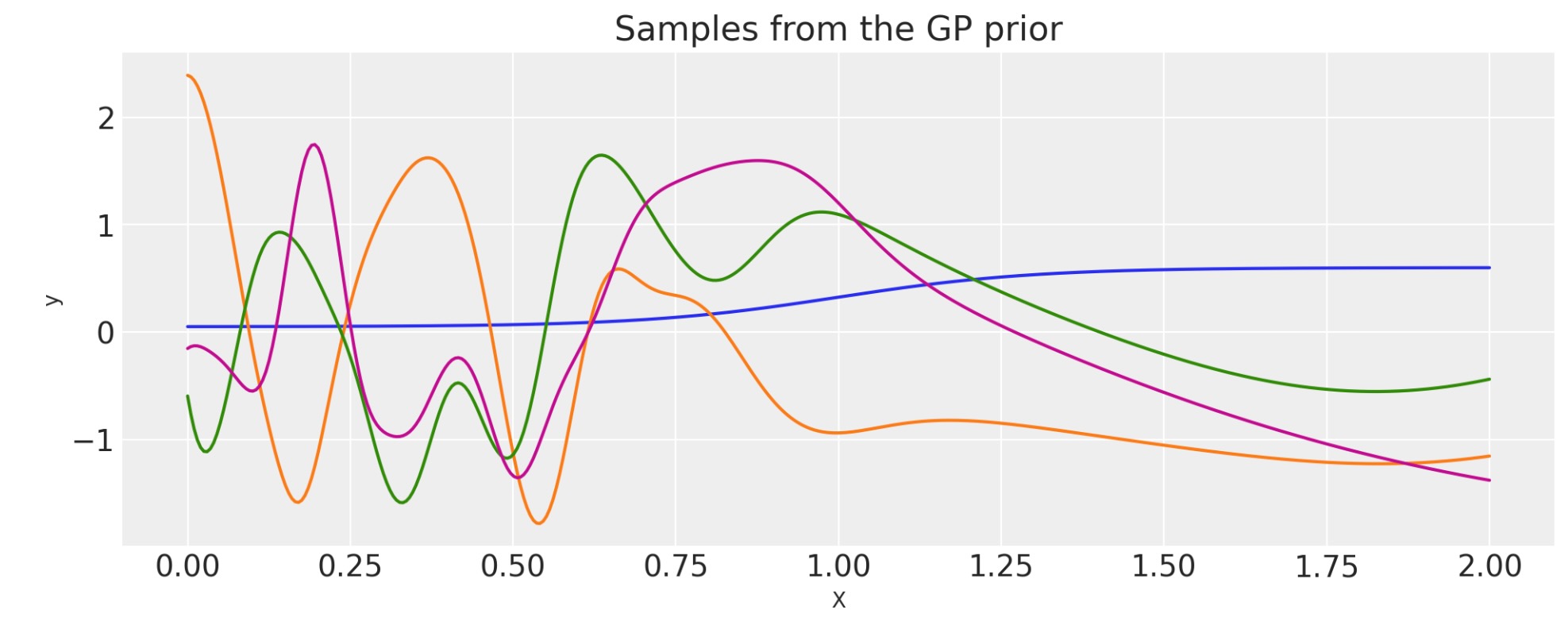

スケールされた共分散

　非負の関数Φ(x)によって任意の基礎カーネルを乗算することによって、新しいカーネルまたは共分散関数を構築します。

　これは、ドメインを超えて振幅が変化する共分散関数を規定するのに使います。

def logistic(x, a, x0, c, d):
    # a is the slope, x0 is the location
    return d * pm.math.invlogit(a * (x - x0)) + c


a = 2.0
x0 = 5.0
c = 0.1
d = 2.0

cov_base = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.ScaledCov(1, scaling_func=logistic, args=(a, x0, c, d), cov_func=cov_base)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)

X = np.linspace(0, 10, 400)[:, None]
lfunc = logistic(X.flatten(), a, b, c, d).eval()

plt.plot(X, lfunc)
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The scaling function")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");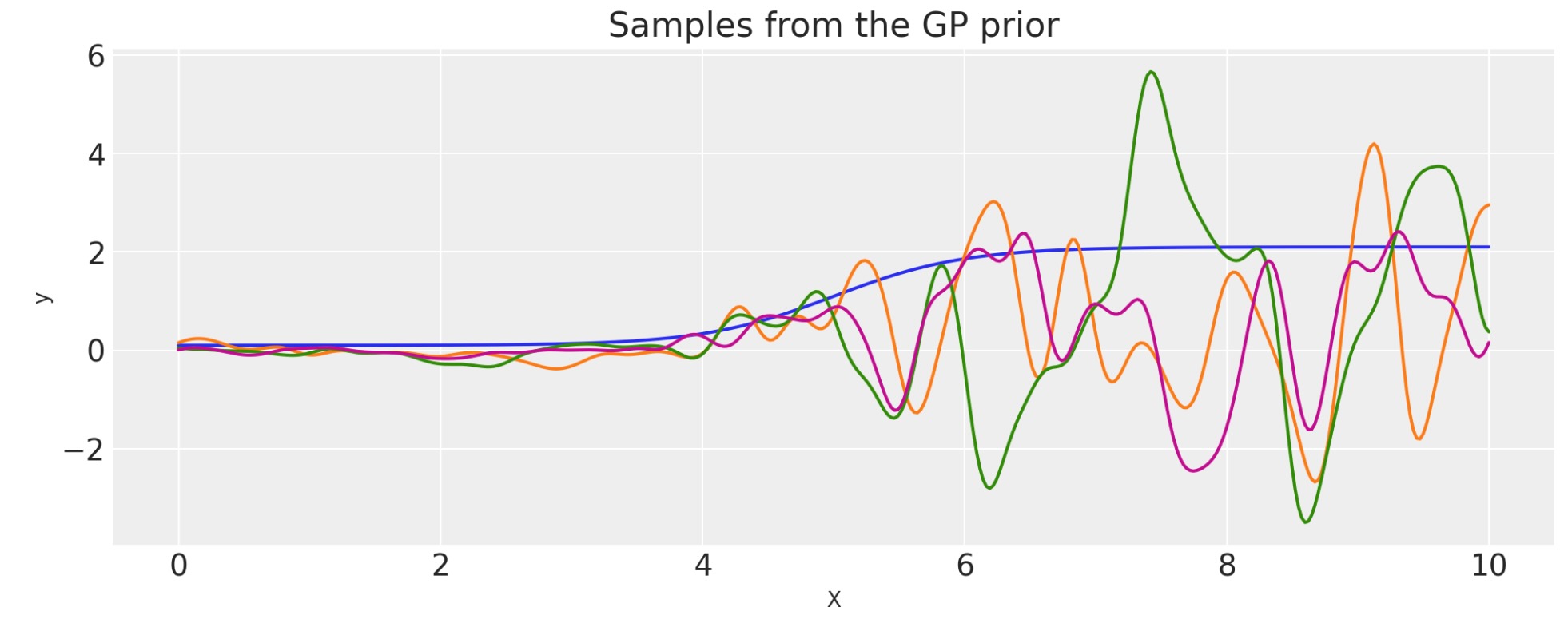

ScaledCovを使ったチェンジポイントカーネルの構築

　ScaledCovカーネルは、Changepoint共分散を生成するのに使うことができます。この共分散は、一つの型の振る舞いから他へ段階的に変換する過程をモデルにします。
チェンジポイントカーネルは、次で与えられます。

　ここで、Φ(x)は、ロジスティック関数です。

def logistic(x, a, x0):
    # a is the slope, x0 is the location
    return pm.math.invlogit(a * (x - x0))


a = 2.0
x0 = 5.0

cov1 = pm.gp.cov.ScaledCov(
    1, scaling_func=logistic, args=(-a, x0), cov_func=pm.gp.cov.ExpQuad(1, 0.2)
)
cov2 = pm.gp.cov.ScaledCov(
    1, scaling_func=logistic, args=(a, x0), cov_func=pm.gp.cov.Cosine(1, 0.5)
)
cov = cov1 + cov2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)

X = np.linspace(0, 10, 400)
plt.fill_between(
    X,
    np.zeros(400),
    logistic(X, -a, x0).eval(),
    label="ExpQuad region",
    color="slateblue",
    alpha=0.4,
)
plt.fill_between(
    X, np.zeros(400), logistic(X, a, x0).eval(), label="Cosine region", color="firebrick", alpha=0.4
)
plt.legend()
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The two scaling functions")

K = cov(X[:, None]).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");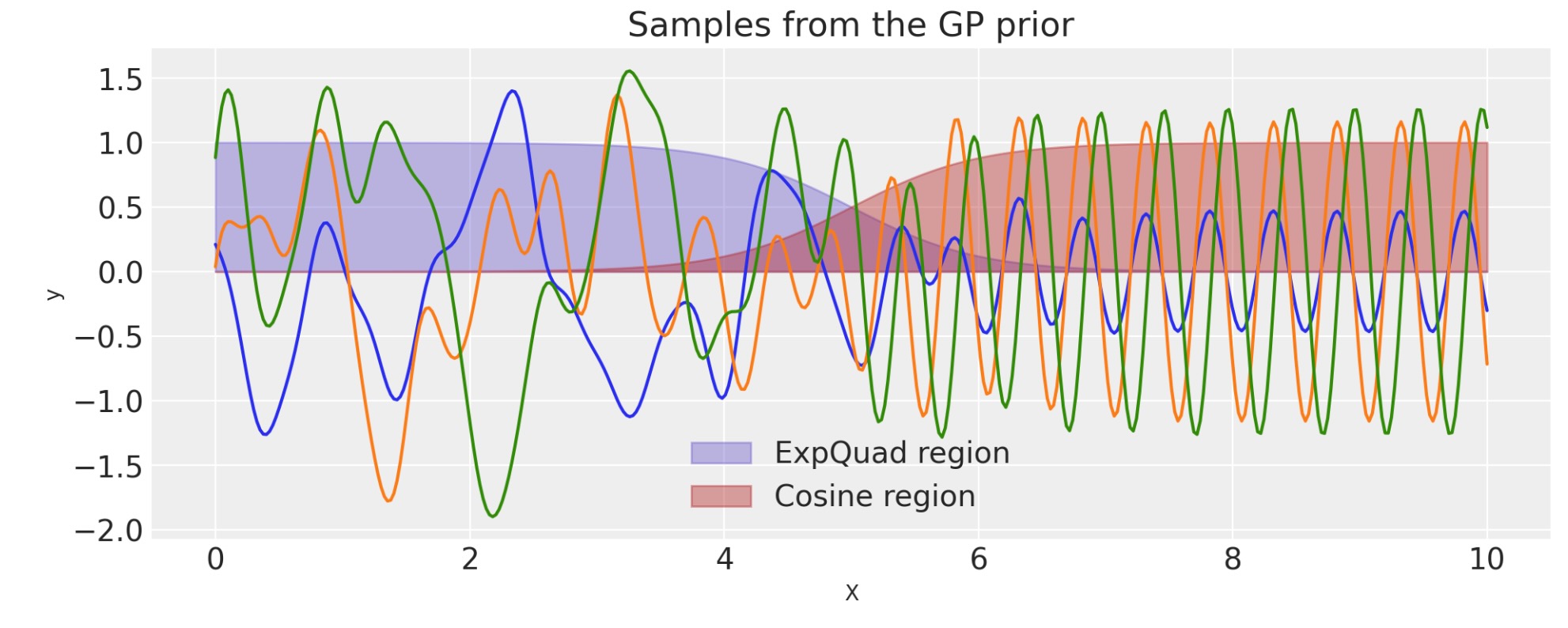

二つ以上の共分散の組み合わせ

　あなたは、複雑なデータをモデル化するのに異なる共分散を組み合わせることができます。
　特に、あなたは、どのような共分散関数でも以下の操作を実行することができます。

最初の共分散関数と同じか広がる次元で他の共分散関数を加算する。
最初の共分散関数と同じか広がる次元でスカラーかまたは共分散関数を乗算する
スカラーの指数

加算

ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)

cov = cov_1 + cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");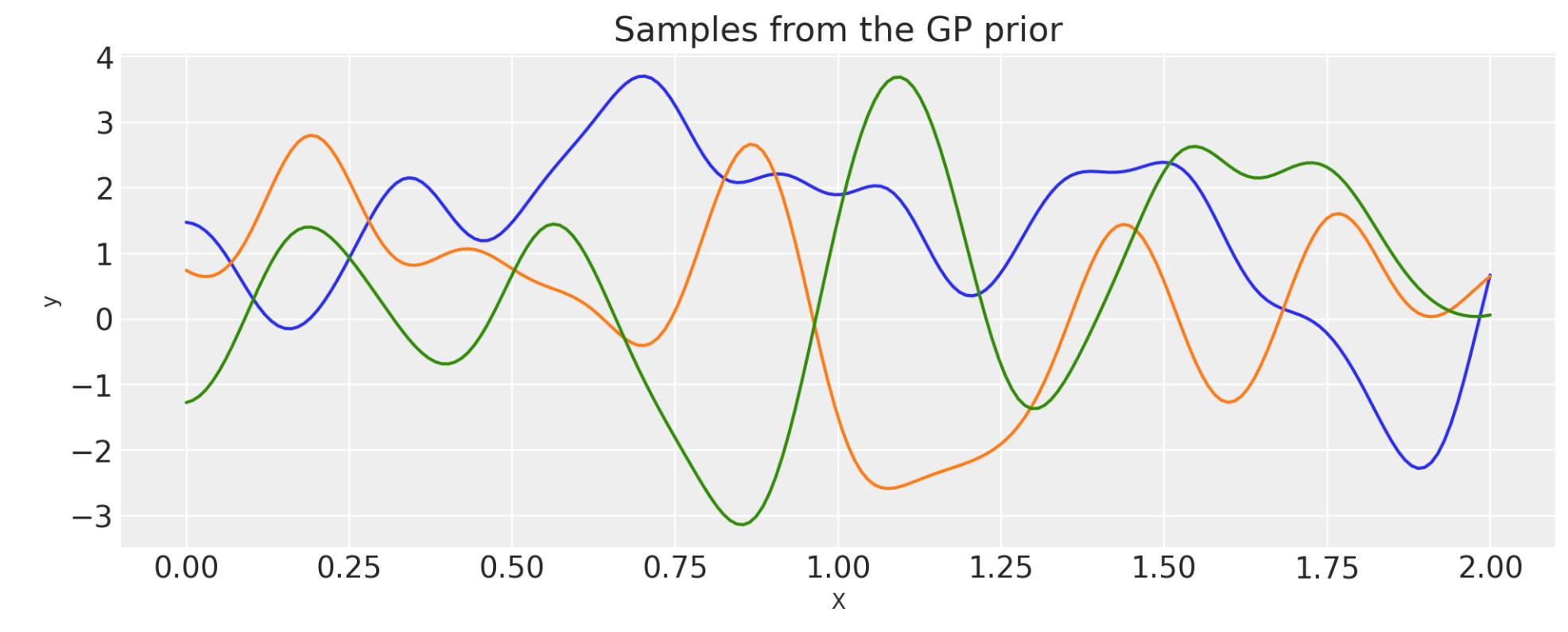

乗算

ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)

cov = cov_1 * cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");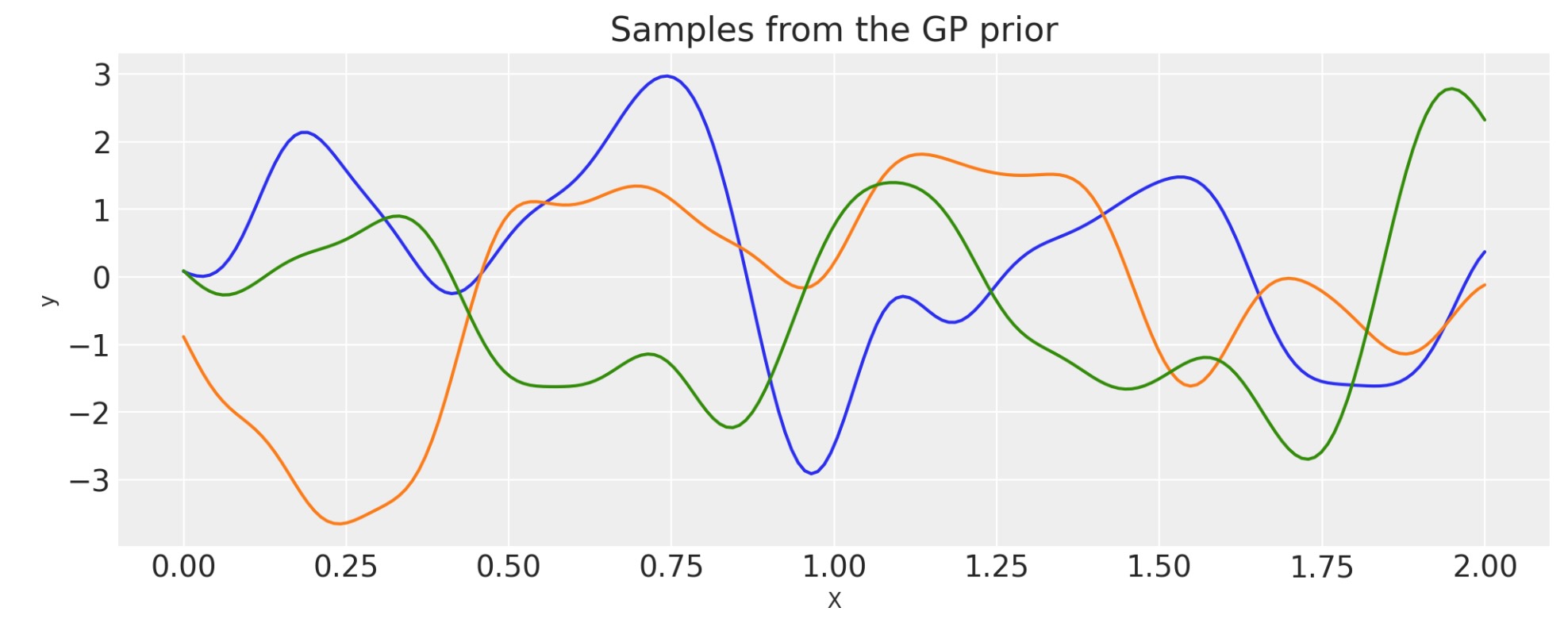

指数

ls_1 = 0.1
tau_1 = 2.0
power = 2
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)

cov = cov_1**power
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");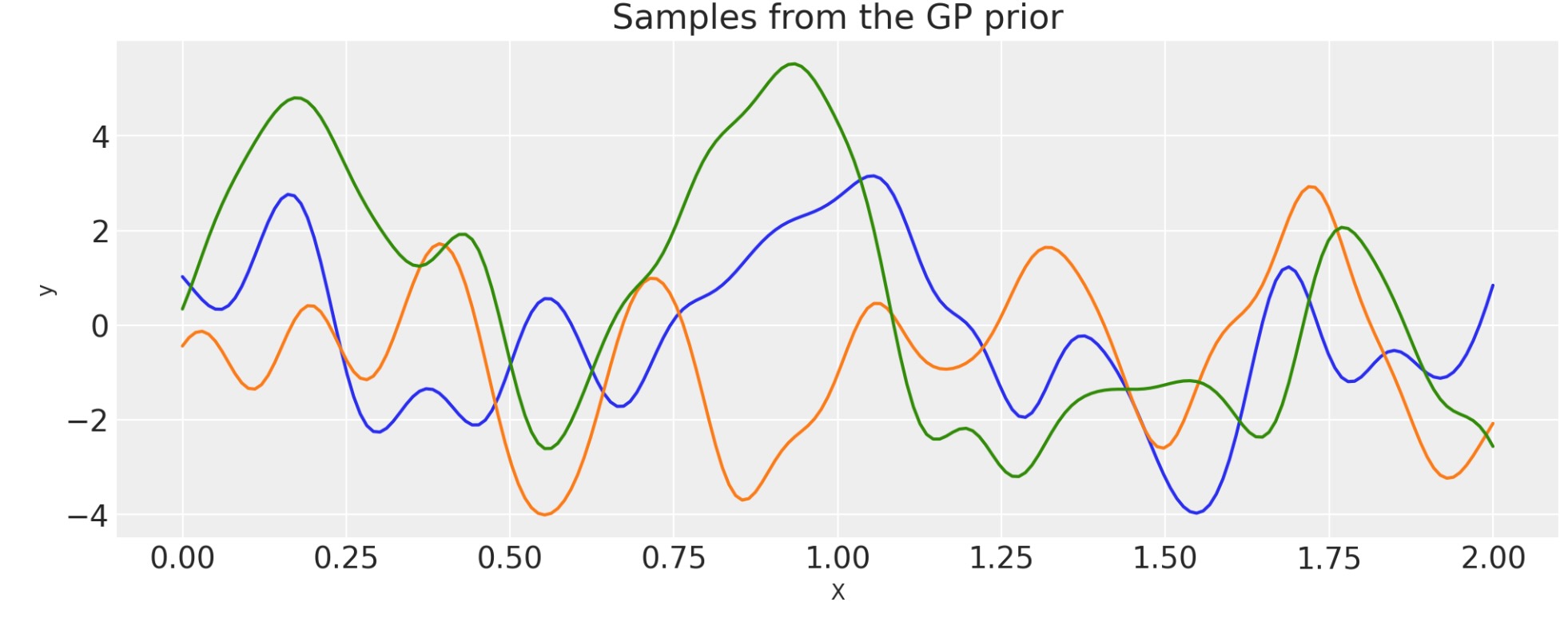

カスタム共分散関数

　PyMCの共分散関数オブジェクトは、__init__,diag,fullメソッドと、gp.cov.Covarianceサブクラスを実装する必要があります。diagは、共分散行列の対角だけを返します。そしてfullは、全共分散行列を返します。fullメソッドは、二つの入力XとXsを持ちます。full(x)は、共分散行列の二乗を返し、full(X,Xs)は、二つの入力セット間のCross共分散を返します。

　例えば、ここは、WhiteNoise共分散関数の実装です。

class WhiteNoise(pm.gp.cov.Covariance):
    def __init__(self, sigma):
        super(WhiteNoise, self).__init__(1, None)
        self.sigma = sigma

    def diag(self, X):
        return tt.alloc(tt.square(self.sigma), X.shape[0])

    def full(self, X, Xs=None):
        if Xs is None:
            return tt.diag(self.diag(X))
        else:
            return tt.alloc(0.0, X.shape[0], Xs.shape[0])

　もし、私たちが重要な共分散関数または、平均関数を忘れていたならば、実装要求を送ってください。

参考資料

Carl Edward Rasmussen and Christopher K. I. Williams. Gaussian Processes for Machine Learning. The MIT Press, 2006. ISBN 026218253X. URL: https://gaussianprocess.org/gpml/.
Espéran Padonou and O Roustant. Polar Gaussian Processes for Predicting on Circular Domains. working paper or preprint, February 2015. URL: https://hal.archives-ouvertes.fr/hal-01119942.

製作者

著者：Bill Engels

更新：Orio Abril Pla 2022年11月　PyMC v4.