import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
from scipy.linalg import cholesky
%matplotlib inlineRANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")このノートブックは、多変量ガウシアン・ランダム・ウォーク(GRWs)を使った相関時系列適合の方法を示します。特に、私たちは、GRWsに依存したモデルに対して時系列データのベイジアン回帰を実行します。
私たちは、3次元時系列としてデータを生成します。
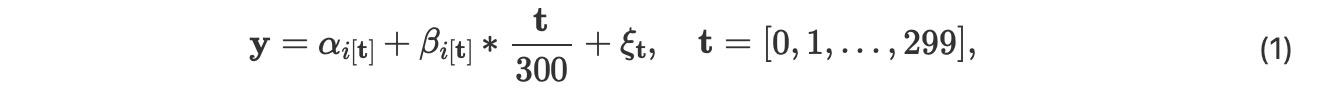
- i -> αi そして i -> βi , i ⊆ {0, 1, 2, 3, 4 }, は、二つの相関行列Σα Σβ のための 二つの3次元ガウシアンランダムウォークです。
- 私たちは、インデックス$ を定義します。
i[t] = j for t= 60j , 60j+1,...,60j + 59, and j=0,1,2,3,4,$
- * は私たちが3 x 300 行列のjー番目のカラムとj-番目のベクターj =0,1,2,...299 のエントリーを乗算することを意味します。
- εtは iid 正規エントリーN(0,σ2 ) の 3x 300行列
系列yは、ステップ0,60,120,180,240の5度、GRW αのために変化します。その間、yは、GRW βのインクリメントのために ステップ1,60,120,180,240 で変化します。そして各ステップのβの重みは t/300です。直感的に、ノイズのあるシステム、それは300ステップの終端を5回経過し時に衝撃を受けます。しかし、βの衝撃の大きさは、段階的に各ステップで大きくなります。
データ生成
データを生成して図示しましょう。
D = 3 # Dimension of random walks
N = 300 # Number of steps
sections = 5 # Number of sections
period = N / sections # Number steps in each section
Sigma_alpha = rng.standard_normal((D, D))
Sigma_alpha = Sigma_alpha.T.dot(Sigma_alpha) # Construct covariance matrix for alpha
L_alpha = cholesky(Sigma_alpha, lower=True) # Obtain its Cholesky decomposition
Sigma_beta = rng.standard_normal((D, D))
Sigma_beta = Sigma_beta.T.dot(Sigma_beta) # Construct covariance matrix for beta
L_beta = cholesky(Sigma_beta, lower=True) # Obtain its Cholesky decomposition
# Gaussian random walks:
alpha = np.cumsum(L_alpha.dot(rng.standard_normal((D, sections))), axis=1).T
beta = np.cumsum(L_beta.dot(rng.standard_normal((D, sections))), axis=1).T
t = np.arange(N)[:, None] / N
alpha = np.repeat(alpha, period, axis=0)
beta = np.repeat(beta, period, axis=0)
# Correlated series
sigma = 0.1
y = alpha + beta * t + sigma * rng.standard_normal((N, 1))
# Plot the correlated series
plt.figure(figsize=(12, 5))
plt.plot(t, y, ".", markersize=2, label=("y_0 data", "y_1 data", "y_2 data"))
plt.title("Three Correlated Series")
plt.xlabel("Time")
plt.legend()
plt.show();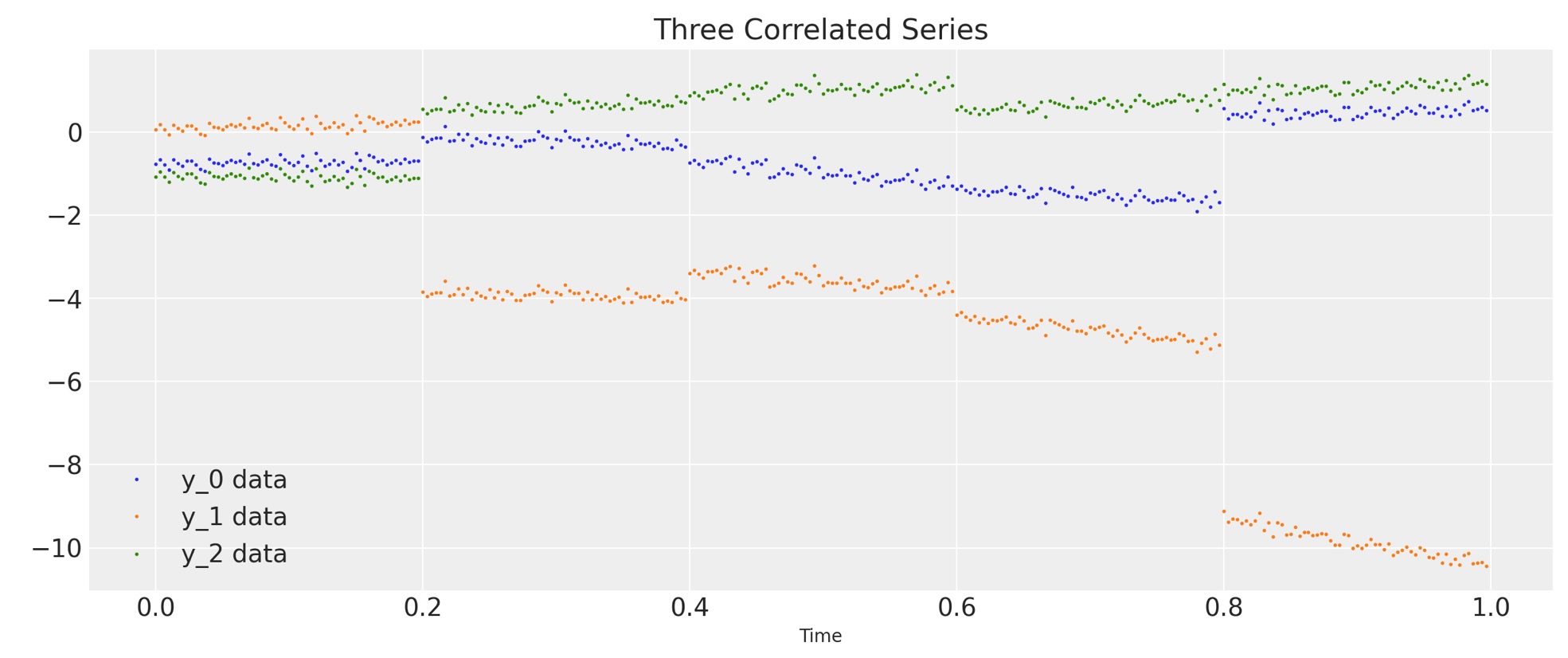
モデル
最初に私たちは、サンプリングの前に私たちのデータと時間パラメータを、再スケール化するためにスケーリングクラスを紹介します。その後、スケールされていないデータにマッチするために予測を再スケールします。
class Scaler:
def __init__(self):
mean_ = None
std_ = None
def transform(self, x):
return (x - self.mean_) / self.std_
def fit_transform(self, x):
self.mean_ = x.mean(axis=0)
self.std_ = x.std(axis=0)
return self.transform(x)
def inverse_transform(self, x):
return x * self.std_ + self.mean_私たちは、ここでGRWs のαとβ、標準偏差σ、コレスキー行列のハイパーパラメータの 事前分布を果たす回帰モデルを構築します。私たちは、コレスキー行列のためにLKJ事前分布[Lewandowski et al., 2009 参考文献]を使います。(以下のコレスキー共分散の記事を参照してください。)
def inference(t, y, sections, n_samples=100):
N, D = y.shape
# Standardize y and t
y_scaler = Scaler()
t_scaler = Scaler()
y = y_scaler.fit_transform(y)
t = t_scaler.fit_transform(t)
# Create a section index
t_section = np.repeat(np.arange(sections), N / sections)
# Create PyTensor equivalent
t_t = pytensor.shared(np.repeat(t, D, axis=1))
y_t = pytensor.shared(y)
t_section_t = pytensor.shared(t_section)
coords = {"y_": ["y_0", "y_1", "y_2"], "steps": np.arange(N)}
with pm.Model(coords=coords) as model:
# Hyperpriors on Cholesky matrices
chol_alpha, *_ = pm.LKJCholeskyCov(
"chol_cov_alpha", n=D, eta=2, sd_dist=pm.HalfCauchy.dist(2.5), compute_corr=True
)
chol_beta, *_ = pm.LKJCholeskyCov(
"chol_cov_beta", n=D, eta=2, sd_dist=pm.HalfCauchy.dist(2.5), compute_corr=True
)
# Priors on Gaussian random walks
alpha = pm.MvGaussianRandomWalk(
"alpha", mu=np.zeros(D), chol=chol_alpha, shape=(sections, D)
)
beta = pm.MvGaussianRandomWalk("beta", mu=np.zeros(D), chol=chol_beta, shape=(sections, D))
# Deterministic construction of the correlated random walk
alpha_r = alpha[t_section_t]
beta_r = beta[t_section_t]
regression = alpha_r + beta_r * t_t
# Prior on noise ξ
sigma = pm.HalfNormal("sigma", 1.0)
# Likelihood
likelihood = pm.Normal("y", mu=regression, sigma=sigma, observed=y_t, dims=("steps", "y_"))
# MCMC sampling
trace = pm.sample(n_samples, tune=1000, chains=4, target_accept=0.9)
# Posterior predictive sampling
pm.sample_posterior_predictive(trace, extend_inferencedata=True)
return trace, y_scaler, t_scaler, t_section推定
私たちは、モデルからサンプルします。そしてトレース、時間と空間のためのスケーリング関数、スケールされた時間にインデックスをリターンします。
trace, y_scaler, t_scaler, t_section = inference(t, y, sections)
私たちは、モデルの収束を視覚チェックのためにarviz.plot_energy()を使ってエナジープロットを表示します。その後、arviz.plot_ppc()を使い、私たちは、観測データyに対して、事後予測サンプルの分布を図示します。この図はモデル(yの値は実際に、yのスケールされたバージョンに一致することに注意してください)の正確さの一般的な考えを提供します。
az.plot_energy(trace)
az.plot_ppc(trace);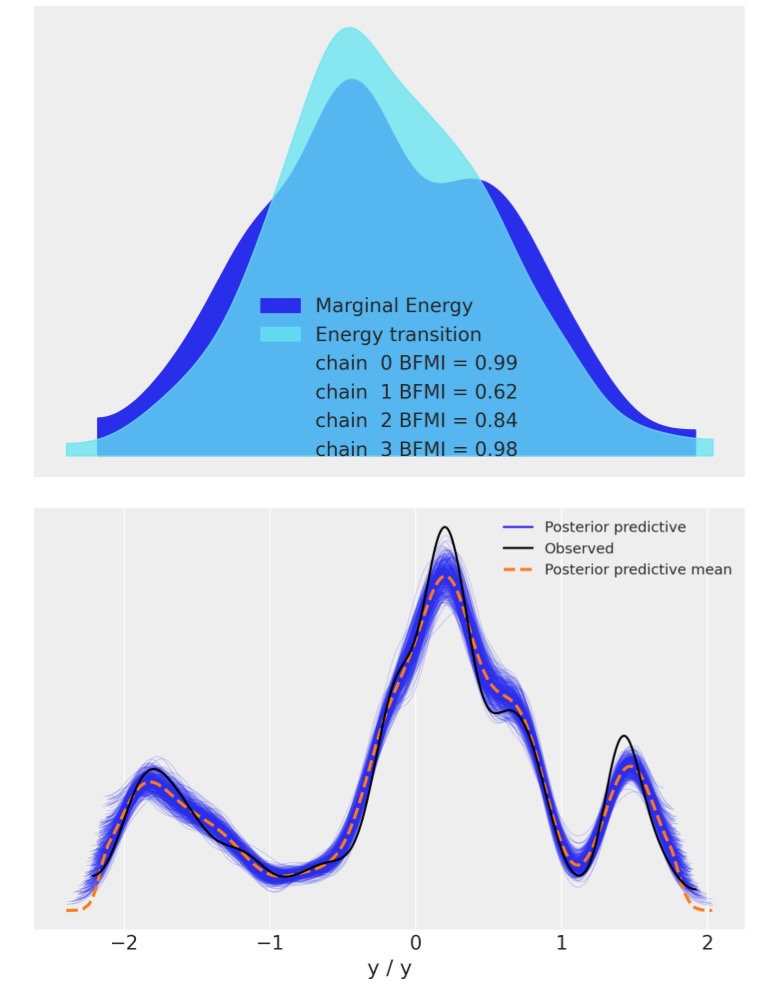
事後分布可視化
上のグラフはよく見えます。ここで、私たちは予測した3次元系列の平均に対して、観測した3次元系列を図示します。言い換えると、私たちはモデルから予測した回帰線に対してデータを図示します。
# Compute the predicted mean of the multivariate GRWs
alpha_mean = trace.posterior["alpha"].mean(dim=("chain", "draw"))
beta_mean = trace.posterior["beta"].mean(dim=("chain", "draw"))
# Compute the predicted mean of the correlated series
y_pred = y_scaler.inverse_transform(
alpha_mean[t_section].values + beta_mean[t_section].values * t_scaler.transform(t)
)
# Plot the predicted mean
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
ax.plot(t, y, ".", markersize=2, label=("y_0 data", "y_1 data", "y_2 data"))
plt.gca().set_prop_cycle(None)
ax.plot(t, y_pred, label=("y_0 pred", "y_1 pred", "y_2 pred"))
ax.set_xlabel("Time")
ax.legend()
ax.set_title("Predicted Mean of Three Correlated Series");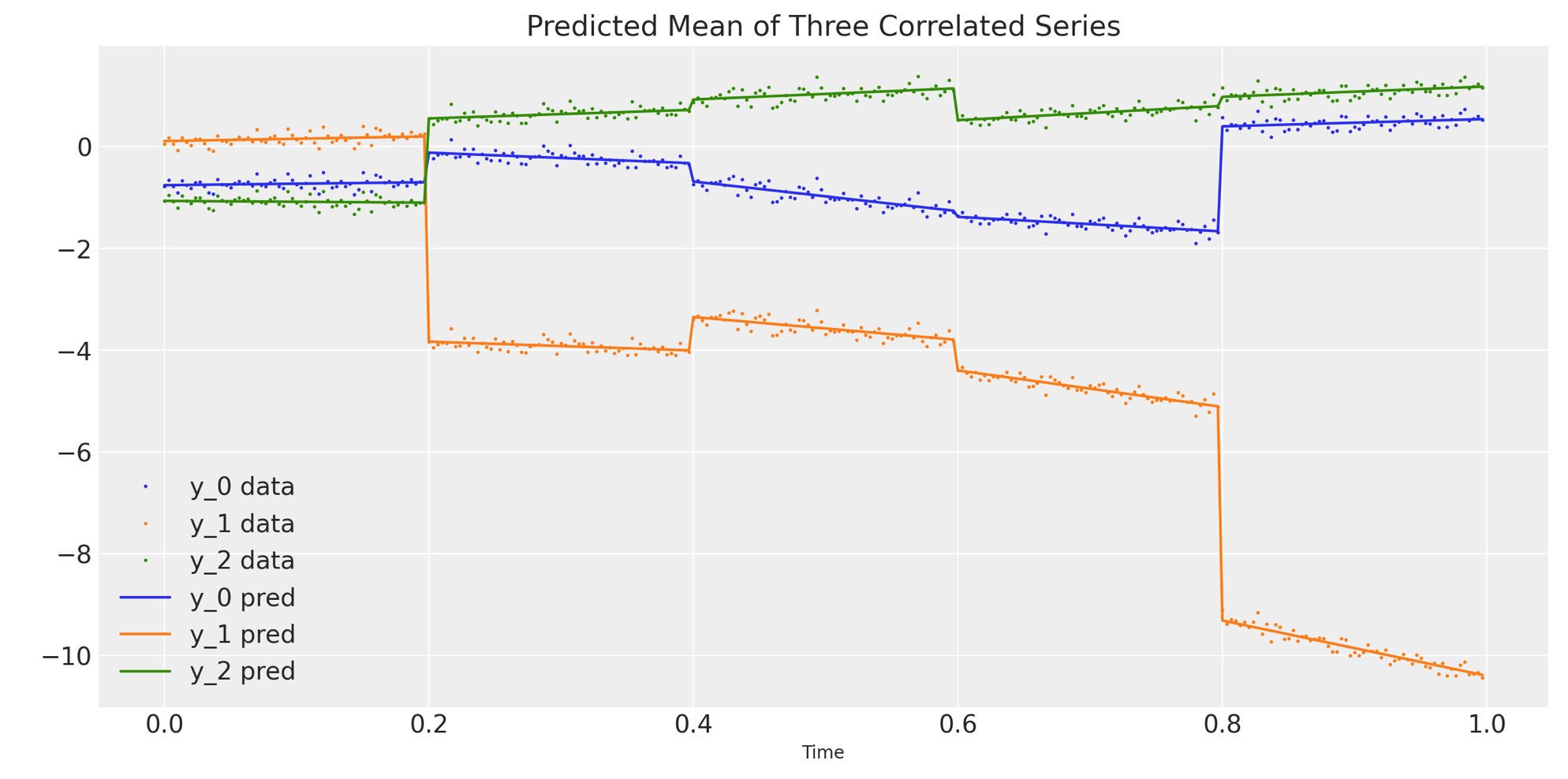
最後に、私たちは事後予測サンプルに対してデータを図示します。
# Rescale the posterior predictive samples
ppc_y = y_scaler.inverse_transform(trace.posterior_predictive["y"].mean("chain"))
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
# Plot the data
ax.plot(t, y, ".", markersize=3, label=("y_0 data", "y_1 data", "y_2 data"))
# Plot the posterior predictive samples
ax.plot(t, ppc_y.sel(y_="y_0").T, color="C0", alpha=0.003)
ax.plot(t, ppc_y.sel(y_="y_1").T, color="C1", alpha=0.003)
ax.plot(t, ppc_y.sel(y_="y_2").T, color="C2", alpha=0.003)
ax.set_xlabel("Time")
ax.legend()
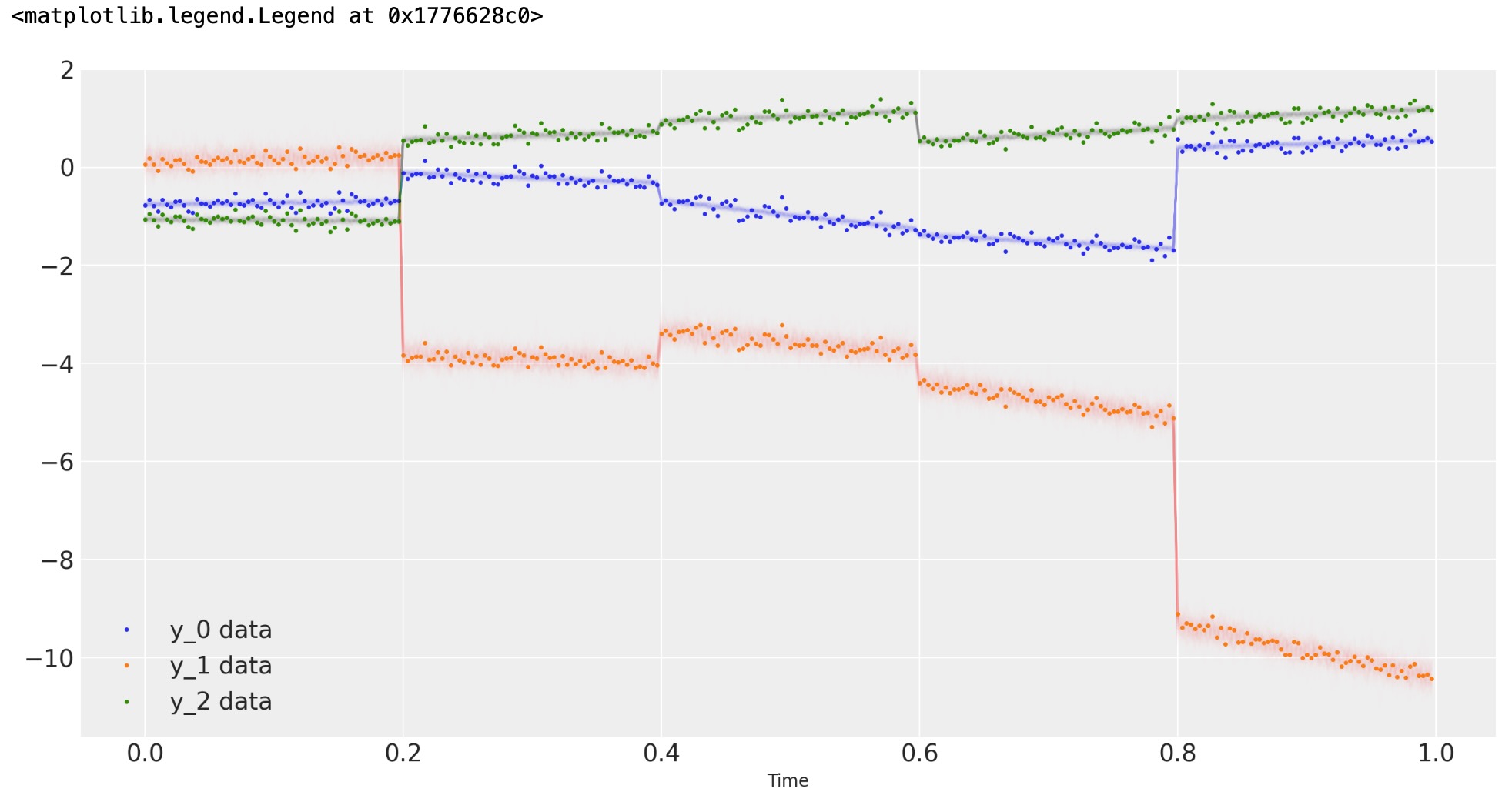
製作者
著者:Lorenzon Itoniazzi 2022年 10月
更新:Chris Fonnesbeck 2023年 2月 PyMC v5
参考文献
- Daniel Lewandowski, Dorota Kurowicka, and Harry Joe. Generating random correlation matrices based on vines and extended onion method. Journal of multivariate analysis, 100(9):1989–2001, 2009.