注記
このノートブックは、PyMCに依存しないライブラリを使います。したがって、このノートブックで走らせるために、特別にインストールされる必要があります。追加のガイダンスは、以下のドロップダウンメニューを開いてください。
import os
import random
from io import StringIO
import arviz as az
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
from lifelines import KaplanMeierFitter, LogNormalFitter, WeibullFitter
from lifelines.utils import survival_table_from_events
from scipy.stats import binom, lognorm, norm, weibull_minRANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
%config InlineBackend.figure_format = 'retina'統計の信頼性
私たちが、生産ラインで誤りを推論したいときは、大なり小なり工場、製品の原料、または、私たちが答えを探している疑問の特性に依存したデータセットのサンプルを取得するでしょう。しかし、全てのケースで、受け入れられる誤りの品質とコストの問題があります。
信頼性の研究は、したがって、誤りが観測に重要であり、間違って特徴づけた調査で稼働するコストと誤りのコストの区間を説明する必要があります。疑問の定義の正確さと、実際のモデリングの性質の要求は、最重要です。
時間と誤りのデータの鍵になる特徴は、この隔たった伝統的な統計的なまとめ方と推定技術と打ち切りのための方法です。このノートブックでは、私たちは、誤った時間の予測に焦点を当て、ベイジアンの見解の較正の予測区間を任意の頻度主義の代替と比較します。私たちは、『信頼データのための統計法」詳細は、(Meeker et al[2022]ハイパーリンク)の成果を書いて置きます。
予測の種類
私たちは、次のような誤りの時間分布の異なる視点について知りたいでしょう。
- 新しいアイテムの失敗のための時間
- 将来のmユニットのサンプルのk個の失敗までの時間
ノンパラメトリックで、これらの疑問の種類の評価に使うことができる説明する方法ですが、私たちが確率モデル、例えば、不定のθによってパラメータ化された誤り時間F(t:θ)の対数正規分布、を持つケースに焦点を当てるつもりです。
プレゼンテーションの構造
私たちは、
- 信頼データに関する累積密度関数CDFの非パラメトリックな推定を議論します。
- いかに頻度主義また同じ関数のMLEが、私たちの予測区間に情報を与えることができるかを示します。
- いかにベイジアンメソッドが稀な情報のケースで同じCDFの分析の引数のために使うことができるかを示します。
いかにCDFの理解が信頼性設定の失敗のリスクを理解するのに役立つことができるかを理解することに焦点を当てます。特に、いかにCDFが、良く較正された予測区間を誘導するのに使うことができるかです。
誤り分布の例
統計の信頼性の研究は、長いテイルの分布を基礎にした位置のスケールに焦点を当てることがあります。そこでは私たちは、正確に、どの分布が私たちの誤りの過程を説明するのかわかります、そして、次の誤りのための信頼区間は、正確に定義されます。
mu, sigma = 6, 0.3
def plot_ln_pi(mu, sigma, xy=(700, 75), title="Exact Prediction Interval for Known Lognormal"):
failure_dist = lognorm(s=sigma, scale=np.exp(mu))
samples = failure_dist.rvs(size=1000, random_state=100)
fig, axs = plt.subplots(1, 3, figsize=(20, 8))
axs = axs.flatten()
axs[0].hist(samples, ec="black", color="slateblue", bins=30)
axs[0].set_title(f"Failure Time Distribution: LN({mu}, {sigma})")
count, bins_count = np.histogram(samples, bins=30)
pdf = count / sum(count)
cdf = np.cumsum(pdf)
axs[1].plot(bins_count[1:], cdf, label="CDF", color="slateblue")
axs[2].plot(bins_count[1:], 1 - cdf, label="Survival", color="slateblue")
axs[2].legend()
axs[1].legend()
axs[1].set_title("Cumulative Density Function")
axs[2].set_title("Survival Curve")
lb = failure_dist.ppf(0.01)
ub = failure_dist.ppf(0.99)
axs[0].annotate(
f"99% Prediction \nInterval: [{np.round(lb, 3)}, {np.round(ub, 3)}]",
xy=(xy[0], xy[1] - 25),
fontweight="bold",
)
axs[0].fill_betweenx(y=range(200), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
axs[1].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
axs[2].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
lb = failure_dist.ppf(0.025)
ub = failure_dist.ppf(0.975)
axs[0].annotate(
f"95% Prediction \nInterval: [{np.round(lb, 3)}, {np.round(ub, 3)}]",
xy=(xy[0], xy[1]),
fontweight="bold",
)
axs[0].fill_betweenx(y=range(200), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[1].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[2].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[0].legend()
axs[1].legend()
axs[2].legend()
plt.suptitle(title, fontsize=20)
plot_ln_pi(mu, sigma)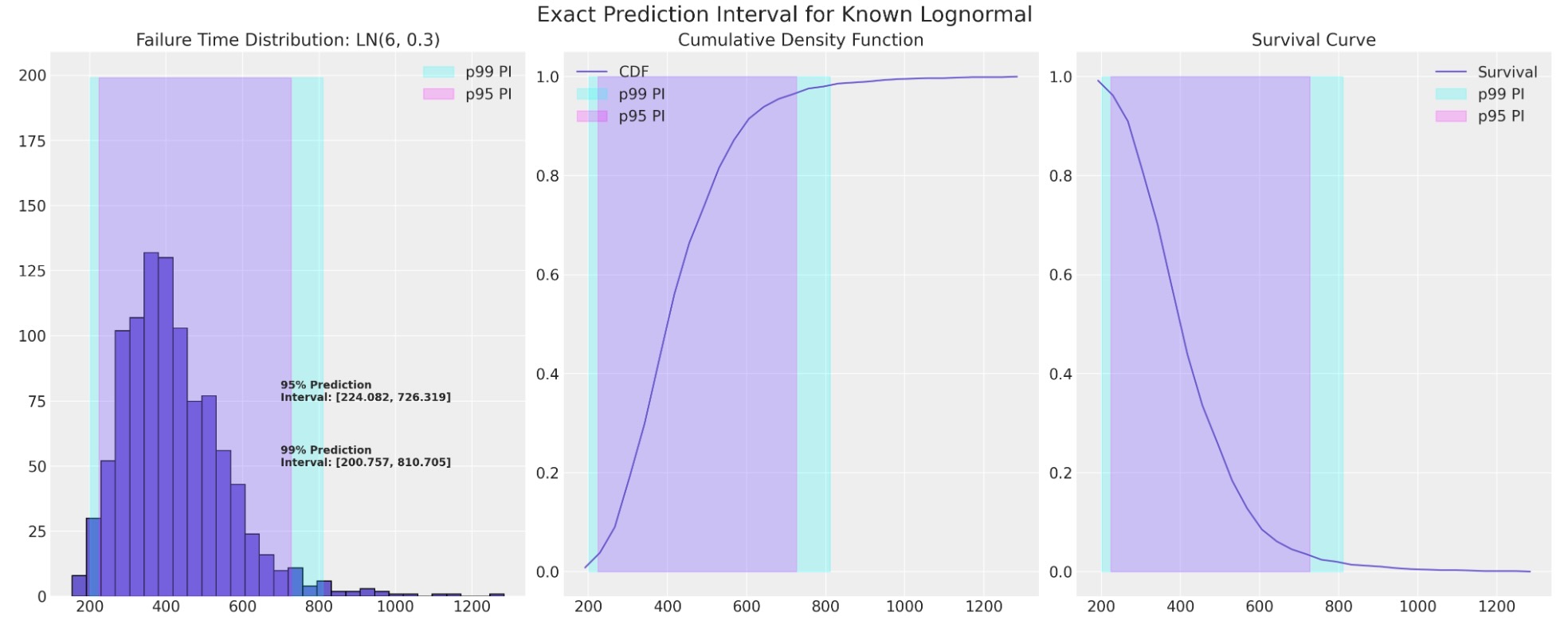
データからの誤り分布の推定
現実の世界では、私たちは、そうした正確な知識を持っていることは稀です。その代わりに、私たちは、はっきりしないデータとともに始めましょう。私たちは、最初に三つの工場間の熱交換に関する誤ったデータで実験します。そして、三つの工場の熱交換の時間の量の情報を集めます。
データは故意に小さくしてあります。そのため、私たちは、時間ー誤りデータの評価を含む説明的な統計に焦点を当てることができます。特に、私たちは、生存関数と、実験に基づいたCDFを推定します。私たちは、その後、この分析のスタイルを大きなデータセットに一般化します。
熱交換データ
打ち切りデータの注記:観測が打ち切りされるかどうか、言い換えれば、私たちが熱交換の期間の全コースを観測したかどうか、どのように誤ったデータがフラグされるか、以下見ていきましょう。これは、誤った時間データの極めて重大な特徴です。統計結果が非常に簡単なので、すべてのアイテムのライフサイクルの全コースに関する研究ではないという事実によって、誤りが蔓延する推定に隔たります。最も蔓延している打ち切りの様式は、"right censored"データを呼ばれます。それは、私たちが、観測値のサブセットに対して、誤った出来事を認識しないことです。データの収集がしかるべき時より早く終わっているため、私たちの履歴は不完全になります。
Left censoring(私たちはそれらの履歴の最初からアイテムの観測をしない) と、interval censoring(right とleft censoringの両方)は、発生できますが、共通していません。
heat_exchange_df| Years Lower | Years Upper | Censoring Indicator | Count | Plant | year_interval | failed | censored | risk_set | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | Left | 1 | 1 | 0,1 | 1 | 0 | 100 |
| 1 | 1 | 2 | Interval | 2 | 1 | 1,2 | 2 | 0 | 99 |
| 2 | 2 | 3 | Interval | 2 | 1 | 2,3 | 2 | 0 | 97 |
| 3 | 3 | Right | 95 | 1 | 3, | 0 | 95 | 0 | |
| 4 | 0 | 1 | Left | 2 | 2 | 0,1 | 2 | 0 | 100 |
| 5 | 1 | 2 | Interval | 3 | 2 | 1,2 | 3 | 0 | 98 |
| 6 | 2 | Right | 95 | 2 | 2, | 0 | 95 | 0 | |
| 7 | 0 | 1 | Left | 1 | 3 | 0,1 | 1 | 0 | 100 |
| 8 | 1 | Right | 99 | 3 | 1, | 0 | 99 | 0 |
actuarial_table = heat_exchange_df.groupby(["Years Upper"])[["failed", "risk_set"]].sum()
actuarial_table = actuarial_table.tail(3)
def greenwood_variance(df):
### Used to estimate the variance in the CDF
n = len(df)
ps = [df.iloc[i]["p_hat"] / (df.iloc[i]["risk_set"] * df.iloc[i]["1-p_hat"]) for i in range(n)]
s = [(df.iloc[i]["S_hat"] ** 2) * np.sum(ps[0 : i + 1]) for i in range(n)]
return s
def logit_transform_interval(df):
### Used for robustness in the estimation of the Confidence intervals in the CDF
df["logit_CI_95_lb"] = df["F_hat"] / (
df["F_hat"]
+ df["S_hat"] * np.exp((1.960 * df["Standard_Error"]) / (df["F_hat"] * df["S_hat"]))
)
df["logit_CI_95_ub"] = df["F_hat"] / (
df["F_hat"]
+ df["S_hat"] / np.exp((1.960 * df["Standard_Error"]) / (df["F_hat"] * df["S_hat"]))
)
df["logit_CI_95_lb"] = np.where(df["logit_CI_95_lb"] < 0, 0, df["logit_CI_95_lb"])
df["logit_CI_95_ub"] = np.where(df["logit_CI_95_ub"] > 1, 1, df["logit_CI_95_ub"])
return df
def make_actuarial_table(actuarial_table):
### Actuarial lifetables are used to describe the nature of the risk over time and estimate
actuarial_table["p_hat"] = actuarial_table["failed"] / actuarial_table["risk_set"]
actuarial_table["1-p_hat"] = 1 - actuarial_table["p_hat"]
actuarial_table["S_hat"] = actuarial_table["1-p_hat"].cumprod()
actuarial_table["CH_hat"] = -np.log(actuarial_table["S_hat"])
### The Estimate of the CDF function
actuarial_table["F_hat"] = 1 - actuarial_table["S_hat"]
actuarial_table["V_hat"] = greenwood_variance(actuarial_table)
actuarial_table["Standard_Error"] = np.sqrt(actuarial_table["V_hat"])
actuarial_table["CI_95_lb"] = (
actuarial_table["F_hat"] - actuarial_table["Standard_Error"] * 1.960
)
actuarial_table["CI_95_lb"] = np.where(
actuarial_table["CI_95_lb"] < 0, 0, actuarial_table["CI_95_lb"]
)
actuarial_table["CI_95_ub"] = (
actuarial_table["F_hat"] + actuarial_table["Standard_Error"] * 1.960
)
actuarial_table["CI_95_ub"] = np.where(
actuarial_table["CI_95_ub"] > 1, 1, actuarial_table["CI_95_ub"]
)
actuarial_table["ploting_position"] = actuarial_table["F_hat"].rolling(1).median()
actuarial_table = logit_transform_interval(actuarial_table)
return actuarial_table
actuarial_table_heat = make_actuarial_table(actuarial_table)
actuarial_table_heat = actuarial_table_heat.reset_index()
actuarial_table_heat.rename({"Years Upper": "t"}, axis=1, inplace=True)
actuarial_table_heat["t"] = actuarial_table_heat["t"].astype(int)
actuarial_table_heat| t | failed | risk_set | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | Standard_Error | CI_95_lb | CI_95_ub | ploting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | 300 | 0.013333 | 0.986667 | 0.986667 | 0.013423 | 0.013333 | 0.000044 | 0.006622 | 0.000354 | 0.026313 | 0.013333 | 0.005013 | 0.034977 |
| 1 | 2 | 5 | 197 | 0.025381 | 0.974619 | 0.961624 | 0.039131 | 0.038376 | 0.000164 | 0.012802 | 0.013283 | 0.063468 | 0.038376 | 0.019818 | 0.073016 |
| 2 | 3 | 2 | 97 | 0.020619 | 0.979381 | 0.941797 | 0.059965 | 0.058203 | 0.000350 | 0.018701 | 0.021550 | 0.094856 | 0.058203 | 0.030694 | 0.107629 |
この例に時間をかけることは価値があります。なぜなら、時間ー誤りモデリングの鍵となる量の推定を作ります。
最初に、いかに私たちが、離散間隔の系列として時間を取り扱うか注意してください。データフォーマットは、時間上で総誤りを記録するので、離散で終端するフォーマットです。私たちは、誤りデータの他のフォーマット-アイテム終端フォーマット-を下で認識します。それは、各個別のアイテムのすべての終端とそれらの対応する状態を記録します。このフォーマットで、鍵の量は、誤ったアイテムのセットと、各終端のrisk_setです。そのほかの全ては、これらの事実から派生します。
最初に私たちは、生産されてその後に故障する熱交換の数を3年の連続した期間で、三つの企業にわたって作ります。これは、年間の故障率:p_hatとその逆1-p_hatの推定を与えます。生存曲線S_hat、それは累積のハザードCH_hatと累積の密度関数F_hatの推定を回復するためにさらに変換される、を推定するために年間のコースをさらに組み合わせます。
次に、私たちは、CDFの私たちの推定の不確実性の拡張を計るために、汚れた方法を取ります。この目的のために、私たちは、推定F_hatのV_hatの変数を推定するために、グリーンウッドの公式を使います。これは、標準のエラーと文献で推薦される信頼区間の二つの変数を私たちに与えます。
私たちは、同じ技術をより大きいデータセットに適用し、いくつかのこれらの量を下に図示します。
衝撃吸収データ:頻度主義の信頼分析
区間のある衝撃吸収データは、打ち切りされる一つのアイテム上で、または各時間間隔で失敗することで、言い換えると正常にテストされて削除されるか、誤りのために削除されるか、時間上で一定間隔でリスクセットが減少されて記録します。これは、終端のあるフォーマットデータの特別なケースです。
actuarial_table_shock = make_actuarial_table(shockabsorbers_events)
actuarial_table_shockt | removed | failed | censored | entrance | risk_set | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | Standard_Error | CI_95_lb | CI_95_ub | ploting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0 | 0 | 0 | 38 | 38 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | NaN | NaN |
| 1 | 6700.0 | 1 | 1 | 0 | 0 | 38 | 0.026316 | 0.973684 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 2 | 6950.0 | 1 | 0 | 1 | 0 | 37 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 3 | 7820.0 | 1 | 0 | 1 | 0 | 36 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 4 | 8790.0 | 1 | 0 | 1 | 0 | 35 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 5 | 9120.0 | 1 | 1 | 0 | 0 | 34 | 0.029412 | 0.970588 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 6 | 9660.0 | 1 | 0 | 1 | 0 | 33 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 7 | 9820.0 | 1 | 0 | 1 | 0 | 32 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 8 | 11310.0 | 1 | 0 | 1 | 0 | 31 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 9 | 11690.0 | 1 | 0 | 1 | 0 | 30 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 10 | 11850.0 | 1 | 0 | 1 | 0 | 29 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 11 | 11880.0 | 1 | 0 | 1 | 0 | 28 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 12 | 12140.0 | 1 | 0 | 1 | 0 | 27 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 13 | 12200.0 | 1 | 1 | 0 | 0 | 26 | 0.038462 | 0.961538 | 0.908698 | 0.095742 | 0.091302 | 0.002594 | 0.050927 | 0.000000 | 0.191119 | 0.091302 | 0.029285 | 0.250730 |
| 14 | 12870.0 | 1 | 0 | 1 | 0 | 25 | 0.000000 | 1.000000 | 0.908698 | 0.095742 | 0.091302 | 0.002594 | 0.050927 | 0.000000 | 0.191119 | 0.091302 | 0.029285 | 0.250730 |
| 15 | 13150.0 | 1 | 1 | 0 | 0 | 24 | 0.041667 | 0.958333 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 16 | 13330.0 | 1 | 0 | 1 | 0 | 23 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 17 | 13470.0 | 1 | 0 | 1 | 0 | 22 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 18 | 14040.0 | 1 | 0 | 1 | 0 | 21 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 19 | 14300.0 | 1 | 1 | 0 | 0 | 20 | 0.050000 | 0.950000 | 0.827294 | 0.189595 | 0.172706 | 0.005191 | 0.072047 | 0.031495 | 0.313917 | 0.172706 | 0.072098 | 0.359338 |
| 20 | 17520.0 | 1 | 1 | 0 | 0 | 19 | 0.052632 | 0.947368 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 21 | 17540.0 | 1 | 0 | 1 | 0 | 18 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 22 | 17890.0 | 1 | 0 | 1 | 0 | 17 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 23 | 18450.0 | 1 | 0 | 1 | 0 | 16 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 24 | 18960.0 | 1 | 0 | 1 | 0 | 15 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 25 | 18980.0 | 1 | 0 | 1 | 0 | 14 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 26 | 19410.0 | 1 | 0 | 1 | 0 | 13 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 27 | 20100.0 | 2 | 1 | 1 | 0 | 12 | 0.083333 | 0.916667 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 28 | 20150.0 | 1 | 0 | 1 | 0 | 10 | 0.000000 | 1.000000 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 29 | 20320.0 | 1 | 0 | 1 | 0 | 9 | 0.000000 | 1.000000 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 30 | 20900.0 | 1 | 1 | 0 | 0 | 8 | 0.125000 | 0.875000 | 0.628635 | 0.464205 | 0.371365 | 0.014203 | 0.119177 | 0.137778 | 0.604953 | 0.371365 | 0.178442 | 0.616380 |
| 31 | 22700.0 | 1 | 1 | 0 | 0 | 7 | 0.142857 | 0.857143 | 0.538830 | 0.618356 | 0.461170 | 0.017348 | 0.131711 | 0.203016 | 0.719324 | 0.461170 | 0.232453 | 0.707495 |
| 32 | 23490.0 | 1 | 0 | 1 | 0 | 6 | 0.000000 | 1.000000 | 0.538830 | 0.618356 | 0.461170 | 0.017348 | 0.131711 | 0.203016 | 0.719324 | 0.461170 | 0.232453 | 0.707495 |
| 33 | 26510.0 | 1 | 1 | 0 | 0 | 5 | 0.200000 | 0.800000 | 0.431064 | 0.841499 | 0.568936 | 0.020393 | 0.142806 | 0.289037 | 0.848835 | 0.568936 | 0.296551 | 0.805150 |
| 34 | 27410.0 | 1 | 0 | 1 | 0 | 4 | 0.000000 | 1.000000 | 0.431064 | 0.841499 | 0.568936 | 0.020393 | 0.142806 | 0.289037 | 0.848835 | 0.568936 | 0.296551 | 0.805150 |
| 35 | 27490.0 | 1 | 1 | 0 | 0 | 3 | 0.333333 | 0.666667 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.913267 |
| 36 | 27890.0 | 1 | 0 | 1 | 0 | 2 | 0.000000 | 1.000000 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.913267 |
| 37 | 28100.0 | 1 | 0 | 1 | 0 | 1 | 0.000000 | 1.000000 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.91326 |
誤ったデータのための最大尤度の適合
私たちのデータの描写的な結果を得ることを追加して、私たちは、単一変数のモデルを誤った時間の分布への適合を推定するためにlifeテーブルデータを使うことができます。そうした適合は、もしよければ、予測区間の特別なセットの予測分布の明快な視界を持つことができます。ここで、私たちは、right-censoredデータのMLE適合を推定するために、Lifelinesパッケージから関数を使います。
lnf = LogNormalFitter().fit(actuarial_table_shock["t"] + 1e-25, actuarial_table_shock["failed"])
lnf.print_summary()| model | lifelines.LogNormalFitter |
|---|---|
| number of observations | 38 |
| number of events observed | 11 |
| log-likelihood | -124.20 |
| hypothesis | mu_ != 0, sigma_ != 1 |
| coef | se(coef) | coef lower 95% | coef upper 95% | cmp to | z | p | -log2(p) | |
|---|---|---|---|---|---|---|---|---|
| mu_ | 10.13 | 0.14 | 9.85 | 10.41 | 0.00 | 71.08 | <0.005 | inf |
| sigma_ | 0.53 | 0.11 | 0.31 | 0.74 | 1.00 | -4.26 | <0.005 | 15.58 |
| AIC | 252.41 |
|---|
このモデルは一時的に実行するものですが、制限したデータにケースに注意する必要があります。例えば、熱交換データでは、私たちは、全体で11の不具合を持つ3年分のデータを持っています。非常に簡単なモデルなので、私たちは、完全に間違います。すぐに、私たちは、衝撃吸収データ、それはノンパラメトリックな描写で簡単な単一の変数でこのデータに適合します、に焦点を当てるでしょう。
plot_cdfs(actuarial_table_shock, title="Shock Absorber");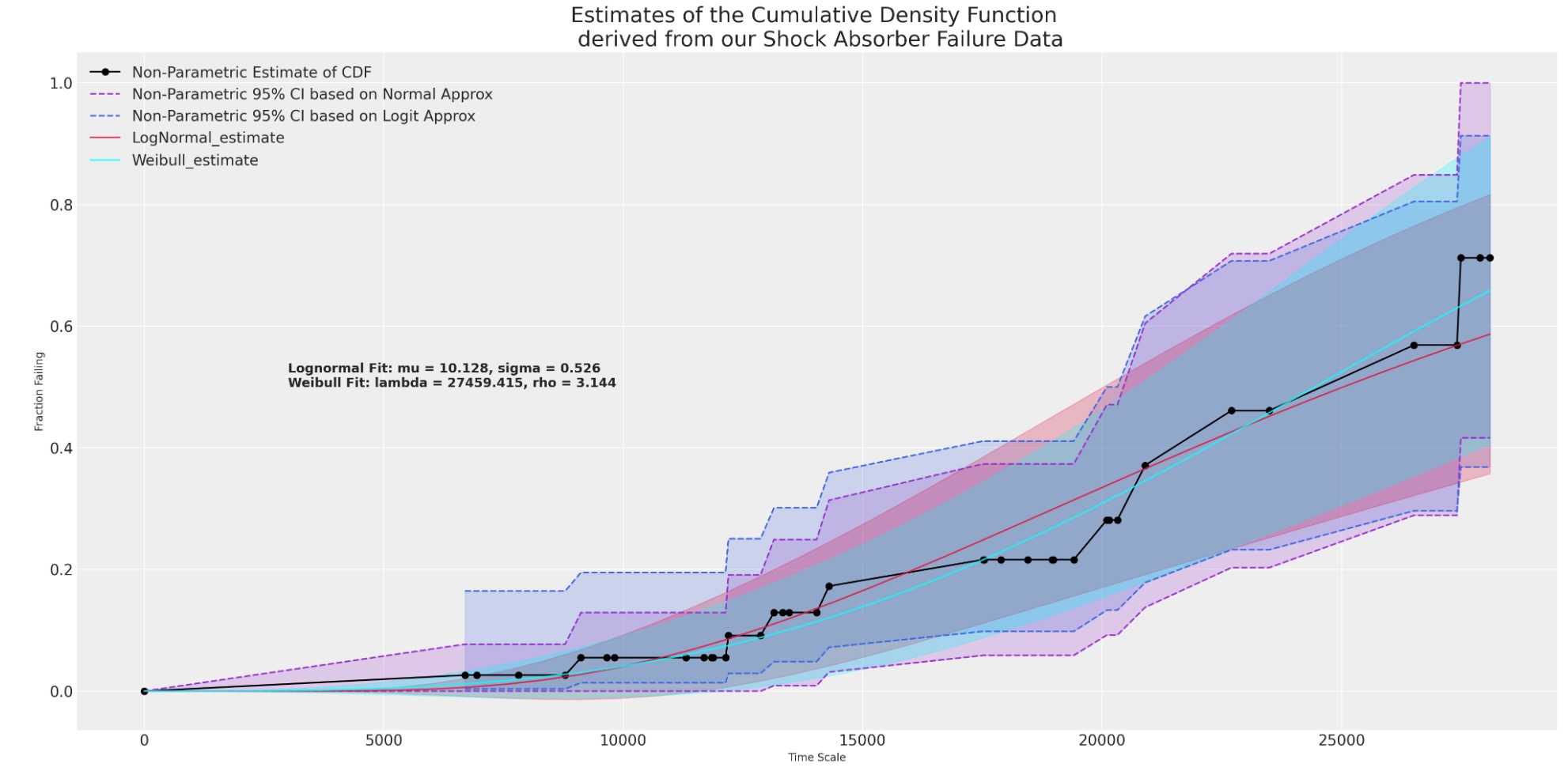
これは、データへの正しい適合を示し、あなたが予期したように、衝撃吸収の不具合の変動がそれらを身につける年齢によって増加するということを示唆します。しかし、どのように私たちは、与えられた推定モデルで、予測を計測しましょう。
統計予測区間の近似の計算のためのプラグイン手続き
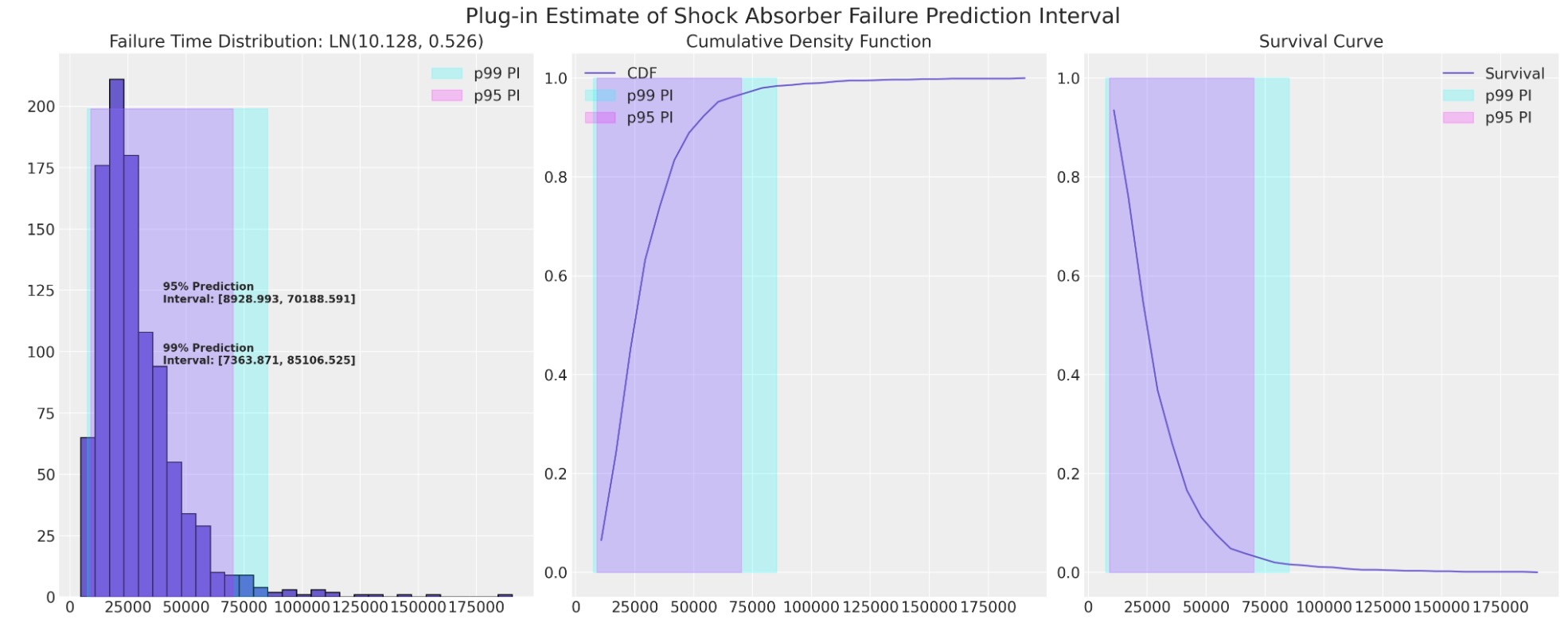
私たちは、衝撃吸収データのCDFのために対数正規適合を推定するので、私たちは、それらの予測区間近似を図示することができます。私たちは、生産者として、低い境界が低すぎる場合、支払のリスクエクスポージャーと保証の請求を認識するかもしれないので、ここでの関心は、予測間隔の短い境界になる可能性が高いことです。
plot_ln_pi(
10.128,
0.526,
xy=(40000, 120),
title="Plug-in Estimate of Shock Absorber Failure Prediction Interval",
)
ブートストラップ較正とカバレッジの推定
私たちは、ここで、信頼区間によって示唆されるカバレッジの推定を求めます。そうすることで、私たちは、95%の信頼区間で上位側と下位側のブートストラップ推定を行います。そして、最後にMLE適合のカバレッジ条件を評価します。私たちは、変動する重みの(ベイジアン)を使います。私たちは、カバレッジ統計を推定する二つの方法を報告します。最初は、知られた範囲からランダムな値のサンプリングを基礎にした実証的なカバレッジ。もし、それが上位と下位の境界の95%MLの間で、誤まれば、評価します。
2番目の方法は、私たちは、評価カバレッジを使います。それは、95%上位と下位の境界でブートストラップ推定します。その後、どのくらいそれらのブートストラップ値が、MLE適合の条件をカバーするか評価します。
def bayes_boot(df, lb, ub, seed=100):
w = np.random.dirichlet(np.ones(len(df)), 1)[0]
lnf = LogNormalFitter().fit(df["t"] + 1e-25, df["failed"], weights=w)
rv = lognorm(s=lnf.sigma_, scale=np.exp(lnf.mu_))
## Sample random choice from implied bootstrapped distribution
choices = rv.rvs(1000)
future = random.choice(choices)
## Check if choice is contained within the MLE 95% PI
contained = (future >= lb) & (future <= ub)
## Record 95% interval of bootstrapped dist
lb = rv.ppf(0.025)
ub = rv.ppf(0.975)
return lb, ub, contained, future, lnf.sigma_, lnf.mu_CIs = [bayes_boot(actuarial_table_shock, 8928, 70188, seed=i) for i in range(1000)]
draws = pd.DataFrame(
CIs, columns=["Lower Bound PI", "Upper Bound PI", "Contained", "future", "Sigma", "Mu"]
)
drawsLower Bound PI | Upper Bound PI | Contained | future | Sigma | Mu | |
|---|---|---|---|---|---|---|
| 0 | 11272.613998 | 49582.094766 | True | 17292.870434 | 0.377878 | 10.070758 |
| 1 | 7991.816789 | 93161.345993 | False | 70864.313494 | 0.626520 | 10.214131 |
| 2 | 10873.715961 | 61376.105119 | True | 25782.887636 | 0.441506 | 10.159440 |
| 3 | 5752.613566 | 125975.249573 | True | 32697.606093 | 0.787369 | 10.200625 |
| 4 | 10599.311448 | 75336.965736 | True | 19192.378160 | 0.500311 | 10.249135 |
| ... | ... | ... | ... | ... | ... | ... |
| 995 | 9642.585462 | 59419.909295 | True | 28284.668918 | 0.463896 | 10.083165 |
| 996 | 6032.791575 | 81430.341065 | False | 89564.056379 | 0.663925 | 10.006234 |
| 997 | 8594.300020 | 65307.015356 | True | 54894.079865 | 0.517357 | 10.072855 |
| 998 | 10491.092455 | 54912.865230 | True | 42479.608921 | 0.422258 | 10.085892 |
| 999 | 10301.395701 | 61648.310891 | True | 44760.037735 | 0.456428 | 10.134618 |
1000 rows × 6 columns
私たちは、さらに予測分布の量を計算するために、これらのブートストラップ統計を使うことができます。私たちのケースでは、簡単なパラメトリックモデルのために、パラメトリックCDFを使います。しかし、私たちは私たちがもっと複雑なモデルの時にも、どのようにこの技術を使うことができるか示すために、私たちは、ここで、実証的なcdfを適合します。
def ecdf(sample):
# convert sample to a numpy array, if it isn't already
sample = np.atleast_1d(sample)
# find the unique values and their corresponding counts
quantiles, counts = np.unique(sample, return_counts=True)
# take the cumulative sum of the counts and divide by the sample size to
# get the cumulative probabilities between 0 and 1
cumprob = np.cumsum(counts).astype(np.double) / sample.size
return quantiles, cumprob
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
hist_data = []
for i in range(1000):
samples = lognorm(s=draws.iloc[i]["Sigma"], scale=np.exp(draws.iloc[i]["Mu"])).rvs(1000)
qe, pe = ecdf(samples)
ax.plot(qe, pe, color="skyblue", alpha=0.2)
lkup = dict(zip(pe, qe))
hist_data.append([lkup[0.05]])
hist_data = pd.DataFrame(hist_data, columns=["p05"])
samples = lognorm(s=draws["Sigma"].mean(), scale=np.exp(draws["Mu"].mean())).rvs(1000)
qe, pe = ecdf(samples)
ax.plot(qe, pe, color="red", label="Expected CDF for Shock Absorbers Data")
ax.set_xlim(0, 30_000)
ax.set_title("Bootstrapped CDF functions for the Shock Absorbers Data", fontsize=20)
ax1.hist(hist_data["p05"], color="slateblue", ec="black", alpha=0.4, bins=30)
ax1.set_title("Estimate of Uncertainty in the 5% Failure Time", fontsize=20)
ax1.axvline(
hist_data["p05"].quantile(0.025), color="cyan", label="Lower Bound CI for 5% failure time"
)
ax1.axvline(
hist_data["p05"].quantile(0.975), color="cyan", label="Upper Bound CI for 5% failure time"
)
ax1.legend()
ax.legend();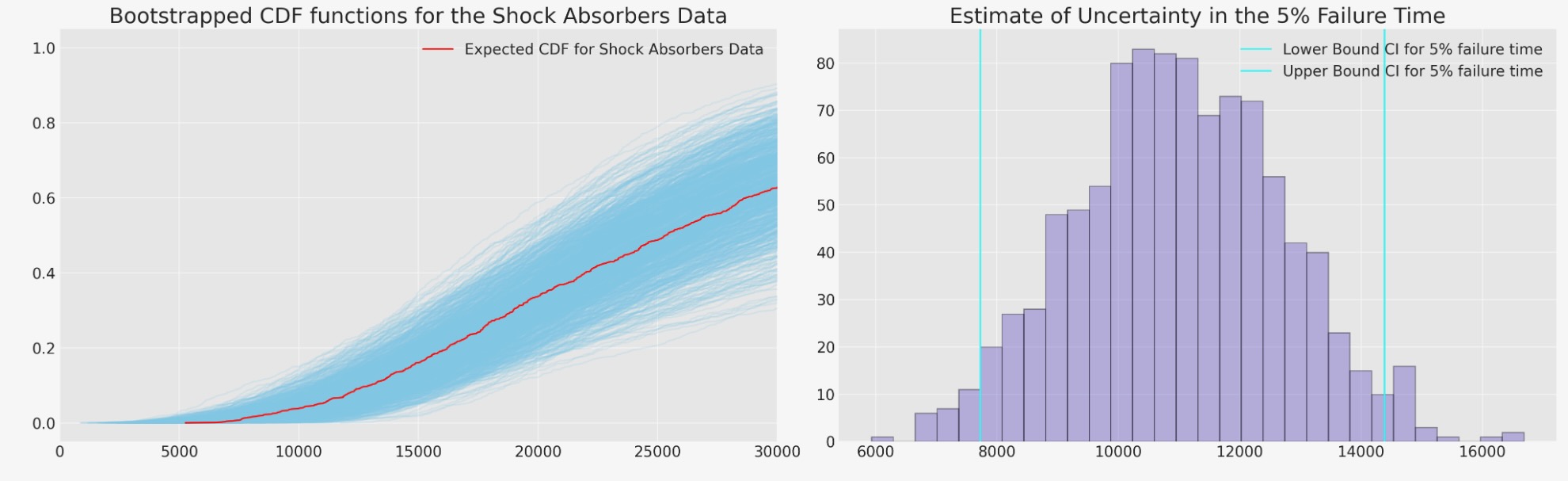
次に、私たちは、ブートストラップしたデータとカバレッジの二つの推定を図示します。私たちはMLE適合の条件でアーカイブします。言い換えると、私たちが、MLE適合を基礎にした予測区間のカバレッジを評価する時に、私たちは、量のためにブートストラップ推定することができます。
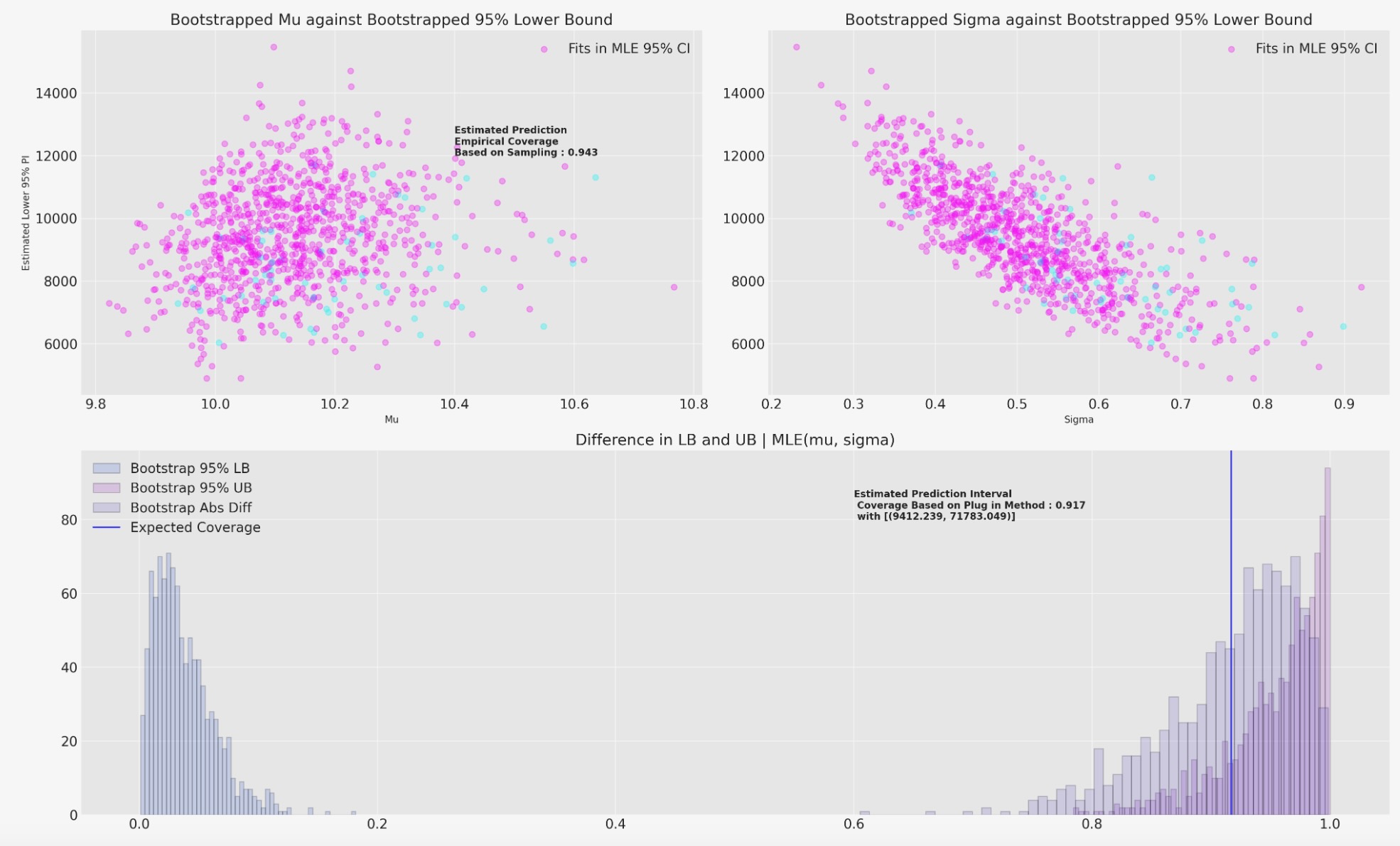
これらのシミュレーションは、私たちがここで実行したよりももっと大きい数の時間を繰り返すべきです。必要とするカバレッジレベルをアーカイブするために、いかにMLE区間を変更できるかわかるのが明白になるでしょう。
ベアリングケージデータ:ベイジアン信頼分析の研究
次に、私たちは、わずかにクリアでないパラメトリック適合を持つデータセットをみましょう。このデータの最も明瞭な特徴は、誤り記録の小さい量です。データは、各ピリオドのrisk_setの拡張を表示する係数の終端の様式が記録されます。
私たちは、衝撃吸収データを推定するために、頻度主義の技術がどのようにうまく働くか示すために、この例で時間をかけます。ベアリングケージデータのケースで議論できます。特に、私たちは、ベイジアンアプローチで解決できる問題がどのように発生するか示します。
actuarial_table_bearings = make_actuarial_table(bearing_cage_events)
actuarial_table_bearings| t | removed | failed | censored | entrance | risk_set | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | Standard_Error | CI_95_lb | CI_95_ub | ploting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0 | 0 | 0 | 1703 | 1703 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 1 | 50.0 | 288 | 0 | 288 | 0 | 1703 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 2 | 150.0 | 148 | 0 | 148 | 0 | 1415 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 3 | 230.0 | 1 | 1 | 0 | 0 | 1267 | 0.000789 | 0.999211 | 0.999211 | 0.000790 | 0.000789 | 6.224491e-07 | 0.000789 | 0.0 | 0.002336 | 0.000789 | 0.000111 | 0.005581 |
| 4 | 250.0 | 124 | 0 | 124 | 0 | 1266 | 0.000000 | 1.000000 | 0.999211 | 0.000790 | 0.000789 | 6.224491e-07 | 0.000789 | 0.0 | 0.002336 | 0.000789 | 0.000111 | 0.005581 |
| 5 | 334.0 | 1 | 1 | 0 | 0 | 1142 | 0.000876 | 0.999124 | 0.998336 | 0.001666 | 0.001664 | 1.386254e-06 | 0.001177 | 0.0 | 0.003972 | 0.001664 | 0.000415 | 0.006641 |
| 6 | 350.0 | 111 | 0 | 111 | 0 | 1141 | 0.000000 | 1.000000 | 0.998336 | 0.001666 | 0.001664 | 1.386254e-06 | 0.001177 | 0.0 | 0.003972 | 0.001664 | 0.000415 | 0.006641 |
| 7 | 423.0 | 1 | 1 | 0 | 0 | 1030 | 0.000971 | 0.999029 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 8 | 450.0 | 106 | 0 | 106 | 0 | 1029 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 9 | 550.0 | 99 | 0 | 99 | 0 | 923 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 10 | 650.0 | 110 | 0 | 110 | 0 | 824 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 11 | 750.0 | 114 | 0 | 114 | 0 | 714 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 12 | 850.0 | 119 | 0 | 119 | 0 | 600 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 13 | 950.0 | 127 | 0 | 127 | 0 | 481 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 14 | 990.0 | 1 | 1 | 0 | 0 | 354 | 0.002825 | 0.997175 | 0.994549 | 0.005466 | 0.005451 | 1.022444e-05 | 0.003198 | 0.0 | 0.011718 | 0.005451 | 0.001722 | 0.017117 |
| 15 | 1009.0 | 1 | 1 | 0 | 0 | 353 | 0.002833 | 0.997167 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 16 | 1050.0 | 123 | 0 | 123 | 0 | 352 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 17 | 1150.0 | 93 | 0 | 93 | 0 | 229 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 18 | 1250.0 | 47 | 0 | 47 | 0 | 136 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 19 | 1350.0 | 41 | 0 | 41 | 0 | 89 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 20 | 1450.0 | 27 | 0 | 27 | 0 | 48 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 21 | 1510.0 | 1 | 1 | 0 | 0 | 21 | 0.047619 | 0.952381 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 22 | 1550.0 | 11 | 0 | 11 | 0 | 20 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 23 | 1650.0 | 6 | 0 | 6 | 0 | 9 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 24 | 1850.0 | 1 | 0 | 1 | 0 | 3 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 25 | 2050.0 | 2 | 0 | 2 | 0 | 2 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
単一の変数または、ノンパラメトリックCDFを推定するために、私たちは、ピリオドフォーマットデータをアイテムーピリオドフォーマットに分解する必要があります。
アイテムピリオドフォーマット
item_period = bearing_cage_df["Hours"].to_list() * bearing_cage_df["Count"].sum()
ids = [[i] * 25 for i in range(bearing_cage_df["Count"].sum())]
ids = [int(i) for l in ids for i in l]
item_period_bearing_cage = pd.DataFrame(item_period, columns=["t"])
item_period_bearing_cage["id"] = ids
item_period_bearing_cage["failed"] = np.zeros(len(item_period_bearing_cage))
## Censor appropriate number of ids
unique_ids = item_period_bearing_cage["id"].unique()
censored = bearing_cage_df[bearing_cage_df["Censoring Indicator"] == "Censored"]
i = 0
stack = []
for hour, count, idx in zip(censored["Hours"], censored["Count"], censored["Count"].cumsum()):
temp = item_period_bearing_cage[
item_period_bearing_cage["id"].isin(unique_ids[i:idx])
& (item_period_bearing_cage["t"] == hour)
]
stack.append(temp)
i = idx
censored_clean = pd.concat(stack)
### Add appropriate number of failings
stack = []
unique_times = censored_clean["t"].unique()
for id, fail_time in zip(
[9999, 9998, 9997, 9996, 9995, 9994],
bearing_cage_df[bearing_cage_df["failed"] == 1]["t"].values,
):
temp = pd.DataFrame(unique_times[unique_times < fail_time], columns=["t"])
temp["id"] = id
temp["failed"] = 0
temp = pd.concat([temp, pd.DataFrame({"t": [fail_time], "id": [id], "failed": [1]}, index=[0])])
stack.append(temp)
failed_clean = pd.concat(stack).sort_values(["id", "t"])
censored_clean
item_period_bearing_cage = pd.concat([failed_clean, censored_clean])
## Transpose for more concise visual
item_period_bearing_cage.head(30).T0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 0 | 1 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | 50.0 | 150.0 | 250.0 | 350.0 | 450.0 | 550.0 | 650.0 | 750.0 | 850.0 | 950.0 | ... | 450.0 | 550.0 | 650.0 | 750.0 | 850.0 | 950.0 | 1009.0 | 50.0 | 150.0 | 250.0 |
| id | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | ... | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9996.0 | 9996.0 | 9996.0 |
| failed | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
3 rows × 30 columns
assert item_period_bearing_cage["id"].nunique() == 1703
assert item_period_bearing_cage["failed"].sum() == 6
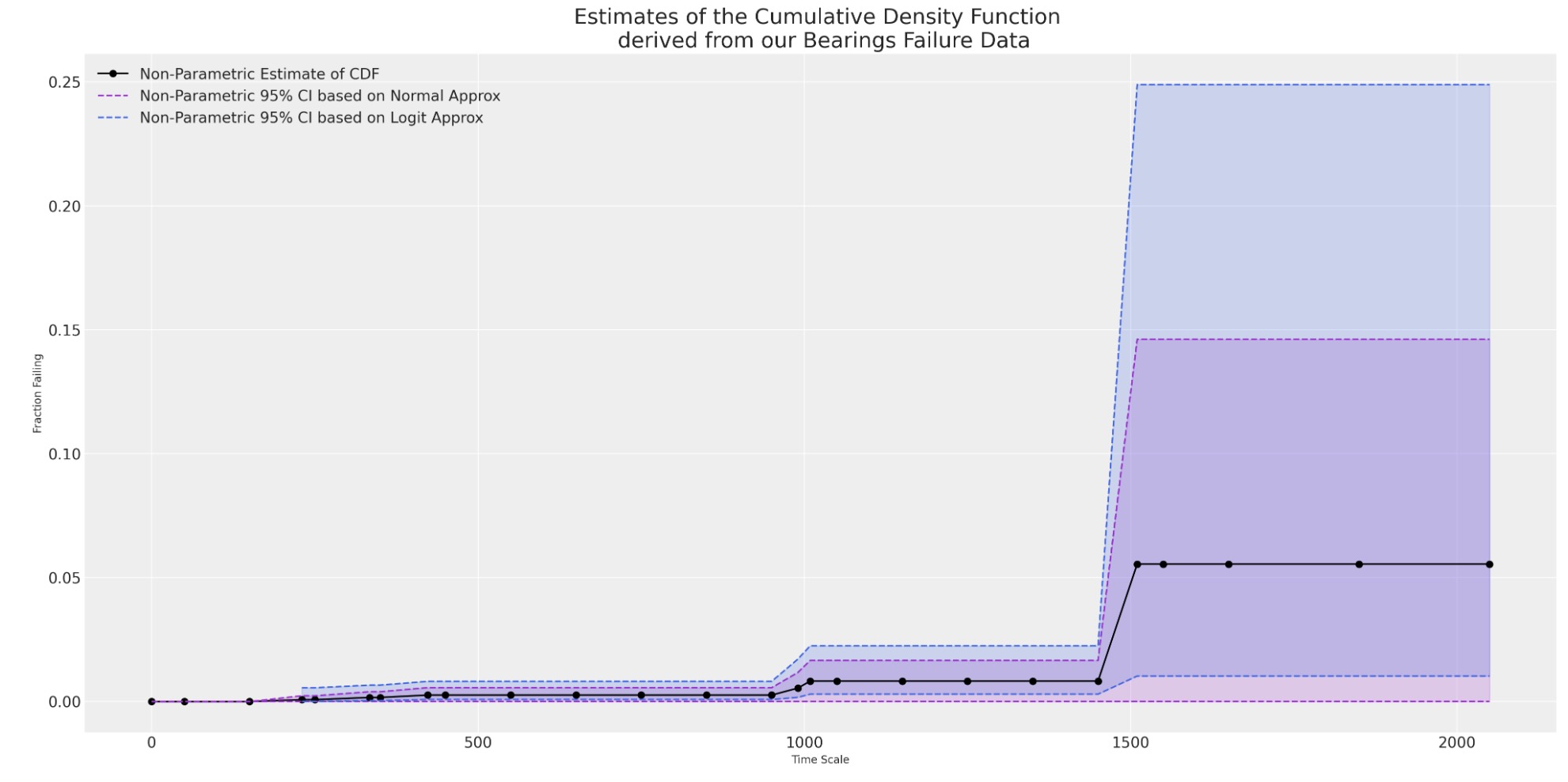
assert item_period_bearing_cage[item_period_bearing_cage["t"] >= 1850]["id"].nunique() == 3私たちは、実証的なCDFを図示するので、私たちは、最大の高さ0.05に達しないy軸だけをみます。単純な(ナイーブ)MLE適合は、データの観測範囲の座標の外で、大きく間違います。
ax = plot_cdfs(
actuarial_table_bearings,
title="Bearings",
dist_fits=False,
xy=(20, 0.7),
item_period=item_period_bearing_cage,
)
確率図示:制限された線形範囲のCDFの比較
このセクションでは、私たちは、視覚的に"適合の正しさ"のチェックを実行できるように、線形のMLE適合の技術を使います。これらの図示の種類は、CDFを線形空間に変えるために、位置とスケールの分布に適用することができる変換に依拠します。
対数正規とWeibull適合の両方、私たちは、ログの値tと、適当なCDF-1の関係として、それらのCDFを線形空間に表します。
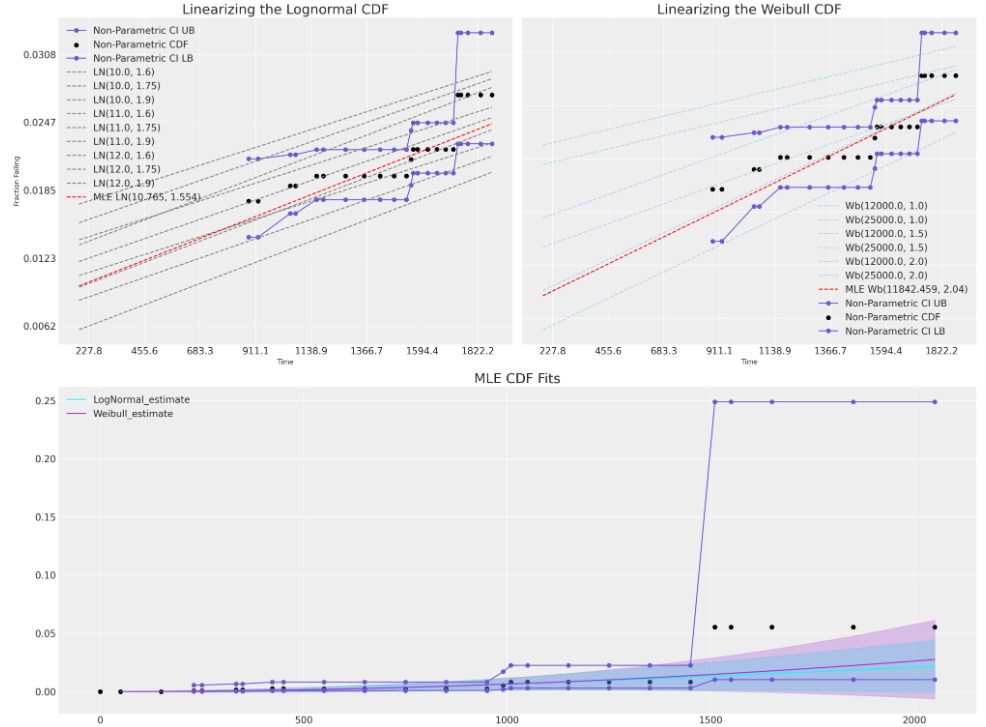
私たちは、ここでどのようにMLE適合が観測データの範囲をカバーしないか見ることができます。
信頼データのベイジアンモデリング
私たちは、ここで、頻度主義とMLEフレームワークを使って、モデルの仕方とパラメトリックモデルの適合が信頼性の希薄さを視覚化するのを見ました。私たちはここで、同じスタイルの推論が、いかにベイジアンパラダイムをアーカイブすることができるか示します。
MLEパラダイムのように、私たちは、打ち切りした尤度のモデルを必要とします。私たちが上で見たほとんどの対数位置分布にとって、尤度は、データポイントが時間ウィンドウで完全に観測されるか、または打ち切りされるかどうかに適切に依存するものとして、適用されるcdfΦと、pdfφの分布の組み合わせの関数として説明されます。
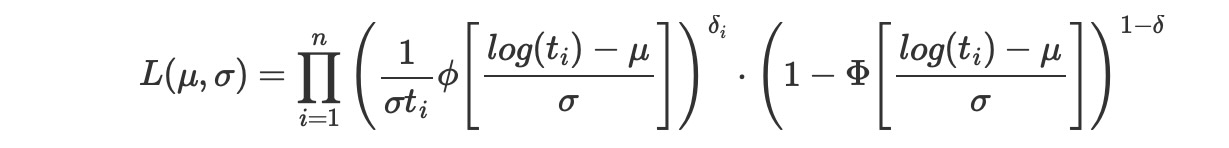
ここで、δiは、観測が失敗するか正しい計測の観測であるかのインジケーターです。もっと複雑な計測の種類は計測した観測の性質に依存するCDFの同様の修正を含むことができます。
Weibull生存の直接のPyMC実装
私たちは、事前分布の仕様の異なる二つのバージョンのモデルを適合します。一つは、データを覆う不明瞭な一様事前分布をとり、もう一つは、MLE適合に近接した事前分布を規定します。私たちは、下の観測データとモデルの較正にためにもっている事前分布の仕様の影響を示します。
def weibull_lccdf(y, alpha, beta):
"""Log complementary cdf of Weibull distribution."""
return -((y / beta) ** alpha)
item_period_max = item_period_bearing_cage.groupby("id")[["t", "failed"]].max()
y = item_period_max["t"].values
censored = ~item_period_max["failed"].values.astype(bool)
priors = {"beta": [100, 15_000], "alpha": [4, 1, 0.02, 8]}
priors_informative = {"beta": [10_000, 500], "alpha": [2, 0.5, 0.02, 3]}
def make_model(p, info=False):
with pm.Model() as model:
if info:
beta = pm.Normal("beta", p["beta"][0], p["beta"][1])
else:
beta = pm.Uniform("beta", p["beta"][0], p["beta"][1])
alpha = pm.TruncatedNormal(
"alpha", p["alpha"][0], p["alpha"][1], lower=p["alpha"][2], upper=p["alpha"][3]
)
y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y[~censored])
y_cens = pm.Potential("y_cens", weibull_lccdf(y[censored], alpha, beta))
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(random_seed=100, target_accept=0.95))
idata.extend(pm.sample_posterior_predictive(idata))
return idata, model
idata, model = make_model(priors)
idata_informative, model = make_model(priors_informative, info=True)
idataarviz.InferenceData
az.plot_trace(idata, kind="rank_vlines");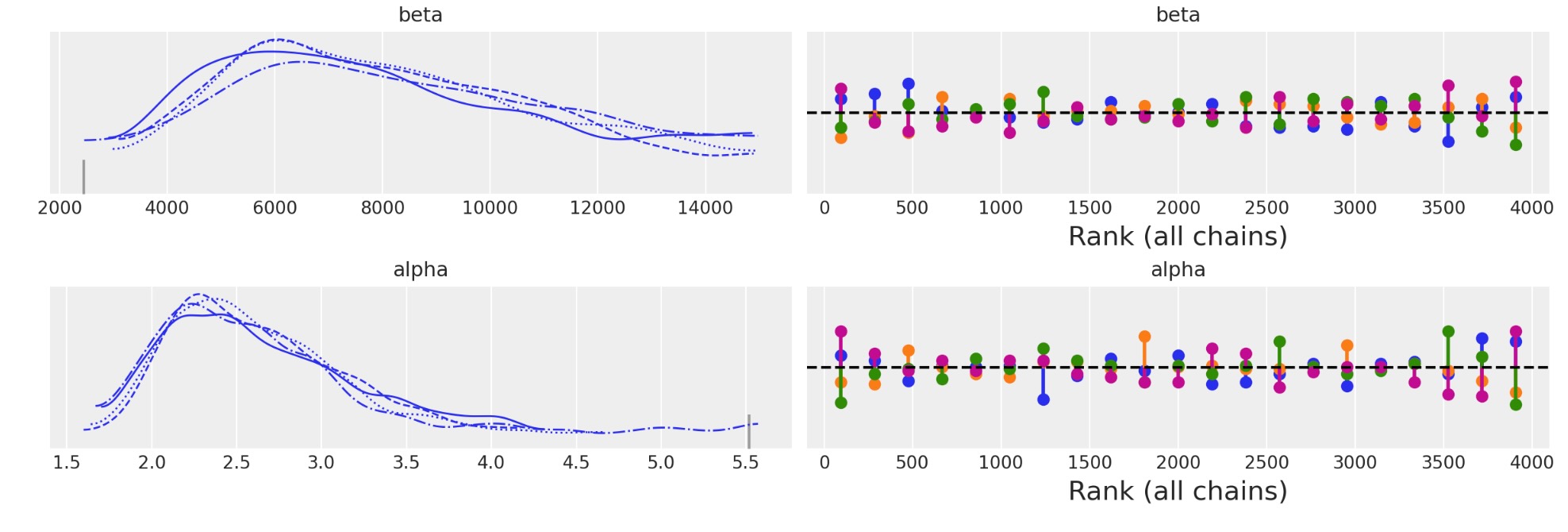
az.plot_trace(idata_informative, kind="rank_vlines");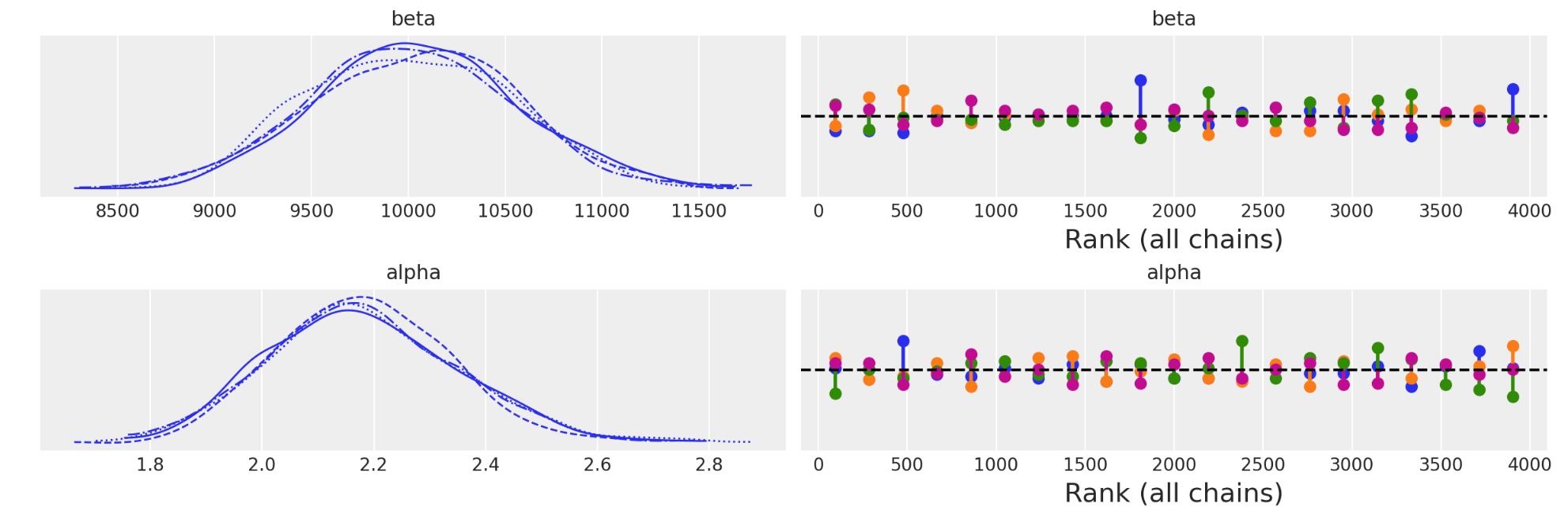
az.summary(idata)| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta | 8149.835 | 2916.378 | 3479.929 | 13787.447 | 111.293 | 78.729 | 612.0 | 371.0 | 1.01 |
| alpha | 2.626 | 0.558 | 1.779 | 3.631 | 0.030 | 0.025 | 616.0 | 353.0 | 1.01 |
az.summary(idata_informative)| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta | 10027.680 | 526.992 | 9013.856 | 10964.301 | 11.848 | 8.400 | 1979.0 | 2241.0 | 1.0 |
| alpha | 2.183 | 0.168 | 1.865 | 2.485 | 0.004 | 0.003 | 2102.0 | 1870.0 | 1.0 |
joint_draws = az.extract(idata, num_samples=1000)[["alpha", "beta"]]
alphas = joint_draws["alpha"].values
betas = joint_draws["beta"].values
joint_draws_informative = az.extract(idata_informative, num_samples=1000)[["alpha", "beta"]]
alphas_informative = joint_draws_informative["alpha"].values
betas_informative = joint_draws_informative["beta"].values
mosaic = """AAAA
BBCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 13))
axs = [axs[k] for k in axs.keys()]
ax = axs[0]
ax1 = axs[2]
ax2 = axs[1]
hist_data = []
for i in range(1000):
draws = pm.draw(pm.Weibull.dist(alpha=alphas[i], beta=betas[i]), 1000)
qe, pe = ecdf(draws)
lkup = dict(zip(pe, qe))
hist_data.append([lkup[0.1], lkup[0.05]])
ax.plot(qe, pe, color="slateblue", alpha=0.1)
hist_data_info = []
for i in range(1000):
draws = pm.draw(pm.Weibull.dist(alpha=alphas_informative[i], beta=betas_informative[i]), 1000)
qe, pe = ecdf(draws)
lkup = dict(zip(pe, qe))
hist_data_info.append([lkup[0.1], lkup[0.05]])
ax.plot(qe, pe, color="pink", alpha=0.1)
hist_data = pd.DataFrame(hist_data, columns=["p10", "p05"])
hist_data_info = pd.DataFrame(hist_data_info, columns=["p10", "p05"])
draws = pm.draw(pm.Weibull.dist(alpha=np.mean(alphas), beta=np.mean(betas)), 1000)
qe, pe = ecdf(draws)
ax.plot(qe, pe, color="purple", label="Expected CDF Uninformative Prior")
draws = pm.draw(
pm.Weibull.dist(alpha=np.mean(alphas_informative), beta=np.mean(betas_informative)), 1000
)
qe, pe = ecdf(draws)
ax.plot(qe, pe, color="magenta", label="Expected CDF Informative Prior")
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_ub"],
"--",
label="Non-Parametric CI UB",
color="black",
)
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["F_hat"],
"-o",
label="Non-Parametric CDF",
color="black",
alpha=1,
)
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_lb"],
"--",
label="Non-Parametric CI LB",
color="black",
)
ax.set_xlim(0, 2500)
ax.set_title(
"Bayesian Estimation of Uncertainty in the Posterior Predictive CDF \n Informative and Non-Informative Priors",
fontsize=20,
)
ax.set_ylabel("Fraction Failing")
ax.set_xlabel("Time")
ax1.hist(
hist_data["p10"], bins=30, ec="black", color="skyblue", alpha=0.4, label="Uninformative Prior"
)
ax1.hist(
hist_data_info["p10"],
bins=30,
ec="black",
color="slateblue",
alpha=0.4,
label="Informative Prior",
)
ax1.set_title("Distribution of 10% failure Time", fontsize=20)
ax1.legend()
ax2.hist(
hist_data["p05"], bins=30, ec="black", color="cyan", alpha=0.4, label="Uninformative Prior"
)
ax2.hist(
hist_data_info["p05"], bins=30, ec="black", color="pink", alpha=0.4, label="Informative Prior"
)
ax2.legend()
ax2.set_title("Distribution of 5% failure Time", fontsize=20)
wbf = WeibullFitter().fit(item_period_bearing_cage["t"] + 1e-25, item_period_bearing_cage["failed"])
wbf.plot_cumulative_density(ax=ax, color="cyan", label="Weibull MLE Fit")
ax.legend()
ax.set_ylim(0, 0.25);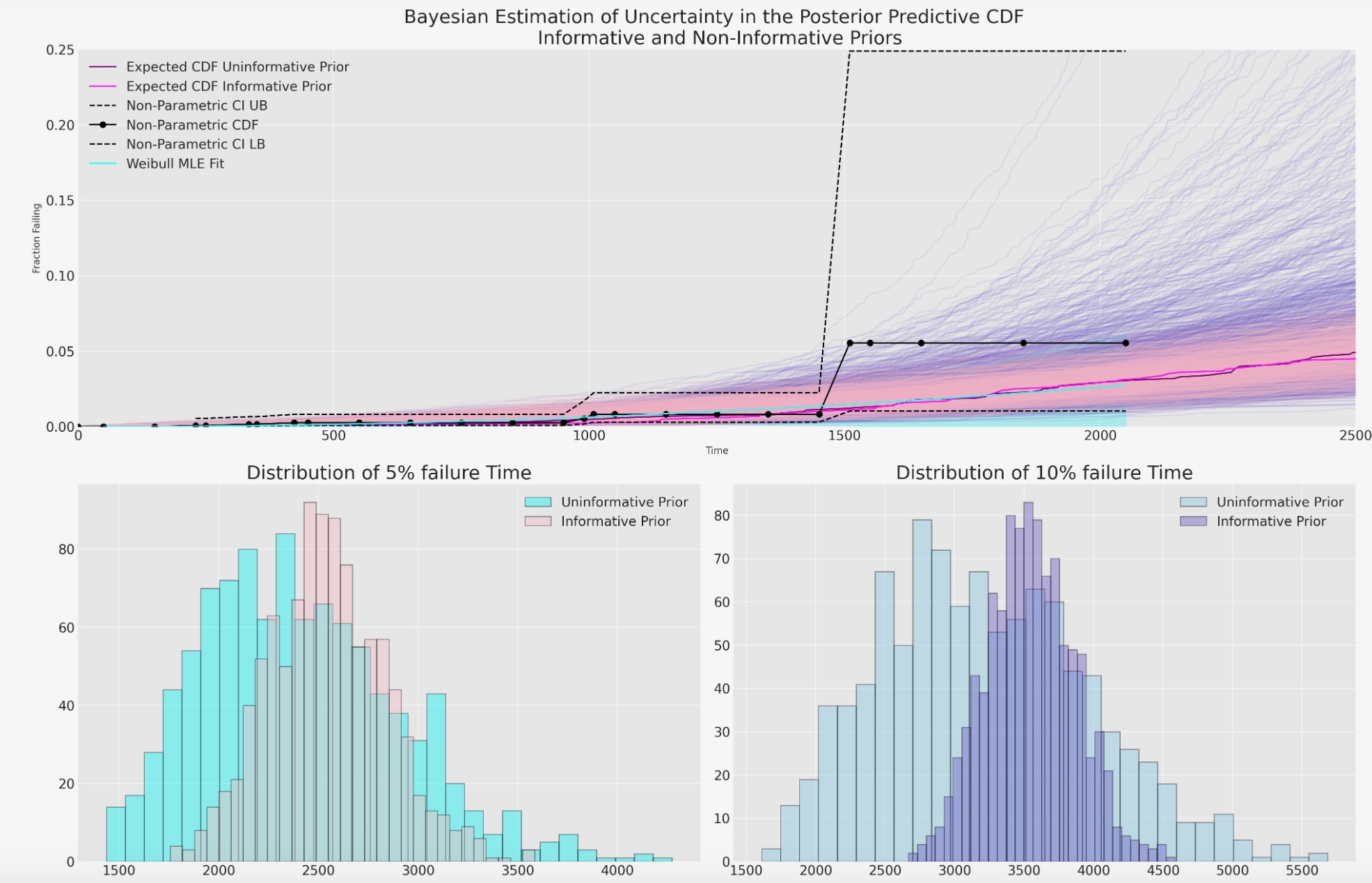
私たちは、故意にぼんやりした事前分布によって駆動させたベイジアン不確実性の推定が、いかに、私たちのMLE適合より、もっと不確実性を包むか見ることができます。そして、情報のない事前分布は、5%と10%の誤り時間の幅広い予測分布を示唆します。情報のない事前分布のベイジアンモデルは、私たちのCDFのノンパラメトリック推定で不確実性を取り扱うのに良い仕事をするように見えます。しかし、さらなる情報なしで、もっと適切なモデルを教えることは困難です。
各モデル適合の時間上の誤り率の具体的な推定は、私たちが希薄なデータを持つこの状況で特に極めて重要です。私たちは、いかに推定と10%の誤り時間の範囲がそれらの生産物にとって、最もらしいかについて、その問題の専門家たちに助言を求めることができる、感覚チェックは有意義です。
区間の誤り数の予測
観測されたデータの誤りが極端に希薄であるため、私たちは、時間の観測範囲に対して、推定について非常に注意深くなければなりません。しかし、私たちは、私たちのcdfの低位のテイルの誤りの予測数について尋ねることができます。これは、このデータに他の視点を与えます。問題に関して専門家と議論するのに役立つことができます。
プラグイン推定
サービスの基礎になる150と600時間の間に、幾つのベアリングが不良なるか知りたいことを想像してくだい。私たちは、推定したCDFと新しい将来のベアリング数を元にして計算することができます。私たちは、最初に、次を計算します。
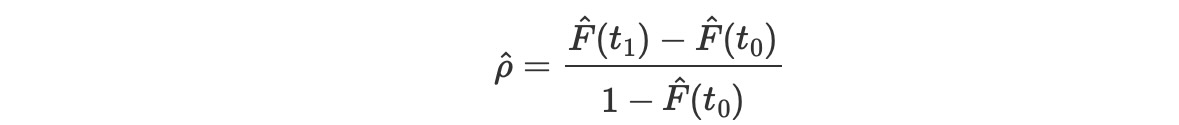
期間で発生する不良品の確率を設定するために、その後、期間の不良品の数のための予測ポイントは、risk_set*ρ で与えられます。
mle_fit = weibull_min(c=2, scale=10_000)
rho = mle_fit.cdf(600) - mle_fit.cdf(150) / (1 - mle_fit.cdf(150))
print("Rho:", rho)
print("N at Risk:", 1700)
print("Expected Number Failing in between 150 and 600 hours:", 1700 * rho)
print("Lower Bound 95% PI :", binom(1700, rho).ppf(0.05))
print("Upper Bound 95% PI:", binom(1700, rho).ppf(0.95))Rho: 0.0033685024546080927 N at Risk: 1700 Expected Number Failing in between 150 and 600 hours: 5.7264541728337575 Lower Bound 95% PI : 2.0 Upper Bound 95% PI: 10.0
ベイズ事後分布の同じ手続きを適用
私たちは、一様なモデルの分布を事後予測に使います。私たちは、ここで、時間間隔の不良品の数の95%予測期間の推定の不確実性を推論する方法を示します。この手続きの代替的な上のMLEで見たように、ブートストラップサンプリングから予測分布を生成することです。ブートストラップ手続きはMLE推定を使ってプラグイン手続きを承認し、そして事前分布の情報を規定することで柔軟性が欠如する傾向があります。
import xarray as xr
from xarray_einstats.stats import XrContinuousRV, XrDiscreteRV
def PI_failures(joint_draws, lp, up, n_at_risk):
fit = XrContinuousRV(weibull_min, joint_draws["alpha"], scale=joint_draws["beta"])
rho = fit.cdf(up) - fit.cdf(lp) / (1 - fit.cdf(lp))
lub = XrDiscreteRV(binom, n_at_risk, rho).ppf([0.05, 0.95])
lb, ub = lub.sel(quantile=0.05, drop=True), lub.sel(quantile=0.95, drop=True)
point_prediction = n_at_risk * rho
return xr.Dataset(
{"rho": rho, "n_at_risk": n_at_risk, "lb": lb, "ub": ub, "expected": point_prediction}
)
output_ds = PI_failures(joint_draws, 150, 600, 1700)
output_dsxarray.Dataset
def cost_func(failures, power):
### Imagined cost function for failing item e.g. refunds required
return np.power(failures, power)
mosaic = """AAAA
BBCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 12))
axs = [axs[k] for k in axs.keys()]
ax = axs[0]
ax1 = axs[1]
ax2 = axs[2]
ax.scatter(
joint_draws["alpha"],
output_ds["expected"],
c=joint_draws["beta"],
cmap=cm.cool,
alpha=0.3,
label="Coloured by function of Beta values",
)
ax.legend()
ax.set_ylabel("Expected Failures")
ax.set_xlabel("Alpha")
ax.set_title(
"Posterior Predictive Expected Failure Count between 150-600 hours \nas a function of Weibull(alpha, beta)",
fontsize=20,
)
ax1.hist(
output_ds["lb"],
ec="black",
color="slateblue",
label="95% PI Lower Bound on Failure Count",
alpha=0.3,
)
ax1.axvline(output_ds["lb"].mean(), label="Expected 95% PI Lower Bound on Failure Count")
ax1.axvline(output_ds["ub"].mean(), label="Expected 95% PI Upper Bound on Failure Count")
ax1.hist(
output_ds["ub"],
ec="black",
color="cyan",
label="95% PI Upper Bound on Failure Count",
bins=20,
alpha=0.3,
)
ax1.hist(
output_ds["expected"], ec="black", color="pink", label="Expected Count of Failures", bins=20
)
ax1.set_title("Uncertainty in the Posterior Prediction Interval of Failure Counts", fontsize=20)
ax1.legend()
ax2.set_title("Expected Costs Distribution(s) \nbased on implied Failure counts", fontsize=20)
ax2.hist(
cost_func(output_ds["expected"], 2.3),
label="Cost(failures,2)",
color="royalblue",
alpha=0.3,
ec="black",
bins=20,
)
ax2.hist(
cost_func(output_ds["expected"], 2),
label="Cost(failures,2.3)",
color="red",
alpha=0.5,
ec="black",
bins=20,
)
ax2.set_xlabel("$ cost")
# ax2.set_xlim(-60, 0)
ax2.legend();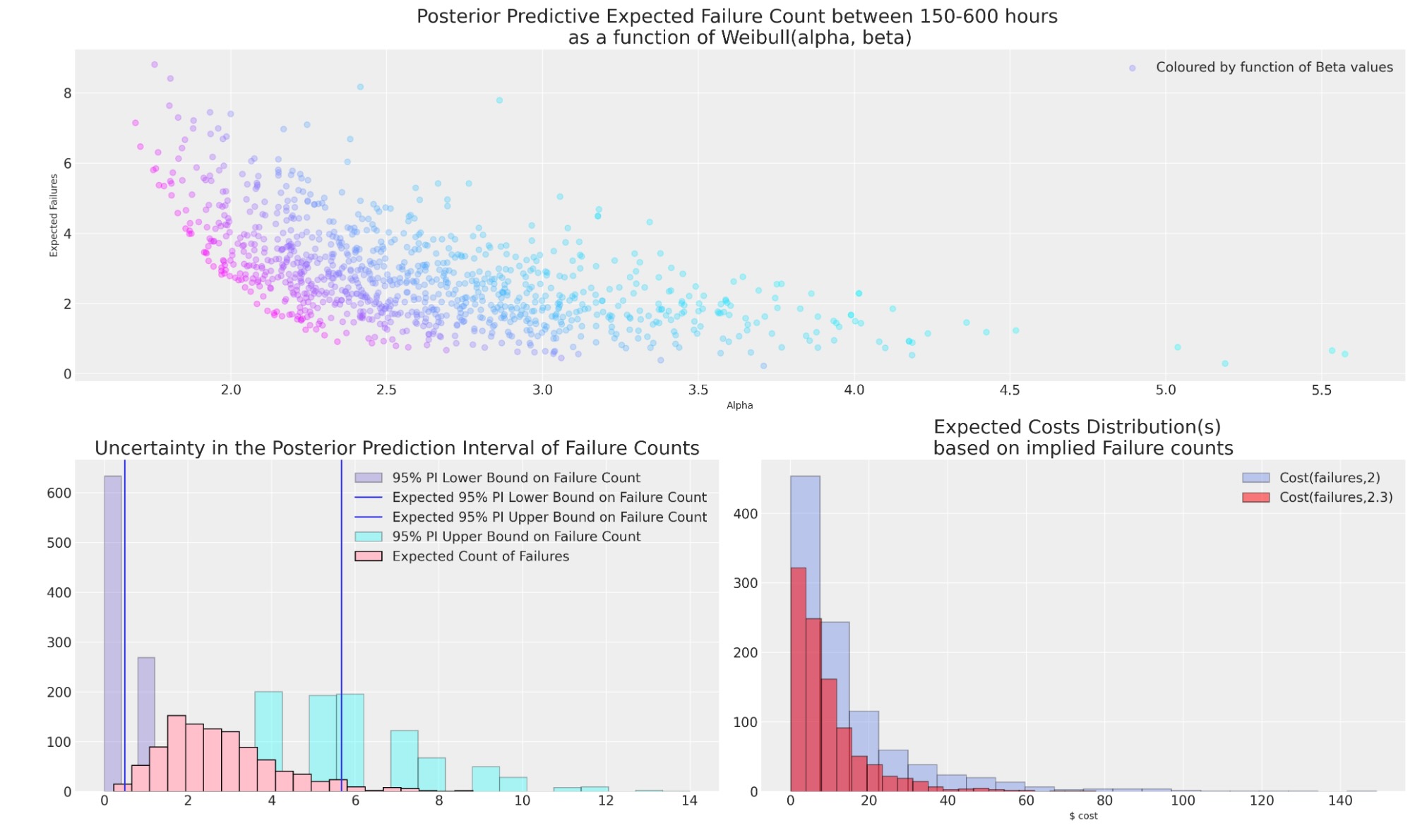
そのようなケースでモデルの選択は、極めて重大です。不良のプロファイルに関する決定は、問題の専門家によって情報を与えられなければならない傾向があります。なぜなら、そうした希薄なデータからの推定は、常に危険が伴います。もし、実際の不良品に付随するコストがあり、問題の専門知識が通常、サービスの600時間内で、2または7の不良品が推定されることがもっともらしいと言うことが、良い適切な値であれば、不確実性を理解することは、極めて重要です。
結論
私たちは、頻度主義とベイジアンの視点からモデルの信頼性と分析の方法を見てきました。そしてノンパラメトリック推定に対して比較しました。私たちは、どのように予測期間がブートストラッピングとベイジアンの両方によって、鍵となる統計の数を推論できるかを示しました。私たちは、再サンプリングメソッドと事前の情報規定を通してこれらの予測区間を較正するためのアプローチを見てきました。問題へのこれらの視点は、補完的であり、その技術の選択は、イデオロギー上の約束ではなく、関心の疑問の要因によって駆動されるのが妥当です。
特に、私たちは、どのようにベアリングデータへのMLE適合が、ベイズ分析の事前分布を作るために、満足できる最初の考えのアプローチを提供するのかを見てきました。私たちはまた、いかにその問題の専門知識が、綿密な検査のためのこれらの事前の影響と予測モデルから鍵となる量を推論することによって、誘導することができるかを見てきました。ベイズ予測区間の選択は、私たちは事前分布の推定を較正します。そして、これらの事前分布は、再度チェックされて適当な費用関数に対して分析されます。
製作者
著者:Nathaniel Forde 2022年1月9日
参考文献
- W.Q. Meeker, L.A. Escobar, and F.G Pascual. Statistical Methods for Reliability Data. Wiley, 2022.