ここでは、以下の項目について記述します。
- シンプソンのパラドックスと混合モデル、または階層混合モデルを使った解決策。これは、グループ内の二つの変数間に負の関係が見られる中で、データが多重グループが結合したものだった場合、その関係が消えるだけでなく全く逆の関係を示す状況です。下の図はその関係をうまく表現しています。
- 線形回帰モデルの作成法、線形回帰から始まり階層線形回帰に進みます。シンプソンのパラドックスはなぜこれが必要なのかを示す好例です。もちろん、できる限るデータ構造についての知識を組み込んだモデルを作るのが目的です。
- 同じモデルで異なるx値を用いて事後予測をやりやすくするためにpm.Dataコンテナを使います。
- 外形の問題に役立つモデルのために次元配列を用います。これはxarrayを使うことを含み、多重階層モデルにおいてとても役に立ちます。
- 事前予測と事後予測分布間の相違。
- ArviZとmatplotlibを使った、データ空間とパラメータ空間におけるモデルの視覚化の方法。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import xarray as xrnfig InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(1234)データの生成
def generate():
group_list = ["one", "two", "three", "four", "five"]
trials_per_group = 20
group_intercepts = rng.normal(0, 1, len(group_list))
group_slopes = np.ones(len(group_list)) * -0.5
group_mx = group_intercepts * 2
group = np.repeat(group_list, trials_per_group)
subject = np.concatenate(
[np.ones(trials_per_group) * i for i in np.arange(len(group_list))]
).astype(int)
intercept = np.repeat(group_intercepts, trials_per_group)
slope = np.repeat(group_slopes, trials_per_group)
mx = np.repeat(group_mx, trials_per_group)
x = rng.normal(mx, 1)
y = rng.normal(intercept + (x - mx) * slope, 1)
data = pd.DataFrame({"group": group, "group_idx": subject, "x": x, "y": y})
return data, group_listデータを生成します。
data, group_list = generate()生成したデータを表示してみます。
display(data)| group | group_idx | x | y | |
|---|---|---|---|---|
| 0 | one | 0 | -0.294574 | -2.338519 |
| 1 | one | 0 | -4.686497 | -1.448057 |
| 2 | one | 0 | -2.262201 | -1.393728 |
| 3 | one | 0 | -4.873809 | -0.265403 |
| 4 | one | 0 | -2.863929 | -0.774251 |
| ... | ... | ... | ... | ... |
| 95 | five | 4 | 3.981413 | 0.467970 |
| 96 | five | 4 | 1.889102 | 0.553290 |
| 97 | five | 4 | 2.561267 | 2.590966 |
| 98 | five | 4 | 0.147378 | 2.050944 |
| 99 | five | 4 | 2.738073 | 0.517918 |
プロットします。以下はプロットするコードです。
for i, group in enumerate(group_list):
plt.scatter(
data.query(f"group_idx=={i}").x,
data.query(f"group_idx=={i}").y,
color=f"C{i}",
label=f"{group}",
)
plt.legend(title="group");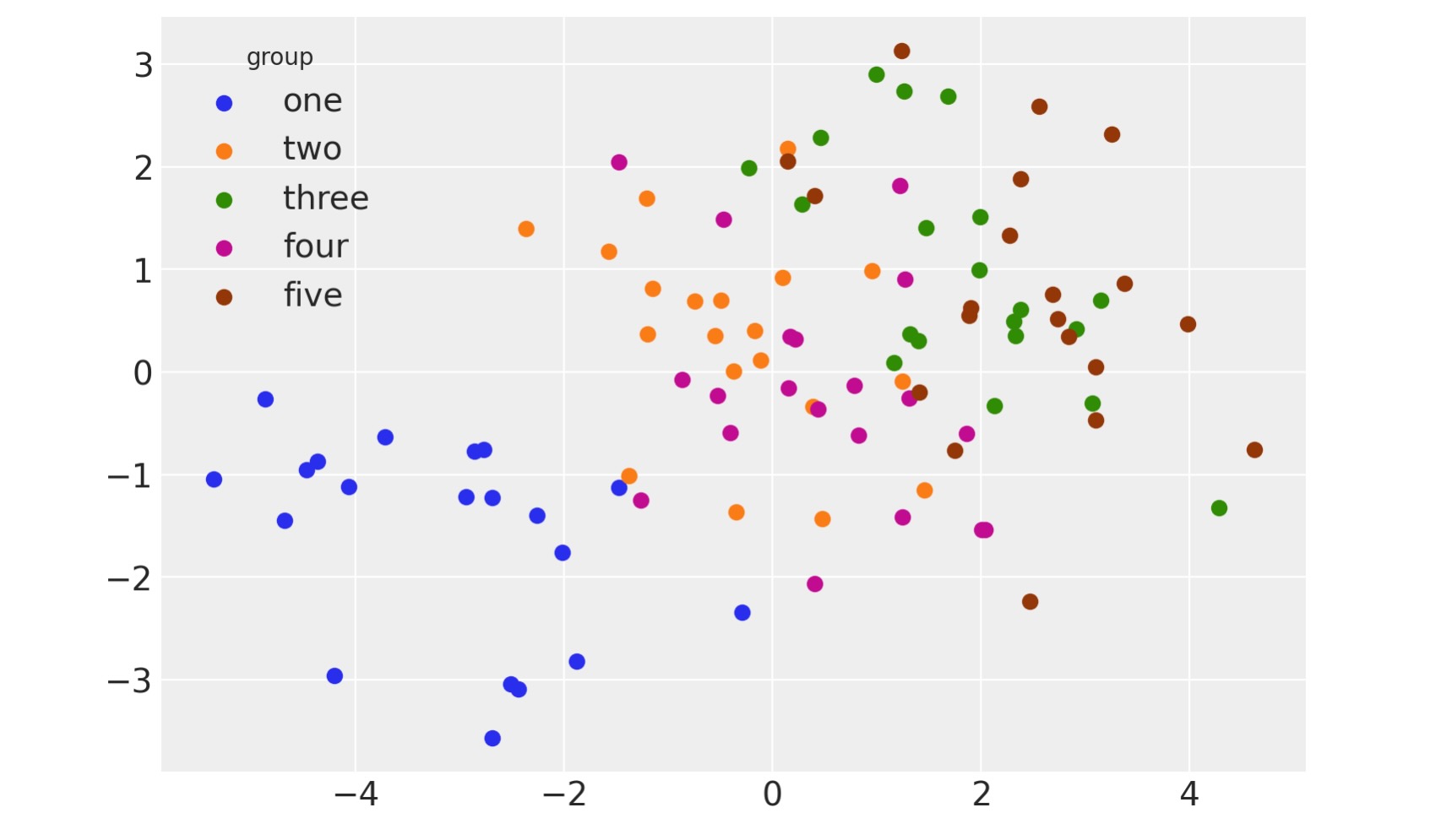
モデル1 基本線形回帰
最初の例は最も簡単な線形回帰モデルです。データの多重構造やグループに関する知識がなく、全てのデータを一塊にしたものです。
モデルを作ります。
with pm.Model() as linear_regression:
sigma = pm.HalfCauchy("sigma", beta=2)
β0 = pm.Normal("β0", 0, sigma=5)
β1 = pm.Normal("β1", 0, sigma=5)
x = pm.MutableData("x", data.x, dims="obs_id")
μ = pm.Deterministic("μ", β0 + β1 * x, dims="obs_id")
pm.Normal("y", mu=μ, sigma=sigma, observed=data.y, dims="obs_id")pm.model_to_graphviz(linear_regression)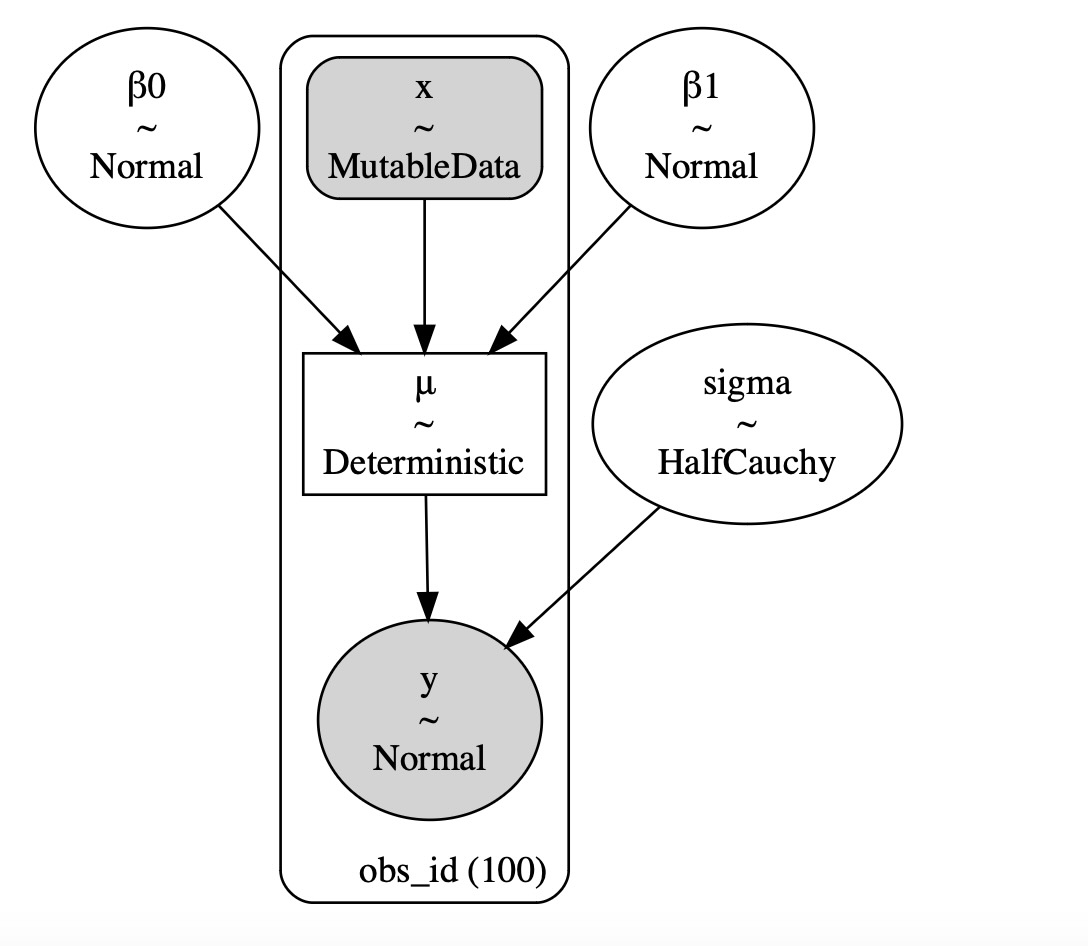
推論を実行します。
with linear_regression:
idata = pm.sample()
結果を出力します。
az.plot_trace(idata, filter_vars="regex", var_names=["~μ"]);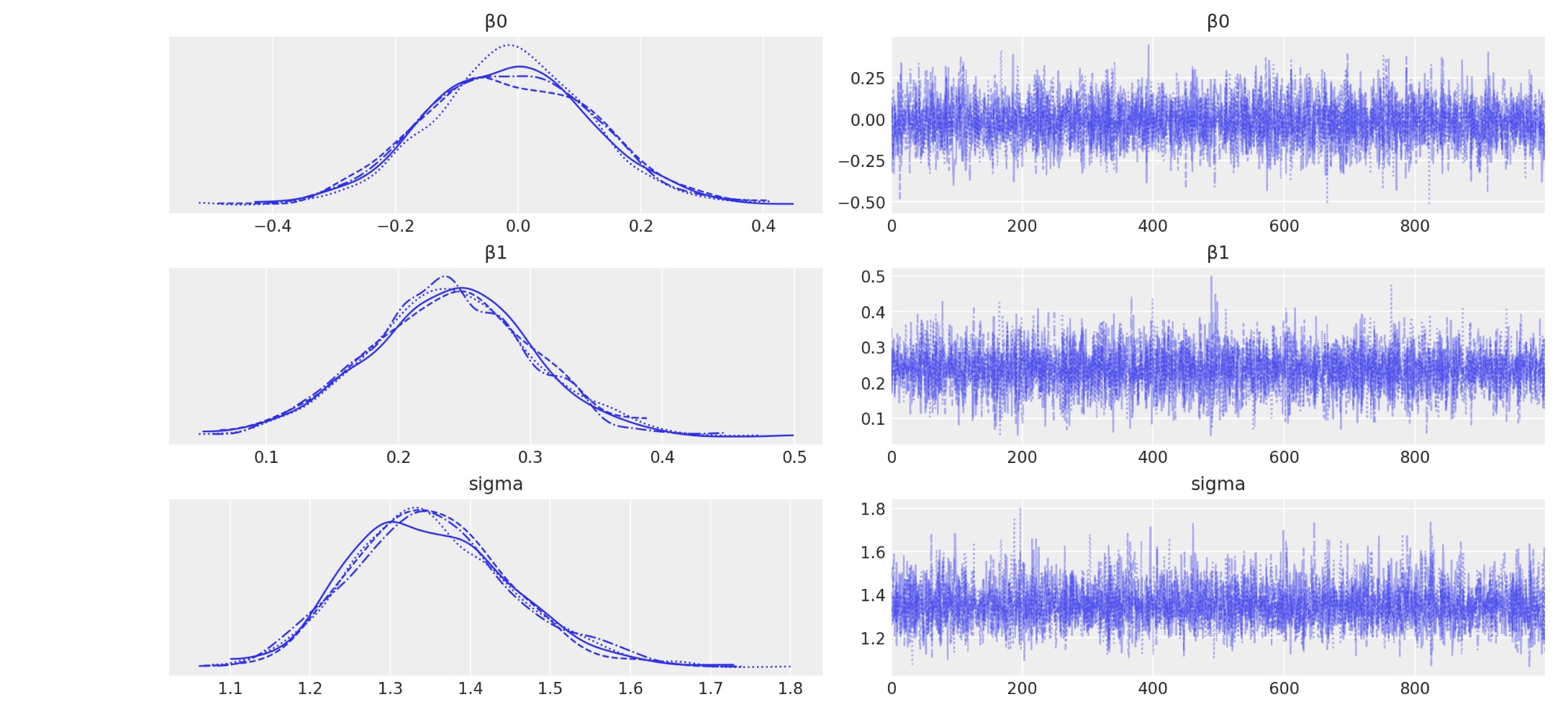
結果の視覚化
# posterior prediction for these x values
xi = np.linspace(data.x.min(), data.x.max(), 20)
# do posterior predictive inference
with linear_regression:
pm.set_data({"x": xi})
idata.extend(pm.sample_posterior_predictive(idata, var_names=["y", "μ"]))
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
# conditional mean plot ---------------------------------------------
# data
ax[0].scatter(data.x, data.y, color="k")
# conditional mean credible intervals
post = az.extract(idata)
xi = xr.DataArray(np.linspace(np.min(data.x), np.max(data.x), 20), dims=["x_plot"])
y = post.β0 + post.β1 * xi
region = y.quantile([0.025, 0.15, 0.5, 0.85, 0.975], dim="sample")
ax[0].fill_between(
xi, region.sel(quantile=0.025), region.sel(quantile=0.975), alpha=0.2, color="k", edgecolor="w"
)
ax[0].fill_between(
xi, region.sel(quantile=0.15), region.sel(quantile=0.85), alpha=0.2, color="k", edgecolor="w"
)
# conditional mean
ax[0].plot(xi, region.sel(quantile=0.5), "k", linewidth=2)
# formatting
ax[0].set(xlabel="x", ylabel="y", title="Conditional mean")
# posterior prediction ----------------------------------------------
# data
ax[1].scatter(data.x, data.y, color="k")
# posterior mean and HDI's
ax[1].plot(xi, idata.posterior_predictive.y.mean(["chain", "draw"]), "k")
az.plot_hdi(
xi,
idata.posterior_predictive.y,
hdi_prob=0.6,
color="k",
fill_kwargs={"alpha": 0.2, "linewidth": 0},
ax=ax[1],
)
az.plot_hdi(
xi,
idata.posterior_predictive.y,
hdi_prob=0.95,
color="k",
fill_kwargs={"alpha": 0.2, "linewidth": 0},
ax=ax[1],
)
# formatting
ax[1].set(xlabel="x", ylabel="y", title="Posterior predictive distribution")
# parameter space ---------------------------------------------------
ax[2].scatter(
az.extract(idata, var_names=["β1"]),
az.extract(idata, var_names=["β0"]),
color="k",
alpha=0.01,
rasterized=True,
)
# formatting
ax[2].set(xlabel="slope", ylabel="intercept", title="Parameter space")
ax[2].axhline(y=0, c="k")
ax[2].axvline(x=0, c="k");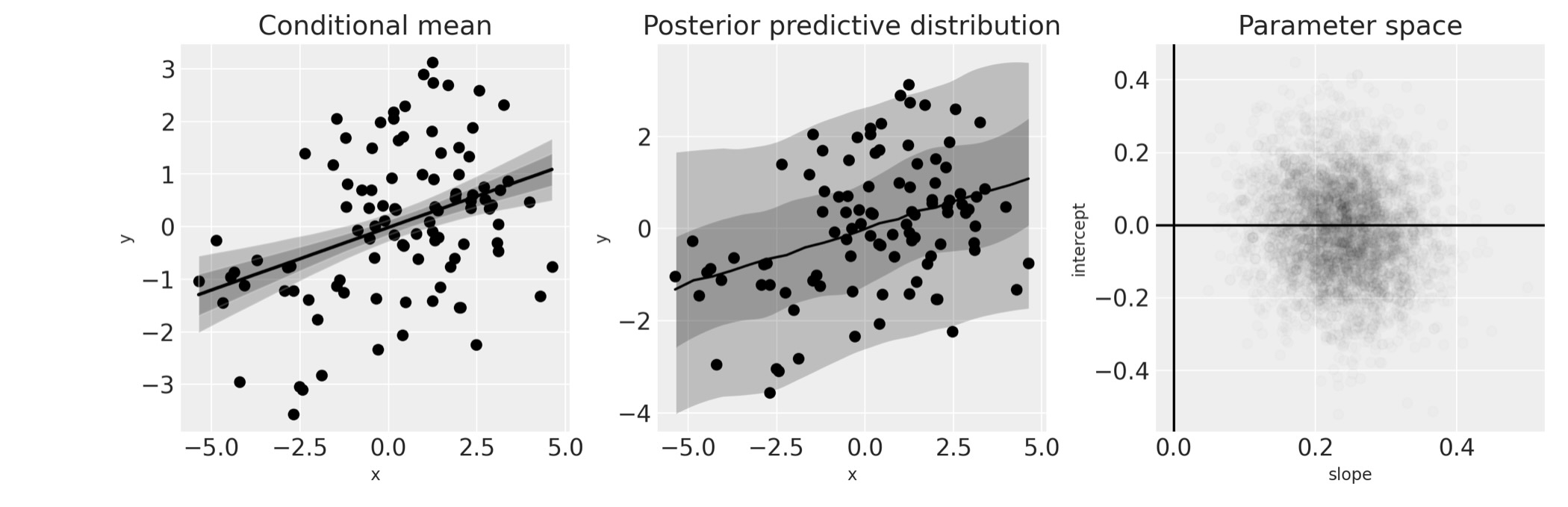
左のプロットはデータと事後の条件平均を示します。与えられたxに対して、モデルの事後分布を取得します。
中のプロットは私たちが予期したデータについて提示した事後予測分布です。直感的にこれは、モデルに関する知識がないだけでなく、エラーの分布に関する知識も含んでいないことがわかります。
右のプロットはパラメータ空間での事後信頼を示しています。
この分析について明らかなことの一つは、xとyが正に相関を持っていることの信頼できる証拠になっていることです。事後の傾きからもこれを見ることができます。
モデル2 独立した傾きと切片のモデル
この分析の同じデータを使います。しかし、今度はデータがグループになっているという知識を使うことにします。より詳しく述べると各グループのデータに独立した回帰を適応させます。
coords = {"group": group_list}
with pm.Model(coords=coords) as ind_slope_intercept:
# Define priors
sigma = pm.HalfCauchy("sigma", beta=2, dims="group")
β0 = pm.Normal("β0", 0, sigma=5, dims="group")
β1 = pm.Normal("β1", 0, sigma=5, dims="group")
# Data
x = pm.MutableData("x", data.x, dims="obs_id")
g = pm.MutableData("g", data.group_idx, dims="obs_id")
# Linear model
μ = pm.Deterministic("μ", β0[g] + β1[g] * x, dims="obs_id")
# Define likelihood
pm.Normal("y", mu=μ, sigma=sigma[g], observed=data.y, dims="obs_id")このモデルのDAGをプロットすることで、今回 各グループ毎に個別の切片、傾き、変数パラメータを持つことが明らかになります。
pm.model_to_graphviz(ind_slope_intercept)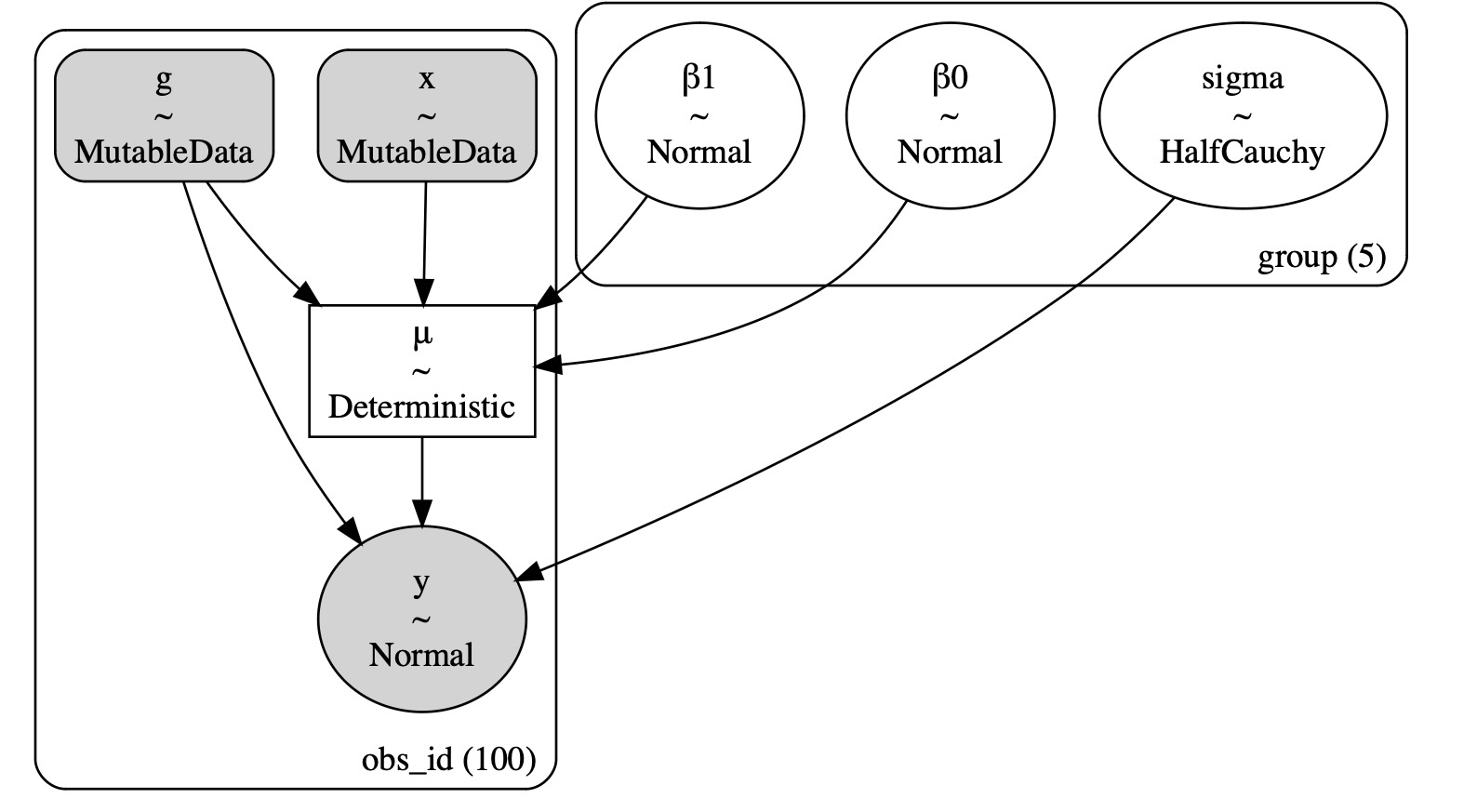
with ind_slope_intercept:
idata = pm.sample()
az.plot_trace(idata, filter_vars="regex", var_names=["~μ"]);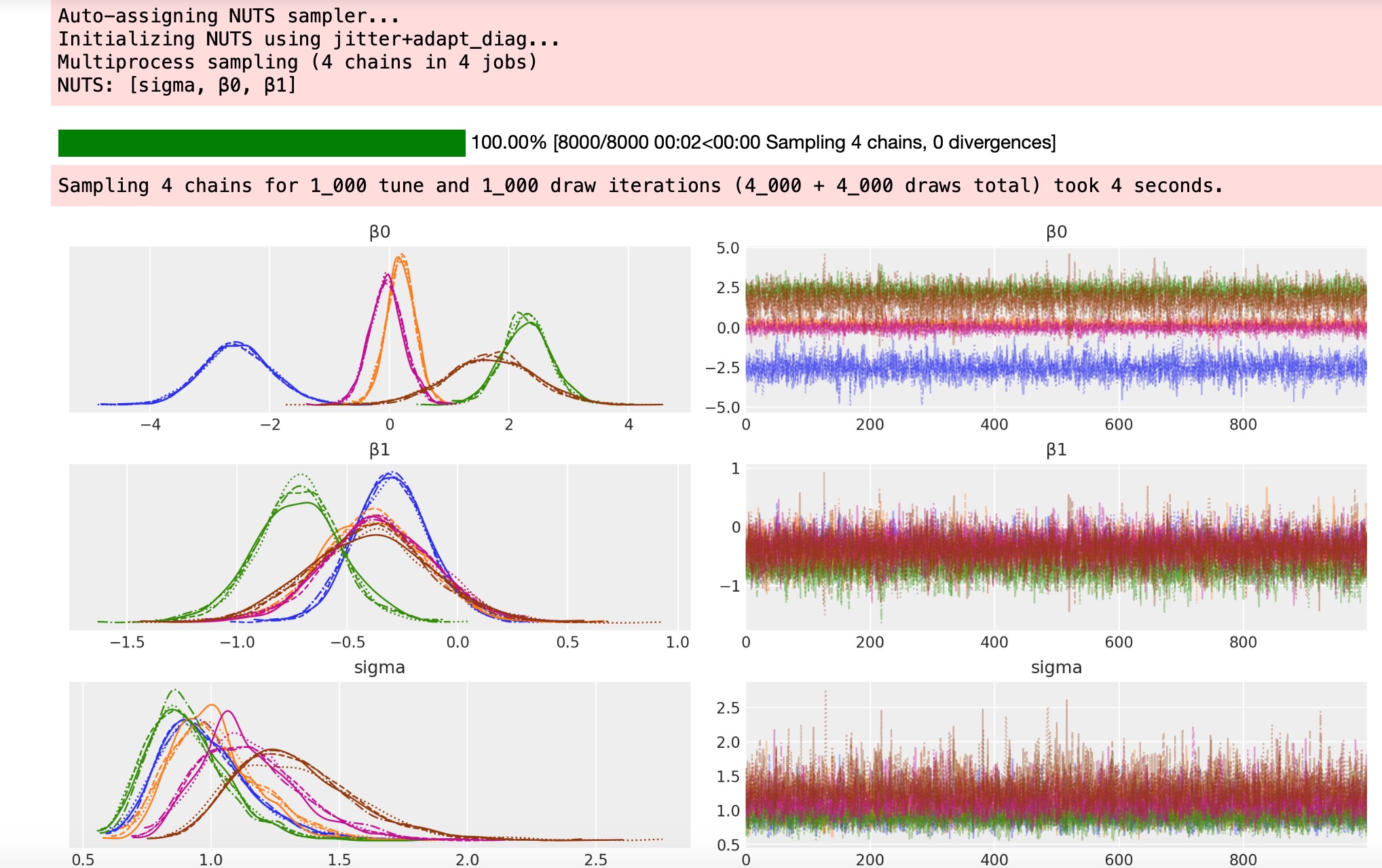
視覚化
# Create values of x and g to use for posterior prediction
xi = [
np.linspace(data.query(f"group_idx=={i}").x.min(), data.query(f"group_idx=={i}").x.max(), 10)
for i, _ in enumerate(group_list)
]
g = [np.ones(10) * i for i, _ in enumerate(group_list)]
xi, g = np.concatenate(xi), np.concatenate(g)
# Do the posterior prediction
with ind_slope_intercept:
pm.set_data({"x": xi, "g": g.astype(int)})
idata.extend(pm.sample_posterior_predictive(idata, var_names=["μ", "y"]))
def get_ppy_for_group(group_list, group):
"""Get posterior predictive outcomes for observations from a given group"""
return idata.posterior_predictive.y.data[:, :, group_list == group]
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
# conditional mean plot ---------------------------------------------
for i, groupname in enumerate(group_list):
# data
ax[0].scatter(data.x[data.group_idx == i], data.y[data.group_idx == i], color=f"C{i}")
# conditional mean credible intervals
post = az.extract(idata)
_xi = xr.DataArray(
np.linspace(np.min(data.x[data.group_idx == i]), np.max(data.x[data.group_idx == i]), 20),
dims=["x_plot"],
)
y = post.β0.sel(group=groupname) + post.β1.sel(group=groupname) * _xi
region = y.quantile([0.025, 0.15, 0.5, 0.85, 0.975], dim="sample")
ax[0].fill_between(
_xi,
region.sel(quantile=0.025),
region.sel(quantile=0.975),
alpha=0.2,
color=f"C{i}",
edgecolor="w",
)
ax[0].fill_between(
_xi,
region.sel(quantile=0.15),
region.sel(quantile=0.85),
alpha=0.2,
color=f"C{i}",
edgecolor="w",
)
# conditional mean
ax[0].plot(_xi, region.sel(quantile=0.5), color=f"C{i}", linewidth=2)
# formatting
ax[0].set(xlabel="x", ylabel="y", title="Conditional mean")
# posterior prediction ----------------------------------------------
for i, groupname in enumerate(group_list):
# data
ax[1].scatter(data.x[data.group_idx == i], data.y[data.group_idx == i], color=f"C{i}")
# posterior mean and HDI's
ax[1].plot(xi[g == i], np.mean(get_ppy_for_group(g, i), axis=(0, 1)), label=groupname)
az.plot_hdi(
xi[g == i],
get_ppy_for_group(g, i), # pp_y[:, :, g == i],
hdi_prob=0.6,
color=f"C{i}",
fill_kwargs={"alpha": 0.4, "linewidth": 0},
ax=ax[1],
)
az.plot_hdi(
xi[g == i],
get_ppy_for_group(g, i),
hdi_prob=0.95,
color=f"C{i}",
fill_kwargs={"alpha": 0.2, "linewidth": 0},
ax=ax[1],
)
ax[1].set(xlabel="x", ylabel="y", title="Posterior predictive distribution")
# parameter space ---------------------------------------------------
for i, _ in enumerate(group_list):
ax[2].scatter(
az.extract(idata, var_names="β1")[i, :],
az.extract(idata, var_names="β0")[i, :],
color=f"C{i}",
alpha=0.01,
rasterized=True,
)
ax[2].set(xlabel="slope", ylabel="intercept", title="Parameter space")
ax[2].axhline(y=0, c="k")
ax[2].axvline(x=0, c="k");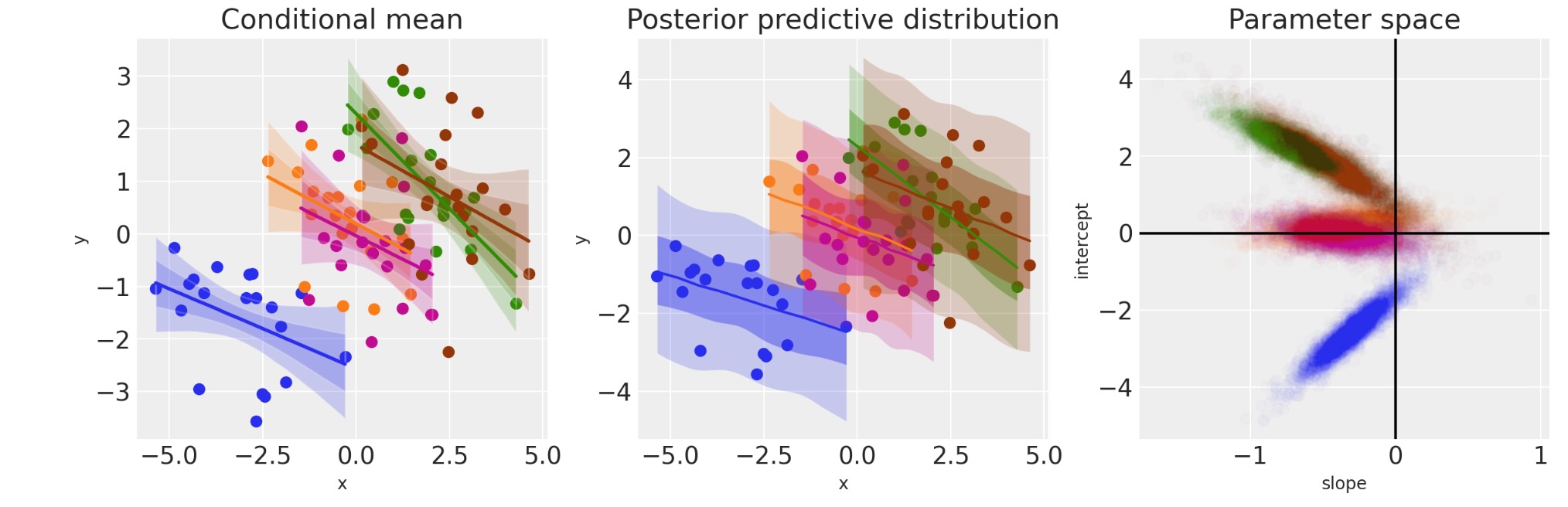
最初のモデルと対照的に、グループレベルでモデルにした時、証拠の点がxとyの間で負の関係にあることがわかります。
モデル3 階層回帰
モデル2に戻り、私たちのデータ構造に対してもっと知識を取り込みます。各グループを完全に独立したものと捉えるよりむしろ、これらのグループが集団レベルの分布から出力されているという知識を使うことができます。これは時にハイパーパラメータと呼ばれます。
モデル2からモデル3へのこの移動はパラメータを追加することでわかります。したがってモデルの複雑性は増加します。しかし、一方でネストしたデータ構造に関する知識の追加は、実際、パラメータ空間の制限をもたらします。
non_centered = True
with pm.Model(coords=coords) as hierarchical:
# Hyperpriors
intercept_mu = pm.Normal("intercept_mu", 0, sigma=1)
intercept_sigma = pm.HalfNormal("intercept_sigma", sigma=2)
slope_mu = pm.Normal("slope_mu", 0, sigma=1)
slope_sigma = pm.HalfNormal("slope_sigma", sigma=2)
sigma_hyperprior = pm.HalfNormal("sigma_hyperprior", sigma=0.5)
# Define priors
sigma = pm.HalfNormal("sigma", sigma=sigma_hyperprior, dims="group")
if non_centered:
β0_offset = pm.Normal("β0_offset", 0, sigma=1, dims="group")
β0 = pm.Deterministic("β0", intercept_mu + β0_offset * intercept_sigma, dims="group")
β1_offset = pm.Normal("β1_offset", 0, sigma=1, dims="group")
β1 = pm.Deterministic("β1", slope_mu + β1_offset * slope_sigma, dims="group")
else:
β0 = pm.Normal("β0", intercept_mu, sigma=intercept_sigma, dims="group")
β1 = pm.Normal("β1", slope_mu, sigma=slope_sigma, dims="group")
# Data
x = pm.MutableData("x", data.x, dims="obs_id")
g = pm.MutableData("g", data.group_idx, dims="obs_id")
# Linear model
μ = pm.Deterministic("μ", β0[g] + β1[g] * x, dims="obs_id")
# Define likelihood
pm.Normal("y", mu=μ, sigma=sigma[g], observed=data.y, dims="obs_id")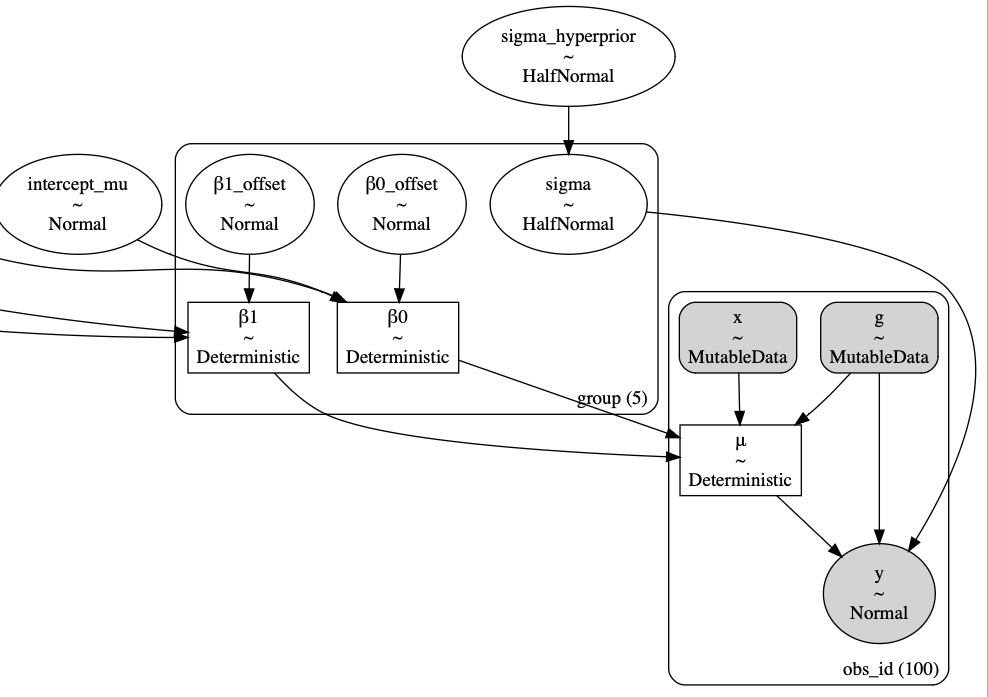
with hierarchical:
idata = pm.sample(tune=2000, target_accept=0.99)
az.plot_trace(idata, filter_vars="regex", var_names=["~μ"]);
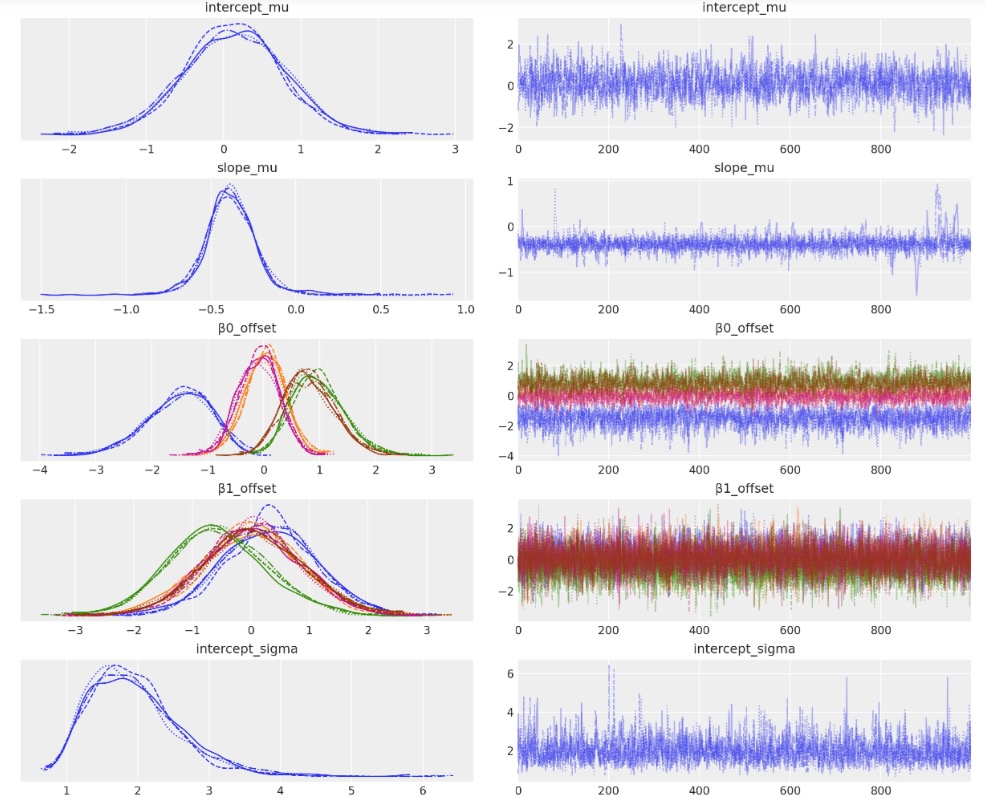
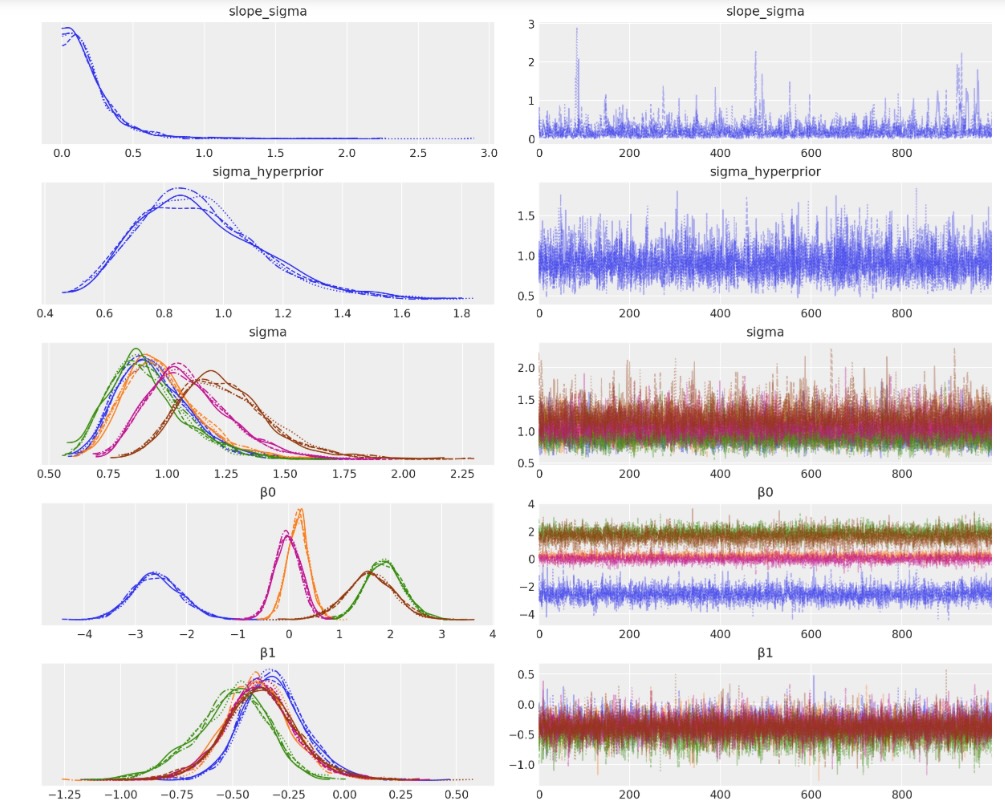
視覚化
# Create values of x and g to use for posterior prediction
xi = [
np.linspace(data.query(f"group_idx=={i}").x.min(), data.query(f"group_idx=={i}").x.max(), 10)
for i, _ in enumerate(group_list)
]
g = [np.ones(10) * i for i, _ in enumerate(group_list)]
xi, g = np.concatenate(xi), np.concatenate(g)
# Do the posterior prediction
with hierarchical:
pm.set_data({"x": xi, "g": g.astype(int)})
idata.extend(pm.sample_posterior_predictive(idata, var_names=["μ", "y"]))
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
# conditional mean plot ---------------------------------------------
for i, groupname in enumerate(group_list):
# data
ax[0].scatter(data.x[data.group_idx == i], data.y[data.group_idx == i], color=f"C{i}")
# conditional mean credible intervals
post = az.extract(idata)
_xi = xr.DataArray(
np.linspace(np.min(data.x[data.group_idx == i]), np.max(data.x[data.group_idx == i]), 20),
dims=["x_plot"],
)
y = post.β0.sel(group=groupname) + post.β1.sel(group=groupname) * _xi
region = y.quantile([0.025, 0.15, 0.5, 0.85, 0.975], dim="sample")
ax[0].fill_between(
_xi,
region.sel(quantile=0.025),
region.sel(quantile=0.975),
alpha=0.2,
color=f"C{i}",
edgecolor="w",
)
ax[0].fill_between(
_xi,
region.sel(quantile=0.15),
region.sel(quantile=0.85),
alpha=0.2,
color=f"C{i}",
edgecolor="w",
)
# conditional mean
ax[0].plot(_xi, region.sel(quantile=0.5), color=f"C{i}", linewidth=2)
# formatting
ax[0].set(xlabel="x", ylabel="y", title="Conditional mean")
# posterior prediction ----------------------------------------------
for i, groupname in enumerate(group_list):
# data
ax[1].scatter(data.x[data.group_idx == i], data.y[data.group_idx == i], color=f"C{i}")
# posterior mean and HDI's
ax[1].plot(xi[g == i], np.mean(get_ppy_for_group(g, i), axis=(0, 1)), label=groupname)
az.plot_hdi(
xi[g == i],
get_ppy_for_group(g, i),
hdi_prob=0.6,
color=f"C{i}",
fill_kwargs={"alpha": 0.4, "linewidth": 0},
ax=ax[1],
)
az.plot_hdi(
xi[g == i],
get_ppy_for_group(g, i),
hdi_prob=0.95,
color=f"C{i}",
fill_kwargs={"alpha": 0.2, "linewidth": 0},
ax=ax[1],
)
ax[1].set(xlabel="x", ylabel="y", title="Posterior Predictive")
# parameter space ---------------------------------------------------
# plot posterior for population level slope and intercept
slope = rng.normal(
az.extract(idata, var_names="slope_mu"),
az.extract(idata, var_names="slope_sigma"),
)
intercept = rng.normal(
az.extract(idata, var_names="intercept_mu"),
az.extract(idata, var_names="intercept_sigma"),
)
ax[2].scatter(slope, intercept, color="k", alpha=0.05)
# plot posterior for group level slope and intercept
for i, _ in enumerate(group_list):
ax[2].scatter(
az.extract(idata, var_names="β1")[i, :],
az.extract(idata, var_names="β0")[i, :],
color=f"C{i}",
alpha=0.01,
)
ax[2].set(xlabel="slope", ylabel="intercept", title="Parameter space", xlim=[-2, 1], ylim=[-5, 5])
ax[2].axhline(y=0, c="k")
ax[2].axvline(x=0, c="k");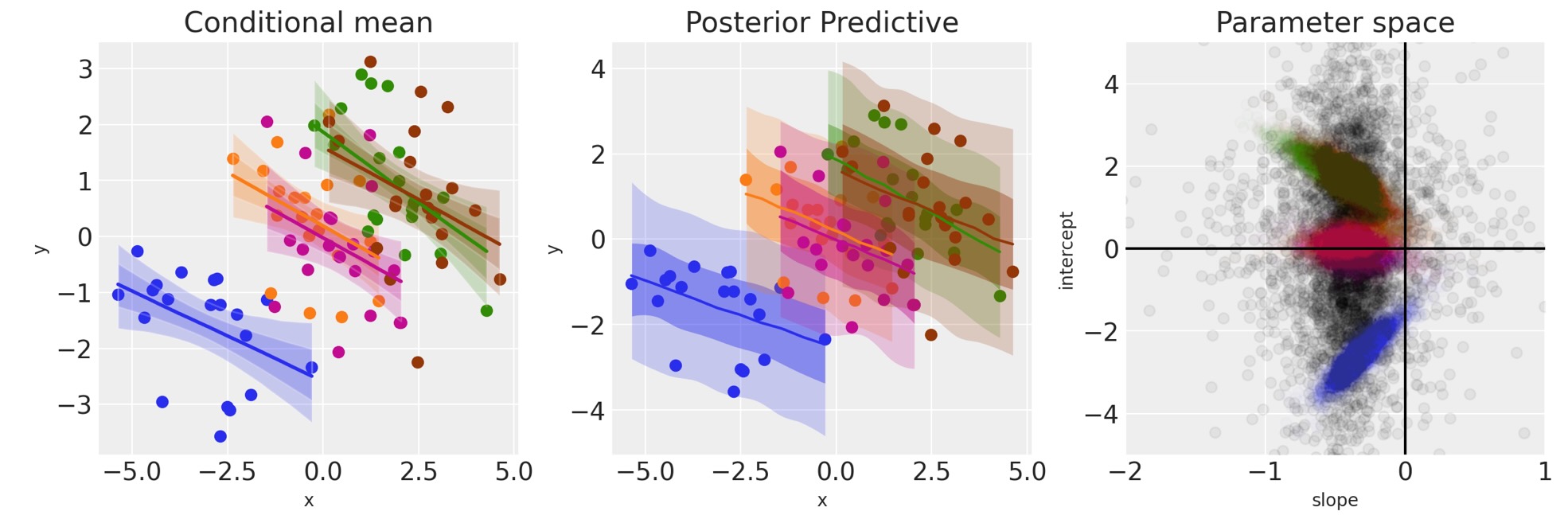
右のパネルは黒で事後の傾きと切片のパラメータの事後のグループレベルを示しています。この特別な視覚化ははっきりしませんが、そのためゼロ以下の傾きにどれくらいの信頼度があるかを見るために、以下の境界分布をプロットすることができます。
az.plot_posterior(slope, ref_val=0)
plt.title("Population level slope parameter");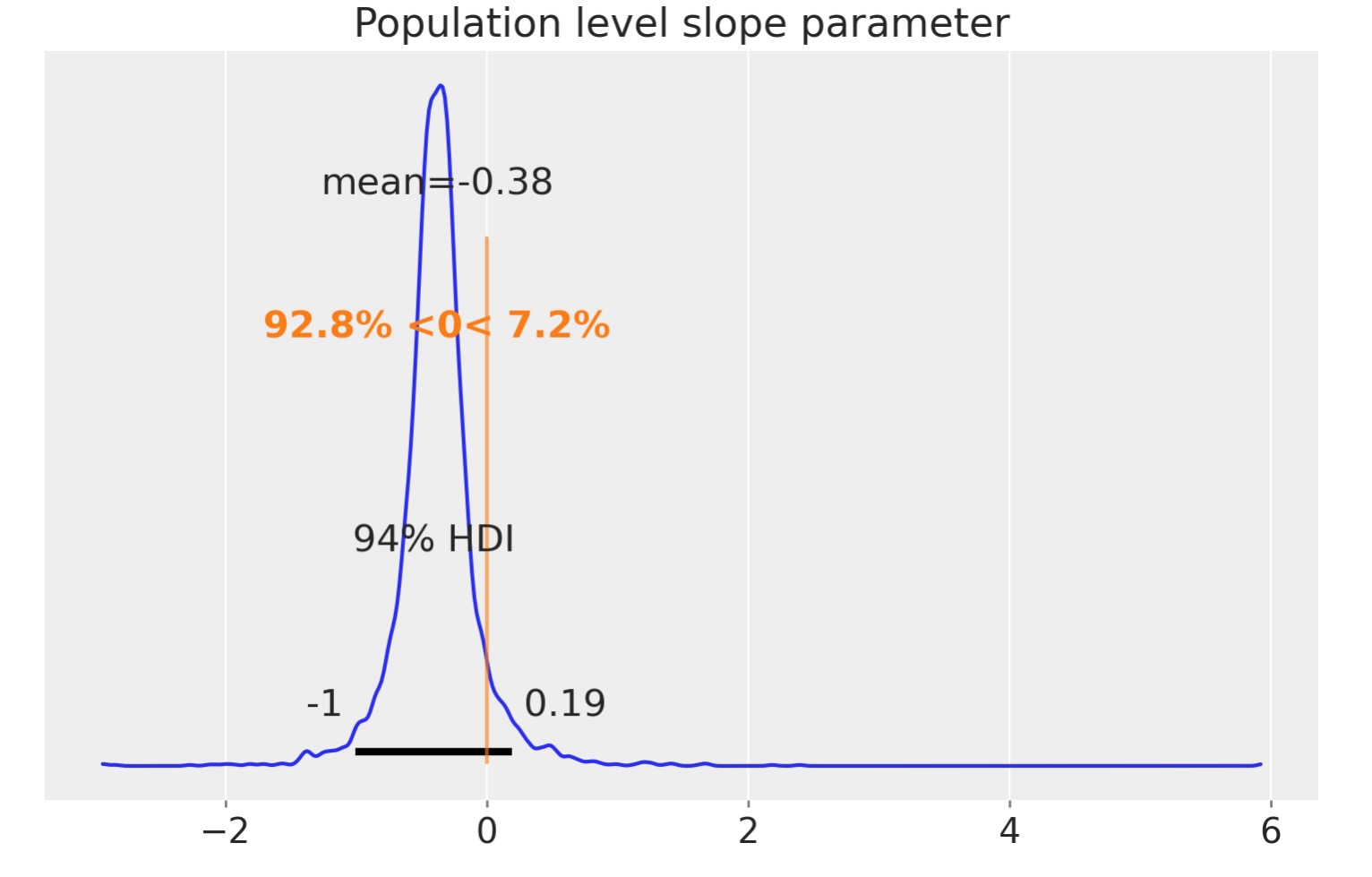
結論
シンプソンのパラドックスを使って、三つのモデルを見てきました。最初は全てのデータが一つのグループからなる簡単な線形回帰。これは回帰の傾きが正になることを私たちに信じさせました。
必ずしも間違いではないのですが、グループ内のデータに対する回帰の傾きが負であることを見た時に、それは矛盾したもの(パラドックス)になります。2番目のモデルで、各グループのデータに対して分離した回帰を適用する方法がわかりました。
3番目の最後のモデルは、全体の集団からこれらのグループの各自をサンプルして私たちの知識を取り込んで、階層に一つ層を追加しました。これはグループレベルばかりでなく、集団レベルにおいてもの回帰パラメータについて推論できることを追加しました。最後のプロットは、私たちが信頼しているグループをサンプルした後の集団レベルの傾きパラメータを示しています。
製作者
- 著作者 Benjamin T.Vincent 2021年7月
- 更新 Benjamin T.Vincent 2022年4月
- 更新 Benjamin T.Vincent 2023年2月 PyMC v5上での動作
- 更新 Benjamin T.Vincent 2023年2月 az.extractを使用
