scikit-learn

Pythonで使える機械学習ライブラリです。

scikit-leanのインストール

　パッケージマネージャーはconda、pip、 オペレーティングシステムは、Windows, MacOS , Linuxが対象です。

　Condaでインストールする場合

conda create -n sklearn-env -c conda-forge scikit-learn
conda activate sklearn-env

sklean用の仮想環境を作ってインストールしています。

PIPでインストール

pip install -U scikit-learn

クイックスタート

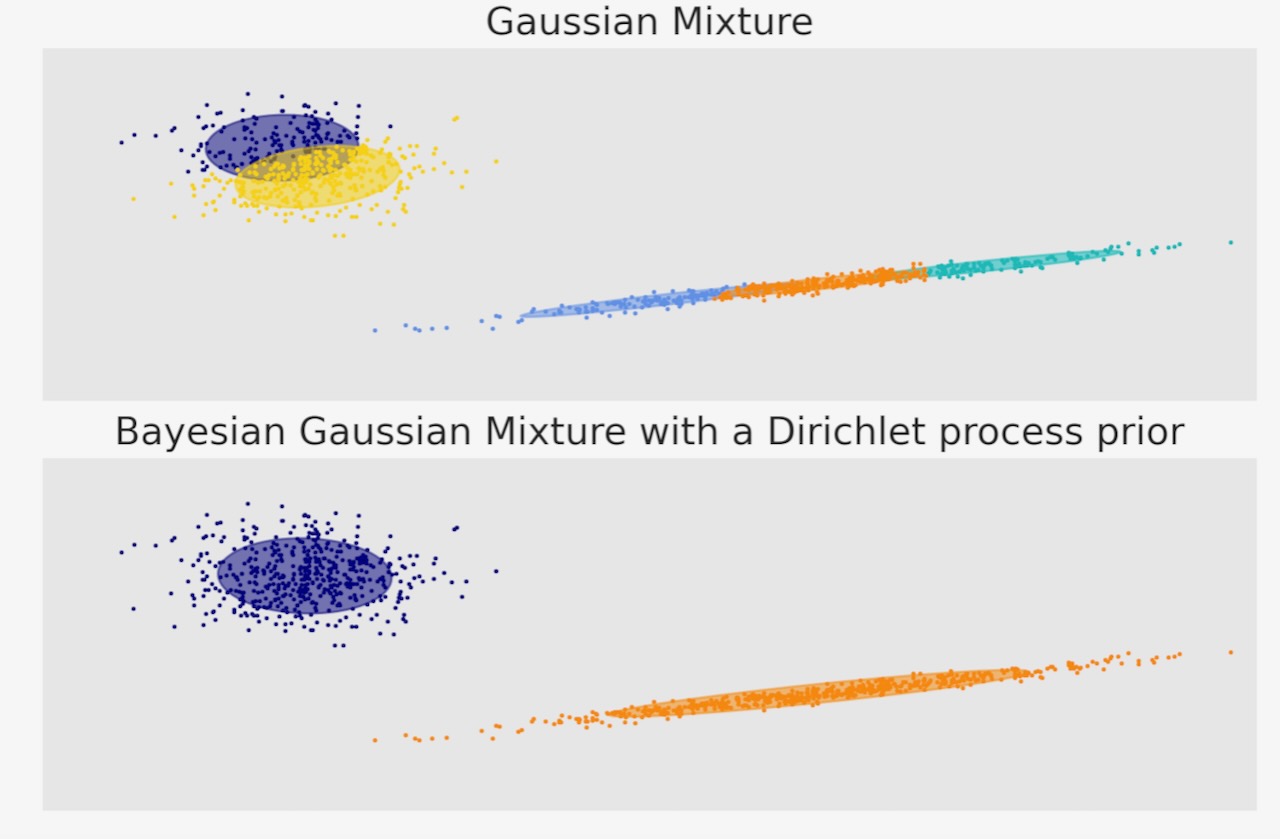
ガウス混合分布 楕円体

　期待最大化(ガウス混合クラス)、変分推論(事前ディリクレ過程によるベイジアンガウス混合クラスモデル)を獲得して二つのガウス混合分布の楕円体をプロットします。両モデルは、データに適合した５つの成分にアクセスします。変分推論モデルは効果的にうまく適合するために必要な数だけを使いますが、期待最大化モデルは５つの成分全てを必要とします。

　期待最大化モデルは多すぎる成分に分離するように試みる為に、このモデルは任意のいくつかの成分に分離します。ディリクレ過程モデルは自動的に状態数を適合させます。

import itertools

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl

from sklearn import mixture

color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])


def plot_results(X, Y_, means, covariances, index, title):
    splot = plt.subplot(2, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y_ == i):
            continue
        plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180.0 * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-9.0, 5.0)
    plt.ylim(-3.0, 6.0)
    plt.xticks(())
    plt.yticks(())
    plt.title(title)


# Number of samples per component
n_samples = 500

# Generate random sample, two components
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
X = np.r_[
    np.dot(np.random.randn(n_samples, 2), C),
    0.7 * np.random.randn(n_samples, 2) + np.array([-6, 3]),
]

# Fit a Gaussian mixture with EM using five components
gmm = mixture.GaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Gaussian Mixture")

# Fit a Dirichlet process Gaussian mixture using five components
dpgmm = mixture.BayesianGaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    1,
    "Bayesian Gaussian Mixture with a Dirichlet process prior",
)

plt.show()