import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy import stats
sns.set_style("darkgrid")
sns.mpl.rc("figure", figsize=(8, 8))%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}システムをモデル化する場合、多重のパラメータが含まれます。これらの各パラメータは、与えられた確率密度関数で記述することができます。もし新しいパラメータセットの値を生成したいならば、私たちはこれらの分布-周辺と呼ばれます(周辺分布)からサンプルされる必要があります。主にふたつのケースがあります。(i) PDFが独立している (ii)従属性がある。従属性をモデル化する方法の一つが、コピュラを使うことです。
コピュラからサンプリング
二項変数の例を使いましょう。最初に、事前分布を持っており、二つの変数間の従属性をモデル化する方法が解っていると仮定します。
このケースでは、私たちは、グンベルコピュラを使います。そしてそのハイパーパラメータをtheta=2に固定します。私たちはこれを2次元のPDFに可視化します。
from statsmodels.distributions.copula.api import (
CopulaDistribution, GumbelCopula, IndependenceCopula)
copula = GumbelCopula(theta=2)
_ = copula.plot_pdf() # returns a matplotlib figure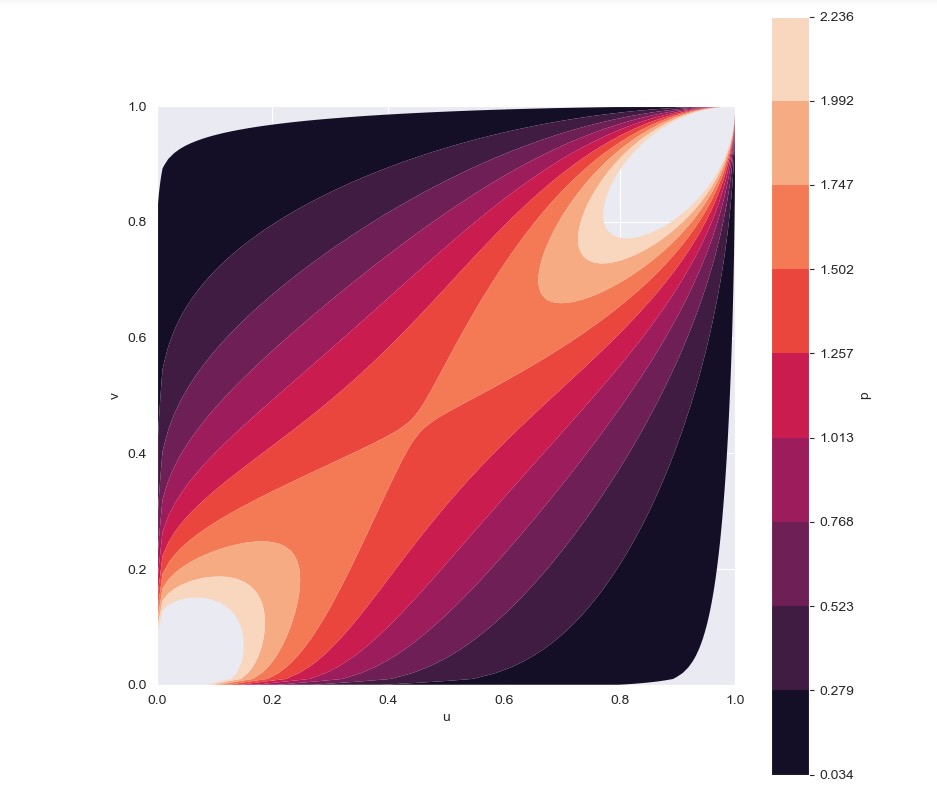
そして、PDFをサンプルすることができます。
sample = copula.rvs(10000)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="hex")
_ = h.set_axis_labels("X1", "X2", fontsize=16)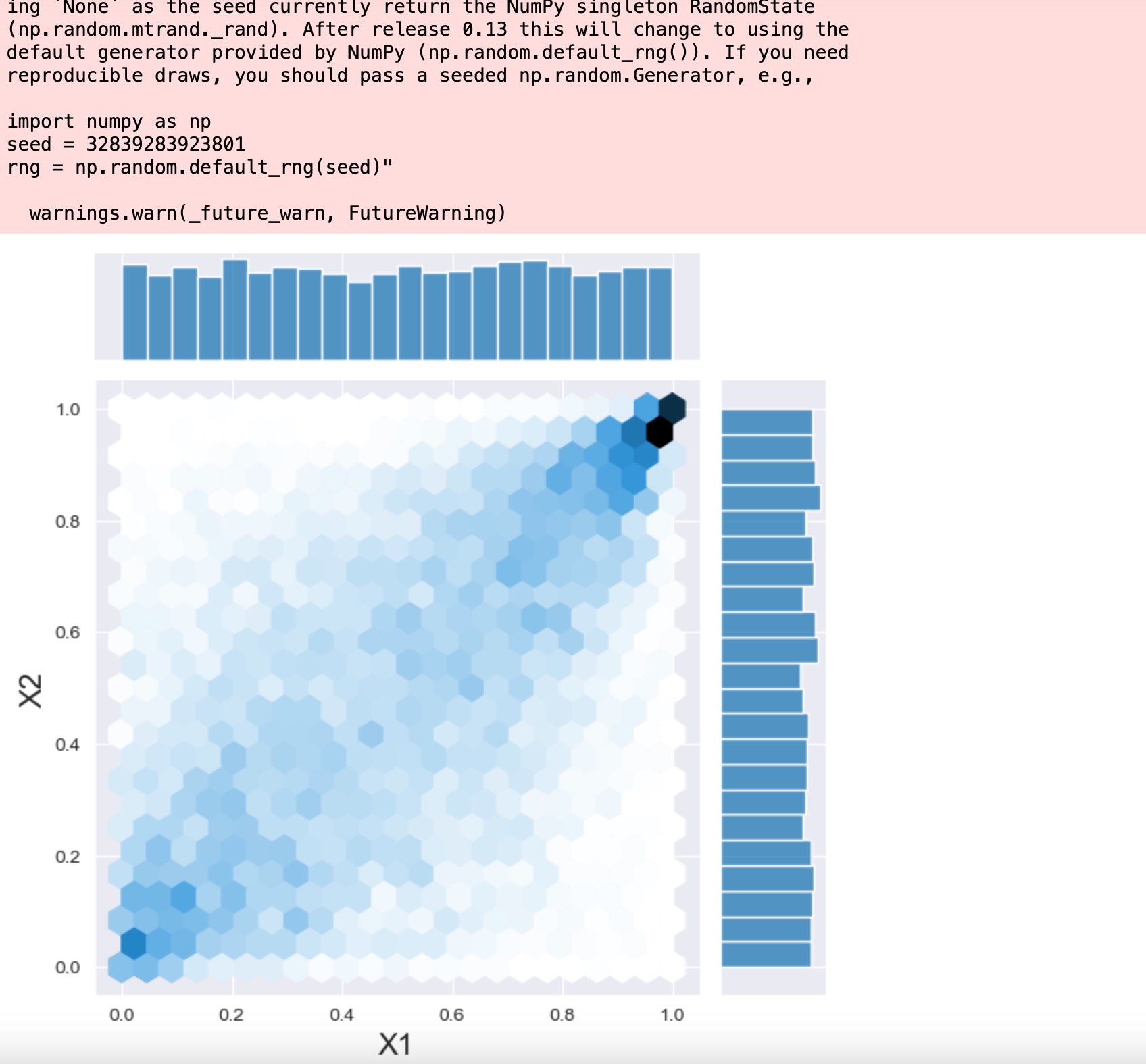
2番目に、二つの変数に戻りましょう。このケースでは、私たちはそれらをガンマと正規分布にすることを考えます。もし、それらが、お互いに独立していれば、私たちは、各PDFから個別にサンプルすることができます。ここで、私たちは同じ操作を実行するために便利なクラスを使います。
再生可能性
seed引数の設定を明確に要求されるコピュラから再生可能なランダム値を生成します。seedは、NumPy Generatorまたは、RandomStateのどちらか一方で生成されることを受け入れます。または、任意の引数は、例えば、整数または整数の系列が、np.random.default_rngへ受け入れられます。この例では、整数を使います。
直接np.random分布に晒される、単独で働くRandomStateは、使われず、np.random.seedの設定は、生成する値に影響を与えません。
marginals = [stats.gamma(2), stats.norm]
joint_dist = CopulaDistribution(copula=IndependenceCopula(), marginals=marginals)
sample = joint_dist.rvs(512, random_state=20210801)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)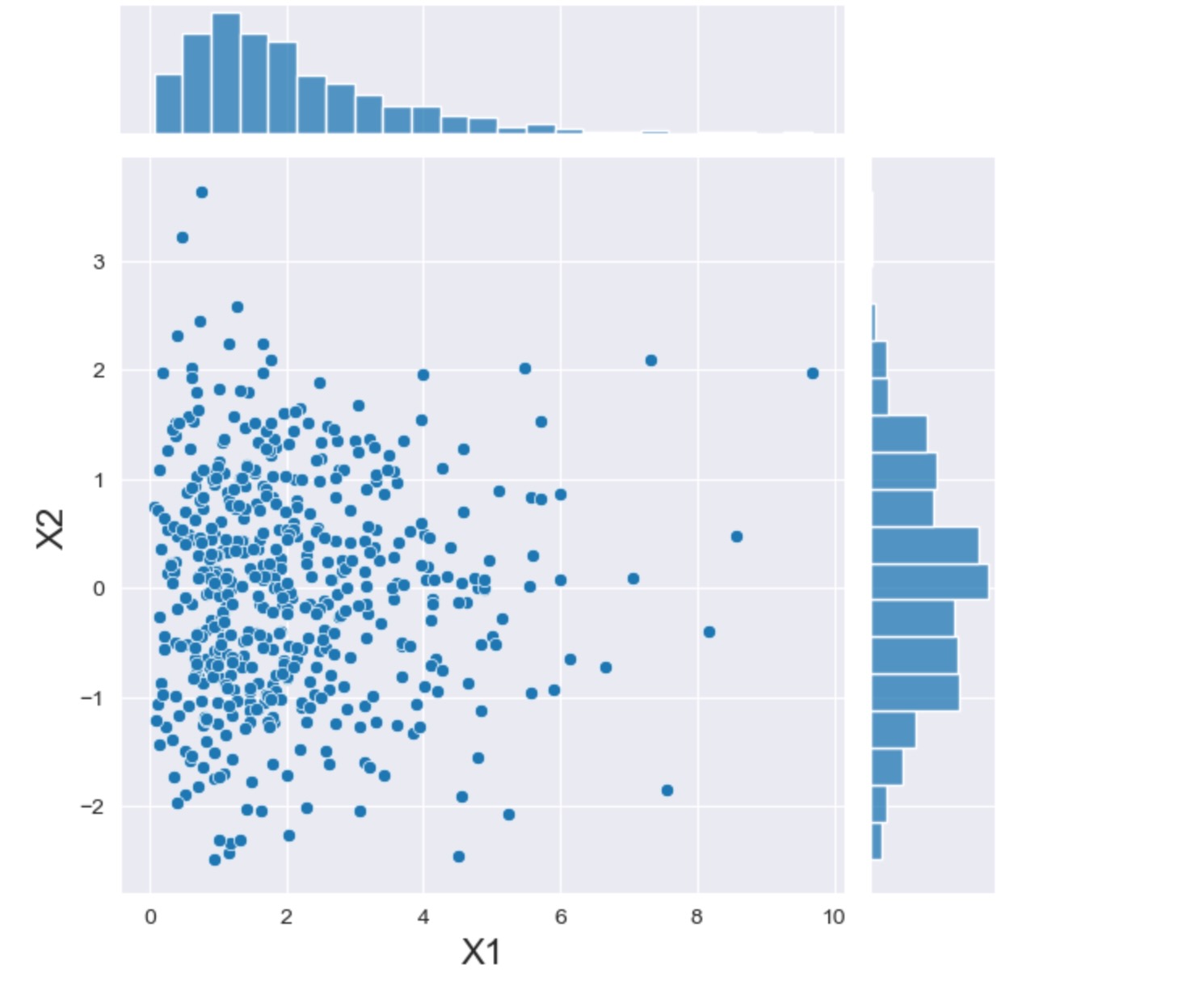
ここで、上記は、コピュラを使った変数間の従属性を説明します。私たちは、同じ便利なクラスの新しいセットの観測をサンプルするためにこのコピュラを使うことができます。
joint_dist = CopulaDistribution(copula, marginals)
# Use an initialized Generator object
rng = np.random.default_rng([2, 0, 2, 1, 0, 8, 0, 1])
sample = joint_dist.rvs(512, random_state=rng)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)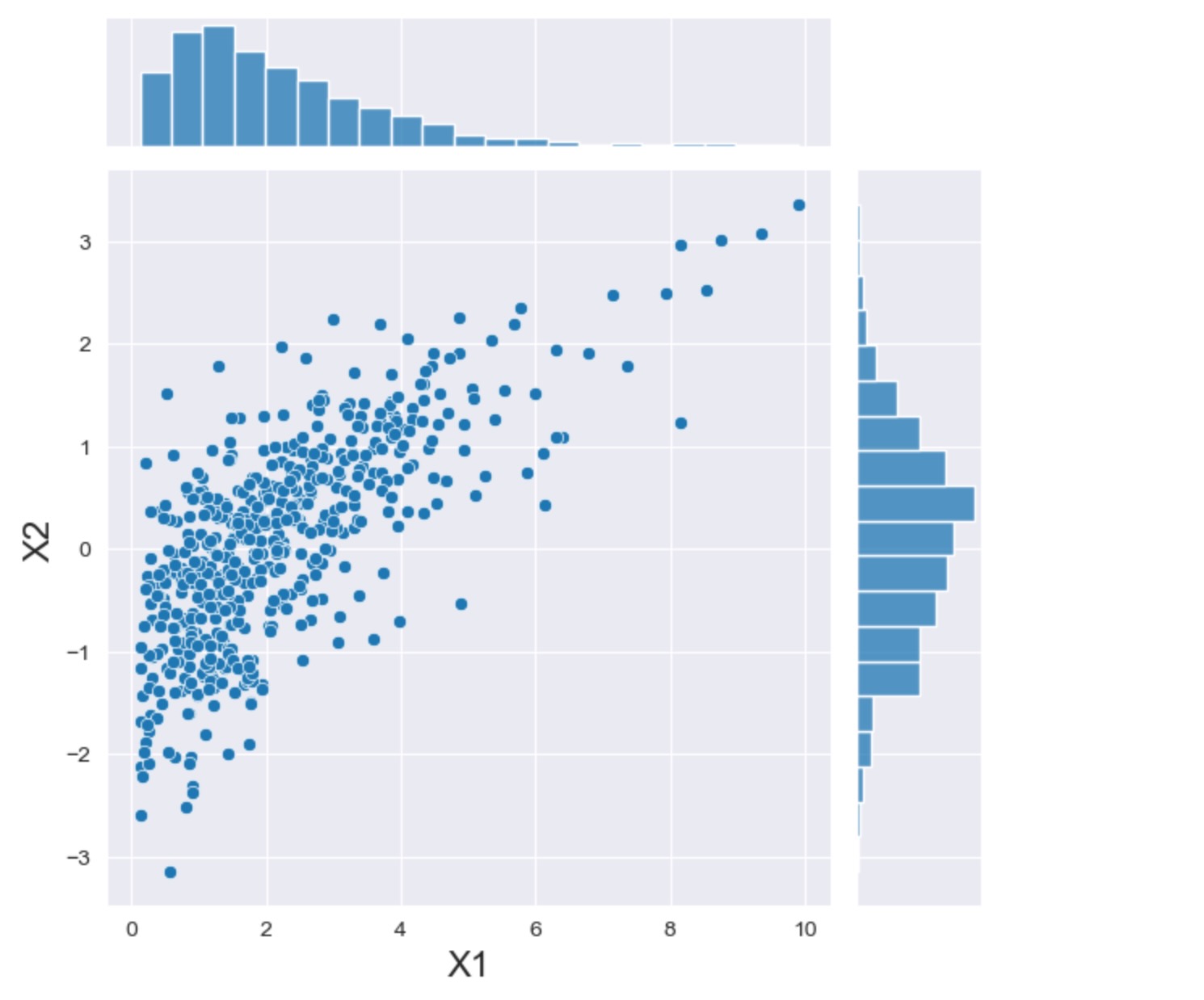
ここで、二点、注意があります。(i)独立したケースでは、周辺は、正確にガンマと正規分布を示しますが、(ii)従属性はふたつの変数間で可視化されます。
コピュラパラメータの推定
ここで、私たちがすでに実験データを持っており、そして、グンベルコピュラを使って説明することができる従属性があることを知っていることを想像してみてください。しかし、私たちは、コピュラにとってのハイパーパラメータの値が何か、私たちは分かっていません。このケースでは、私たちはその値を推定することができます。
私たちは生成したサンプルを使って、私たちがすでに知っているハイパーパラメータの値である、theta=2を取得します。
copula = GumbelCopula()
theta = copula.fit_corr_param(sample)
print(theta)2.049379621506455私たちは、予測したハイパーパラメータが、以前に設定した値と近いことがわかります。