このノートブックは、KimとNelson(1999)に発表された結果の検証を、statsmodelのマルコフ・スィッチングモデルを使った例を提供します。Hamiltonフィルター(1989)、Kim(1994)スムーサーを適用します。
これは、E-view 8からのマルコフ・スイッチング・モデルに対してテストされます。それは、"http://www.eviews.com/EViews8/ev8ecswitch_n.html#MarkovAR"で見つけることができ、Stata14のマルコフ・スイッチング・モデルは" http://www.stata.com/manuals14/tsmswitch.pdf."で参照できます。
%matplotlib inline
from datetime import datetime
from io import BytesIO
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import statsmodels.api as sm
# NBER recessions
from pandas_datareader.data import DataReader
usrec = DataReader(
"USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)GNPのハミルトン・スィッチング・モデル(1989)
これはハミルトンの講義論文で紹介しているマルコフ・スイッチング・モデルの検証です。モデルは4次の自己回帰モデルで過程の平均は二つのレジーム間で切り替わります。それは、次のように書けます。
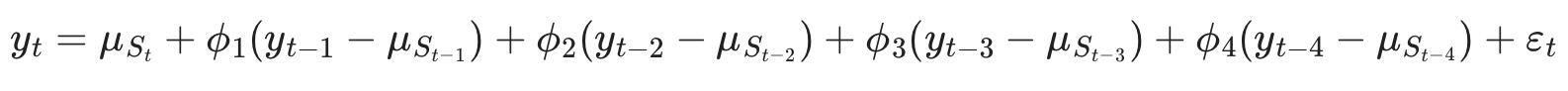
各終端で、レジームが以下の遷移確率行列に従って遷移します。
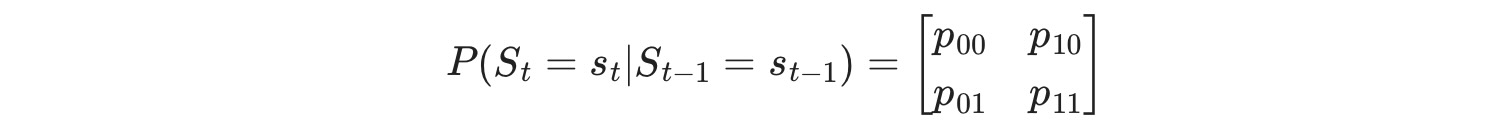
ここでpij は、レジームi からレジームj への遷移確率です。
モデルクラスは、statsmodelの時系列パートのMarkovAutoregressionです。モデルを生成するために、私たちは、レジームの数をk_regimes=2、自己回帰の次元をorder=4に規定しなければなりません。デフォルトのモデルは、スイッチング自己回帰係数を含んでおり、そのためここで、それを避けるために、switching_ar=Falseを規定する必要があります。
生成後に、モデルは最大尤度推定を通してfit します。その状態下で、予測最大化(EM)アルゴリズムのステップ数を使うことで、良い開始パラメータが発見されます。そして、凖ニュートン(BFGS)・アルゴリズムが最大値をすぐに発見するために適用されます。
# Get the RGNP data to replicate Hamilton
dta = pd.read_stata("https://www.stata-press.com/data/r14/rgnp.dta").iloc[1:]
dta.index = pd.DatetimeIndex(dta.date, freq="QS")
dta_hamilton = dta.rgnp
# Plot the data
dta_hamilton.plot(title="Growth rate of Real GNP", figsize=(12, 3))
# Fit the model
mod_hamilton = sm.tsa.MarkovAutoregression(
dta_hamilton, k_regimes=2, order=4, switching_ar=False
)
res_hamilton = mod_hamilton.fit()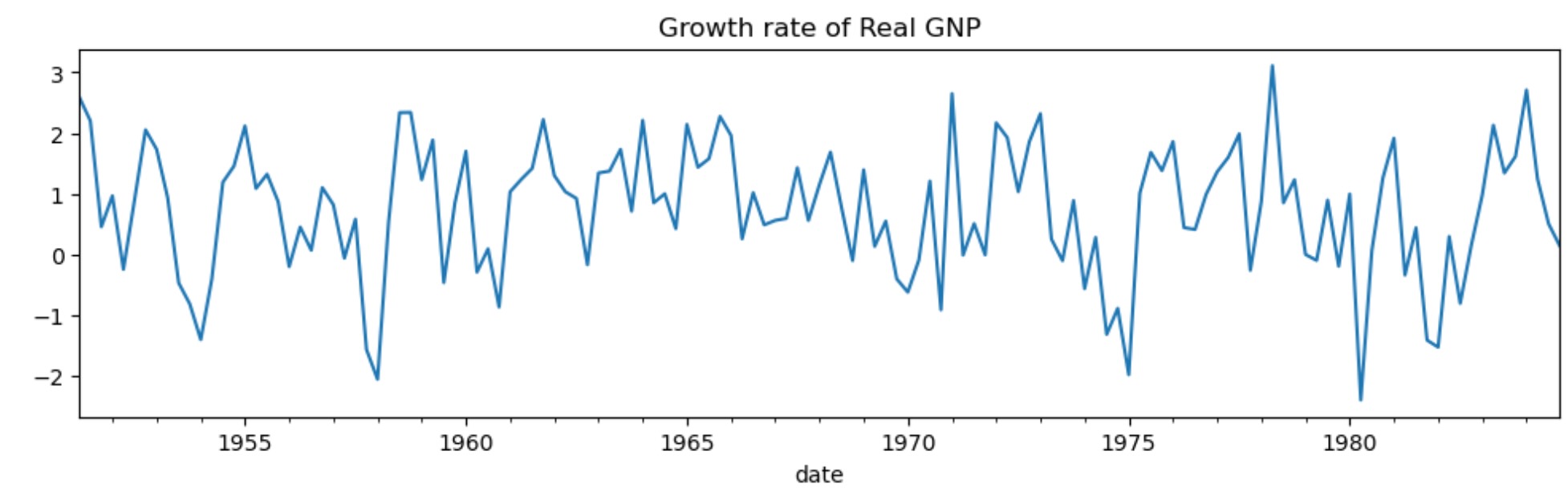
res_hamilton.summary()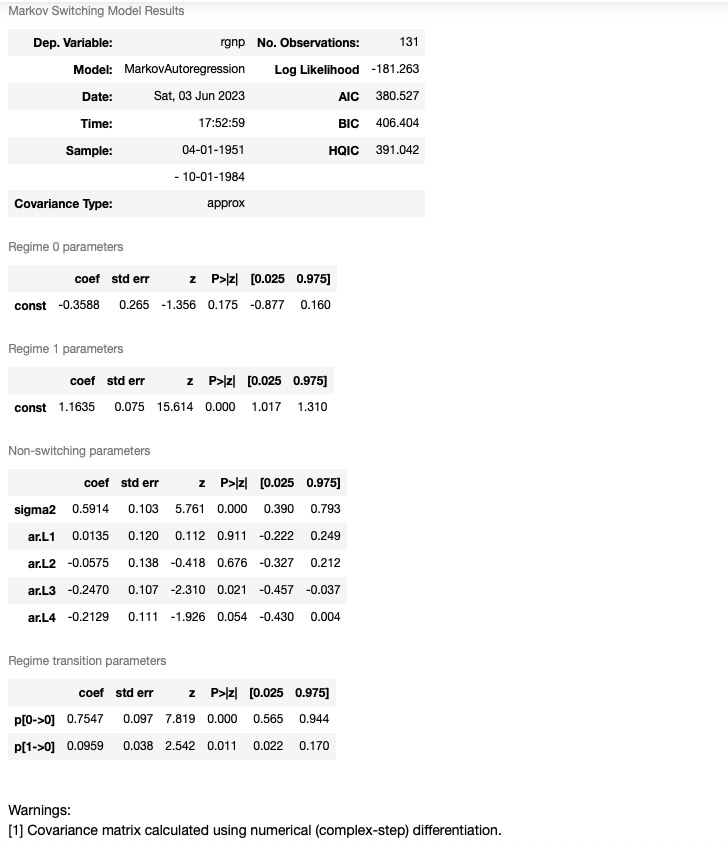
私たちは、フィルターとスムーサーによるリセッションの確率を図示します。フィルターは、時間tを含むtまでのデータを元にした確率の推定を参照します。(しかし、時間t+1,...Tは含みません)スムーサーは、サンプルのすべてのデータを使って、時間tの確率の推定を参照します。
参照のため、編みかけの終端はNBERのリセッションを表しています。
fig, axes = plt.subplots(2, figsize=(7, 7))
ax = axes[0]
ax.plot(res_hamilton.filtered_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Filtered probability of recession")
ax = axes[1]
ax.plot(res_hamilton.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Smoothed probability of recession")
fig.tight_layout()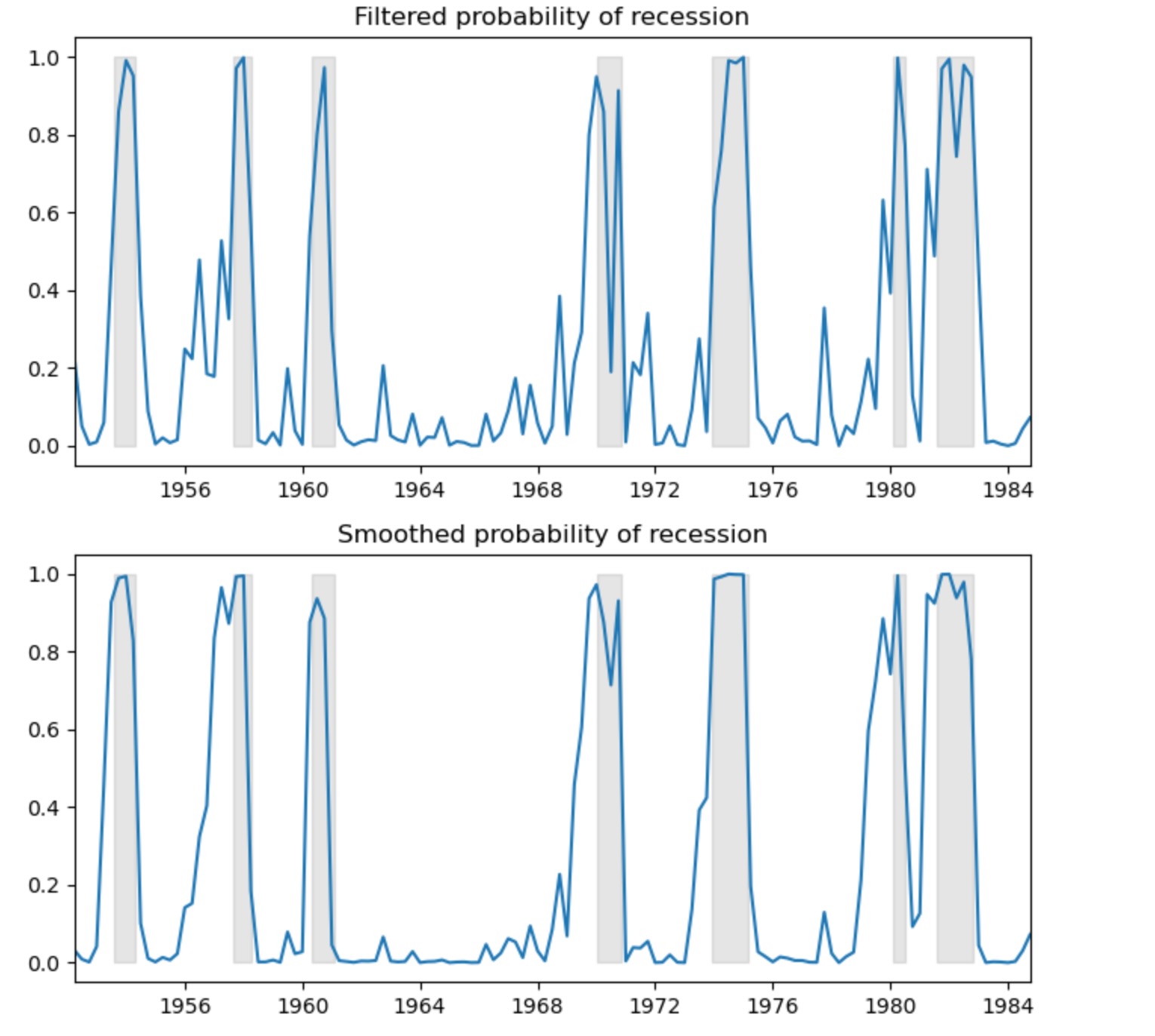
推定遷移行列から、リセッションと拡張機の予測期間を計算することができます。
print(res_hamilton.expected_durations)[ 4.07604744 10.4258939 ]このケースでは、リセッションがおよそ1年(4Q)と拡張期が2年半と予測されます。
Kim,NelsonとStartz(1998) 3状態変量スイッチング
このモデルは、レジーム不均一(変量のスイッチング)、平均効果のない推定を示します。データセットは、ここから(http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn.)取得できます。
モデルの多項式は、
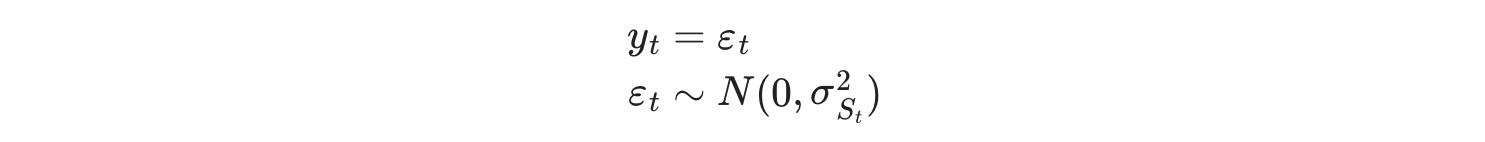
自己回帰成分がないので、このモデルは、MarkovRegressionクラスを用いて適合できます。平均の効果がないため、trend='n' を規定します。変量のスイッチングに三つのレジームがあると仮定しています。そのため私たちは、k_regimes=3 と switching_variance=True (デフォルトで、変量は三つのレジーム間で同じであることを仮定しています)
# Get the dataset
ew_excs = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn").content
raw = pd.read_table(BytesIO(ew_excs), header=None, skipfooter=1, engine="python")
raw.index = pd.date_range("1926-01-01", "1995-12-01", freq="MS")
dta_kns = raw.loc[:"1986"] - raw.loc[:"1986"].mean()
# Plot the dataset
dta_kns[0].plot(title="Excess returns", figsize=(12, 3))
# Fit the model
mod_kns = sm.tsa.MarkovRegression(
dta_kns, k_regimes=3, trend="n", switching_variance=True
)
res_kns = mod_kns.fit()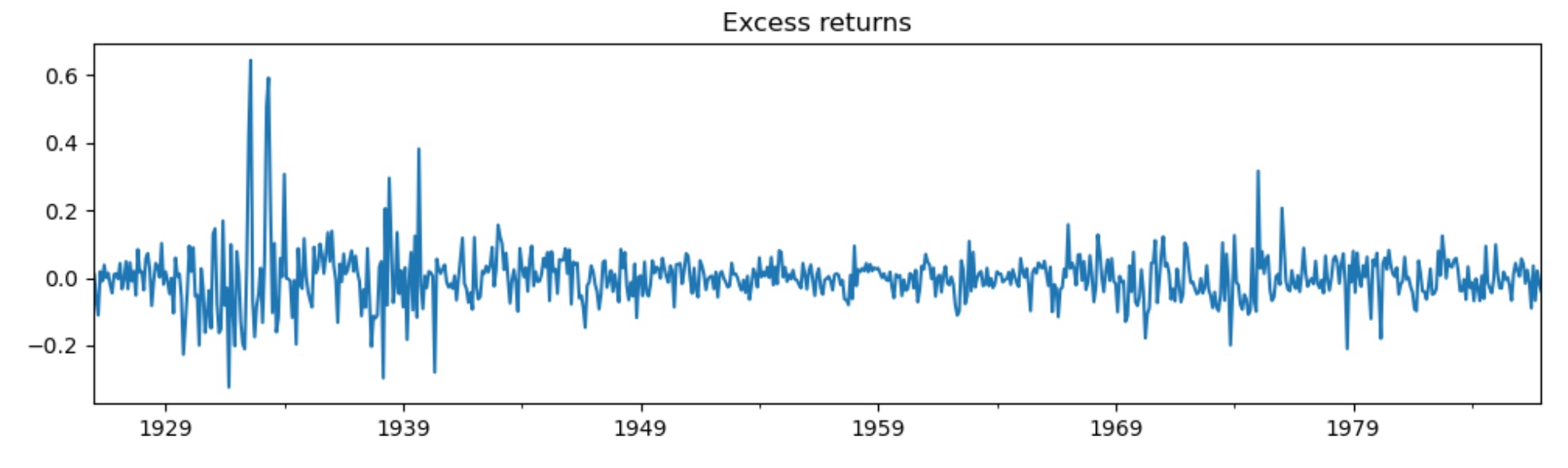
res_kns.summary()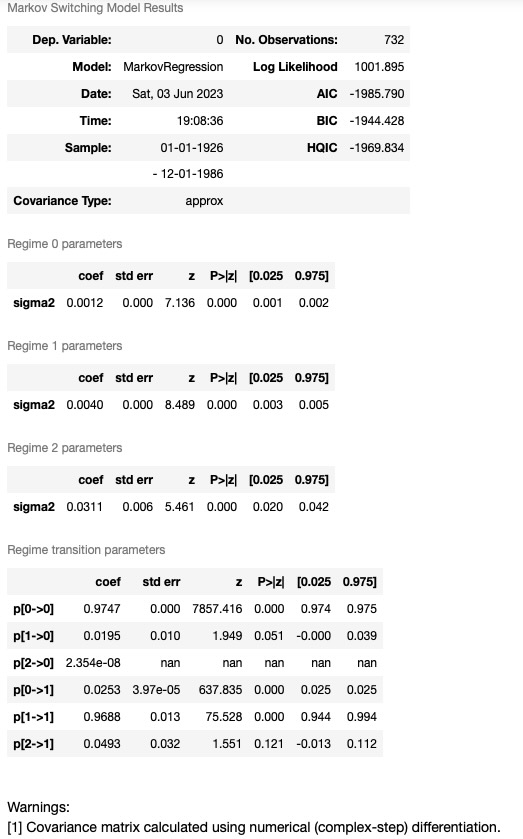
下に私たちは、各レジームにある確率を図示しています。ほんの僅かな終端で高い変動のレジームが起こりそうです。
fig, axes = plt.subplots(3, figsize=(10, 7))
ax = axes[0]
ax.plot(res_kns.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-variance regime for stock returns")
ax = axes[1]
ax.plot(res_kns.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-variance regime for stock returns")
ax = axes[2]
ax.plot(res_kns.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-variance regime for stock returns")
fig.tight_layout()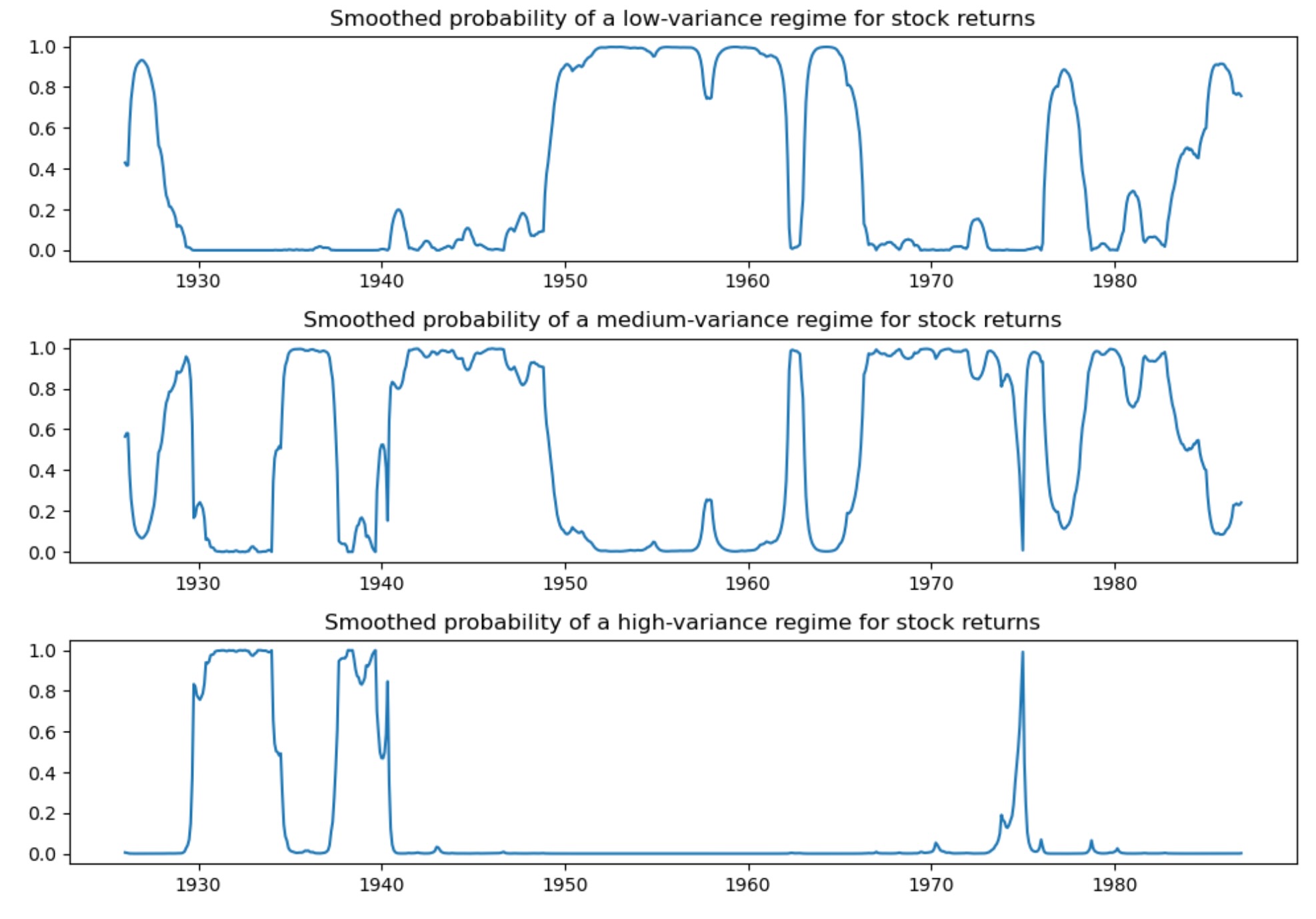
Filardo(1994)の 時変遷移確率
このモデルは、時変遷移確率の推定を示します。データセットはここから(http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn.)取得できます。
上のモデルでは、私たちは遷移確率は時間に対して一定であると仮定しました。ここでは私たちは、経済の状態で変化する確率を許容します。そうでなければ、モデルは、Hamilton(1989)のマルコフ自己回帰と同じです。
各終端でレジームは、以下の時変遷移確率行列に従って遷移します。
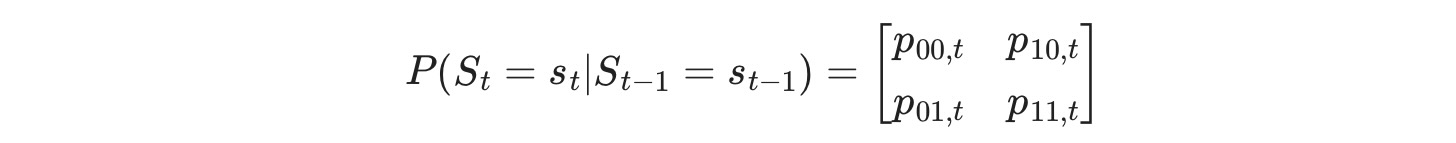
ここでpijは、時間tでのレジームi からレジームj への遷移確率です。それは次に定義されます。
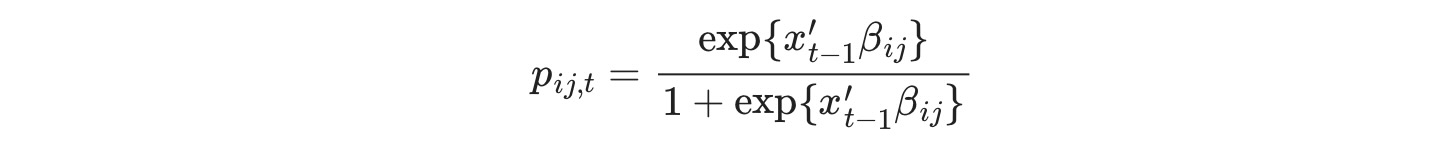
最大尤度の部分として遷移確率を推定する代わりに、回帰係数βij を推定します。これらの係数は遷移確率を事前決定のベクターまたは外因性の回帰xt-1 に関連付けます。
# Get the dataset
filardo = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn").content
dta_filardo = pd.read_table(
BytesIO(filardo), sep=" +", header=None, skipfooter=1, engine="python"
)
dta_filardo.columns = ["month", "ip", "leading"]
dta_filardo.index = pd.date_range("1948-01-01", "1991-04-01", freq="MS")
dta_filardo["dlip"] = np.log(dta_filardo["ip"]).diff() * 100
# Deflated pre-1960 observations by ratio of std. devs.
# See hmt_tvp.opt or Filardo (1994) p. 302
std_ratio = (
dta_filardo["dlip"]["1960-01-01":].std() / dta_filardo["dlip"][:"1959-12-01"].std()
)
dta_filardo["dlip"][:"1959-12-01"] = dta_filardo["dlip"][:"1959-12-01"] * std_ratio
dta_filardo["dlleading"] = np.log(dta_filardo["leading"]).diff() * 100
dta_filardo["dmdlleading"] = dta_filardo["dlleading"] - dta_filardo["dlleading"].mean()
# Plot the data
dta_filardo["dlip"].plot(
title="Standardized growth rate of industrial production", figsize=(13, 3)
)
plt.figure()
dta_filardo["dmdlleading"].plot(title="Leading indicator", figsize=(13, 3))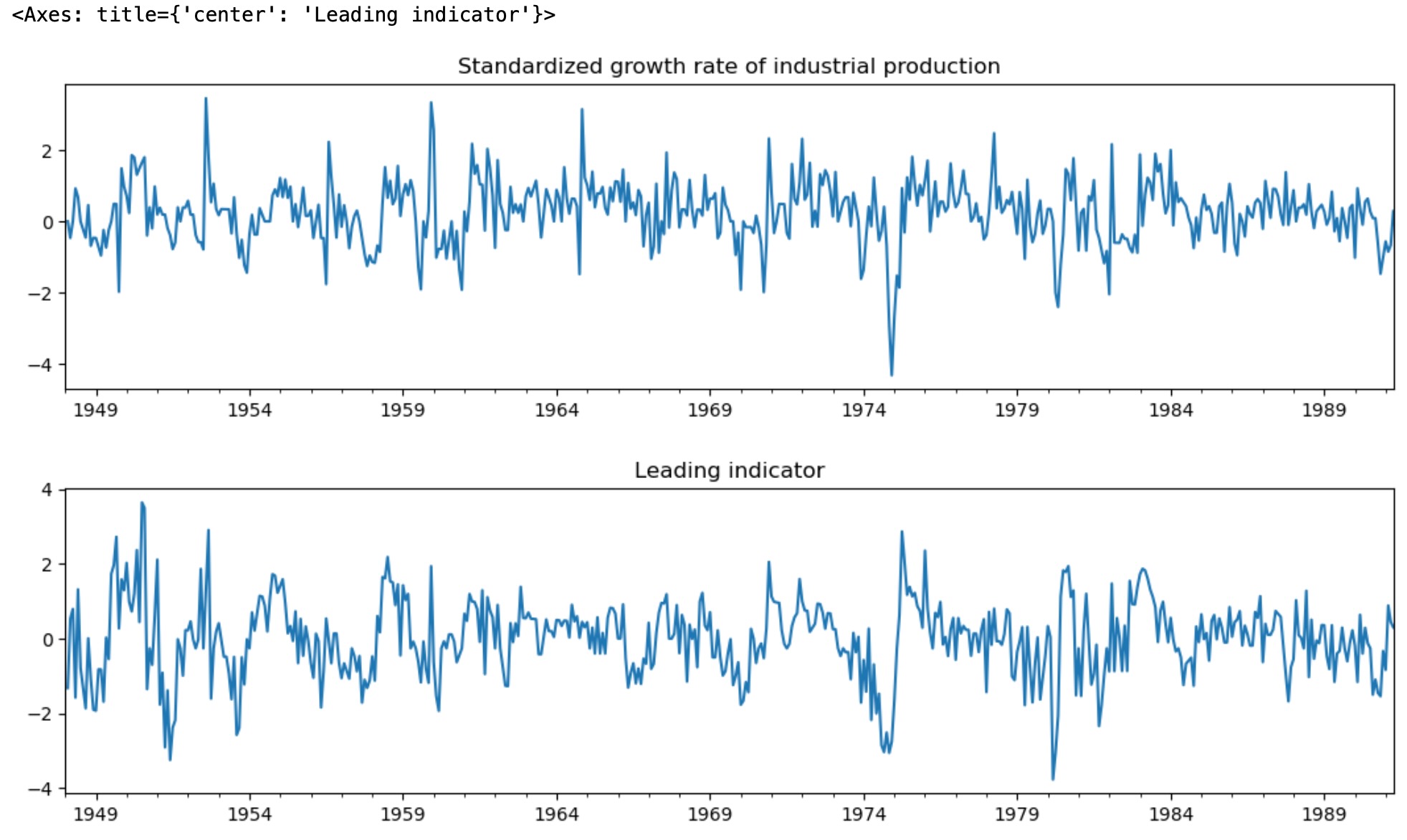
時変遷移確率はexog_tvtpパラメータによって規定されます。
ここで、私たちは、モデル適合の他の特徴ーMLE開始パラメータのランダムサーチの使用を示します。なぜなら、マルコフスイッチングモデルはしばしば、尤度関数の多くの局所的最大値で特徴づけられます。初期最適化ステップを実行することは最適なパラメータを見つけることに役立ちます。
以下は、開始パラメータベクターから20のランダムな影響が検証され、最適な一つが実際の開始パラメータとして使われることを規定します。サーチのランダムな性質のため、私たちは結果の検証を許すため、あらかじめ乱数生成の種を蒔きます。
mod_filardo = sm.tsa.MarkovAutoregression(
dta_filardo.iloc[2:]["dlip"],
k_regimes=2,
order=4,
switching_ar=False,
exog_tvtp=sm.add_constant(dta_filardo.iloc[1:-1]["dmdlleading"]),
)
np.random.seed(12345)
res_filardo = mod_filardo.fit(search_reps=20)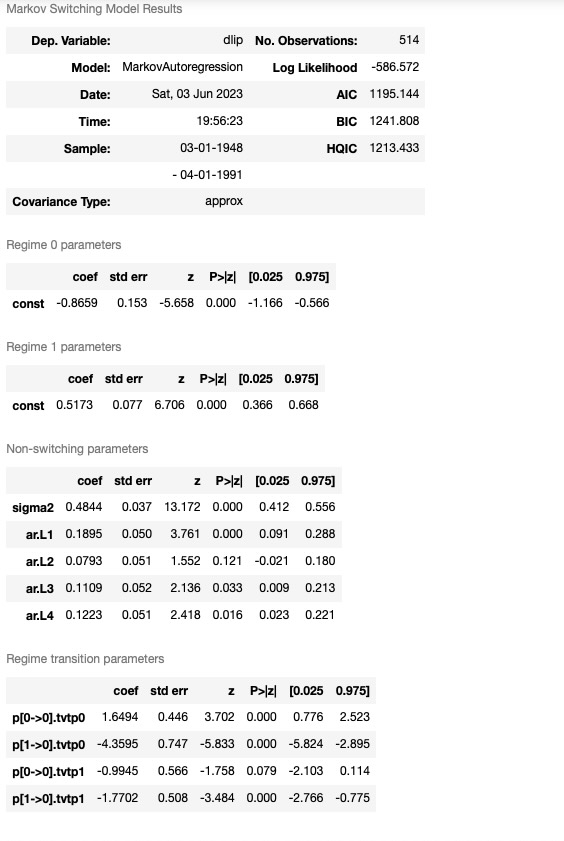
下は、低い生産状態の経済運営のスムース化した確率を図示しています。そして再度、比較のためにNBERリセッションの図を含みます。
fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(res_filardo.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="gray", alpha=0.2)
ax.set_xlim(dta_filardo.index[6], dta_filardo.index[-1])
ax.set(title="Smoothed probability of a low-production state")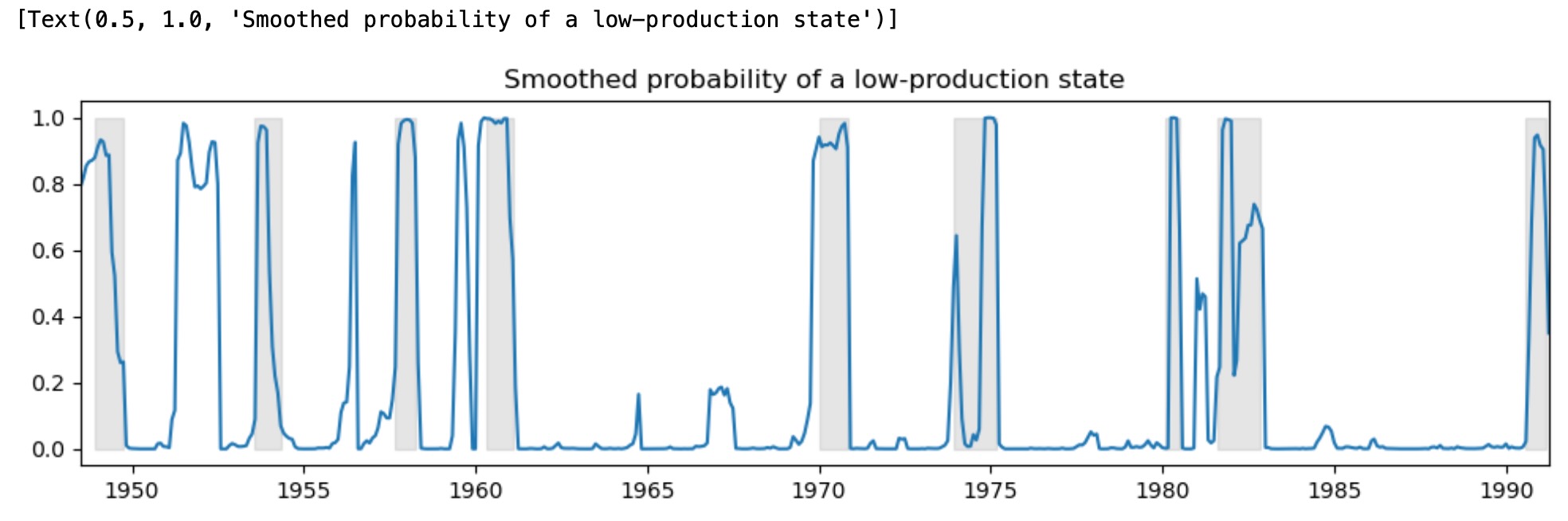
時変遷移確率を使うことで、私たちは、どのように低生産状態の予測期間が時間を超えて変化するか見ることができます。
res_filardo.expected_durations[0].plot(
title="Expected duration of a low-production state", figsize=(12, 3)
)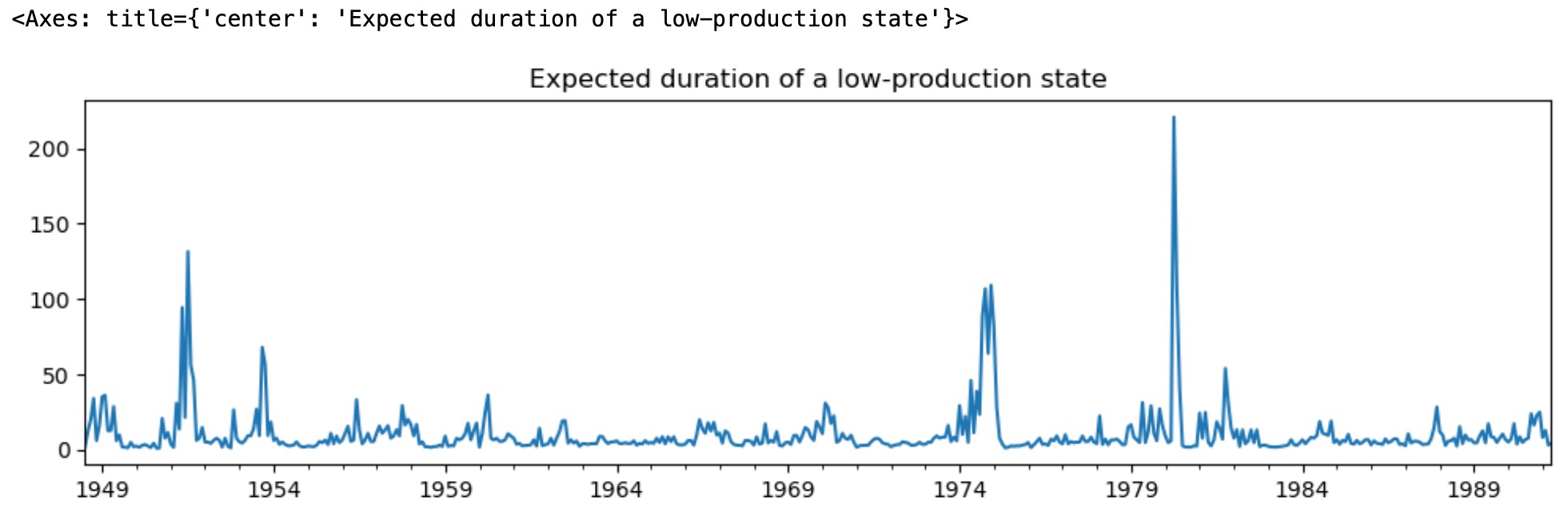
リセッションの期間、低生産状態の予測期間は、拡張期間よりもっと大きくなります。