このノートブックでは、私たちは、世界銀行からデータを入手して、192か国の出生率の時系列データを分析するために、主成分分析を使います。主なゴールは、国と国の間で異なる時間経過の出生率のトレンドがどれくらいか理解することです。これは、データが時系列のために、少々、不規則なPCAの解説です。機能的PCAのような方法は、この設定のために開発されました。しかし、出生率のデータはとてもスムースなので、このケースで標準的なPCAを使うことに、実際に不便な点はありません。
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.multivariate.pca import PCA
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)データは、世界現行のサイトにから取得することができます。しかし、ここで、私たちは少しデータを修正したバージョンを使います。
data = sm.datasets.fertility.load_pandas().data
data.head()| Country Name | Country Code | Indicator Name | Indicator Code | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | ... | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Aruba | ABW | Fertility rate, total (births per woman) | SP.DYN.TFRT.IN | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | ... | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 | NaN | NaN |
| 1 | Andorra | AND | Fertility rate, total (births per woman) | SP.DYN.TFRT.IN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | 1.240 | 1.180 | 1.250 | 1.190 | 1.220 | NaN | NaN | NaN |
| 2 | Afghanistan | AFG | Fertility rate, total (births per woman) | SP.DYN.TFRT.IN | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 | NaN | NaN |
| 3 | Angola | AGO | Fertility rate, total (births per woman) | SP.DYN.TFRT.IN | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | ... | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 | NaN | NaN |
| 4 | Albania | ALB | Fertility rate, total (births per woman) | SP.DYN.TFRT.IN | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | ... | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 | NaN | NaN |
5 rows × 58 columns
ここで、データフレームを構築します。それは、出生率の数値データだけを含んでおり、国名にインデックスを設定します。
columns = list(map(str, range(1960, 2012)))
data.set_index("Country Name", inplace=True)
dta = data[columns]
dta = dta.dropna()
dta.head()| 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | ... | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country Name | |||||||||||||||||||||
| Aruba | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | 3.625 | 3.417 | 3.226 | 3.054 | ... | 1.825 | 1.805 | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 |
| Afghanistan | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.484 | 7.321 | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 |
| Angola | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | 7.422 | 7.403 | 7.375 | 7.339 | ... | 6.778 | 6.743 | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 |
| Albania | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | 5.483 | 5.376 | 5.268 | 5.160 | ... | 2.195 | 2.097 | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 |
| United Arab Emirates | 6.928 | 6.910 | 6.893 | 6.877 | 6.861 | 6.841 | 6.816 | 6.783 | 6.738 | 6.679 | ... | 2.428 | 2.329 | 2.236 | 2.149 | 2.071 | 2.004 | 1.948 | 1.903 | 1.868 | 1.841 |
5 rows × 52 columns
対角の行列を分析するためにPCAを使うふたつの方法があります。私たちは、縦列をオブジェクト、横列を変数、逆もまた同様に、整えることができます。ここで私たちは、出生率の尺度を変数として整え、国の尺度をオブジェクトとして使います。このようにゴールは、年間の出生率の値を、異なる国の時間を超えた多くの種類を取り込んだ少数の出生率"プロファイル"または"基礎機能"に減少させることです。
平均のトレンドは、PCAから除外されますが、それを観測することは役に立ちます。出生率は、このデータでカバーする時間経過に応じてしっかりと減少していくことを示しています。平均値は、分析ユニットとして、人口の大きさを無視した国を使って計算していることに注意してください。これもまた、以下で導出される主成分分析の真実です。もっと洗練された分析は、例えば1980年の人口によって、国を重みづけするかもしれません。
ax = dta.mean().plot(grid=False)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility rate", size=17)
ax.set_xlim(0, 51)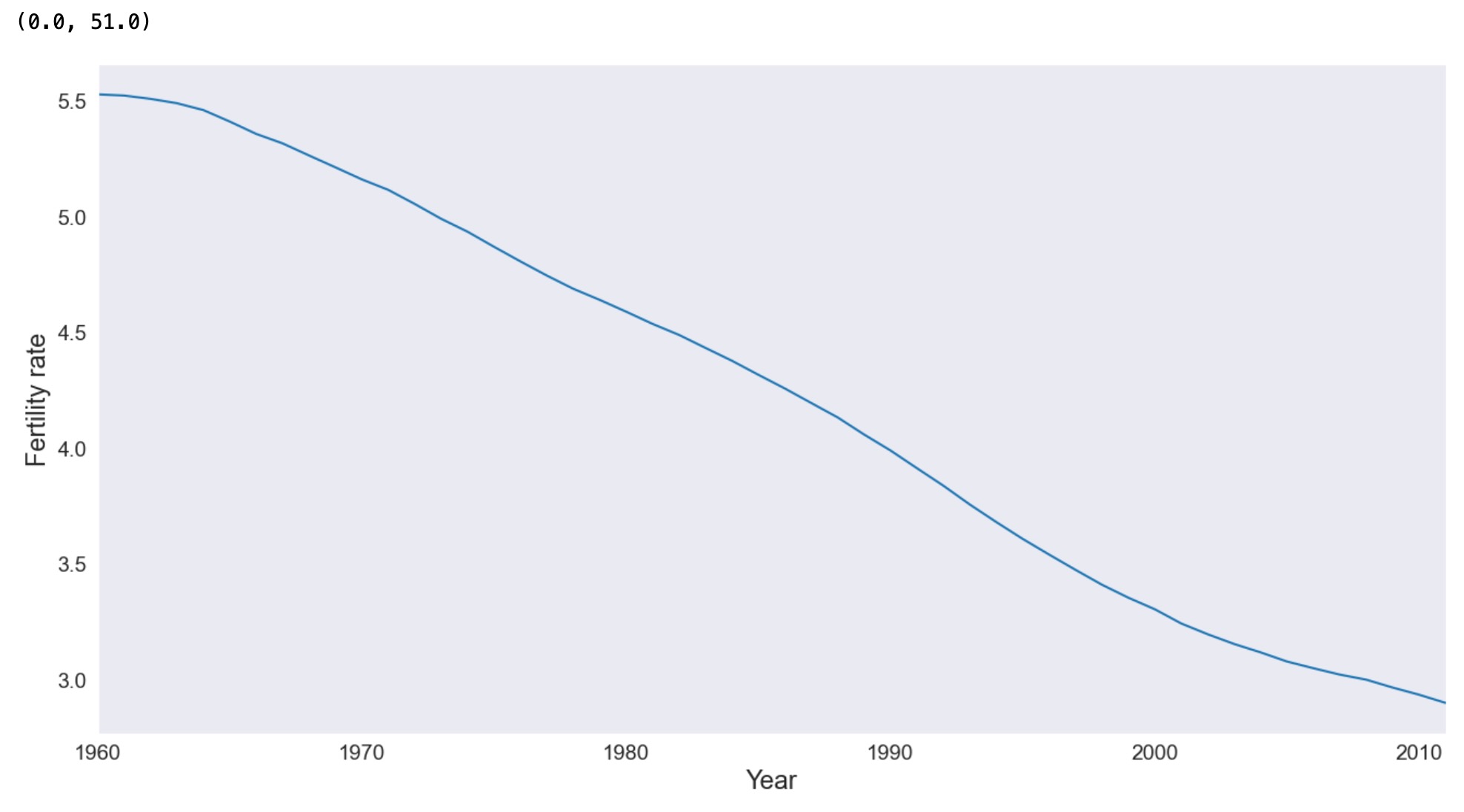
次に私たちは、PCAを実行します。
pca_model = PCA(dta.T, standardize=False, demean=True)固有値を基礎にして、私たちは、2番目と3番目の主成分を取り込んだ、おそらく少量の有意義な(意味のある)変異とともに、最初の強い影響のある主成分を見ます。
fig = pca_model.plot_scree(log_scale=False)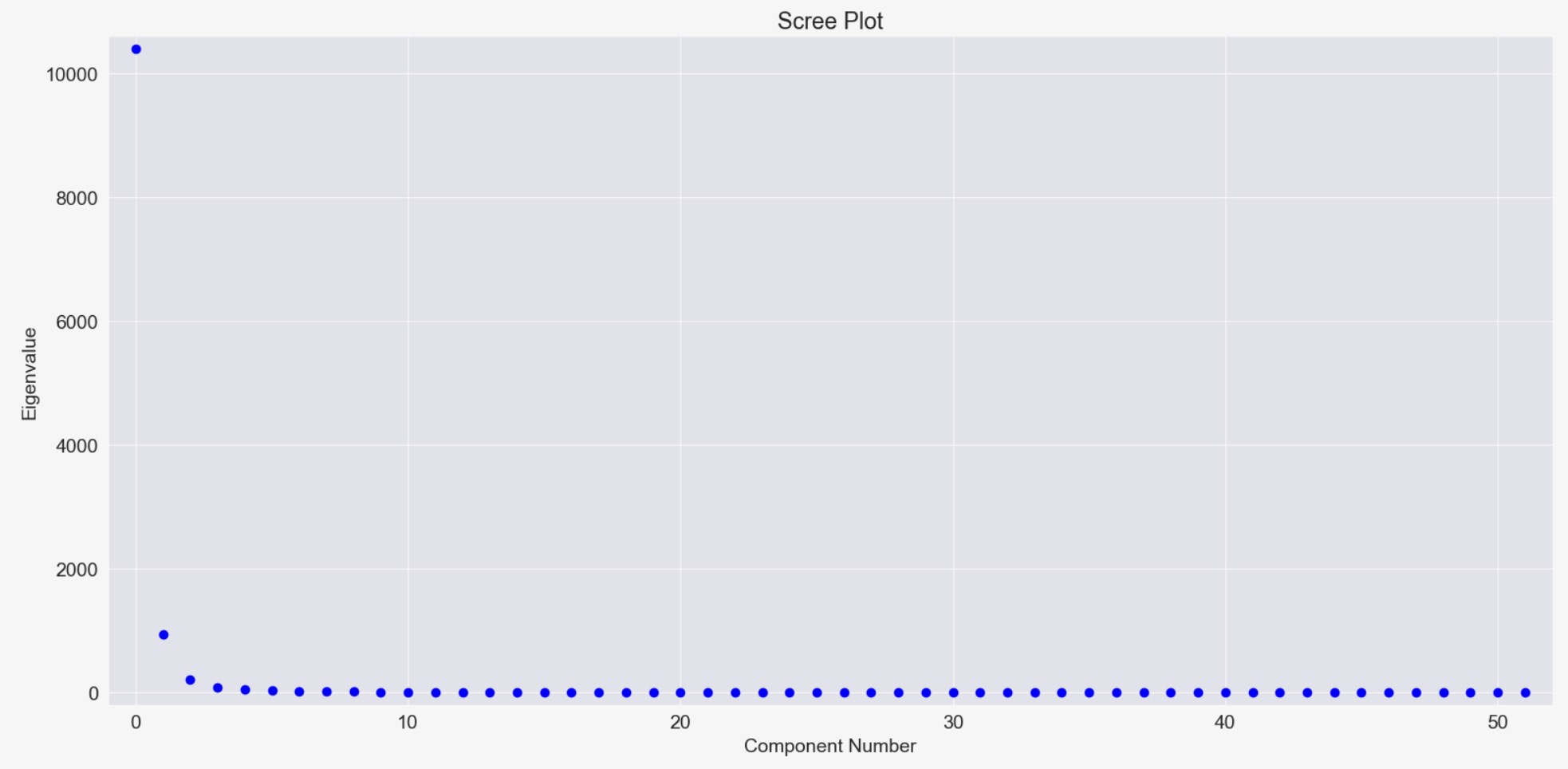
次に、私たちは、主成分因子を図示します。強い影響のある因子は、一本調子で増加します。最初の因子が正のスコアの国々は、上に示す平均と比較してより速く増加(またはより遅く減少)します。最初の因子が負のスコアの国々は、平均よりもっと速く減少します。2番目の因子は、1985年の周辺でせいのピークを持つU字型をしています。2番目の因子が大きな正の値を持つ国々は、最初から終端までのデータの範囲の平均出生率より低くなります。しかし、中間の範囲の平均出生率より高くなります。
fig, ax = plt.subplots(figsize=(8, 4))
lines = ax.plot(pca_model.factors.iloc[:, :3], lw=4, alpha=0.6)
ax.set_xticklabels(dta.columns.values[::10])
ax.set_xlim(0, 51)
ax.set_xlabel("Year", size=17)
fig.subplots_adjust(0.1, 0.1, 0.85, 0.9)
legend = fig.legend(lines, ["PC 1", "PC 2", "PC 3"], loc="center right")
legend.draw_frame(False)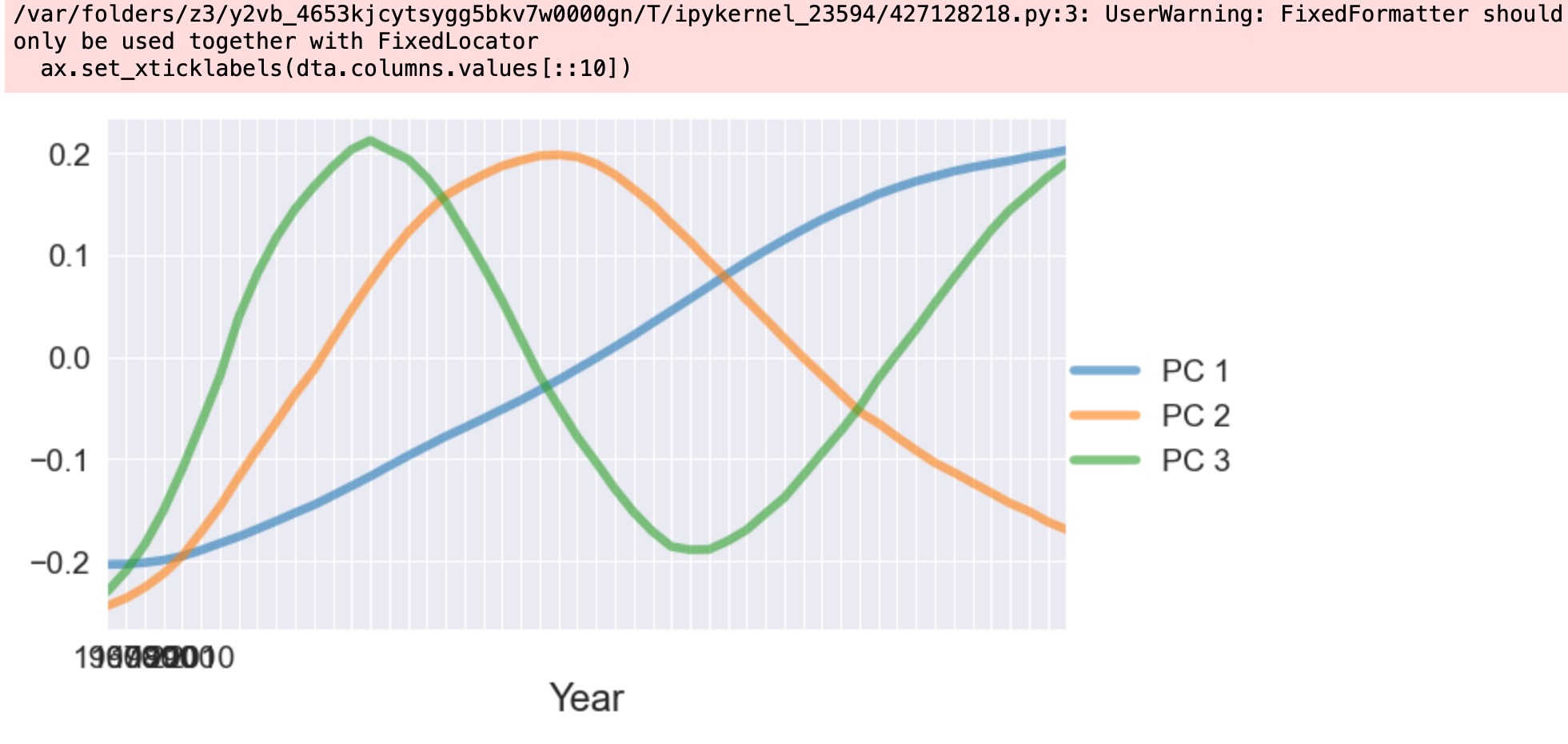
何が起きているかよりよく理解するために、同様の主成分スコアのくのセットのために出生率の足跡を、私たちは図示 します。下の便利な関数は、そうした図を提供します。
idx = pca_model.loadings.iloc[:, 0].argsort()最初に、主成分1の最も大きいスコアを持つ五つの国を図示します。これらの国は、全体の平均より高い出生率で増加します。
def make_plot(labels):
fig, ax = plt.subplots(figsize=(9, 5))
ax = dta.loc[labels].T.plot(legend=False, grid=False, ax=ax)
dta.mean().plot(ax=ax, grid=False, label="Mean")
ax.set_xlim(0, 51)
fig.subplots_adjust(0.1, 0.1, 0.75, 0.9)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility", size=17)
legend = ax.legend(
*ax.get_legend_handles_labels(), loc="center left", bbox_to_anchor=(1, 0.5)
)
legend.draw_frame(False)labels = dta.index[idx[-5:]]
make_plot(labels)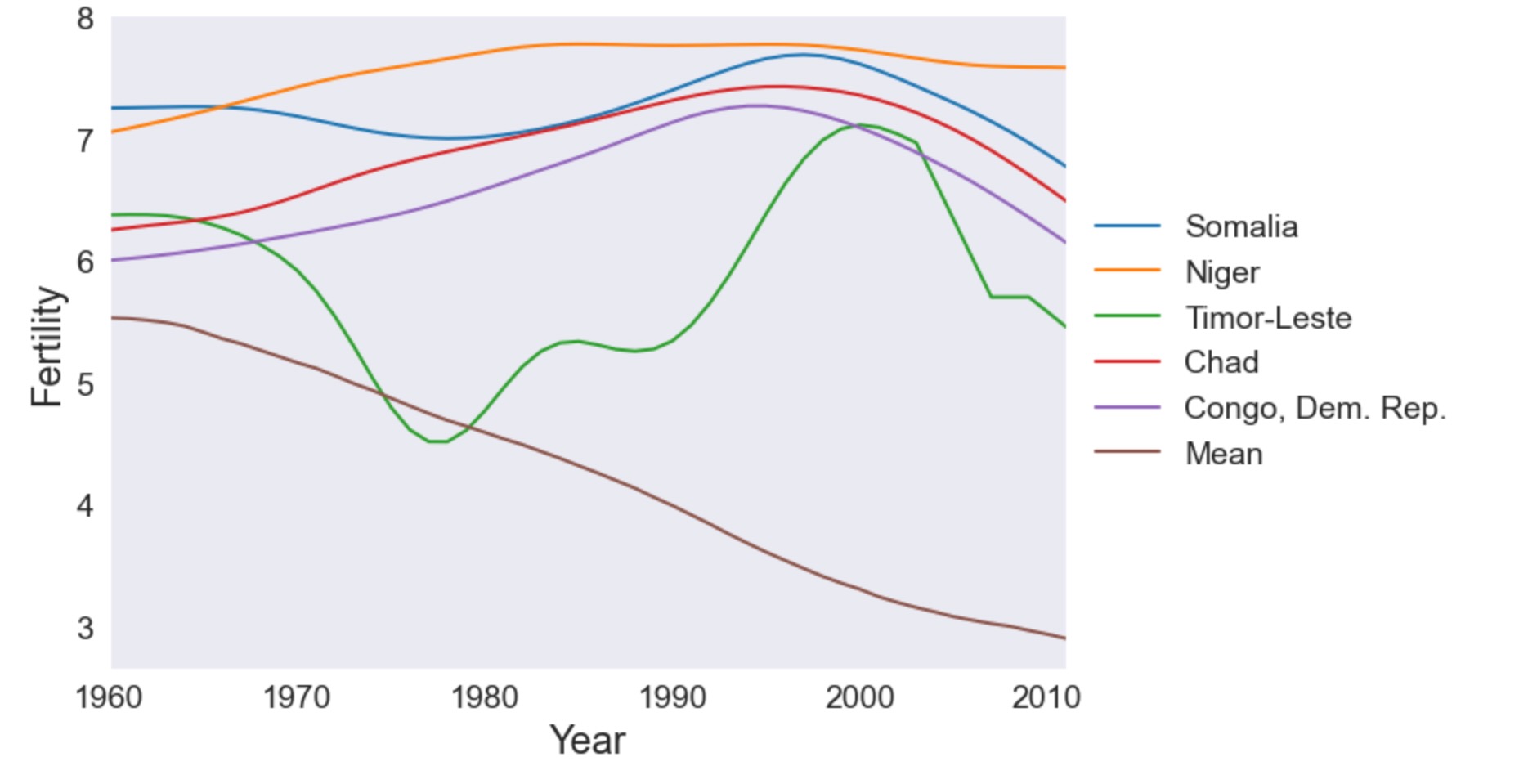
ここは、因子2の最も大きいスコアを持つ五つの国です。残りの多くの世界よりも遅く、1980年の周辺で出生率がピークに達する国です。その後急速に出生率が減少します。
idx = pca_model.loadings.iloc[:, 1].argsort()
make_plot(dta.index[idx[-5:]])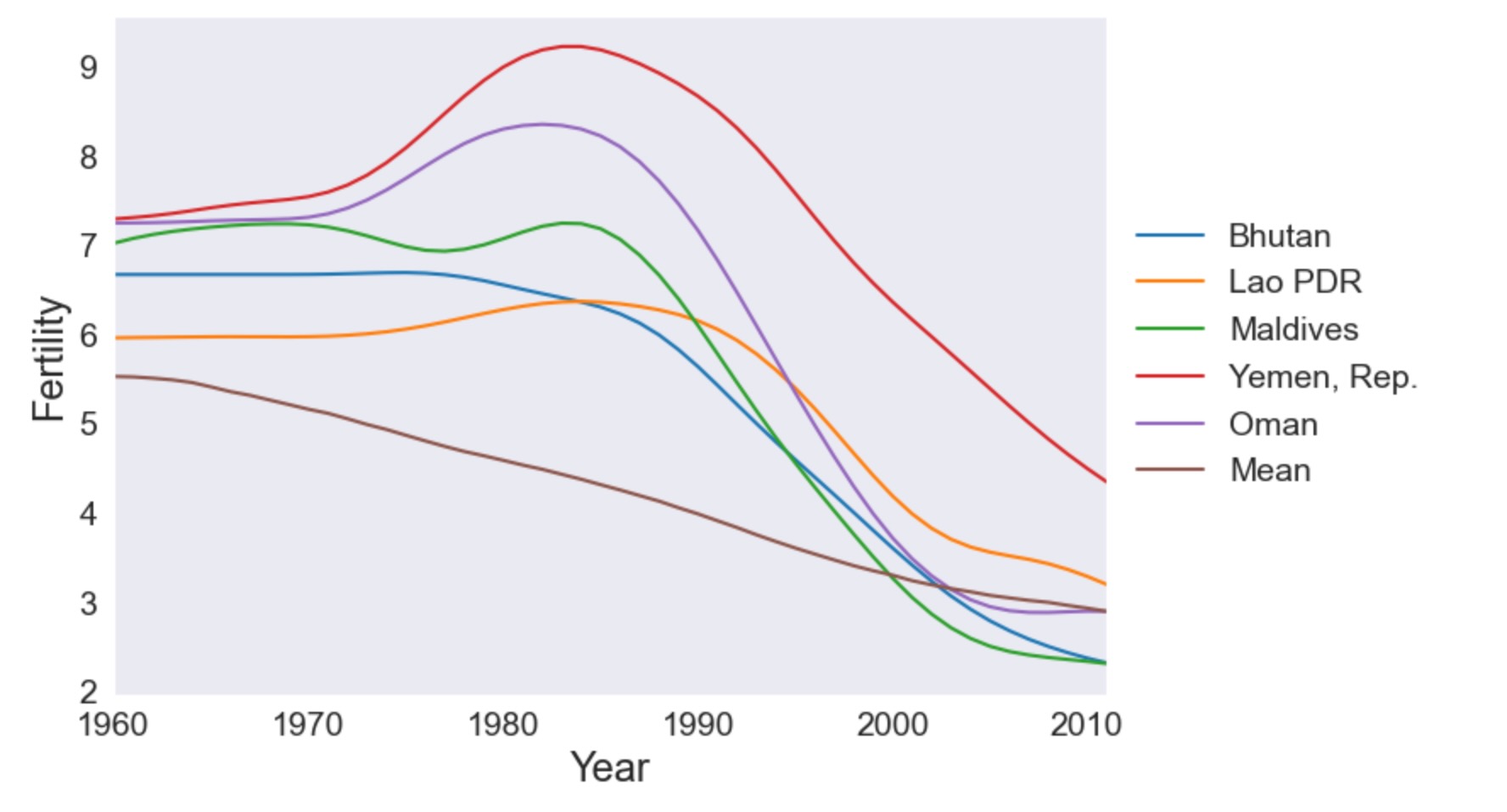
最後に、因子2のスコアが最も大きな負を持つ国です。これらは、出生率が1960年代と1970年代の間で全体の平均よりもっと速く減少します。その後、平坦になります。
make_plot(dta.index[idx[:5]])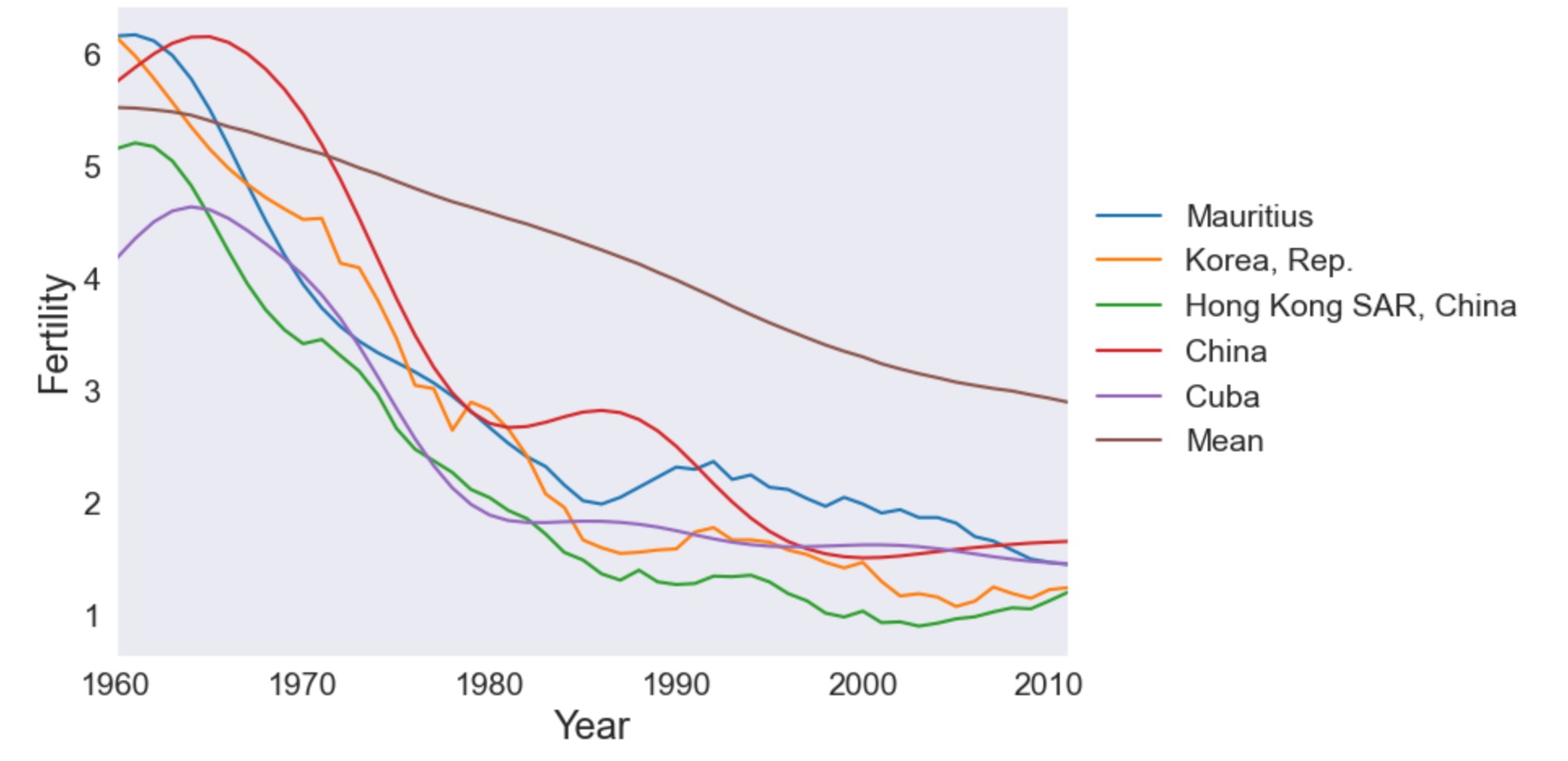
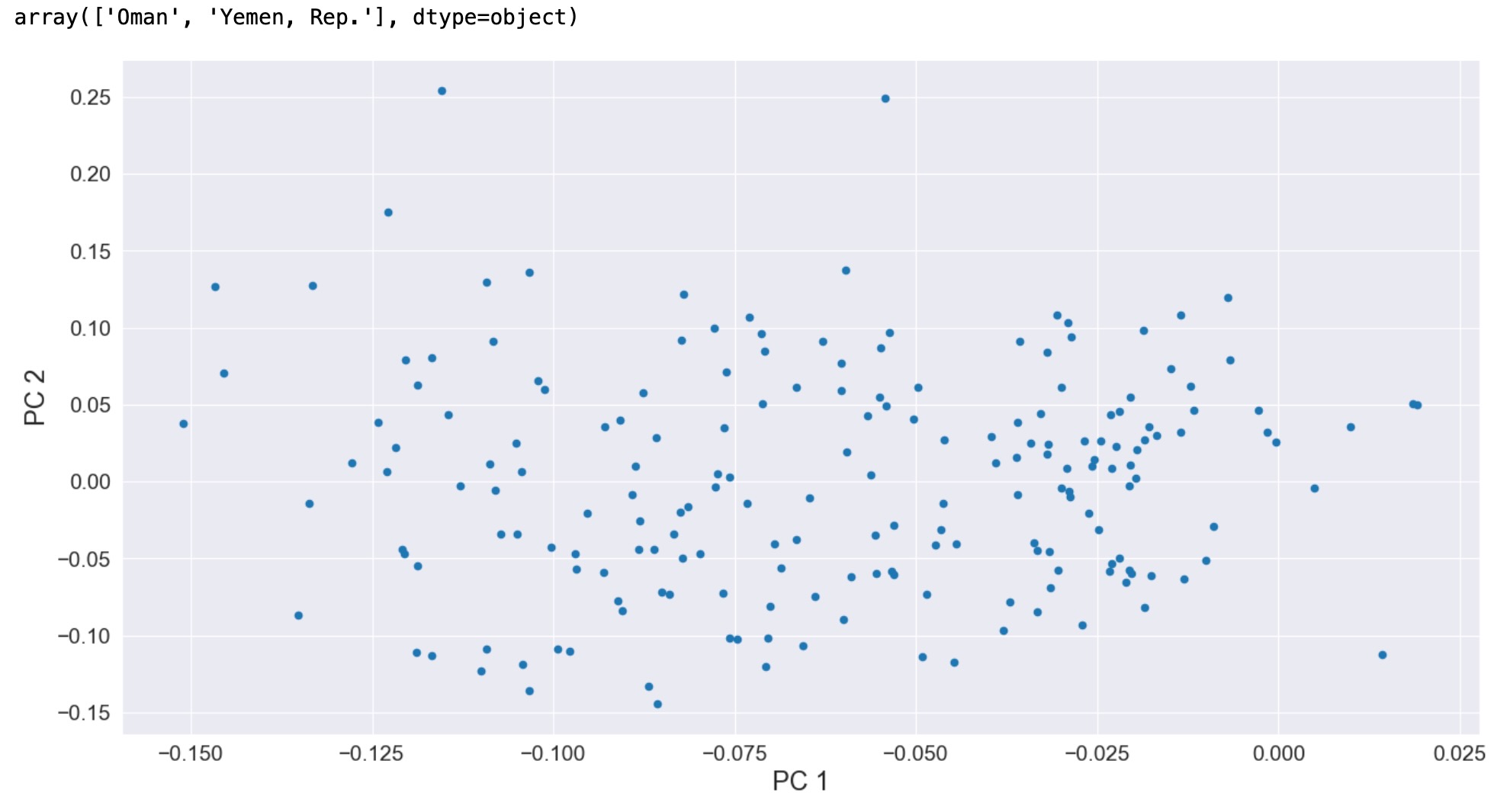
私たちは、最初の二つに主成分のスコアのスキャッタープロットを見ることができます。私たちは、国の間の多様さが、結構連続的で、おそらく、他の点から何かが分離される主成分2で最も高いスコアを持つふたつの国をのぞきます。これらの国、オマーンとイエメン、は、1980年の周りで出生率に鋭い頂点を持っており、特別です。他の国はそうした頂点は持っていません。対照的に、因子1が高いスコアの国は、(持続して出生率が増加しています。)は、変化が連続している部分です。
fig, ax = plt.subplots()
pca_model.loadings.plot.scatter(x="comp_00", y="comp_01", ax=ax)
ax.set_xlabel("PC 1", size=17)
ax.set_ylabel("PC 2", size=17)
dta.index[pca_model.loadings.iloc[:, 1] > 0.2].values