θモデルは、Assimakopulos とNikolopoulos(2000)のシータモデルは、二つのシータラインを適合することを含むフォーキャストのための簡単な方法です。簡単な指数スムーサーを使ってラインをフォーキャストします。その後、最終的なフォーキャストを産むために、二つのラインからのフォーキャストを結合します。モデルは以下のステップで実装されます。
- 季節性のテスト
- 季節性を検出すると、季節性の除去
- SESモデルをデータに適合することによりαを、OLSによりb0を推定
- 系列のフォーキャスト
- データが季節性を除去されたならば、再季節性
季節性のテストは、季節性遅延でACFを検証します。もし、この遅延がゼロから相当異なっていれば、データは、乗法か加法のどちらかを使うstatsmodels.tsa.seasonal_decomposeを使って季節性除去します。
モデルのパラメータは、b0とαです。ここでb0は、OLS回帰から推定されます。
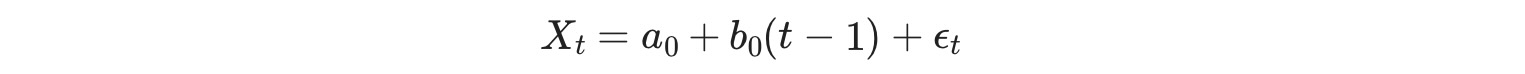
そして、αは、SESスムーシングパラメータ
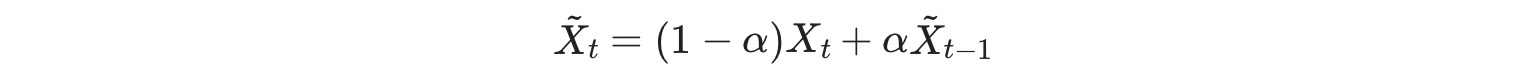
フォーキャストは、
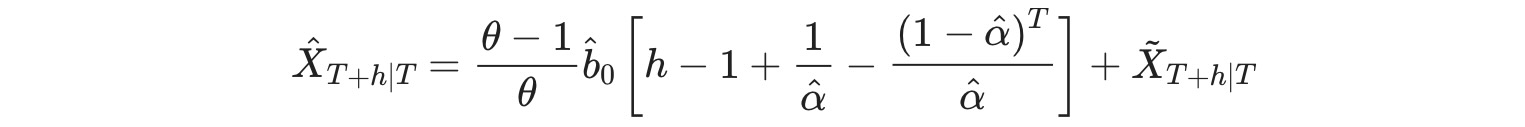
最高のθは、どのくらいトレンドがdumpedか決定する役割をもつ。もし、θがとても大きければ、モデルのフォーキャストは、ドリフト付きの移動平均を統合したものち一致します。
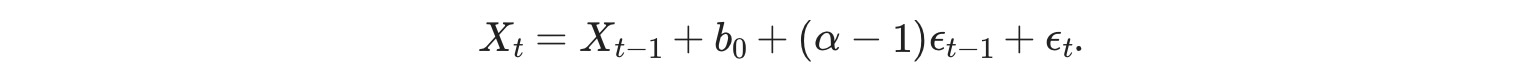
最後に、フォーキャストは、必要ならば、再度、季節化されます。
このモジュールは、以下を基礎にしています。
- Assimakopoulos, V., & Nikolopoulos, K. (2000). The theta model: a decomposition approach to forecasting. International journal of forecasting, 16(4), 521-530.
- Hyndman, R. J., & Billah, B. (2003). Unmasking the Theta method. International Journal of Forecasting, 19(2), 287-290.
- Fioruci, J. A., Pellegrini, T. R., Louzada, F., & Petropoulos, F. (2015). The optimized theta method. arXiv preprint arXiv:1503.03529.
インポート
私たちは、インポートの標準セットとデフォルトのmatplotlibスタイルを幾らか微調整して開始します。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=15)
plt.rc("lines", linewidth=3)
sns.set_style("darkgrid")任意のデータの読み込み
私たちは、USデータを使ってハウジングの開始を最初に見ていきます。この系列は、明らかに季節性がありますが、同時期に明確なトレンドはありません。
reader = pdr.fred.FredReader(["HOUST"], start="1980-01-01", end="2020-04-01")
data = reader.read()
housing = data.HOUST
housing.index.freq = housing.index.inferred_freq
ax = housing.plot()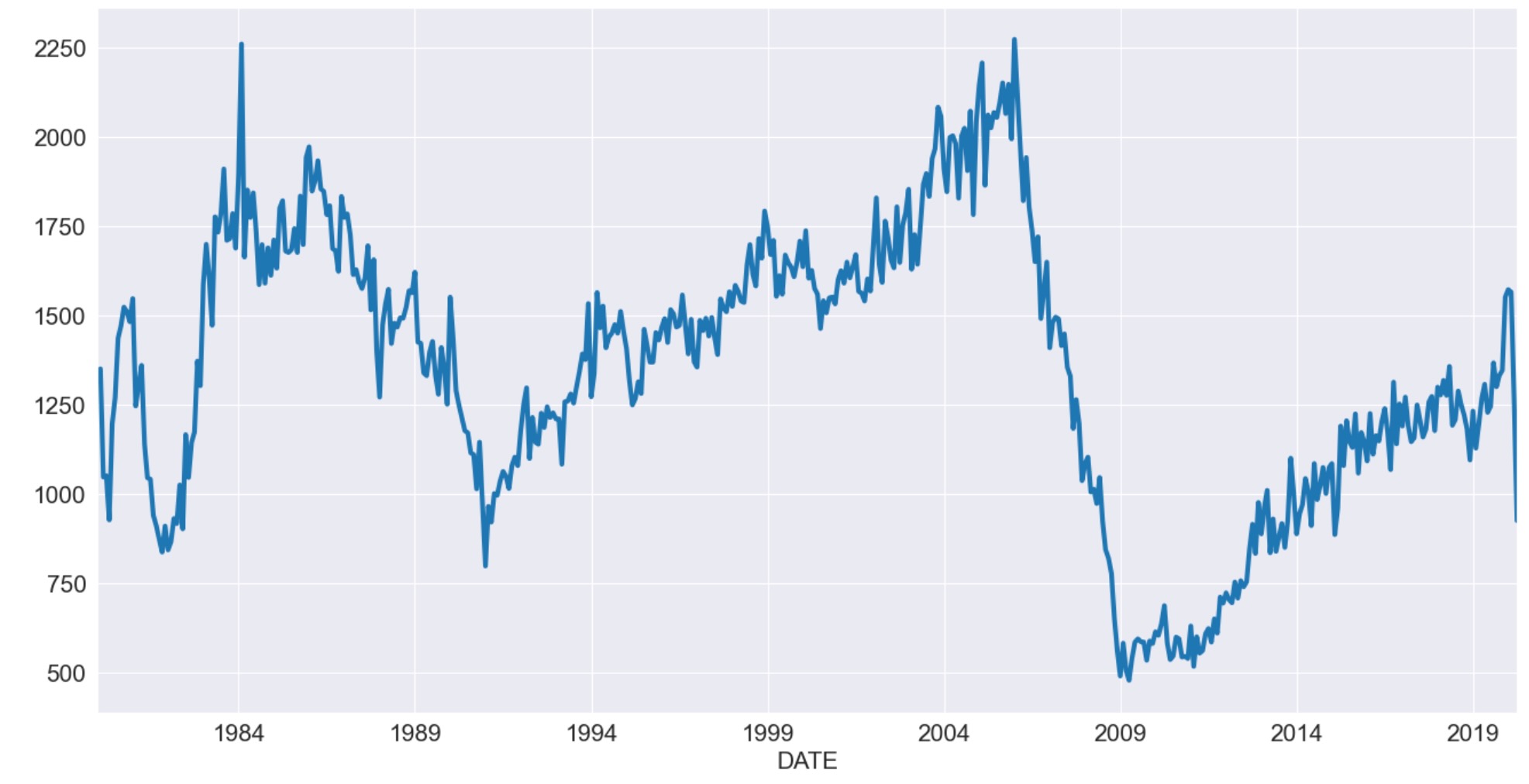
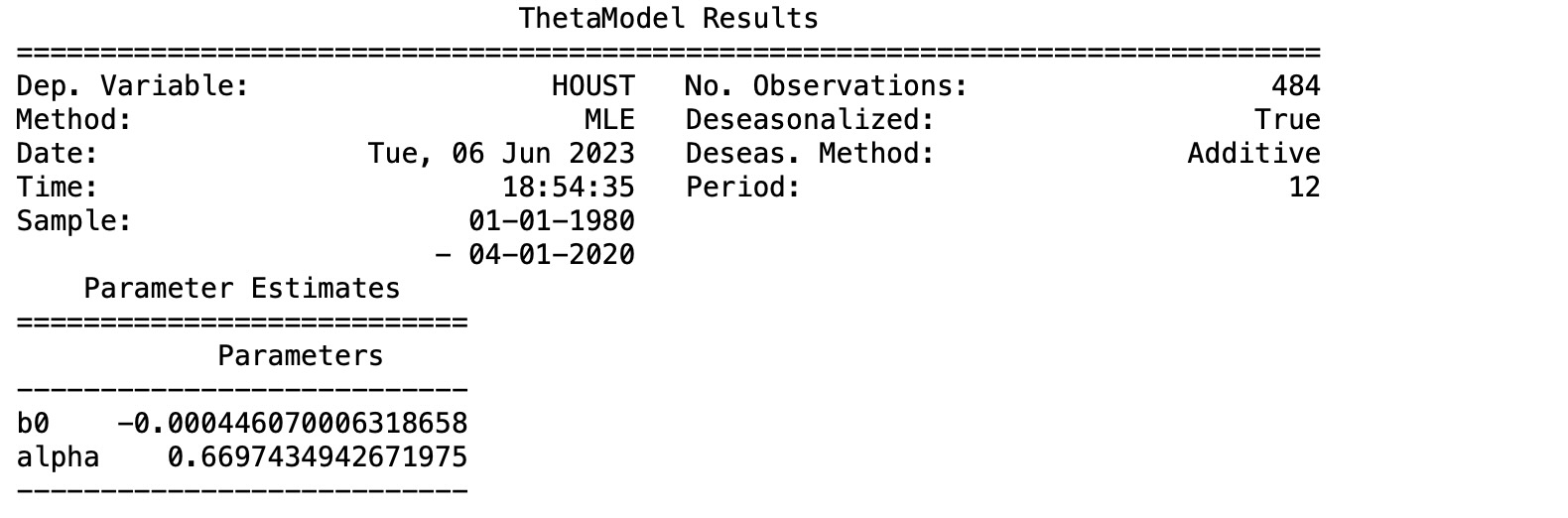
私たちは、どのようなオプションとその適合もなしにモデルを規定して適合します。結果はデータが乗数の方法を使って季節性を除去したことを示しています。ドリフトは控えめで、ネガティブです。そしてスムーシングパラメータはかなり低くくなります。
from statsmodels.tsa.forecasting.theta import ThetaModel
tm = ThetaModel(housing)
res = tm.fit()
print(res.summary())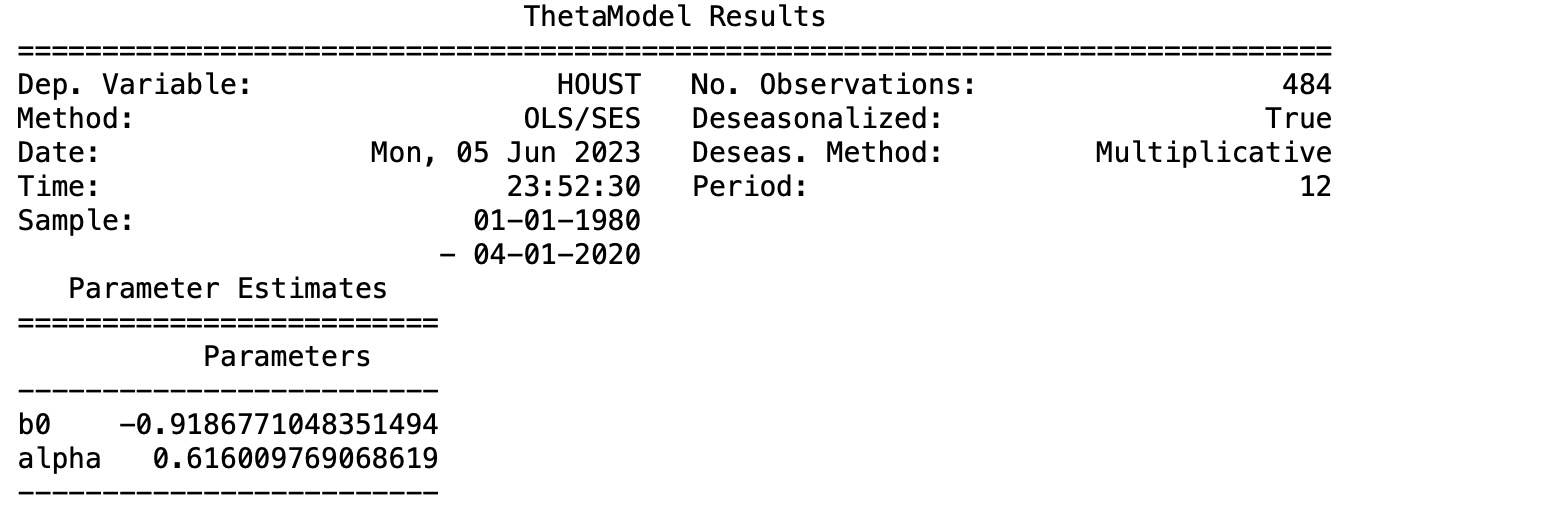
モデルは、最初のそしてもっとも重要な予測の方法です。予測は、forecastメソッドを使って、適合したモデルから生産されます。以下、私たちは2年ごとに2年先の予測によってヘッジホッグ(ハリネズミ)図を生み出します。
デフォルトのθが2 であることに注意してください。
forecasts = {"housing": housing}
for year in range(1995, 2020, 2):
sub = housing[: str(year)]
res = ThetaModel(sub).fit()
fcast = res.forecast(24)
forecasts[str(year)] = fcast
forecasts = pd.DataFrame(forecasts)
ax = forecasts["1995":].plot(legend=False)
children = ax.get_children()
children[0].set_linewidth(4)
children[0].set_alpha(0.3)
children[0].set_color("#000000")
ax.set_title("Housing Starts")
plt.tight_layout(pad=1.0)
私たちは、代わりに、データの対数を適合することができます。ここに、もし必要であれば、強制して加法メソッドを使って季節性を削除することはもっと理解しやすいことです。私たちは、MLEを使ってモデルパラメータを適合します。このメソッドはIMAを適合します。
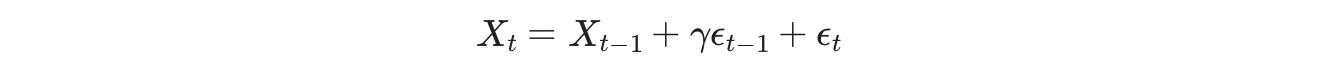
ここで、α~ = min(γ +1, 0.9998) statsmodels.tsa.SARIMAXを使っています。パラメータは似ていますが、ドリフトはゼロに近くなります。
フォーキャストは、フォーキャストトレンド成分にだけ依存します。
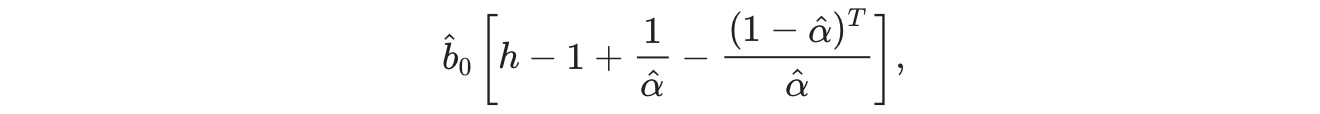
SES(それは範囲を変化させない)と季節性からのフォーキャスト。これらの三つの成分が、forecast_componentsを使って利用できます。これは、上の重みの式を使ったθの多重な選択を使用して、フォーキャストを構築することを許容します。
res.forecast_components(12)| trend | ses | seasonal | |
|---|---|---|---|
| 2020-05-01 | -0.000666 | 6.957192 | -0.000969 |
| 2020-06-01 | -0.001112 | 6.957192 | -0.007192 |
| 2020-07-01 | -0.001558 | 6.957192 | 0.003105 |
| 2020-08-01 | -0.002004 | 6.957192 | -0.003966 |
| 2020-09-01 | -0.002450 | 6.957192 | -0.004147 |
| 2020-10-01 | -0.002896 | 6.957192 | -0.003889 |
| 2020-11-01 | -0.003342 | 6.957192 | 0.008512 |
| 2020-12-01 | -0.003789 | 6.957192 | -0.000737 |
| 2021-01-01 | -0.004235 | 6.957192 | 0.005350 |
| 2021-02-01 | -0.004681 | 6.957192 | 0.010091 |
| 2021-03-01 | -0.005127 | 6.957192 | -0.004445 |
| 2021-04-01 | -0.005573 | 6.957192 | -0.001713 |
個人消費支出
私たちは次に個人消費支出を見ていきます。この系列は明確に季節性の成分をもち、それはドリフトします。
reader = pdr.fred.FredReader(["NA000349Q"], start="1980-01-01", end="2020-04-01")
pce = reader.read()
pce.columns = ["PCE"]
pce.index.freq = "QS-OCT"
_ = pce.plot()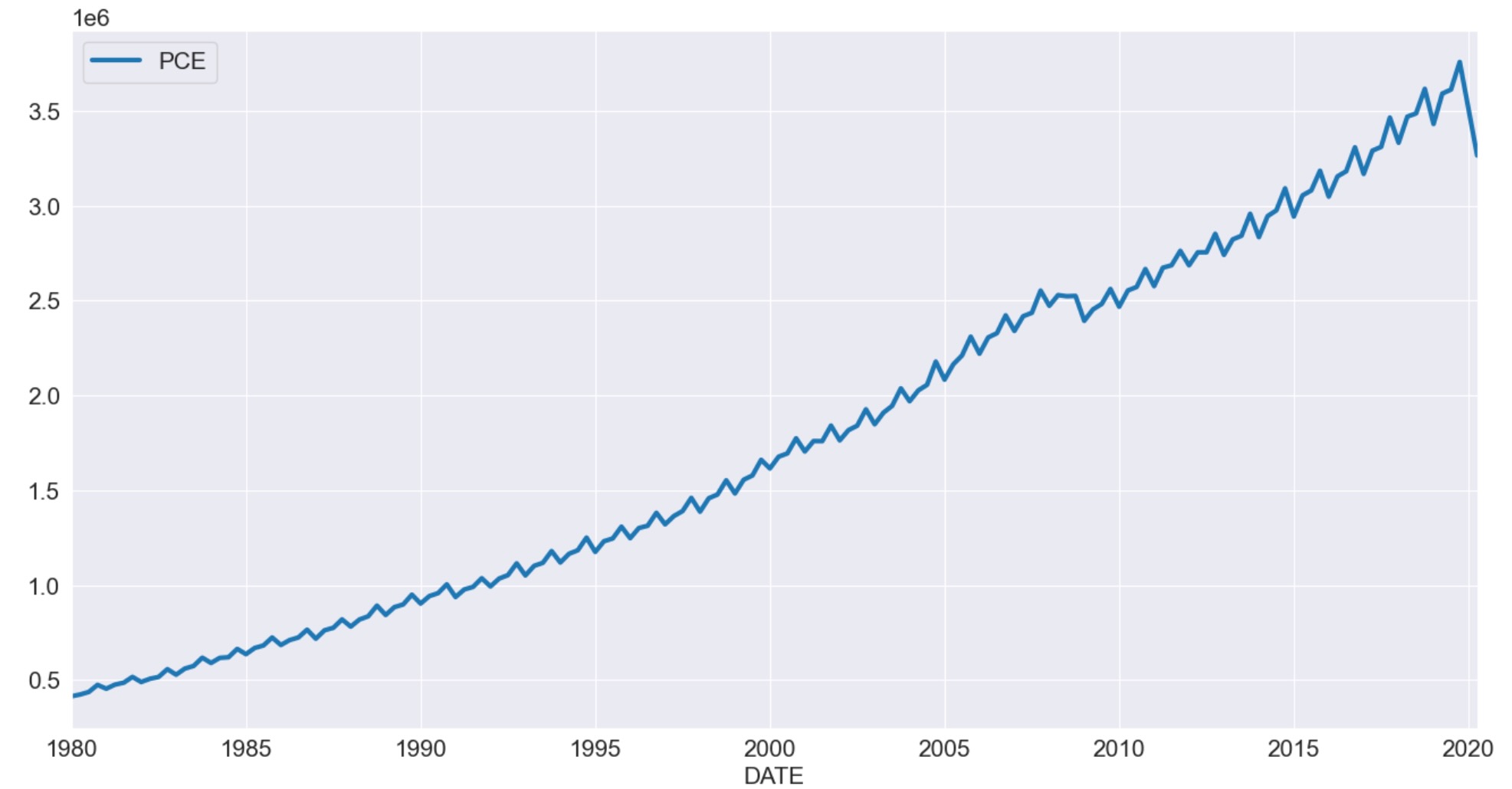
この系列jは常に正なので、私たちはlnでモデルにします。
mod = ThetaModel(np.log(pce))
res = mod.fit()
print(res.summary())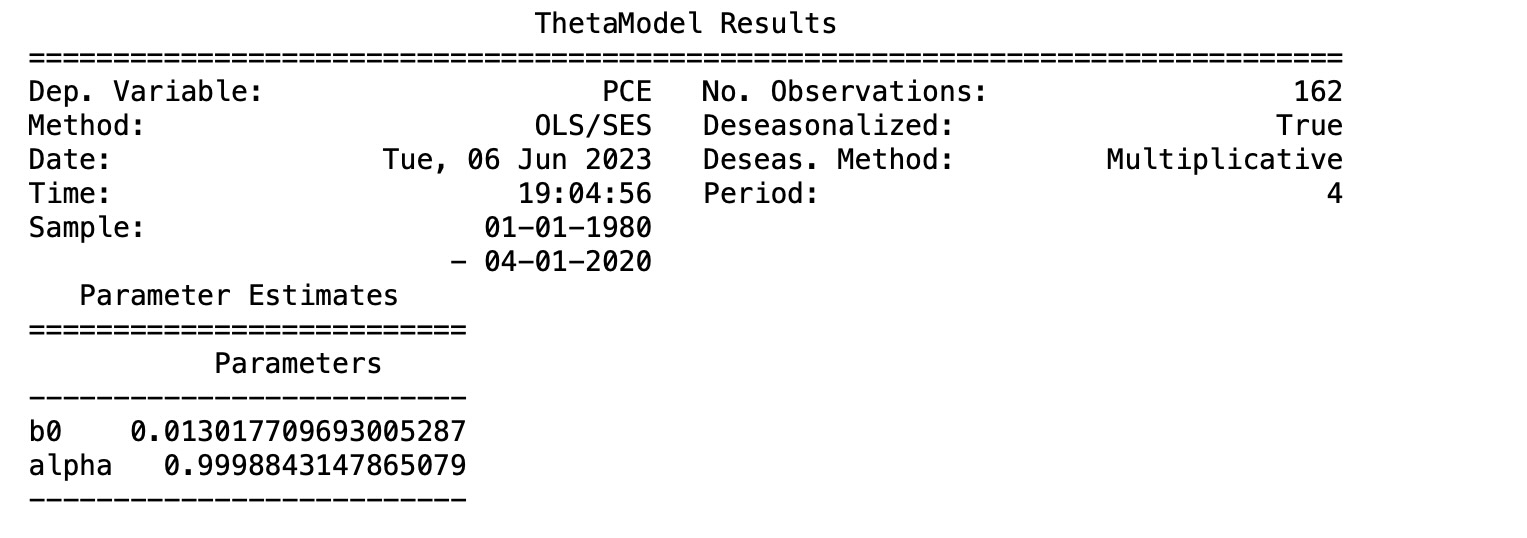
次に、θが変化するため、フォーキャストの相違を探します。θが1に近いとき、ドリフトはほぼなくなります。θは増加するので、ドリフトはもっとはっきしてきます。
forecasts = pd.DataFrame(
{
"ln PCE": np.log(pce.PCE),
"theta=1.2": res.forecast(12, theta=1.2),
"theta=2": res.forecast(12),
"theta=3": res.forecast(12, theta=3),
"No damping": res.forecast(12, theta=np.inf),
}
)
_ = forecasts.tail(36).plot()
plt.title("Forecasts of ln PCE")
plt.tight_layout(pad=1.0)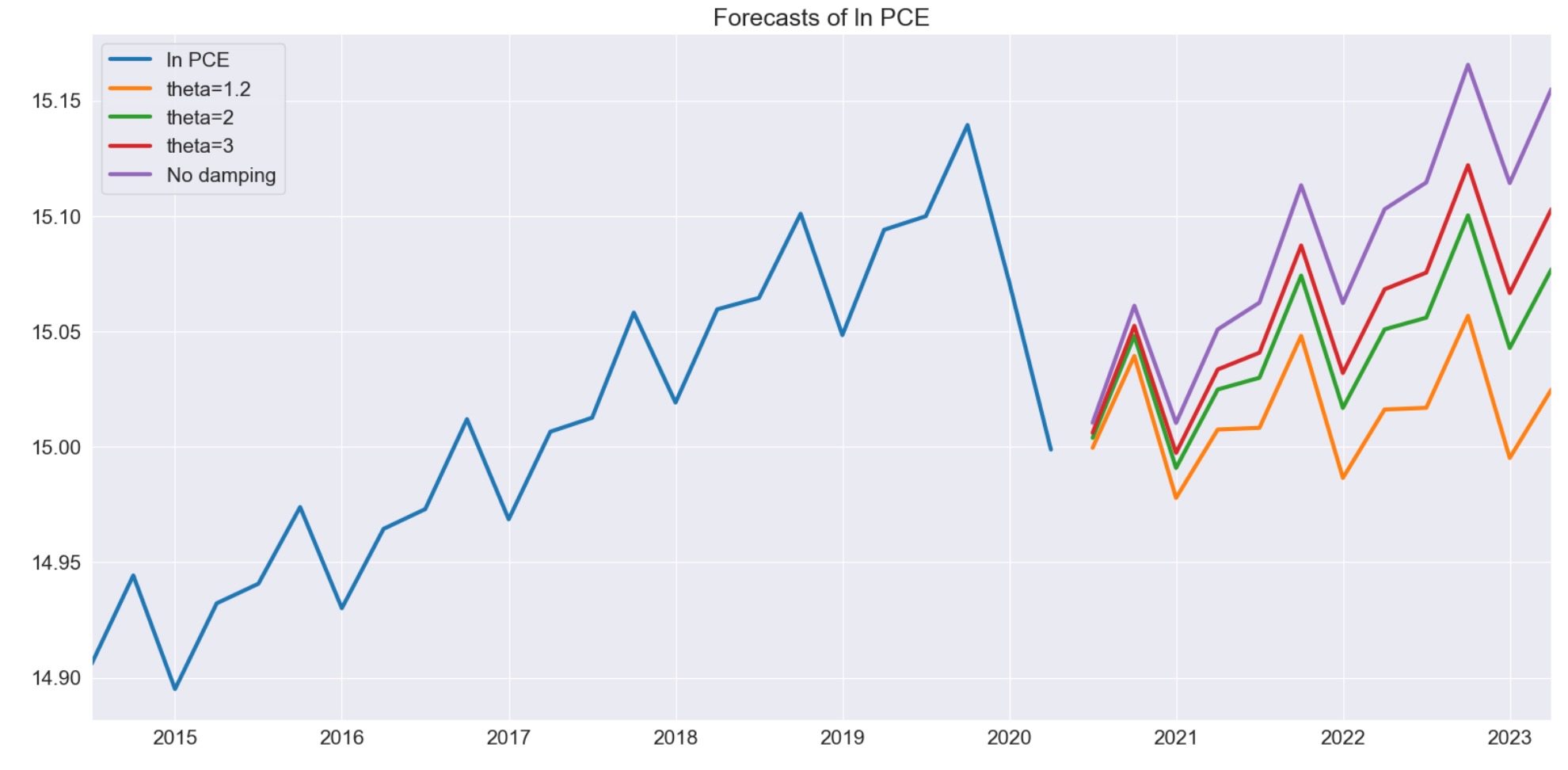
最後に、plot_predictは、IMAが真であることを仮定して構築される予測と予測のインターバルを可視化するのに使います。
ax = res.plot_predict(24, theta=2)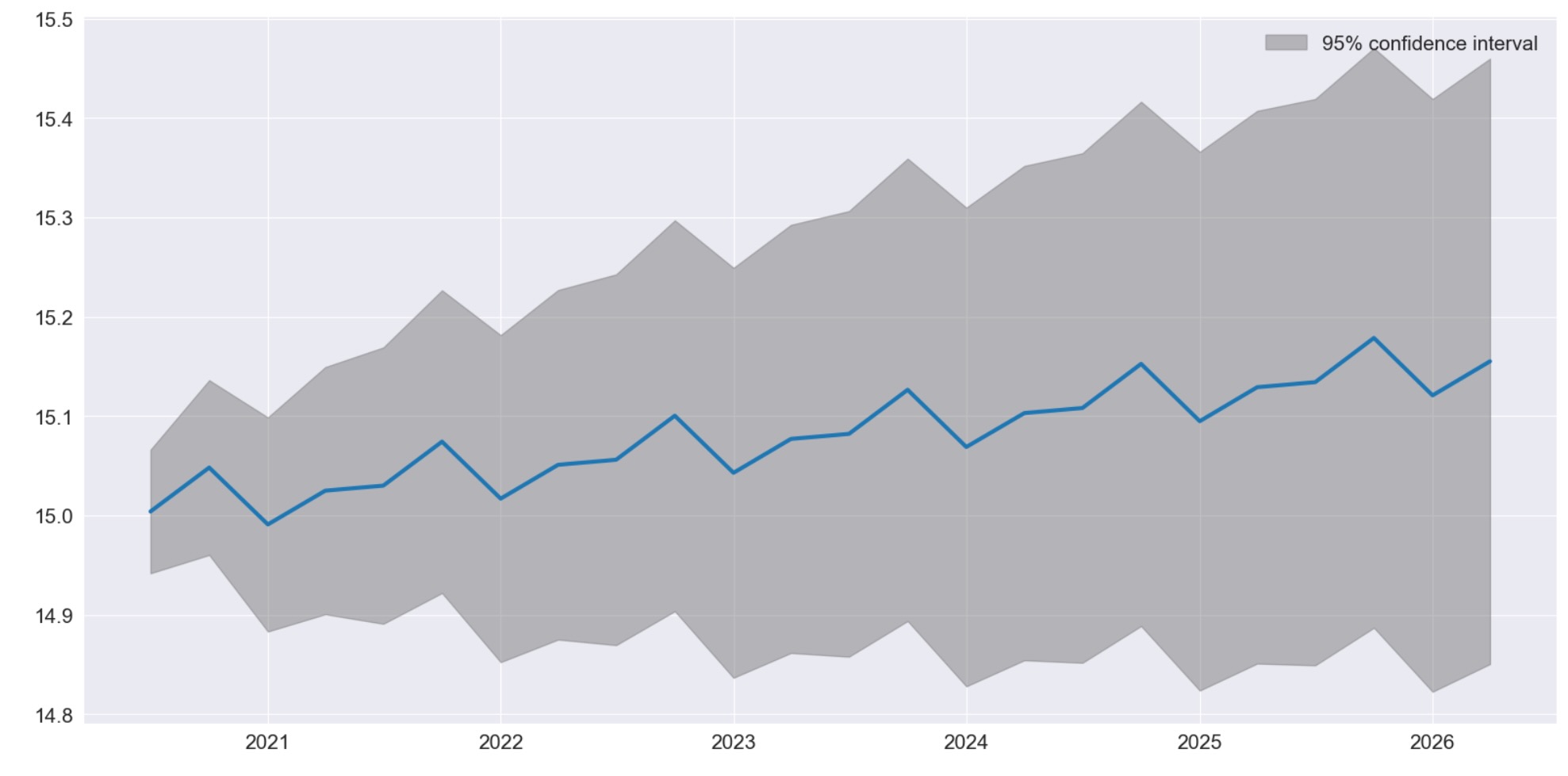
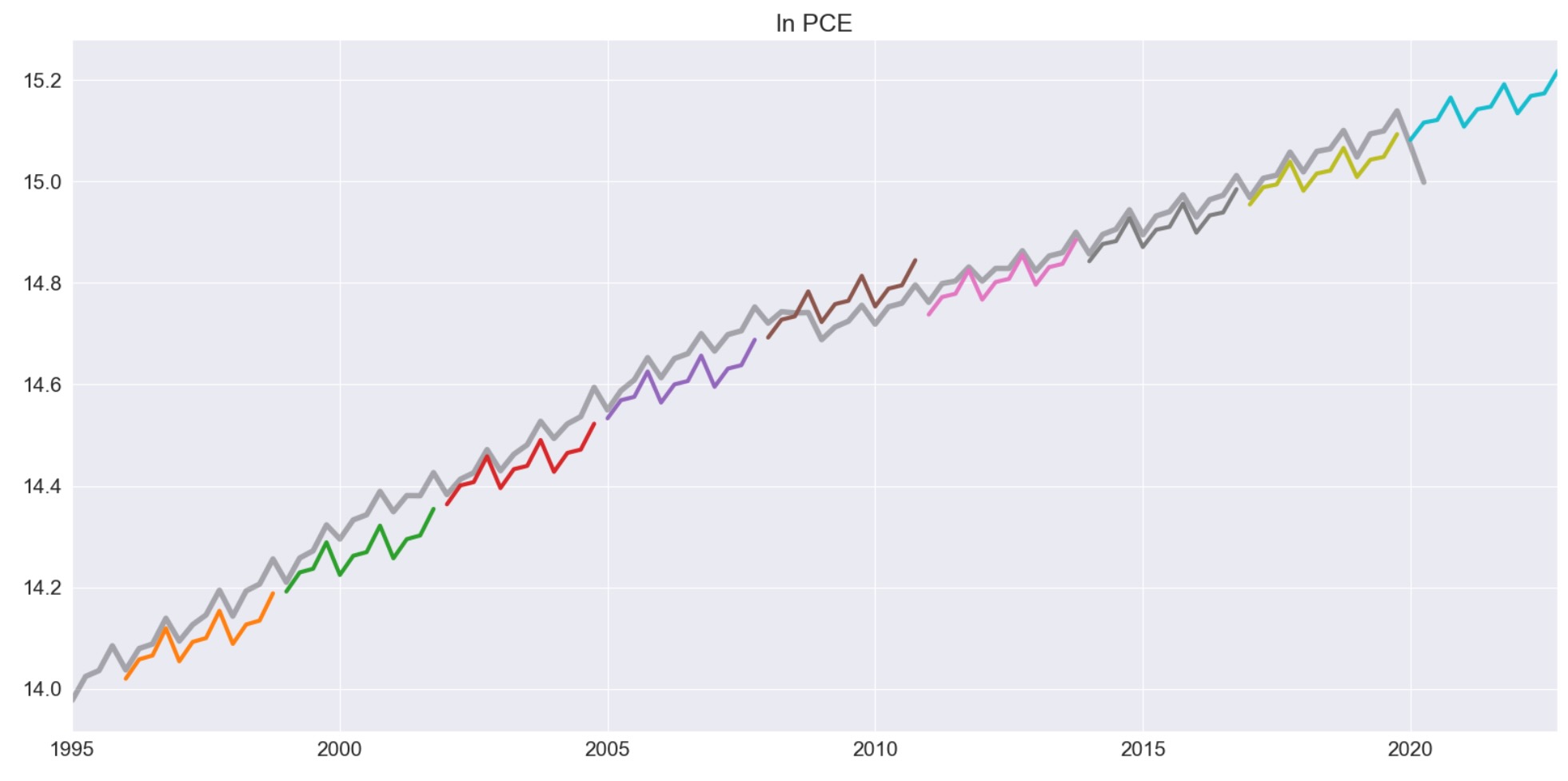
私たちは、2年の重ならないサンプルを用いてヘッジホッグプロットを出力して締めくくります。
ln_pce = np.log(pce.PCE)
forecasts = {"ln PCE": ln_pce}
for year in range(1995, 2020, 3):
sub = ln_pce[: str(year)]
res = ThetaModel(sub).fit()
fcast = res.forecast(12)
forecasts[str(year)] = fcast
forecasts = pd.DataFrame(forecasts)
ax = forecasts["1995":].plot(legend=False)
children = ax.get_children()
children[0].set_linewidth(4)
children[0].set_alpha(0.3)
children[0].set_color("#000000")
ax.set_title("ln PCE")
plt.tight_layout(pad=1.0)