TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。
PCMCIはここに記述されています: J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996
PCMCIのさらに進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。
このチュートリアルは、因果の仮定を説明し、事例の解説を提供します。
最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.models import LinearMediation, Prediction因果の仮定
基本的な機能を紹介します。私たちは、因果の解釈の基盤になる仮定を議論に取り掛かります。
- 正確性/安定性:データの独立性は、偶然の一致からではなく、因果の構造または、異なった表現から発生します。もし、任意の他の変数のサブセットで与えられる、二つの変数が独立していれば、その時、それらはグラフの因果リンクによって接続されません。
- 因果の充分性:計測した変数は全ての共通の原因を含みます。
- 因果のマルコフ条件:全ての関連する確率情報は、システムから得ることができる直接の原因と相違の表現、もし、任意の条件のセット(Runge 2018 のより深い定義を参照してください)で与えられる因果グラフで二つの変数が接続されていないならば、それらは条件付き独立です。
- 非同時性の効果:ラグがゼロの場合、因果関係はありません。
- ステーショナリティー
- 独立テストのパラメトリック仮定(すでに基本的なチュートリアルで議論しました。)
正確性
正確性は、上に規定されるように、私たちが、因果の構造、すなわち時系列グラフ、からの起因を測定する独立性の仮定の表現です。そして、パラメータの適切な調整のために見られなくなります。一方の不正確なケースは、純粋な決定的な従属性、いわゆるノイズなしのY=f(X)、を含む過程です。
適切な調整
私たちのモデルは、X0がX2の原因となる直接的な一つ、と以下のようなモデルで実現されるX0->X1->X2 関節的な結果、の二つの方法のモデルについて考えます。
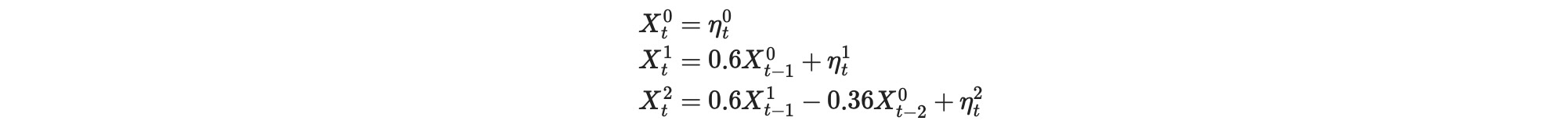
seed=1
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((500, 3))
for t in range(1, 500):
# data[t, 0] += 0.6*data[t-1, 1]
data[t, 1] += 0.6*data[t-1, 0]
data[t, 2] += 0.6*data[t-1, 1] - 0.36*data[t-2, 0]
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']
dataframe = pp.DataFrame(data, var_names=var_names)
# tp.plot_timeseries(dataframe)ここで、Xt2 = 0.6Xt-11 - 0.36Xt-20 + ηt2 = 0.6(0.6Xt-20 + ηt-11 ) - 0.36 Xt-20 + ηt2 = 0.36Xt-20 - 0.36Xt-20 …., 無条件の従属性 Xt-20 -> Xt2 はありません。そして、リンクは、条件選択ステップでは検出されません。
parcorr = ParCorr()
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)
all_parents = pcmci_parcorr.run_pc_stable(tau_max=2, pc_alpha=0.2)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 2
pc_alpha = [0.2]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X^0$ has 1 link(s):
($X^0$ -1): max_pval = 0.09500, min_val = -0.075
Variable $X^1$ has 1 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.527
Variable $X^2$ has 2 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.394
($X^0$ -1): max_pval = 0.15990, min_val = -0.063しかし、X2の他の親、名称はXt-11は検出されるので、Xt-11のMCステップは、真の基礎となるグラフ(この特別なケースで)を明らかにすることができます。
results = pcmci_parcorr.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
## ## Step 1: PC1 algorithm with lagged conditions ## Parameters: independence test = par_corr tau_min = 1 tau_max = 2 pc_alpha = [0.2] max_conds_dim = None max_combinations = 1 ## Resulting lagged parent (super)sets: Variable $X^0$ has 1 link(s): ($X^0$ -1): max_pval = 0.09500, min_val = -0.075 Variable $X^1$ has 1 link(s): ($X^0$ -1): max_pval = 0.00000, min_val = 0.527 Variable $X^2$ has 2 link(s): ($X^1$ -1): max_pval = 0.00000, min_val = 0.394 ($X^0$ -1): max_pval = 0.15990, min_val = -0.063 ## ## Step 2: MCI algorithm ## Parameters: independence test = par_corr tau_min = 0 tau_max = 2 max_conds_py = None max_conds_px = None ## Significant links at alpha = 0.01: Variable $X^0$ has 0 link(s): Variable $X^1$ has 1 link(s): ($X^0$ -1): pval = 0.00000 | val = 0.530 Variable $X^2$ has 2 link(s): ($X^1$ -1): pval = 0.00000 | val = 0.479 ($X^0$ -2): pval = 0.00000 | val = -0.294
しかし、これは必ずしもそうした取り消しのケースではありません。理不尽なケースですが、特にサンプラーのサンプルサイズに関して問題を表すことができます。
決定論的な従属性
その他の正確さの違反は、ここに示されるような、純粋に決定論的な従属性のために発生します。
seed=1
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((500, 3))
for t in range(1, 500):
data[t, 0] = 0.4*data[t-1, 1]
data[t, 2] += 0.3*data[t-2, 1] + 0.7*data[t-1, 0]
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()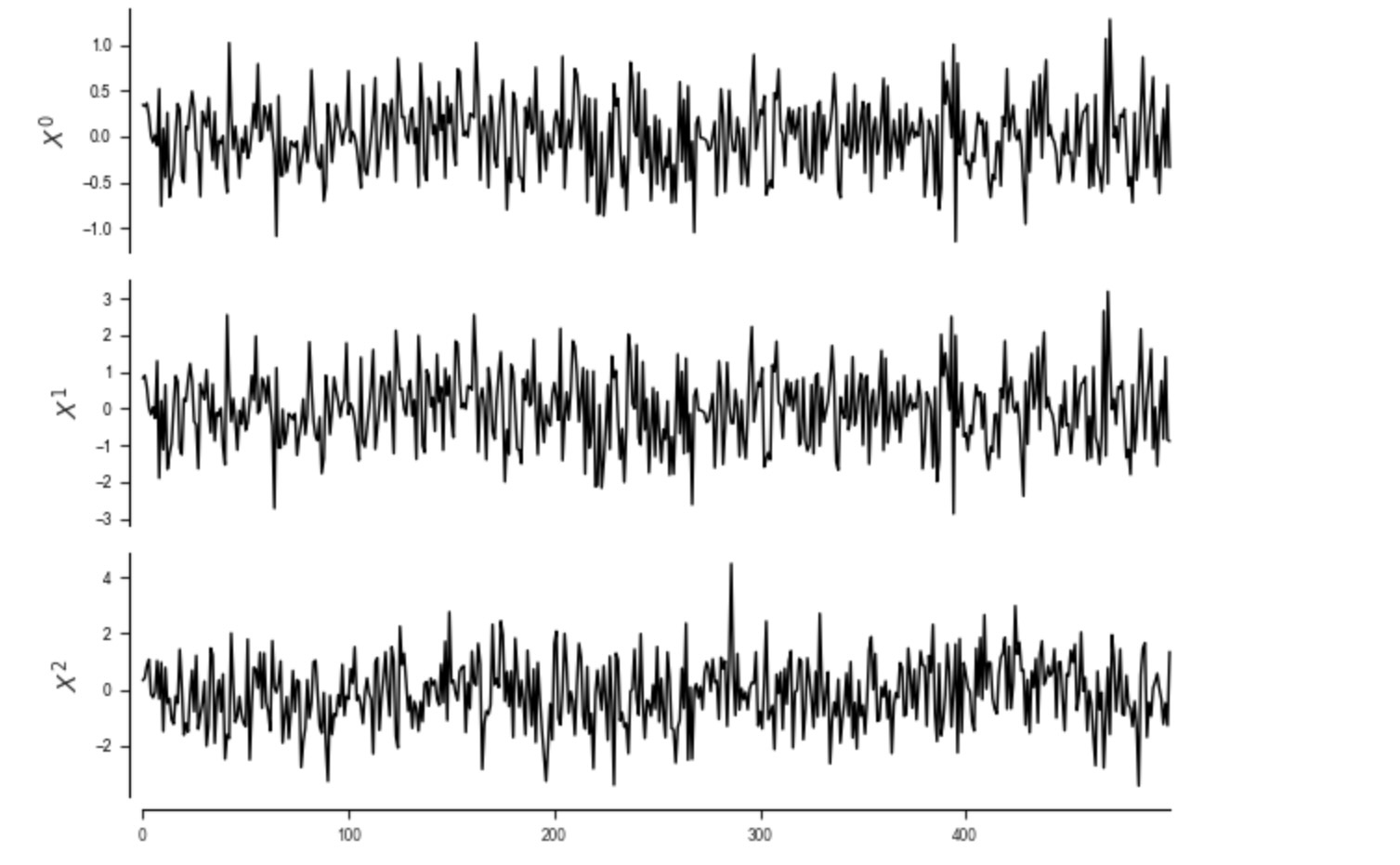
parcorr = ParCorr()
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=2)
results = pcmci_parcorr.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 2
pc_alpha = [0.2]
max_conds_dim = None
max_combinations = 1
## Variable $X^0$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^0$ (1/6):
Subset 0: () gives pval = 0.51104 / val = 0.030
Non-significance detected.
Link ($X^0$ -2) -?> $X^0$ (2/6):
Subset 0: () gives pval = 0.77977 / val = 0.013
Non-significance detected.
Link ($X^1$ -1) -?> $X^0$ (3/6):
Subset 0: () gives pval = 0.00000 / val = 1.000
No conditions of dimension 0 left.
Link ($X^1$ -2) -?> $X^0$ (4/6):
Subset 0: () gives pval = 0.51104 / val = 0.030
Non-significance detected.
Link ($X^2$ -1) -?> $X^0$ (5/6):
Subset 0: () gives pval = 0.20746 / val = -0.057
Non-significance detected.
Link ($X^2$ -2) -?> $X^0$ (6/6):
Subset 0: () gives pval = 0.19827 / val = -0.058
No conditions of dimension 0 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^0$ has 2 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 1.000
($X^2$ -2): max_pval = 0.19827, min_val = 0.058
Testing condition sets of dimension 1:
Link ($X^1$ -1) -?> $X^0$ (1/2):
Subset 0: ($X^2$ -2) gives pval = 0.00000 / val = 1.000
No conditions of dimension 1 left.
Link ($X^2$ -2) -?> $X^0$ (2/2):
Subset 0: ($X^1$ -1) gives pval = 0.93185 / val = 0.004
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^0$ has 1 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 1.000
Algorithm converged for variable $X^0$
## Variable $X^1$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^1$ (1/6):
Subset 0: () gives pval = 0.82511 / val = 0.010
Non-significance detected.
Link ($X^0$ -2) -?> $X^1$ (2/6):
Subset 0: () gives pval = 0.67752 / val = 0.019
Non-significance detected.
Link ($X^1$ -1) -?> $X^1$ (3/6):
Subset 0: () gives pval = 0.49082 / val = 0.031
Non-significance detected.
Link ($X^1$ -2) -?> $X^1$ (4/6):
Subset 0: () gives pval = 0.82511 / val = 0.010
Non-significance detected.
Link ($X^2$ -1) -?> $X^1$ (5/6):
Subset 0: () gives pval = 0.21189 / val = -0.056
Non-significance detected.
Link ($X^2$ -2) -?> $X^1$ (6/6):
Subset 0: () gives pval = 0.77424 / val = -0.013
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^1$ has 0 link(s):
Algorithm converged for variable $X^1$
## Variable $X^2$
Iterating through pc_alpha = [0.2]:
# pc_alpha = 0.2 (1/1):
Testing condition sets of dimension 0:
Link ($X^0$ -1) -?> $X^2$ (1/6):
Subset 0: () gives pval = 0.00000 / val = 0.493
No conditions of dimension 0 left.
Link ($X^0$ -2) -?> $X^2$ (2/6):
Subset 0: () gives pval = 0.67625 / val = -0.019
Non-significance detected.
Link ($X^1$ -1) -?> $X^2$ (3/6):
Subset 0: () gives pval = 0.71172 / val = -0.017
Non-significance detected.
Link ($X^1$ -2) -?> $X^2$ (4/6):
Subset 0: () gives pval = 0.00000 / val = 0.493
No conditions of dimension 0 left.
Link ($X^2$ -1) -?> $X^2$ (5/6):
Subset 0: () gives pval = 0.44687 / val = 0.034
Non-significance detected.
Link ($X^2$ -2) -?> $X^2$ (6/6):
Subset 0: () gives pval = 0.62733 / val = 0.022
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^2$ has 2 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.493
($X^1$ -2): max_pval = 0.00000, min_val = 0.493
Testing condition sets of dimension 1:
Link ($X^0$ -1) -?> $X^2$ (1/2):
Subset 0: ($X^1$ -2) gives pval = 0.87812 / val = 0.007
Non-significance detected.
Link ($X^1$ -2) -?> $X^2$ (2/2):
Subset 0: ($X^0$ -1) gives pval = 0.87812 / val = -0.007
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^2$ has 0 link(s):
Algorithm converged for variable $X^2$
## Resulting lagged parent (super)sets:
Variable $X^0$ has 1 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 1.000
Variable $X^1$ has 0 link(s):
Variable $X^2$ has 0 link(s):
##
## Step 2: MCI algorithm
##
Parameters:
independence test = par_corr
tau_min = 0
tau_max = 2
max_conds_py = None
max_conds_px = None
link ($X^0$ -1) -?> $X^0$ (1/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ($X^1$ -2) ]
link ($X^0$ -2) -?> $X^0$ (2/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ($X^1$ -3) ]
link ($X^1$ 0) o?o $X^0$ (3/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ]
link ($X^1$ -1) -?> $X^0$ (4/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^1$ -2) -?> $X^0$ (5/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ]
link ($X^2$ 0) o?o $X^0$ (6/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ]
link ($X^2$ -1) -?> $X^0$ (7/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ]
link ($X^2$ -2) -?> $X^0$ (8/8):
with conds_y = [ ($X^1$ -1) ]
with conds_x = [ ]
link ($X^0$ 0) o?o $X^1$ (1/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -1) ]
link ($X^0$ -1) -?> $X^1$ (2/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -2) ]
link ($X^0$ -2) -?> $X^1$ (3/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -3) ]
link ($X^1$ -1) -?> $X^1$ (4/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^1$ -2) -?> $X^1$ (5/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^2$ 0) o?o $X^1$ (6/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^2$ -1) -?> $X^1$ (7/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^2$ -2) -?> $X^1$ (8/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^0$ 0) o?o $X^2$ (1/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -1) ]
link ($X^0$ -1) -?> $X^2$ (2/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -2) ]
link ($X^0$ -2) -?> $X^2$ (3/8):
with conds_y = [ ]
with conds_x = [ ($X^1$ -3) ]
link ($X^1$ 0) o?o $X^2$ (4/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^1$ -1) -?> $X^2$ (5/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^1$ -2) -?> $X^2$ (6/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^2$ -1) -?> $X^2$ (7/8):
with conds_y = [ ]
with conds_x = [ ]
link ($X^2$ -2) -?> $X^2$ (8/8):
with conds_y = [ ]
with conds_x = [ ]
## Significant links at alpha = 0.01:
Variable $X^0$ has 2 link(s):
($X^1$ -1): pval = 0.00000 | val = 1.000
($X^0$ -1): pval = 0.00295 | val = 0.133
Variable $X^1$ has 0 link(s):
Variable $X^2$ has 1 link(s):
($X^1$ -2): pval = 0.00000 | val = 0.493
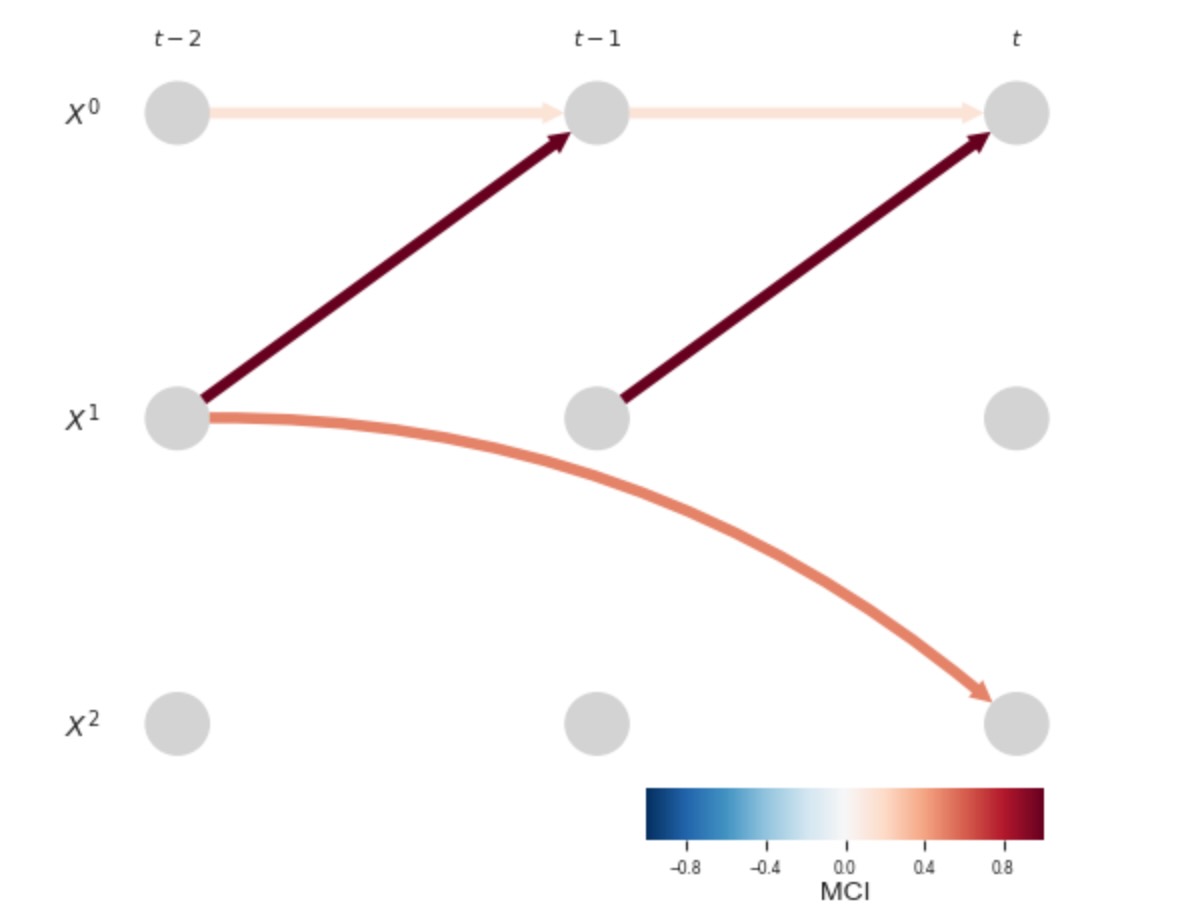
ここで部分的な相関Xt-11->Xt0は正確に1になります。ここで、同じ変数を表すので、私たちの条件がXt-2 1なので、真のリンク Xt-10 ->Xt2 は、もはや検出できません。他の変数の決定論的な複製は分析から除外されます。
因果の充分性
因果の充分性は、変数のセットが、任意の二つの変数の全ての共通の原因を含むことを要求します。この仮定は、解放した外部の制限された実験の設定を分析するときに、ほとんど違反されます。もし、もっと変数が分析に含まれるならば、因果の発見アルゴリズムから推定される任意のリンクは、特徴がなくなります。因果の充分性を仮定した観測上の因果推論は、理解できる物理的な過程への一つのステップとして、一般的にもっとよくわかります。しかしこれらのアルゴリズムの存在は、理解でき、困惑させるリンク(例えば、FCIアルゴリズムとLPCMCI)を外部に表すことができます。因果の発見は、潜在的なドライバーの考えを得るために、モデルの構築の分析を探索するのに大いに役立つことができます。特に、リンクの欠如はもっと確実な結果を許容します。もし、静的な従属性の証拠がない場合、そのとき、物理的なメカニズムはありそうにありません。(他の仮定を保持すると仮定して)
Runge Jakobの2018年の“Causal Network Reconstruction from Time Series: From Theoretical Assumptions to Practical Estimation.” Chaos: An Interdisciplinary Journal of Nonlinear Science 28 (7): 075310.は、因果の充分性を必要としない代替的なアプローチ を参照してください。
無測定ドライバー/潜在変数
共通のドライバー過程のために、共通のドライバーが測定されないことを考えます。
seed=1
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((10000, 5))
a = 0.8
for t in range(5, 10000):
data[t, 0] += a*data[t-1, 0]
data[t, 1] += a*data[t-1, 1] + 0.5*data[t-1, 0]
data[t, 2] += a*data[t-1, 2] + 0.5*data[t-1, 1] + 0.5*data[t-1, 4]
data[t, 3] += a*data[t-1, 3] + 0.5*data[t-2, 4]
data[t, 4] += a*data[t-1, 4]
# tp.plot_timeseries(dataframe)
obsdata = data[:,[0, 1, 2, 3]]
var_names_lat = ['W', 'Y', 'X', 'Z', 'U']for data_here in [data, obsdata]:
dataframe = pp.DataFrame(data_here)
parcorr = ParCorr()
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_max=5, pc_alpha=0.1, alpha_level = 0.001)
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names_lat,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
); plt.show()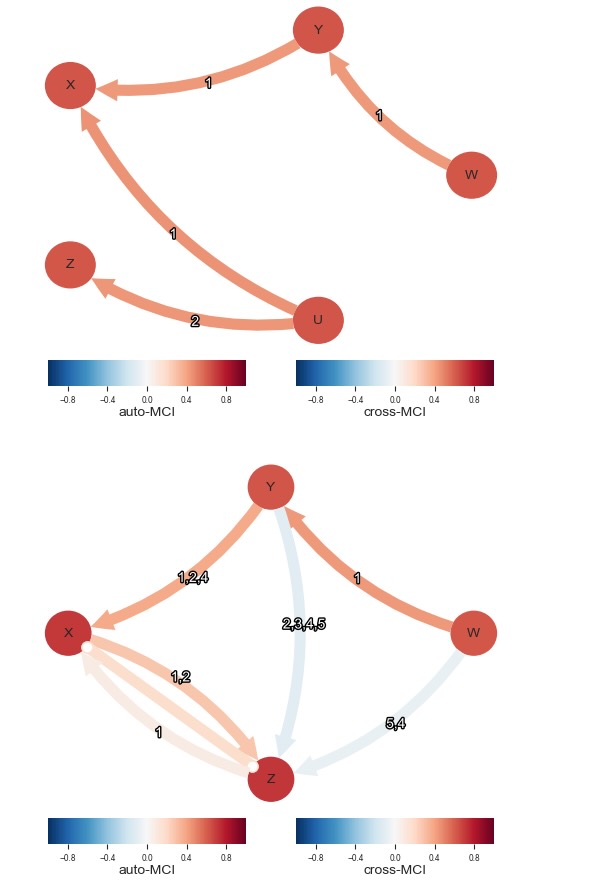
上位の図は、もし全ての変数が観測される場合、真の因果グラフを示します。下側のグラフは、変数Uが隠されているケースを示しています。そのときいくつかの不確かなリンクが現れます。(1)X->Z そして、(2) YとWからZへのリンク、それは、可能な関節的な経路がないため、直感に反しています。理由は何でしょう?原因となっているのは、Zの親が条件になっている YとZの間のX:MCI(またはFullMCIと過去全体を条件にした、任意の他の因果の測定)のビームです。それは、低位の潜在グラフの個々のXを含みます。しかし、そのときYとWからZへの経路を開くビーム(collider)を条件にして、それらの従属性を形成します。
太陽の力
地球科学の文脈では、太陽の力は典型的に、多くの過程の共通のドライバーです。この自明な効果を削除するために、時系列は、典型的に異常になります。それは、季節周期の平均が減算されることです。しかし、ここの人工的な例での正弦波を経由してに見られるように明白に太陽の力は含んでいます。私たちは、それらの過去の値への自動依存性を追加することによって、もっと現実的な時系列を作ります。
T = 2000
seed=42
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((T, 4))
# Simple sun
data[:,3] = np.sin(np.arange(T)*20/np.pi) + 0.1*np.random.randn(T)
c = 0.8
for t in range(1, T):
data[t, 0] += 0.4*data[t-1, 0] + 0.4*data[t-1, 1] + c*data[t-1,3]
data[t, 1] += 0.5*data[t-1, 1] + c*data[t-1,3]
data[t, 2] += 0.6*data[t-1, 2] + 0.3*data[t-2, 1] + c*data[t-1,3]
dataframe = pp.DataFrame(data, var_names=[r'$X^0$', r'$X^1$', r'$X^2$', 'Sun'])
tp.plot_timeseries(dataframe); plt.show()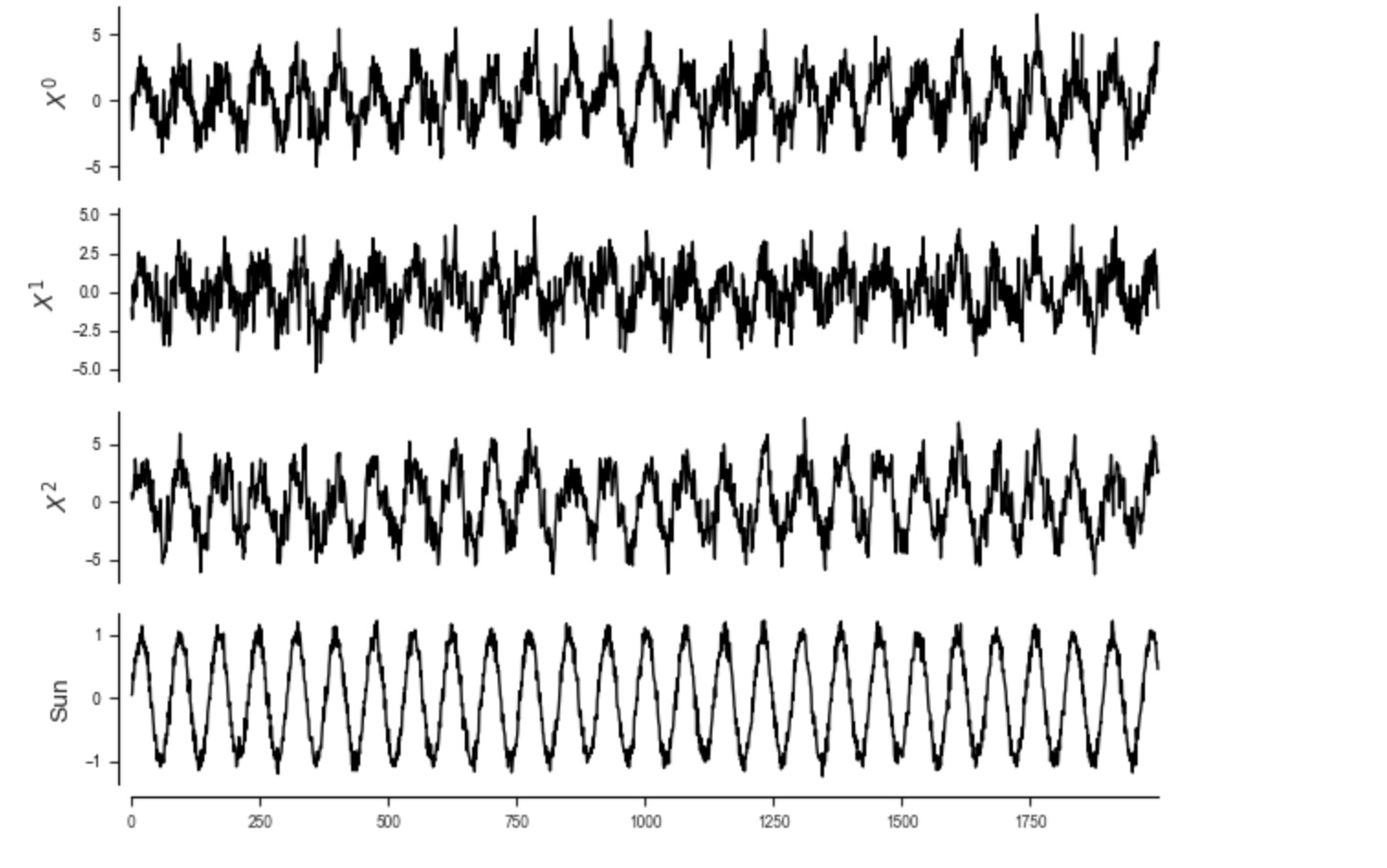
もし、共通の太陽の力を説明しないならば、多くの不確かなリンクがあることになります。
parcorr = ParCorr()
dataframe_nosun = pp.DataFrame(data[:,[0,1,2]], var_names=[r'$X^0$', r'$X^1$', r'$X^2$'])
pcmci_parcorr = PCMCI(
dataframe=dataframe_nosun,
cond_ind_test=parcorr,
verbosity=0)
tau_max = 2
results = pcmci_parcorr.run_pcmci(tau_max=tau_max, pc_alpha=0.2, alpha_level = 0.01)
# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()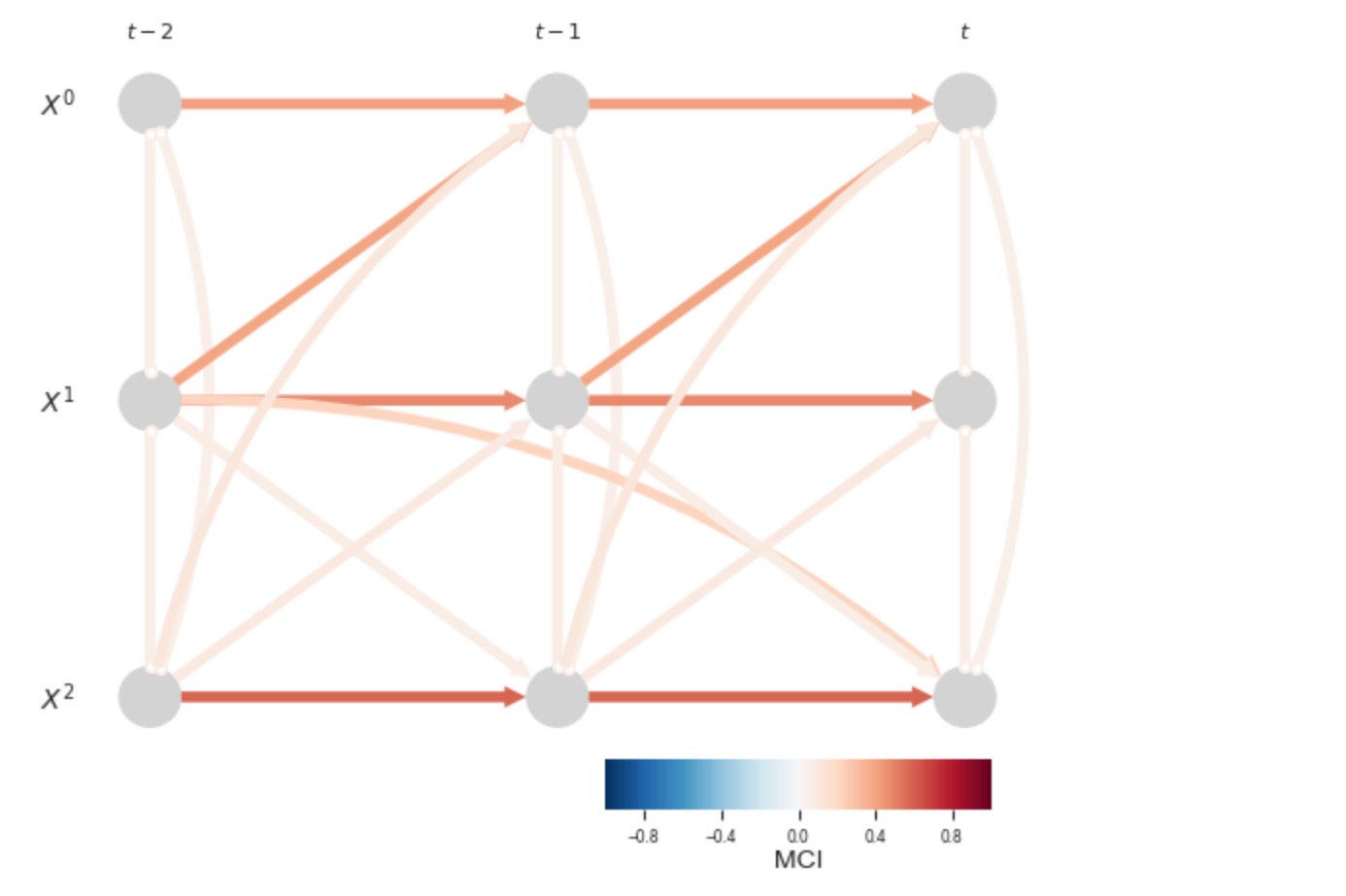
しかしながら、もし私たちが太陽の力の変数を明白に含むならば(それは私たちはこのケースでよく知られていると仮定します)、私たちは、正しい因果グラフを識別することができます。私たちは、太陽の力の変数のドライバーには関心がないので、私たちはその親の再構築に達しません。これは、link_assumtions(selected_linksは、ここで不可になります)によって再制限することによって、アーカイブされます。
parcorr = ParCorr()
# Only estimate parents of variables 0, 1, 2
link_assumptions = {}
for j in range(4):
if j in [0, 1, 2]:
# Directed lagged links
link_assumptions[j] = {(var, -lag): '-?>' for var in [0, 1, 2]
for lag in range(1, tau_max + 1)}
# Unoriented contemporaneous links
link_assumptions[j].update({(var, 0): 'o?o' for var in [0, 1, 2] if var != j})
# Directed lagged and contemporaneous links from the sun (3)
link_assumptions[j].update({(var, -lag): '-?>' for var in [3]
for lag in range(0, tau_max + 1)})
else:
link_assumptions[j] = {}
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_max=tau_max, pc_alpha=0.2,
link_assumptions=link_assumptions, alpha_level = 0.01)
# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=[r'$X^0$', r'$X^1$', r'$X^2$', 'Sun'],
link_colorbar_label='MCI',
); plt.show()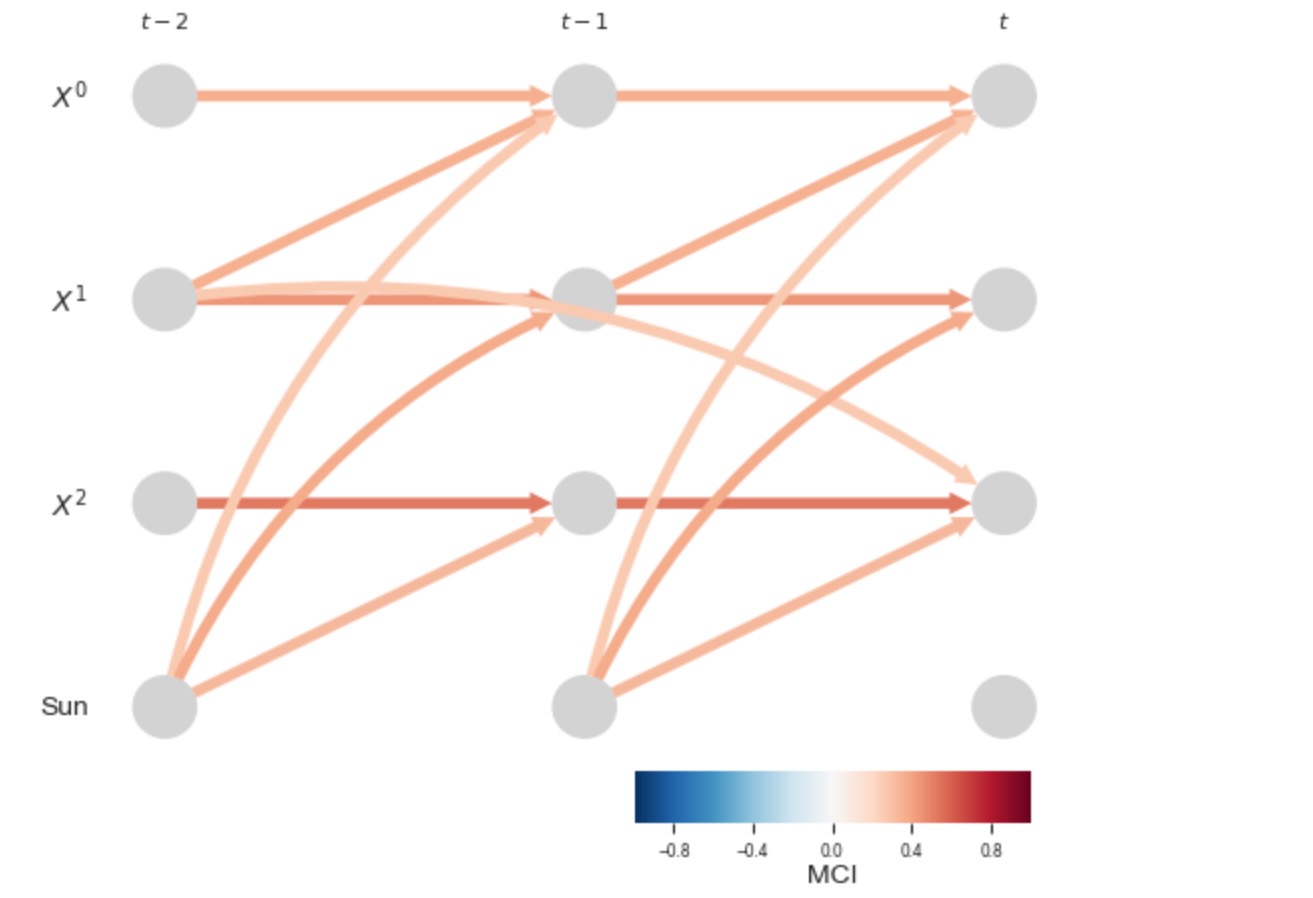
時間のサブサンプリング
ときに、時系列は、サブサンプルされます。それは、真の時間従属性をもとにしたものよりも低い頻度で測定されます。以下の過程を考えます。
seed=1
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((1000, 3))
for t in range(1, 1000):
data[t, 0] += 0.*data[t-1, 0] + 0.6*data[t-1,2]
data[t, 1] += 0.*data[t-1, 1] + 0.6*data[t-1,0]
data[t, 2] += 0.*data[t-1, 2] + 0.6*data[t-1,1]
dataframe = pp.DataFrame(data, var_names=[r'$X^0$', r'$X^1$', r'$X^2$'])
tp.plot_timeseries(dataframe); plt.show()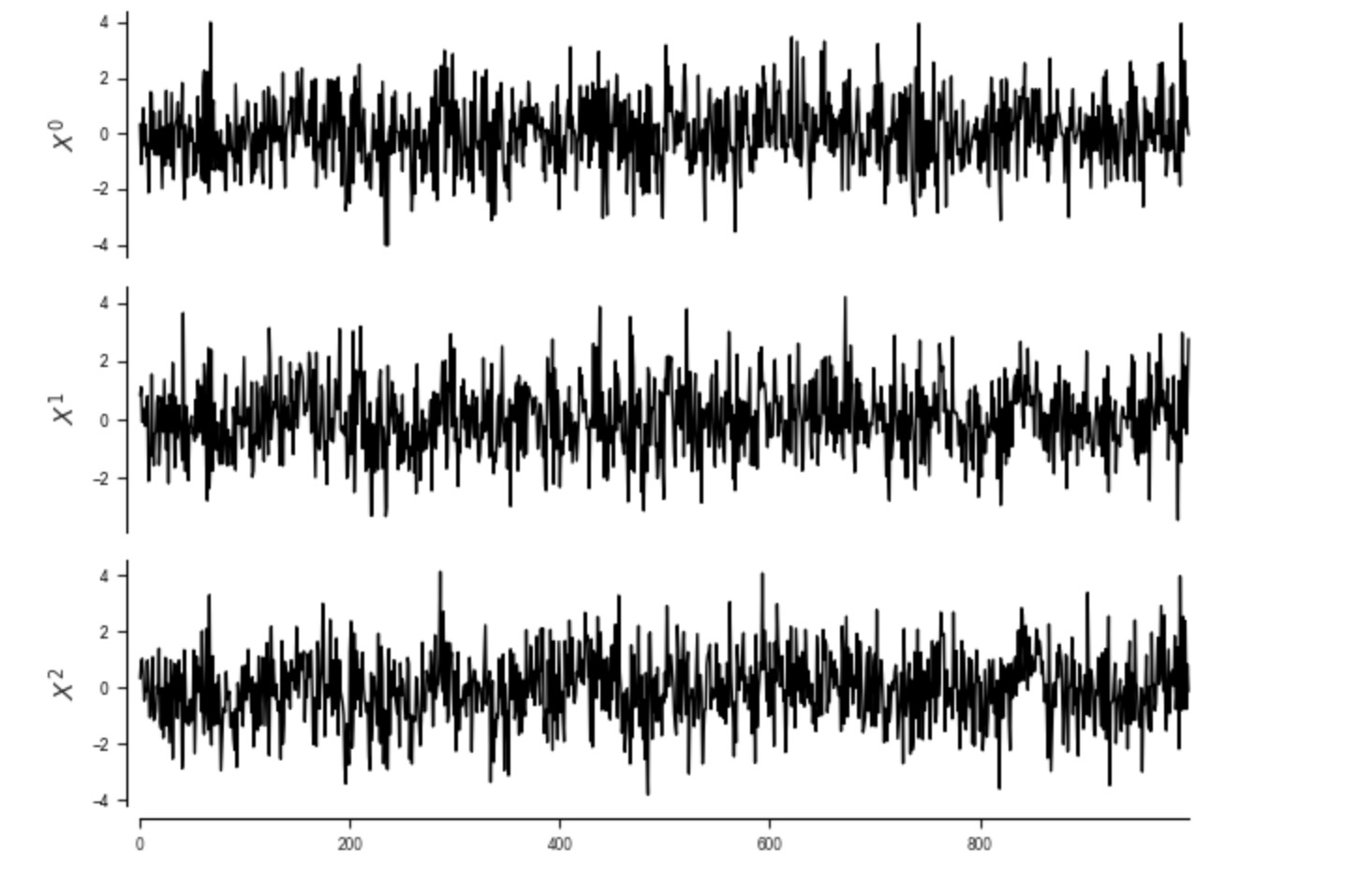
元の時間サンプリングに伴って、私たちは正しい因果グラフを得ます。
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr())
results = pcmci_parcorr.run_pcmci(tau_min=0,tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()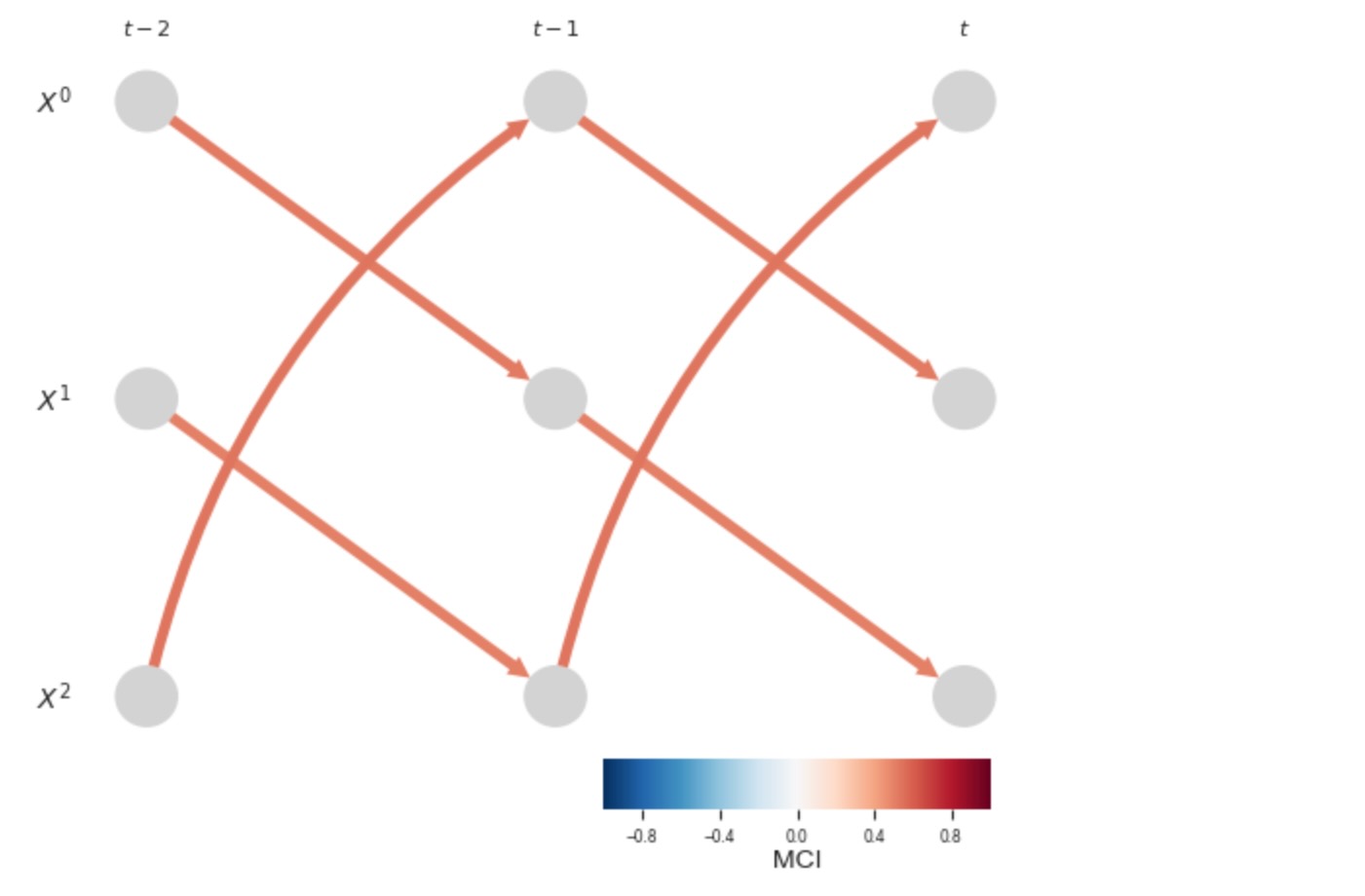
もし、私たちがデータをサブサンプルすれば、非常に直感に反したリンクが現れます。真の因果のループは、間違った方向に検出されることになります。
sampled_data = data[::2]
pcmci_parcorr = PCMCI(dataframe=pp.DataFrame(sampled_data, var_names=var_names),
cond_ind_test=ParCorr(), verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_min=0, tau_max=2, pc_alpha=0.2, alpha_level=0.01)
# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()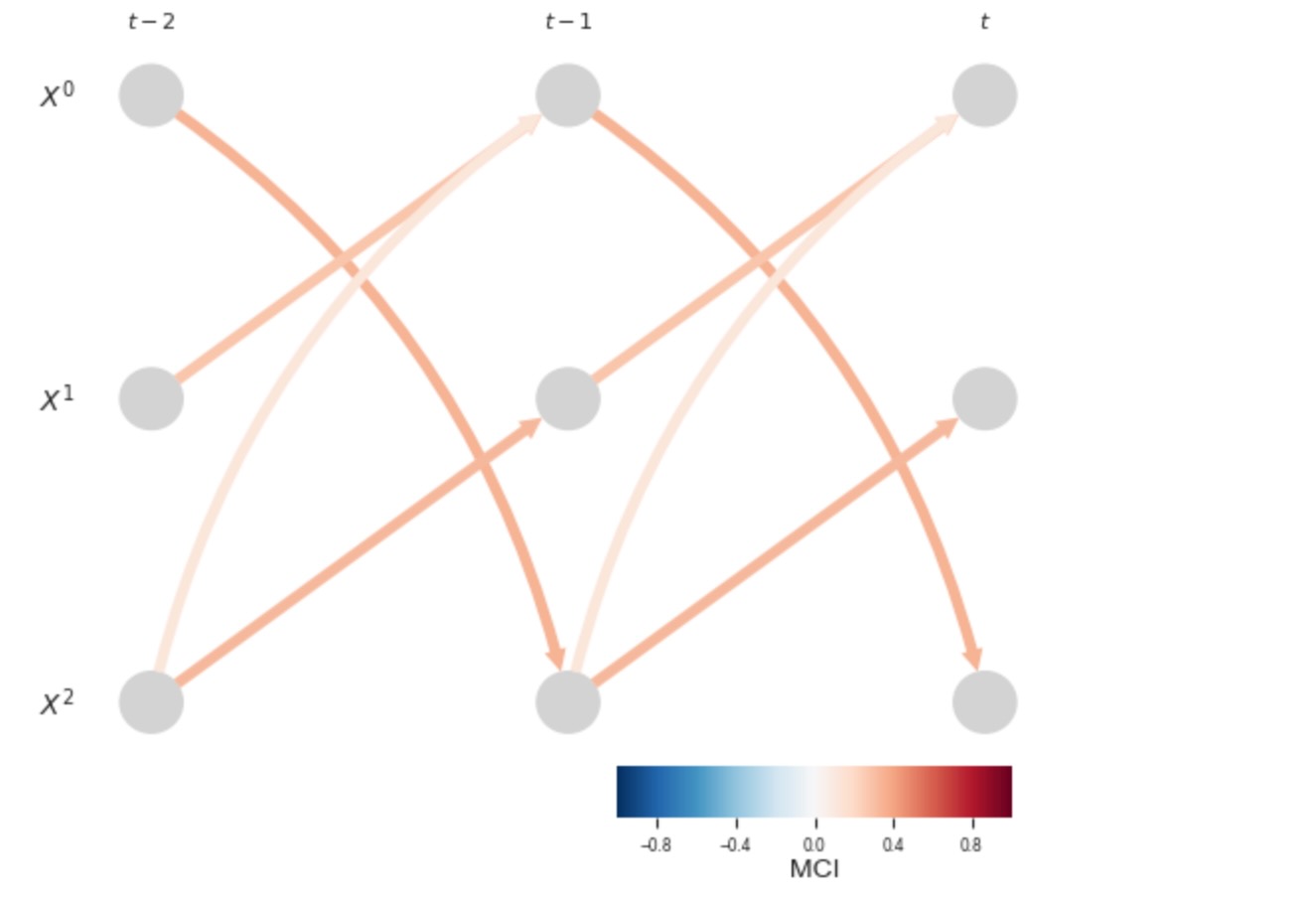
もし、因果のラグが、時間のサンプリングよりも小さいならば、そのような問題が発生します。サブサンプルデータのための因果推論は、まだ活発な研究領域です。
因果マルコフ条件
マルコフ条件は、各変数が互いに独立で、時間にも独立して動かされるノイズを仮定するように言い換えることができます。これは、以下の例の違反です。そこで各変数は、パワーススペクトラムのスケーリングを参照する、1/f ノイズで駆動されます。1/f ノイズは、AR(1)過程(http://www.scholarpedia.org/article/1/f_noise)の平均によって生成することができます。それは(AR過程)それ以上(各個別変数のノイズ項はまだ独立です。)ノイズが時間に独立しないことを意味しています。これは、観測過程のマルコフ条件の違反だけの構成要素であることに注意してください。そのため、これをむしろ因果の充分性の違反と呼ばれるかもしれません。
seed=1
random_state = np.random.default_rng(seed=seed)
T = 10000
# Generate 1/f noise by averaging AR1-process with wide range of coeffs
# (http://www.scholarpedia.org/article/1/f_noise)
def one_over_f_noise(T, n_ar=20):
whitenoise = random_state.standard_normal((T, n_ar))
ar_coeffs = np.linspace(0.1, 0.9, n_ar)
for t in range(T):
whitenoise[t] += ar_coeffs*whitenoise[t-1]
return whitenoise.sum(axis=1)
data = random_state.standard_normal((T, 3))
data[:,0] += one_over_f_noise(T)
data[:,1] += one_over_f_noise(T)
data[:,2] += one_over_f_noise(T)
for t in range(1, T):
data[t, 0] += 0.4*data[t-1, 1]
data[t, 2] += 0.3*data[t-2, 1]
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()
# plt.psd(data[:,0],return_line=True)[2]
# plt.psd(data[:,1],return_line=True)[2]
# plt.psd(data[:,2],return_line=True)[2]
# plt.gca().set_xscale("log", nonposx='clip')
# plt.gca().set_yscale("log", nonposy='clip')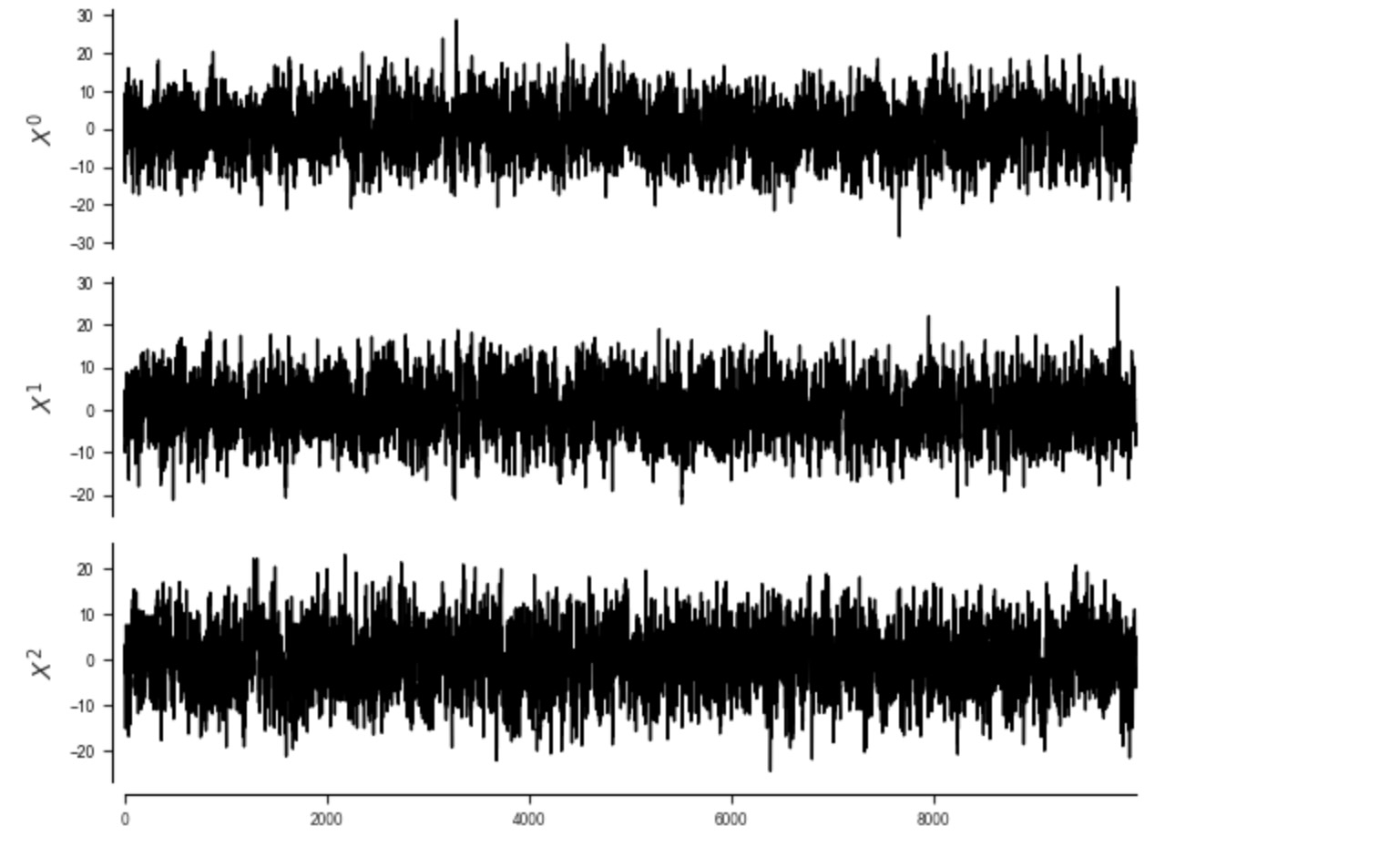
ここで、過程は長い記憶があり、そして現在の状態は、いくつかの親のセットで与えられる遠い過去から独立ではないので、特に自動依存性で、PCMCIは、多くの不確かなリンクを検出します。
parcorr = ParCorr()
pcmci_parcorr = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)
results = pcmci_parcorr.run_pcmci(tau_max=5, pc_alpha=0.2, alpha_level = 0.01)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 5
pc_alpha = [0.2]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X^0$ has 9 link(s):
($X^0$ -1): max_pval = 0.00000, min_val = 0.601
($X^1$ -1): max_pval = 0.00000, min_val = 0.294
($X^0$ -2): max_pval = 0.00000, min_val = 0.062
($X^0$ -4): max_pval = 0.00001, min_val = 0.044
($X^1$ -3): max_pval = 0.00480, min_val = 0.028
($X^0$ -5): max_pval = 0.00490, min_val = 0.028
($X^0$ -3): max_pval = 0.01260, min_val = 0.025
($X^1$ -4): max_pval = 0.05417, min_val = -0.019
($X^1$ -5): max_pval = 0.10577, min_val = -0.016
Variable $X^1$ has 5 link(s):
($X^1$ -1): max_pval = 0.00000, min_val = 0.615
($X^1$ -2): max_pval = 0.00000, min_val = 0.073
($X^1$ -3): max_pval = 0.00613, min_val = 0.027
($X^2$ -2): max_pval = 0.04390, min_val = 0.020
($X^0$ -5): max_pval = 0.06550, min_val = 0.018
Variable $X^2$ has 7 link(s):
($X^2$ -1): max_pval = 0.00000, min_val = 0.614
($X^1$ -2): max_pval = 0.00000, min_val = 0.177
($X^2$ -2): max_pval = 0.00000, min_val = 0.064
($X^2$ -5): max_pval = 0.00284, min_val = 0.030
($X^2$ -3): max_pval = 0.00652, min_val = 0.027
($X^2$ -4): max_pval = 0.08027, min_val = 0.018
($X^1$ -5): max_pval = 0.18810, min_val = 0.013
##
## Step 2: MCI algorithm
##
Parameters:
independence test = par_corr
tau_min = 0
tau_max = 5
max_conds_py = None
max_conds_px = None
## Significant links at alpha = 0.01:
Variable $X^0$ has 8 link(s):
($X^0$ -1): pval = 0.00000 | val = 0.464
($X^1$ -1): pval = 0.00000 | val = 0.371
($X^1$ -2): pval = 0.00000 | val = -0.178
($X^1$ -3): pval = 0.00000 | val = -0.100
($X^0$ -2): pval = 0.00000 | val = 0.089
($X^0$ -4): pval = 0.00009 | val = 0.039
($X^0$ -3): pval = 0.00096 | val = 0.033
($X^1$ -4): pval = 0.00312 | val = -0.030
Variable $X^1$ has 3 link(s):
($X^1$ -1): pval = 0.00000 | val = 0.476
($X^1$ -2): pval = 0.00000 | val = 0.073
($X^1$ -3): pval = 0.00707 | val = 0.027
Variable $X^2$ has 7 link(s):
($X^2$ -1): pval = 0.00000 | val = 0.470
($X^1$ -2): pval = 0.00000 | val = 0.280
($X^1$ -3): pval = 0.00000 | val = -0.119
($X^1$ -4): pval = 0.00000 | val = -0.087
($X^2$ -2): pval = 0.00000 | val = 0.084
($X^1$ -5): pval = 0.00000 | val = -0.068
($X^2$ -3): pval = 0.00000 | val = 0.046総時間
重要な選択は、総時系列の測定です。例えば、気候時系列は、日次で測定されます。しかし、ノイズの少ない時間と、月次の総数を分析するのに関心があるかもしれません。以下の過程を考えます。
seed=1
random_state = np.random.default_rng(seed=seed)
data = random_state.standard_normal((1000, 3))
for t in range(1, 1000):
data[t, 0] += 0.7*data[t-1, 0]
data[t, 1] += 0.6*data[t-1, 1] + 0.6*data[t-1,0]
data[t, 2] += 0.5*data[t-1, 2] + 0.6*data[t-1,1]
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()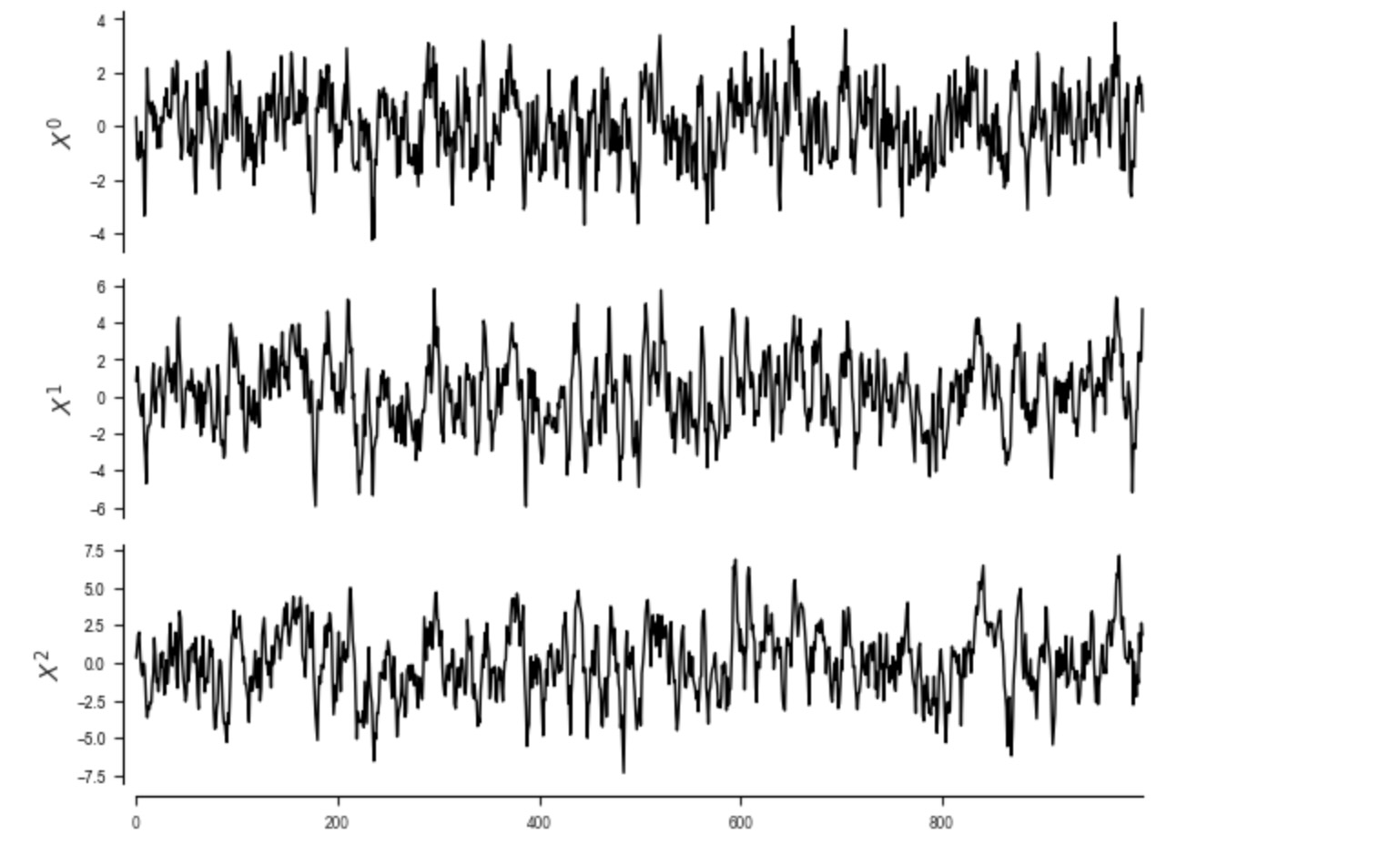
オリジナルの総時間とともに、私たちは、正確な因果グラフを得ます。
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr())
results = pcmci_parcorr.run_pcmci(tau_min=0,tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()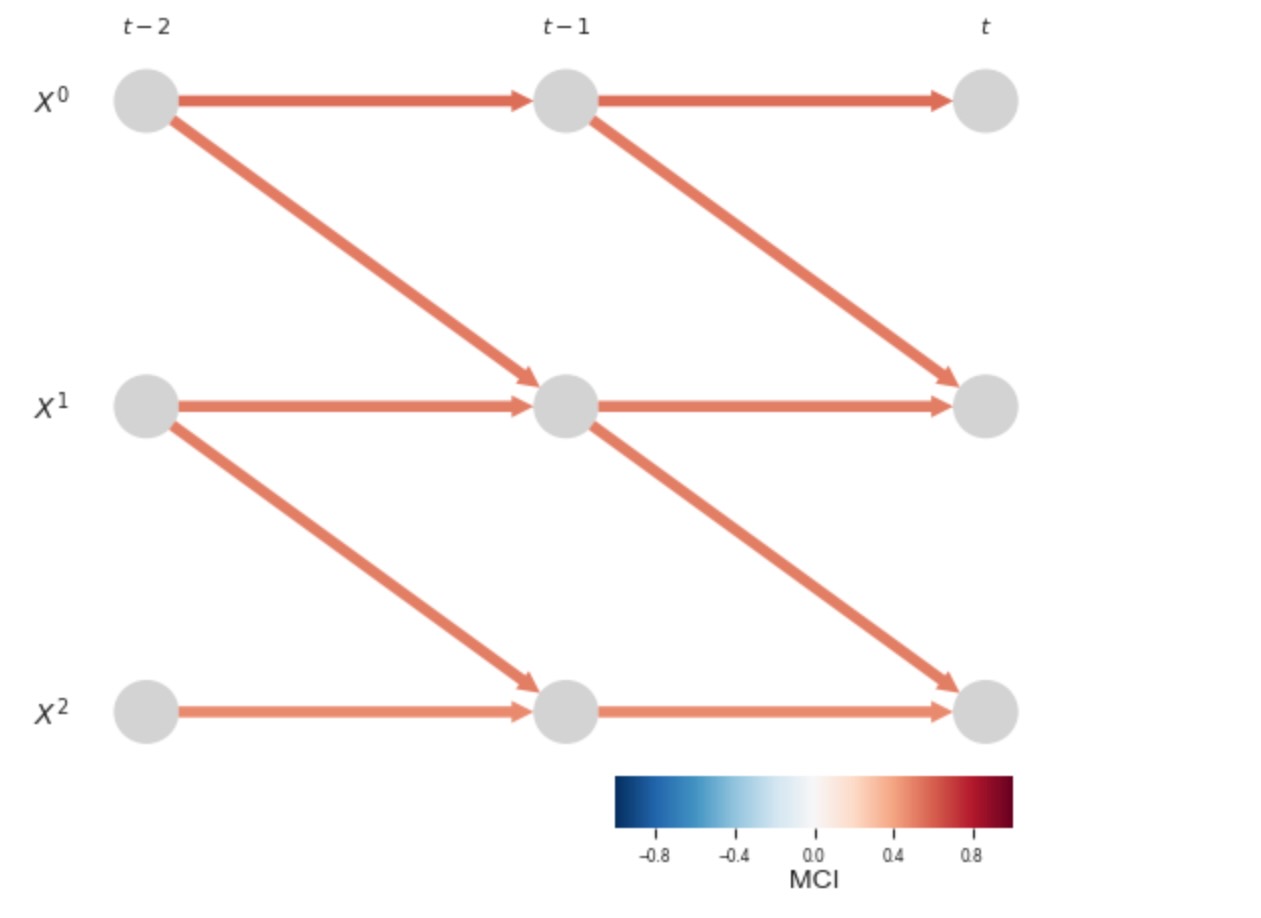
もし、私たちがデータを総和すれば、私たちは、このフレームワークでは原因の方向性が評価できない、同時に発生する依存性を検出します。そして私たちは、いくつかのラグのある不確かなリンクを得ます。特に、私たちはここで、総時間スケールの中で、同時に発生して現れる直接の原因を持っています。総時間のための因果推論もまた、活発な研究領域です。再度、これは観測過程のマルコフ条件の違反だけの構成要素であることに注意してください。
aggregated_data = pp.time_bin_with_mask(data, time_bin_length=4)
pcmci_parcorr = PCMCI(dataframe=pp.DataFrame(aggregated_data[0], var_names=var_names), cond_ind_test=ParCorr(),
verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_min=0, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Plot time series graph
tp.plot_time_series_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()