TIGRAMITEは時系列pythonモジュールです。PCMCIフレームワークを基礎にした離散または連続した値の時系列からグラフィカルモデルを再構築し、結果の高品質な図を生成します。
このチュートリアルは、causal_effect.pyからCausalEffectsクラスを説明します。それは、一般線形、非線形の因果の影響を推定することと最適化し調整したセットの調停ができるようになります。主要な背景の最適化調整理論を説明する論文は、
J.Runge, Necessary and sufficient graphical conditions for optimal adjustment sets in causal graphical models with hidden variables, Advances in Neural Information Processing Systems, 2021, 34 https://proceedings.neurips.cc/paper/2021/hash/8485ae387a981d783f8764e508151cd9-Abstract.html
注記:CausalEffectクラスは、明らかに時系列だけでなく、非時系列データにも取り組みます。
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
from scipy.stats import gaussian_kde
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.models import Models
from tigramite.causal_effects import CausalEffects
import sklearn
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.gaussian_process import GaussianProcessRegressor
# Find more estimators in sklearn!背景:Pearlの因果フレームワークと最適化調整
因果推論の標準的な問題設定は、因果グラフィカルモデルで与えられるY上の変数Xの因果の影響を推定することです。それは、隠された混乱させる変数の可能な表現を含んでいる観測した変数の間の量的な因果関係を規定します。PCアルゴリズムは典型的な因果の発見方法です。そしてPCMCI法とその派生のPCMCIplusとLPCMCIは時系列のための修正です。一旦、因果グラフが因果発見法で推定されると、量的な因果の影響を推定するためにそれが使えます。
因果関係 (Causal effects)
Yに対してX = xに設定するPearlの因果(causal effect)のフレームワークは、介入分布 p(Y| do(X=x))の関数です。この分布は原理的に条件確率p(Y|X=x)!からは異なります。Pearlのフレームワークの基本は、ランダム変数の間の根底にある構造因果モデルを(しかし未知の)仮定します。例えば、
X:= fX(Z,ηx)
Y:= fY(X,Z,ηx)
Z:= fZ(ηz)ここでf()は、左辺のランダム変数の値が、右辺の直接の原因(parentsと呼ばれます)とノイズ項ηによって決定される、代入関数として理解されます。これらのノイズ項はお互いに独立していることが仮定される、さらに進んだ因果ドライバーとして表されます。関連するグラフの中で端は、例えば、Xが代入関数の中で引数として発生するならば、ZからXへの出力になります。因果グラフは、非周期性を仮定し、因果関係の性質を表しています。

このSCMではp(Y|do(X=x)) は、介入されたSCMの確率分布として解釈されるものです。ここでXの代入式は取り替えられます。
X:= x
Y:= fY(X,Z,ηx)
Z:= fZ(ηz)これは、実験的な介入の設定の模倣です。介入された変数への全てのリンクに一致するグラフは削除されます。与えられたこのSCMで、介入do(X=x’)と比較した介入do(x=x)の平均因果の影響は、以下で定義されます。
Δyxx'|s = E[Y|do(x)] - E[Y| do(x')]条件付き因果 (Conditional causal effects)
時に、グラフの他の変数S の値 S=s の条件での因果に関心を向けるかもしれません。条件付き因果分布は、次のように示されます。
P(Y| do(X=x), S=s)そして最初の介入設定X=xの実験そ基礎にして、その後、S = s のための条件介入分布を考えます。その時、S = s の条件で介入 do(X=x’) と比較した 介入 do(X=x)の 平均条件因果の影響は、次のように定義されます。
Δyxx'|s = E[Y|do(x),s] - E[Y| do(x'),s]多変量因果 (Multivariate causal effects)
X,Yの多変量因果は、それ相応に定義されます。多変量Yの因果は、常に個別の影響 Y ⊆ Y に分解できることに注意してください。一方で、単一の介入 X ⊆ X は、全体の多変量Xの介入より原理的に異なる実験を参照します。
調整
Pearlの理論は、観測変数Vの間でYにおけるXの因果関係が識別できるかどうかの性質があわかる尺度を利用するための純粋なグラフィカルな知識を与えます。例えば、介入の対象かどうかの疑問は、次のように書けます。
p(Y| do(X=x)) = q(p(V))ここで、q(p(V))は、観測分布のesitmandと呼ばれる、任意の関数です。一般的なdo-calculasは、(Pearl2009 Shpister et al.,2010)は、このケースでは、完全に特徴づけられて使用されます。あるクラスのestimandはbackdoor調整を基礎にしています。ここで調整変数Zの適切なセットは、観測分布の項の設定do(X=x)のための介入分布を、次のように表現することができます。
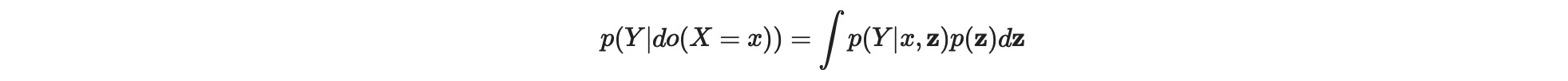
空でないZの、そして空のZ=0には、p( Y|do(X=x)) = p(Y|x). そうしたセットは、(X,Y)に対する正しい調整セットと呼ばれます。繰り返すために、ここの糸口は、介入の因果関係が介入なしで計算できることです。しかし、グラフの仮定が正しければ、観測データだけを基礎にします。
ここで、私たちは、一般化バックドア調整だけを考えます。その率は、十分です。しかし、因果を識別する評価基準は必要ありません。この終端は、XからYへの因果の経路の中間値Mと禁止されたノード forb(X,Y)=X ∪ des(YM) によって示します。ここで、desはグラフの派生を示します。一般化バックドア基準によれば、 調整セットZは以下の条件を保持する時のみ、正しくなります。
- Z ∩ forb = 0 そして
- 全ての非因果のXからYへの経路はZによってブロックされます。
XからYへの因果の経路は、直接のYへの終端だけからなります。全ての他の経路は非因果と呼ばれます。調整セットは、もしZの制限のないサブセットがまだ正しければ、minimalと呼ばれます。
最適調整セット
私たちは、正しい引数のセットZ、Δyxx'|s,zとして、で与えれらる推定値を示します。共変量としてそのような正しい調整セットを基礎にした因果の推定は、隔たりません。しかし、異なる調整セットのための推定変数は、強力に変化します。最適調整セットは、最小の漸近の推定変数を持つものとして特徴づけられます。もっと形式的には、タスクは、正しい最適セットZを選択するために、グラフと(X,Y,S)(Sはおそらく空)で与えられます。そのような因果の影響の推定の漸近変数は、Var(Δyxx'|s,z) = E[Δyxx'|s - Δyxx|s,z)2] は最小の
Zoptimal ⊆ argminz Var(Δyxx'|s,z)隠れ変数付きの一般化グラフィカルモデルのための最適調整セットは、 隠れ変数なしのケースのためのHeckel et al(2019)による仕事に続く、Rungeに派生しました。正しいanestors ancs = an(XYS)\forb により定義。その時、0-セットは次に定義されます。
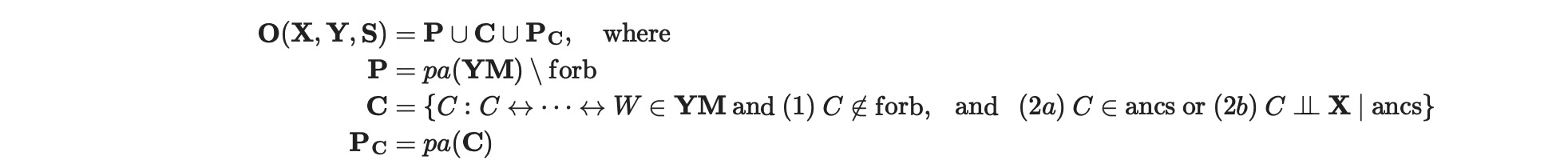
ここで、W <-> … <-> C ビームのパスを示します。もし、隠れ変数が、提供されないと(両方向の終端で)、その時、O= pa(YM)\ forb, それはHeckel et al(2019)により派生されました。
DAGsにとって0-セットは常に最適です。そこに隠れ変数があるグラフにとって、最適化調整セットが存在しない、ケースにできます。それは、グラフからなる任意の分布のための全ての調整セットの間で最小の変数を持ちます(論文参照)。最適調整セットが存在するtuples(graph,X,Y,S)では、私たちは、グラフィカル最適性保持と言います。
Rungeの理論的な寄与は、状況の理論的命題は、
- もし正しいバックドア調整が存在する場合、その時にだけ、 O-セットは正しい調整セットになります。
- O-セットは、任意のグラフの調整セットより小さい変数を持ちます。
- 完全に、tuples(graph,X,Y,S)で特徴づけられるグラフィカル最適性は、保持します。
これらの結果は、線形な推定を保持するために証明されました。しかし、数値的な実験は、Oセットまたは共変量が典型的に、他の調整、ニューラルネット、kー最近某、rランダムフォレスト、ガウス過程を基礎にした推定、を上回っていることが示されました。
あるそのようなOセットの共変量が、コライダー最小化O-セットです。そこで、非因果経路をブロックしないコライダーノードは、削除されます。このセットは、次元の呪いに苦しむもっと複雑な推定に役立つことができるO-セットより小さい座標を持ちます。
調整を通る因果の推定
私たちは次で定義される処置の効果平均に焦点を当てます。
Δyxx' = E[Y|do(x)] - E[Y|do(x')]個別の項は、次の調整セットZを使って推定することができます。
E[Y|do(x)] = Ez[EY|X,Z[Y|X=x, Z=z]]Tigramite CausalEfectクラスに実装されている現在のアプローチは、(X,Y,Z)のための観測データからの任意のモデルのY=f(X,Z)内部予想で推定されます。その時、介入された値、X=xで、f(X=x,Z=z)を評価します。そして、その時、期待値をとります。
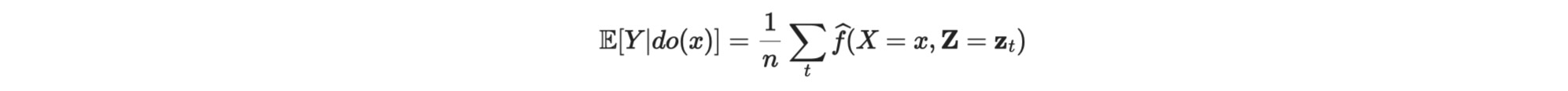
ここで、nは、Zのサンプルサイズです。
線形ケース
線形のケースでは、しかし、ここでXの多変量介入を仮定すると、Xへの因果 wrtは次のように書けます。
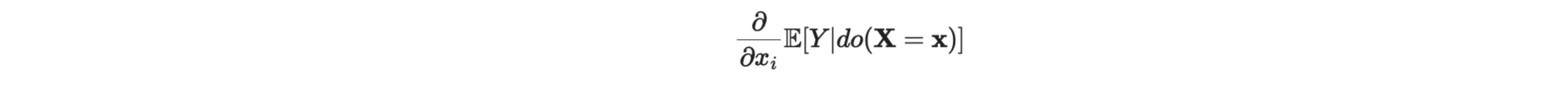
それは、モデルの回帰係数 βY,X,ZZ\Xi に等しくなります。
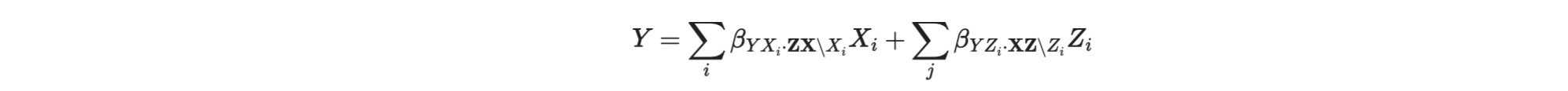
条件付き因果の推定
条件の効果は、線形モデルでは発生できません。そのため、これは、非線形モデルにだけ適用されます。
S=sで与えられる介入do(X=x')と比較される潜在的多変量介入 do(X=x)の処置の影響の条件付き平均は、以下で定義されます。
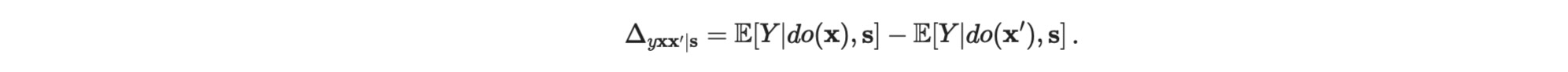
個別項は、次のように調整セットZを使って、推定することができます。
その現在の実装で、これらのネストされた予測は、ネストされた回帰によって推定されます。そこで、内部の予期は、estimatorモデルを使い、外部の予測はconditional_estimatorモデルを使います。もっと明確には、ステップは、
- 観測データのesimatorモデルを使った内部予期 Y=f(X=x,Z=z,S=s)の適合
- ztが観測データ、xが介入値、そしてsが条件値の場合、Y XZS = f(X=x,Z=z,S=s)の予測
- Sの観測値のモデルconditional_estimatorを使った外部予期 Y xzsの適合
- sが条件値Sである場合の Y do(X),S = g(S=s)の予測
Wright推定と線形効果の推定
Swall Wright(Wright1921)は、特別な方法で線形モデルの因果を推定することを、すでに100年前に提案しました。それは、最初に、パス係数と呼ばれる因果パスに属する全てのリンクを推定します。そして、その後、これらのパス係数の積の全ての因果パスの総和をとります。
このアプローチは、DAGsにだけ適用されます。そして推定のステップは、
- XからYへの因果パスに属する全ての因果リンク i->j は、全てのその親と、親に属する係数を取ることでjを回帰することによって、パス係数βi->jを推定します。
- その後、因果の影響は、
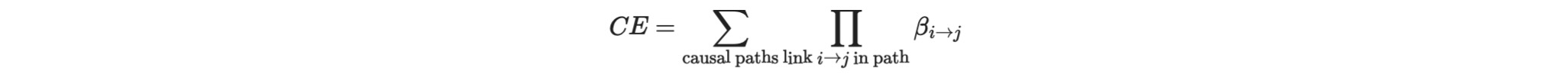
この推定を、選択された中間値M* の間の少なくとも一つのノードを通すパスだけに制限することによって、中間の因果の影響を計算することができます。
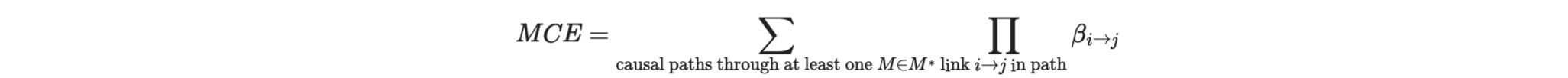
これは、また、パラメータmediationを通すクラスに実装されます。mediation='direct'は、係数βX->Yの direct effectだけ、もし0でなければ、返されます。
質的な因果の知識を記述するグラフの種別
非時系列データ
質的な知識は、異なる様式で現れます。例えば、 有向非周期性(directed acyclic)グラフ(DAG)の任意の変数、ここではL、が観測されないことを仮定しても構いません。

隠れ変数の存在を表現するもう一方の方法は、非周期性有向混合(acyclic directed mixed graph)グラフ(ADMG)を通すことです。それはここでは、

ADMGは、直接、関節に終端で一つ以上の潜在的な混乱させる変数を表現します。
時系列データ
この時系列の文脈では、私たちは時間に従属スタSCMsを考えます。重要な仮定は、ステーショナリティーです。言い換えると、SCMは時点 t に依存しません。その時、ステーショナリーDAGの結果のノードとして、異なる時間のインスタンスで、各変数を表現してよいでしょう。
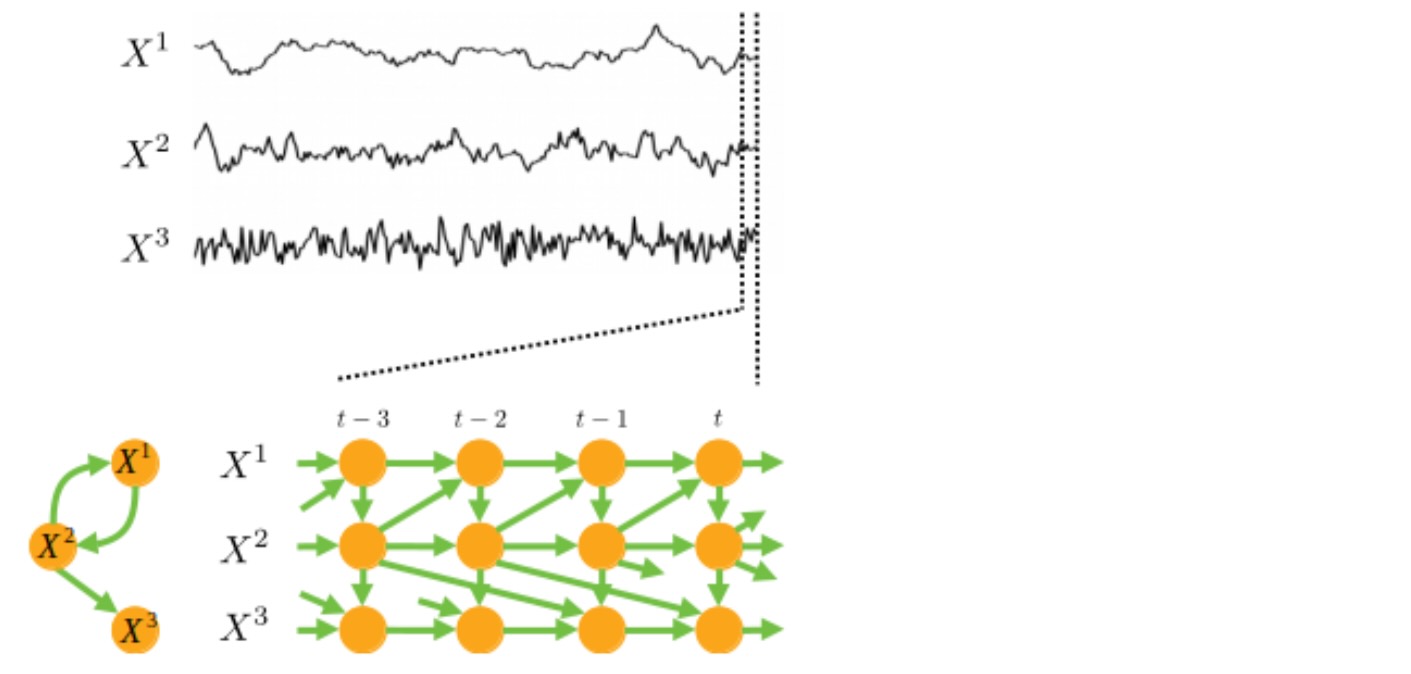
ステーショナリー仮定は、このグラフが過去、未来において繰り返されること示唆しています。時間tの全ての因果の終端の知識は、その時全ての因果関係を表現するために十分です。最大の時間ラグを伴う因果のリンクは、その時、仮定の順序として定義します。上の例では、あなたは、実際、まだ非周期の時系列グラフである結果のグラフのフィードバック周期を見ることができます。
現在の実装法の制限
隠れ変数付きのステーショナリー時系列DAGsの理論は、もっと複雑で、現在Tigramiteでは取り上げていません。しかし、ADMGsは非時系列ケースを取り上げます。
上に述べたように、最適調整セットの理論的結果は、線形最小二乗推定と単一のXのために設定された。しかし、数値的結果は、O-セットまたは、最小化した変形は、多変量Xを保持することを示します。そして、kNN、ニューラルネットワーク、ガウス過程またはランダムフォレストのような非パラメトリック推定と非最適化設定内の、小さい変化にしばしば分離します。
参考文献
- Pearl, J. (2009). Causality: Models, reasoning, and inference. Cambridge University Press.
- Perković, E., Textor, J., and Kalisch, M. (2018). Complete graphical characterization and construction of adjustment sets in markov equivalence classes of ancestral graphs. Journal of Machine Learning Research, 18:1–62.
- Shpitser, I., VanderWeele, T., and Robins, J. M. (2010). On the validity of covariate adjustment for estimating causal effects.
- Runge, J. (2021). Necessary and sufficient graphical conditions for optimal adjustment sets in causal graphical models with hidden variables. Advances in Neural Information Processing Systems, 34.
- Henckel, L.; Perković, E. & Maathuis, M. H. (2019). Graphical criteria for efficient total effect estimation via adjustment in causal linear models arXiv preprint arXiv:1907.02435
- Wright, S. (1921). Correlation and causation. J. Agric. Res., 20, 557-585
Causal Effect クラス
初期化
CausalEffets は以下の引数をとります。
graph, graph_type と hidden_variables
graphは、graph_typeに依存する異なるシェイプのdtype ='<U3'の文字列配列です。
- graph_type ='dag' 非時系列DAGを示します。ここでgraphは、(N,N)のシェイプで、Nはノード数を示します。
- graph_type='admg' 非時系列ADMGを示します。ここで、graphは(N,N)のシェイプです。
- graph_type ='stationary_dag' は、ステーショナリー時系列DAGを示します。ここで、graphは、(N ,N,tau_max±1)シェイプで、tau_maxは最大時間ラグです。'+1'は、同時に存在する関係を示します。
hidden_variablesは、それは隠れた変数、または時系列グラフ、もっと一般的には、変数Kの選択された隠れた時点だけを含むtuples[(k,-tau),...]のリストです。例えば、(k,-tau)は、 X t-r k を示しています。現在、隠れた変数は、時系列用にサポートされていないことに注意してください。
各ケースでグラフのエントリーは、dtype='<U3':
graph_type='dag'用の終端は、'<--' または、'-->'. 例えば、上のDAGの変数(L,X,Z,Y)は次のように与えられます。
graph = np.array([['', '-->', '-->', ''],
['<--', '', '', '-->'],
['<--', '', '', '-->'],
['', '<--', '<--', '']], dtype='<U3')hidden_variables=[(0,0)]に設定します。
ADMGには、graph_type='admg' の終端は、'<--', '-->', '<->', '+->', または '<-+'. 例えば、変数(X,Z,Y)は、
graph = np.array([['', '<->', '-->'],
['<->', '', '-->'],
['<--', '<--', '']], dtype='<U3')終端の種別'+->', '<-+' は、方向と双方向の終端の両方の存在を表します。
hidden_variablesは、ADMG入力に特徴づけることができます。その後、内部で修正したADMGは潜在プロジェクション操作を基礎に構築されることに注意してください。
最後に、graph_type='stationary_dag'の終端は、時間ラグと双方向リンクが'-->'、そして'<--'が、例えばgraph[:,:,0]の中の双方向リンクのためだけに設定できます。例えば、変数(X1,X2,X3) 上のセクションのグラフは、次で与えられます。
graph = np.array([[['', '-->', ''],
['', '', ''],
['', '', '']],
[['', '-->', ''],
['', '-->', ''],
['-->', '', '-->']],
[['', '', ''],
['<--', '', ''],
['', '-->', '']]], dtype='<U3')全てのケースで、graphは非周期的に違いなく、一致する終端を持ちます。例えば、graph[i,j,taui,tauj]='-->' は、 graph[j,i,tauj,taui]='<--'を要求します。ステーショナリーDAGには、これは、ゼロラグに関係します。例えば、graph[:,:,0]
内部では、CausalEffectクラスは、ステーショナリーDAGをADMGへ、シェイプ(N,N,tau_max+1, tau_max + 1)の潜在プロジェクション操作を経由して変換します。このADMG内の調整セットは、その後計算されます。そうしたグラフはgraph_type='tsg_admg'または、graph_type='tsg_dag'へのgraphとして与えられることのよって直接表されます。
X, Y, と オプションで S
これらは、因果変数X、結果変数Y, そして、オプションで条件変数 S と表現します。全ては、tau>0の時のtuple[(i, tau), ...]のリストです。graphが与えられると、クラスはオーバーラップが存在しないかチェックします。そして実際にXからYへ因果のパスがあります。さらに、条件Sは、禁じられたセットしてはなりません。
上の隠れ変数のある簡単なDAGで始めましょう。
graph = np.array([['', '-->', '-->', ''],
['<--', '', '', '-->'],
['<--', '', '', '-->'],
['', '<--', '<--', '']], dtype='<U3')
hidden_variables = [(0,0)]
X = [(1,0)]
Y = [(3,0)]
causal_effects = CausalEffects(graph, graph_type='dag', X=X, Y=Y, S=None,
hidden_variables=hidden_variables,
verbosity=1)
## ## Initializing CausalEffects class ## Input: graph_type = dag X = [(1, 0)] Y = [(3, 0)] S = [] M = [] hidden_variables = {(0, 0)}
内部で、隠れ変数のあるDAGは、潜在プロジェクション操作を通して、ADMGに転換されます。tigramite.plottingモジュールからplot_graph関数を使ってADMGを図示しましょう。ノードの位置、色付け、その他を変化させるためのさらなるオプションを見るために、ドキュメント文字列を見ることができます。
# Just for plotting purposes
var_names = ['$L$', '$X$', '$Z$', '$Y$']
tp.plot_graph(graph = causal_effects.graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (4, 4),
); plt.show()
次に、私たちは上の'plot_time_series_graph'関数の使用からステーショナリー時系列を示します。
graph = np.array([[['', '-->', ''],
['', '', ''],
['', '', '']],
[['', '-->', ''],
['', '-->', ''],
['-->', '', '-->']],
[['', '', ''],
['<--', '', ''],
['', '-->', '']]], dtype='<U3')
X = [(1,-2)]
Y = [(2,0)]
causal_effects = CausalEffects(graph, graph_type='stationary_dag', X=X, Y=Y, S=None,
hidden_variables=None, #[(1, -1)],
verbosity=1)
var_names = ['$X^0$', '$X^1$', '$X^2$']
tp.plot_time_series_graph(graph = graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 4),
); plt.show()
## ## Initializing CausalEffects class ## Input: graph_type = stationary_dag X = [(1, -2)] Y = [(2, 0)] S = [] M = [(1, 0), (2, -1), (2, -2), (1, -1)]
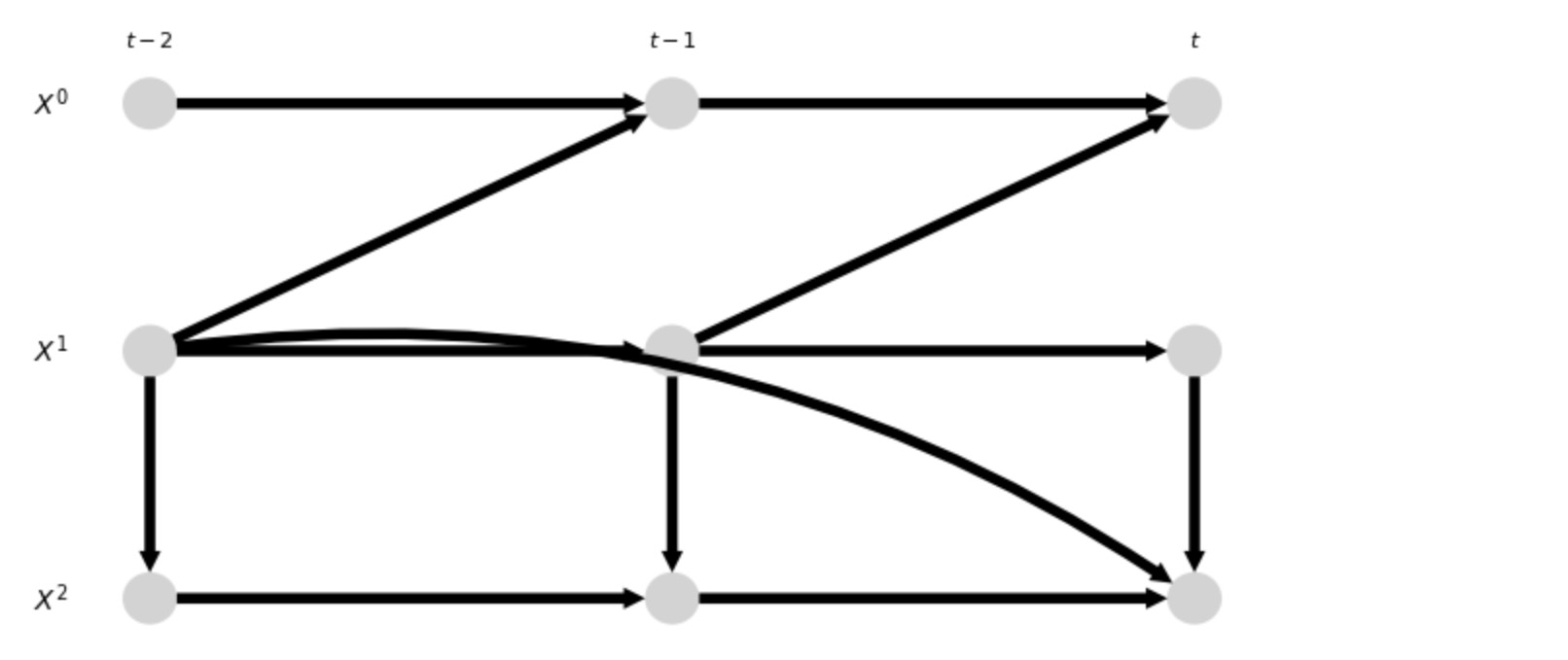
上のグラフは、ステーショナリーを仮定している時系列グラフです。そして、このように上の終端を過去と未来へ向けて繰り返します。CausalEffectsクラスは、これらの無限のグラフを処理しませんが、むしろ、ステーショナリーグラフのための潜在プロジェクション操作を経由して同じd-separationsによる有限のADMGを構築します。
以下は調整とパスが基礎にしているこの有限のtsg_admgです。
tp.plot_time_series_graph(graph = causal_effects.graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 4),
); plt.show()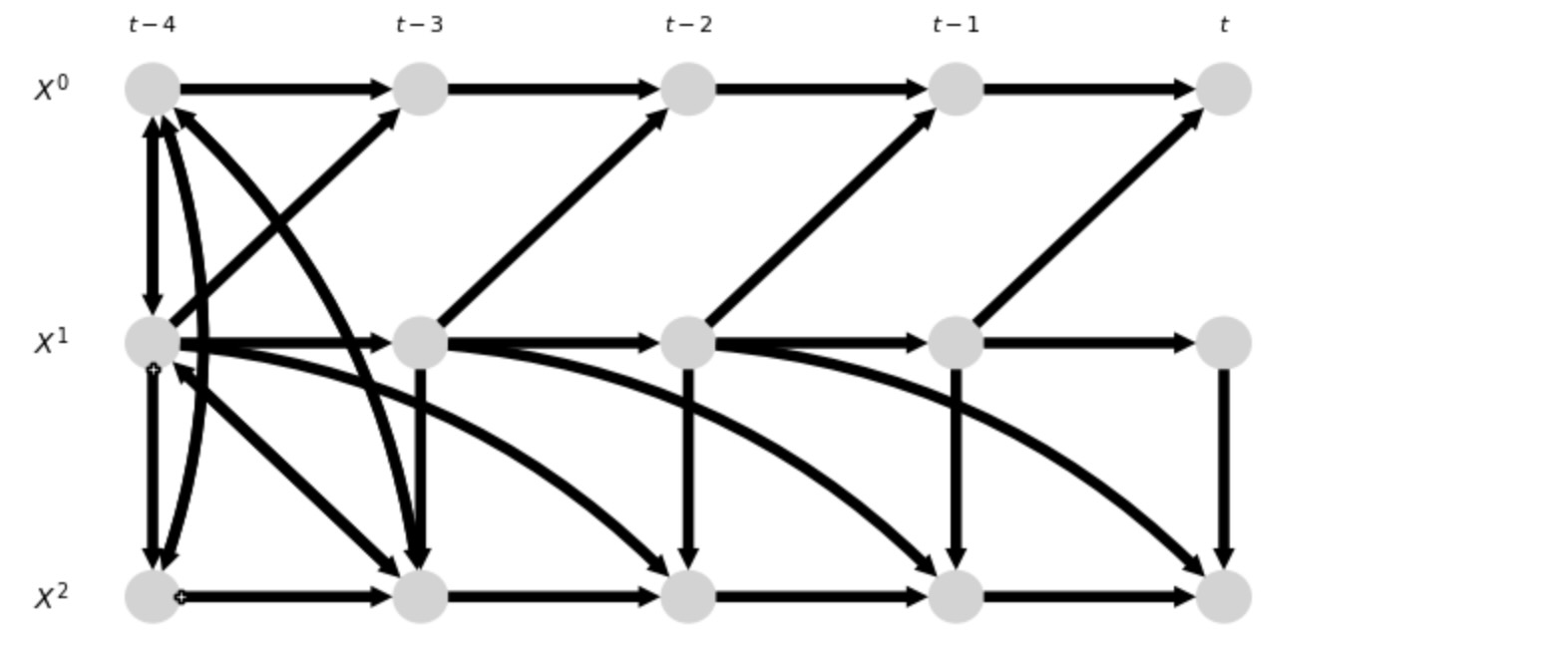
このグラフが示しているのは、τ max = maxlag(X,Y,S) + graph.shape[2] -1( here τ max = 4) に拡張したADMGです。この選択の理由は親YとMからなる0-セットは、ここで、正しい調整セットに完全に再構築されます。リンク '+->' は双方向<-> と因果リンク -> の両方の存在を示しています。
あなたは、また静的なメソッド CausalEffects.get_graph_from_dict(links,tau_max=None) をtigmaiteの様式モデルデータの辞書リンクからグラフを生成するために使えます。また、フォーマット{0:[((0,-1), coeff, func), ...], 1:[...],...}は、tigmaiteのtoyモデルデータの使用そ許容します。coeffとfuncパラメータは、グラフの生成時に無視されます。graphのシェイプは、(N,N,tau_max+1) ここで tau_maxは、辞書から自動で推定するか、引数として与えることができます。もしあなたが、シェイプ(N,N)の大きな非時系列のDAGが必要ならば、ゼロラグのリンクを与え、それからグラフを絞り出してください。:dag_graph = graph.squeeze().
それは、静的なメソッドなので、あなたはCausalEffectsを前もって初期化する必要はありません。
def lin_f(x): return x
links = {0: [(0, -1)],
1: [(1, -1), (0, -3)],
2: [(2, -1), (1, 0)],
}
graph = CausalEffects.get_graph_from_dict(links, tau_max=None)
print(graph)[[['' '-->' '' ''] ['' '' '' '-->'] ['' '' '' '']] [['' '' '' ''] ['' '-->' '' ''] ['-->' '' '' '']] [['' '' '' ''] ['<--' '' '' ''] ['' '-->' '' '']]]
多変量Xのもっと複雑な非時系列ADMGを考えてみましょう。
graph = np.array([['', '-->', '', '', '', '', ''],
['<--', '', '-->', '-->', '', '<--', ''],
['', '<--', '', '-->', '', '<--', ''],
['', '<--', '<--', '', '<->', '', '<--'],
['', '', '', '<->', '', '<--', ''],
['', '-->', '-->', '', '-->', '', ''],
['', '', '', '-->', '', '', '']], dtype='<U3')
X = [(0,0), (1,0)]
Y = [(3,0)]
causal_effects = CausalEffects(graph, graph_type='admg', X=X, Y=Y, S=None, hidden_variables=None,
verbosity=1)
# Just for plotting purposes
var_names = ['$X_1$', '$X_2$', '$M$', '$Y$', '$Z_1$', '$Z_2$', '$Z_3$']## ## Initializing CausalEffects class ## Input: graph_type = admg X = [(0, 0), (1, 0)] Y = [(3, 0)] S = [] M = [(2, 0)]
tp.plot_graph(graph = graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 6),
); plt.show()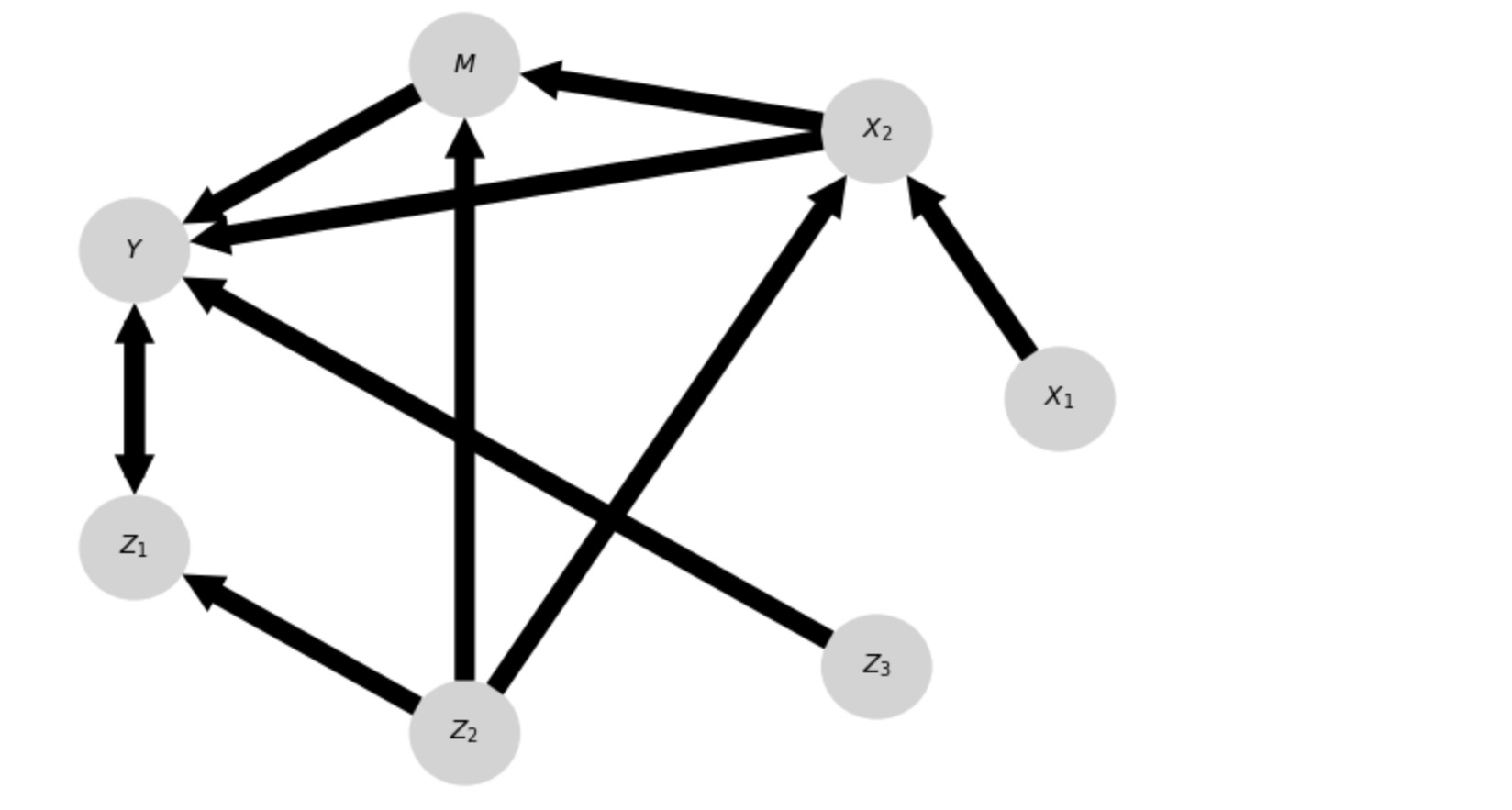
チェック
中間値Mは、グラフから自動で計算されます。これは、YとZ1の間の双方向に終端のあるADMGです。
調整セットを熟考する前に、私たちは、適切な因果パスに寄与しないノードがX(またはY)から、実際に削除できるかどうかチェックすることができます。
newX, newY = causal_effects.check_XYS_paths()Consider pruning X = {(1, 0), (0, 0)} to X = {(1, 0)} since only these have causal path to Yここで、これはケースです。しかし、それが因果の推定を変化しないので、私たちは、オリジナルXを維持するだろう。
調整セット
私たちは、ここで、直接fit_total_effectとpredict_total_effect関数へ移ることができます。それは、自動的に、最適な適合セットに使います。しかし、その前に、私たちは、異なる可能な調整セットを簡潔に議論します。
デフォルトのクラスの実装は、0-セットです。上のグラフは
opt = causal_effects.get_optimal_set()
print("Oset = ", [(var_names[v[0]], v[1]) for v in opt])Oset = [('$Z_1$', 0), ('$Z_2$', 0), ('$Z_3$', 0)]special_nodes = {}
for node in causal_effects.X:
special_nodes[node] = 'red'
for node in causal_effects.Y:
special_nodes[node] = 'blue'
for node in opt:
special_nodes[node] = 'orange'
for node in causal_effects.M:
special_nodes[node] = 'lightblue'
tp.plot_graph(graph = graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 6),
special_nodes=special_nodes,
); plt.show()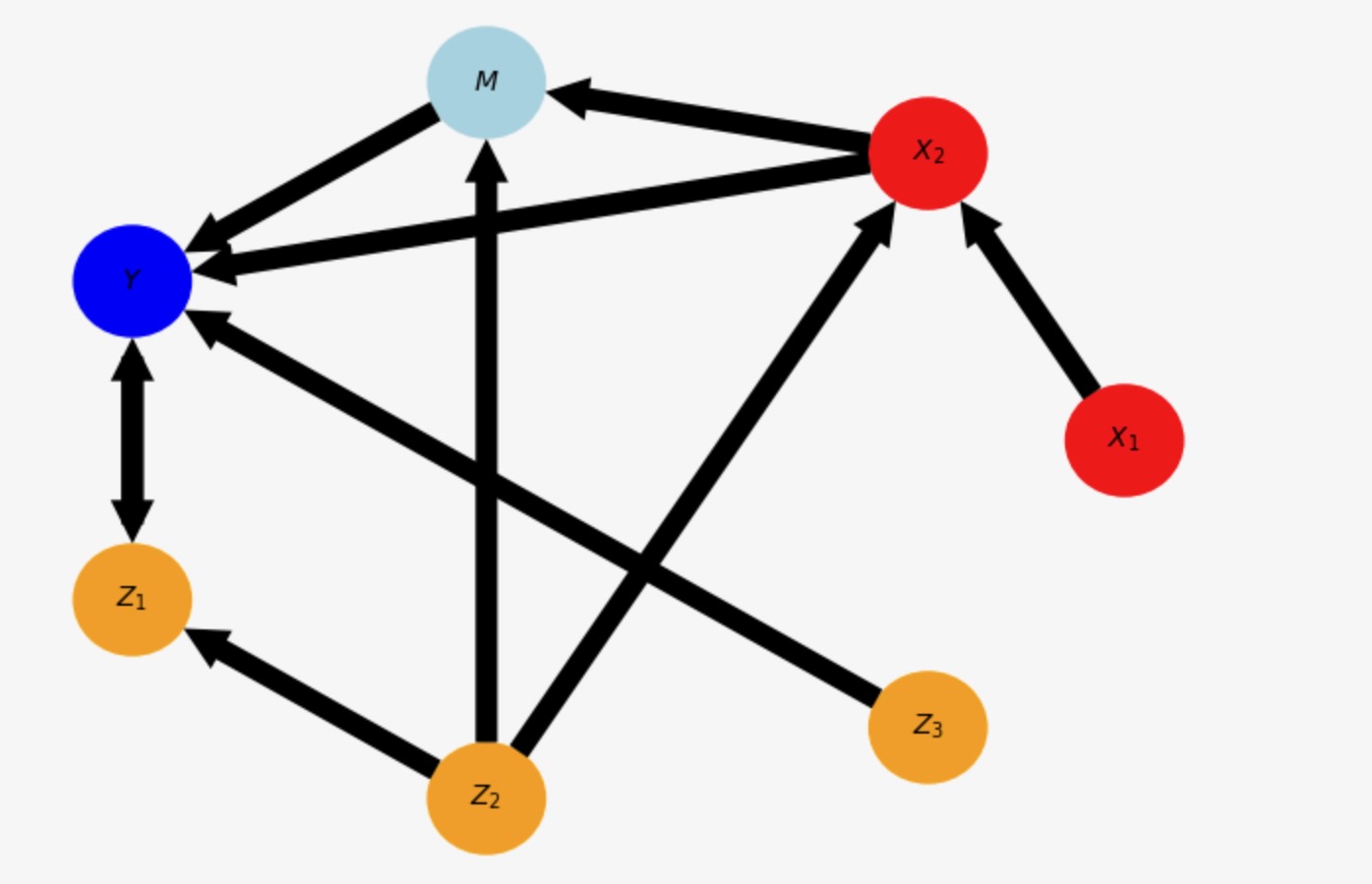
ここで、親YとM(ここでZ3,Z2)からなります。YM(ここではY<->Z1)から出る正しいビームパス、これらの正しいビームの親(ここで、Z2はすでにセットの一部です)
代替は、上に定義したancs-セットです。(Perkovic et al.,2018) それはXとY(オプションでS)の先祖からなります。そこから禁じられたノードは削除されます。
adj = causal_effects._get_adjust_set()
print("Adjust-set = ", [(var_names[v[0]], v[1]) for v in adj])Adjust-set = [('$Z_2$', 0), ('$Z_3$', 0)]special_nodes = {}
for node in causal_effects.X:
special_nodes[node] = 'red'
for node in causal_effects.Y:
special_nodes[node] = 'blue'
for node in adj:
special_nodes[node] = 'orange'
for node in causal_effects.M:
special_nodes[node] = 'lightblue'
tp.plot_graph(graph = graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 6),
special_nodes=special_nodes,
); plt.show()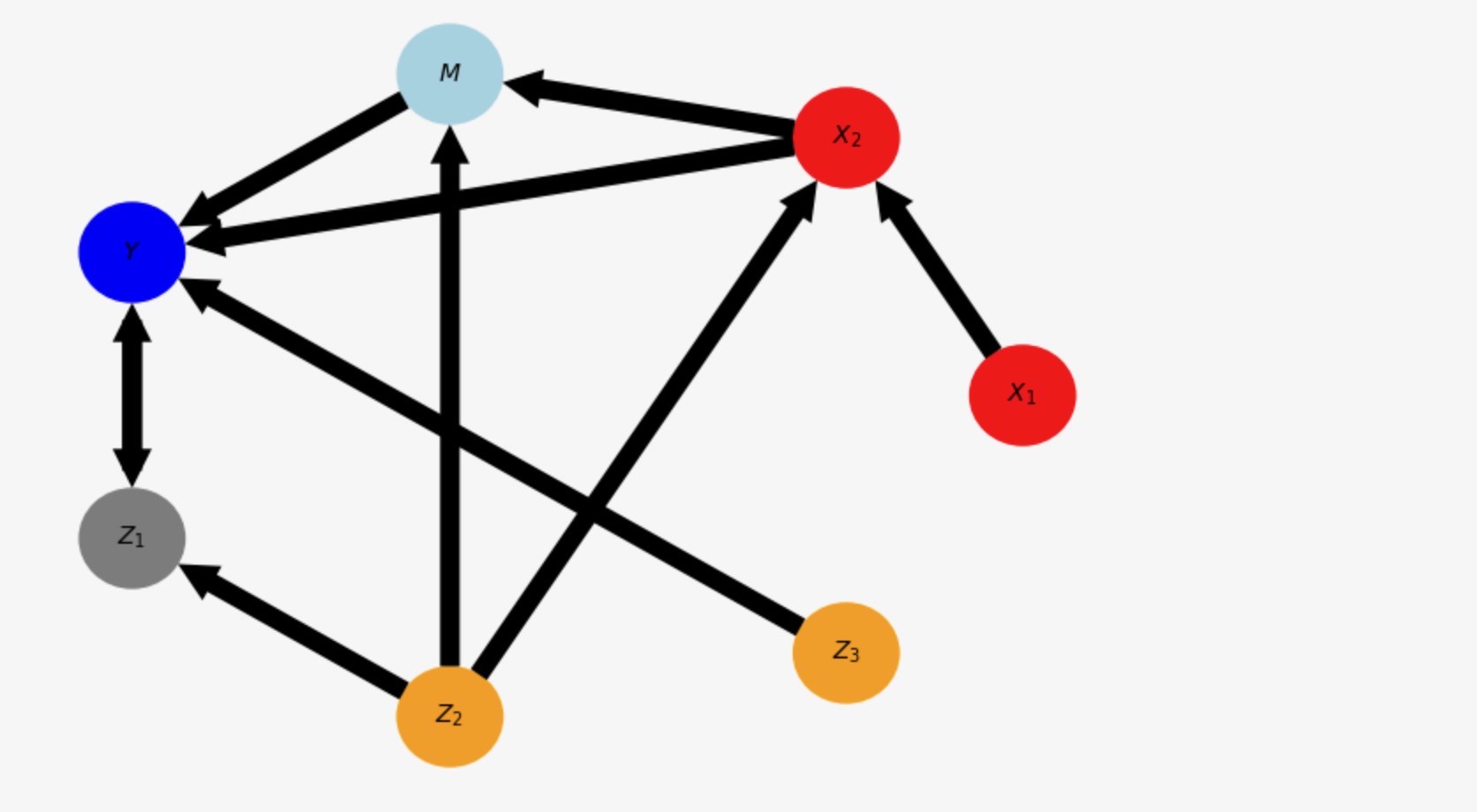
最適セットとの相違は、ノードZ1が調整セットの一部ではないことです。しかし、研究論文によると、YとMノードの正しいビームパスを調整セットに追加することは、推定の変化を減少させます。
ここで、最小化O-セットは、
cminopt = causal_effects.get_optimal_set(minimize='colliders_only')
print("Cmin-Oset = ", [(var_names[v[0]], v[1]) for v in cminopt])
special_nodes = {}
for node in causal_effects.X:
special_nodes[node] = 'red'
for node in causal_effects.Y:
special_nodes[node] = 'blue'
for node in cminopt:
special_nodes[node] = 'orange'
for node in causal_effects.M:
special_nodes[node] = 'lightblue'
tp.plot_graph(graph = graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 6),
special_nodes=special_nodes,
); plt.show()Cmin-Oset = [('$Z_2$', 0), ('$Z_3$', 0)]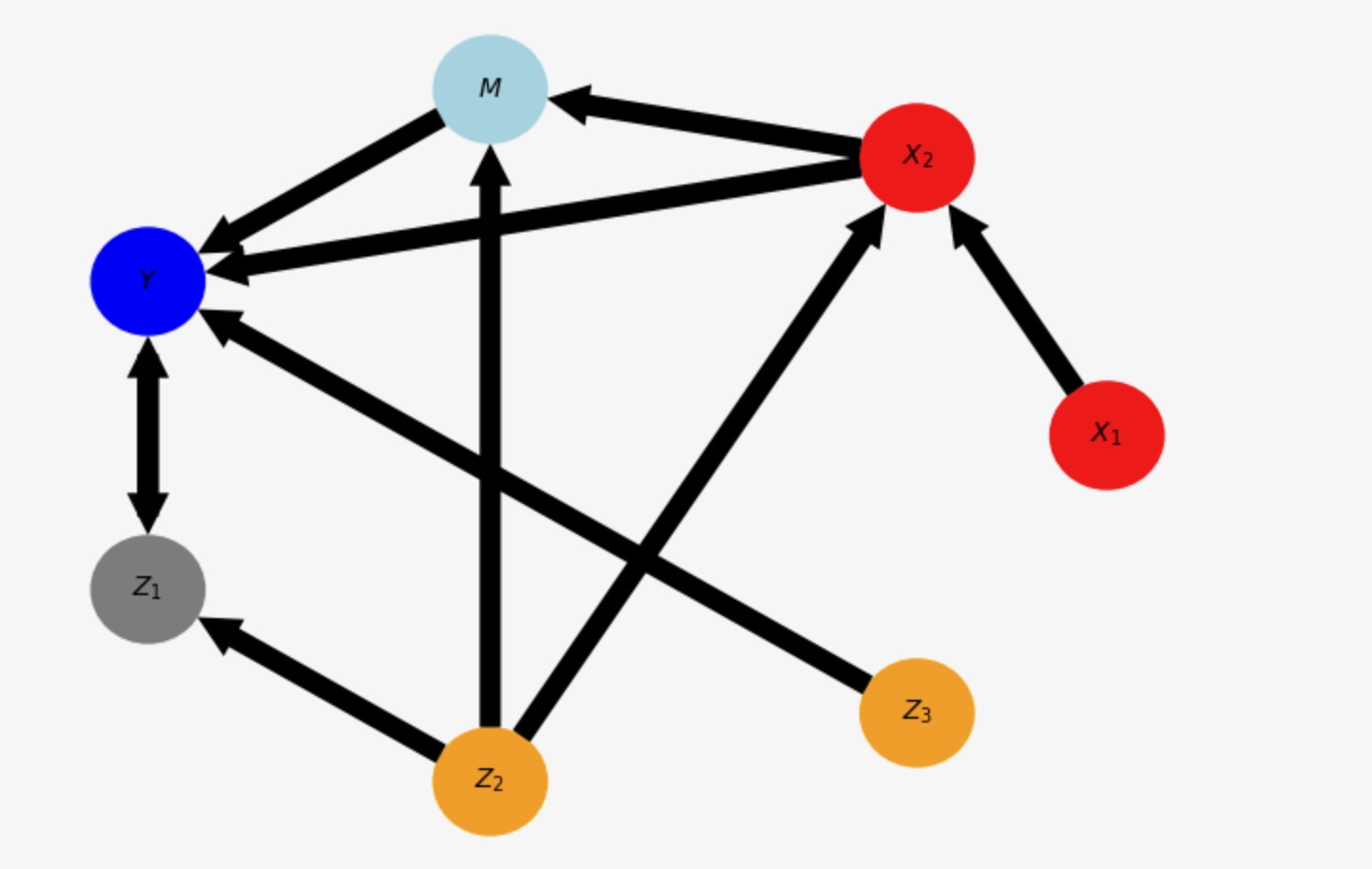
ここでZ1は削除されます。
この設定が、最適なグラフを保持しているかチェックしましょう。
optimality = causal_effects.check_optimality()
print("(Graph, X, Y, S) fulfills optimality: ", optimality)Optimality = True with cond_0 = False, cond_I = True, cond_II = True (Graph, X, Y, S) fulfills optimality: True
しかし、このグラフでO-セットは、少なくとも線形推定では、グラフと一致する任意の分布への最小に漸近推定変数に分岐します。
一般総因果の推定
私たちは、最適長せセットに伴うグラフィカル一般化バックドア調整を応用した総因果の推定に移ります。
toyモデルの正解データ
最初に、ガウスユニット変数ノイズとともにtigmaite関数、toys.structual_causal_processを使った上のグラフのSCMから、いくつかデータを生成しましょう。
def lin_f(x): return x
coeff = .5
links_coeffs = {
0: [],
1: [((0, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
2: [((1, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
3: [((1, 0), coeff, lin_f), ((2, 0), coeff, lin_f), ((6, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
4: [((5, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
5: [],
6: [],
7: [],
}
T = 10000
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
# Time series no 7 is unobserved confounder
data = data[:, [0,1,2,3,4,5,6]]
dataframe = pp.DataFrame(data)最初に、私たちはデータをプロットします。これは、関数tp.plot_timeseriesで実行できます。
tp.plot_timeseries(dataframe); plt.show()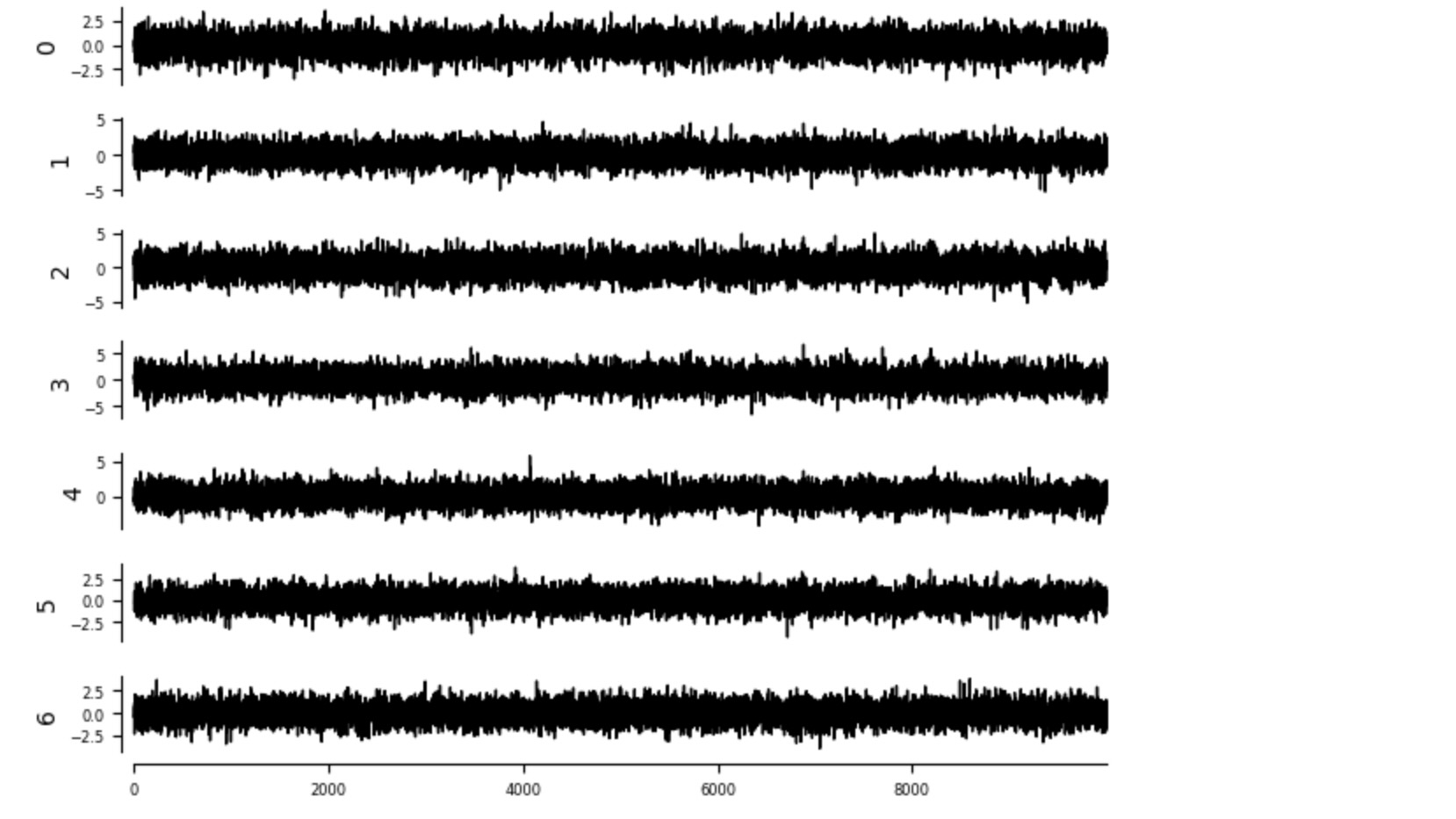
介入データの正解データ
介入の効果の予測の前に、私たちは、正解データを見ていきます。それは、私たちは基礎になるSCMを持っているのでここで生成することができます。私たちは、二つの介入x1 = x2 =1 と x1’ = x2' = 0 のために介入データを生成します。
T = 10000
intervention1 = np.ones(T)
intervention_data1, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7,
intervention={X[0][0]:intervention1, X[1][0]:intervention1},
intervention_type='hard',)
# Time series no 7 is unobserved confounder
intervention_data1 = intervention_data1[:, [0,1,2,3,4,5,6]]
tp.plot_timeseries(pp.DataFrame(intervention_data1)); plt.show()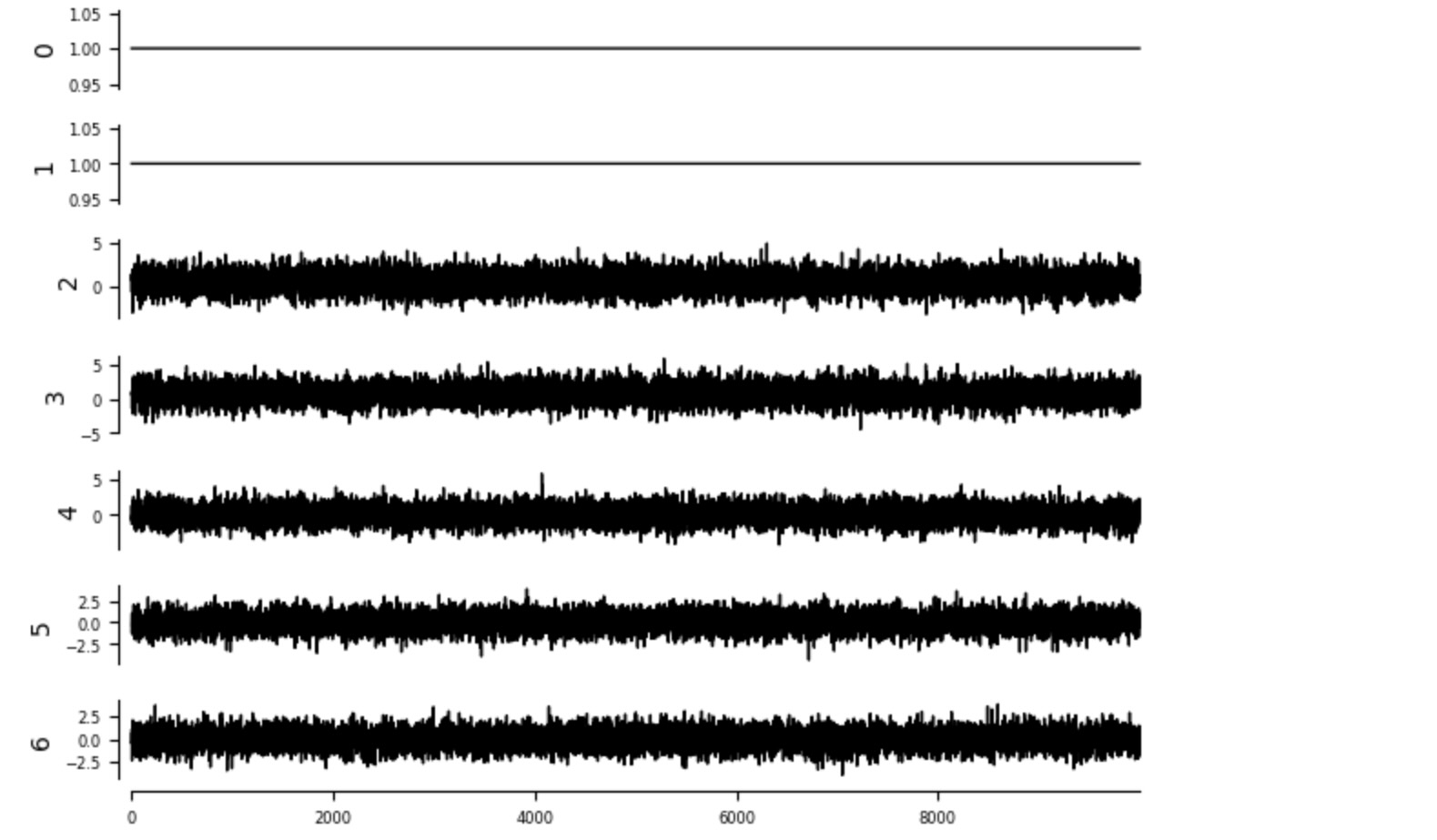
intervention2 = 0.*np.ones(T)
intervention_data2, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7,
intervention={X[0][0]:intervention2, X[1][0]:intervention2},
intervention_type='hard',)
# Time series no 7 is unobserved confounder
intervention_data2 = intervention_data2[:, [0,1,2,3,4,5,6]]
tp.plot_timeseries(pp.DataFrame(intervention_data2)); plt.show()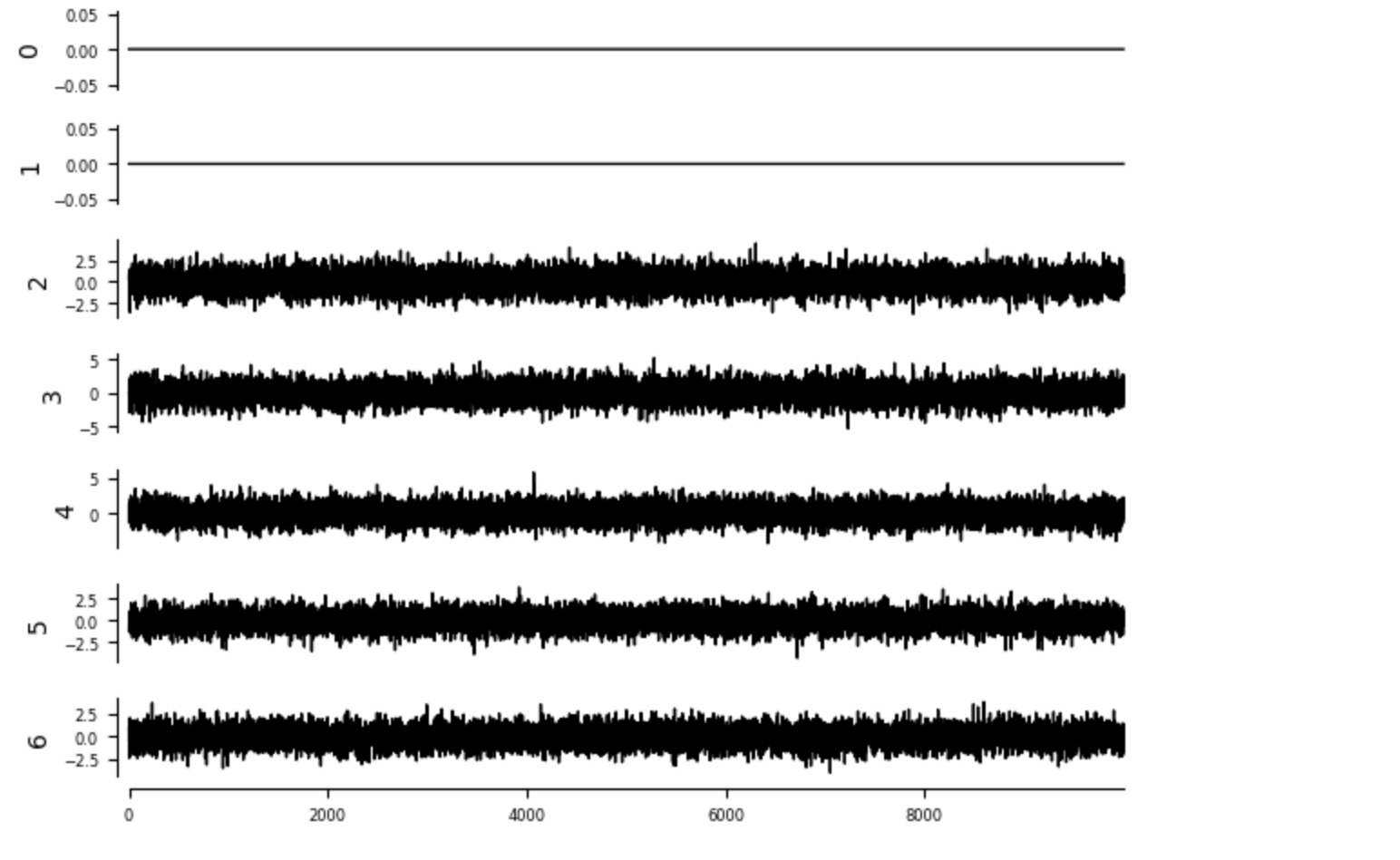
処置の効果の真の平均は、単純にY-データの平均の相違です。
true_effect = (intervention_data1[:,Y[0][0]] - intervention_data2[:,Y[0][0]]).mean()
print("True effect = %.2f" %true_effect)True effect = 0.75
ここで値、0.75は、係数0.5の X2 ->Yの 有向因果リンクと 間接パス X2 -> M -> Y、ここで効果は 積 0.5 x 0.5 = 0.25、の合計として現れます。
因果調整モデルの適合
私たちは、関数fit_total_effect と predict_total_effectに実装された平均処置効果に焦点を当てます。様式は、最も関係のある入力としてdata_frameとestimatorオブジェクト、ここで線形回帰、としてskleanモデルをとります。adjustment_setのデフォルトは最適セットです。Sは空なので、ここで、私たちは、条件付き因果は考えません。このケースは以下で詳細に議論します。
ここでは、私たちはそれ自身非標準化の実行としてデータを離れます。それは、data_transformで実行されます。mask_typeはデータサンプルのマスキングに使われます。
causal_effects.fit_total_effect(
dataframe=dataframe,
estimator=LinearRegression(),
adjustment_set='optimal',
conditional_estimator=None,
data_transform=None,
mask_type=None,
)<tigramite.causal_effects.CausalEffects at 0x15b1561d0>
介入の効果の予測
ここで私たちは、Yの推定値の分離である二つの介入 x1 = x2 = 1 と x1 = x2 = 0の効果を予測するために、適合された因果モデルを使います。関数 predict_total_effect は、intervention_data, conditions_data, そして pred_paramsを引数としてとります。pred_paramsはオプションのパラメータで、skleanの予測関数に渡されます。intervention_dataは、単一の値X=x の介入、または Txの長さの値の範囲の効果を予測するために、シェイプ(1, len(x)) にします。一致して、conditions_dataはシェイプ(T_x, len(S))、言い換えれば、intervention_dataと同じ長さに、する必要があります。
intervention_data = 1.*np.ones((1, 2))
y1 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
# conditions_data=conditions_data,
)
print("y1 = ",y1)
intervention_data = 0.*np.ones((1, 2))
y2 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
# conditions_data=conditions_data,
)
print("y2 = ",y2)y1 = [[0.73288075]] y2 = [[-0.00799763]]
predict_total_effectは、シェイプ(T_x, len(Y))の配列で推定された因果の効果を返します。平均処置効果は、その時、相違によって与えられます。
beta = (y1 - y2)
print("Causal effect = %.2f" %(beta))Causal effect = 0.74
見てわかるように、上の因果の結果はほぼ真実です。
私たちは、また、介入の値の範囲の効果を直接計算できます。
intervention_data = np.tile(np.linspace(-2, 2, 20).reshape(20, 1), (1, 2))
estimated_causal_effects = causal_effects.predict_total_effect(
intervention_data=intervention_data,
# conditions_data=conditions_data,
)
plt.scatter(intervention_data[:,0], estimated_causal_effects[:,0], label="Estimated")
# plt.plot(intervention_values, true_causal_effects, 'k-', label="True")
# plt.title(r"NRMSE = %.2f" % (np.abs(estimated_causal_effects - true_causal_effects).mean()/true_causal_effects.std()))
plt.xlabel('Intervention / X-value range')
plt.ylabel('Causal effect')
plt.legend()
plt.show()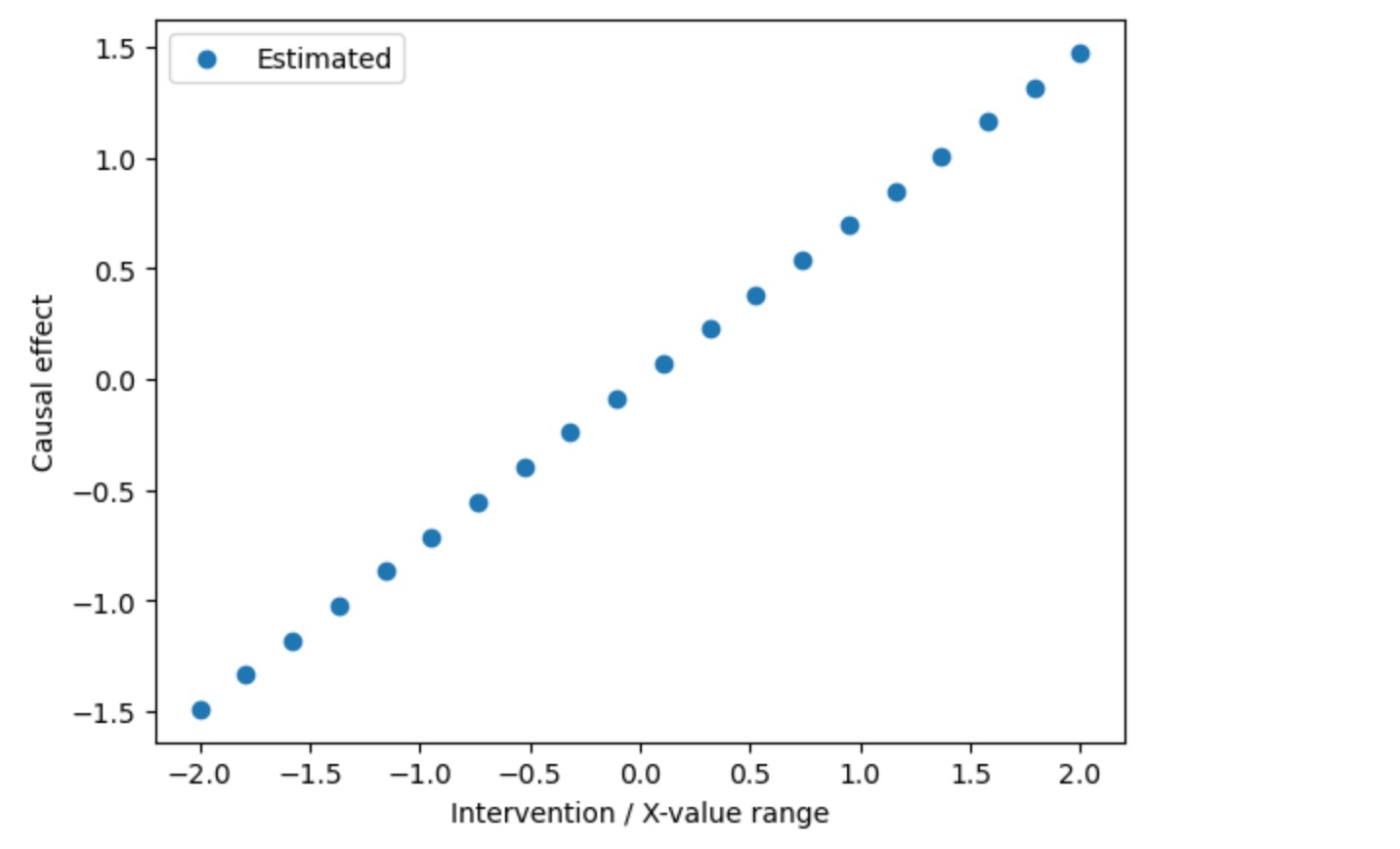
ここで、これは、私たちは線形モデルで処理しているので、丁度傾き0.75の直線になります。
その他の推定モデル
非線形/ノンパラメトリック推定
ここで正解データは、線形です。そのため、線形推定を使うことがわかります。非線形の正解データを考えましょう。そして、介入の値の範囲のための介入の正解データのデータと同様に観測値を生成しましょう。
def lin_f(x): return x
def nonlin_f(x): return (x + 5. * x ** 2 * np.exp(-x ** 2 / 20.))
coeff = .5
links_coeffs = {
0: [],
1: [((0, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
2: [((1, 0), -coeff, nonlin_f), ((5, 0), coeff, lin_f)],
3: [((1, 0), 1., nonlin_f), ((2, 0), coeff, lin_f), ((6, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
4: [((5, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
5: [],
6: [],
7: [],
}
# Observational data
T = 1000
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
# Time series no 7 is unobserved confounder
data = data[:, [0,1,2,3,4,5,6]]
dataframe = pp.DataFrame(data)
# Interventional data for a range of intervention values
intervention_data = np.linspace(-10, 10, 30)
true_causal_effects = np.zeros(len(intervention_data))
for i, int_val in enumerate(intervention_data):
intervention1 = int_val*np.ones(T)
intervention_data1, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7,
intervention={0:intervention1, 1:intervention1},
intervention_type='hard',)
# Time series no 7 is unobserved confounder
intervention_data1 = intervention_data1[:, [0,1,2,3,4,5,6]]
true_causal_effects[i] = intervention_data1[:,Y[0][0]].mean()tp.plot_timeseries(dataframe); plt.show()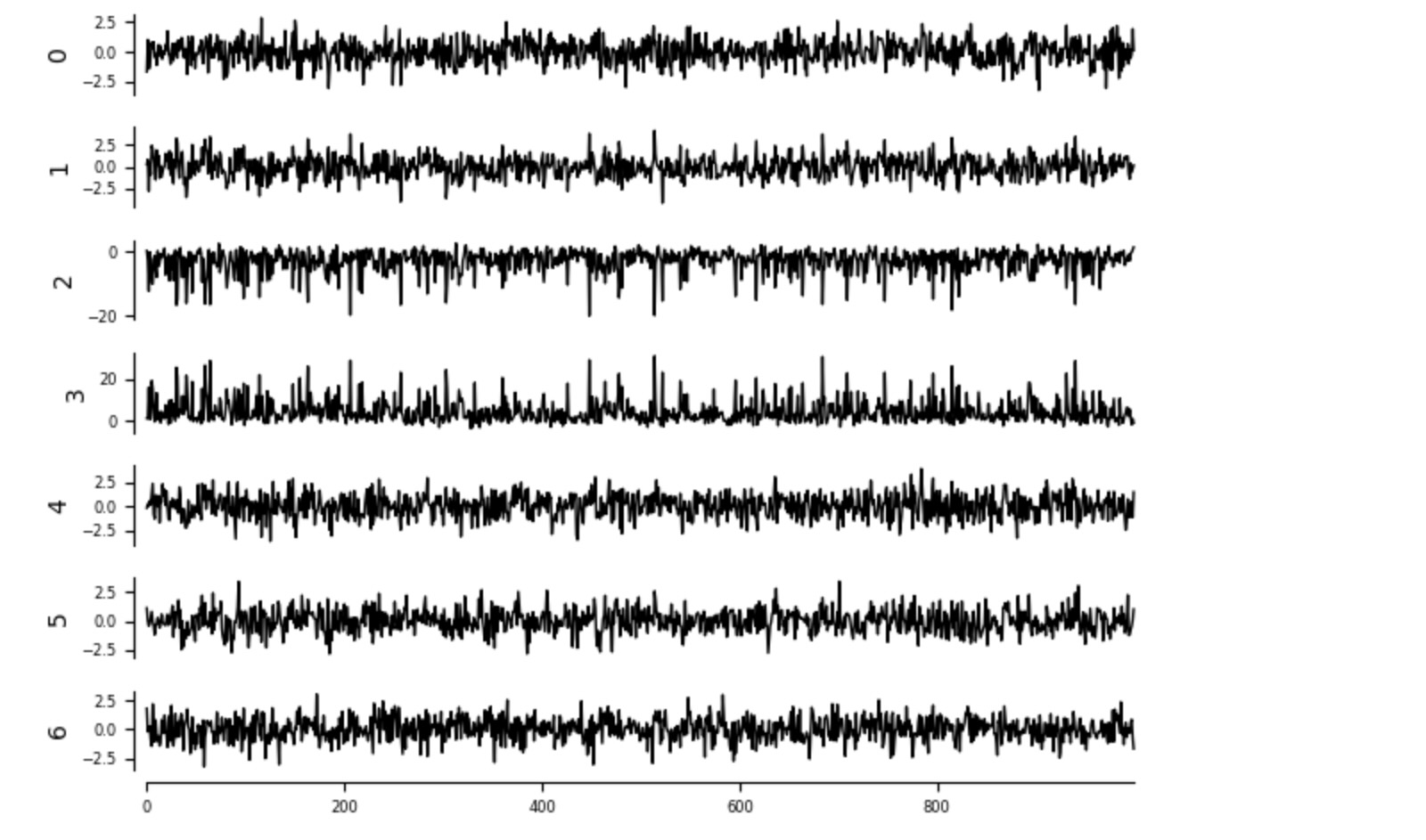
ここで、私たちはノンパラメトリック KNeighborsRegressor()を使って観測データを適合します。そして、上の重要な介入の効果を推定します。
# Fit causal effect model from observational data
causal_effects.fit_total_effect(
dataframe=dataframe,
estimator=KNeighborsRegressor(),
adjustment_set='optimal',
conditional_estimator=None,
data_transform=None,
mask_type=None,
)
# Predict effect of interventions
intervention_data_here = np.tile(intervention_data.reshape(30, 1), (1, 2))
estimated_causal_effects = causal_effects.predict_total_effect(
intervention_data=intervention_data_here,
# conditions_data=conditions_data,
)下は、x軸の介入の値Xで与えられる 予測された因果の影響の値Y(y軸)と正解の比較です。
追加で、私たちはX1(赤色)の観測密度を表示します。
plt.scatter(intervention_data, estimated_causal_effects[:,0], label="Estimated")
plt.plot(intervention_data, true_causal_effects, 'k-', label="True")
plt.title(r"NRMSE = %.2f" % (np.abs(estimated_causal_effects[:,0] - true_causal_effects).mean()/true_causal_effects.std()))
plt.xlabel('Intervention / X-value range')
plt.ylabel('Causal effect')
plt.legend()
# Also show observational density of X1
ax2 = plt.gca().twinx()
density = gaussian_kde(data[:,1])
ax2.plot(intervention_data, density(intervention_data), 'r-', label=r"$p(X_1)$")
ax2.set_ylabel(r'$p(X_1)$')
ax2.legend(loc='upper right')
plt.show()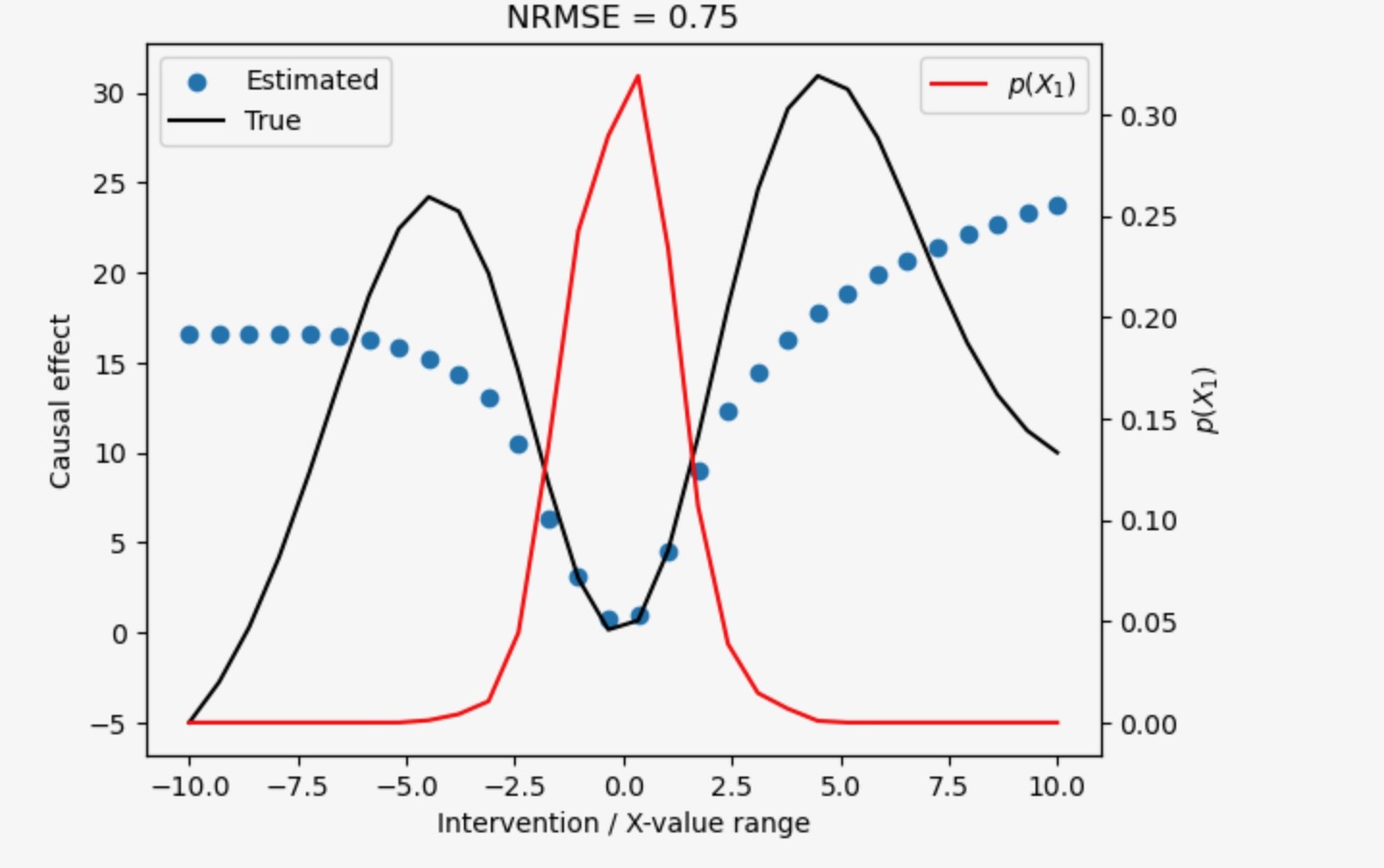
因果推定は値の範囲に対してよく働きます。ここでXの観測分布は非ゼロです。kNN-推定モデルはこの範囲の外の機能を学習できません。
ロジスティック回帰
ここで、LogisticRegressionを見ていきましょう。それは、連続入力変数のために分類する対象の変数を適合することを許容します。これを修了するために、私たちはここで、対象Yの分類 toyデータを得るために、pp.quantile_bin_arrayを使います。
def lin_f(x): return x
coeff = .5
links_coeffs = {
0: [],
1: [((0, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
2: [((1, 0), -coeff, lin_f), ((5, 0), coeff, lin_f)],
3: [((1, 0), 1., lin_f), ((2, 0), coeff, lin_f), ((6, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
4: [((5, 0), coeff, lin_f), ((7, 0), coeff, lin_f)],
5: [],
6: [],
7: [],
}
# Observational data
T = 1000
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
# Let's make Y a categorical variable using quantile binning
bins = 3
data[:,Y[0][0]] = pp.quantile_bin_array(data[:,Y[0][0]].reshape(len(data), 1), bins=bins).squeeze()
# Time series no 7 is unobserved confounder
data = data[:, [0,1,2,3,4,5,6]]
dataframe = pp.DataFrame(data)
tp.plot_timeseries(dataframe); plt.show()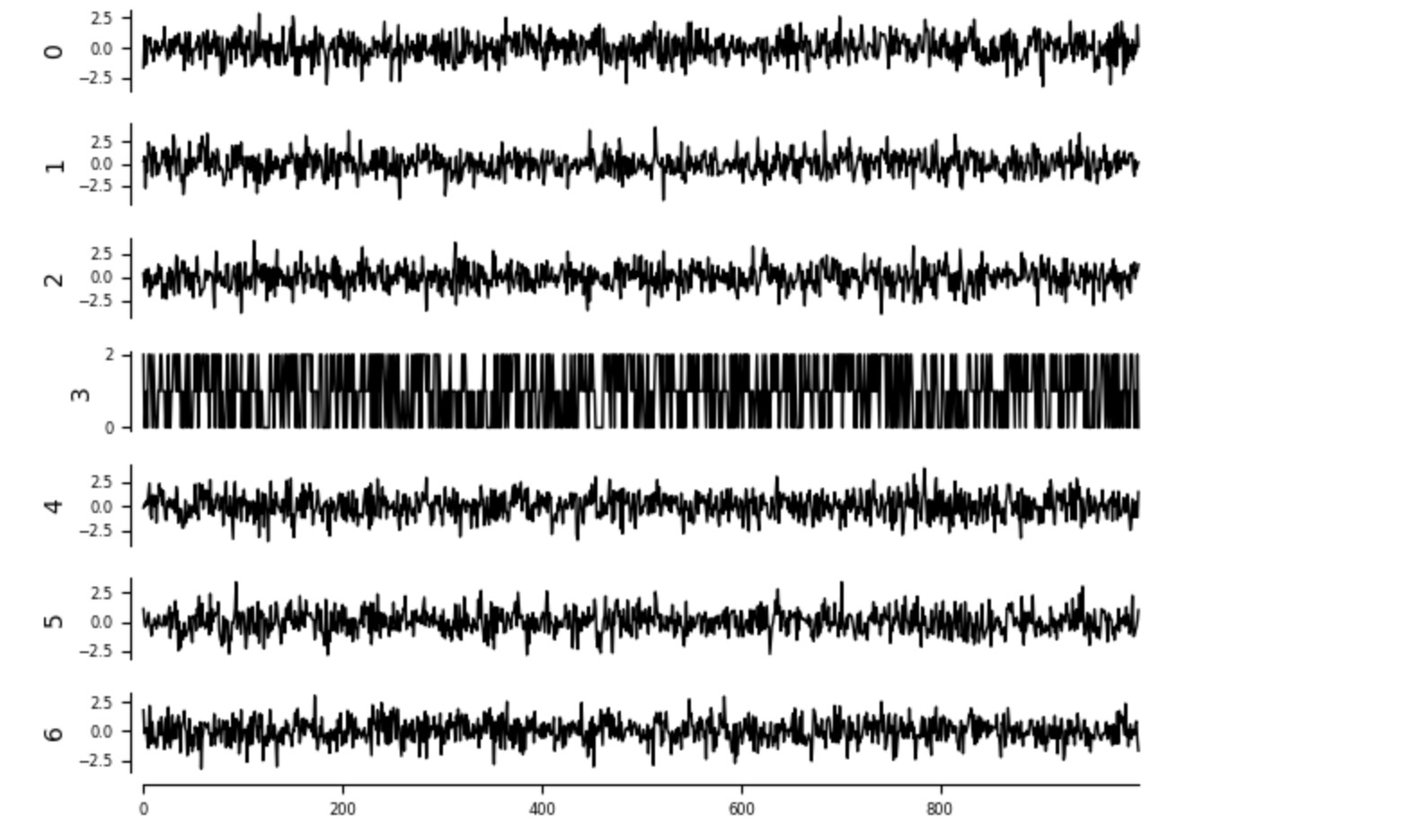
その時、私たちはLogisticRegressionを使って総効果を適合します。デフォルトでpredict(...)の出力は、平均されます。それは連続した対象変数とわかります。ここで、代わりに、私たちは分類予測を得ます。そして、各介入の予測分布を得るためにnp.bincount(カテゴリの正しい数値)を適用します。
# Interventional data for a range of intervention values
intervention_data = np.linspace(-5, 5, 10)
# Fit causal effect model from observational data
causal_effects.fit_total_effect(
dataframe=dataframe,
estimator=LogisticRegression(),
adjustment_set='optimal',
conditional_estimator=None,
data_transform=None,
mask_type=None,
)
# Predict effect of interventions
intervention_data_here = np.tile(intervention_data.reshape(10, 1), (1, 2))
# Instead of the default mean function for continuous target variables, here we get categorical predictions
# and apply np.bincount to get their interventional distribution
def aggregation_func(x):
x = x.astype('int64')
return np.bincount(x, minlength=bins)
estimated_causal_effects = causal_effects.predict_total_effect(
intervention_data=intervention_data_here,
# conditions_data=conditions_data,
aggregation_func = aggregation_func,
)
for ido, dox in enumerate(intervention_data):
print("Interventional distribution for do(X=%.3f) = %s" %(dox, str(estimated_causal_effects[ido, 0])))Interventional distribution for do(X=-5.000) = [1000 0 0] Interventional distribution for do(X=-3.889) = [1000 0 0] Interventional distribution for do(X=-2.778) = [997 3 0] Interventional distribution for do(X=-1.667) = [918 73 9] Interventional distribution for do(X=-0.556) = [441 457 102] Interventional distribution for do(X=0.556) = [ 60 474 466] Interventional distribution for do(X=1.667) = [ 2 146 852] Interventional distribution for do(X=2.778) = [ 0 19 981] Interventional distribution for do(X=3.889) = [ 0 1 999] Interventional distribution for do(X=5.000) = [ 0 0 1000]
ここで、分布は低位から上位のカテゴリーへ段階的にシフトします。
条件付き因果
私たちは、グラフのその他の変数の任意の値S=sの条件で因果の効果E[Y|do(X=x),S=s]のための応用例を与えます。
Sは連続変数になります。しかし、ここで私たちはバイナリ{-1,1}と二つの因果レジームで定義されるケースを考えます。
Y = 0.7 * S * X + Z + ηY言い換えると、S = 1 の時、Y = 0.7 * X + Z + ηY , そして S = -1 の時、 Y = -0.7 * X + Z + ηY . ここでS はZの原因で、ZはXの原因です。
T = 10000
Sdata = np.random.choice([-1., 1.], size=T)
Zdata = Sdata*np.random.randn(T)
Xdata = np.random.randn(T) + Zdata
Ydata = 0.7*Sdata*Xdata + Zdata + np.random.randn(T)
data = np.vstack((Xdata, Ydata, Sdata, Zdata)).T
dataframe = pp.DataFrame(data)graph = np.array([['', '-->', '', '<--'],
['<--', '', '<--', '<--'],
['', '-->', '', '-->'],
['-->', '-->', '<--', '']], dtype='<U3')
X = [(0,0)]
Y = [(1,0)]
S = [(2,0)]
causal_effects = CausalEffects(graph, graph_type='admg', X=X, Y=Y, S=S, hidden_variables=None,
verbosity=1)
# Just for plotting purposes
var_names = ['$X$', '$Y$', '$S$', '$Z$']
tp.plot_graph(graph = causal_effects.graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (4, 4),
); plt.show()
## ## Initializing CausalEffects class ## Input: graph_type = admg X = [(0, 0)] Y = [(1, 0)] S = [(2, 0)] M = []
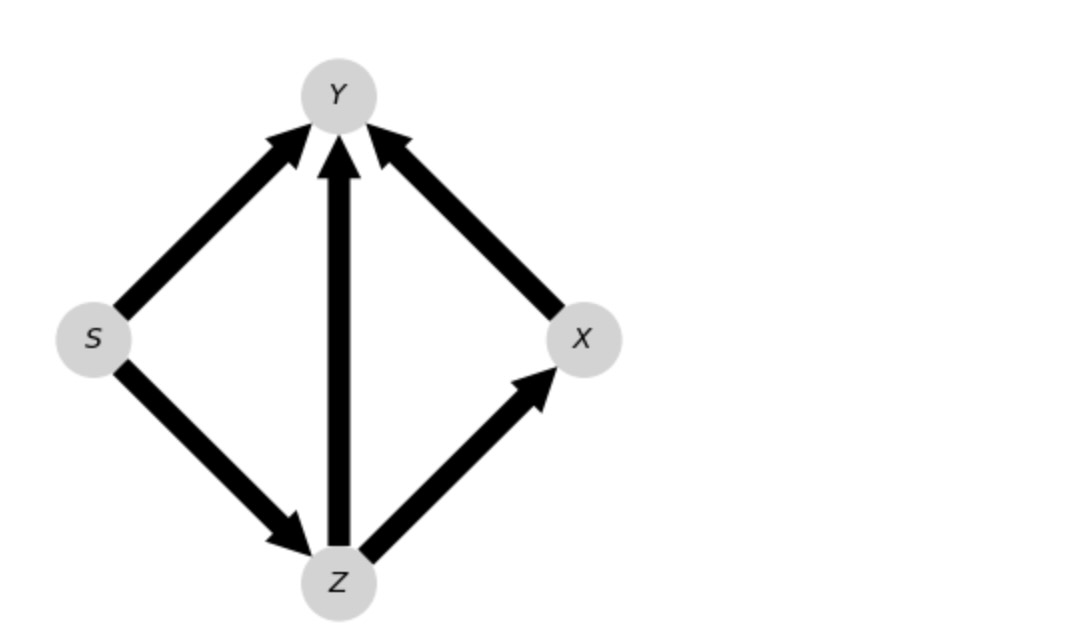
ここで、私たちは推定のためのニューラルネットワークと条件推定のために線形推定を選択します。
# Fit causal effect model from observational data
causal_effects.fit_total_effect(
dataframe=dataframe,
estimator=MLPRegressor(max_iter=200),
adjustment_set='optimal',
conditional_estimator=LinearRegression(),
data_transform=None,
mask_type=None,
)<tigramite.causal_effects.CausalEffects at 0x1569844f0>
# Set X to intervened values given S=-1, 1
# S=-1
for cond_value in [-1, 1]:
conditions_data=cond_value*np.ones((1, 1))
intervention_data = 1.*np.ones((1, 1))
y1 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
conditions_data=conditions_data,
)
intervention_data = 0.*np.ones((1, 1))
y2 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
conditions_data=conditions_data,
)
beta = (y1 - y2)
print("Causal effect for S = % .2f is %.2f" %(cond_value, beta))Causal effect for S = -1.00 is -0.67 Causal effect for S = 1.00 is 0.67
これは完全にうまく正しい因果を推定します。S=1の場合、β=0.7, S= -1 β= -0.7
時系列DAGsの因果関係
次に、私たちは上のステーショナリーDAGから因果推定を調査します。
graph = np.array([[['', '-->', ''],
['', '', ''],
['', '', '']],
[['', '-->', ''],
['', '-->', ''],
['-->', '', '-->']],
[['', '', ''],
['<--', '', ''],
['', '-->', '']]], dtype='<U3')
X = [(1,-2)]
Y = [(2,0)]
causal_effects = CausalEffects(graph, graph_type='stationary_dag', X=X, Y=Y, S=None,
hidden_variables=None,
verbosity=1)
var_names = ['$X^0$', '$X^1$', '$X^2$']
opt = causal_effects.get_optimal_set()
print("Oset = ", [(var_names[v[0]], v[1]) for v in opt])
special_nodes = {}
for node in causal_effects.X:
special_nodes[node] = 'red'
for node in causal_effects.Y:
special_nodes[node] = 'blue'
for node in opt:
special_nodes[node] = 'orange'
for node in causal_effects.M:
special_nodes[node] = 'lightblue'
tp.plot_time_series_graph(graph = causal_effects.graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (8, 4),
special_nodes=special_nodes
); plt.show()
## ## Initializing CausalEffects class ## Input: graph_type = stationary_dag X = [(1, -2)] Y = [(2, 0)] S = [] M = [(1, 0), (2, -1), (2, -2), (1, -1)] Oset = [('$X^2$', -3), ('$X^1$', -4), ('$X^1$', -3)]
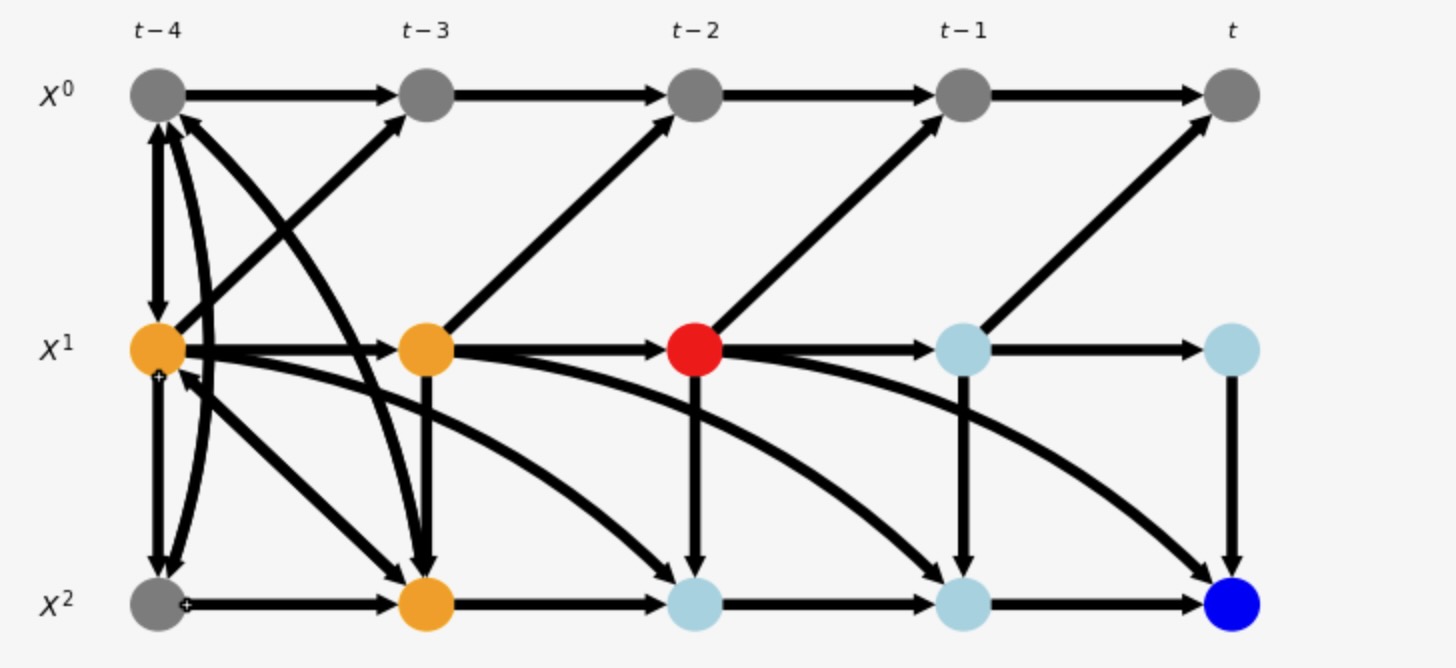
ステーショナリー入力DAG(上に記述したように)から構築されたこの拡張されたADMGで、最適調整セットは、オレンジ、中間値は明るいブルーで色付けされます。全体の最適調整セットはこのラグ範囲に含まれるので、調整は正しいものです。
ステーショナリーDAGのSCMためにいくつかのデータを生成します。
coeff = .5
links_coeffs = {
0: [((0, -1), coeff, lin_f), ((1, -1), coeff, lin_f)],
1: [((1, -1), coeff, lin_f),],
2: [((2, -1), coeff, lin_f), ((1, 0), coeff, lin_f), ((1,-2), coeff, lin_f)],
}
# Observational data
T = 10000
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
dataframe = pp.DataFrame(data)ここで、私たちは、x=1とx'=0 の二つの介入の効果を予測し、適合します。
# Fit causal effect model from observational data
causal_effects.fit_total_effect(
dataframe=dataframe,
estimator=LinearRegression(),
adjustment_set='optimal',
)<tigramite.causal_effects.CausalEffects at 0x15717c190>
intervention_data = 1.*np.ones((1, 1))
y1 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
)
intervention_data = 0.*np.ones((1, 1))
y2 = causal_effects.predict_total_effect(
intervention_data=intervention_data,
)
beta = (y1 - y2)
print("Causal effect is %.2f" %(beta))Causal effect is 0.85
この線形モデルの効果は、Xt-2 1から Xt 2までの間の因果パス全ての係数の積の総和に等しくなります。
Write 推定と線形予測の推定
私たちは、イントとダクションの複雑なグラフのDAGバージョンを考えます。
graph = np.array([['', '-->', '', '', '', '', ''],
['<--', '', '-->', '-->', '', '<--', ''],
['', '<--', '', '-->', '', '<--', ''],
['', '<--', '<--', '', '<--', '', '<--'],
['', '', '', '-->', '', '<--', ''],
['', '-->', '-->', '', '-->', '', ''],
['', '', '', '-->', '', '', '']], dtype='<U3')
X = [(0,0), (1,0)]
Y = [(3,0)]
causal_effects = CausalEffects(graph, graph_type='dag', X=X, Y=Y, S=None, hidden_variables=None,
verbosity=1)
# Just for plotting purposes
var_names = ['$X_1$', '$X_2$', '$M$', '$Y$', '$Z_1$', '$Z_2$', '$Z_3$']
opt = causal_effects.get_optimal_set()
print("Oset = ", [(var_names[v[0]], v[1]) for v in opt])
special_nodes = {}
for node in causal_effects.X:
special_nodes[node] = 'red'
for node in causal_effects.Y:
special_nodes[node] = 'blue'
for node in opt:
special_nodes[node] = 'orange'
for node in causal_effects.M:
special_nodes[node] = 'lightblue'
tp.plot_graph(graph = causal_effects.graph,
var_names=var_names,
# save_name='Example.pdf',
figsize = (6, 6),
special_nodes=special_nodes
); plt.show()
## ## Initializing CausalEffects class ## Input: graph_type = dag X = [(0, 0), (1, 0)] Y = [(3, 0)] S = [] M = [(2, 0)] Oset = [('$Z_1$', 0), ('$Z_2$', 0), ('$Z_3$', 0)]
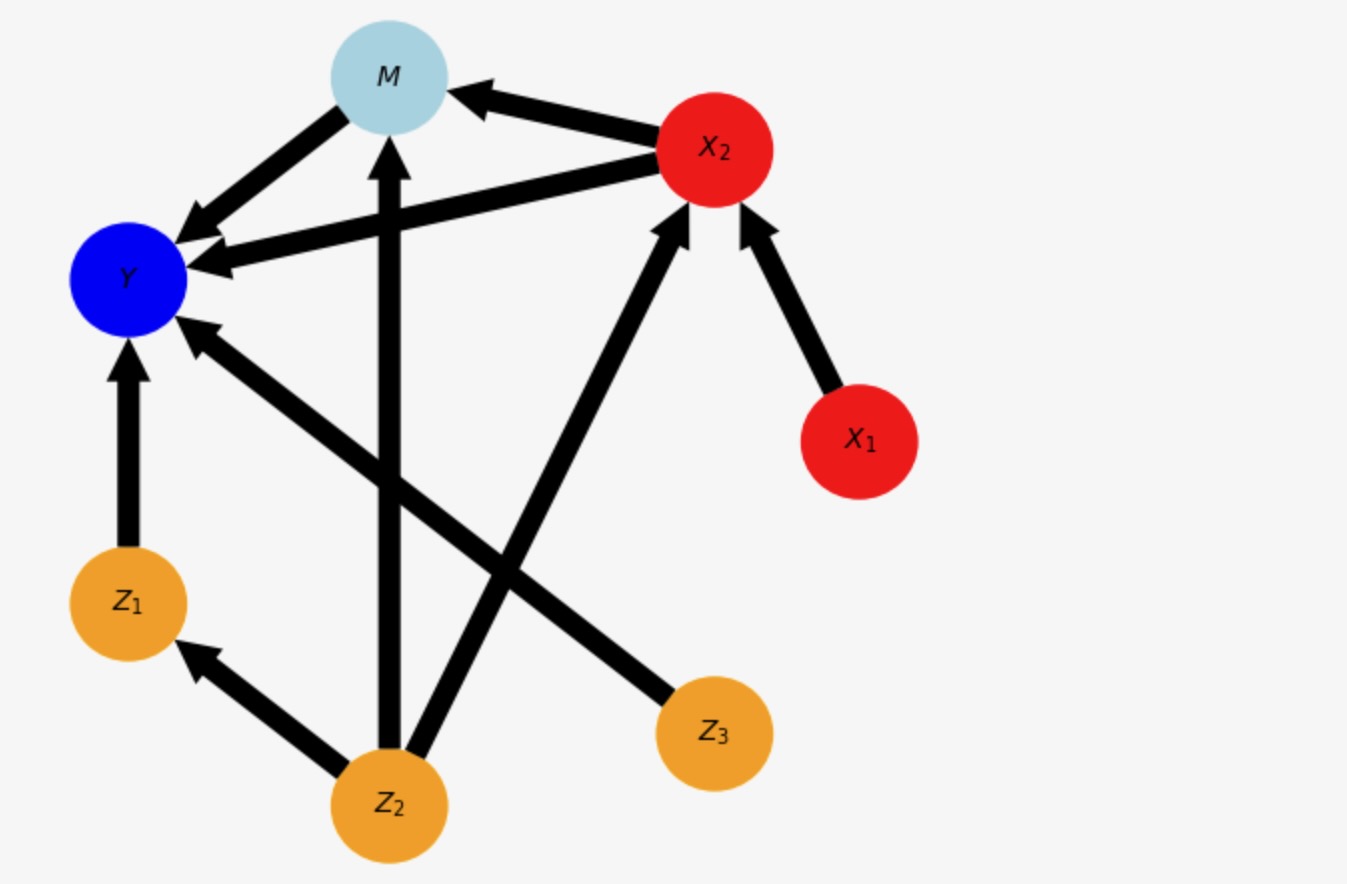
いくつかのデータを生成しましょう。
def lin_f(x): return x
coeff = .5
links_coeffs = {
0: [],
1: [((0, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
2: [((1, 0), coeff, lin_f), ((5, 0), coeff, lin_f)],
3: [((1, 0), coeff, lin_f), ((2, 0), coeff, lin_f), ((6, 0), coeff, lin_f), ((4, 0), coeff, lin_f)],
4: [((5, 0), coeff, lin_f)],
5: [],
6: [],
}
T = 10000
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
dataframe = pp.DataFrame(data)私たちは、Writeのメソッドの予測と適合します。次のデータハンドリング引数 fit_wrights_effect は以下をとります。
- mediation:Noneまたは ’direct’ または tuplesのリスト:もしなければ、総効果が推定されます。もし'direct'ならば、直接の効果だけが推定されます。そうでなければ、それらの因果パスだけは、少なくともこれらの中間ノードの一つを通って、渡されることが考えられます。
- method:{'parents','links_coeffs','optimal'}: Wrightのパス係数の推定に使われるメソッド。もし'optimal'ならば、Oセットが使用され、もし'links_coeffs'ならば、links_coeffsの係数が使用されます。もし'parents'ならば、親が使用されます。(もし中間値やYへの双方向リンクの調整がない場合だけ、正しくなります)あなたがtoyモデルで動作させる時、'links_coeffs'は、テスト目的で使用できます。
- link_coeffs : dict: method='links_coeffs'の場合にだけ使用されます。全ての変数のためのフォーマットの辞書は、{0:[((i, -tau), coeff),...], 1:[...], ...} ここで、I は 変数の数Nである [0..N-1] 、tau >= 0に設定します。係数coeffは浮動小数点(float)です。
デフォルトは method='parents'です。DAGを処理するので、ここでは、妥当です。
causal_effects.fit_wright_effect(dataframe=dataframe)
intervention_data = 1.*np.ones((1, 2))
y1 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
intervention_data = 0.*np.ones((1, 2))
y2 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
beta = (y1 - y2)
print("Causal effect is %.2f" %(beta))Causal effect is 0.75
これは、係数0.5の一つの有向リンクと0.5*0.5の結果の間接パスがあるので、推定の結果です。
最後に、オプション mediationは、直接と中間の効果だけを考えることを許容します。Mを通って成立する総効果がどれくらいか測定しましょう。
considered_mediators = [(2, 0)]
causal_effects.fit_wright_effect(dataframe=dataframe, mediation=considered_mediators)
intervention_data = 1.*np.ones((1, 2))
y1 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
intervention_data = 0.*np.ones((1, 2))
y2 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
beta = (y1 - y2)
print("Mediated causal effect through M = %s is %.2f" %(considered_mediators, beta))Mediated causal effect through M = [(2, 0)] is 0.23
そして直接の影響は、
causal_effects.fit_wright_effect(dataframe=dataframe, mediation='direct')
intervention_data = 1.*np.ones((1, 2))
y1 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
intervention_data = 0.*np.ones((1, 2))
y2 = causal_effects.predict_wright_effect(
intervention_data=intervention_data,
)
beta = (y1 - y2)
print("Direct causal effect is %.2f" %(beta))Direct causal effect is 0.51
CausalEffectsクラスはtigramiteのLinearMediationクラスを一般化します。それは、時系列グラフにだけ適用されます。その実装のため、LinearMediationは相当速くなります。
ブートストラップを基礎にした信頼度
あなたは、一般的な総効果とWrightを基礎にした推定の両方の信頼度を推定できます。
# Let's generate shorter length data
T = 100
data, nonstat = toys.structural_causal_process(links_coeffs, T=T, noises=None, seed=7)
dataframe = pp.DataFrame(data)
# First for the Wright method with effect estimate being 0.75 above
causal_effects.fit_bootstrap_of(
method='fit_wright_effect',
method_args={'dataframe':dataframe},
boot_samples=1000)
intervention_data = 1.*np.ones((1, 2))
conf = causal_effects.predict_bootstrap_of(
method='predict_wright_effect',
method_args={'intervention_data':intervention_data})
print(conf.shape)## ## Running Bootstrap of fit_wright_effect ## boot_samples = 1000 boot_blocklength = 1 (2, 1)
# Now the total effect estimate
# First fit
causal_effects.fit_total_effect(dataframe=dataframe, estimator=LinearRegression())
# Then its confidence interval
causal_effects.fit_bootstrap_of(
method='fit_total_effect',
method_args={'dataframe':dataframe,
'estimator':LinearRegression()},
boot_samples=1000)
# Then predict
intervention_data = np.tile(np.linspace(-2, 2, 20).reshape(20, 1), (1, 2))
estimated_causal_effects = causal_effects.predict_total_effect(
intervention_data=intervention_data,
# conditions_data=conditions_data,
)
estimated_confidence_intervals = causal_effects.predict_bootstrap_of(
method='predict_total_effect',
method_args={'intervention_data':intervention_data},
conf_lev=0.9)
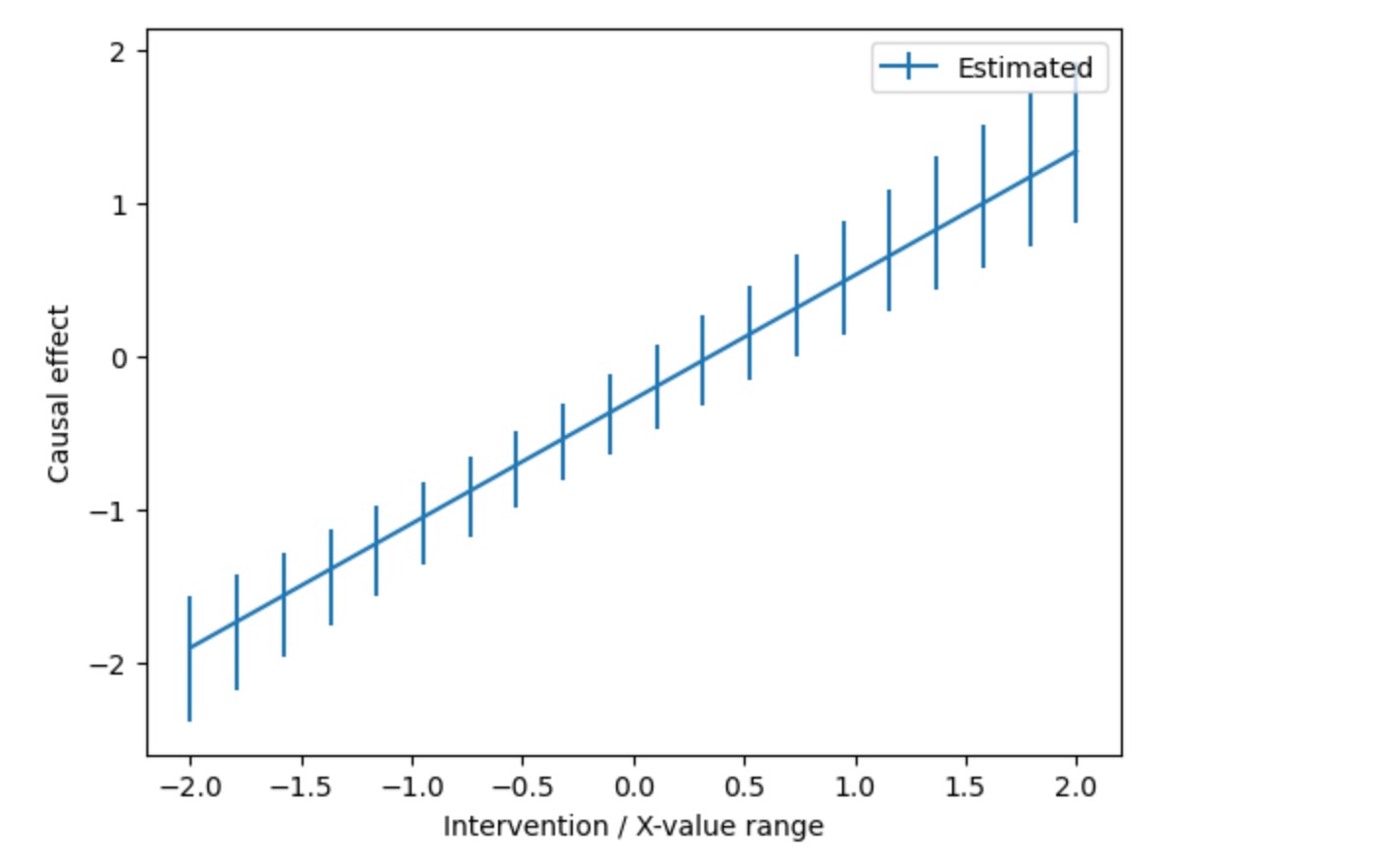
plt.errorbar(intervention_data[:,0], estimated_causal_effects[:,0],
np.abs(estimated_confidence_intervals - estimated_causal_effects[:,0]), label="Estimated")
plt.xlabel('Intervention / X-value range')
plt.ylabel('Causal effect')
plt.legend()
plt.show()## ## Running Bootstrap of fit_total_effect ## boot_samples = 1000 boot_blocklength = 1