TIGRAMITEによる因果探索　(FullCI)

　TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。

　PCMCIはここに記述されています： J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996

　PCMCIのさらに進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。

　このチュートリアルはPCMCIとFullCIを比較します。理論的な背景は以下の論文を参照してください。Runge, Jakob. 2018. “Causal Network Reconstruction from Time Series: From Theoretical Assumptions to Practical Estimation.” Chaos: An Interdisciplinary Journal of Nonlinear Science 28 (7): 075310.

　最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例)： https://www.nature.com/articles/s41467-019-10105-3

# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline     
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn

import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.models import LinearMediation, Prediction

PCMCI vs FullCI

　時系列グラフを推定するために代替的な方法は、それらの定義する恒等式でリンクを直接テストすることです。(FullCI)

      X_t-rⁱ ⊥ X_t^j | X_t^-

　ここでX_t^- = (X_t-1,X_t-2,...) は、全体の過程の過去です。これは、Granger Causalityまたはエントロピー転送のラグ仕様バージョンです。このアプローチは二つの理由で検出力が低下します。

MCIと比べてFullCIのより小さい効果のサイズ
もっと高い次元

1. MCIに比べてFullCIのより小さい効果サイズ

　以下のシステムを考えます。

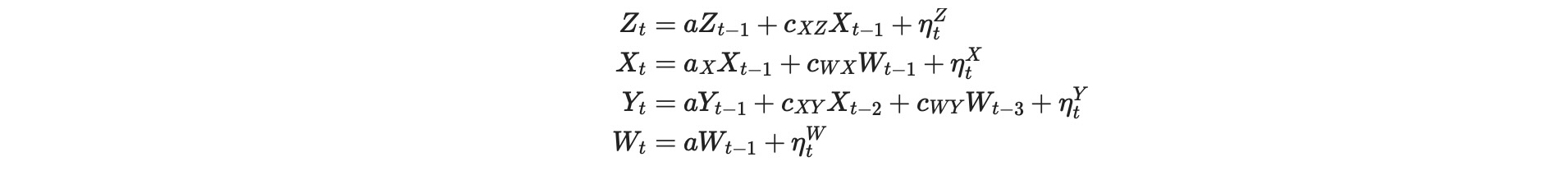
分散がσ²の独立ガウスホワイトノイズ過程η_t . リンクX_t-2 -> Y_tを考えます。ここで、一般的に静的テスト I ^FullCI ( X_t-2 -> Y_t) ≦ I ^MCI (X_t-2 -> Y_t) を見ること(解説論文を参照してください)ができます。論文では、これは、恣意的なモデルの証明です。

# Setup analysis
np.random.seed(42)     # Fix random seed
links_coeffs = {0: [((0, -1), 0.9), ((1, -1), -0.25)],
                1: [((1, -1), 0.95), ((3, -1), 0.3)],
                2: [((2, -1), 0.85), ((1, -2), 0.3), ((3, -3), 0.3)],
                3: [((3, -1), 0.8)],
                }
T = 100     # time series length
N = len(links_coeffs)
tau_max = 5
realizations = 100
alpha_level = 0.05

var_names = [r'$Z$', r'$X$', r'$Y$', r'$W$']
# # Define whole past
# whole_past = {}
# for j in range(N):
#     whole_past[j] = [(var, -lag)
#                          for var in range(N)
#                          for lag in range(1, tau_max + 1)
#                     ]
def get_sig_links():
    p_matrices = {'PCMCI':np.ones((realizations, N, N, tau_max+1)),
                  'FullCI':np.ones((realizations, N, N, tau_max+1))}
    val_matrices = {'PCMCI':np.zeros((realizations, N, N, tau_max+1)),
                  'FullCI':np.zeros((realizations, N, N, tau_max+1))}  
    for i in range(realizations):
        data, true_parents_neighbors = toys.var_process(links_coeffs, T=T)
        dataframe = pp.DataFrame(data)
        
        # PCMCI
        pcmci = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr())
        results = pcmci.run_pcmci(tau_max=tau_max, pc_alpha=0.2)
        p_matrices['PCMCI'][i] = results['p_matrix']
        val_matrices['PCMCI'][i] = results['val_matrix']

        # Condition on whole past
        results = pcmci.run_fullci(tau_max=tau_max)
        p_matrices['FullCI'][i] = results['p_matrix']
        val_matrices['FullCI'][i] = results['val_matrix']

    # Get true positive rate (=power) and false positive rate 
    sig_links = {'PCMCI':(p_matrices['PCMCI'] <= alpha_level).mean(axis=0),
                  'FullCI':(p_matrices['FullCI'] <= alpha_level).mean(axis=0),}
    ave_val_matrices = {'PCMCI':val_matrices['PCMCI'].mean(axis=0),
                  'FullCI':val_matrices['FullCI'].mean(axis=0),}
    return sig_links, ave_val_matrices

sig_links, ave_val_matrices = get_sig_links()

　私たちは、どれくらいの頻度で所与のalpha_levelでリンクが検出されるか推定します。そして、各リンクの効果の平均サイズは色で与えられますが、この比率をリンクの幅として図示します。

# Showing detection power as width of links
min_sig = 0.2
vminmax = 0.4
graph = (sig_links['PCMCI'] > min_sig)
tp.plot_graph(val_matrix=ave_val_matrices['PCMCI'],
              graph=graph, var_names=var_names,
              link_width=sig_links['PCMCI'],
              vmin_edges=-vminmax,
              vmax_edges=vminmax,

)
graph = (sig_links['FullCI'] > min_sig)
tp.plot_graph(val_matrix=ave_val_matrices['FullCI'],
              graph=graph, var_names=var_names,
              link_width=sig_links['FullCI'], 
              link_colorbar_label='FullCI',
              node_colorbar_label='auto-FullCI',
              vmin_edges=-vminmax,
              vmax_edges=vminmax,
); plt.show()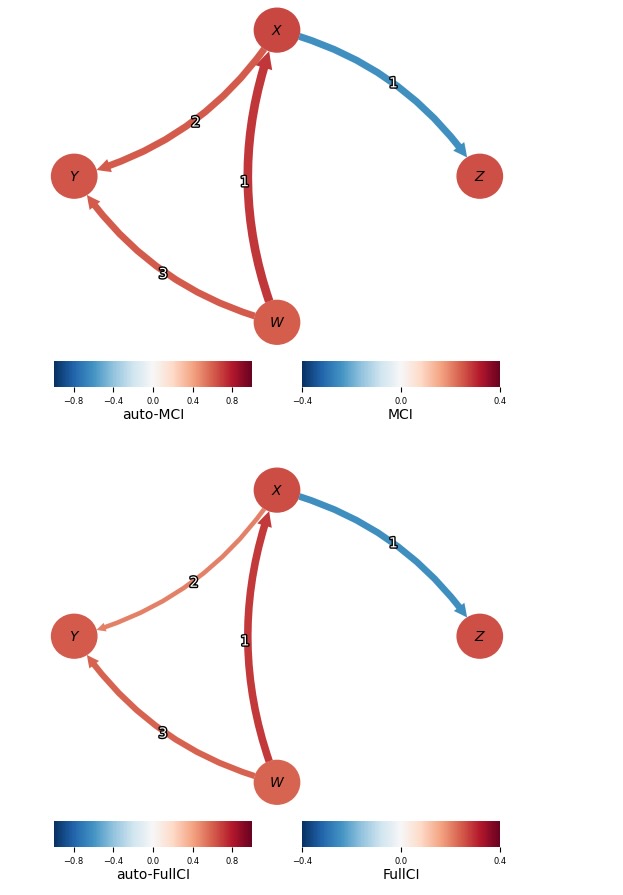

　明らかに、FullCIの静的テスト効果サイズがより小さくなるために、FullCIの力は、低下します。MCIは、論文で議論されているように、因果の強さの正確な見当を推定するために構築されます。MCIは、こうして、特定のリンクの他の従属性の影響を緩和します。大規模な研究では、この特徴は、それらの因果の強さによって、リンクを順序付けることができます。

高い次元性

　FullCIの明白な欠点は、より低い力の結果で非常に高い次元の推定を導くことを条件として、常に全体の過去を含むことです。以下で、私たちは、多くの無関係な独立変数のモデルを考えます。

# Setup analysis
np.random.seed(42)     # Fix random seed
links_coeffs = {0: [((0, -1), 0.9), ((1, -1), -0.25)],
                1: [((1, -1), 0.95), ((3, -1), 0.3)],
                2: [((2, -1), 0.85), ((1, -2), 0.3), ((3, -3), 0.3)],
                3: [((3, -1), 0.8)],
                }
T = 80     # time series length
tau_max = 5
realizations = 100
alpha_level = 0.05
n_variables = 9

# Add independent autocorrelated variables
for d in range(4, n_variables):
    links_coeffs[d] = [((d, -1), 0.2 + np.random.rand()*0.7)]
    
var_names = [r'$Z$', r'$X$', r'$Y$', r'$W$'] + list(range(4, n_variables))

N = len(links_coeffs)
# # Define whole past
# whole_past = {}
# for j in range(N):
#     whole_past[j] = [(var, -lag)
#                          for var in range(N)
#                          for lag in range(1, tau_max + 1)
#                     ]

# This cell may take some minutes
sig_links, ave_val_matrices = get_sig_links()

# Showing detection power as width of links
min_sig = 0.05
vminmax = 0.5
graph = (sig_links['PCMCI'] > min_sig)
tp.plot_graph(val_matrix=ave_val_matrices['PCMCI'],
              graph=graph, 
              link_width=sig_links['PCMCI'],
              vmin_edges=-vminmax,
              vmax_edges=vminmax,
              var_names = var_names,

)
graph = (sig_links['FullCI'] > min_sig)
tp.plot_graph(val_matrix=ave_val_matrices['FullCI'],
              graph=graph, 
              link_width=sig_links['FullCI'], 
              link_colorbar_label='FullCI',
              node_colorbar_label='auto-FullCI',
              vmin_edges=-vminmax,
              vmax_edges=vminmax,
             var_names = var_names,

); plt.show()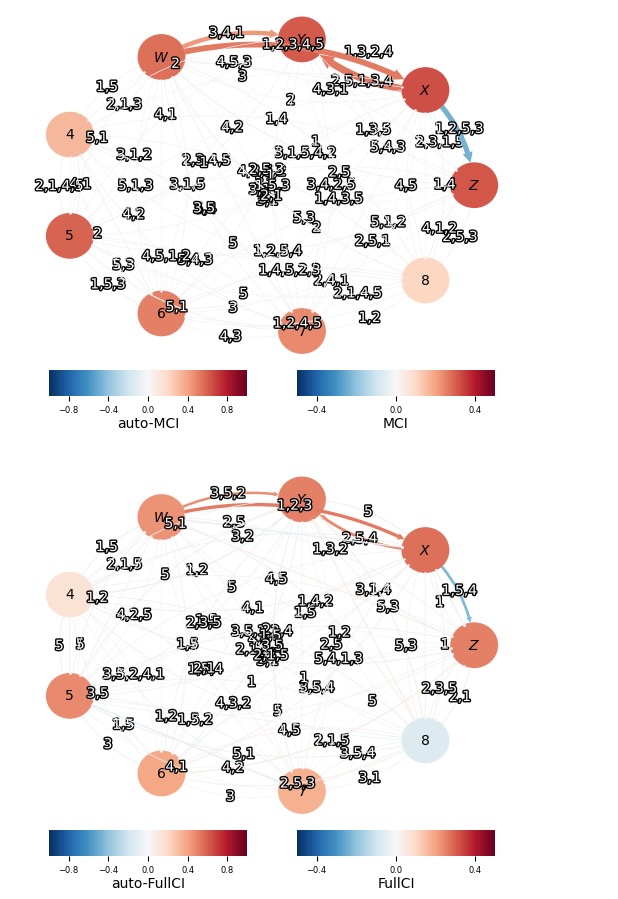

　ここで、５つの独立変数の追加は、PCMCIはまだ、前もって、予期値５％のレベルで、誤ったの見込み(positives)をうまく抑制し(真の有望な割合はもっと信頼できるけれども、100の実現値は、誤った有望な割合を推定するのに使われます、それらを作ることは、とても信頼できないことに注意してください)、ほとんど同じ力でそれらを検出しますが、FullCIで真のリンクを検出することが既に不可能になります。

true_links = np.zeros((N, N, tau_max+1))
for var in list(links_coeffs):
    for par in links_coeffs[var]:
        true_links[par[0][0], var, abs(par[0][1])] = True
# print true_links
print ("Mean true  positives PCMCI ", np.mean(sig_links['PCMCI'][:,:,1:]
                                                [true_links[:,:,1:]==True]).round(3))
print ("Mean false positives PCMCI ", np.mean(sig_links['PCMCI'][:,:,1:]
                                                [true_links[:,:,1:]==False]).round(3))
print ("Mean true  positives FullCI    ", np.mean(sig_links['FullCI'][:,:,1:]
                                                [true_links[:,:,1:]==True]).round(3))
print ("Mean false positives FullCI    ", np.mean(sig_links['FullCI'][:,:,1:]
                                                [true_links[:,:,1:]==False]).round(3))

Mean true  positives PCMCI  0.781
Mean false positives PCMCI  0.054
Mean true  positives FullCI     0.471
Mean false positives FullCI     0.052

TIGRAMITEによる因果探索 (FullCI)

PCMCI vs FullCI

1. MCIに比べてFullCIのより小さい効果サイズ

高い次元性

TIGRAMITEによる因果探索　(FullCI)