TIGRAMITEによる潜在因果探索

　TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。

　このチュートリアルは、Latent-PCMCI(LPCMCI)アルゴリズムを説明します。それは、関数LPCMCI.run_lpcmiとして実装されています。PCMCI.run _PCMCIとPCMCCCI.run_pcmciplusとして対応して実装されているPCMCIとPCMCIplusアルゴリズムと対照的に、LPCMCIは非観測の時系列を許容します。

　注記：まだハイパーパラメータのデフォルト設定が最適に調整されている最中なので、この方法は、まだ実験段階です。この問題へのフィードバックには感謝します。

　このチュートリアルの構造は以下のとおりです。

1. セクション１は、LPCMCIによって学習される因果グラフィカルモデルの解釈について説明します。
2. セクション２は、LPCMCIが、どのように重要なパラメータと出力を扱って説明するかの紹介を与えます。
3. セクション３は、合成データで応用例を示すことでLPCMCIの実際の使用を説明します。

import numpy as np

from matplotlib import pyplot as plt
%matplotlib inline     

import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.lpcmci import LPCMCI
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
# from tigramite.independence_tests.gpdc import GPDC
# from tigramite.independence_tests.cmiknn import CMIknn
# from tigramite.independence_tests.cmisymb import CMIsymb

1.構造因果過程とグラフィカル表示

　私たちは、複雑な動的システム下での因果の構造の学習に関心があります。対応する時系列はV_t = (V_t¹,…V_t^N)は、以下の因果過程、例えば次の様式、を仮定します。

　　　　　　　　　　　　　　Vtj = fi(P(Vtj),ηtj)

　ここでfiは、任意の測定可能な平凡でない従属性を持つ関数です、そのすべての引数は、排他的に表され(i≠ j)連続(t'≠t) して動的ノイズに独立し、P(Vtj)⊆Vt+1- = (Vt,Vt-1,…) \ {Vtj}. 重要にも、恒等式は、動的なノイズηtjの値とともに、P(V_t^j)の変数の値から決定されるV_t^jの値によって物理的な機構を表す、因果的な意味を持つことでアサートされます。これは、P(Vtj)の変数が、V_t^jの因果的な親として参照される理由です。私たちは、さらに、もしVt-ri ⊆ P(Vt-Δt j)、その属性は因果的にステーショナリーとして参照される、の場合にのみ、Vt-ri ⊆ P(Vtj)を要求します。そして、周期的な因果の関係はありません。(両方のこれらの性質は、直感的なグラフィカルな意味を持ちます。下のセクション1.1を参照してください。)
　LPCMCIのゴールは、データ生成した構造的因果過程のDPAG時系列を学習することです。それは、観測した変数間だけの因果的に継承する部分的知識をグラフにします。これらのグラフは、このセクションの残りで誘導され説明されます。

　補足：
　この点でもっと詳細な説明は、私たちは構造因果モデルの文献を参照します。例えば、[1]と[2]を参照してください。(参考文献はこの投稿の末尾にリストしています)

1.1 時系列DAGs

　構造的因果過程によって規定される因果上の親は、有向非周期グラフ(DAG)gによって便利に表現することができます。それは、

1. 変数V_t^jあたり、一つの頂点(akaノード)を持ちます。
2. V_t-rⁱ ⊆ P(V_t^j)のとき、Vt-ri -> Vtjの終端(aka リンク)を持ちます。

　それは正確に非周期です。なぜなら、周期的な因果の関係がない仮定によります。そしてその構造は、因果的なステーショナリティーのために、時間上で頻発します。TIGRAMITE 他のチュートリアルで　gは、時系列グラフとして参照されます。

　τ > 0 の時、Vt-ri -> Vtjの終端は、整数τをそのラグとして、参照されます。終端V_tⁱ -> V_t^jは、同時と呼ばれます。過程の順序は、最大ラグptsによって示されます。

　説明のために、ここと、その後の議論で、私たちは、動作例として、四つの要素時系列からなるpts=2の順序の以下の線形構造過程を考えます。

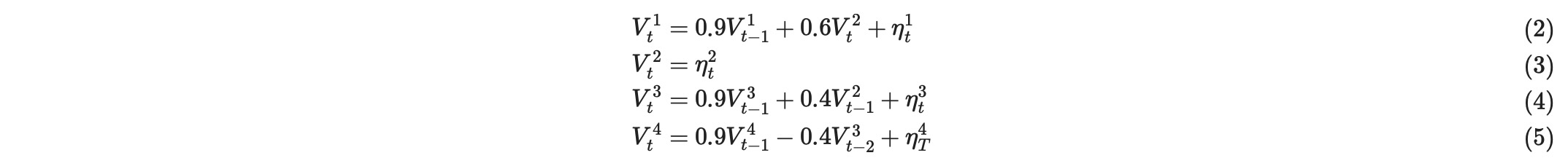
　以下の図は、時系列DAG gの関係を示します。

　左から右への水平のドットは、この基本的なグラフが過去から未来へ無限に拡張していることを示します。しかし、繰り返す構造のせいで、因果のステーショナリティーによって果されるので、少なくとも[t-pts,t]の大きさの時間ウインドウで制限するのが十分です。(上の例では、これは、one時間ステップ少なくしても十分であることを意味します。)。慣例で、私たちは、時間ウィンドウで示されるの中に完全に含まれている、それらの終端だけを表示します。例えば、V_t-1¹ -> V_t+1³は、時間ウィンドウ[t-3,t]で示されるV_t-1¹に関わらず、出力されません。なぜならV_t+1³は、時間ウィンドウの外部にあります。

1.2 時系列　DMAGs

　PCMCIとPCMCIplusから区別されるLPCMCIの設定は、要素時系列のサブセットで、観測されないことを許容します。言い換えると、要素時系列のセット、V1,…,VNは、観測された時系列X1,…,XN Nx>1 と、観測していない時系列のセット、L1,…,LN NL>0 ,N = Nx + NL, に分離します。

　これは、観測した変数のためだけの頂点のあるグラフの基礎になる過程の因果的な関係を表示する方法として疑問を生じさせます。LPCMCIが基礎にする一つのアプローチは、有向最大継承グラフ(DMAGs)を利用することです。有向混合グラフの種別があります。そしてこのように、有向終端と双方向に終端を持つことができます。それらは、[3]で紹介された最大継承グラフのもっと一般的なクラスがまだ専門化しています。それは、追加で選択バイアスを表現することを許容します。LPCMCIには、しかし、選択バイアスの欠如が仮定されます。

　基本の考えは以下のとおりです

　観測していない変数のサブセットで与えられた　DAG gを与えられることは、観測変数を覆う特別なDMAG M(g)に関連づけることができます。それは、以下の性質を持っています。

1. 隣接

　それらの情報の流れが任意の観測された変数のサブセットの条件によって、ブロックできないならば、その時だけ、例えば、もしXとYが独立となる条件で観測された変数のサブセットがないならばその場合だけ、XとYの交点、例えばX->Y,X<-Y,X<->Y、に終端があります。

2. 終端の種別

1. X->Y は、gに、XからYへの有向経路があることを示唆しています。なぜならgが非周期的です。これは、さらに、YからXへの有向経路がないことを示唆しています。
2. X<->Y は、gに、XからYへの有向経路がなく、YからXへの有向経路がないことを示唆しています。

DAGgは、有向終端が、因果の親性を示すセンスの(判別する力)原因の意味を運ぶので、関連するDMAG M(G)は因果の意味を運びます。

1. X->Yは
   　A. Xは、(潜在的に間接の)Yの原因の一つ
   　B. Yは、Xの原因ではない
2. X<->Y は
   　A. Xは、Yの原因ではない
   　B. Yは、Xの原因ではない
   　C. XとYは、同時に発生することが観測されていない対象、例えば、それはXとYの両方の原因となる、観測されていない変数Zが存在する。

　別の言い方をすると、DMAG M(G)は、過程を生成するデータの下での因果の継承関係を表現します。変数のペアの間の終端の欠如と表現は、しかしながら、真っ直ぐに原因の解釈とはなりません。

　ここで考えるこの時系列の設定は、一つの追加の様相が影響し始めます。：過去と未来全体でなく、有限の数の時間ステップだけが、観測されます。この観測する時間のウィンドウ[t-τmax,t],ここでτmax > 0 ,の選択の量が、最大考慮される時間ラグとして参照されます。さらに、DAG gの下の繰り返し構造は、その時、観測される時間ウィンドウの外側の時間ステップで推定する(外挿法により)、DMAGに関係した繰り返し構造、を示唆するために使うことができます。セクション1.2.2でより詳細に説明したように、一般的にDMAGの結果は、τ_maxの選択に依存します。この理由で、私たちは、時系列設定を特別に参照するときに、M^τ_max(g)を利用します。

　前の議論で説明するために、動作例に戻らせてください。要素時系列V²は、V¹,.V³,V⁴が観測されたときに観測されません。対応する時系列　DMAG M²(g)は、そしてτ_max = 2を選択して、以下の図の右側で示されます。

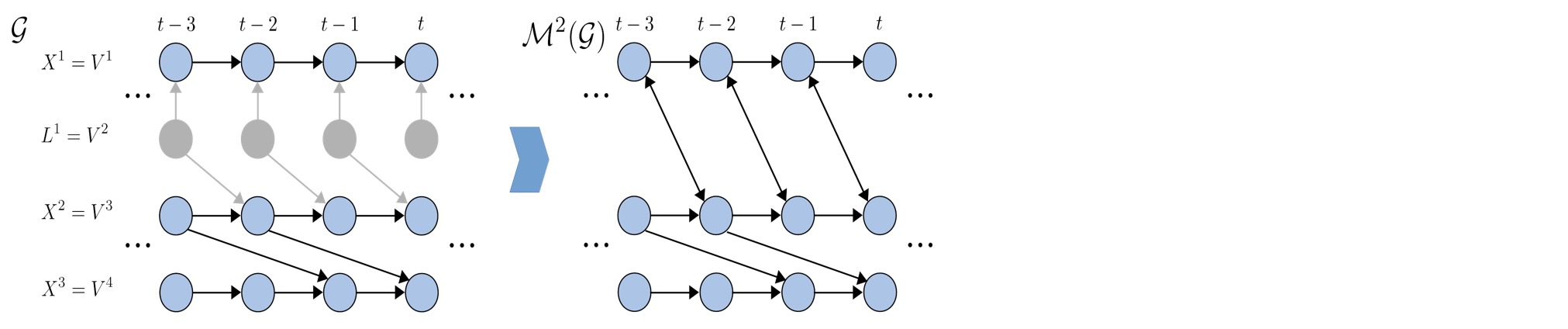
　観測されていない変数L_t-1¹ は、経路Xt-11 <-Lt-11 ->Xt2によって、観測変数X_t-1¹とX_t²を交絡させます。これは、X_t-1¹とX_t²の間の独立性を伝えます。それは、条件L_t-1¹によってのみブロックできます。それはL_t-1¹が観測されないので、実行できません。このように、X_t-1¹とX_t²はM(g）で交絡されます。gでは、X_t-1¹からX_t²への有向経路と、X_t²からX_t-1¹への有向経路がありません。後者は、不可能な方法です。なぜなら、P(V_t^j)のセットがV_t^j--それらの間の終端は双方向です、例えばM2(g)においてXt-11<->Xt2 、--の前と過去で制限されることによって、最初から強制されるので、時間上で後方への因果の影響はありません。

　補足：τ_maxは、過程の順序P_tsと等価ではあrません。"最大考慮時間ラグ"の考慮は区別の強さを判断します。

1.2.1 DMAGsの解釈の詳細

　DMAGsの解釈は、時々困難になります。特に有向終端に懸念があります。混乱を避けるために、私たちは、DMAG M(g)が何を結果として生じないか強調します。

1. XからYへの有向終端は、XがgにおいてYの原因になるとは言えません。
   Xから Yへの有向経路よりむしろ、一つ以上の単一の終端を含んでよいでしょう。例えば、YにおけるXの因果の影響は、間接的です。
2. XからYへの有向終端は、XとYは、観測されていない交絡の対象にならないとは言えません。γにおいてXからYへの有向経路を追加すると、XとYの両方の原因となる一つ以上の観測していないZがあるかもしれません。(しかし、正確な有向終端には、観測していない交絡の欠如を推測する可能性があります、このサブセクション1.2.1の、さらに次の記述を参照してください)

　これらのポイントの両方は、以下の例で説明されます。左側は時系列DAG gを示し、右側はそれに対応する時系列DAG M² (g)を示します。

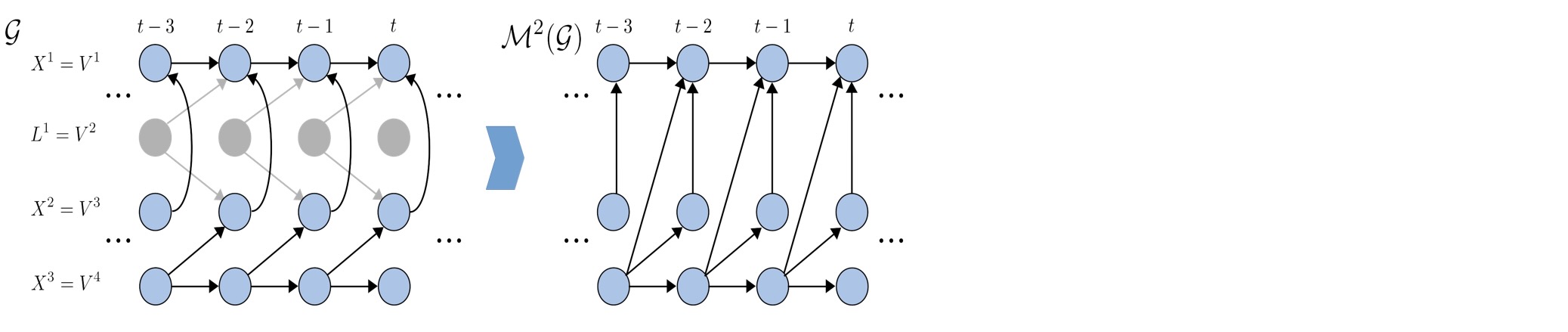
　Xt-13 -> Xt2 -> Xt1の経路によって伝えられX _t-1³とX_t¹の依存をブロックすることは、X_t²の条件を要求します。これはしかし、X_t-1³ -> X_t² <- L_t-1¹ ->X_t¹ の経路の間に依存して伝えることです。したがって、X_t-1³とX_t¹が独立になる条件の観測された変数のセットはありません。有向経路X_t-1³ -> X_t² -> X_t¹のせいで、この終端は方向があります。例えば、M2(g)のX_t-1³ -> X_t¹。しかし、X_t-1³は、gにおけるX_t¹の因果上の親ではありません。このように、上のリストの最初のポイントは説明されます。2番目のポイントは、X_t²->X_t¹の終端によって説明されます。それは、経路 X_t² <- L_t-1¹ -> X_t¹を通って、観測していない変数L_t-1¹によって交絡させられます。

　しかし、正確な条件下で、XとYが未観測の交絡の対象にならず、M(g)のX->Yから推論することは可能です。そのような有向終端は、[4]で見ることができます。視認性の必要条件ででなく十分条件は、次のとおりです。

1. もし第三の変数Zがあり、M(g)において、Z->X->Y または、Z <->X ->Y 、そしてZとYがM(g)で交絡されないならば、そのとき、終端X-> Yは、見ることができます。例えば、XtoYは未観測の交絡の対象にはなりません。

　前の例でX_t² -> X_t¹の終端のための条件は、適切であり、一致しないことに注意してください。

1.2.2 最大考慮時間ラグτ_maxの効果

　上で述べたように、時系列 DMAG M^τ_max(g)は最大考慮ログ時間τ_maxの選択に依存します。これを説明するために、下の図の右側は、私たちの動作例に関連したτ_max=1の時系列DMAG M¹(g)を示します。

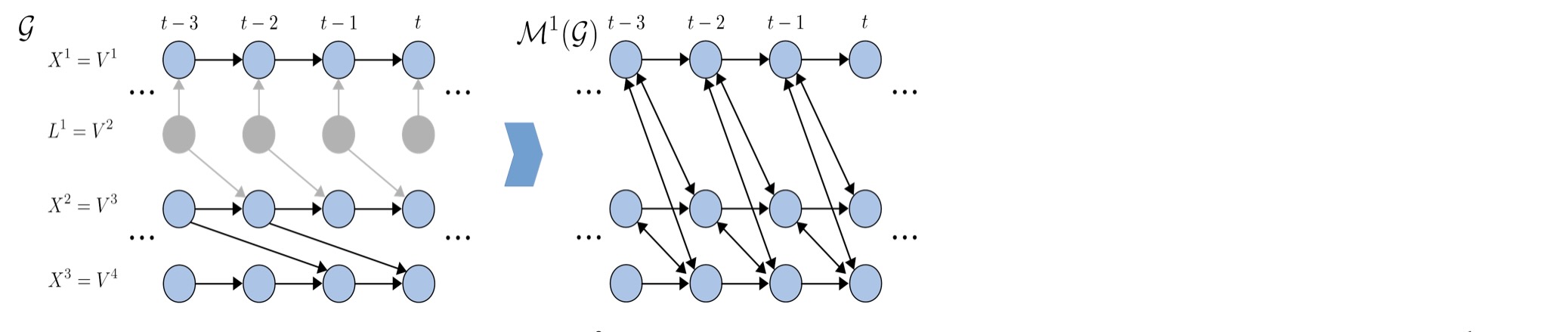
　これを、対応する時系列DMAG M²(g)を比較します。それはセクション１.２.１の前のセクション１.２で表現したものです。M¹(g)の一つの相違は、M²(g)ではX_t-2²->X_t³があるけれども、X _t-2²とX_t³の間の終端にはないことです。理由は明白です。M¹(g)は、観測された時間ウィンドウ[t-τmax,1] = [t-1,1]を基礎にしているので、τ_max =1より大きなラグの終端を含むことができません。さらに、より小さな観測された時間ウィンドウは、もっと独立して伝達する経路を導きます。それは、ブロックすることができません：最初に、経路X_t-1² <- X_t-2² ->X_t³は、ブロックできません、なぜならこれは、条件X_t-2²を要求します。これは、しかしながら、実行できません。なぜなら、X_t-2²は、観測された時間ウィンドウ[t-1,1]内にないからです。これは、M¹(g)内の終端X_t-1² <-> X_t³ を導きます。2番目に、同様に、経路X_t-1¹ <- X_t-2¹ <- X_t-3¹ <-L_t-3¹ ->X_t-2² ->X_t³は、ブロックされますそしてこのように、M¹(g)の終端X_t-1¹ <-> X_t³があります。

　この例のτ_max = 1 < p_tsの間、私たちは、この条件はτ_maxとともにM^τ_max(g)の観測された変化を必要としないことを強調します。もっと複雑なgでは、τ_max >p_tsとτ'_max > p_tsであっても 、M^τ_max(g)とM^τ'_max(g)の間の相違があって構いません。

1.3 時系列DPAGs

　このポイントのタスクは観測した時系列の観測からDMAGsの時系列を学習すると一言で言えます。LPCMCIは、データの中で独立性を使用して因果関係を開示するために制約されたアプローチでこれを実行します。それは、静的な平均によってテストされます。

　これは、しかしながら、決定論的な元で問題になります、なぜなら、厳密なDMAGsは、正確な同じ独立性のセットの増加を与えることができます。マルコフ同値として参照される現象です。それは、DMAG M(g)を特別に学習するのは不可能です。それは、データを生成した過程の下で、因果の継承関係を表現します。しかし、それはM(g)を含み、M(g)のマルコフ同値類からなる、時系列DMAG M(g)M₁,…M_m,,の候補のセットだけを好まれます。これは、M(g)のマルコフ同値類のすべてのメンバーによって共有されるそれらの特徴だけが、学習されることを意味しています。これらの共有する特徴は、直接部分継承クラスによって順番に表現することができます。それは、部分継承グラフの特徴です。それは、MAGs[5,6]のマルコフ同値類を表現するのに使われます。

　これらの基本的な考えは以下の通りです：

　マルコフ同値類のすべてのメンバーは、交絡を承認します。　ーー例えば、XとYはM(g)の終端で接続されます。もし、それらがマルコフ同値類のすべてのメンバーの終端によって接続されるならば、その時だけ、--しかし、メンバーは、終端の種別をみなすものから異なってよいでしょう。、例えば、もし X-> Y がM(g)内ならば、その時、それらは,X<-YまたはX<->Yの代わりに、マルコフ同値類のメンバーにできます。これらの多様性は、明らかに、部分方向終端Xo->Yと無方向の終端Xo-oYという、二つの新しい種類の終端によって表現されます。M(g)に対応するDPAG P(g)は、以下のように構築されます。

1. 隣接

　M(g)のそれらの間の終端がある場合に、その場合にだけ、XとYの頂点に終端があります。

2. 終端の種類

1. X->YはM(g)のマルコフ同値類のすべてのメンバーのX->Yを示唆しています。特に、M(g)内にX->Y
2. X<->Yは、M(g)のマルコフ同値類のすべてのメンバーのX<->Yを示唆しています。特に、M(g）のX<->Y.
3. Xo->Yは、以下の保持全てを示唆しています。(1)M(g)のすべてのマルコフ同値類のすべてのメンバー内で、X->YまたはX<->Yがあります。特に、M(g)のX->YまたはX<->Y。(2)M₁でのX->Yのような、M(g)のマルコフ同値類のメンバーM1があります。(3)M2でのX<->Yのような、M(g)のマルコフ同値類のメンバーM₂があります。
4. Xo-oYは、以下で保持するすべてを示唆しています。(1)M₁のX->Yのような、M(g)のマルコフ同値類のメンバーM₁があります。(2) M₂のX<-Yのような、M(g)のマルコフ同値類のメンバーM₂があります。

　M(g)は因果的な意味を運ぶので、その終端は、DPAG P(g)に関連した関係もまた、因果継承関係を示すことがわかります。

1. X->Yは、 M(g)と同様です。例えば、
   A. Xは、(潜在的に間接)Yの原因になります。
   B. Y は、Xの原因になりません
2. X<->Y は、M（g）と同様です。例えば、
   A. XはYの原因になりません
   B. YはXの原因になりません
   C. XとYは、観測されない交絡の対象になります。例えば、XとYの両方の原因となる観測されれない変数Zがあります。
3. Xo->Yは次のことが言えます。
   A. Xは、Yの原因になるかもしれないし、ならないかもしれません
   B. Yは、Xの原因になりません
4. Xo-oY は次にことが言えます。
   A. Xは、Yの原因になるかもしれないし、ならないかもしれません
   B. Yは、Xの原因になるかもしれないし、ならないかもしれません。

　言い換えれば、DPAG P(g)は、データ生成過程の元で因果継承関係の部分的な知識を表現しています。M(g)なので、変数のペア間の終端の欠如と表現は真っ直ぐに因果的な解釈を持ちません。
　以前の議論を説明するために、私たちの動作例に戻らせてください。M²(g)に関連した時系列DPAG P²(g)は、下の図の右側に表示されます。

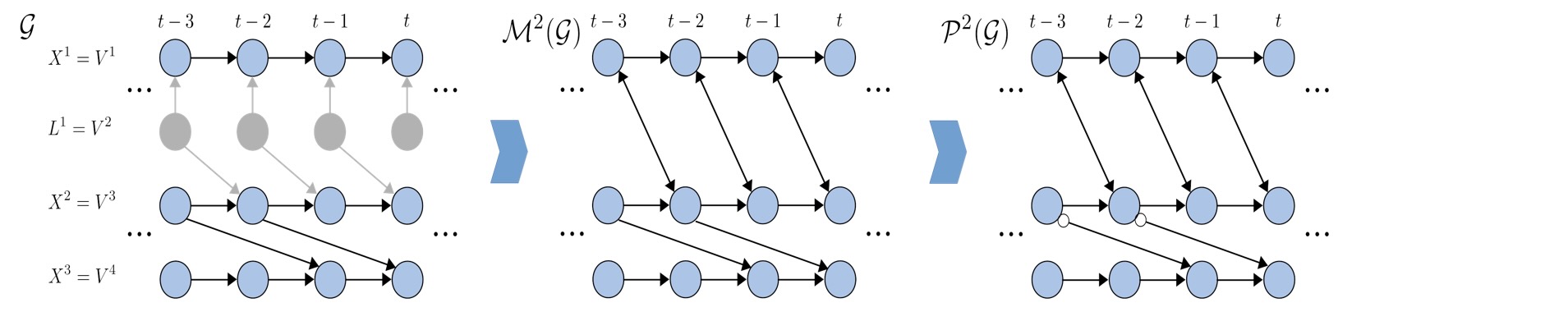
補足：選択バイアスのないケースで特徴づけます。

2. LPCMCI:観測されない交絡の時系列のための因果探索

　PCMCIのゴールは、時系列DPAG P ^τ_max(g)を学習することです。それは、構造因果過程の下の因果継承関係の部分的知識を明らかにしたセクション１で説明されています。τ_maxの値は、ユーザーによって選択された入力パラメータです。

　このセクションは、どのようにアルゴリズムが働くかの概要を与えます。LPCMCIを適用してそれらのクイックスタートを始めたければ、サブセクション2.1から2.4をスキップして、サブセクション2.5と2.6へ直接進んでください。

2.1 原理的基礎：　FCIアルゴリズム

　LPCMCIの円理的基礎は、FCIアルゴリズムです[7,,8,6].このアルゴリズムは一時的でない設定とPAGsの学習で開発されました。例えば、グラフは、、選択バイアスと観測されない交絡の両方の潜在的表現の因果継承関係の部分的知識を表します。選択バイアスの可能性は、しかしながら、少数の簡単な修正によって簡単に除外できます。アルゴリズムは四つのステップで働きます。

1. 最初の終端削除フェイズ
   完全に接続されたグラフから始めましょう。すべての終端は,X⚪︎-⚪︎Yの種別です。アルゴリズムはすべての隣接変数(X,Y)のペアを通って繰り返されます。そして、XとYは、（条件で)任意の他の変数のサブセットから独立しています。もしこれがそのケースであれば、X⚪︎-⚪︎Yは削除されます。テストされた条件のセットは、Xの隣接したサブセットとYの隣接したサブセットのセットです。

2. あらかじめ衝突する方針のフェイズ
   正確な方針のルールを元にして、任意の残りのリンクは、X⚪︎-⚪︎ YからX⚪︎->Y または、X<-⚪︎YまたはX<->Y
3. 2番目の終端の削除フェイズ
   アルゴリズムは、隣接変数(X,Y)のすべてのペアを通って、一度以上繰り返されます。そして、XとYが、与えられた任意の他の変数のサブセットと（条件つき）独立であるかどうかテストされます。この時、しかしながら、テストされた条件のセットは、Xに隣接しないサブセットまたはYに隣接したサブセットです。しかし、むしろ可能な-D-Sep(X,Y) と可能な-D-Sep(Y,X)として参照する大きなセットです。終端の種別の残りのこれらのセットの識別は、前のステップで作られて更新します。
4. ルールアプリケーションのフェイズ
   (1)すべての残りの終端は、X⚪︎-⚪︎Yに移ります。(例えば、すべての終端の種別はステップ２で更新され、実行されない) (2)ステップ２と同じ方針のルールが適用されます。(3)他の方針のルール、いくつかの終端に、X⚪︎->Yまたは、X<-⚪︎Y または　X->Yまたは　X<-Y または　X<->Yに移るルールが、余す所なく適応されます。

　FCIアルゴリズムの他の、わずかにもっと正確で詳細な説明は、LPCMCIの論文への補足資料のセクションS2を参照してください。

重要にも、制約を元にした因果探索のアプローチは、データの独立性の間の１対１の対応、とデータ生成過程の因果的な親を表現するDAGのd-separationのグラフィカルな表記、に関係します。d-separationは、対応する(条件付き)独立性を示唆します。因果マルコフ条件として知られる性質は、構造因果モデルに従って生成されたデータ、または構造因果過程に従うここで考慮する時系列設定、によってすでに示唆されています。逆の影響は、すなわち、(条件付き)独立性は、対応するd-separationを示唆し、因果の信頼条件と追加の仮定の量として参照されます。直感的にこれは、正確にその影響を取り消す逆らう仕組みのせいで、偶然の(条件付き)独立性を除外します。

2.2 時系列設定の基本修正

　私たちがここで考える時系列設定で、いくつかの基本修正がFCIアルゴリズムに適用されます。これらの間には

1. すべてのラグ付きの終端X_t-rⁱ ⚪︎-⚪︎ X_t^j , ここで私たちが呼ぶ"ラグ付き"は、τ > 0, X_t-r⚪︎->X_t^jに映ることができます。これは、X_t-rⁱ ⚪︎-> X_t^jなので、X_t^jはX_t-rⁱの原因にならない、それは単純に時間を遡る因果の影響がないことを反映します。
2. ラグ付きの終端X_t-rⁱ ⚪︎-> X_t^jは、X_t-rⁱ -> X_t^j または、X_t-rⁱ <- X_t^jに移る時はいつでも、同じ終端の種類の更新は、すべてのΔtに置いてX_t-r-Δtⁱ ⚪︎-> X_t-Δt ^jに適用されます。同様に、同時に発生する終端はX_tⁱ ⚪︎-⚪︎ X_t^j がX_tⁱ <-⚪︎ X_t^j またはX_tⁱ <- X_t^jまたはX_tⁱ ⚪︎-> X_t^j またはX_tⁱ -> X_t^j または　X_tⁱ <->X_t^jに移るときはいつでも、同じ終端の種類の更新は、すべてのΔtに対して終端X_t-Δtⁱ ⚪︎-> Xt-Δtjが適用されます。これは因果のステーショナリティーを反映しています。
3. X_t-rⁱとX_t^jの間のラグ付き、または同時に発生する終端が削除されるときはいつでも、すべてのΔtに対するX_t-r-ΔtⁱとX_t-Δt^jの間の終端も削除されます。これは因果のステーショナリーによって許容されます。

2.3 PCMCIアイデアの結合

　LPCMCIの主要な特徴は、PCMCIのアイデアを結合することです。それは、PCMCI[9]とPCMCIplus[10]アルゴリズムを使うことです。強い自己相関は、(条件)独立テストの効果的なサイズを減少させる傾向があるという観測に基づきます。それによって、これらのテストの統計的な力を減少させ、こうして、アルゴリズムの統計的な性能全体を落とします。このアイデアは、条件付き自己相関の方法によって、この問題を緩和させます。これは、デフォルトの条件Sde(Xt-ri,Xtj)による(条件)独立テストの標準的条件セットを拡張することによってアーカイブされます。概略的に

　　Test whether Xt-ri ⊥ Xtj | S  ->   Test whether  Xt-ri ⊥ Xtj | S ∪ Sdef(Xt-ri, Xtj)

　PCMCIとPCMCIplusの設定は、観測していない変数がない仮定によって、デフォルト条件S_def(X_t-rⁱ,X_t^j)が、この目的のために、Xt-riとXtjの因果的な親を結合させます。初期には、しかしながら、因果的な協力は、結局知られていません。これのアルゴリズムの目的は、因果的な協力を学習することです。PCMCIとPCMCIplusは、観測しない変数の欠如において、不確かな従属性を伝えることの危険性なしに、すべてのラグ付きの変数とともに、条件セットが、原理的に、拡張してよいことを記すことによって、この複雑さを動き回ります。言い換えると：デフォルト条件S_def(X_t-rⁱ,X_t^j)は、基本的に、t-1またはより早く、すべての変数セットとして選択されます。そのような高次の条件セットは、しかしながら、特に、(条件)独立テストの次元の推定を増加します。そして、再びそれによって、それらの統計的な力を減少させます。中間物(妥協案)はラグ付きのリンクのPCアルゴリズムの最初に実行する貪欲なバージョンによって出力されます。そしてその後、デフォルトの条件で、ラグ付きの隣接を使います。詳細は[9],[10]を参照してください。

　LPCMCIの設定で、観測しない変数の存在が許容されると、状況は、もっと複雑になります。：ラグ付き変数の条件は、不確かな従属性を伝えるでしょう。そうして、PCMCIとPCMCIplusのアプローチは、簡単に複製されません。しかし、条件セットは、不確かな従属性を伝える危険なしに、まだ、因果の継承を拡張することができます。もし因果の継承を定義した知識が、すべての(条件)独立テストがすでに実行される前に、推論できるならば、PCMCIのアイデアは、このように実装されます。これは、正確に、LPCMCIがすることです：FCIアルゴリズムを拡張することで、方針のルールの最新のセットを使用します。それは、アルゴリズムがまだ、さらなる(条件)独立性をテストする間、因果の継承関係を学習することを許します。この方法で識別される因果の継承元は、残りのテストのために、デフォルト条件S_def(X_t-rⁱ,X_t^j)として使います。なぜなら、最新の方針のルールは、もっと因果の継承関係、もっとすでに削除されている終端を識別することができます。アルゴリズムは独立性テストの実行中、繰り返され、方針ルールの適用されます。

2.4 LPCMCIアルゴリズム

　LPCMCIの基本構造は、以下のとおりです。

　これを理解するために、最初にステップ2を仮定します。k=0が選択されるためにスキップされます。(kの値は、LPCMCI.run_lpcmciの引数で、以下のセクション2.5を参照してください。)LPCMCIのステップ１と３の組み合わせは、そのとき、サブセクション2.2と2.3で議論に従って修正された、FCI(上のサブセクション2.1を参照)のステップ1と2の組み合わせに一致します。同様に、LPCMCIのステップ4は、修正に従うFCIのステップ3と４の組み合わせに一致します。これは、LPCMCIの正しいアプリケーションです--理論的にも正しく--真の時系列DAG P ^τ_max (g)を学習します。

　k>0でのステップ２の目的は、LPCMCIの有限のサンプル実行をさらに改良します。これは、LPCMCIの論文の数値実験のデモです。これに対する理由は以下の通り、もし、k＝０が選択されれば、そのとき、LPCMCIのステップ３が、因果的な継承関係の知識なしに始まります。最初の(条件付き)独立性テストは、このように空のデフォルト条件Sdef(Xt-ri,xtj)を持ちます。それは、低い統計的な力に悩むことを意味します。従って誤った判断の傾向があります。ステップ３のコースでは、任意の因果的な継承関係は、識別され、(条件)独立性テストの結果のデフォルトの条件として使用されます。しかし、前のテストのエラー決定が修復されることはありません。そしてこれが、正確になぜk>0のステップ２が役に立つか：一旦ステップ２が完了すると、いくかの因果的継承関係が識別されます。アルゴリズムはそのとき、すべての削除した終端のレストアを開始します。しかし、いくつかの因果の継承関係は覚えておきます。これは、ステップ３の最初の(条件)独立テストの空ではないデフォルト条件Sdef(Xt-ri,Xtj)の結果です。このように、それらの統計的な力を増やし、エラーのあるテストの決定に対してもっと堅牢なこのステップを作ります。　k > 1では、終端をレストアする過程は、ステップ2.Aが空でないデフォルト条件で開始するのと同様に、(最初の繰り返し数を除いて)一度以上繰り返されます。

　これは、LPCMCIの論文の中で、LPCMCIのステップ２の繰り返しの冗長な出力と同様に、、(最後の)継承フェイズとしてステップ３、継承のないフェイズとしてステップ４の仮の相として参照されます。

2.5 LPCMCIのパラメータ

　LPCMCIは、任意の種類の（条件付き）静的独立性テストの柔軟に結合することができます。従って、従属性の様式を過程するのと同じように、データの種類(連続か離散)を適合します。（条件付き）独立テストは、tigmite.independence_testsで利用できます。

　LPCMCIの主要な自由パラメータは、（条件付き）独立性テストのそれらに追加して、

1. 最大考慮時間ラグ τ_max(tau_max). これは、観測ウィンドウ[t-τmax,t]と、学習されることが考えられる時系列 DPAG P τmax (g).
2. 個別の(条件付き)独立性テストの重要な閾値 αpc (pc_alpha)。より高いαpc日して、推定されたグラフは密集する傾向があります。
3. アルゴリズムのステップ２の仮の回数　k、(n_preliminary_iterations)。デフォルトでは、n_preliminary_iteratuons = 1.

　LPCMCIの非継承フェイズ（ステップ４）は、時々、非常に遅くなります。なぜなら、標準の条件セットSが、大きいセットのサブセットを通って実行するためです。それは、大きな数の（条件)独立性テストが伝達されることを意味しています。このケースでは、ここでステップ４の実行時に、引数max_p_non_ancestralを使うことによって、Sの基数の制限と、LCMCIの正確な漸近の可能性を約束することができます。

2.6 LPCMCIの出力

　関数LPCMCI.run_lpcmciは、三つのエントリーの辞書を返します。それは文字列'graph','p_matrix', 'val_matrix'で対応してアクセスされます。私たちは、ここで、三つのエントリーを、それらをそれらのキーによって参照して、順番に議論していきます。

graph:
これは、LPCMCIの中央の出力です、それは、シェイプ(N_X,N_X,tau_max + 1)の３次元の配列です。ここでgraph[i,j,tau]は、象徴的にX_t-rⁱからX_t^jへの終端を表す文字列です。次のように規定されます。

1. graph[i, j, tau] = '-->' は、X_t-rⁱ -> X_t^jを意味します。
2. graph[i, j, tau] = '<->' は、X_t-rⁱ <-> X_t^j を意味します
3. graph[i, j, tau] = 'o->' は、X_t-rⁱ o-> X_t^j を意味します
4. graph[i, j, tau] = '' (空文字列) は、X_t-rⁱ とX_t^jの間に終端がないことを
5. graph[i, j, 0] = '-->' と graph[j, i, 0] = '<--' は、X_tⁱ -> X_t^j
6. graph[i, j, 0] = '<--' と graph[j, i, 0] = '-->' は、X_tⁱ <- X_t^j
7. graph[i, j, 0] = '<->' と graph[j, i, 0] = '<->' は、X_tⁱ <-> X_t^j
8. graph[i, j, 0] = 'o->' と graph[j, i, 0] = '<-o' は、X_tⁱ o-> X_t^j
9. graph[i, j, 0] = '<-o' と graph[j, i, 0] = 'o->' は、X_tⁱ <-o X_t^j
10. graph[i, j, 0] = 'o-o' と graph[j, i, 0] = 'o-o' は、X_tⁱ o-o X_t^j
11. graph[i, j, 0] = '' と graph[j, i, 0] = '' (空文字列)は、X_tⁱとX_t^jの間に終端がないことを意味します。

　(条件付き）独立性に関するエラーのあるテスト決定のせいで、終端の方針ルールが終端の種類の更新で競合を推定することが発生します。例えば、一つの方針ルールがX_t-rⁱ o-> Xtjの終端が、X_t-rⁱ -> X_t^jに更新できると主張し、同じ時に、他の方針ルールがX_t-rⁱ <->X_t^jに更新できると伝えます。そうした競合は、競合を表記するシンボルXで、X_t-rⁱ x-x X_t^j と　X_t-rⁱ x-> X_t^jという、追加の終端の種類を明白にそれらに導入することによって、処理されます。例では、終端は、X_t-rⁱ x->X_t^jに更新されます。なぜなら、競合は、X_t^jがX_t-rⁱの原因ではないというコンセンサスがある間に、X_t-rⁱがX_t^jの原因でないかどうかの時に懸念されます。

1. graph[i, j, tau] = 'x->' は、X_t-rⁱ -> X_t^j　と X_t-rⁱ <-> X_t^jの両方が提案されます。
2. graph[i, j, 0] = 'x->' と graph[j, i, 0] = '<-x' は、これらの競合の一つは、 A. X_tⁱ -> X_t^j と　X_tⁱ <-> X_t^j
   B. X_tⁱ -> X_t^j と　X_tⁱ<-o X_t^j
3. graph[i, j, 0] = '<-x' と graph[j, i, 0] = 'x->' は、これらの競合の中の一つは、
   A. X_tⁱ -> X_t^j と X_tⁱ <-> X_t^j
   B. X_tⁱ <- X_t^j と X_tⁱ o-> X_t^j
4. graph[i, j, 0] = 'x-x' と graph[j, i, 0] = 'x-x' は、X_tⁱ->X_t^jとX_tⁱ <- X_t^jの両方が提案されます。

グラフは、TIGRAMITEの描画関数で可視化できます。セクション3以下の応用例を参照してください。

p_matrix:
シェイプ(N_X,N_X,tau_max+1)の３次元配列、ここで、p_matrix[i,j,tau] は変数X_t-rⁱとX_t^jの変数ペアのすべての(条件)独立性テストのp-値の最大値です。τ=0 で、対称性 p_matrix[i,j,0] = p_matrix[j,i,0]が保持されます。

　独立性テストは制限を基礎にしたパラダイムを使う方法のために、最小p-値よりむしろ最大p-値が、記録されます。：対応する終端が削除されるケースでは、αpcより大きいp-値は、独立性の帰無仮説を拒否しません。

val_matrix:
　シェイプ(N_X,N_X,tau_max + 1 )の３次元配列、ここでval_matrix[i,j,tau] p-値がp_matrix[i,j,tau]にストアされる、特別な（条件付き）独立性の静的なテストです。変数X_t-rⁱとX_t^jの同じペアに、異なる基数の条件セットでテストされます。このように異なるnull分布に導くことで、この値は、すべての(条件)独立性テストを通って、最小のテスト統計と等しくなる必要なありません。τ=0では、対称性val_matrix[i,j,0] = val_matrix[j,i,0]を保持します。

　それに従って、終端に色付けするために、プロッティング関数tp.plot_graphとtp.plot_time_series_graphにval_matrixを渡します。下のセクション３の応用例を参照してください。

3. 応用例

　このセクションは、合成データ上で、LPCMCIのアプリケーションを説明し、デモンストレーとします。サブセクション3.7は最初の読みkみでスキップしても構いません。

3.1 データ生成

　私たちは、構造因果過程に戻ります。セクション1は、そこでは、上で私たちが観測されないものとして2番目の成分の時系列を取り扱うように、動作例として取り扱われます。観測した時系列のためにシンボルXiと、過程が読み込む観測されない時系列Liを使うことによって、これを明らかにします。

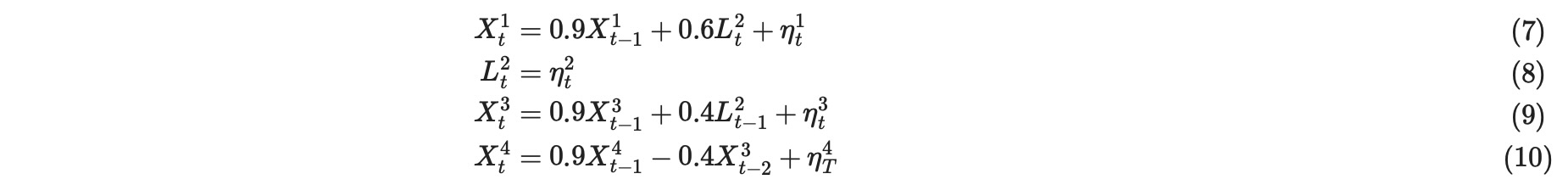
　関数 toy.structual_causal_processは、以下のように、この過程の実現を生成することができます。

# Set a seed for reproducibility
seed = 19

# Choose the time series length
T = 500

# Specify the model (note that here, unlike in the typed equations, variables
# are indexed starting from 0)
def lin(x): return x

links = {0: [((0, -1), 0.9, lin), ((1, 0), 0.6, lin)],
         1: [],
         2: [((2, -1), 0.9, lin), ((1, -1), 0.4, lin)],
         3: [((3, -1), 0.9, lin), ((2, -2), -0.5, lin)]                                    
        }

# Specify dynamical noise term distributions, here unit variance Gaussians
random_state = np.random.RandomState(seed)
noises = noises = [random_state.randn for j in links.keys()]

# Generate data according to the full structural causal process
data_full, nonstationarity_indicator = toys.structural_causal_process(
    links=links, T=T, noises=noises, seed=seed)
assert not nonstationarity_indicator

# Remove the unobserved component time series
data_obs = data_full[:, [0, 2, 3]]

# Number of observed variables
N = data_obs.shape[1]

# Initialize dataframe object, specify variable names
var_names = [r'$X^{%d}$' % j for j in range(N)]
dataframe = pp.DataFrame(data_obs, var_names=var_names)

3.2 時系列の図示

　時系列は関数tp.plot_timeseriesで図示することができます。

tp.plot_timeseries(dataframe, figsize=(15, 5));
plt.show()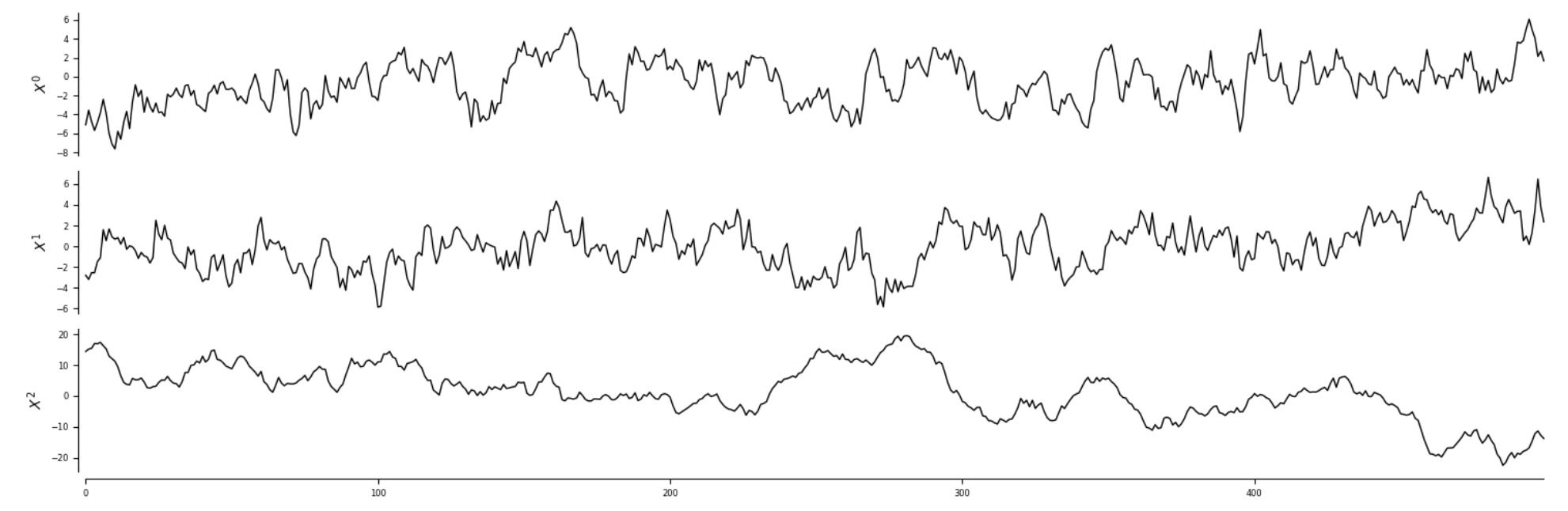

3.3 探索：二項ラグ付き条件独立性

　選択のためtau_maxの考えを得る目的で、関数run_bivciを実行させるでしょう。それは、二項ラグ付き条件独立性テストを実装しています。(二項Granger因果と似ています。しかし、ラグ付きです)。この関数は、PCMCIクラスによって実装されています。

# Create a (conditional) independence test object
# Here, the partial correlation test is used
parcorr = ParCorr(significance='analytic')

# Create a PCMCI object, passing the the dataframe and (conditional)
# independence test object.
pcmci = PCMCI(dataframe=dataframe, 
              cond_ind_test=parcorr,
              verbosity=1)

# Run the `PCMCI.run_bivci` function
correlations = pcmci.run_bivci(tau_max=20, val_only=True)['val_matrix']

# Plot the results
setup_args = {'var_names':var_names,
              'figsize':(10, 6),
              'x_base':5,
              'y_base':.5}
lag_func_matrix = tp.plot_lagfuncs(val_matrix=correlations, 
                                   setup_args=setup_args)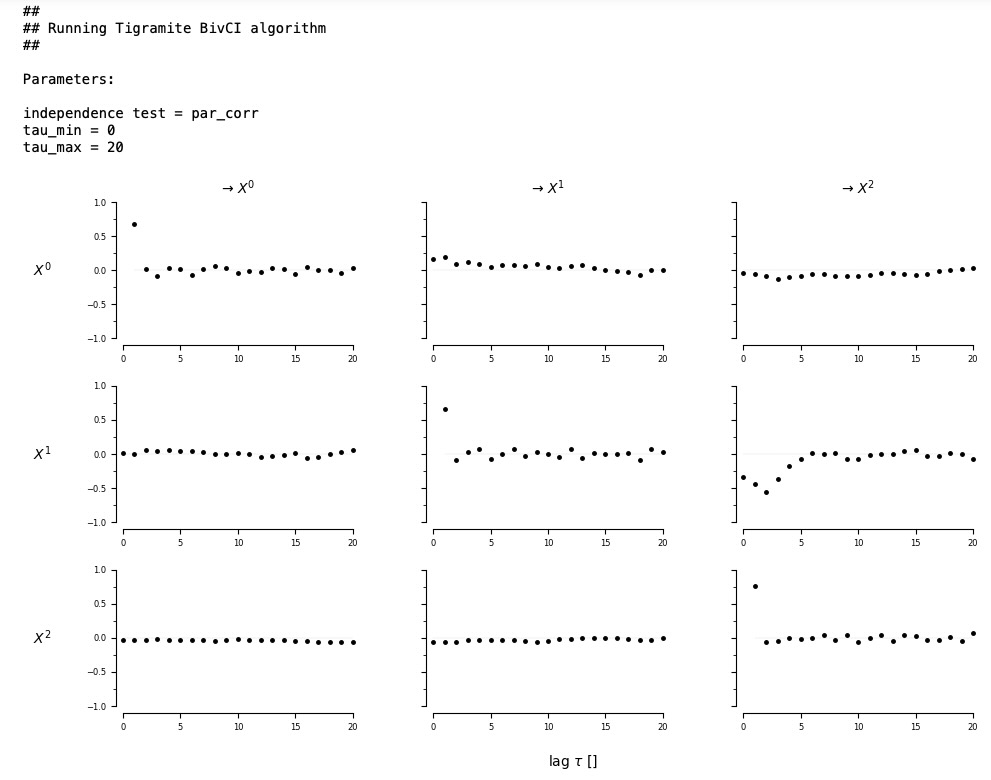

3.4 LPCMCIの応用

　run_bivciの結果を基礎にして、私たちは、LPCMCIにtau_max=5、を適用することを選択します。そのラグの後、ラグ関数は０に衰退します。
これはヒューリスティックだけ(経験に基づく)であることに注意してください。加えて、あなたは、適当な条件独立性テストを選択するために、PCMCIのチュートリアルで実行したように、スキャッタープロットをチェックして良いでしょう。私たちは、pc_alpha=0.01をさらに、選択します。そしてそこから離れて、デフォルトのハイパーパラメータの設定を修正することはありません。

# Create a LPCMCI object, passing the dataframe and (conditional)
# independence test objects.
# parcorr = ParCorr(significance='analytic')
lpcmci = LPCMCI(dataframe=dataframe, 
                cond_ind_test=parcorr,
                verbosity=1)

# Define the analysis parameters.
tau_max = 5
pc_alpha = 0.01

# Run LPCMCI
results = lpcmci.run_lpcmci(tau_max=tau_max,
                            pc_alpha=pc_alpha)

=======================================================
=======================================================
Starting preliminary phase  1

Starting test phase

p = 0

Test phase complete
p = 1
(0,-5) independent (0, 0) given ((0, -1),) union set()
(0,-4) independent (0, 0) given ((0, -1),) union set()
(0,-3) independent (0, 0) given ((0, -1),) union set()
(0,-2) independent (0, 0) given ((0, -1),) union set()
(1,-5) independent (1, 0) given ((1, -1),) union set()
(1,-4) independent (1, 0) given ((1, -1),) union set()
(1,-3) independent (1, 0) given ((1, -1),) union set()
(1,-2) independent (1, 0) given ((1, -1),) union set()
Writing:   (0,-5) oL> (0, 0) ==> (0,-5)     (0, 0) 
Writing:   (0,-4) oL> (0, 0) ==> (0,-4)     (0, 0) 
Writing:   (0,-3) oL> (0, 0) ==> (0,-3)     (0, 0) 
Writing:   (0,-2) oL> (0, 0) ==> (0,-2)     (0, 0) 
Writing:   (1,-5) oL> (1, 0) ==> (1,-5)     (1, 0) 
Writing:   (1,-4) oL> (1, 0) ==> (1,-4)     (1, 0) 
Writing:   (1,-3) oL> (1, 0) ==> (1,-3)     (1, 0) 
Writing:   (1,-2) oL> (1, 0) ==> (1,-2)     (1, 0) 
(0, 0) independent (1, 0) given ((0, -1),) union set()
(0, 0) independent (1, 0) given ((0, -1),) union set()
(0, 0) independent (2, 0) given ((2, -1),) union set()
(0, 0) independent (2, 0) given ((0, -1),) union set()
Writing:   (0, 0) o?o (1, 0) ==> (0, 0)     (1, 0) 
Writing:   (1, 0) o?o (0, 0) ==> (1, 0)     (0, 0) 
Writing:   (0, 0) o?o (2, 0) ==> (0, 0)     (2, 0) 
Writing:   (2, 0) o?o (0, 0) ==> (2, 0)     (0, 0) 
(0,-1) independent (1, 0) given ((0, -2),) union set()
(0,-1) independent (2, 0) given ((2, -1),) union set()
(1,-1) independent (0, 0) given ((0, -1),) union set()
(2,-1) independent (0, 0) given ((0, -1),) union set()
Writing:   (1,-1) oL> (0, 0) ==> (1,-1)     (0, 0) 
Writing:   (2,-1) oL> (0, 0) ==> (2,-1)     (0, 0) 
Writing:   (0,-1) oL> (1, 0) ==> (0,-1)     (1, 0) 
Writing:   (0,-1) oL> (2, 0) ==> (0,-1)     (2, 0) 
(0,-2) independent (1, 0) given ((1, -1),) union set()
(0,-2) independent (2, 0) given ((2, -1),) union set()
(1,-2) independent (0, 0) given ((0, -1),) union set()
(2,-2) independent (0, 0) given ((0, -1),) union set()
Writing:   (1,-2) oL> (0, 0) ==> (1,-2)     (0, 0) 
Writing:   (2,-2) oL> (0, 0) ==> (2,-2)     (0, 0) 
Writing:   (0,-2) oL> (1, 0) ==> (0,-2)     (1, 0) 
Writing:   (0,-2) oL> (2, 0) ==> (0,-2)     (2, 0) 
(0,-3) independent (1, 0) given ((1, -1),) union set()
(0,-3) independent (2, 0) given ((1, -5),) union set()
(1,-3) independent (0, 0) given ((0, -1),) union set()
(2,-3) independent (0, 0) given ((0, -1),) union set()
(2,-3) independent (1, 0) given ((1, -1),) union set()
Writing:   (1,-3) oL> (0, 0) ==> (1,-3)     (0, 0) 
Writing:   (2,-3) oL> (0, 0) ==> (2,-3)     (0, 0) 
Writing:   (0,-3) oL> (1, 0) ==> (0,-3)     (1, 0) 
Writing:   (2,-3) oL> (1, 0) ==> (2,-3)     (1, 0) 
Writing:   (0,-3) oL> (2, 0) ==> (0,-3)     (2, 0) 
(0,-4) independent (1, 0) given ((1, -1),) union set()
(0,-4) independent (2, 0) given ((2, -1),) union set()
(1,-4) independent (0, 0) given ((0, -1),) union set()
(2,-4) independent (0, 0) given ((0, -1),) union set()
(2,-4) independent (1, 0) given ((1, -1),) union set()
Writing:   (1,-4) oL> (0, 0) ==> (1,-4)     (0, 0) 
Writing:   (2,-4) oL> (0, 0) ==> (2,-4)     (0, 0) 
Writing:   (0,-4) oL> (1, 0) ==> (0,-4)     (1, 0) 
Writing:   (2,-4) oL> (1, 0) ==> (2,-4)     (1, 0) 
Writing:   (0,-4) oL> (2, 0) ==> (0,-4)     (2, 0) 
(0,-5) independent (1, 0) given ((1, -1),) union set()
(0,-5) independent (2, 0) given ((2, -1),) union set()
(1,-5) independent (0, 0) given ((0, -1),) union set()
(2,-5) independent (0, 0) given ((0, -1),) union set()
(2,-5) independent (1, 0) given ((1, -1),) union set()
Writing:   (1,-5) oL> (0, 0) ==> (1,-5)     (0, 0) 
Writing:   (2,-5) oL> (0, 0) ==> (2,-5)     (0, 0) 
Writing:   (0,-5) oL> (1, 0) ==> (0,-5)     (1, 0) 
Writing:   (2,-5) oL> (1, 0) ==> (2,-5)     (1, 0) 
Writing:   (0,-5) oL> (2, 0) ==> (0,-5)     (2, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-09'], ['ER-10']]

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Marked:    (0,-1) oL> (0, 0) ==> (0,-1) -L> (0, 0) 
Marked:    (1,-1) oL> (1, 0) ==> (1,-1) -L> (1, 0) 
Writing:   (0,-1) oL> (0, 0) ==> (0,-1) -L> (0, 0) 
Update:    Marking (0, -1) as anc of (0, 0)
Writing:   (1,-1) oL> (1, 0) ==> (1,-1) -L> (1, 0) 
Update:    Marking (1, -1) as anc of (1, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

Orientation phase complete

Middle mark updates


Starting test phase

p = 0

Test phase complete
p = 1
Writing:   (0,-1) -L> (0, 0) ==> (0,-1) -!> (0, 0) 
(1, 0) independent (2, 0) given ((2, -1),) union {(1, -1)}
(1, 0) independent (2, 0) given ((2, -2),) union {(1, -1)}
Writing:   (1, 0) o?o (2, 0) ==> (1, 0)     (2, 0) 
Writing:   (2, 0) o?o (1, 0) ==> (2, 0)     (1, 0) 
(1,-1) independent (2, 0) given ((2, -1),) union {(1, -2)}
(2,-1) independent (1, 0) given ((2, -2),) union {(1, -1)}
Writing:   (2,-1) oL> (1, 0) ==> (2,-1)     (1, 0) 
Writing:   (1,-1) oL> (2, 0) ==> (1,-1)     (2, 0) 
Writing:   (2,-2) oL> (1, 0) ==> (2,-2) o!> (1, 0) 
(1,-3) independent (2, 0) given ((1, -2),) union {(1, -4)}
Writing:   (1,-3) oL> (2, 0) ==> (1,-3)     (2, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-09'], ['ER-10']]

APR:
Marked:    (0,-1) -!> (0, 0) ==> (0,-1) --> (0, 0) 
Writing:   (0,-1) -!> (0, 0) ==> (0,-1) --> (0, 0) 

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Marked:    (1,-2) oL> (2, 0) ==> (1,-2) -L> (2, 0) 
Writing:   (1,-2) oL> (2, 0) ==> (1,-2) -L> (2, 0) 
Update:    Marking (1, -2) as anc of (2, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-09:
Marked:    (1,-4) oL> (2, 0) ==> (1,-4) -L> (2, 0) 
Writing:   (1,-4) oL> (2, 0) ==> (1,-4) -L> (2, 0) 
Update:    Marking (1, -4) as anc of (2, 0)

APR:
Found nothing

ER-08:
Marked:    (1,-5) oL> (2, 0) ==> (1,-5) -L> (2, 0) 
Writing:   (1,-5) oL> (2, 0) ==> (1,-5) -L> (2, 0) 
Update:    Marking (1, -5) as anc of (2, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

Orientation phase complete

Middle mark updates


Starting test phase

p = 0

Test phase complete
p = 1
(2,-5) independent (2, 0) given ((2, -1),) union {(1, -5), (1, -4), (1, -2)}
(2,-4) independent (2, 0) given ((2, -1),) union {(1, -5), (1, -4), (1, -2)}
(2,-3) independent (2, 0) given ((2, -1),) union {(1, -5), (1, -4), (1, -2)}
(2,-2) independent (2, 0) given ((2, -1),) union {(1, -5), (1, -4), (1, -2)}
Writing:   (2,-5) oL> (2, 0) ==> (2,-5)     (2, 0) 
Writing:   (2,-4) oL> (2, 0) ==> (2,-4)     (2, 0) 
Writing:   (2,-3) oL> (2, 0) ==> (2,-3)     (2, 0) 
Writing:   (2,-2) oL> (2, 0) ==> (2,-2)     (2, 0) 
(1,-4) independent (2, 0) given ((2, -1),) union {(1, -5), (1, -2)}
Writing:   (1,-4) -L> (2, 0) ==> (1,-4)     (2, 0) 
(1,-5) independent (2, 0) given ((2, -1),) union {(1, -2)}
Writing:   (1,-5) -L> (2, 0) ==> (1,-5)     (2, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-09'], ['ER-10']]

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Marked:    (2,-1) oL> (2, 0) ==> (2,-1) -L> (2, 0) 
Writing:   (2,-1) oL> (2, 0) ==> (2,-1) -L> (2, 0) 
Update:    Marking (2, -1) as anc of (2, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

Orientation phase complete

Middle mark updates


Starting test phase

p = 0

Test phase complete
p = 1
Writing:   (2,-1) -L> (2, 0) ==> (2,-1) -!> (2, 0) 
Writing:   (1,-2) -L> (2, 0) ==> (1,-2) -!> (2, 0) 

Test phase complete
p = 2
Writing:   (1,-1) -L> (1, 0) ==> (1,-1) -!> (1, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-00-d'], ['ER-00-c'], ['ER-03'], ['R-04'], ['ER-09'], ['ER-10'], ['ER-00-b'], ['ER-00-a']]

APR:
Marked:    (1,-2) -!> (2, 0) ==> (1,-2) --> (2, 0) 
Marked:    (2,-1) -!> (2, 0) ==> (2,-1) --> (2, 0) 
Marked:    (1,-1) -!> (1, 0) ==> (1,-1) --> (1, 0) 
Writing:   (1,-1) -!> (1, 0) ==> (1,-1) --> (1, 0) 
Writing:   (1,-2) -!> (2, 0) ==> (1,-2) --> (2, 0) 
Writing:   (2,-1) -!> (2, 0) ==> (2,-1) --> (2, 0) 

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Marked:    (2,-2) o!> (1, 0) ==> (2,-2) <!> (1, 0) 
Writing:   (2,-2) o!> (1, 0) ==> (2,-2) <!> (1, 0) 
Update:    Marking (2, -2) as non-anc of (1, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Found nothing

ER-03:
Found nothing

R-04:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

ER-00-b:
Found nothing

ER-00-a:
Marked:    (2,-2) <!> (1, 0) ==> (2,-2)     (1, 0) 
Writing:   (2,-2) <!> (1, 0) ==> (2,-2)     (1, 0) 

Links were removed by rules


APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Found nothing

ER-03:
Found nothing

R-04:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

ER-00-b:
Found nothing

ER-00-a:
Found nothing

Orientation phase complete

Middle mark updates


Preliminary phase  1 complete

Graph:
--------------------------------
(0,-1) --> (0, 0)
(1,-1) --> (1, 0)
(1,-2) --> (2, 0)
(2,-1) --> (2, 0)
--------------------------------
Writing:   (0,-1) oL> (0, 0) ==> (0,-1) -L> (0, 0) 
Update:    Marking (0, -1) as anc of (0, 0)
Writing:   (1,-1) oL> (1, 0) ==> (1,-1) -L> (1, 0) 
Update:    Marking (1, -1) as anc of (1, 0)
Writing:   (2,-1) oL> (2, 0) ==> (2,-1) -L> (2, 0) 
Update:    Marking (2, -1) as anc of (2, 0)
Writing:   (1,-2) oL> (2, 0) ==> (1,-2) -L> (2, 0) 
Update:    Marking (1, -2) as anc of (2, 0)

=======================================================
=======================================================
Starting final ancestral phase

Starting test phase

p = 0
(0,-5) independent (0, 0) given () union {(0, -1)}
(0,-4) independent (0, 0) given () union {(0, -5), (0, -1)}
(0,-3) independent (0, 0) given () union {(0, -4), (0, -1)}
(0,-2) independent (0, 0) given () union {(0, -3), (0, -1)}
(1,-5) independent (1, 0) given () union {(1, -1)}
(1,-4) independent (1, 0) given () union {(1, -5), (1, -1)}
(1,-3) independent (1, 0) given () union {(1, -4), (1, -1)}
(1,-2) independent (1, 0) given () union {(1, -3), (1, -1)}
(2,-5) independent (2, 0) given () union {(2, -1), (1, -2)}
(2,-4) independent (2, 0) given () union {(2, -1), (1, -2), (2, -5)}
(2,-3) independent (2, 0) given () union {(1, -5), (2, -1), (1, -2), (2, -4)}
(2,-2) independent (2, 0) given () union {(2, -3), (2, -1), (1, -4), (1, -2)}
Writing:   (0,-5) oL> (0, 0) ==> (0,-5)     (0, 0) 
Writing:   (0,-4) oL> (0, 0) ==> (0,-4)     (0, 0) 
Writing:   (0,-3) oL> (0, 0) ==> (0,-3)     (0, 0) 
Writing:   (0,-2) oL> (0, 0) ==> (0,-2)     (0, 0) 
Writing:   (1,-5) oL> (1, 0) ==> (1,-5)     (1, 0) 
Writing:   (1,-4) oL> (1, 0) ==> (1,-4)     (1, 0) 
Writing:   (1,-3) oL> (1, 0) ==> (1,-3)     (1, 0) 
Writing:   (1,-2) oL> (1, 0) ==> (1,-2)     (1, 0) 
Writing:   (2,-5) oL> (2, 0) ==> (2,-5)     (2, 0) 
Writing:   (2,-4) oL> (2, 0) ==> (2,-4)     (2, 0) 
Writing:   (2,-3) oL> (2, 0) ==> (2,-3)     (2, 0) 
Writing:   (2,-2) oL> (2, 0) ==> (2,-2)     (2, 0) 
(0, 0) independent (1, 0) given () union {(0, -1), (1, -1)}
(0, 0) independent (1, 0) given () union {(0, -1), (1, -1)}
(0, 0) independent (2, 0) given () union {(2, -1), (0, -1), (1, -2)}
(0, 0) independent (2, 0) given () union {(2, -1), (0, -1), (1, -2)}
(1, 0) independent (2, 0) given () union {(2, -1), (1, -2), (1, -1)}
(1, 0) independent (2, 0) given () union {(2, -1), (1, -1), (1, -2)}
Writing:   (0, 0) o?o (1, 0) ==> (0, 0)     (1, 0) 
Writing:   (1, 0) o?o (0, 0) ==> (1, 0)     (0, 0) 
Writing:   (0, 0) o?o (2, 0) ==> (0, 0)     (2, 0) 
Writing:   (2, 0) o?o (0, 0) ==> (2, 0)     (0, 0) 
Writing:   (1, 0) o?o (2, 0) ==> (1, 0)     (2, 0) 
Writing:   (2, 0) o?o (1, 0) ==> (2, 0)     (1, 0) 
(0,-1) independent (2, 0) given () union {(2, -1), (0, -2), (1, -2)}
(1,-1) independent (0, 0) given () union {(0, -1), (1, -2)}
(1,-1) independent (2, 0) given () union {(2, -1), (1, -2)}
(2,-1) independent (0, 0) given () union {(2, -2), (1, -3), (0, -1)}
(2,-1) independent (1, 0) given () union {(2, -2), (1, -3), (1, -1)}
Writing:   (1,-1) oL> (0, 0) ==> (1,-1)     (0, 0) 
Writing:   (2,-1) oL> (0, 0) ==> (2,-1)     (0, 0) 
Writing:   (2,-1) oL> (1, 0) ==> (2,-1)     (1, 0) 
Writing:   (0,-1) oL> (2, 0) ==> (0,-1)     (2, 0) 
Writing:   (1,-1) oL> (2, 0) ==> (1,-1)     (2, 0) 
(0,-2) independent (1, 0) given () union {(0, -3), (1, -1)}
(0,-2) independent (2, 0) given () union {(2, -1), (0, -3), (1, -2)}
(1,-2) independent (0, 0) given () union {(1, -3), (0, -1)}
(2,-2) independent (0, 0) given () union {(2, -3), (1, -4), (0, -1)}
(2,-2) independent (1, 0) given () union {(2, -3), (1, -4), (1, -1)}
Writing:   (1,-2) oL> (0, 0) ==> (1,-2)     (0, 0) 
Writing:   (2,-2) oL> (0, 0) ==> (2,-2)     (0, 0) 
Writing:   (0,-2) oL> (1, 0) ==> (0,-2)     (1, 0) 
Writing:   (2,-2) oL> (1, 0) ==> (2,-2)     (1, 0) 
Writing:   (0,-2) oL> (2, 0) ==> (0,-2)     (2, 0) 
(0,-3) independent (1, 0) given () union {(0, -4), (1, -1)}
(0,-3) independent (2, 0) given () union {(2, -1), (1, -2), (0, -4)}
(1,-3) independent (0, 0) given () union {(1, -4), (0, -1)}
(1,-3) independent (2, 0) given () union {(2, -1), (1, -4), (1, -2)}
(2,-3) independent (0, 0) given () union {(1, -5), (0, -1), (2, -4)}
(2,-3) independent (1, 0) given () union {(1, -5), (1, -1), (2, -4)}
Writing:   (1,-3) oL> (0, 0) ==> (1,-3)     (0, 0) 
Writing:   (2,-3) oL> (0, 0) ==> (2,-3)     (0, 0) 
Writing:   (0,-3) oL> (1, 0) ==> (0,-3)     (1, 0) 
Writing:   (2,-3) oL> (1, 0) ==> (2,-3)     (1, 0) 
Writing:   (0,-3) oL> (2, 0) ==> (0,-3)     (2, 0) 
Writing:   (1,-3) oL> (2, 0) ==> (1,-3)     (2, 0) 
(0,-4) independent (1, 0) given () union {(0, -5), (1, -1)}
(0,-4) independent (2, 0) given () union {(0, -5), (2, -1), (1, -2)}
(1,-4) independent (0, 0) given () union {(1, -5), (0, -1)}
(1,-4) independent (2, 0) given () union {(1, -5), (2, -1), (1, -2)}
(2,-4) independent (0, 0) given () union {(0, -1), (2, -5)}
(2,-4) independent (1, 0) given () union {(1, -1), (2, -5)}
Writing:   (1,-4) oL> (0, 0) ==> (1,-4)     (0, 0) 
Writing:   (2,-4) oL> (0, 0) ==> (2,-4)     (0, 0) 
Writing:   (0,-4) oL> (1, 0) ==> (0,-4)     (1, 0) 
Writing:   (2,-4) oL> (1, 0) ==> (2,-4)     (1, 0) 
Writing:   (0,-4) oL> (2, 0) ==> (0,-4)     (2, 0) 
Writing:   (1,-4) oL> (2, 0) ==> (1,-4)     (2, 0) 
(0,-5) independent (1, 0) given () union {(1, -1)}
(0,-5) independent (2, 0) given () union {(2, -1), (1, -2)}
(1,-5) independent (0, 0) given () union {(0, -1)}
(1,-5) independent (2, 0) given () union {(2, -1), (1, -2)}
(2,-5) independent (0, 0) given () union {(0, -1)}
(2,-5) independent (1, 0) given () union {(1, -1)}
Writing:   (1,-5) oL> (0, 0) ==> (1,-5)     (0, 0) 
Writing:   (2,-5) oL> (0, 0) ==> (2,-5)     (0, 0) 
Writing:   (0,-5) oL> (1, 0) ==> (0,-5)     (1, 0) 
Writing:   (2,-5) oL> (1, 0) ==> (2,-5)     (1, 0) 
Writing:   (0,-5) oL> (2, 0) ==> (0,-5)     (2, 0) 
Writing:   (1,-5) oL> (2, 0) ==> (1,-5)     (2, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-09'], ['ER-10']]

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

Orientation phase complete
p = 1
Writing:   (0,-1) -L> (0, 0) ==> (0,-1) -!> (0, 0) 
Writing:   (2,-1) -L> (2, 0) ==> (2,-1) -!> (2, 0) 
Writing:   (0,-1) oL> (1, 0) ==> (0,-1) o!> (1, 0) 
Writing:   (1,-2) -L> (2, 0) ==> (1,-2) -!> (2, 0) 

Test phase complete
p = 2
Writing:   (1,-1) -L> (1, 0) ==> (1,-1) -!> (1, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-00-d'], ['ER-00-c'], ['ER-03'], ['R-04'], ['ER-09'], ['ER-10'], ['ER-00-b'], ['ER-00-a']]

APR:
Marked:    (1,-2) -!> (2, 0) ==> (1,-2) --> (2, 0) 
Marked:    (2,-1) -!> (2, 0) ==> (2,-1) --> (2, 0) 
Marked:    (0,-1) -!> (0, 0) ==> (0,-1) --> (0, 0) 
Marked:    (1,-1) -!> (1, 0) ==> (1,-1) --> (1, 0) 
Writing:   (0,-1) -!> (0, 0) ==> (0,-1) --> (0, 0) 
Writing:   (1,-1) -!> (1, 0) ==> (1,-1) --> (1, 0) 
Writing:   (1,-2) -!> (2, 0) ==> (1,-2) --> (2, 0) 
Writing:   (2,-1) -!> (2, 0) ==> (2,-1) --> (2, 0) 

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Marked:    (0,-1) o!> (1, 0) ==> (0,-1) <!> (1, 0) 
Writing:   (0,-1) o!> (1, 0) ==> (0,-1) <!> (1, 0) 
Update:    Marking (0, -1) as non-anc of (1, 0)

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Found nothing

ER-03:
Found nothing

R-04:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

ER-00-b:
Found nothing

ER-00-a:
Found nothing

Orientation phase complete

Middle mark updates


Final ancestral phase complete

Graph:
--------------------------------
(0,-1) --> (0, 0)
(0,-1) <!> (1, 0)
(1,-1) --> (1, 0)
(1,-2) --> (2, 0)
(2,-1) --> (2, 0)
--------------------------------

=======================================================
=======================================================
Starting non-ancestral phase

Middle mark updates


Starting test phase

p = 0

Test phase complete
p = 1
Writing:   (0,-1) <!> (1, 0) ==> (0,-1) <-> (1, 0) 

Test phase complete

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-00-d'], ['ER-00-c'], ['ER-03'], ['R-04'], ['ER-09'], ['ER-10'], ['ER-00-b'], ['ER-00-a']]

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Found nothing

ER-03:
Found nothing

R-04:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

ER-00-b:
Found nothing

ER-00-a:
Found nothing

Orientation phase complete

Non-ancestral phase complete

Graph:
--------------------------------
(0,-1) --> (0, 0)
(0,-1) <-> (1, 0)
(1,-1) --> (1, 0)
(1,-2) --> (2, 0)
(2,-1) --> (2, 0)
--------------------------------

=======================================================
=======================================================
Final rule application phase

Setting all middle marks to '-'

Starting orientation phase
with rule list:  [['APR'], ['ER-08'], ['ER-02'], ['ER-01'], ['ER-00-d'], ['ER-00-c'], ['ER-03'], ['R-04'], ['ER-09'], ['ER-10'], ['ER-00-b'], ['ER-00-a']]

APR:
Found nothing

ER-08:
Found nothing

ER-02:
Found nothing

ER-01:
Found nothing

ER-00-d:
Found nothing

ER-00-c:
Found nothing

ER-03:
Found nothing

R-04:
Found nothing

ER-09:
Found nothing

ER-10:
Found nothing

ER-00-b:
Found nothing

ER-00-a:
Found nothing

Orientation phase complete

=======================================================
=======================================================

LPCMCI has converged

Final graph:
--------------------------------
--------------------------------
(0,-1) --> (0, 0)
(0,-1) <-> (1, 0)
(1,-1) --> (1, 0)
(1,-2) --> (2, 0)
(2,-1) --> (2, 0)
--------------------------------
--------------------------------

Max search set: 0
Max na-pds set: 1

　次に、私たちは、学習した時系列DPAG(これらの図では、時間ウィンドウ[t-τmax,t]が表示されます)を図示するために、関数tp.plot_time_series_graphを使います。現在のケースでは、学習されたグラフは、正確に、真の時系列DPAG P5(g)で承認されます。特に、LPCMCIは正しく、X _t-1¹とX_t²を、観測されない変数のせいで、相関して識別します。終端は、LPCMCI.run_lpcmciによって戻されたテストの静的な値に従って、色付けされます。例えば、val_matrix[i,j,tau]の値は、末尾のカラースケールに従って、X_t-rⁱとX_t^jの間の終端の色を決定します。

# Plot the learned time series DPAG
tp.plot_time_series_graph(graph=results['graph'],
                          val_matrix=results['val_matrix'])
plt.show()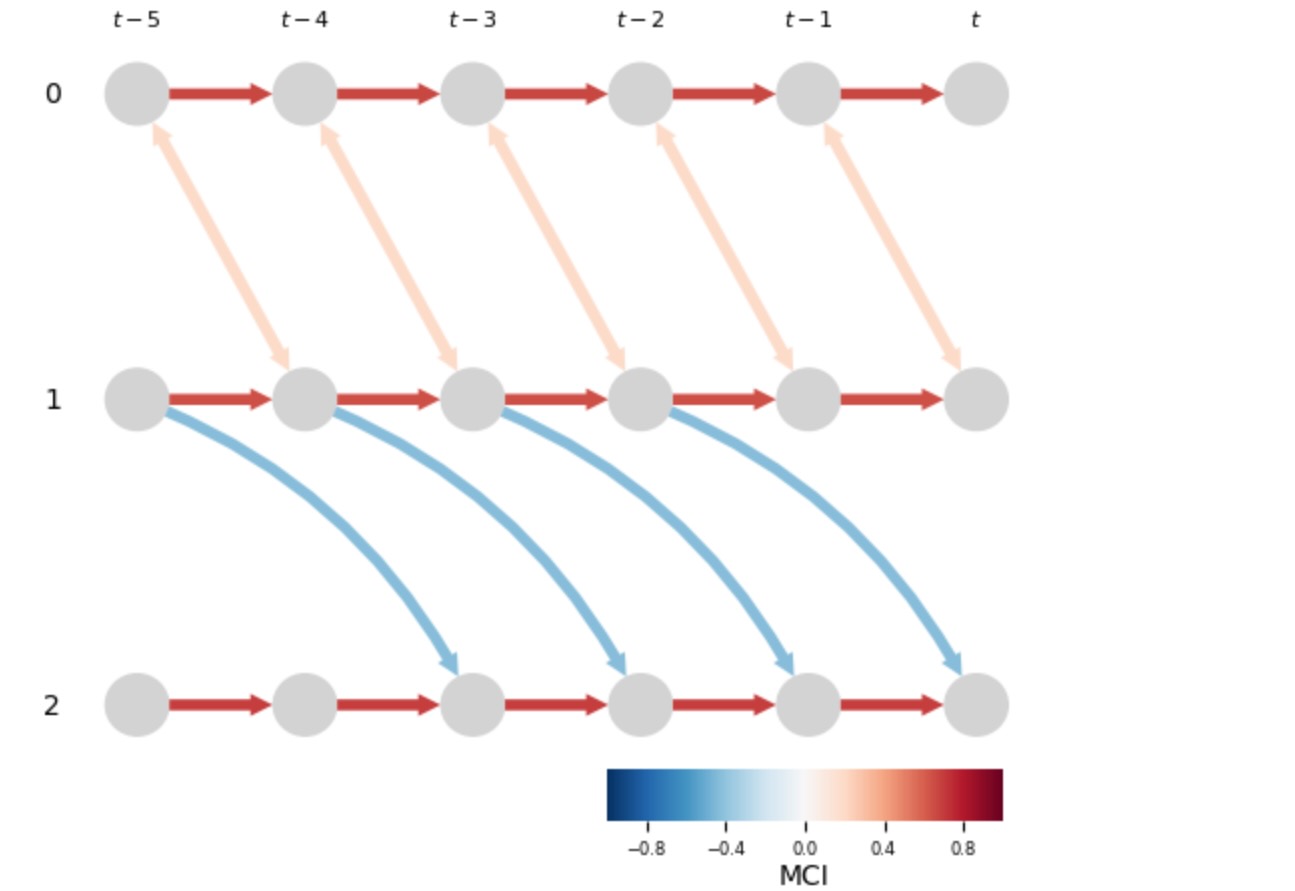

そのほかの可視化は関数tp.plot_graphによって提案されます。それは、直感的に言えば、tp.plot_time_series_graphと比較されるので、時間の次元上でグラフは衝突します。そしてこうして、観測した成分時系列Xiごとに単一のノードiを含みます。τ > 0 で、X_t-rⁱとX_t^jの間のすべての終端の間で、それはgraphの中にあります。もっとも強い一つは、(ここでもっとも強いは、val_matrixの中のテストの静的な値の絶対値に従って計測されます)、曲線上のノードi と j の間に出力されます。そして、上のこの終端の小さ数字は、それらの強さのために、すべてのこれらの終端のラグを列挙します。τ > 0で、X_t-r^j と X_tⁱ の間のすべての終端も同様です。同時に発生する終端は、直線で(曲線でなく)描画されます。ノード i の色は、すべての 1 ≦ τ ≦ τ_max にまたがって、val_matrix[i,j,tau]の絶対値の最大値を示します。

# Plot the learned time series DPAG
tp.plot_graph(graph=results['graph'],
              val_matrix=results['val_matrix'])
plt.show()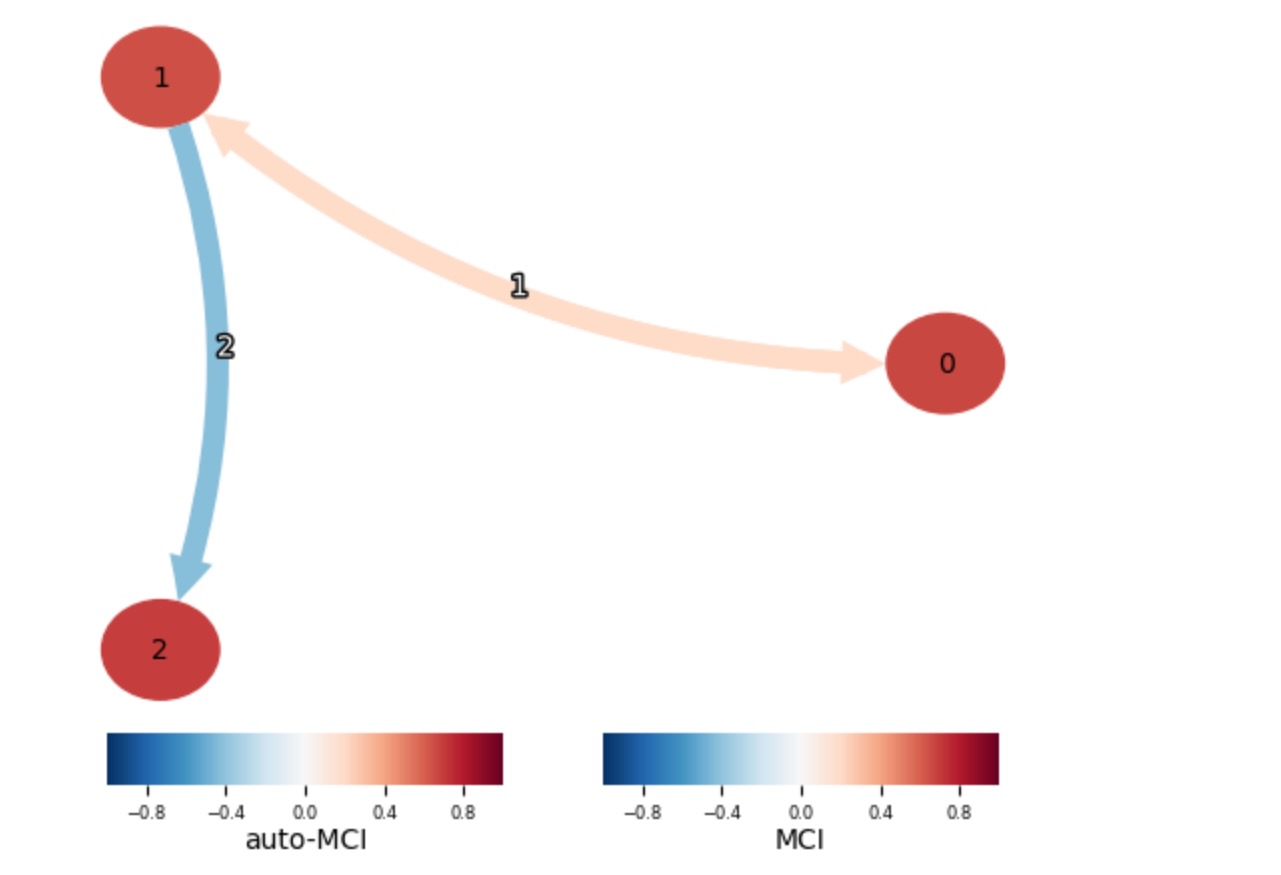

　参照のため、私たちは、ここで、上のLPCMCI.run_lpcmciのアプリケーションによって戻される値を出力します。

print("Graph:\n", results['graph'])
print("\n Maximum p-values:\n", results['p_matrix'])
print("\n Associated test statistic values:\n", results['val_matrix'])

Graph:
 [[['' '-->' '' '' '' '']
  ['' '<->' '' '' '' '']
  ['' '' '' '' '' '']]

 [['' '' '' '' '' '']
  ['' '-->' '' '' '' '']
  ['' '' '-->' '' '' '']]

 [['' '' '' '' '' '']
  ['' '' '' '' '' '']
  ['' '-->' '' '' '' '']]]

 Maximum p-values:
 [[[0.00000000e+00 3.27587534e-64 6.51860685e-01 1.66931792e-01
   3.04058020e-01 2.69057386e-01]
  [4.98048581e-01 1.89519997e-05 8.15648178e-01 3.92853868e-01
   1.53679047e-01 1.45390533e-01]
  [9.95865145e-01 8.18453415e-01 2.04903614e-01 9.50878192e-01
   8.78253544e-01 6.62506913e-01]]

 [[4.98048581e-01 3.32516869e-01 9.33958624e-01 4.00491240e-01
   3.51910362e-01 6.25033647e-01]
  [0.00000000e+00 4.98134664e-59 7.65326966e-02 9.28068279e-01
   6.83166024e-02 1.95806341e-01]
  [6.17173477e-01 6.30054174e-01 3.96189863e-23 6.53400676e-01
   8.99607194e-01 2.03196828e-01]]

 [[9.95865145e-01 5.72581038e-01 4.83793121e-01 7.79203868e-02
   4.34900758e-01 5.91366004e-01]
  [6.17173477e-01 4.41473048e-01 1.86116180e-02 3.31451935e-01
   5.04650462e-01 1.93950990e-02]
  [0.00000000e+00 1.06277039e-69 9.53625058e-01 7.81342882e-01
   5.31474674e-02 7.35232346e-01]]]

 Associated test statistic values:
 [[[ 0.00000000e+00  6.66897489e-01  2.04742700e-02 -6.26652856e-02
   -4.66192187e-02 -5.00772924e-02]
  [ 3.07434432e-02  1.92483930e-01 -1.05808544e-02  3.87641554e-02
    6.46799201e-02  6.59400183e-02]
  [-2.35437253e-04 -1.04277206e-02  5.75454268e-02 -2.79873031e-03
    6.95920792e-03  1.98062275e-02]]

 [[ 3.07434432e-02 -4.39586631e-02 -3.76076836e-03 -3.81426689e-02
    4.22289160e-02  2.21550718e-02]
  [ 0.00000000e+00  6.46212245e-01 -8.02534748e-02 -4.09707020e-03
    8.25901624e-02  5.85979495e-02]
  [-2.27062599e-02 -2.18567451e-02 -4.27743225e-01 -2.03983801e-02
    5.73142688e-03  5.77031774e-02]]

 [[-2.35437253e-04 -2.56304694e-02 -3.18034655e-02  7.99613413e-02
   -3.54264011e-02 -2.43362250e-02]
  [-2.27062599e-02  3.49579770e-02 -1.06604502e-01 -4.41008932e-02
   -3.02730069e-02 -1.05695388e-01]
  [ 0.00000000e+00  6.88594441e-01 -2.64477634e-03 -1.26228091e-02
   -8.76817489e-02  1.53468564e-02]]]

3.5 τ_max の異なる選択

　以下のコードは同じデータでτmax = 2 に設定してLPCMCIを実行します。学習したグラフは、完全に、上のセクション1.3で表示した 真の時系列DPAG P² (g) を承認します。私たちは、P⁵(g)からP²(g)の相違を注記します。それは、P⁵(g)はX_t-2² -> X_t³の終端のあるけれども、P2(g)はX_t-2² ⚪︎-> X_t³の終端のあります。これは、エラーのあるテストの決定のせいで、有限のサンプルの結果になりません。しかしむしろ、P^τ_maxがτ_maxに依存できる事実のもう一つの例です。

# Create a LPCMCI object, passing the dataframe and (conditional)
# independence test objects.
# parcorr = ParCorr(significance='analytic')
lpcmci = LPCMCI(dataframe=dataframe, 
                cond_ind_test=parcorr,
                verbosity=0)

# Define the analysis parameters.
tau_max = 2
pc_alpha = 0.01

# Run LPCMCI
results = lpcmci.run_lpcmci(tau_max=tau_max,
                            pc_alpha=pc_alpha)

# Plot the learned time series DPAG
tp.plot_time_series_graph(graph=results['graph'],
                          val_matrix=results['val_matrix'])
plt.show()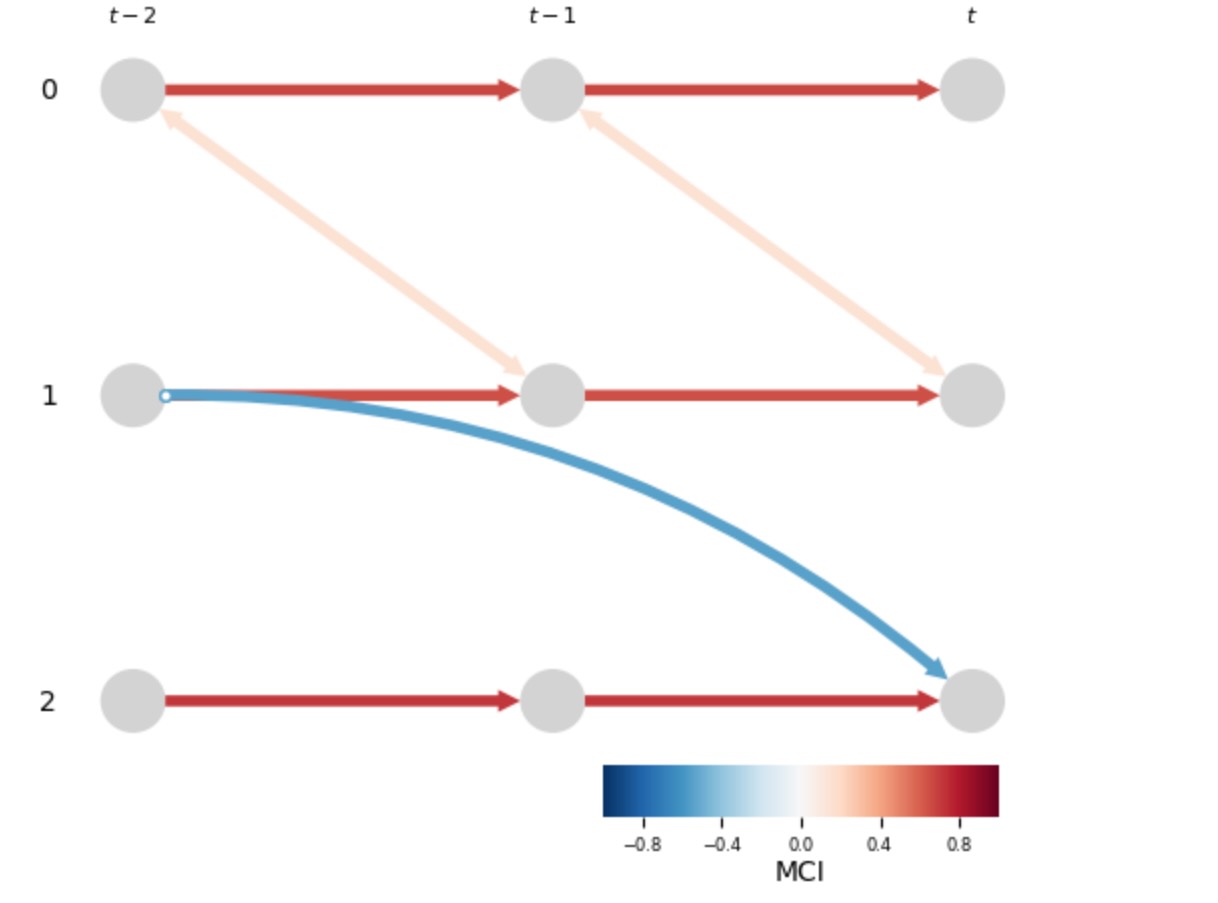

3.6 PCMCIplusとの比較

　PCMCIplusアルゴリズムは、観測していない変数の欠如を仮定します。この仮定は、現在の例では違反するので、私たちがそれをデータに適用したときに何が起きるか見てみましょう。

# Create a PCMCI object, passing the dataframe and (conditional)
# independence test objects.
# parcorr = ParCorr(significance='analytic')
pcmci = PCMCI(dataframe=dataframe, 
              cond_ind_test=parcorr,
              verbosity=0)

# Define the analysis parameters.
tau_max = 5
pc_alpha = 0.01

# Run LPCMCI
results = pcmci.run_pcmciplus(tau_max=tau_max,
                              pc_alpha=pc_alpha)

# Plot the learned time series DPAG
tp.plot_time_series_graph(graph=results['graph'],
                          val_matrix=results['val_matrix'])
plt.show()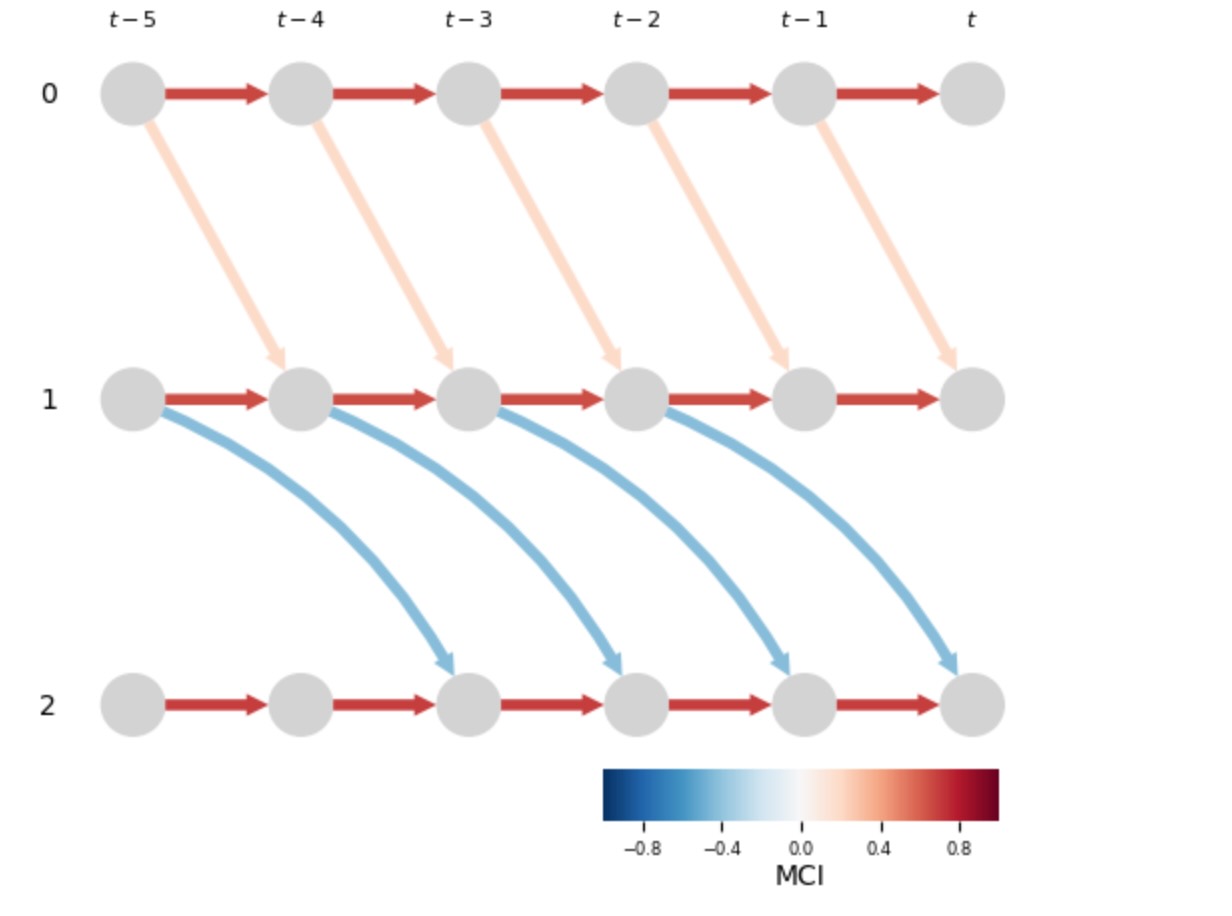

私たちは、PCMCIplusが正しく近接を推論し、多くの終端が正しい終端の種別であることがわかります。しかし、X_t-1⁰ <-> X_t¹の代わりに、X_t-1⁰ -> X_t¹という間違った推論になり、それは、X_t¹上でX_t-1⁰の間違った因果推論を主張します。これは、観測していない変数の仮定の早急な影響です。観測していない変数なしで、可能な終端の方針は、X_t-1⁰ -> X_t¹ とX_t-1⁰ <- X_t¹だけです。時間上で後方への因果の影響はないため、後者は除外されます。

3.7 仮のフェイズの重要性

　サブセクション2.4で、私たちは、例えば、アルゴリズムのステップ２で、LPCMCIplusの仮のフェイズの重要性を議論し、紹介しました。デフォルトで、LPCMCIは、n_preliminary_iterations=1(アルゴリズムのステップ２でk=1）、例えば、デフォルトで、ある仮のフェイズを実行することによって、使います。私たちは、上で見たように、これは、現在の例に良い結果を導きます。私たちは、ここで、仮のフェイズなしで、例えば、tau_max=0とtau_max=2の両方でn_preliminary_itelatons=0の設定で、LPCMCIを実行した結果を見せます。

# Create a LPCMCI object, passing the dataframe and (conditional)
# independence test objects.
# parcorr = ParCorr(significance='analytic')
lpcmci = LPCMCI(dataframe=dataframe, 
                cond_ind_test=parcorr,
                verbosity=0)

# Define the analysis parameters.
tau_max = 5
pc_alpha = 0.01
n_preliminary_iterations = 0

# Run LPCMCI
results = lpcmci.run_lpcmci(tau_max=tau_max,
                            pc_alpha=pc_alpha,
                            n_preliminary_iterations=n_preliminary_iterations)

# Plot the learned time series DPAG
tp.plot_time_series_graph(graph=results['graph'],
                          val_matrix=results['val_matrix'])
plt.show()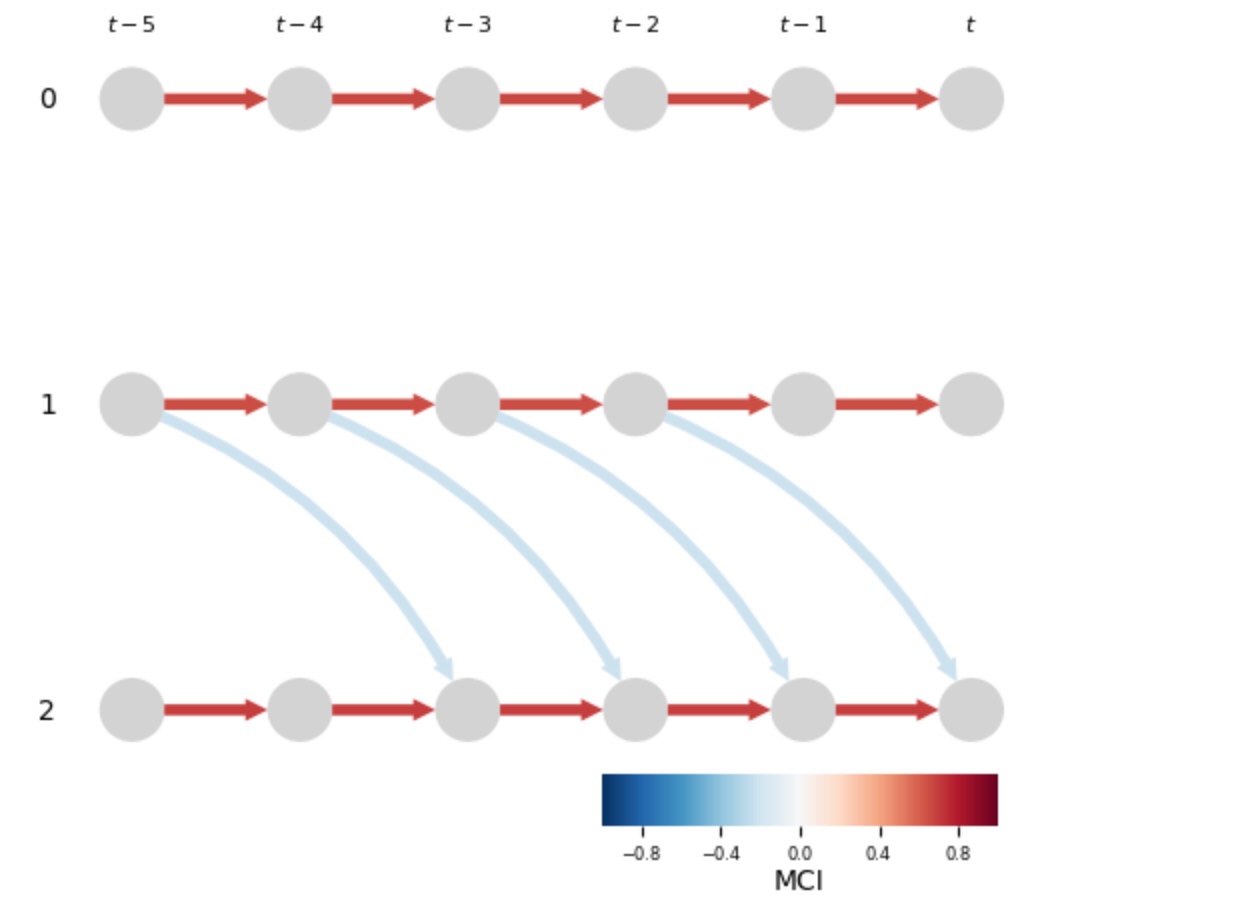

# Create a LPCMCI object, passing the dataframe and (conditional)
# independence test objects.
# parcorr = ParCorr(significance='analytic')
lpcmci = LPCMCI(dataframe=dataframe, 
                cond_ind_test=parcorr,
                verbosity=0)

# Define the analysis parameters.
tau_max = 2
pc_alpha = 0.01
n_preliminary_iterations = 0

# Run LPCMCI
results = lpcmci.run_lpcmci(tau_max=tau_max,
                            pc_alpha=pc_alpha,
                            n_preliminary_iterations=n_preliminary_iterations)

# Plot the learned time series DPAG
tp.plot_time_series_graph(graph=results['graph'],
                          val_matrix=results['val_matrix'])
plt.show()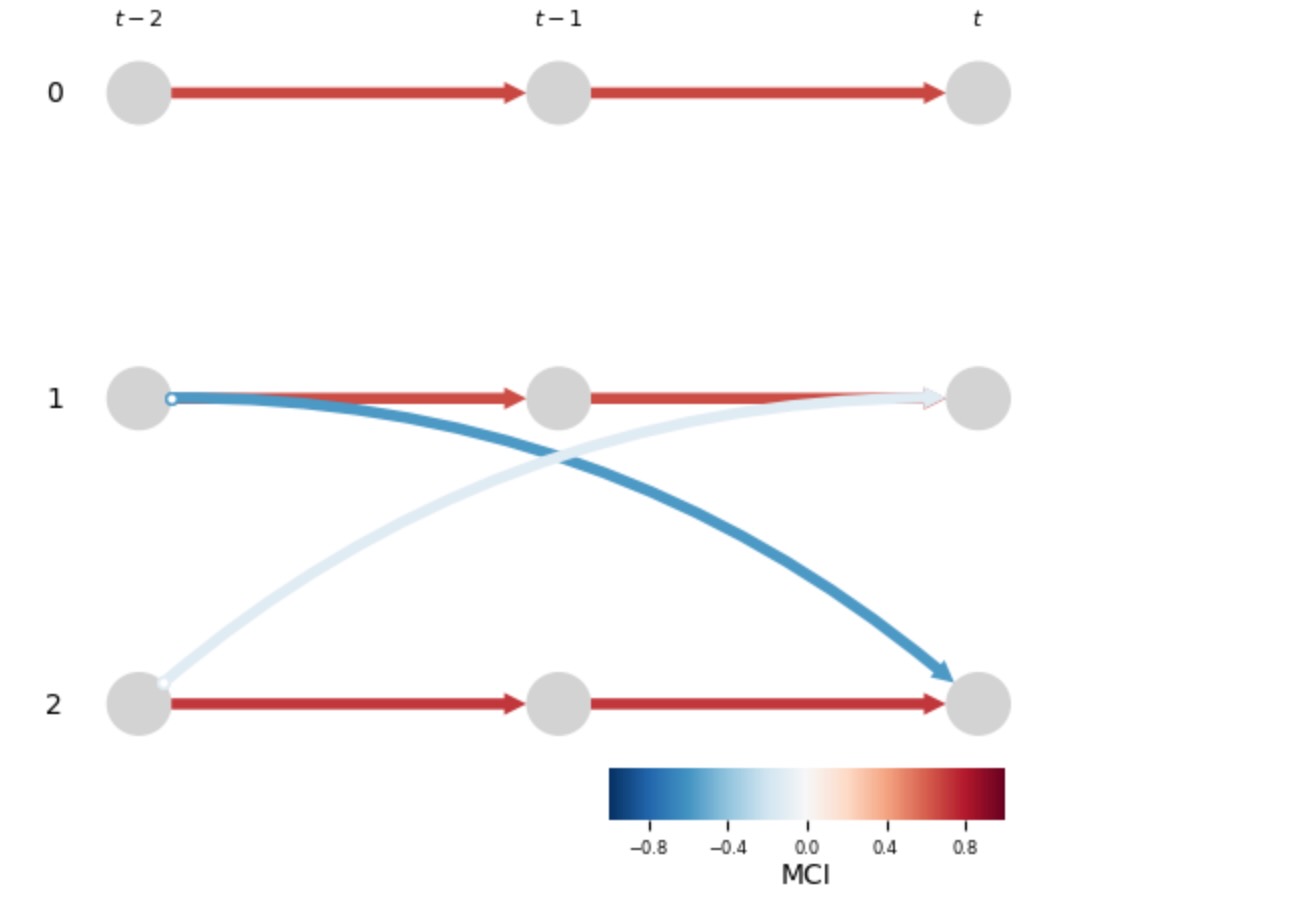

　私たちは、デフォルトの設定と違い、アルゴリズムがXt-10<-> Xt1の終端の検出で失敗するのがわかります。これは、サブセクション2.3で議論したこと、時系列の自己相関のせいの低効果サイズ、の証明です。デフォルト設定では、n_preliminary_iterations = 1であり、この問題は、仮のフェイズの後のすべての終端が削除されてレストアされることによって、導かれます。その後、アルゴリズムの最後の継承フェイズ(ステップ３)で、より大きいデフォルト条件セットS_def(X_t-rⁱ,X_t^j) で働きます。

　詳細にはこのポイントを妥当と認めることに関心があるため：X_t-2⁰の条件でX_t-1⁰とX_t¹の独立性を判断する(条件)独立性テストが間違って判断するため、X_t-1⁰とX_t¹の間の終端は、削除されます。これを見るために、前の二つのセルのLPCCMIオブジェクトを生成するときに、verbosity=1を設定します。そして、 ANC(Y): (0, -1) _|_ (1, 0) | S_def = , S_pc = (0, -2): val = 0.10 / pval = 0.0287を探します。(ここで、S_pcは、標準条件セットSとSdef ,デフォルト条件セットSdefを参照します)。その後、上のサブセクション2.3と3.5でLPCMCIのデフォルトのアプリケーションでverbosity=2に設定します。そして、それらを走らせる仮のフェイズで同じことが起きるのがわかります。しかし、これらのケースで、アルゴリズムは、X_t-1¹のがX_t¹の因果上の祖先であることX_t-2⁰がX_t-1⁰の因果上の祖先であることを覚えているので、最終の継承フェイズへ移る前にこの終端をレストアします。最終の継承フェイズでは、従って、S_def(X_t-1⁰,X_t⁰) = {X_t-2⁰,X_t-1¹}を使います。X_t-1⁰とX_t¹がX_t-2⁰で与えられる条件で独立であるかどうかテストは２度と実行されません。実際は、冗長的な出力でANC(Y): (0, -1) _|_ (1, 0) | S_def = (0, -2) (1, -1), S_pc = : val = 0.19 / pval = 0.0000を探します。

　tau_max = 2では、さらに間違って、X_t-2²とX_t¹が近接していると推論します。

4. 背景知識の取り入れ

　いくつかのケースで、あなたは、確実なリンクの方針について確かなリンクの存在と欠如に関する事前知識を持っているかもしれません。あなたは、関数LPCMCI.run_lpcmciに渡すオプションのキーワード引数link_assumptionsを使うことで、この背景知識についてLPCMCIに知らせることができます。デフォルトのlink_assumptionsは、Noneです。

link_assumptionsに渡す値は、様式{j: {(i, lag_i): link, ...}, ...}で２段階にネストされる必要があります。ここで、linkは、以下のルールに従った変数Xt-lagiiとXtjの間のリンクについてあなたの事前知識を規定します。：

重要にも、link_assumptionのエントリーが何を意味するかの上の説明の最後の重点項目を覚えておいてください：もし、link_assumptions がそのデフォルト値のNoneを取らずに、link_assumptions[j][(i, lag_i)]が存在しないならば、その時、この事実の組み合わせは、link_assumptions[j][(i, lag_i)] = ''を規定することと同じです。

　可能な少数のリンクだけの背景知識を持っており、 完全にネストされた辞書を作るのに効率が悪いケースがあるでしょう。そこで背景知識の欠如は、lagi < 0の時に、link_assumptions[j][(i, lag_i)] = 'o?> とlagi = 0の場合のlink_assumptions[j][(i, 0)] = 'o?o' によって規定される必要があります。そのようなケースでは、あなたは、以下の便利な関数をあなたのコードやノートブックで使うことができます。

def build_link_assumptions(link_assumptions_absent_link_means_no_knowledge,
                           n_component_time_series,
                           tau_max,
                           tau_min=0):

    out = {j: {(i, -tau_i): ("o?>" if tau_i > 0 else "o?o")
         for i in range(n_component_time_series) for tau_i in range(tau_min, tau_max+1)
         if (tau_i > 0 or i != j)} for j in range(n_component_time_series)}

    for j, links_j in link_assumptions_absent_link_means_no_knowledge.items():
        for (i, lag_i), link_ij in links_j.items():
            if link_ij == "": 
                del out[j][(i, lag_i)]
            else:
                out[j][(i, lag_i)] = link_ij
    return out

　前の例に戻って、あなたは以下を規定できます。

link_assumptions_absent_link_means_no_knowledge = {0: {(1, 0): 'o?>', (1, -1): '-->'}, 1: {(0, 0): '<?o'}}

そして、link_assumptions = build_link_assumptions(link_assumptions_absent_link_means_no_knowledge, 2, 1)としてlink_assumptionsを構築します。