TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。このチュートリアルは、事例を通して主要な特徴を説明します。これは以下をカバーします。
- 基本の使い方
- 図示
- リンクに関する仮定の統合
- ベンチマークと検証
- 因果推定
- データセットの難題
- スライディングウインドウ分析
理論的な背景は、以下の論文を算用してください:Runge, Jakob. 2018. “Causal Network Reconstruction from Time Series: From Theoretical Assumptions to Practical Estimation.” Chaos: An Interdisciplinary Journal of Nonlinear Science 28 (7): 075310.
最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
1. 基本の使い方
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.lpcmci import LPCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.parcorr_wls import ParCorrWLS
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.independence_tests.gsquared import Gsquared
from tigramite.independence_tests.regressionCI import RegressionCITigramiteは、PCMCIフレームワークからいくつかの因果の発見メソッドを提供します。それは、異なる仮定のもとで、使用することができます。アプリケーションは常に、メソッドと、選択された条件独立性のテスト、例えば、 PArCorrを伴うPCMCI、からなります。以下の二つのテーブルは、仮定が含んでいる概要を与えます。
| Method | Assumptions | Output |
|---|---|---|
| (in addition to Causal Markov Condition and Faithfulness) | ||
| PCMCI | Causal stationarity, no contemporaneous causal links, no hidden variables | Directed lagged links, undirected contemporaneous links (for tau_min=0) |
| PCMCIplus | Causal stationarity, no hidden variables | Directed lagged links, directed and undirected contemp. links (Time series CPDAG) |
| LPCMCI | Causal stationarity | Time series PAG |
| Conditional independence test | Assumptions |
|---|---|
| ParCorr | univariate, continuous variables with linear dependencies and Gaussian noise |
| RobustParCorr | univariate, continuous variables with linear dependencies, robust for different marginal distributions |
| ParCorrWLS | univariate, continuous variables with linear dependencies, can account for heteroskedastic data |
| GPDC / GPDCtorch | univariate, continuous variables with additive dependencies |
| CMIknn | multivariate, continuous variables with more general dependencies (permutation-based test) |
| Gsquared | univariate discrete/categorical variables |
| CMIsymb | multivariate discrete/categorical variables (permutation-based test) |
| RegressionCI | mixed datasets with univariate discrete/categorical and (linear) continuous variables |
メソッドの参照は、以下の通り:PCMCI: J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996
PCMCIplus: J. Runge (2020), Discovering contemporaneous and lagged causal relations in autocorrelated nonlinear time series datasets http://www.auai.org/uai2020/proceedings/579_main_paper.pdf
LPCMCI: Gerhardus, Andreas and Runge, Jakob (2020). High-recall causal discovery for autocorrelated time series with latent confounders. In Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M. F., and Lin, H., editors, Advances in Neural Information Processing Systems, volume 33, pages 12615–12625. Curran Associates, Inc. https://proceedings.neurips.cc/paper/2020/file/94e70705efae423efda1088614128d0b-Paper.pdf.
条件独立テストの参照は、対応したチュートリアルconditional_independence_testsでカバーされています。以下のステップは典型的な因果分析に導きます。
toyモデル
データ生成過程から時系列を考えます。
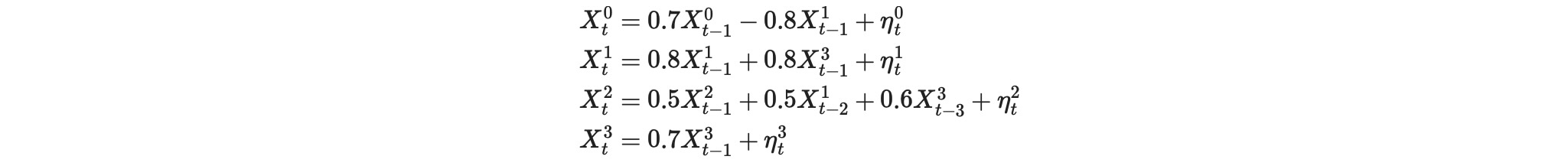
ここで、ηは、独立したゼロ平均のユニット分散のランダム変数です。私たちのゴールは、各変数のドライバーを再構築することです。Tigramiteではそうした過程は、関数う toy.structual_causal_processで生成することができます。
seed = 42
np.random.seed(seed) # Fix random seed
def lin_f(x): return x
links_coeffs = {0: [((0, -1), 0.7, lin_f), ((1, -1), -0.8, lin_f)],
1: [((1, -1), 0.8, lin_f), ((3, -1), 0.8, lin_f)],
2: [((2, -1), 0.5, lin_f), ((1, -2), 0.5, lin_f), ((3, -3), 0.6, lin_f)],
3: [((3, -1), 0.4, lin_f)],
}
T = 1000 # time series length
data, _ = toys.structural_causal_process(links_coeffs, T=T, seed=seed)
T, N = data.shape
# Initialize dataframe object, specify time axis and variable names
var_names = [r'$X^0$', r'$X^1$', r'$X^2$', r'$X^3$']
dataframe = pp.DataFrame(data,
datatime = {0:np.arange(len(data))},
var_names=var_names)常に最初のステップ:データの図示
これは関数tp.plot_timeseriesで実行できます。
tp.plot_timeseries(dataframe); plt.show()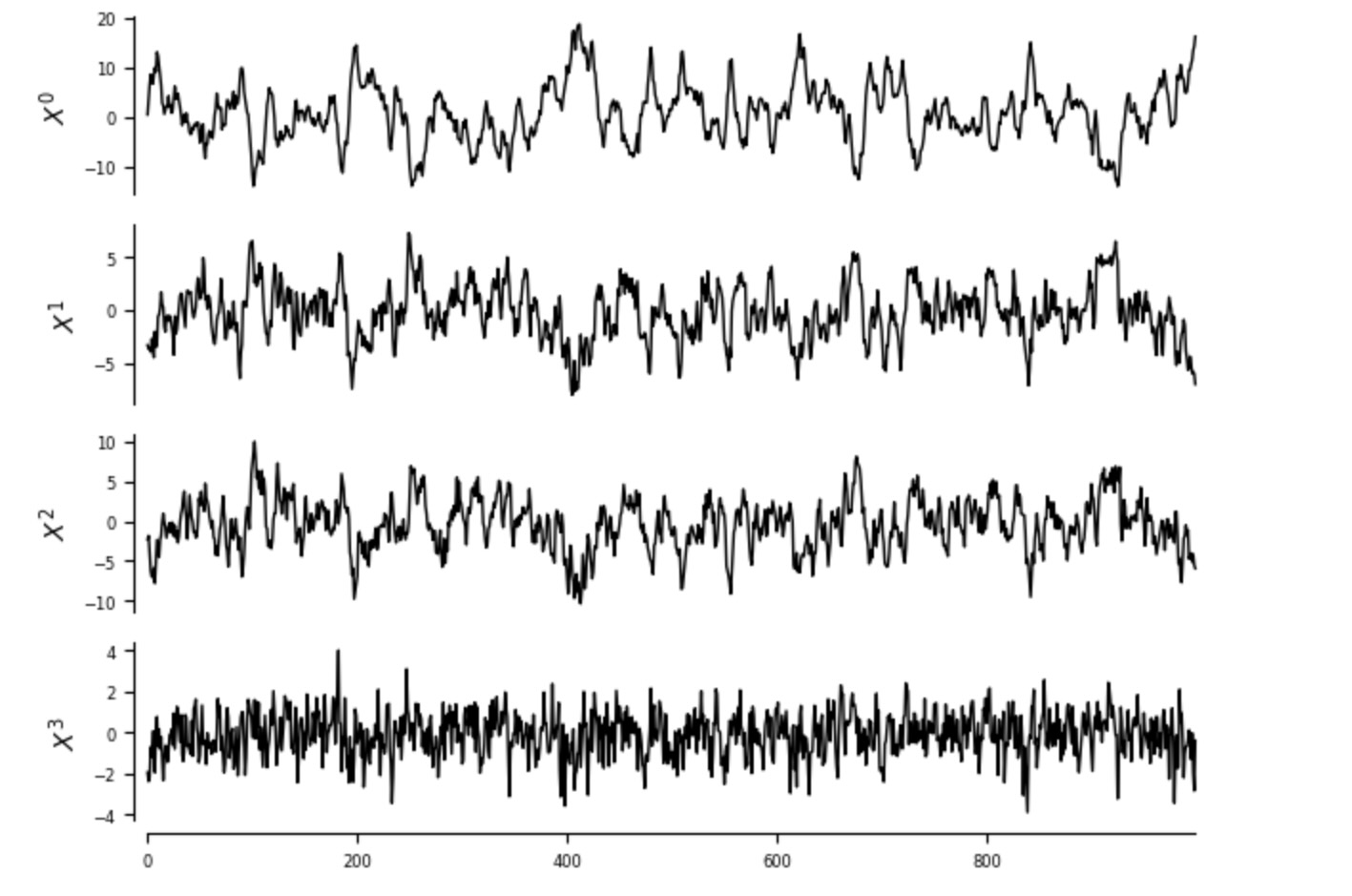
それはステーショナリーであり、(追加でチェックすることができます。)欠測値を含みません。(チュートリアルmissing_making)
私たちは、因果のステーショナリーを、ここで仮定します。隠れ変数ななく、ラグの依存性だけがあります。こうして、私たちは、因果発見メソッドとして、PCMCIを選択します。次に、私たちは、最大ラグ時間tau_maxのような、条件独立テストとハイパーパラメータを選択する必要があります。そうすることによって、私たちは、データを検査することができます。
データの独立性とラグ関数の調査
依存性の種別を調査するために、私たちは、従属性が本当に線形かどうかをみるためにplot_scatterplotsとplot_densityplotsを使います。引数matrix_lags をnumpy整数配列の(N,N)に設定して、あなたは、全ての変数ペアにどのラグを使うか選択することができます。ここで、左のNoneはラグゼロを意味しています。
parcorr = ParCorr(significance='analytic')
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)
correlations = pcmci.get_lagged_dependencies(tau_max=20, val_only=True)['val_matrix']## ## Estimating lagged dependencies ## Parameters: independence test = par_corr tau_min = 0 tau_max = 20
matrix_lags = None #np.argmax(np.abs(correlations), axis=2)
tp.plot_scatterplots(dataframe=dataframe, add_scatterplot_args={'matrix_lags':matrix_lags}); plt.show()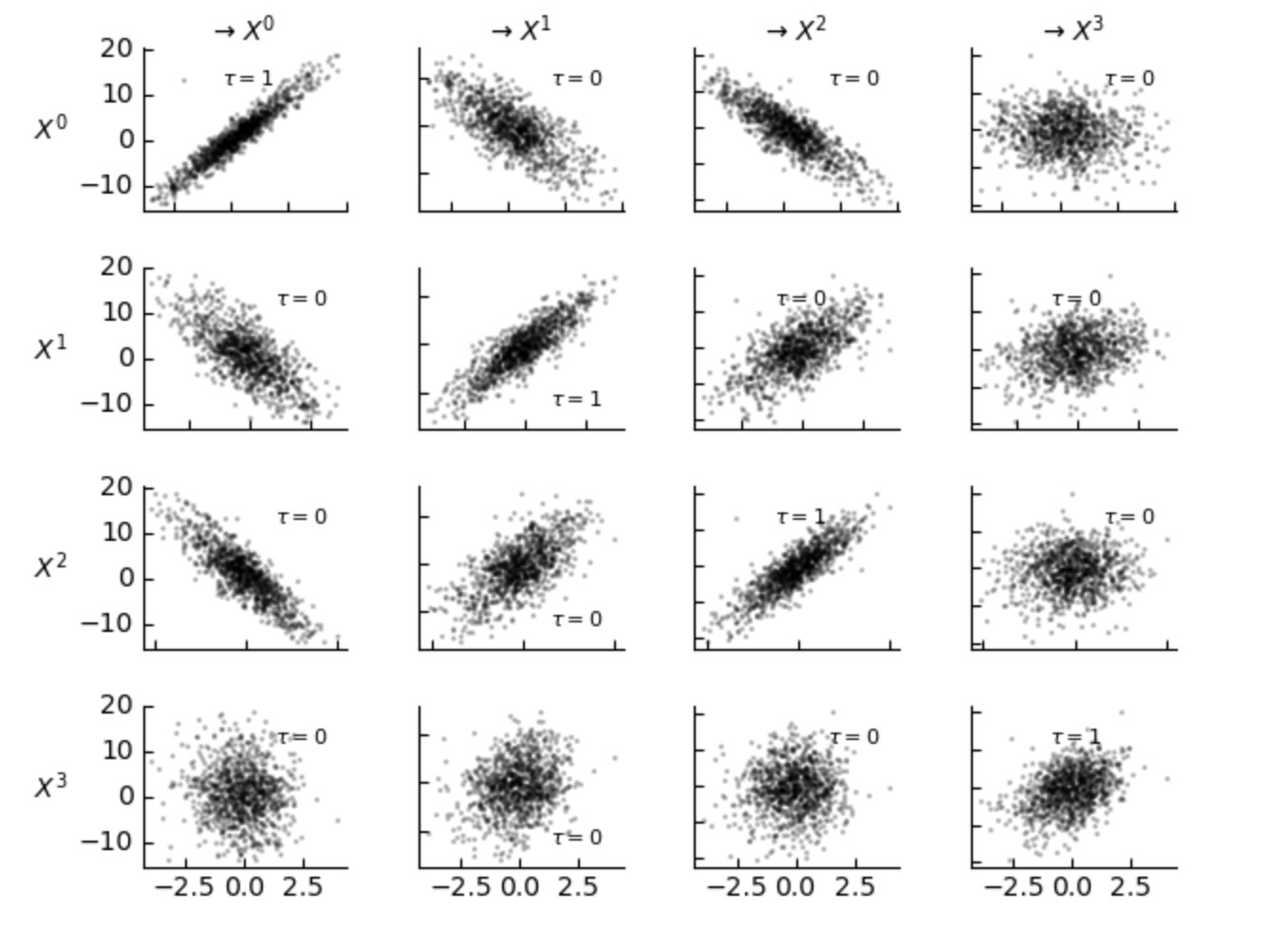
(オリジナルの対角面のパネルは、ここでは変数それ自身のラグゼロスキャッタープロットを示しています)
次に、私たちはカーネル密度が推定する結合と周辺密度を調査します。
tp.plot_densityplots(dataframe=dataframe, add_densityplot_args={'matrix_lags':matrix_lags})
plt.show()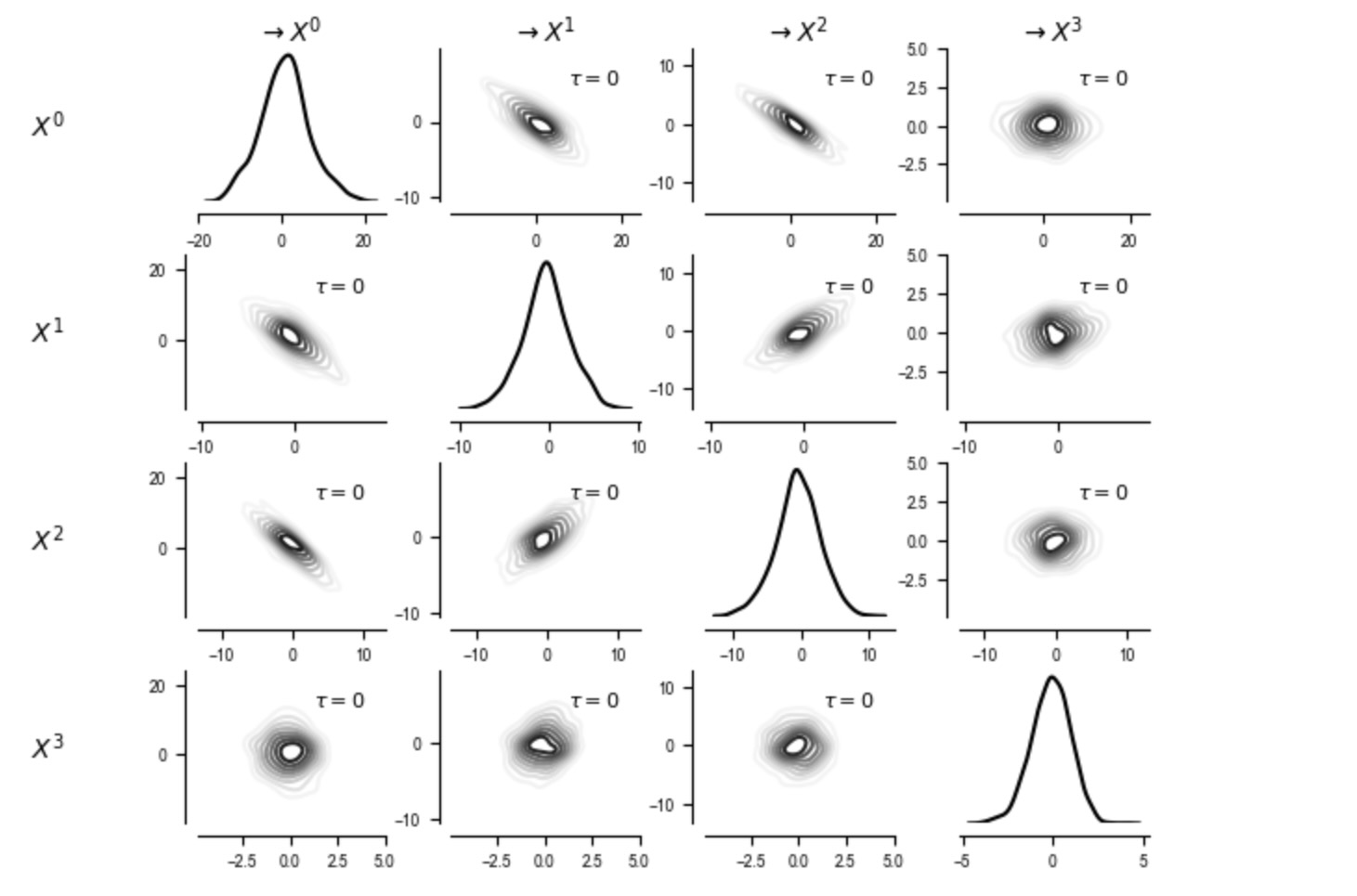
私たちのモデルでは、従属性は、妥当な線形とガウス分布で現れるので、私たちは、線形部分相関で実装されたParCorr条件独立テストを使います。significance='analytic'の場合、null分布はステユーデントのTを仮定します。
次に、ラグの無条件従属性、例えば、ParCorrクラスを使ったラグ相関、を図示するのは良い考えです。これは、因果アルゴリズムを選択するために、最大時間ラグtau_maxを識別するのに役立ちます。
これを終わらせるために、私たちは、cond_ind_testとして、dataframe, ParCorrとともにPCMCIメソッドで初期化します。
parcorr = ParCorr(significance='analytic')
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)correlations = pcmci.get_lagged_dependencies(tau_max=20, val_only=True)['val_matrix']
lag_func_matrix = tp.plot_lagfuncs(val_matrix=correlations, setup_args={'var_names':var_names,
'x_base':5, 'y_base':.5}); plt.show()## ## Estimating lagged dependencies ## Parameters: independence test = par_corr tau_min = 0 tau_max = 20
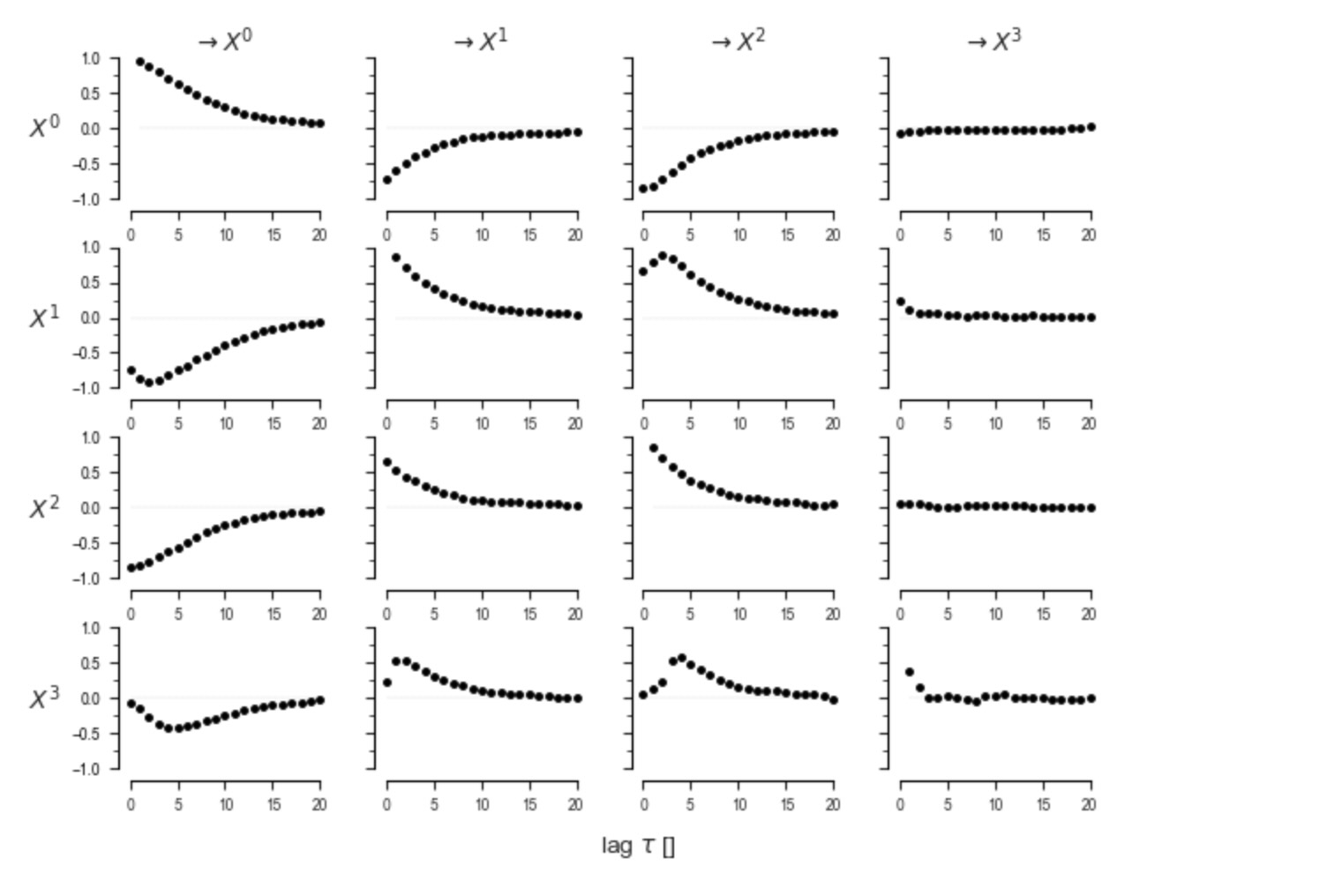
代替的にスキャッタープロットとラグゼロの時の上の密度を調査するために、従属性が持っているそれらの最大絶対値のラグを選択しても良いでしょう。もちろん、あなたは、最大従属性のラグにアクセスするために、非線形の条件独立性テストを使いたいかもしれません。例えば、非線形測度(いわゆる、CMIknnまたは条件独立性テストのチュートリアルで紹介されているGPDC)で初期化されたPCMCIのpcmci.get _lagged_dependenciesを実行します。
PCMCI因果探索
こうして、ラグ関数の従属性は、8の周りの最大ラグに対する減衰を上に図示します。私たちは、PCMCIにtau_max=8 を選択します。他の主要なパラメータpc_alphaは、条件選択ステップで特徴あるレベルを設定します。ここで、私たちは、pc_alpha=Noneへ設定することによって、PCMCIに最適な値を選択させます。そのとき、PCMCIは、妥当な値(例えば、pc_alpha=[0.05,0.1,0.2,0.3,0.4,0.5])のデフォルトのリストの間で、Akaike情報量基準によってParCorrケースのパラメータを最適化します。パラメータaplpha_level=0.01は、グラフを得るために、この特徴的なレベルでのp-値の行列の結果を閾値にすることを示します。
pcmci.verbosity = 1
results = pcmci.run_pcmci(tau_max=8, pc_alpha=None, alpha_level=0.01)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 8
pc_alpha = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X^0$ has 5 link(s):
##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 8
pc_alpha = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5]
max_conds_dim = None
max_combinations = 1
## Resulting lagged parent (super)sets:
Variable $X^0$ has 5 link(s):
[pc_alpha = 0.1]
($X^0$ -1): max_pval = 0.00000, min_val = 0.816
($X^1$ -1): max_pval = 0.00000, min_val = -0.729
($X^3$ -4): max_pval = 0.04439, min_val = 0.064
($X^2$ -5): max_pval = 0.06669, min_val = -0.059
($X^3$ -1): max_pval = 0.08886, min_val = -0.054
Variable $X^1$ has 2 link(s):
[pc_alpha = 0.05]
($X^1$ -1): max_pval = 0.00000, min_val = 0.700
($X^3$ -1): max_pval = 0.00000, min_val = 0.522
Variable $X^2$ has 3 link(s):
[pc_alpha = 0.1]
($X^2$ -1): max_pval = 0.00000, min_val = 0.450
($X^1$ -2): max_pval = 0.00000, min_val = 0.429
($X^3$ -3): max_pval = 0.00000, min_val = 0.171
Variable $X^3$ has 3 link(s):
[pc_alpha = 0.2]
($X^3$ -1): max_pval = 0.00000, min_val = 0.350
($X^1$ -3): max_pval = 0.14772, min_val = 0.046
($X^3$ -8): max_pval = 0.18318, min_val = -0.042
##
## Step 2: MCI algorithm
##
Parameters:
independence test = par_corr
tau_min = 0
tau_max = 8
max_conds_py = None
max_conds_px = None
## Significant links at alpha = 0.01:
Variable $X^0$ has 2 link(s):
($X^1$ -1): pval = 0.00000 | val = -0.619
($X^0$ -1): pval = 0.00000 | val = 0.559
Variable $X^1$ has 2 link(s):
($X^3$ -1): pval = 0.00000 | val = 0.638
($X^1$ -1): pval = 0.00000 | val = 0.628
Variable $X^2$ has 3 link(s):
($X^3$ -3): pval = 0.00000 | val = 0.452
($X^1$ -2): pval = 0.00000 | val = 0.429
($X^2$ -1): pval = 0.00000 | val = 0.422
Variable $X^3$ has 1 link(s):
($X^3$ -1): pval = 0.00000 | val = 0.350 出力からわかるように、PCMCIは、各変数のために異なるpc_alphaを選択しました。run_pcmciの結果は、p-値を行列、静的値のテストの行列(ここで、MCI部分相関)、オプションでその(ParCorrを初期化して特徴づけられる)信頼境界、グラフ行列を含む辞書です。p_matrixとval_matrixは、シェイプ(N,N,tau_max+1) エントリー(i,j,γ)、それはリンクXit-r -> Xjtのテストを示します。γ=0のMCI値は、その他の同時に発生した結果を除外しません。tに関して経過した(past)変数だけが、条件づけられます。同じシェイプのgraphの配列は、alpha_levelで規定したp_matrixの閾値から得られます。それは文字列配列で、因果のリンクを'-->'によって、同時に発生したリンク(方針はPCMCIで決定されません)を'⚪︎-⚪︎'によって示します。PCMCIplusメソッドでは、同時性リンクは順応できません。
注記:静的値のテストは、(例えば、部分相関)従属性の強さの質的な直感を与えます。しかし、適切な因果分析は、CausalEffectクラスとチュートリアルを参照してくさい。
print("p-values")
print (results['p_matrix'].round(3))
print("MCI partial correlations")
print (results['val_matrix'].round(2))p-values [[[1. 0. 0.552 0.504 0.935 0.954 0.59 0.699 0.095] [0.434 0.389 0.769 0.14 0.643 0.155 0.148 0.15 0.675] [0.97 0.191 0.846 0.441 0.688 0.815 0.736 0.066 0.765] [0.185 0.761 0.643 0.078 0.262 0.176 0.535 0.757 0.282]] [[0.434 0. 0.844 0.629 0.566 0.83 0.265 0.62 0.921] [1. 0. 0.324 0.885 0.074 0.17 0.861 0.639 0.766] [0.425 0.654 0. 0.478 0.663 0.202 0.34 0.618 0.359] [0.354 0.276 0.909 0.097 0.981 0.617 0.882 0.947 0.654]] [[0.97 0.986 0.887 0.16 0.794 0.065 0.555 0.563 0.024] [0.425 0.048 0.752 0.759 0.846 0.314 0.63 0.763 0.876] [1. 0. 0.474 0.664 0.371 0.991 0.647 0.874 0.336] [0.306 0.721 0.473 0.861 0.97 0.143 0.569 0.931 0.123]] [[0.185 0.119 0.851 0.775 0.029 0.449 0.782 0.552 0.322] [0.354 0. 0.548 0.087 0.651 0.894 0.046 0.898 0.407] [0.306 0.341 0.756 0. 0.389 0.226 0.819 0.336 0.566] [1. 0. 0.277 0.07 0.316 0.616 0.43 0.677 0.023]]] MCI partial correlations [[[ 0. 0.56 0.02 0.02 0. 0. -0.02 0.01 -0.05] [ 0.03 -0.03 0.01 -0.05 0.01 -0.05 0.05 0.05 -0.01] [-0. 0.04 0.01 -0.02 0.01 -0.01 -0.01 -0.06 0.01] [ 0.04 0.01 0.01 0.06 0.04 -0.04 -0.02 0.01 0.03]] [[ 0.03 -0.62 -0.01 -0.02 0.02 -0.01 -0.04 0.02 0. ] [ 0. 0.63 -0.03 -0. -0.06 0.04 -0.01 0.01 0.01] [ 0.03 0.01 0.43 -0.02 0.01 0.04 0.03 -0.02 -0.03] [ 0.03 0.03 0. 0.05 -0. 0.02 0. 0. 0.01]] [[-0. -0. 0. -0.05 0.01 -0.06 -0.02 -0.02 0.07] [ 0.03 -0.06 -0.01 -0.01 0.01 0.03 0.02 0.01 0.01] [ 0. 0.42 0.02 0.01 0.03 0. -0.01 0.01 0.03] [-0.03 0.01 0.02 0.01 -0. -0.05 -0.02 -0. -0.05]] [[ 0.04 -0.05 -0.01 -0.01 0.07 -0.02 0.01 0.02 0.03] [ 0.03 0.64 0.02 -0.05 0.01 -0. 0.06 -0. 0.03] [-0.03 0.03 0.01 0.45 0.03 -0.04 0.01 0.03 -0.02] [ 0. 0.35 0.03 -0.06 -0.03 -0.02 -0.03 -0.01 -0.07]]]
誤った発見率の制御
もし、私たちが、ここで伝えるN2 τmaxテストの制御したいのであれば、私たちは、さらに一層p-値、例えば、q_matrixを分岐した偽の発見率(FDR)制御によって、正しくできます。グラフはそのとき、p_matrixとget_graph_from_matrixを使った異なるalpha_levelに適応して更新されます。
q_matrix = pcmci.get_corrected_pvalues(p_matrix=results['p_matrix'], tau_max=8, fdr_method='fdr_bh')
pcmci.print_significant_links(
p_matrix = q_matrix,
val_matrix = results['val_matrix'],
alpha_level = 0.01)
graph = pcmci.get_graph_from_pmatrix(p_matrix=q_matrix, alpha_level=0.01,
tau_min=0, tau_max=8, link_assumptions=None)
results['graph'] = graph## Significant links at alpha = 0.01:
Variable $X^0$ has 2 link(s):
($X^1$ -1): pval = 0.00000 | val = -0.619
($X^0$ -1): pval = 0.00000 | val = 0.559
Variable $X^1$ has 2 link(s):
($X^3$ -1): pval = 0.00000 | val = 0.638
($X^1$ -1): pval = 0.00000 | val = 0.628
Variable $X^2$ has 3 link(s):
($X^3$ -3): pval = 0.00000 | val = 0.452
($X^1$ -2): pval = 0.00000 | val = 0.429
($X^2$ -1): pval = 0.00000 | val = 0.422
Variable $X^3$ has 1 link(s):
($X^3$ -1): pval = 0.00000 | val = 0.350さらに関連する方法のチュートリアル
チュートリアルassumtionsは、因果発見の基礎となる仮定とそれらの違反がどのようにメソッドに影響するかを説明しています。
ここで、私たちは、同時発生の因果リンクがないことを仮定するrun_pcmciの事例を見てきました。run_pcmciplusを見ると、その一致するチュートリアルはpcmciplusであり、そのメソッドは、同時に発生する因果リンク(そのせいで交絡することを説明する)を検出できます。
チュートリアルlatent-pcmciは、LPCMCIクラスを説明します。あなたが、同時性リンクに追加して、隠れた交絡を許容するならば、それは使うことができます。
チュートリアル、conditional_independence_testsは、非線形とカテゴリー変数を含むtigramiteで利用できるる全ての条件独立テストの概要を与えます。
チュートリアルpcmci_fullciは、PCMCIとベクター自己回帰モデルの代替の推定を比較します。
2.図示
Tigramiteはいくつかの描画オプションを提案します。ラグ関数行列は、時系列グラフ、過程グラフは、それは、時系列グラフの情報を集計します。グラフ配列、オプションのval_matrixそして、もっと深いリンク属性、両方を引数として取ります。
過程グラフでは、ノードの色は、自動MCI値、リンクの色は、cross-MCOIの値を示します。もし、リンクが二つの変数間で多重ラグが存在するならば、リンクの色はもっとも強い一つを示し、ラベルは、それらの強さを示すために、全ての特定のラグをリストします。追加で、show_autodependency_lags=Trueの設定は、対応するノードラベルの下に、特別な自動従属性を表示します。
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI',
node_colorbar_label='auto-MCI',
show_autodependency_lags=False
); plt.show()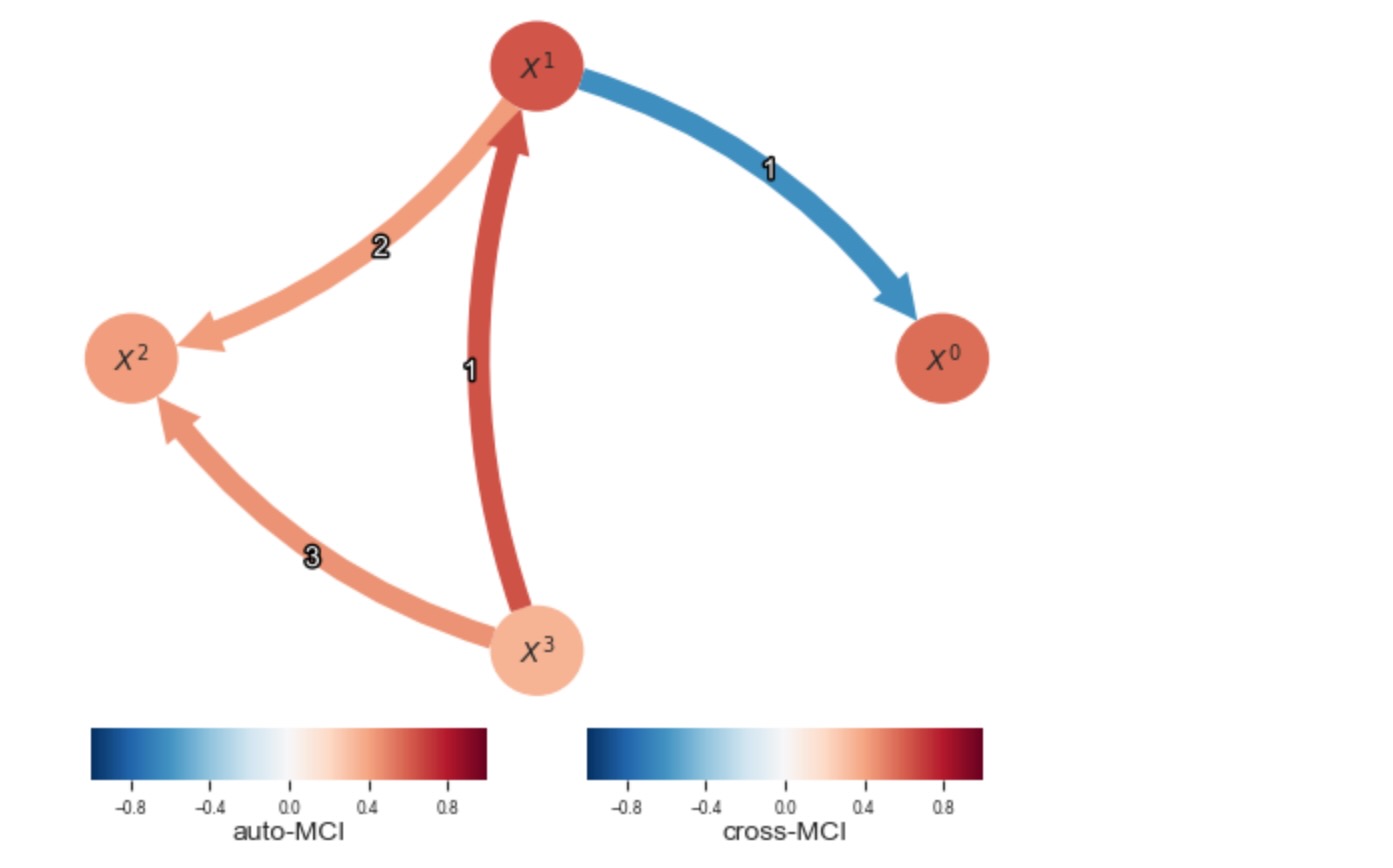
# Plot time series graph
tp.plot_time_series_graph(
figsize=(6, 4),
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()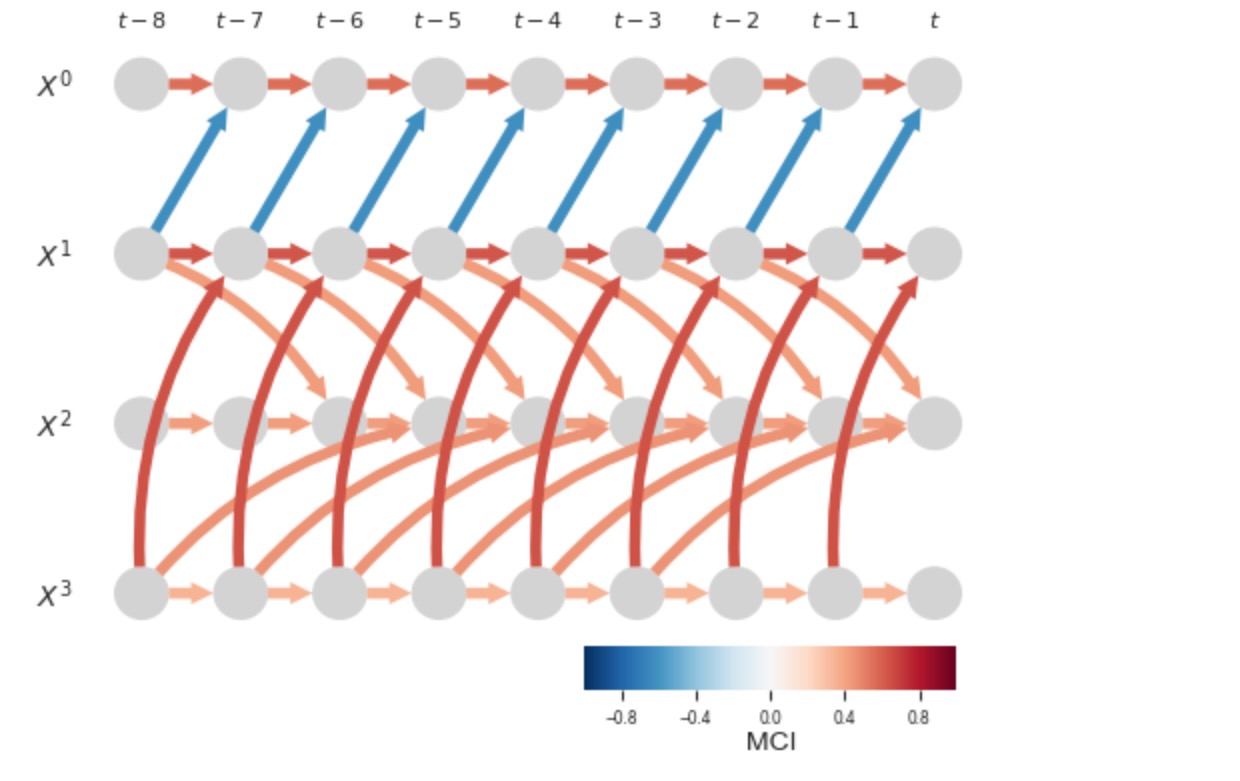
過程グラフは視覚的に高品質で、時系列グラフは、そこから因果の経路が読み取れる一時的な空間の依存構造を適切に表します。あなたは、node_sizeとnode_aspectパラメータでサイズと相の割合を調整することができます。そして、多くの他の性質を修正します。パラメータplot_graphとplot_time_series_graphを参照してください。
他の方法として、リンクはcsvファイルに出力することができます。
tp.write_csv(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
save_name='test_graph.csv',
digits=5,
)3.リンクに関する専門家の仮定の統合
しばしば、リンクの存在と欠如、そしてそれらの方針について事前の知識を持っているでしょう。そのような専門知識はlink_assumptions引数を経由して統合できます。
link_assumptionsは、リンクに関する仮定を規定した 形式{j:(i,-tau): link_type,…},…}の辞書です。内部では、この引数の設定は、グラフを次のように初期化します。graph[i,j,tau] =link_type 、辞書のエントリーのために、link_assumptions[i][(i,tau)] = link_type. 以下の仕様が許されます。
graph[i,j,0] = '-->':ラグ0のiからjへの指向性のリンクが存在graph[i,j,0] = '-?>':隣接のためのメソッドにテストさせ、もし存在していれば、方針はラグ0でiからjへの指向性を持つgraph[i,j,0] = '⚪︎-⚪︎':ラグ0でiとjの間で隣接、しかし、メソッドがその方針を決定する。graph[i,j,0] = '⚪︎?⚪︎':メソッドが隣接をテストし、その方針を決定する。
リンクの仮定は一定になる必要があります。いわゆる、graph[i,j,0] = '-->'はgraph[i,j,0] = '<--'を必要とし、非周期性は保持しなければなりません。もしリンクが辞書には現れないならば、欠如を仮定します。それは、もし、link_assumtionsがNoneでなければ、そのとき全てのリンクは規定されなければならないかあるいは、リンクは欠如と仮定されます。
小さな数値の可能なリンクだけに背景知識を持っているようなケースがあるでしょう。sそして、それは完全にネストされた辞書を構築するのに、複雑で能率の悪いものです、そこでは背景知識の欠如は、tau < 0の場合、link_assumptions[j][(i,tau)] = '-?>' 、tau = 0の場合、link_assumptions[j][(i,0)] = '⚪︎?⚪︎'によって規定される必要があります。そのようなケースでは、あなたは静的な便利な関数pcmci.build_link_assumptions(…)をあなたのコードまたはノートブックで使うことができます。それは、link_assumptions_absent_link_means_no_knowledge(エントリーの欠如はリンクに関するデフォルトの仮定です)によってlink_assumptions(リンクを欠如させるためにエントリーの欠如を仮定します)を実装して構築することを許します。
以下の例を考えます。
links_coeffs = {0: [((0, -1), 0.7, lin_f)],
1: [((1, -1), 0.7, lin_f), ((0, 0), 0.2, lin_f), ((2, -2), 0.2, lin_f)],
2: [((2, -1), 0.9, lin_f)],
}
T = 100 # time series length
data, _ = toys.structural_causal_process(links_coeffs, T=T, seed=8)
T, N = data.shape
# Initialize dataframe object
dataframe = pp.DataFrame(data)
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=ParCorr(),
verbosity=0)私たちは、最初にPCMCIplus(同時に発生するリンクの検出を許可します)をリンクの仮定なしで実行します。
tau_max = 2
pc_alpha = 0.05
link_assumptions = None
results = pcmci.run_pcmciplus(tau_max=tau_max,
pc_alpha=pc_alpha,
link_assumptions=link_assumptions,
)
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
); plt.show()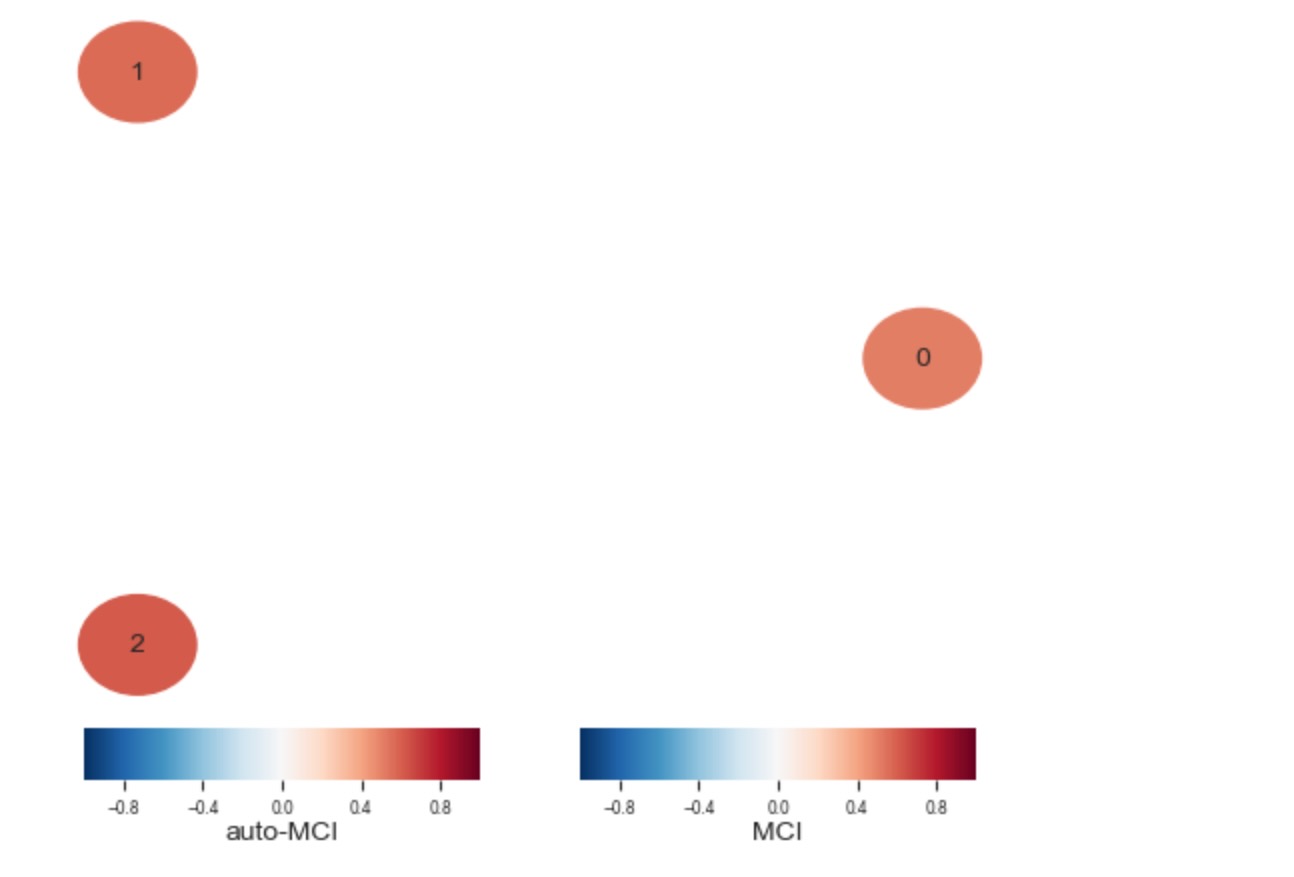
このように、小さなサンプルサイズのために、リンクの強度が弱くなります。私たちは、0から1と2から1へのリンクの両方で紛失し、偽の正を取得します。
ここで、私たちは、ラグ0で0から1のリンクがそこにあることを仮定しまが、その方針は固定されません。そしてラグ2の2から1へのリンク(方針は時間の順序によって与えられます)を仮定します。さらに私たちは、0と2の間(任意のラグ)にはリンクがないことを仮定します。
link_assumptions = {j:{(i, -tau):'o?o' for i in range(N) for tau in range(tau_max + 1) if (i, -tau) != (j, 0)}
for j in range(N)}
# Exclude all links between 0 and 2
link_assumptions[0] = {(i, -tau):'o?o' for i in range(N) for tau in range(tau_max + 1)
if ((i, -tau) != (0, 0)
and i != 2)}
link_assumptions[2] = {(i, -tau):'o?o' for i in range(N) for tau in range(tau_max + 1)
if ((i, -tau) != (2, 0)
and i != 0)}
# Set link 1 o-o 0 at lag 0
link_assumptions[1][(0, 0)] = 'o-o'
link_assumptions[0][(1, 0)] = 'o-o' # Required for consistency of contemporaneous links, would be internally added if not present
# Set link 2 --> 1 at lag 2
link_assumptions[1][(2, -2)] = '-->'
results = pcmci.run_pcmciplus(tau_max=tau_max,
pc_alpha=pc_alpha,
link_assumptions=link_assumptions,
)
print(results['graph'][:,:,0])
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
); plt.show()[['' '-->' ''] ['<--' '' ''] ['' '' '']]
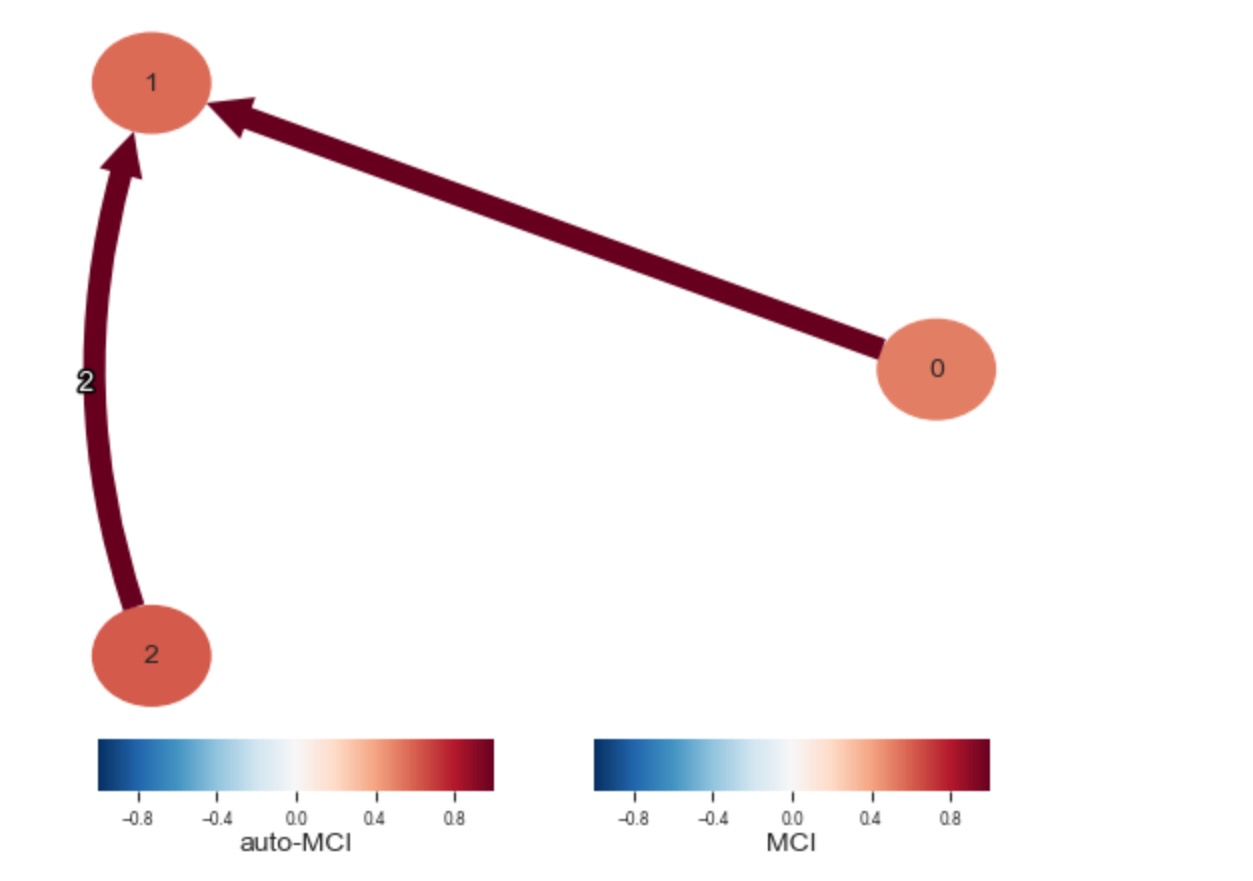
これは、正しいグラフを与えます。私たちは、1 ⚪︎-⚪︎ 0の隣接だけで、リンク1<-⚪︎の方針を規定していないことに注意してください。方針は、PCMCIによってビーム(collider)のルールで推論されました。対応するPCMCIplusのチュートリアルを参照してください。
4. ベンチマークと検証
モデルのデータをあなた自身で生成することは助言できます。特徴は、あなたの現実のデータと同様の同じ難問です。しかし、正解データが知られているところでは、どのメソッドがもっともよく機能するか、そしてまたハイパーパラメータを選択するために、あなたが評価することができるということです。
対応するフォルダーのチュートリアルを参照してください。
5. 因果結果の推定
上の図は、対応する独立テストの静的なテストの値としてリンクの因果の強度を示しています。しかし、これは、因果の結果の測度として真っ直ぐに解釈することはできません。これは、CausalEffectとLinearMediationクラスによってカバーされます。
対応するフォルダーのチュートリアルを参照してください。
6.データセットの難題
最後に、あなたは、tigramiteのDataFrameの機能によってカバーされる 欠測、またはマスキングのような難題の一つ以上のデータセットを扱うでしょう。
対応するフォルダのチュートリアルを参照してください。
7.スライディング・ウィンドウの分析
チュートリアルsliding_wondow_analysisは、関数PCMCI.run_sliding_window_ofを説明します。それは、便利な関数で、全てのPCMCIの因果の発見メソッドを、多変量時系列スライディングウィンドウで実行させることができます。
