TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。
このチュートリアルは、関数PCMCI.run_pcmciplusを説明します。標準のPCMCI.run_pcmciと対照的に、PCMCIplusは、因果充分性、信頼性、マルコフ条件の標準の仮定の元で、完全な、遅延および同時発生の、因果グラフ(同時に発生するリンクのマルコフ同値類までの)を識別できます。
PCMCIplusはここに記述されています: . Runge (2020), Discovering contemporaneous and lagged causal relations in autocorrelated nonlinear time series datasetshttp://www.auai.org/uai2020/proceedings/579_main_paper.pdf
最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例): https://www.nature.com/articles/s41467-019-10105-3
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb1. 同時性と遅延従属性の構造的因果過程
私たちは、時系列グラフを再構築することに関心があります。それは、複雑な動的システム下で、一時的な従属性構造を表現し使用することができます。時間に依存したシステムXt = (Xt1,...XtN)
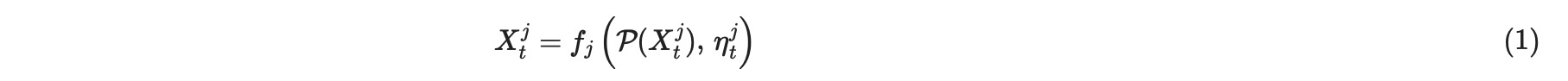
ここで、任意の測定できるその引数に平凡でない従属性を持つ関数で、ηtjは、排他的で(i≠j) 、連続的(t'≠t) 独立した動的ノイズです。時系列グラフのノードは、異なる遅延時間と変数のセット、を持つ変数Xtjを表します。そのXtjが依存している変数のセットは、因果的な親P(Xtj) ⊆Xt+1- =(Xt,Xt-1,...)\{Xtj}を定義します。因果リンクXt-ri ->Xtjは、Xt-ri ⊆P(Xtj) の場合に存在します。τ>0 で、私たちはそれを遅延リンクと呼び、τ = 0 で Xti -> Xtjを同時性リンクと呼びます。その時、変数Xtj ⊆ Xtは、それらの親とともに、時系列グラフ gで表します。
Tigramiteでこの過程の変位は、(一般化加法モデル)関数toys.structual_causal_processで生成することができます。toys.var_processと対称的に、ここのリンクは様式((i,-tau), coeff,func) を持ち、ここで、funcは、Pythonから一つの引数を指定して呼び出すことができるように提供される任意の(非線形)関数です。coeffは、乗算する因子です。それは、toys.structual_causal_processで、以下の様式の過程を生成します。
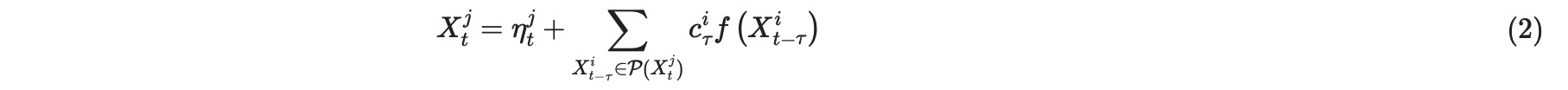
ηjのノイズ分布は、toys.structual_causal_processで規定されます。重要にも、τ = 0の時、私たちは同時に発生させて生成することがきます。また、即座に因果従属性を呼び出されます。これらが非周期的である必要性に注意してください。そうでなければ、エラーが上がります。PCMCIplusの解説論文から、以下の例を取り上げて考えます。
seed = 7
auto_coeff = 0.95
coeff = 0.4
T = 500
def lin(x): return x
links ={0: [((0, -1), auto_coeff, lin),
((1, -1), coeff, lin)
],
1: [((1, -1), auto_coeff, lin),
],
2: [((2, -1), auto_coeff, lin),
((3, 0), -coeff, lin),
],
3: [((3, -1), auto_coeff, lin),
((1, -2), coeff, lin),
],
4: [((4, -1), auto_coeff, lin),
((3, 0), coeff, lin),
],
5: [((5, -1), 0.5*auto_coeff, lin),
((6, 0), coeff, lin),
],
6: [((6, -1), 0.5*auto_coeff, lin),
((5, -1), -coeff, lin),
],
7: [((7, -1), auto_coeff, lin),
((8, 0), -coeff, lin),
],
8: [],
}
# Specify dynamical noise term distributions, here unit variance Gaussians
random_state = np.random.RandomState(seed)
noises = noises = [random_state.randn for j in links.keys()]
data, nonstationarity_indicator = toys.structural_causal_process(
links=links, T=T, noises=noises, seed=seed)
T, N = data.shape
# Initialize dataframe object, specify variable names
var_names = [r'$X^{%d}$' % j for j in range(N) ]
dataframe = pp.DataFrame(data, var_names=var_names) 真のグラフはここで、真の最大遅延時間はtau_max = 2なので、シェイプ(N,N,2+1)を持ちます。τ≧0のときエントリーtrue_graph[i,j,tau]="-->" は、因果リンクXt-ri -> Xtjを示し、true_graph[i,j,0]="<--" は、(τ=0の時だけ)因果リンクXti <- Xtjを示します。そして、true_graph[i,j,tau]="" は因果リンクの欠如を示します。
true_graph = toys.links_to_graph(links=links)2. PCMCI+:同時性と遅延従属性の因果探索
PCMCIplusのゴールは、グラフgを再構築することです。私たちは、無限のサンプルサイズと全ての仮定を満たすときでも、これは必ずしも可能でなく、グラフはマルコフ同値類までだけが再構築できることがわかります。
一般的アイデア
PCMCIplusに対する一般的アイデアは、次のPCアルゴリズムに従います。
- 概略探索フェイズ:完全に接続されたグラフから始めます。最初に、Xt-ri - Xtjに近接した概略は、ノードのペアは、他のノードの正確なサブセットへの条件独立であることを識別することによって推定されます。条件を選択する特別な方法は論文を参照してください。それは、オリジナルのPCアルゴリズムからは相違します。条件独立ペア間の近接は削除されます。概略の中の遅延のある近接は、その時自動的に、時間の順序で指向されます。例えば、無向リンクXt-2i - Xtjは、因果の影響が時間上でさかのぼることができないので、Xt-2i -> Xtjとしてだけ指向することができます。
- Collider 方針フェイズ:同時に発生する Xti-Xtjの近接は、その時、以下のColliderルールを基礎にして、指向されます。:もし、Xtiが条件セットの部分でなければ、それはXt-rkとXtjを独立にします。その時、Xt-rk- Xti - Xtjの向は、Xt-rk ->Xti <- Xtjになります。このルールは、全てのシールドされない三つに適用されます。(
contemp_collider_rule={'none', 'majority', 'conservative'}) 中間ノードXtiが分離する条件のセットであるかないかを決定するために、三つのオプションがあります。オリジナルのPCアルゴリズムでは、概略探索フェイズで条件独立を導く条件は、ストアされ(Tigramiteではsepset)、そして、その後colliderフェイズで使用されます。代替的に、全ての分離条件セットはXt-rkとXtjの近傍を基礎にして再計算されます、そしてcolliderモチーフは、論文で議論されるようにmajorityまたはconservativeルールを基礎にして指向されます。 - ルール指向フェイズ:さらに近接したグラフの方針は、周期性を含みません(ルールR1-R3)
このアルゴリズムは、グラフに有向(遅延と同時性)リンクXt-ri -> Xtjを含んでいるグラフの結果になります。しかし、同時性リンクXt-ri -> Xtjもまた、上のフェイズに従って指向することはできません。例えば、もし完全に同時に発生する三つXti - Xtk - Xtjの中間ノードXtkが、XtiとXtjを独立にする条件セットの部分であれば、その時、私たちは、真の因果の関係がXti->Xtk->Xtj または、Xti <- Xtk <- Xtjであるか区別をつけることができません。これらは、その時、マルコフ同値類の様式です。τ > 0の時、遅延 Xt-riを含む三つは本当に、最初にモチーフが可能なときだけ、リンクの指向に役立ちます。
順位独立性;オリジナルPCアルゴリズムの重要な不必要な性質は、N 変数の順序依存です。これは、(Tigramiteに実装されている)概略フェイズの少し修正したバージョンを使うことによって、上で述べた多数派の保守的なcolliderルール、そして、方針ルールが相互に衝突している全てのリンクを作ることによって(conflict_resolution=True)、乗り越えることができます。
PCMCIplusアルゴリズム
時系列の適用する標準のPCアルゴリズムと比較して、PCMCIplusは二つの中心的アイデアを基にしています。最初は、概略フェイズは、遅延と同時性条件のセットに分離して伝達されます。そして遅延フェイズは、もっと大きな力を出すのにより少ないテストを使います。2番目に、PCMCIplusは、自己相関の下でもっとよく校正できるように、条件セットを個別の条件独立性テストのために修正します。そして、一瞬の条件独立性アプローチを使うことによって、検出力を増大させます。結果として、PCMCIplusは、4つのフェイズのアルゴリズムによって、時間遅延と、同時性因果リンクを推定します。(論文の仮のコードを参照してください):
- 遅延条件の概略探索フェイズ(PCMCIと同じ): 各変数Xtjに対して、
run_pc_stableとして実装されている、PC1アルゴリズムの繰り返し数とともに、遅延(τ > 0 )親Bt-(Xtj)のスーパーセットを推定します。 - 同時性条件と一瞬の条件独立テストを伴う概略探索フェイズ:同時に発生する近接のサブセットS⊆Xtを通って繰り返し、Xtj⊆Xtでかつ、Xt-ri ⊆ Xt ∪ Bt-(Xtj)である、全ての順序のペア(Xt-ri,Xtj)の近接を削除します。もし、MCI条件独立性が、(Bt-r-(Xt-ri) がXt-riの親で)以下のを保持するならば、
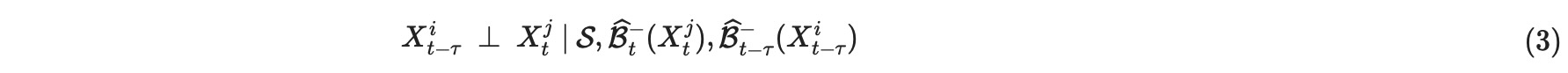
3. Collider方針フェイズ:同時性リンクをシールドされない三つを基礎にして正しい位置に置きます。オプションで、保守的で(MCIテストを基礎にした)主要なルールを適用します。
4. ルール方針フェイズ:論文のR1-R3のルールを基礎にして同時性リンクを、正しい位置に置きます。
フェイズ;2-4はrun_pcalgにパラメータmode='contemp_conds'で実装されています。MCIテストは、Xt-riとXtjの両方の親の遅延スーパーセットで条件づけられます。それは、PCMCIのアイデアと同じです。これに対する妥当性は、この論文で詳細に議論されています。ここでまた、PCMCIplusの定常性と独立の秩序もまた、証明されます。
PCMCIと対称的に、PCMCIplusの関連出力は、graphの配列になります。それは以下のように解釈されてエントリーされます。
graph[i,j,tau]='-->' tau > 0は、有向遅延因果リンクXt-ri -> Xtjを示します。graph[i,j,0]='-->'とgraph[j,i,0]='<--'は、有向同時性因果リンクXti -> Xtjを示します。graph[i,j,0]='o-o'とgraph[j,i,0]='o-o'は、無向同時性近接Xti - Xtjを示し、colliderと方針ルールは適用されません。 (Markov equivalence)graph[i,j,0]='x-x'とgraph[j,i,0]='x-x'は、Xti とXtj間の衝突、同時性、近接を示し。その方向は方針ルールが衝突しているために決定されません。
衝突の例は、Xti - Xtjの近接が二つのトリプルの部分のときに、他のトリプルはXti <- Xtjを提案しますが、一つのトリプルに適用されるcolliderルールが、Xti->Xtjを提案します。これは、有限のサンプル効果または、仮定の違反のために発生します。
重要にも、PCMCIplusのp_matrixとval_matrixは、不確実性と強度の量計は、フェイズ2の近接のためだけでなく、しかし、フェイズ3と4で決定される同時性リンクの方向性のためでもありません。遅延リンクは常に、時間上の順序であることに注意してください。
パラメータ
PCMCIplusは、データの種類(連続、または離散)に対応し、従属性の種類が仮定されて、静的に任意の種類の条件独立性テストを柔軟に組み合わせることができます。それらは、tigmaite.indepencdence_testsで利用できます。
PCMCIplusの主要な自由パラメータは、(条件独立性テストの自由パラメータを追加して)、最大時間遅延τmax(tau_max)と重要な閾値αPC(pc_alpha)があります。もし、リストまたはNoneがpc_alphaに渡されると、重要なレベルが与えられたpc_alphaの値に沿って、cond_ind_test.get_model_selection_criterion()で計算されたスコアを使って、全てのグラフで最適化されます。最大時間遅延は、アプリケーションに依存します。そして、複雑なシステムで予期される最大因果遅延時間に従って選択されます。私たちは、むしろ、関数run_bivciのピークを含む、大きな選択を推薦します。もう一つの重要なパラメータは、contemp_collider_ruleです。conflict_resolution=True(デフォルト値)と一緒にmajority(デフォルト値)または、conservativeが設定されたときだけ、PCMCIplusは、上で議論したように、完全に順序に独立になります。それはデータフレームのN変数の順序が問題ではないことを意味します。最後に、デフォルトのオプションreset_laggged_links =Falseは、フェイズ2の遅延リンクの検出を、Bt-(Xtj)で与えられるフェイズ1で見つけた重要な近接に、制限します。reset_lagged_links=Falseであれば、全ての遅延リンクは、再度考慮されます。それは、遅延リンクの検出力を改善しますが、実行時に大きく導きます。さらにオプションパラメータは論文またはドキュメントで議論されます。
3. 応用例
上の例の過程でPCMCIplusの分析へ伝達するために、最初に私たちは、時系列を図示します。これは、関数tp.plot_timeseriesで実行できます。
tp.plot_timeseries(dataframe, figsize=(15, 5)); plt.show()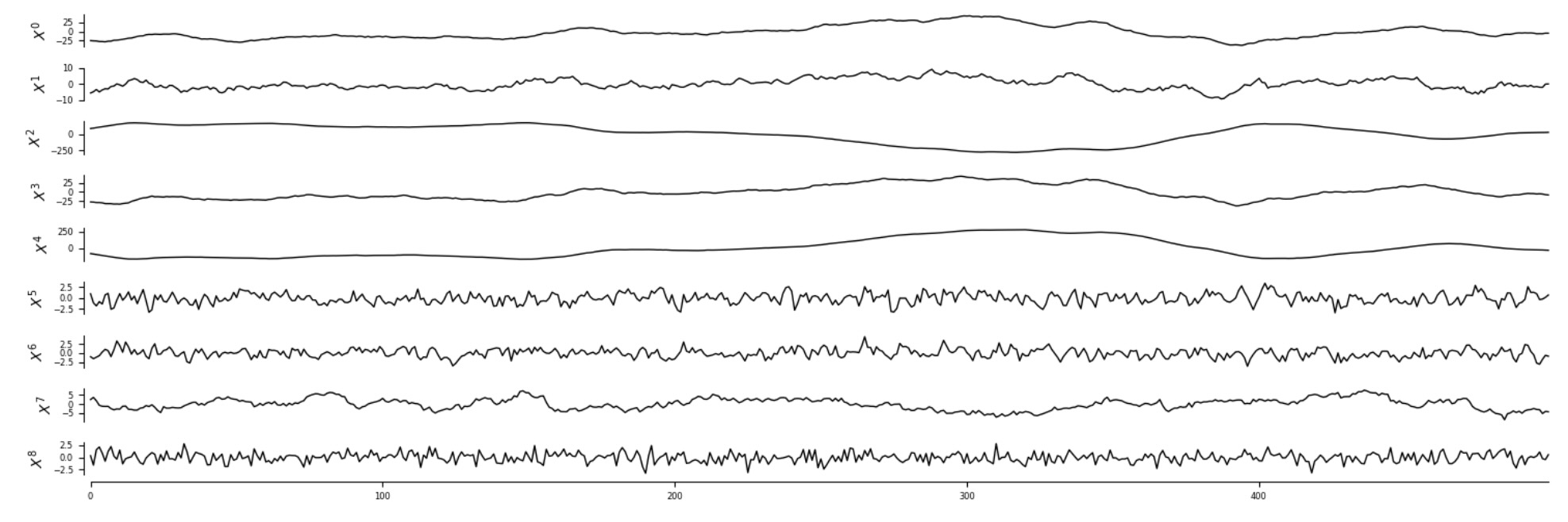
高い自己相関にも関わらず、それはステーショナリーで、欠測値を含んでいます。非ステーショナリーと欠測値に議論については他のチュートリアルをチェックしてください。
次に、私たちは、条件独立テストを選択します。ここで、私たちは、線形部分相関で実装されたParCorrの線形従属性を仮定します。signicance='analytics'のnull分布は、スチューデントのTが仮定されます。そのとき、私たちは、 PCMCIクラスを初期化します。それは、dataframeとcond_ind_testとともに、PCMCIplus同様、PCMCIをカバーします。
parcorr = ParCorr(significance='analytic')
pcmci = PCMCI(
dataframe=dataframe,
cond_ind_test=parcorr,
verbosity=1)PCMCI plusを実行する前に、関数run_bivciを実行して図示するのは良いアイデアです。それは、二項で、遅延条件独立テストに実装されています。(二項Granger因果同様ですが、遅延仕様です)これは、最大時間遅延tau_maxを選択するのに役立つことができます。その他のオプションは、図示するためのget_lagged_dependenciesです。しかし大きな自己相関は、遅延のピークを増幅します( https://journals.ametsoc.org/doi/full/10.1175/JCLI-D-13-00159.1 を参照してください。)。run_bivciは少なくとも自己相関のいくつかで条件外になります。
correlations = pcmci.run_bivci(tau_max=10, val_only=True)['val_matrix']
lag_func_matrix = tp.plot_lagfuncs(val_matrix=correlations,
setup_args={'var_names':var_names, 'figsize':(15, 10),
'x_base':5, 'y_base':.5})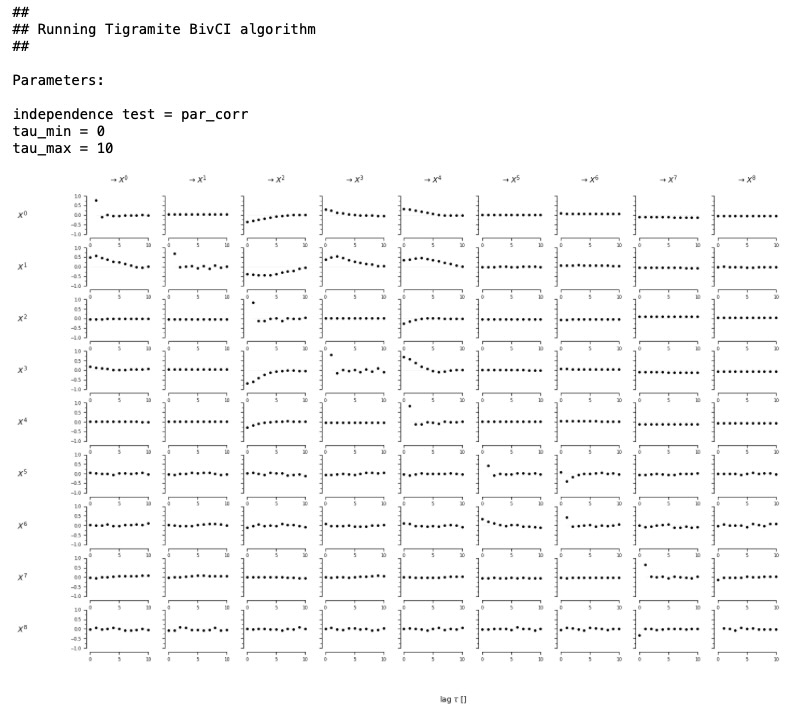
matrix_lags = np.argmax(np.abs(correlations), axis=2)
tp.plot_densityplots(dataframe=dataframe, setup_args={'figsize':(15, 10)}, add_densityplot_args={'matrix_lags':matrix_lags}); plt.show()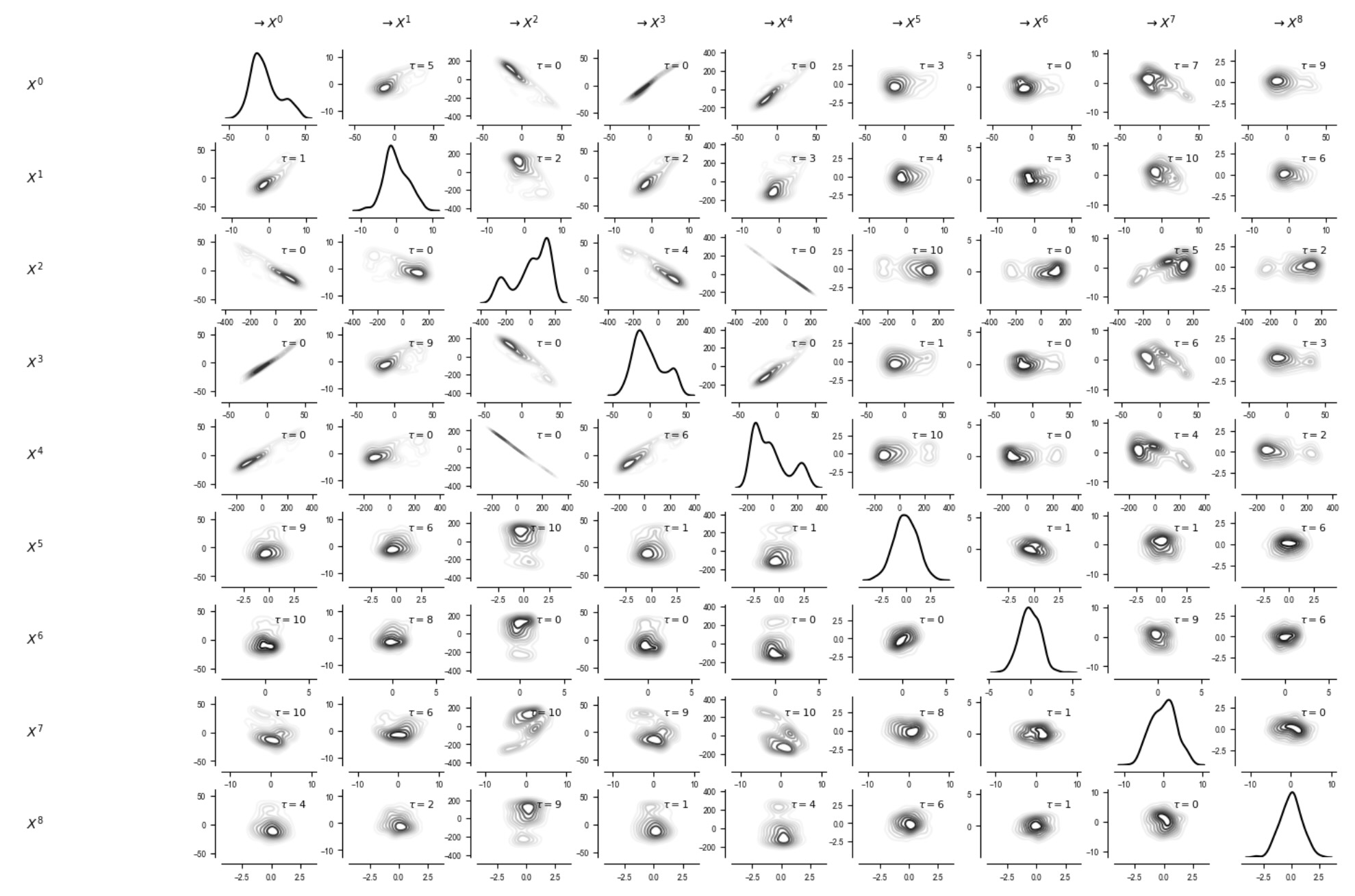
従属性は、図示関数の遅延の3の周りで最大のピークを持つため、私たちはPCMCIplusにtau_max = 3を選択します。この選択は、しかしながら、システムの専門家の知識に強く依存しています。明白に、同時性因果探索で、私たちは、デフォルト値tau_min=0から離れます。その他の主要なパラメータは、pc_alphaです。それは、PCMCIplusの全てのテストの重要なレベルを設定します。こればPCMCIとは対照的です、ここでpc_alphaは、MCIテストではない、条件選択フェイズで、重要なテストだけを操作します。PCMCIplusはまた、最適化の値を選択するための自動手続(PCMCIのように)があります。もし、リストまたはNoneがpc_alphaに渡されると、cond_ind_test.get_model_selections_criterion()で計算されたスコアを使ってpc_alphaに与えられた値に沿って、全てのグラフを重要なレベルが最適化します。PCMCIplusの出力は、DAGだけでなく、DAGの同値クラスも出力するので、最初にこのクラスのあるメンバーは、計算され、その後、スコアが全てのモデルの平均して計算され、各変数に適合されます。スコアは、クラスの全てのメンバーで同じ値です。
ここで、私たちは、pc_alpha=0.01を設定します。アプリケーションで異なる数値は、テストされ、透過して議論される結果になります。
verbosity=2設定するのは命令的で、論文と仮のコードを読んだ後、PCMCIplusの出力を理解します。同時性近接の出力は、⚪︎--⚪︎によって記される無指向でなく、すでに'-->'によって指向性のある近接です。
tau_max = 3
pc_alpha = 0.01
pcmci.verbosity = 2
results = pcmci.run_pcmciplus(tau_min=0, tau_max=tau_max, pc_alpha=pc_alpha)##
## Step 1: PC1 algorithm with lagged conditions
##
Parameters:
independence test = par_corr
tau_min = 1
tau_max = 3
pc_alpha = [0.01]
max_conds_dim = None
max_combinations = 1
## Variable $X^{0}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{0}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = 0.997
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{0}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = 0.992
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{0}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = 0.984
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{0}$ (4/27):
Subset 0: () gives pval = 0.00000 / val = 0.703
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{0}$ (5/27):
Subset 0: () gives pval = 0.00000 / val = 0.738
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{0}$ (6/27):
Subset 0: () gives pval = 0.00000 / val = 0.768
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{0}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = -0.826
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{0}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = -0.811
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{0}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = -0.796
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{0}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = 0.971
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{0}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = 0.965
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{0}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = 0.956
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{0}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = 0.829
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{0}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = 0.814
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{0}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = 0.799
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{0}$ (16/27):
Subset 0: () gives pval = 0.69874 / val = 0.017
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{0}$ (17/27):
Subset 0: () gives pval = 0.62546 / val = 0.022
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{0}$ (18/27):
Subset 0: () gives pval = 0.58808 / val = 0.024
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{0}$ (19/27):
Subset 0: () gives pval = 0.02699 / val = 0.100
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{0}$ (20/27):
Subset 0: () gives pval = 0.02388 / val = 0.102
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{0}$ (21/27):
Subset 0: () gives pval = 0.01621 / val = 0.108
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{0}$ (22/27):
Subset 0: () gives pval = 0.00000 / val = -0.372
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{0}$ (23/27):
Subset 0: () gives pval = 0.00000 / val = -0.366
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{0}$ (24/27):
Subset 0: () gives pval = 0.00000 / val = -0.361
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{0}$ (25/27):
Subset 0: () gives pval = 0.45960 / val = -0.033
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{0}$ (26/27):
Subset 0: () gives pval = 0.43451 / val = -0.035
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{0}$ (27/27):
Subset 0: () gives pval = 0.39192 / val = -0.039
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{0}$ has 18 link(s):
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.997
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.992
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.984
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.971
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.965
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.956
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.829
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.826
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.814
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.811
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.799
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.796
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.768
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.738
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.703
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.372
($X^{7}$ -2): max_pval = 0.00000, min_val = 0.366
($X^{7}$ -3): max_pval = 0.00000, min_val = 0.361
Testing condition sets of dimension 1:
Link ($X^{0}$ -1) -?> $X^{0}$ (1/18):
Subset 0: ($X^{0}$ -2) gives pval = 0.00000 / val = 0.846
No conditions of dimension 1 left.
Link ($X^{0}$ -2) -?> $X^{0}$ (2/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.434
No conditions of dimension 1 left.
Link ($X^{0}$ -3) -?> $X^{0}$ (3/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.478
No conditions of dimension 1 left.
Link ($X^{3}$ -1) -?> $X^{0}$ (4/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.04324 / val = -0.091
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{0}$ (5/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.211
No conditions of dimension 1 left.
Link ($X^{3}$ -3) -?> $X^{0}$ (6/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.295
No conditions of dimension 1 left.
Link ($X^{4}$ -1) -?> $X^{0}$ (7/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.285
No conditions of dimension 1 left.
Link ($X^{2}$ -1) -?> $X^{0}$ (8/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.284
No conditions of dimension 1 left.
Link ($X^{4}$ -2) -?> $X^{0}$ (9/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.287
No conditions of dimension 1 left.
Link ($X^{2}$ -2) -?> $X^{0}$ (10/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.285
No conditions of dimension 1 left.
Link ($X^{4}$ -3) -?> $X^{0}$ (11/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = -0.287
No conditions of dimension 1 left.
Link ($X^{2}$ -3) -?> $X^{0}$ (12/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.285
No conditions of dimension 1 left.
Link ($X^{1}$ -3) -?> $X^{0}$ (13/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.602
No conditions of dimension 1 left.
Link ($X^{1}$ -2) -?> $X^{0}$ (14/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.659
No conditions of dimension 1 left.
Link ($X^{1}$ -1) -?> $X^{0}$ (15/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.00000 / val = 0.714
No conditions of dimension 1 left.
Link ($X^{7}$ -1) -?> $X^{0}$ (16/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.62195 / val = 0.022
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{0}$ (17/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.20225 / val = 0.058
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{0}$ (18/18):
Subset 0: ($X^{0}$ -1) gives pval = 0.15295 / val = 0.064
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{0}$ has 14 link(s):
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.846
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.703
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.659
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.602
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.478
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.434
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.295
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.287
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.287
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.285
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.285
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.285
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.284
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.211
Testing condition sets of dimension 2:
Link ($X^{0}$ -1) -?> $X^{0}$ (1/14):
Subset 0: ($X^{1}$ -1) ($X^{1}$ -2) gives pval = 0.00000 / val = 0.997
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{0}$ (2/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -2) gives pval = 0.00000 / val = 0.366
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{0}$ (3/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.67004 / val = 0.019
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{0}$ (4/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.48923 / val = 0.031
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{0}$ (5/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.55674 / val = 0.027
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{0}$ (6/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.88577 / val = 0.006
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{0}$ (7/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.98726 / val = 0.001
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{0}$ (8/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.58358 / val = 0.025
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{0}$ (9/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.55963 / val = 0.026
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{0}$ (10/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.59255 / val = -0.024
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{0}$ (11/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.55313 / val = 0.027
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{0}$ (12/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.59990 / val = -0.024
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{0}$ (13/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.59587 / val = -0.024
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{0}$ (14/14):
Subset 0: ($X^{0}$ -1) ($X^{1}$ -1) gives pval = 0.81624 / val = 0.011
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{0}$ has 2 link(s):
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.846
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.366
Algorithm converged for variable $X^{0}$
## Variable $X^{1}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{1}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = 0.627
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{1}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = 0.592
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{1}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = 0.559
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{1}$ (4/27):
Subset 0: () gives pval = 0.00000 / val = 0.954
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{1}$ (5/27):
Subset 0: () gives pval = 0.00000 / val = 0.906
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{1}$ (6/27):
Subset 0: () gives pval = 0.00000 / val = 0.860
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{1}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = -0.371
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{1}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = -0.355
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{1}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = -0.340
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{1}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = 0.590
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{1}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = 0.559
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{1}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = 0.529
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{1}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = 0.372
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{1}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = 0.356
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{1}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = 0.341
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{1}$ (16/27):
Subset 0: () gives pval = 0.70965 / val = -0.017
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{1}$ (17/27):
Subset 0: () gives pval = 0.77260 / val = -0.013
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{1}$ (18/27):
Subset 0: () gives pval = 0.85351 / val = -0.008
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{1}$ (19/27):
Subset 0: () gives pval = 0.01056 / val = 0.115
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{1}$ (20/27):
Subset 0: () gives pval = 0.02124 / val = 0.104
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{1}$ (21/27):
Subset 0: () gives pval = 0.03360 / val = 0.096
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{1}$ (22/27):
Subset 0: () gives pval = 0.00154 / val = -0.142
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{1}$ (23/27):
Subset 0: () gives pval = 0.00331 / val = -0.132
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{1}$ (24/27):
Subset 0: () gives pval = 0.00963 / val = -0.116
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{1}$ (25/27):
Subset 0: () gives pval = 0.39701 / val = -0.038
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{1}$ (26/27):
Subset 0: () gives pval = 0.83871 / val = -0.009
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{1}$ (27/27):
Subset 0: () gives pval = 0.84067 / val = 0.009
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{1}$ has 18 link(s):
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.954
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.906
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.860
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.627
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.592
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.590
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.559
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.559
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.529
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.372
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.371
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.356
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.355
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.341
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.340
($X^{7}$ -1): max_pval = 0.00154, min_val = 0.142
($X^{7}$ -2): max_pval = 0.00331, min_val = 0.132
($X^{7}$ -3): max_pval = 0.00963, min_val = 0.116
Testing condition sets of dimension 1:
Link ($X^{1}$ -1) -?> $X^{1}$ (1/18):
Subset 0: ($X^{1}$ -2) gives pval = 0.00000 / val = 0.702
No conditions of dimension 1 left.
Link ($X^{1}$ -2) -?> $X^{1}$ (2/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.44734 / val = -0.034
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{1}$ (3/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.47865 / val = -0.032
Non-significance detected.
Link ($X^{0}$ -1) -?> $X^{1}$ (4/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.50432 / val = -0.030
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{1}$ (5/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.53196 / val = -0.028
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{1}$ (6/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.66032 / val = -0.020
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{1}$ (7/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.58334 / val = -0.025
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{1}$ (8/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.64219 / val = -0.021
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{1}$ (9/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.68004 / val = -0.019
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{1}$ (10/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.98930 / val = 0.001
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{1}$ (11/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.98493 / val = -0.001
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{1}$ (12/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.97777 / val = 0.001
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{1}$ (13/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.96279 / val = -0.002
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{1}$ (14/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.94991 / val = 0.003
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{1}$ (15/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.93372 / val = -0.004
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{1}$ (16/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.99454 / val = -0.000
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{1}$ (17/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.82437 / val = 0.010
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{1}$ (18/18):
Subset 0: ($X^{1}$ -1) gives pval = 0.49291 / val = 0.031
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{1}$ has 1 link(s):
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.702
Algorithm converged for variable $X^{1}$
## Variable $X^{2}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{2}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = -0.854
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{2}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = -0.867
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{2}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = -0.879
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{2}$ (4/27):
Subset 0: () gives pval = 0.00000 / val = -0.407
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{2}$ (5/27):
Subset 0: () gives pval = 0.00000 / val = -0.427
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{2}$ (6/27):
Subset 0: () gives pval = 0.00000 / val = -0.448
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{2}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = 1.000
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{2}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = 0.998
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{2}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = 0.996
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{2}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = -0.893
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{2}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = -0.905
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{2}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = -0.916
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{2}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = -0.999
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{2}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = -0.998
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{2}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = -0.996
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{2}$ (16/27):
Subset 0: () gives pval = 0.36310 / val = -0.041
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{2}$ (17/27):
Subset 0: () gives pval = 0.35303 / val = -0.042
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{2}$ (18/27):
Subset 0: () gives pval = 0.34502 / val = -0.043
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{2}$ (19/27):
Subset 0: () gives pval = 0.23647 / val = -0.053
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{2}$ (20/27):
Subset 0: () gives pval = 0.22617 / val = -0.055
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{2}$ (21/27):
Subset 0: () gives pval = 0.20075 / val = -0.058
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{2}$ (22/27):
Subset 0: () gives pval = 0.00000 / val = 0.400
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{2}$ (23/27):
Subset 0: () gives pval = 0.00000 / val = 0.395
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{2}$ (24/27):
Subset 0: () gives pval = 0.00000 / val = 0.392
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{2}$ (25/27):
Subset 0: () gives pval = 0.18375 / val = 0.060
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{2}$ (26/27):
Subset 0: () gives pval = 0.17016 / val = 0.062
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{2}$ (27/27):
Subset 0: () gives pval = 0.14489 / val = 0.066
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{2}$ has 18 link(s):
($X^{2}$ -1): max_pval = 0.00000, min_val = 1.000
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.999
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.998
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.998
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.996
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.996
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.916
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.905
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.893
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.879
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.867
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.854
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.448
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.427
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.407
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.400
($X^{7}$ -2): max_pval = 0.00000, min_val = 0.395
($X^{7}$ -3): max_pval = 0.00000, min_val = 0.392
Testing condition sets of dimension 1:
Link ($X^{2}$ -1) -?> $X^{2}$ (1/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.741
No conditions of dimension 1 left.
Link ($X^{4}$ -1) -?> $X^{2}$ (2/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.72841 / val = -0.016
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{2}$ (3/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.928
No conditions of dimension 1 left.
Link ($X^{4}$ -2) -?> $X^{2}$ (4/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = 0.610
No conditions of dimension 1 left.
Link ($X^{2}$ -3) -?> $X^{2}$ (5/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.937
No conditions of dimension 1 left.
Link ($X^{4}$ -3) -?> $X^{2}$ (6/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = 0.810
No conditions of dimension 1 left.
Link ($X^{3}$ -3) -?> $X^{2}$ (7/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.914
No conditions of dimension 1 left.
Link ($X^{3}$ -2) -?> $X^{2}$ (8/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.941
No conditions of dimension 1 left.
Link ($X^{3}$ -1) -?> $X^{2}$ (9/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.960
No conditions of dimension 1 left.
Link ($X^{0}$ -3) -?> $X^{2}$ (10/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.851
No conditions of dimension 1 left.
Link ($X^{0}$ -2) -?> $X^{2}$ (11/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.869
No conditions of dimension 1 left.
Link ($X^{0}$ -1) -?> $X^{2}$ (12/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.881
No conditions of dimension 1 left.
Link ($X^{1}$ -3) -?> $X^{2}$ (13/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.765
No conditions of dimension 1 left.
Link ($X^{1}$ -2) -?> $X^{2}$ (14/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.727
No conditions of dimension 1 left.
Link ($X^{1}$ -1) -?> $X^{2}$ (15/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = -0.679
No conditions of dimension 1 left.
Link ($X^{7}$ -1) -?> $X^{2}$ (16/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00062 / val = -0.154
No conditions of dimension 1 left.
Link ($X^{7}$ -2) -?> $X^{2}$ (17/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00053 / val = -0.155
No conditions of dimension 1 left.
Link ($X^{7}$ -3) -?> $X^{2}$ (18/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00038 / val = -0.159
No conditions of dimension 1 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{2}$ has 17 link(s):
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.937
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.928
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.914
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.905
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.893
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.867
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.854
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.851
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.810
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.741
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.610
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.448
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.427
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.407
($X^{7}$ -3): max_pval = 0.00038, min_val = 0.159
($X^{7}$ -2): max_pval = 0.00053, min_val = 0.155
($X^{7}$ -1): max_pval = 0.00062, min_val = 0.154
Testing condition sets of dimension 2:
Link ($X^{2}$ -3) -?> $X^{2}$ (1/17):
Subset 0: ($X^{2}$ -2) ($X^{3}$ -3) gives pval = 0.00000 / val = -0.344
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{2}$ -2) -?> $X^{2}$ (2/17):
Subset 0: ($X^{2}$ -3) ($X^{3}$ -3) gives pval = 0.00000 / val = 0.619
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -3) -?> $X^{2}$ (3/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.498
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -2) -?> $X^{2}$ (4/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.703
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -1) -?> $X^{2}$ (5/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.841
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -2) -?> $X^{2}$ (6/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.450
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -1) -?> $X^{2}$ (7/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.502
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -3) -?> $X^{2}$ (8/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.377
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{4}$ -3) -?> $X^{2}$ (9/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.64621 / val = -0.021
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{2}$ (10/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = 0.862
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{4}$ -2) -?> $X^{2}$ (11/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00013 / val = -0.171
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -3) -?> $X^{2}$ (12/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.509
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{2}$ (13/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.496
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{2}$ (14/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.454
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{7}$ -3) -?> $X^{2}$ (15/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.84769 / val = 0.009
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{2}$ (16/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.78099 / val = 0.013
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{2}$ (17/17):
Subset 0: ($X^{2}$ -3) ($X^{2}$ -2) gives pval = 0.98124 / val = -0.001
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{2}$ has 13 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.841
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.741
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.703
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.619
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.502
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.498
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.450
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.448
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.427
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.407
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.377
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.344
($X^{4}$ -2): max_pval = 0.00013, min_val = 0.171
Testing condition sets of dimension 3:
Link ($X^{3}$ -1) -?> $X^{2}$ (1/13):
Subset 0: ($X^{2}$ -1) ($X^{3}$ -2) ($X^{2}$ -2) gives pval = 0.00000 / val = -0.528
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{2}$ -1) -?> $X^{2}$ (2/13):
Subset 0: ($X^{3}$ -1) ($X^{3}$ -2) ($X^{2}$ -2) gives pval = 0.00000 / val = 0.662
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{3}$ -2) -?> $X^{2}$ (3/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{2}$ -2) gives pval = 0.00000 / val = 0.207
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{2}$ -2) -?> $X^{2}$ (4/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.57973 / val = -0.025
Non-significance detected.
Link ($X^{0}$ -1) -?> $X^{2}$ (5/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.94749 / val = -0.003
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{2}$ (6/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.04690 / val = 0.090
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{2}$ (7/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.26052 / val = 0.051
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{2}$ (8/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.00094 / val = -0.149
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{2}$ (9/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.00000 / val = -0.216
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{2}$ (10/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.00000 / val = -0.216
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{0}$ -3) -?> $X^{2}$ (11/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.10329 / val = 0.074
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{2}$ (12/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.46520 / val = -0.033
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{2}$ (13/13):
Subset 0: ($X^{3}$ -1) ($X^{2}$ -1) ($X^{3}$ -2) gives pval = 0.93596 / val = -0.004
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{2}$ has 6 link(s):
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.662
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.528
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.216
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.216
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.207
($X^{1}$ -3): max_pval = 0.00094, min_val = 0.149
Testing condition sets of dimension 4:
Link ($X^{2}$ -1) -?> $X^{2}$ (1/6):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -1) ($X^{1}$ -2) ($X^{3}$ -2) gives pval = 0.00000 / val = 1.000
Still subsets of dimension 4 left, but q_max = 1 reached.
Link ($X^{3}$ -1) -?> $X^{2}$ (2/6):
Subset 0: ($X^{2}$ -1) ($X^{1}$ -1) ($X^{1}$ -2) ($X^{3}$ -2) gives pval = 0.00000 / val = -0.411
Still subsets of dimension 4 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{2}$ (3/6):
Subset 0: ($X^{2}$ -1) ($X^{3}$ -1) ($X^{1}$ -2) ($X^{3}$ -2) gives pval = 0.21703 / val = -0.056
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{2}$ (4/6):
Subset 0: ($X^{2}$ -1) ($X^{3}$ -1) ($X^{1}$ -1) ($X^{3}$ -2) gives pval = 0.22099 / val = -0.055
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{2}$ (5/6):
Subset 0: ($X^{2}$ -1) ($X^{3}$ -1) ($X^{1}$ -1) ($X^{1}$ -2) gives pval = 0.10135 / val = 0.074
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{2}$ (6/6):
Subset 0: ($X^{2}$ -1) ($X^{3}$ -1) ($X^{1}$ -1) ($X^{1}$ -2) gives pval = 0.36314 / val = 0.041
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{2}$ has 2 link(s):
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.662
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.411
Algorithm converged for variable $X^{2}$
## Variable $X^{3}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{3}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = 0.977
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{3}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = 0.976
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{3}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = 0.973
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{3}$ (4/27):
Subset 0: () gives pval = 0.00000 / val = 0.660
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{3}$ (5/27):
Subset 0: () gives pval = 0.00000 / val = 0.698
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{3}$ (6/27):
Subset 0: () gives pval = 0.00000 / val = 0.731
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{3}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = -0.867
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{3}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = -0.852
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{3}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = -0.838
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{3}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = 0.997
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{3}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = 0.992
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{3}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = 0.985
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{3}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = 0.867
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{3}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = 0.852
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{3}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = 0.838
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{3}$ (16/27):
Subset 0: () gives pval = 0.60906 / val = 0.023
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{3}$ (17/27):
Subset 0: () gives pval = 0.58229 / val = 0.025
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{3}$ (18/27):
Subset 0: () gives pval = 0.55619 / val = 0.027
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{3}$ (19/27):
Subset 0: () gives pval = 0.05614 / val = 0.086
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{3}$ (20/27):
Subset 0: () gives pval = 0.04584 / val = 0.090
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{3}$ (21/27):
Subset 0: () gives pval = 0.03463 / val = 0.095
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{3}$ (22/27):
Subset 0: () gives pval = 0.00000 / val = -0.287
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{3}$ (23/27):
Subset 0: () gives pval = 0.00000 / val = -0.283
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{3}$ (24/27):
Subset 0: () gives pval = 0.00000 / val = -0.280
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{3}$ (25/27):
Subset 0: () gives pval = 0.26265 / val = -0.050
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{3}$ (26/27):
Subset 0: () gives pval = 0.24432 / val = -0.052
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{3}$ (27/27):
Subset 0: () gives pval = 0.18291 / val = -0.060
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{3}$ has 18 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.997
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.992
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.985
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.977
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.976
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.973
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.867
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.867
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.852
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.852
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.838
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.838
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.731
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.698
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.660
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.287
($X^{7}$ -2): max_pval = 0.00000, min_val = 0.283
($X^{7}$ -3): max_pval = 0.00000, min_val = 0.280
Testing condition sets of dimension 1:
Link ($X^{3}$ -1) -?> $X^{3}$ (1/18):
Subset 0: ($X^{3}$ -2) gives pval = 0.00000 / val = 0.865
No conditions of dimension 1 left.
Link ($X^{3}$ -2) -?> $X^{3}$ (2/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = -0.497
No conditions of dimension 1 left.
Link ($X^{3}$ -3) -?> $X^{3}$ (3/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = -0.512
No conditions of dimension 1 left.
Link ($X^{0}$ -1) -?> $X^{3}$ (4/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.271
No conditions of dimension 1 left.
Link ($X^{0}$ -2) -?> $X^{3}$ (5/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.02885 / val = 0.098
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{3}$ (6/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.22552 / val = -0.055
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{3}$ (7/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.324
No conditions of dimension 1 left.
Link ($X^{4}$ -1) -?> $X^{3}$ (8/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = -0.321
No conditions of dimension 1 left.
Link ($X^{2}$ -2) -?> $X^{3}$ (9/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.324
No conditions of dimension 1 left.
Link ($X^{4}$ -2) -?> $X^{3}$ (10/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = -0.322
No conditions of dimension 1 left.
Link ($X^{2}$ -3) -?> $X^{3}$ (11/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.322
No conditions of dimension 1 left.
Link ($X^{4}$ -3) -?> $X^{3}$ (12/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = -0.319
No conditions of dimension 1 left.
Link ($X^{1}$ -3) -?> $X^{3}$ (13/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.654
No conditions of dimension 1 left.
Link ($X^{1}$ -2) -?> $X^{3}$ (14/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.708
No conditions of dimension 1 left.
Link ($X^{1}$ -1) -?> $X^{3}$ (15/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.00000 / val = 0.659
No conditions of dimension 1 left.
Link ($X^{7}$ -1) -?> $X^{3}$ (16/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.33035 / val = 0.044
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{3}$ (17/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.32084 / val = 0.045
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{3}$ (18/18):
Subset 0: ($X^{3}$ -1) gives pval = 0.35647 / val = 0.042
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{3}$ has 13 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.865
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.698
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.659
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.654
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.512
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.497
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.324
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.324
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.322
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.322
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.321
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.319
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.271
Testing condition sets of dimension 2:
Link ($X^{3}$ -1) -?> $X^{3}$ (1/13):
Subset 0: ($X^{1}$ -2) ($X^{1}$ -1) gives pval = 0.00000 / val = 0.997
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{3}$ (2/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -1) gives pval = 0.00000 / val = 0.345
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{3}$ (3/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.64261 / val = 0.021
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{3}$ (4/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.72598 / val = 0.016
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{3}$ (5/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.11704 / val = -0.071
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{3}$ (6/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.02482 / val = -0.101
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{3}$ (7/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.43627 / val = -0.035
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{3}$ (8/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.43166 / val = -0.036
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{3}$ (9/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.43284 / val = -0.035
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{3}$ (10/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.44519 / val = 0.034
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{3}$ (11/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.44618 / val = 0.034
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{3}$ (12/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.43643 / val = 0.035
Non-significance detected.
Link ($X^{0}$ -1) -?> $X^{3}$ (13/13):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) gives pval = 0.60484 / val = 0.023
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{3}$ has 2 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.865
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.345
Algorithm converged for variable $X^{3}$
## Variable $X^{4}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{4}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = 0.856
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{4}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = 0.869
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{4}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = 0.881
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{4}$ (4/27):
Subset 0: () gives pval = 0.00000 / val = 0.408
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{4}$ (5/27):
Subset 0: () gives pval = 0.00000 / val = 0.428
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{4}$ (6/27):
Subset 0: () gives pval = 0.00000 / val = 0.450
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{4}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = -0.999
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{4}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = -0.998
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{4}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = -0.996
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{4}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = 0.893
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{4}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = 0.905
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{4}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = 0.915
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{4}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = 1.000
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{4}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = 0.998
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{4}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = 0.996
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{4}$ (16/27):
Subset 0: () gives pval = 0.34746 / val = 0.042
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{4}$ (17/27):
Subset 0: () gives pval = 0.33956 / val = 0.043
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{4}$ (18/27):
Subset 0: () gives pval = 0.33630 / val = 0.043
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{4}$ (19/27):
Subset 0: () gives pval = 0.20119 / val = 0.058
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{4}$ (20/27):
Subset 0: () gives pval = 0.18668 / val = 0.060
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{4}$ (21/27):
Subset 0: () gives pval = 0.16615 / val = 0.062
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{4}$ (22/27):
Subset 0: () gives pval = 0.00000 / val = -0.412
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{4}$ (23/27):
Subset 0: () gives pval = 0.00000 / val = -0.408
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{4}$ (24/27):
Subset 0: () gives pval = 0.00000 / val = -0.405
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{4}$ (25/27):
Subset 0: () gives pval = 0.19485 / val = -0.058
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{4}$ (26/27):
Subset 0: () gives pval = 0.18521 / val = -0.060
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{4}$ (27/27):
Subset 0: () gives pval = 0.15990 / val = -0.063
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{4}$ has 18 link(s):
($X^{4}$ -1): max_pval = 0.00000, min_val = 1.000
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.999
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.998
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.998
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.996
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.996
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.915
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.905
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.893
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.881
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.869
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.856
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.450
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.428
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.412
($X^{7}$ -2): max_pval = 0.00000, min_val = 0.408
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.408
($X^{7}$ -3): max_pval = 0.00000, min_val = 0.405
Testing condition sets of dimension 1:
Link ($X^{4}$ -1) -?> $X^{4}$ (1/18):
Subset 0: ($X^{2}$ -1) gives pval = 0.00000 / val = 0.737
No conditions of dimension 1 left.
Link ($X^{2}$ -1) -?> $X^{4}$ (2/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.42104 / val = -0.036
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{4}$ (3/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = -0.926
No conditions of dimension 1 left.
Link ($X^{2}$ -2) -?> $X^{4}$ (4/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.606
No conditions of dimension 1 left.
Link ($X^{4}$ -3) -?> $X^{4}$ (5/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = -0.937
No conditions of dimension 1 left.
Link ($X^{2}$ -3) -?> $X^{4}$ (6/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.815
No conditions of dimension 1 left.
Link ($X^{3}$ -3) -?> $X^{4}$ (7/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.914
No conditions of dimension 1 left.
Link ($X^{3}$ -2) -?> $X^{4}$ (8/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.941
No conditions of dimension 1 left.
Link ($X^{3}$ -1) -?> $X^{4}$ (9/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.960
No conditions of dimension 1 left.
Link ($X^{0}$ -3) -?> $X^{4}$ (10/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.865
No conditions of dimension 1 left.
Link ($X^{0}$ -2) -?> $X^{4}$ (11/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.881
No conditions of dimension 1 left.
Link ($X^{0}$ -1) -?> $X^{4}$ (12/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.891
No conditions of dimension 1 left.
Link ($X^{1}$ -3) -?> $X^{4}$ (13/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.776
No conditions of dimension 1 left.
Link ($X^{1}$ -2) -?> $X^{4}$ (14/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.733
No conditions of dimension 1 left.
Link ($X^{7}$ -1) -?> $X^{4}$ (15/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00050 / val = 0.156
No conditions of dimension 1 left.
Link ($X^{7}$ -2) -?> $X^{4}$ (16/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00044 / val = 0.158
No conditions of dimension 1 left.
Link ($X^{1}$ -1) -?> $X^{4}$ (17/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00000 / val = 0.684
No conditions of dimension 1 left.
Link ($X^{7}$ -3) -?> $X^{4}$ (18/18):
Subset 0: ($X^{4}$ -1) gives pval = 0.00047 / val = 0.157
No conditions of dimension 1 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{4}$ has 17 link(s):
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.937
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.926
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.914
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.905
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.893
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.869
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.865
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.856
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.815
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.737
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.606
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.450
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.428
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.408
($X^{7}$ -2): max_pval = 0.00044, min_val = 0.158
($X^{7}$ -3): max_pval = 0.00047, min_val = 0.157
($X^{7}$ -1): max_pval = 0.00050, min_val = 0.156
Testing condition sets of dimension 2:
Link ($X^{4}$ -3) -?> $X^{4}$ (1/17):
Subset 0: ($X^{4}$ -2) ($X^{3}$ -3) gives pval = 0.00000 / val = -0.336
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{4}$ -2) -?> $X^{4}$ (2/17):
Subset 0: ($X^{4}$ -3) ($X^{3}$ -3) gives pval = 0.00000 / val = 0.613
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -3) -?> $X^{4}$ (3/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.501
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -2) -?> $X^{4}$ (4/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.710
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -1) -?> $X^{4}$ (5/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.852
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -2) -?> $X^{4}$ (6/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.480
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -3) -?> $X^{4}$ (7/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.409
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{0}$ -1) -?> $X^{4}$ (8/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.522
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{2}$ -3) -?> $X^{4}$ (9/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.55941 / val = 0.026
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{4}$ (10/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.861
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{2}$ -2) -?> $X^{4}$ (11/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00674 / val = -0.122
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -3) -?> $X^{4}$ (12/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.529
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{4}$ (13/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.490
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{1}$ -1) -?> $X^{4}$ (14/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.436
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{7}$ -2) -?> $X^{4}$ (15/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.92613 / val = 0.004
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{4}$ (16/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.75665 / val = -0.014
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{4}$ (17/17):
Subset 0: ($X^{4}$ -3) ($X^{4}$ -2) gives pval = 0.90831 / val = 0.005
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{4}$ has 13 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.852
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.737
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.710
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.613
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.522
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.501
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.480
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.450
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.428
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.409
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.408
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.336
($X^{2}$ -2): max_pval = 0.00674, min_val = 0.122
Testing condition sets of dimension 3:
Link ($X^{3}$ -1) -?> $X^{4}$ (1/13):
Subset 0: ($X^{4}$ -1) ($X^{3}$ -2) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.542
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{4}$ -1) -?> $X^{4}$ (2/13):
Subset 0: ($X^{3}$ -1) ($X^{3}$ -2) ($X^{4}$ -2) gives pval = 0.00000 / val = 0.637
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{3}$ -2) -?> $X^{4}$ (3/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{4}$ -2) gives pval = 0.00000 / val = -0.215
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{4}$ -2) -?> $X^{4}$ (4/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.60164 / val = 0.024
Non-significance detected.
Link ($X^{0}$ -1) -?> $X^{4}$ (5/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.01294 / val = 0.112
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{4}$ (6/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.04191 / val = -0.092
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{4}$ (7/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.13304 / val = 0.068
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{4}$ (8/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.00000 / val = 0.229
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{4}$ (9/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.00000 / val = 0.264
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{0}$ -3) -?> $X^{4}$ (10/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.23015 / val = 0.054
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{4}$ (11/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.00000 / val = 0.252
Still subsets of dimension 3 left, but q_max = 1 reached.
Link ($X^{4}$ -3) -?> $X^{4}$ (12/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.78604 / val = 0.012
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{4}$ (13/13):
Subset 0: ($X^{3}$ -1) ($X^{4}$ -1) ($X^{3}$ -2) gives pval = 0.67180 / val = 0.019
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{4}$ has 6 link(s):
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.637
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.542
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.264
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.252
($X^{1}$ -3): max_pval = 0.00000, min_val = 0.229
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.215
Testing condition sets of dimension 4:
Link ($X^{4}$ -1) -?> $X^{4}$ (1/6):
Subset 0: ($X^{3}$ -1) ($X^{1}$ -2) ($X^{1}$ -1) ($X^{1}$ -3) gives pval = 0.00000 / val = 1.000
Still subsets of dimension 4 left, but q_max = 1 reached.
Link ($X^{3}$ -1) -?> $X^{4}$ (2/6):
Subset 0: ($X^{4}$ -1) ($X^{1}$ -2) ($X^{1}$ -1) ($X^{1}$ -3) gives pval = 0.00000 / val = 0.908
Still subsets of dimension 4 left, but q_max = 1 reached.
Link ($X^{1}$ -2) -?> $X^{4}$ (3/6):
Subset 0: ($X^{4}$ -1) ($X^{3}$ -1) ($X^{1}$ -1) ($X^{1}$ -3) gives pval = 0.12058 / val = 0.070
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{4}$ (4/6):
Subset 0: ($X^{4}$ -1) ($X^{3}$ -1) ($X^{1}$ -2) ($X^{1}$ -3) gives pval = 0.39172 / val = 0.039
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{4}$ (5/6):
Subset 0: ($X^{4}$ -1) ($X^{3}$ -1) ($X^{1}$ -2) ($X^{1}$ -1) gives pval = 0.55067 / val = 0.027
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{4}$ (6/6):
Subset 0: ($X^{4}$ -1) ($X^{3}$ -1) ($X^{1}$ -2) ($X^{1}$ -1) gives pval = 0.23099 / val = -0.054
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{4}$ has 2 link(s):
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.637
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.542
Algorithm converged for variable $X^{4}$
## Variable $X^{5}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{5}$ (1/27):
Subset 0: () gives pval = 0.74380 / val = 0.015
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{5}$ (2/27):
Subset 0: () gives pval = 0.72045 / val = 0.016
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{5}$ (3/27):
Subset 0: () gives pval = 0.67021 / val = 0.019
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{5}$ (4/27):
Subset 0: () gives pval = 0.88741 / val = 0.006
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{5}$ (5/27):
Subset 0: () gives pval = 0.82116 / val = 0.010
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{5}$ (6/27):
Subset 0: () gives pval = 0.61026 / val = 0.023
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{5}$ (7/27):
Subset 0: () gives pval = 0.33111 / val = -0.044
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{5}$ (8/27):
Subset 0: () gives pval = 0.32365 / val = -0.044
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{5}$ (9/27):
Subset 0: () gives pval = 0.31390 / val = -0.045
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{5}$ (10/27):
Subset 0: () gives pval = 0.50349 / val = 0.030
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{5}$ (11/27):
Subset 0: () gives pval = 0.51049 / val = 0.030
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{5}$ (12/27):
Subset 0: () gives pval = 0.59454 / val = 0.024
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{5}$ (13/27):
Subset 0: () gives pval = 0.31129 / val = 0.046
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{5}$ (14/27):
Subset 0: () gives pval = 0.30728 / val = 0.046
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{5}$ (15/27):
Subset 0: () gives pval = 0.29857 / val = 0.047
Non-significance detected.
Link ($X^{5}$ -1) -?> $X^{5}$ (16/27):
Subset 0: () gives pval = 0.00000 / val = 0.416
No conditions of dimension 0 left.
Link ($X^{5}$ -2) -?> $X^{5}$ (17/27):
Subset 0: () gives pval = 0.05232 / val = 0.087
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{5}$ (18/27):
Subset 0: () gives pval = 0.70821 / val = -0.017
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{5}$ (19/27):
Subset 0: () gives pval = 0.00000 / val = 0.283
No conditions of dimension 0 left.
Link ($X^{6}$ -2) -?> $X^{5}$ (20/27):
Subset 0: () gives pval = 0.00000 / val = 0.208
No conditions of dimension 0 left.
Link ($X^{6}$ -3) -?> $X^{5}$ (21/27):
Subset 0: () gives pval = 0.01627 / val = 0.108
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{5}$ (22/27):
Subset 0: () gives pval = 0.11534 / val = -0.071
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{5}$ (23/27):
Subset 0: () gives pval = 0.21199 / val = -0.056
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{5}$ (24/27):
Subset 0: () gives pval = 0.19469 / val = -0.058
Non-significance detected.
Link ($X^{8}$ -1) -?> $X^{5}$ (25/27):
Subset 0: () gives pval = 0.50817 / val = -0.030
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{5}$ (26/27):
Subset 0: () gives pval = 0.82302 / val = 0.010
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{5}$ (27/27):
Subset 0: () gives pval = 0.36814 / val = 0.041
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{5}$ has 3 link(s):
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.416
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.283
($X^{6}$ -2): max_pval = 0.00000, min_val = 0.208
Testing condition sets of dimension 1:
Link ($X^{5}$ -1) -?> $X^{5}$ (1/3):
Subset 0: ($X^{6}$ -1) gives pval = 0.00000 / val = 0.383
No conditions of dimension 1 left.
Link ($X^{6}$ -1) -?> $X^{5}$ (2/3):
Subset 0: ($X^{5}$ -1) gives pval = 0.00000 / val = 0.224
No conditions of dimension 1 left.
Link ($X^{6}$ -2) -?> $X^{5}$ (3/3):
Subset 0: ($X^{5}$ -1) gives pval = 0.02180 / val = 0.103
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{5}$ has 2 link(s):
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.383
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.224
Algorithm converged for variable $X^{5}$
## Variable $X^{6}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{6}$ (1/27):
Subset 0: () gives pval = 0.03189 / val = 0.097
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{6}$ (2/27):
Subset 0: () gives pval = 0.03543 / val = 0.095
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{6}$ (3/27):
Subset 0: () gives pval = 0.04794 / val = 0.089
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{6}$ (4/27):
Subset 0: () gives pval = 0.01699 / val = 0.107
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{6}$ (5/27):
Subset 0: () gives pval = 0.01816 / val = 0.106
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{6}$ (6/27):
Subset 0: () gives pval = 0.00643 / val = 0.122
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{6}$ (7/27):
Subset 0: () gives pval = 0.26750 / val = -0.050
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{6}$ (8/27):
Subset 0: () gives pval = 0.28480 / val = -0.048
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{6}$ (9/27):
Subset 0: () gives pval = 0.30125 / val = -0.047
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{6}$ (10/27):
Subset 0: () gives pval = 0.10377 / val = 0.073
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{6}$ (11/27):
Subset 0: () gives pval = 0.17521 / val = 0.061
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{6}$ (12/27):
Subset 0: () gives pval = 0.24251 / val = 0.053
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{6}$ (13/27):
Subset 0: () gives pval = 0.23355 / val = 0.054
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{6}$ (14/27):
Subset 0: () gives pval = 0.25198 / val = 0.052
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{6}$ (15/27):
Subset 0: () gives pval = 0.26405 / val = 0.050
Non-significance detected.
Link ($X^{5}$ -1) -?> $X^{6}$ (16/27):
Subset 0: () gives pval = 0.00000 / val = -0.278
No conditions of dimension 0 left.
Link ($X^{5}$ -2) -?> $X^{6}$ (17/27):
Subset 0: () gives pval = 0.00000 / val = -0.295
No conditions of dimension 0 left.
Link ($X^{5}$ -3) -?> $X^{6}$ (18/27):
Subset 0: () gives pval = 0.00035 / val = -0.160
No conditions of dimension 0 left.
Link ($X^{6}$ -1) -?> $X^{6}$ (19/27):
Subset 0: () gives pval = 0.00000 / val = 0.454
No conditions of dimension 0 left.
Link ($X^{6}$ -2) -?> $X^{6}$ (20/27):
Subset 0: () gives pval = 0.00105 / val = 0.147
No conditions of dimension 0 left.
Link ($X^{6}$ -3) -?> $X^{6}$ (21/27):
Subset 0: () gives pval = 0.54157 / val = 0.028
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{6}$ (22/27):
Subset 0: () gives pval = 0.14362 / val = -0.066
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{6}$ (23/27):
Subset 0: () gives pval = 0.24131 / val = -0.053
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{6}$ (24/27):
Subset 0: () gives pval = 0.29751 / val = -0.047
Non-significance detected.
Link ($X^{8}$ -1) -?> $X^{6}$ (25/27):
Subset 0: () gives pval = 0.27585 / val = 0.049
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{6}$ (26/27):
Subset 0: () gives pval = 0.10906 / val = 0.072
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{6}$ (27/27):
Subset 0: () gives pval = 0.43574 / val = 0.035
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{6}$ has 6 link(s):
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.454
($X^{5}$ -2): max_pval = 0.00000, min_val = 0.295
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.278
($X^{5}$ -3): max_pval = 0.00035, min_val = 0.160
($X^{6}$ -2): max_pval = 0.00105, min_val = 0.147
($X^{1}$ -3): max_pval = 0.00643, min_val = 0.122
Testing condition sets of dimension 1:
Link ($X^{6}$ -1) -?> $X^{6}$ (1/6):
Subset 0: ($X^{5}$ -2) gives pval = 0.00000 / val = 0.405
No conditions of dimension 1 left.
Link ($X^{5}$ -2) -?> $X^{6}$ (2/6):
Subset 0: ($X^{6}$ -1) gives pval = 0.00001 / val = -0.197
No conditions of dimension 1 left.
Link ($X^{5}$ -1) -?> $X^{6}$ (3/6):
Subset 0: ($X^{6}$ -1) gives pval = 0.00000 / val = -0.423
No conditions of dimension 1 left.
Link ($X^{5}$ -3) -?> $X^{6}$ (4/6):
Subset 0: ($X^{6}$ -1) gives pval = 0.50427 / val = -0.030
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{6}$ (5/6):
Subset 0: ($X^{6}$ -1) gives pval = 0.09760 / val = -0.075
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{6}$ (6/6):
Subset 0: ($X^{6}$ -1) gives pval = 0.05740 / val = 0.086
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{6}$ has 3 link(s):
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.405
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.278
($X^{5}$ -2): max_pval = 0.00001, min_val = 0.197
Testing condition sets of dimension 2:
Link ($X^{6}$ -1) -?> $X^{6}$ (1/3):
Subset 0: ($X^{5}$ -1) ($X^{5}$ -2) gives pval = 0.00000 / val = 0.513
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{5}$ -1) -?> $X^{6}$ (2/3):
Subset 0: ($X^{6}$ -1) ($X^{5}$ -2) gives pval = 0.00000 / val = -0.383
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{5}$ -2) -?> $X^{6}$ (3/3):
Subset 0: ($X^{6}$ -1) ($X^{5}$ -1) gives pval = 0.66754 / val = 0.019
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{6}$ has 2 link(s):
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.405
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.278
Algorithm converged for variable $X^{6}$
## Variable $X^{7}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{7}$ (1/27):
Subset 0: () gives pval = 0.00000 / val = -0.379
No conditions of dimension 0 left.
Link ($X^{0}$ -2) -?> $X^{7}$ (2/27):
Subset 0: () gives pval = 0.00000 / val = -0.384
No conditions of dimension 0 left.
Link ($X^{0}$ -3) -?> $X^{7}$ (3/27):
Subset 0: () gives pval = 0.00000 / val = -0.388
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{7}$ (4/27):
Subset 0: () gives pval = 0.00060 / val = -0.154
No conditions of dimension 0 left.
Link ($X^{1}$ -2) -?> $X^{7}$ (5/27):
Subset 0: () gives pval = 0.00042 / val = -0.158
No conditions of dimension 0 left.
Link ($X^{1}$ -3) -?> $X^{7}$ (6/27):
Subset 0: () gives pval = 0.00024 / val = -0.164
No conditions of dimension 0 left.
Link ($X^{2}$ -1) -?> $X^{7}$ (7/27):
Subset 0: () gives pval = 0.00000 / val = 0.408
No conditions of dimension 0 left.
Link ($X^{2}$ -2) -?> $X^{7}$ (8/27):
Subset 0: () gives pval = 0.00000 / val = 0.412
No conditions of dimension 0 left.
Link ($X^{2}$ -3) -?> $X^{7}$ (9/27):
Subset 0: () gives pval = 0.00000 / val = 0.416
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{7}$ (10/27):
Subset 0: () gives pval = 0.00000 / val = -0.297
No conditions of dimension 0 left.
Link ($X^{3}$ -2) -?> $X^{7}$ (11/27):
Subset 0: () gives pval = 0.00000 / val = -0.301
No conditions of dimension 0 left.
Link ($X^{3}$ -3) -?> $X^{7}$ (12/27):
Subset 0: () gives pval = 0.00000 / val = -0.307
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{7}$ (13/27):
Subset 0: () gives pval = 0.00000 / val = -0.421
No conditions of dimension 0 left.
Link ($X^{4}$ -2) -?> $X^{7}$ (14/27):
Subset 0: () gives pval = 0.00000 / val = -0.425
No conditions of dimension 0 left.
Link ($X^{4}$ -3) -?> $X^{7}$ (15/27):
Subset 0: () gives pval = 0.00000 / val = -0.428
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{7}$ (16/27):
Subset 0: () gives pval = 0.04273 / val = -0.091
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{7}$ (17/27):
Subset 0: () gives pval = 0.04554 / val = -0.090
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{7}$ (18/27):
Subset 0: () gives pval = 0.05366 / val = -0.087
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{7}$ (19/27):
Subset 0: () gives pval = 0.05250 / val = -0.087
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{7}$ (20/27):
Subset 0: () gives pval = 0.02394 / val = -0.102
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{7}$ (21/27):
Subset 0: () gives pval = 0.02013 / val = -0.105
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{7}$ (22/27):
Subset 0: () gives pval = 0.00000 / val = 0.939
No conditions of dimension 0 left.
Link ($X^{7}$ -2) -?> $X^{7}$ (23/27):
Subset 0: () gives pval = 0.00000 / val = 0.887
No conditions of dimension 0 left.
Link ($X^{7}$ -3) -?> $X^{7}$ (24/27):
Subset 0: () gives pval = 0.00000 / val = 0.838
No conditions of dimension 0 left.
Link ($X^{8}$ -1) -?> $X^{7}$ (25/27):
Subset 0: () gives pval = 0.01379 / val = -0.111
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{7}$ (26/27):
Subset 0: () gives pval = 0.02306 / val = -0.102
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{7}$ (27/27):
Subset 0: () gives pval = 0.00844 / val = -0.118
No conditions of dimension 0 left.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{7}$ has 19 link(s):
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.939
($X^{7}$ -2): max_pval = 0.00000, min_val = 0.887
($X^{7}$ -3): max_pval = 0.00000, min_val = 0.838
($X^{4}$ -3): max_pval = 0.00000, min_val = 0.428
($X^{4}$ -2): max_pval = 0.00000, min_val = 0.425
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.421
($X^{2}$ -3): max_pval = 0.00000, min_val = 0.416
($X^{2}$ -2): max_pval = 0.00000, min_val = 0.412
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.408
($X^{0}$ -3): max_pval = 0.00000, min_val = 0.388
($X^{0}$ -2): max_pval = 0.00000, min_val = 0.384
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.379
($X^{3}$ -3): max_pval = 0.00000, min_val = 0.307
($X^{3}$ -2): max_pval = 0.00000, min_val = 0.301
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.297
($X^{1}$ -3): max_pval = 0.00024, min_val = 0.164
($X^{1}$ -2): max_pval = 0.00042, min_val = 0.158
($X^{1}$ -1): max_pval = 0.00060, min_val = 0.154
($X^{8}$ -3): max_pval = 0.00844, min_val = 0.118
Testing condition sets of dimension 1:
Link ($X^{7}$ -1) -?> $X^{7}$ (1/19):
Subset 0: ($X^{7}$ -2) gives pval = 0.00000 / val = 0.668
No conditions of dimension 1 left.
Link ($X^{7}$ -2) -?> $X^{7}$ (2/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.30497 / val = 0.046
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{7}$ (3/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.44596 / val = 0.034
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{7}$ (4/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.03570 / val = -0.095
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{7}$ (5/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.03696 / val = -0.094
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{7}$ (6/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.03796 / val = -0.093
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{7}$ (7/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.03941 / val = 0.093
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{7}$ (8/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.04207 / val = 0.092
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{7}$ (9/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.04291 / val = 0.091
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{7}$ (10/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.04776 / val = -0.089
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{7}$ (11/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.04476 / val = -0.090
Non-significance detected.
Link ($X^{0}$ -1) -?> $X^{7}$ (12/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.05812 / val = -0.085
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{7}$ (13/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.09367 / val = -0.076
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{7}$ (14/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.11701 / val = -0.071
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{7}$ (15/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.11666 / val = -0.071
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{7}$ (16/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.30749 / val = -0.046
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{7}$ (17/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.35285 / val = -0.042
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{7}$ (18/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.35919 / val = -0.041
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{7}$ (19/19):
Subset 0: ($X^{7}$ -1) gives pval = 0.18921 / val = -0.059
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{7}$ has 1 link(s):
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.668
Algorithm converged for variable $X^{7}$
## Variable $X^{8}$
Iterating through pc_alpha = [0.01]:
# pc_alpha = 0.01 (1/1):
Testing condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{8}$ (1/27):
Subset 0: () gives pval = 0.37290 / val = -0.040
Non-significance detected.
Link ($X^{0}$ -2) -?> $X^{8}$ (2/27):
Subset 0: () gives pval = 0.38421 / val = -0.039
Non-significance detected.
Link ($X^{0}$ -3) -?> $X^{8}$ (3/27):
Subset 0: () gives pval = 0.37278 / val = -0.040
Non-significance detected.
Link ($X^{1}$ -1) -?> $X^{8}$ (4/27):
Subset 0: () gives pval = 0.95511 / val = 0.003
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{8}$ (5/27):
Subset 0: () gives pval = 0.89218 / val = -0.006
Non-significance detected.
Link ($X^{1}$ -3) -?> $X^{8}$ (6/27):
Subset 0: () gives pval = 0.66042 / val = -0.020
Non-significance detected.
Link ($X^{2}$ -1) -?> $X^{8}$ (7/27):
Subset 0: () gives pval = 0.17912 / val = 0.061
Non-significance detected.
Link ($X^{2}$ -2) -?> $X^{8}$ (8/27):
Subset 0: () gives pval = 0.18026 / val = 0.060
Non-significance detected.
Link ($X^{2}$ -3) -?> $X^{8}$ (9/27):
Subset 0: () gives pval = 0.18481 / val = 0.060
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{8}$ (10/27):
Subset 0: () gives pval = 0.18260 / val = -0.060
Non-significance detected.
Link ($X^{3}$ -2) -?> $X^{8}$ (11/27):
Subset 0: () gives pval = 0.19184 / val = -0.059
Non-significance detected.
Link ($X^{3}$ -3) -?> $X^{8}$ (12/27):
Subset 0: () gives pval = 0.18215 / val = -0.060
Non-significance detected.
Link ($X^{4}$ -1) -?> $X^{8}$ (13/27):
Subset 0: () gives pval = 0.18419 / val = -0.060
Non-significance detected.
Link ($X^{4}$ -2) -?> $X^{8}$ (14/27):
Subset 0: () gives pval = 0.18413 / val = -0.060
Non-significance detected.
Link ($X^{4}$ -3) -?> $X^{8}$ (15/27):
Subset 0: () gives pval = 0.18831 / val = -0.059
Non-significance detected.
Link ($X^{5}$ -1) -?> $X^{8}$ (16/27):
Subset 0: () gives pval = 0.72763 / val = 0.016
Non-significance detected.
Link ($X^{5}$ -2) -?> $X^{8}$ (17/27):
Subset 0: () gives pval = 0.74336 / val = 0.015
Non-significance detected.
Link ($X^{5}$ -3) -?> $X^{8}$ (18/27):
Subset 0: () gives pval = 0.81871 / val = -0.010
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{8}$ (19/27):
Subset 0: () gives pval = 0.24371 / val = 0.053
Non-significance detected.
Link ($X^{6}$ -2) -?> $X^{8}$ (20/27):
Subset 0: () gives pval = 0.77071 / val = 0.013
Non-significance detected.
Link ($X^{6}$ -3) -?> $X^{8}$ (21/27):
Subset 0: () gives pval = 0.65536 / val = 0.020
Non-significance detected.
Link ($X^{7}$ -1) -?> $X^{8}$ (22/27):
Subset 0: () gives pval = 0.74986 / val = -0.014
Non-significance detected.
Link ($X^{7}$ -2) -?> $X^{8}$ (23/27):
Subset 0: () gives pval = 0.81212 / val = -0.011
Non-significance detected.
Link ($X^{7}$ -3) -?> $X^{8}$ (24/27):
Subset 0: () gives pval = 0.91442 / val = -0.005
Non-significance detected.
Link ($X^{8}$ -1) -?> $X^{8}$ (25/27):
Subset 0: () gives pval = 0.56284 / val = 0.026
Non-significance detected.
Link ($X^{8}$ -2) -?> $X^{8}$ (26/27):
Subset 0: () gives pval = 0.97721 / val = 0.001
Non-significance detected.
Link ($X^{8}$ -3) -?> $X^{8}$ (27/27):
Subset 0: () gives pval = 0.22643 / val = -0.055
Non-significance detected.
Sorting parents in decreasing order with
weight(i-tau->j) = min_{iterations} |val_{ij}(tau)|
Updating parents:
Variable $X^{8}$ has 0 link(s):
Algorithm converged for variable $X^{8}$
## Resulting lagged parent (super)sets:
Variable $X^{0}$ has 2 link(s):
($X^{0}$ -1): max_pval = 0.00000, min_val = 0.846
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.366
Variable $X^{1}$ has 1 link(s):
($X^{1}$ -1): max_pval = 0.00000, min_val = 0.702
Variable $X^{2}$ has 2 link(s):
($X^{2}$ -1): max_pval = 0.00000, min_val = 0.662
($X^{3}$ -1): max_pval = 0.00000, min_val = -0.411
Variable $X^{3}$ has 2 link(s):
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.865
($X^{1}$ -2): max_pval = 0.00000, min_val = 0.345
Variable $X^{4}$ has 2 link(s):
($X^{4}$ -1): max_pval = 0.00000, min_val = 0.637
($X^{3}$ -1): max_pval = 0.00000, min_val = 0.542
Variable $X^{5}$ has 2 link(s):
($X^{5}$ -1): max_pval = 0.00000, min_val = 0.383
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.224
Variable $X^{6}$ has 2 link(s):
($X^{6}$ -1): max_pval = 0.00000, min_val = 0.405
($X^{5}$ -1): max_pval = 0.00000, min_val = -0.278
Variable $X^{7}$ has 1 link(s):
($X^{7}$ -1): max_pval = 0.00000, min_val = 0.668
Variable $X^{8}$ has 0 link(s):
##
## Step 2: PC algorithm with contemp. conditions and MCI tests
##
Parameters:
independence test = par_corr
tau_min = 0
tau_max = 3
pc_alpha = 0.01
contemp_collider_rule = majority
conflict_resolution = True
reset_lagged_links = False
max_conds_dim = None
max_conds_py = None
max_conds_px = None
max_conds_px_lagged = None
fdr_method = none
--------------------------
Skeleton discovery phase
--------------------------
Testing contemporaneous condition sets of dimension 0:
Link ($X^{0}$ -1) -?> $X^{0}$ (1/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{1}$ -1) ]
with conds_x = [ ($X^{0}$ -2) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.682
No conditions of dimension 0 left.
Link ($X^{0}$ 0) o?o $X^{1}$ (2/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{1}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.58230 / val = -0.025
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{2}$ (3/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.35848 / val = 0.042
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{3}$ (4/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.65989 / val = -0.020
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{4}$ (5/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.16523 / val = -0.063
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{5}$ (6/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.42604 / val = 0.036
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{6}$ (7/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.20779 / val = 0.057
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{7}$ (8/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.57550 / val = 0.025
Non-significance detected.
Link ($X^{0}$ 0) o?o $X^{8}$ (9/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{0}$ -1) ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.26252 / val = -0.051
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{0}$ (10/86):
Already removed.
Link ($X^{1}$ -1) -?> $X^{0}$ (11/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{0}$ -1) ]
with conds_x = [ ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.366
No conditions of dimension 0 left.
Link ($X^{1}$ -1) -?> $X^{1}$ (12/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.702
No conditions of dimension 0 left.
Link ($X^{1}$ 0) o?o $X^{2}$ (13/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.38736 / val = 0.039
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{3}$ (14/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.03807 / val = -0.094
Non-significance detected.
Link ($X^{1}$ -2) -?> $X^{3}$ (15/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = 0.360
No conditions of dimension 0 left.
Link ($X^{1}$ 0) o?o $X^{4}$ (16/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.83948 / val = 0.009
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{5}$ (17/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.61402 / val = -0.023
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{6}$ (18/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.34689 / val = 0.043
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{7}$ (19/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.55754 / val = -0.027
Non-significance detected.
Link ($X^{1}$ 0) o?o $X^{8}$ (20/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{1}$ -1) ]
Subset 0: () gives pval = 0.15053 / val = -0.065
Non-significance detected.
Link ($X^{2}$ 0) o?o $X^{0}$ (21/86):
Already removed.
Link ($X^{2}$ 0) o?o $X^{1}$ (22/86):
Already removed.
Link ($X^{2}$ -1) -?> $X^{2}$ (23/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{2}$ -2) ($X^{3}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.662
No conditions of dimension 0 left.
Link ($X^{2}$ 0) o?o $X^{3}$ (24/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.382
No conditions of dimension 0 left.
Link ($X^{2}$ 0) o?o $X^{4}$ (25/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.243
No conditions of dimension 0 left.
Link ($X^{2}$ 0) o?o $X^{5}$ (26/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.66846 / val = 0.019
Non-significance detected.
Link ($X^{2}$ 0) o?o $X^{6}$ (27/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.06850 / val = -0.082
Non-significance detected.
Link ($X^{2}$ 0) o?o $X^{7}$ (28/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.54563 / val = -0.027
Non-significance detected.
Link ($X^{2}$ 0) o?o $X^{8}$ (29/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.66989 / val = 0.019
Non-significance detected.
Link ($X^{3}$ 0) o?o $X^{0}$ (30/86):
Already removed.
Link ($X^{3}$ 0) o?o $X^{1}$ (31/86):
Already removed.
Link ($X^{3}$ 0) o?o $X^{2}$ (32/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = -0.382
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{2}$ (33/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = -0.402
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{3}$ (34/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{1}$ -2) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = 0.727
No conditions of dimension 0 left.
Link ($X^{3}$ 0) o?o $X^{4}$ (35/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.375
No conditions of dimension 0 left.
Link ($X^{3}$ -1) -?> $X^{4}$ (36/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = 0.369
No conditions of dimension 0 left.
Link ($X^{3}$ 0) o?o $X^{5}$ (37/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.73680 / val = -0.015
Non-significance detected.
Link ($X^{3}$ 0) o?o $X^{6}$ (38/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.01284 / val = 0.112
Non-significance detected.
Link ($X^{3}$ 0) o?o $X^{7}$ (39/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.10808 / val = 0.073
Non-significance detected.
Link ($X^{3}$ 0) o?o $X^{8}$ (40/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: () gives pval = 0.36038 / val = -0.041
Non-significance detected.
Link ($X^{4}$ 0) o?o $X^{0}$ (41/86):
Already removed.
Link ($X^{4}$ 0) o?o $X^{1}$ (42/86):
Already removed.
Link ($X^{4}$ 0) o?o $X^{2}$ (43/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.243
No conditions of dimension 0 left.
Link ($X^{4}$ 0) o?o $X^{3}$ (44/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = 0.375
No conditions of dimension 0 left.
Link ($X^{4}$ -1) -?> $X^{4}$ (45/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{4}$ -2) ($X^{3}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.637
No conditions of dimension 0 left.
Link ($X^{4}$ 0) o?o $X^{5}$ (46/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.80091 / val = -0.011
Non-significance detected.
Link ($X^{4}$ 0) o?o $X^{6}$ (47/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.41566 / val = 0.037
Non-significance detected.
Link ($X^{4}$ 0) o?o $X^{7}$ (48/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.36068 / val = -0.041
Non-significance detected.
Link ($X^{4}$ 0) o?o $X^{8}$ (49/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.68371 / val = 0.018
Non-significance detected.
Link ($X^{5}$ 0) o?o $X^{0}$ (50/86):
Already removed.
Link ($X^{5}$ 0) o?o $X^{1}$ (51/86):
Already removed.
Link ($X^{5}$ 0) o?o $X^{2}$ (52/86):
Already removed.
Link ($X^{5}$ 0) o?o $X^{3}$ (53/86):
Already removed.
Link ($X^{5}$ 0) o?o $X^{4}$ (54/86):
Already removed.
Link ($X^{5}$ -1) -?> $X^{5}$ (55/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ]
with conds_x = [ ($X^{5}$ -2) ($X^{6}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.343
No conditions of dimension 0 left.
Link ($X^{5}$ 0) o?o $X^{6}$ (56/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
with conds_x = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = 0.292
No conditions of dimension 0 left.
Link ($X^{5}$ -1) -?> $X^{6}$ (57/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ]
with conds_x = [ ($X^{5}$ -2) ($X^{6}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = -0.383
No conditions of dimension 0 left.
Link ($X^{5}$ 0) o?o $X^{7}$ (58/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
Subset 0: () gives pval = 0.93945 / val = 0.003
Non-significance detected.
Link ($X^{5}$ 0) o?o $X^{8}$ (59/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
Subset 0: () gives pval = 0.63977 / val = -0.021
Non-significance detected.
Link ($X^{6}$ 0) o?o $X^{0}$ (60/86):
Already removed.
Link ($X^{6}$ 0) o?o $X^{1}$ (61/86):
Already removed.
Link ($X^{6}$ 0) o?o $X^{2}$ (62/86):
Already removed.
Link ($X^{6}$ 0) o?o $X^{3}$ (63/86):
Already removed.
Link ($X^{6}$ 0) o?o $X^{4}$ (64/86):
Already removed.
Link ($X^{6}$ 0) o?o $X^{5}$ (65/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ($X^{6}$ -1) ]
with conds_x = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = 0.292
No conditions of dimension 0 left.
Link ($X^{6}$ -1) -?> $X^{5}$ (66/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ]
with conds_x = [ ($X^{6}$ -2) ($X^{5}$ -2) ]
Subset 0: () gives pval = 0.00022 / val = 0.166
No conditions of dimension 0 left.
Link ($X^{6}$ -1) -?> $X^{6}$ (67/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ]
with conds_x = [ ($X^{6}$ -2) ($X^{5}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.452
No conditions of dimension 0 left.
Link ($X^{6}$ 0) o?o $X^{7}$ (68/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
Subset 0: () gives pval = 0.64517 / val = 0.021
Non-significance detected.
Link ($X^{6}$ 0) o?o $X^{8}$ (69/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{6}$ -1) ($X^{5}$ -1) ]
Subset 0: () gives pval = 0.18018 / val = -0.061
Non-significance detected.
Link ($X^{7}$ 0) o?o $X^{0}$ (70/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{1}$ (71/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{2}$ (72/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{3}$ (73/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{4}$ (74/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{5}$ (75/86):
Already removed.
Link ($X^{7}$ 0) o?o $X^{6}$ (76/86):
Already removed.
Link ($X^{7}$ -1) -?> $X^{7}$ (77/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{7}$ -2) ]
Subset 0: () gives pval = 0.00000 / val = 0.668
No conditions of dimension 0 left.
Link ($X^{7}$ 0) o?o $X^{8}$ (78/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{7}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.342
No conditions of dimension 0 left.
Link ($X^{8}$ 0) o?o $X^{0}$ (79/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{1}$ (80/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{2}$ (81/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{3}$ (82/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{4}$ (83/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{5}$ (84/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{6}$ (85/86):
Already removed.
Link ($X^{8}$ 0) o?o $X^{7}$ (86/86):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{7}$ -1) ]
with conds_x = [ ]
Subset 0: () gives pval = 0.00000 / val = -0.342
No conditions of dimension 0 left.
Updated contemp. adjacencies:
Variable $X^{0}$ has 0 link(s):
Variable $X^{1}$ has 0 link(s):
Variable $X^{2}$ has 2 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.382
($X^{4}$ 0): max_pval = 0.00000, min_val = 0.243
Variable $X^{3}$ has 2 link(s):
($X^{2}$ 0): max_pval = 0.00000, min_val = 0.382
($X^{4}$ 0): max_pval = 0.00000, min_val = 0.375
Variable $X^{4}$ has 2 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.375
($X^{2}$ 0): max_pval = 0.00000, min_val = 0.243
Variable $X^{5}$ has 1 link(s):
($X^{6}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{6}$ has 1 link(s):
($X^{5}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{7}$ has 1 link(s):
($X^{8}$ 0): max_pval = 0.00000, min_val = 0.342
Variable $X^{8}$ has 1 link(s):
($X^{7}$ 0): max_pval = 0.00000, min_val = 0.342
Testing contemporaneous condition sets of dimension 1:
Link ($X^{1}$ -2) -?> $X^{3}$ (1/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -3) ]
Subset 0: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.358
Subset 1: ($X^{4}$ 0) gives pval = 0.00000 / val = 0.358
No conditions of dimension 1 left.
Link ($X^{2}$ -1) -?> $X^{2}$ (2/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{2}$ -2) ($X^{3}$ -2) ]
Subset 0: ($X^{3}$ 0) gives pval = 0.00000 / val = 0.696
Subset 1: ($X^{4}$ 0) gives pval = 0.00000 / val = 0.663
No conditions of dimension 1 left.
Link ($X^{2}$ 0) o?o $X^{3}$ (3/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: ($X^{4}$ 0) gives pval = 0.00000 / val = -0.381
No conditions of dimension 1 left.
Link ($X^{2}$ 0) o?o $X^{4}$ (4/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: ($X^{3}$ 0) gives pval = 0.60740 / val = -0.023
Non-significance detected.
Link ($X^{3}$ 0) o?o $X^{2}$ (5/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: ($X^{4}$ 0) gives pval = 0.00000 / val = -0.381
No conditions of dimension 1 left.
Link ($X^{3}$ -1) -?> $X^{2}$ (6/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{2}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: ($X^{3}$ 0) gives pval = 0.57260 / val = -0.026
Non-significance detected.
Link ($X^{3}$ -1) -?> $X^{3}$ (7/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{1}$ -2) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.726
Subset 1: ($X^{4}$ 0) gives pval = 0.00000 / val = 0.726
No conditions of dimension 1 left.
Link ($X^{3}$ 0) o?o $X^{4}$ (8/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
Subset 0: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.374
No conditions of dimension 1 left.
Link ($X^{3}$ -1) -?> $X^{4}$ (9/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{4}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: ($X^{3}$ 0) gives pval = 0.90731 / val = 0.005
Non-significance detected.
Link ($X^{4}$ 0) o?o $X^{2}$ (10/17):
Already removed.
Link ($X^{4}$ 0) o?o $X^{3}$ (11/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.374
No conditions of dimension 1 left.
Link ($X^{4}$ -1) -?> $X^{4}$ (12/17):
Iterate through 2 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{4}$ -2) ($X^{3}$ -2) ]
Subset 0: ($X^{3}$ 0) gives pval = 0.00000 / val = 0.676
Subset 1: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.637
No conditions of dimension 1 left.
Link ($X^{5}$ -1) -?> $X^{5}$ (13/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ]
with conds_x = [ ($X^{5}$ -2) ($X^{6}$ -2) ]
Subset 0: ($X^{6}$ 0) gives pval = 0.00000 / val = 0.425
No conditions of dimension 1 left.
Link ($X^{5}$ -1) -?> $X^{6}$ (14/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{6}$ -1) ]
with conds_x = [ ($X^{5}$ -2) ($X^{6}$ -2) ]
Subset 0: ($X^{5}$ 0) gives pval = 0.00000 / val = -0.456
No conditions of dimension 1 left.
Link ($X^{6}$ -1) -?> $X^{5}$ (15/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ]
with conds_x = [ ($X^{6}$ -2) ($X^{5}$ -2) ]
Subset 0: ($X^{6}$ 0) gives pval = 0.67680 / val = 0.019
Non-significance detected.
Link ($X^{6}$ -1) -?> $X^{6}$ (16/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{5}$ -1) ]
with conds_x = [ ($X^{6}$ -2) ($X^{5}$ -2) ]
Subset 0: ($X^{5}$ 0) gives pval = 0.00000 / val = 0.427
No conditions of dimension 1 left.
Link ($X^{7}$ -1) -?> $X^{7}$ (17/17):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ]
with conds_x = [ ($X^{7}$ -2) ]
Subset 0: ($X^{8}$ 0) gives pval = 0.00000 / val = 0.689
No conditions of dimension 1 left.
Updated contemp. adjacencies:
Variable $X^{0}$ has 0 link(s):
Variable $X^{1}$ has 0 link(s):
Variable $X^{2}$ has 1 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.381
Variable $X^{3}$ has 2 link(s):
($X^{2}$ 0): max_pval = 0.00000, min_val = 0.381
($X^{4}$ 0): max_pval = 0.00000, min_val = 0.374
Variable $X^{4}$ has 1 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.374
Variable $X^{5}$ has 1 link(s):
($X^{6}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{6}$ has 1 link(s):
($X^{5}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{7}$ has 1 link(s):
($X^{8}$ 0): max_pval = 0.00000, min_val = 0.342
Variable $X^{8}$ has 1 link(s):
($X^{7}$ 0): max_pval = 0.00000, min_val = 0.342
Testing contemporaneous condition sets of dimension 2:
Link ($X^{1}$ -2) -?> $X^{3}$ (1/2):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -3) ]
Subset 0: ($X^{2}$ 0) ($X^{4}$ 0) gives pval = 0.00000 / val = 0.358
Still subsets of dimension 2 left, but q_max = 1 reached.
Link ($X^{3}$ -1) -?> $X^{3}$ (2/2):
Iterate through 1 subset(s) of conditions:
with conds_y = [ ($X^{1}$ -2) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: ($X^{2}$ 0) ($X^{4}$ 0) gives pval = 0.00000 / val = 0.726
Still subsets of dimension 2 left, but q_max = 1 reached.
Updated contemp. adjacencies:
Variable $X^{0}$ has 0 link(s):
Variable $X^{1}$ has 0 link(s):
Variable $X^{2}$ has 1 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.381
Variable $X^{3}$ has 2 link(s):
($X^{2}$ 0): max_pval = 0.00000, min_val = 0.381
($X^{4}$ 0): max_pval = 0.00000, min_val = 0.374
Variable $X^{4}$ has 1 link(s):
($X^{3}$ 0): max_pval = 0.00000, min_val = 0.374
Variable $X^{5}$ has 1 link(s):
($X^{6}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{6}$ has 1 link(s):
($X^{5}$ 0): max_pval = 0.00000, min_val = 0.292
Variable $X^{7}$ has 1 link(s):
($X^{8}$ 0): max_pval = 0.00000, min_val = 0.342
Variable $X^{8}$ has 1 link(s):
($X^{7}$ 0): max_pval = 0.00000, min_val = 0.342
Algorithm converged at p = 2.
----------------------------
Collider orientation phase
----------------------------
contemp_collider_rule = majority
conflict_resolution = True
Triple ($X^{1}$ -2) --> $X^{3}$ o-o $X^{2}$ (1/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00013 / val = -0.172
Subset 1: ($X^{3}$ 0) gives pval = 0.53799 / val = -0.028
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{3}$ -1) --> $X^{3}$ o-o $X^{2}$ (2/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{2}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = -0.402
Subset 1: ($X^{3}$ 0) gives pval = 0.57260 / val = -0.026
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{4}$ 0) o-o $X^{3}$ o-o $X^{2}$ (3/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.243
Subset 1: ($X^{3}$ 0) gives pval = 0.60740 / val = -0.023
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{2}$ -1) --> $X^{2}$ o-o $X^{3}$ (4/10)
Iterate through 4 condition subset(s) of neighbors:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{2}$ -2) ($X^{3}$ -2) ]
Subset 0: ($X^{2}$ 0) ($X^{4}$ 0) gives pval = 0.00000 / val = 0.247
Subset 1: ($X^{4}$ 0) gives pval = 0.62679 / val = -0.022
Subset 2: () gives pval = 0.62897 / val = -0.022
Subset 3: ($X^{2}$ 0) gives pval = 0.00000 / val = 0.248
Fraction of separating subsets containing ($X^{2}$ 0) is < 0.5 --> collider found
Triple ($X^{4}$ -1) --> $X^{4}$ o-o $X^{3}$ (5/10)
Iterate through 4 condition subset(s) of neighbors:
with conds_y = [ ($X^{3}$ -1) ($X^{1}$ -2) ]
with conds_x = [ ($X^{4}$ -2) ($X^{3}$ -2) ]
Subset 0: ($X^{2}$ 0) ($X^{4}$ 0) gives pval = 0.00000 / val = -0.253
Subset 1: ($X^{4}$ 0) gives pval = 0.00000 / val = -0.254
Subset 2: () gives pval = 0.94570 / val = -0.003
Subset 3: ($X^{2}$ 0) gives pval = 0.94498 / val = -0.003
Fraction of separating subsets containing ($X^{4}$ 0) is < 0.5 --> collider found
Triple ($X^{1}$ -2) --> $X^{3}$ o-o $X^{4}$ (6/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00266 / val = 0.135
Subset 1: ($X^{3}$ 0) gives pval = 0.87116 / val = -0.007
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{2}$ 0) o-o $X^{3}$ o-o $X^{4}$ (7/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{4}$ -1) ($X^{3}$ -1) ]
with conds_x = [ ($X^{2}$ -1) ($X^{3}$ -1) ]
Subset 0: () gives pval = 0.00000 / val = -0.243
Subset 1: ($X^{3}$ 0) gives pval = 0.60740 / val = -0.023
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{3}$ -1) --> $X^{3}$ o-o $X^{4}$ (8/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{4}$ -1) ]
with conds_x = [ ($X^{3}$ -2) ($X^{1}$ -3) ]
Subset 0: () gives pval = 0.00000 / val = 0.369
Subset 1: ($X^{3}$ 0) gives pval = 0.90731 / val = 0.005
Fraction of separating subsets containing ($X^{3}$ 0) is > 0.5 --> non-collider found
Triple ($X^{6}$ -1) --> $X^{6}$ o-o $X^{5}$ (9/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ($X^{5}$ -1) ]
with conds_x = [ ($X^{6}$ -2) ($X^{5}$ -2) ]
Subset 0: () gives pval = 0.00022 / val = 0.166
Subset 1: ($X^{6}$ 0) gives pval = 0.67680 / val = 0.019
Fraction of separating subsets containing ($X^{6}$ 0) is > 0.5 --> non-collider found
Triple ($X^{7}$ -1) --> $X^{7}$ o-o $X^{8}$ (10/10)
Iterate through 2 condition subset(s) of neighbors:
with conds_y = [ ]
with conds_x = [ ($X^{7}$ -2) ]
Subset 0: ($X^{7}$ 0) gives pval = 0.00000 / val = 0.228
Subset 1: () gives pval = 0.78143 / val = -0.013
Fraction of separating subsets containing ($X^{7}$ 0) is < 0.5 --> collider found
Orienting links among colliders:
Collider ($X^{2}$ -1) --> $X^{2}$ o-o $X^{3}$:
Orient $X^{3}$ o-o $X^{2}$ as $X^{3}$ --> $X^{2}$
Collider ($X^{4}$ -1) --> $X^{4}$ o-o $X^{3}$:
Orient $X^{3}$ o-o $X^{4}$ as $X^{3}$ --> $X^{4}$
Collider ($X^{7}$ -1) --> $X^{7}$ o-o $X^{8}$:
Orient $X^{8}$ o-o $X^{7}$ as $X^{8}$ --> $X^{7}$
Updated adjacencies:
Variable $X^{0}$ has 2 link(s):
($X^{0}$ -1)
($X^{1}$ -1)
Variable $X^{1}$ has 1 link(s):
($X^{1}$ -1)
Variable $X^{2}$ has 2 link(s):
($X^{2}$ -1)
($X^{3}$ 0)
Variable $X^{3}$ has 4 link(s):
($X^{1}$ -2)
($X^{2}$ 0)
($X^{3}$ -1)
($X^{4}$ 0)
Variable $X^{4}$ has 2 link(s):
($X^{3}$ 0)
($X^{4}$ -1)
Variable $X^{5}$ has 2 link(s):
($X^{5}$ -1)
($X^{6}$ 0)
Variable $X^{6}$ has 3 link(s):
($X^{5}$ 0)
($X^{5}$ -1)
($X^{6}$ -1)
Variable $X^{7}$ has 2 link(s):
($X^{7}$ -1)
($X^{8}$ 0)
Variable $X^{8}$ has 1 link(s):
($X^{7}$ 0)
----------------------------
Rule orientation phase
----------------------------
Try rule(s) [1 2 3]
R1: Found ($X^{6}$ -1) --> $X^{6}$ o-o $X^{5}$, orient as $X^{6}$ --> $X^{5}$
Try rule(s) [1]
Updated adjacencies:
Variable $X^{0}$ has 2 link(s):
($X^{0}$ -1)
($X^{1}$ -1)
Variable $X^{1}$ has 1 link(s):
($X^{1}$ -1)
Variable $X^{2}$ has 2 link(s):
($X^{2}$ -1)
($X^{3}$ 0)
Variable $X^{3}$ has 4 link(s):
($X^{1}$ -2)
($X^{2}$ 0)
($X^{3}$ -1)
($X^{4}$ 0)
Variable $X^{4}$ has 2 link(s):
($X^{3}$ 0)
($X^{4}$ -1)
Variable $X^{5}$ has 2 link(s):
($X^{5}$ -1)
($X^{6}$ 0)
Variable $X^{6}$ has 3 link(s):
($X^{5}$ 0)
($X^{5}$ -1)
($X^{6}$ -1)
Variable $X^{7}$ has 2 link(s):
($X^{7}$ -1)
($X^{8}$ 0)
Variable $X^{8}$ has 1 link(s):
($X^{7}$ 0)
-----------------------------
PCMCIplus algorithm finished.
-----------------------------
## Significant links at alpha = 0.01:
Variable $X^{0}$ has 2 link(s):
($X^{0}$ -1): pval = 0.00000 | val = 0.682
($X^{1}$ -1): pval = 0.00000 | val = 0.366
Variable $X^{1}$ has 1 link(s):
($X^{1}$ -1): pval = 0.00000 | val = 0.702
Variable $X^{2}$ has 2 link(s):
($X^{2}$ -1): pval = 0.00000 | val = 0.662
($X^{3}$ 0): pval = 0.00000 | val = -0.381
Variable $X^{3}$ has 2 link(s):
($X^{3}$ -1): pval = 0.00000 | val = 0.726
($X^{1}$ -2): pval = 0.00000 | val = 0.358
Variable $X^{4}$ has 2 link(s):
($X^{4}$ -1): pval = 0.00000 | val = 0.637
($X^{3}$ 0): pval = 0.00000 | val = 0.374
Variable $X^{5}$ has 2 link(s):
($X^{5}$ -1): pval = 0.00000 | val = 0.343
($X^{6}$ 0): pval = 0.00000 | val = 0.292
Variable $X^{6}$ has 2 link(s):
($X^{6}$ -1): pval = 0.00000 | val = 0.427
($X^{5}$ -1): pval = 0.00000 | val = -0.383
Variable $X^{7}$ has 2 link(s):
($X^{7}$ -1): pval = 0.00000 | val = 0.668
($X^{8}$ 0): pval = 0.00000 | val = -0.342
Variable $X^{8}$ has 0 link(s): 関数print_results(results)の出力は、(上の出力の終端に見られる)、各変数の親をの情報を与えます。そしてまた、無指向のリンクと衝突を示します。それは、研究用レポートとして重要です。
run_pcmciplusの結果は、グラフ、p-値の行列、静的テストの行列値(ここではMCIの部分相関)、曖昧なトリプル値を含む辞書です。graph,p_matrix,val_matrixは、上で述べたようにシェイプ(N,N,tau_max+1)になります。
注記:静的テスト値は、(例えば、部分相関)は、従属性のstrengthの直感的な性質を与えるでよう。しかし、最適な因果分析は、CausalEffectsクラスとチュートリアルを参照してください。
print("Graph")
print (results['graph'])
print("Adjacency MCI partial correlations")
print (results['val_matrix'].round(2))
print("Adjacency p-values")
print (results['p_matrix'].round(3))Graph [[['' '-->' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '-->' '' ''] ['' '-->' '' ''] ['' '' '' ''] ['' '' '-->' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '-->' '' ''] ['<--' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['-->' '' '' ''] ['' '-->' '' ''] ['-->' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['<--' '' '' ''] ['' '-->' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '-->' '' ''] ['<--' '-->' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['-->' '' '' ''] ['' '-->' '' ''] ['' '' '' ''] ['' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '-->' '' ''] ['<--' '' '' '']] [['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['' '' '' ''] ['-->' '' '' ''] ['' '' '' '']]] Adjacency MCI partial correlations [[[ 0. 0.68 0.01 0.03] [-0.02 -0.03 -0.03 -0.02] [ 0.04 -0. 0.05 0.07] [-0.02 0.02 0.1 -0.05] [-0.06 0.11 0.07 0.05] [ 0.04 0.01 0.02 0.02] [ 0.06 0.1 0.09 0.09] [ 0.03 -0.09 -0.09 -0.09] [-0.05 -0.04 -0.04 -0.04]] [[-0.02 0.37 0.02 0.03] [ 0. 0.7 -0.03 -0.03] [ 0.04 -0.06 -0.06 0.04] [-0.09 0.02 0.36 0.02] [ 0.01 0.04 0.07 0.03] [-0.02 0.01 0.01 0.02] [ 0.04 0.11 0.11 0.09] [-0.03 -0.04 -0.04 -0.05] [-0.06 0. -0.01 -0.02]] [[ 0.04 -0.02 -0.02 -0.02] [ 0.04 -0. -0. -0. ] [ 0. 0.66 -0.03 -0.03] [-0.38 -0.04 -0.04 -0.04] [-0.02 -0.04 0.02 0.03] [ 0.02 -0.04 -0.04 -0.05] [-0.08 -0.05 -0.05 -0.05] [-0.03 0.09 0.09 0.09] [ 0.02 0.06 0.06 0.06]] [[-0.02 -0.09 0.01 0. ] [-0.09 -0.02 -0.02 -0.02] [-0.38 -0.03 0.07 0.09] [ 0. 0.73 -0.1 -0.07] [ 0.37 0.01 -0.05 -0.09] [-0.02 0.03 0.03 0.02] [ 0.11 0.07 0.06 0.05] [ 0.07 -0.07 -0.07 -0.08] [-0.04 -0.06 -0.06 -0.06]] [[-0.06 0.03 0.03 0.02] [ 0.01 0. 0. 0. ] [-0.02 -0.02 -0. -0.02] [ 0.37 0.03 0.03 0.04] [ 0. 0.64 0.02 0.01] [-0.01 0.05 0.05 0.05] [ 0.04 0.05 0.05 0.05] [-0.04 -0.09 -0.09 -0.09] [ 0.02 -0.06 -0.06 -0.06]] [[ 0.04 0.02 0.02 0.02] [-0.02 -0.02 -0.01 -0.01] [ 0.02 -0.04 -0.04 -0.04] [-0.02 0.02 0.02 0.03] [-0.01 0.04 0.04 0.04] [ 0. 0.34 0.09 -0.02] [ 0.29 -0.38 0.02 -0.03] [ 0. -0.09 -0.09 -0.09] [-0.02 0.02 0.01 -0.01]] [[ 0.06 0.1 0.1 0.11] [ 0.04 0.11 0.1 0.1 ] [-0.08 -0.05 -0.05 -0.06] [ 0.11 0.09 0.09 0.1 ] [ 0.04 0.06 0.06 0.06] [ 0.29 0.02 0.1 0.11] [ 0. 0.43 -0.07 0.03] [ 0.02 -0.09 -0.1 -0.1 ] [-0.06 0.05 0.01 0.02]] [[ 0.03 0.02 0.06 0.06] [-0.03 -0. 0.01 0.03] [-0.03 -0. 0.01 0.01] [ 0.07 0.04 0.04 0.04] [-0.04 0.01 0. -0.01] [ 0. -0.07 -0.06 -0.06] [ 0.02 -0.07 -0.05 -0.05] [ 0. 0.67 0.05 0.03] [-0.34 -0.01 -0.01 -0. ]] [[-0.05 -0.03 -0.04 -0.04] [-0.06 -0.04 -0.01 0.01] [ 0.02 0.06 0.06 0.07] [-0.04 -0.05 -0.05 -0.06] [ 0.02 -0.06 -0.06 -0.06] [-0.02 -0.03 0.01 0.04] [-0.06 0.05 0.07 0.04] [-0.34 -0.11 -0.1 -0.06] [ 0. 0.03 0. -0.05]]] Adjacency p-values [[[1. 0. 0.886 0.557] [0.582 0.504 0.532 0.583] [0.358 0.947 0.261 0.103] [0.66 0.605 0.029 0.226] [0.165 0.013 0.133 0.23 ] [0.426 0.744 0.72 0.67 ] [0.208 0.032 0.035 0.048] [0.575 0.058 0.045 0.048] [0.263 0.373 0.384 0.373]] [[0.582 0. 0.67 0.489] [1. 0. 0.447 0.479] [0.387 0.217 0.221 0.363] [0.038 0.643 0. 0.726] [0.839 0.392 0.121 0.551] [0.614 0.887 0.821 0.61 ] [0.347 0.017 0.018 0.057] [0.558 0.359 0.353 0.307] [0.151 0.955 0.892 0.66 ]] [[0.358 0.596 0.593 0.6 ] [0.387 0.985 0.963 0.934] [1. 0. 0.58 0.465] [0. 0.432 0.436 0.433] [0.607 0.421 0.672 0.559] [0.668 0.331 0.324 0.314] [0.069 0.268 0.285 0.301] [0.546 0.043 0.042 0.039] [0.67 0.179 0.18 0.185]] [[0.66 0.043 0.816 0.987] [0.038 0.66 0.642 0.68 ] [0. 0.573 0.101 0.047] [1. 0. 0.025 0.117] [0. 0.907 0.231 0.042] [0.737 0.503 0.51 0.595] [0.013 0.104 0.175 0.243] [0.108 0.117 0.117 0.094] [0.36 0.183 0.192 0.182]] [[0.165 0.553 0.56 0.584] [0.839 0.989 0.978 0.95 ] [0.607 0.728 0.936 0.646] [0. 0.446 0.445 0.436] [1. 0. 0.602 0.786] [0.801 0.311 0.307 0.299] [0.416 0.234 0.252 0.264] [0.361 0.038 0.037 0.036] [0.684 0.184 0.184 0.188]] [[0.426 0.699 0.625 0.588] [0.614 0.71 0.773 0.854] [0.668 0.363 0.353 0.345] [0.737 0.609 0.582 0.556] [0.801 0.347 0.34 0.336] [1. 0. 0.052 0.708] [0. 0. 0.668 0.504] [0.939 0.043 0.046 0.054] [0.64 0.728 0.743 0.819]] [[0.208 0.027 0.024 0.016] [0.347 0.011 0.021 0.034] [0.069 0.236 0.226 0.201] [0.013 0.056 0.046 0.035] [0.416 0.201 0.187 0.166] [0. 0.677 0.022 0.016] [1. 0. 0.098 0.542] [0.645 0.053 0.024 0.02 ] [0.18 0.244 0.771 0.655]] [[0.575 0.622 0.202 0.153] [0.558 0.995 0.824 0.493] [0.546 0.981 0.781 0.848] [0.108 0.33 0.321 0.356] [0.361 0.908 0.926 0.757] [0.939 0.115 0.212 0.195] [0.645 0.144 0.241 0.298] [1. 0. 0.305 0.446] [0. 0.75 0.812 0.914]] [[0.263 0.46 0.435 0.392] [0.151 0.397 0.839 0.841] [0.67 0.184 0.17 0.145] [0.36 0.263 0.244 0.183] [0.684 0.195 0.185 0.16 ] [0.64 0.508 0.823 0.368] [0.18 0.276 0.109 0.436] [0. 0.014 0.023 0.189] [1. 0.563 0.977 0.226]]]
上で述べたように、PCMCIplusのp_matrixとval_matrixは、しかし、フェイズ3、4で決定した同時性リンクの方向のためでなく、対して、フェイズ2の近接のためだけに、不確実性と強さの量を測ります。同時性リンクには対称性の性質があるので、graphとは異なり、p_matrixとval_matrixは、tau=0で、対称になります。私たちは、q_matrixの歩留まりをFalseDiscovery Rate(FDR)によって制御することで、p-値を訂正することができます。
q_matrix = pcmci.get_corrected_pvalues(p_matrix=results['p_matrix'], fdr_method='fdr_bh',
exclude_contemporaneous=False) しかし、PCMCIplusの重要な出力は、graphです。
Tigramaiteは、いくつかの図示オプションを提案します。遅延関数行列は、(上に見られるように)、時系列グラフ、時系列グラフの情報を集計した過程グラフがあります。両方、引数graphを取ります。val_matrixは、リンクの強さを示すのに使うことができます。
過程グラフでは、graphの異なるエントリーは以下のように可視化されます。
graph[i,j,tau]='-->'任意のtau > 0は、有向遅延因果リンクXt-ri -> Xtjを示します。そして、XiからXjへの曲線の矢印によって表現されます。もし、他の方向の遅延リンクXt-ri->Xtjが表されると、両方の曲線は、それらが交わらないように反対に湾曲されて描画されます。graph[i,j,0]='-->'とgraph[j,i,0]='<--'は、有向同時性因果リンクXti->Xtjを示します。そして、XiからXjへの直線の矢印で表現されます。graph[i,j,0]='o-o'とgraph[j,i,0]='o-o'は、XtiとXtj間の無向の同時性因果リンクを示します。colliderと方針ルールは適用されません(マルコフ同値)。そして、XiとXj間の円で終端された直線によって表現されます。graph[i,j,0]='x-x'とgraph[j,i,0]='x-x'は、XtiとXtjの間の衝突、同時性、近接を示します。方向性は、方針ルールの衝突のせいで、決定されません。そして、XiとXjの間で終端を結んで直線で表現されます。
各ケースでは、リンクの色はcross-MCIの値で参照されます。もし、リンクが二つの変数間で多重の遅延が発生すれば、リンクの色と種別は、最も強い色で示されます。そして、ラベルは、それらの強さのために、全ての重要なラグがリストされます。ノードの色は、ラグにおいて最大絶対値の自動MCIを表現します。仮に、 val_matrixがすでに同時性の値に対して対称でない場合、最大絶対値が示されます。
tp.plot_graph(
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='cross-MCI (edges)',
node_colorbar_label='auto-MCI (nodes)',
); plt.show()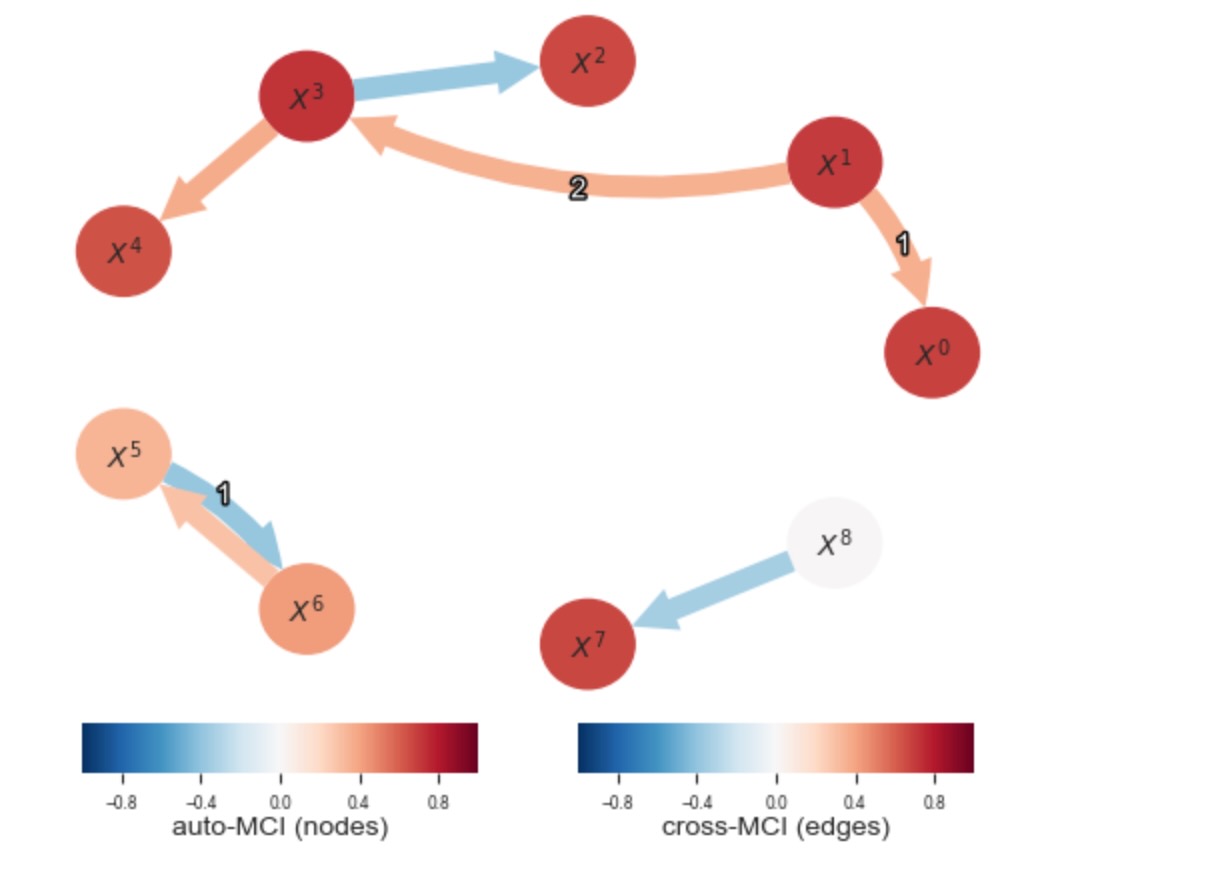
過程グラフは、よく表示されています。時系列グラフは、読み取れる因果の経路から一時的空間上従属構造をよく表しています。
時系列グラフでは、graphの各エントリーは、直接可視化できます。有向遅延または、同時性リンクは、対応する直線の矢印、指向性のない、または衝突する同時性リンクとして、出力されます。各ケースで、リンクの色は、val_matrixのMCI値を参照します。また、ここでval_matrixが同時性の値にすでに対称でなければ、最大絶対値が表示されます。
# Plot time series graph
tp.plot_time_series_graph(
figsize=(8, 8),
node_size=0.05,
val_matrix=results['val_matrix'],
graph=results['graph'],
var_names=var_names,
link_colorbar_label='MCI',
); plt.show()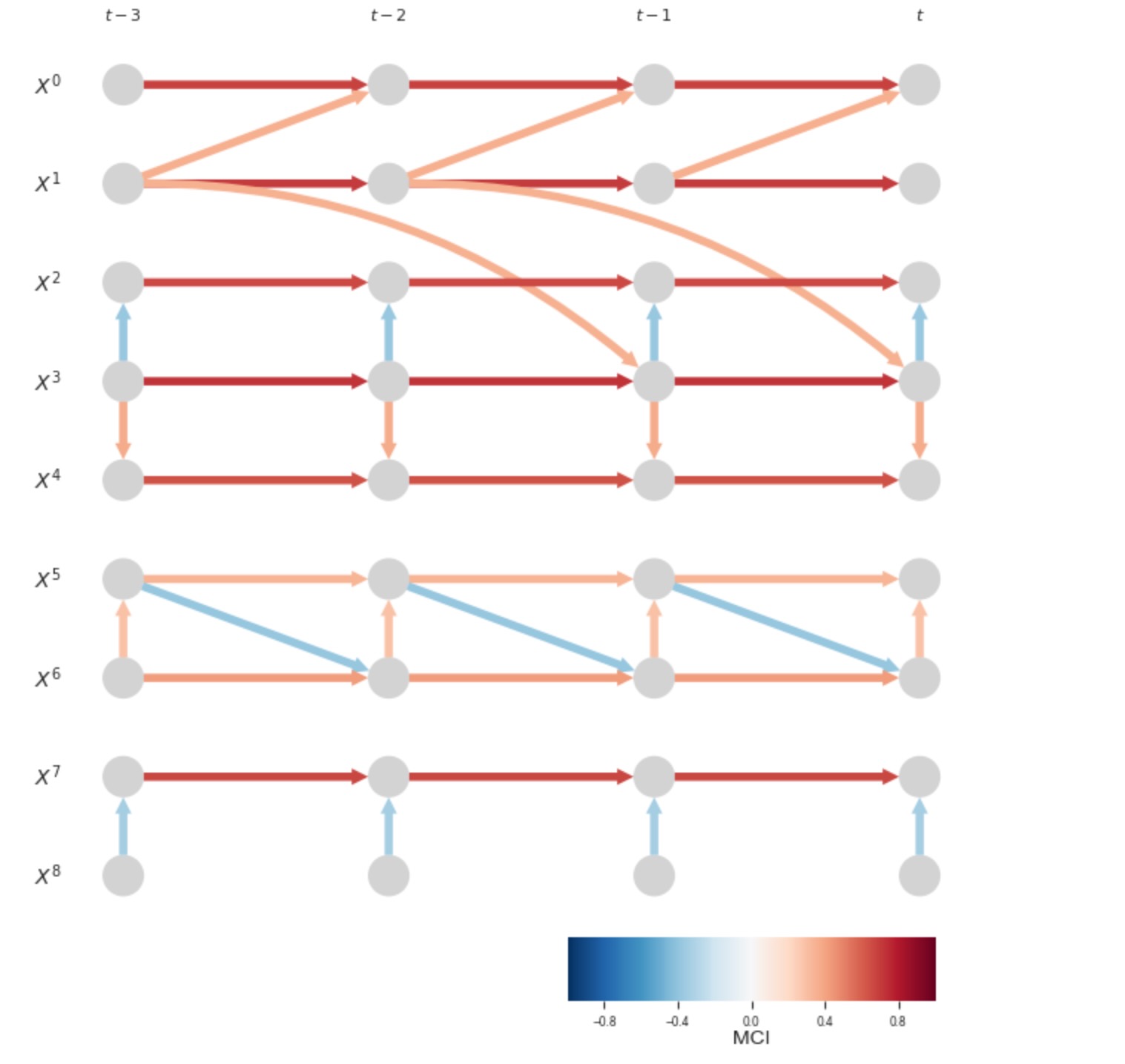
ここで、PCMCIplusは、正しく遅延と、同時性リンクと近接の両方に従う因果グラフの下で、推定します。
ペア(X5,X6)は、フィードバックサイクルを表示します。これらはしばしば、現実のデータで発生し、例は、他のグラフモデリングアプローチは、周期的依存性を表すことはできませんが、その時系列グラフが、時間のフィードバックを解決することを示します。
同時に発生する1組のペア(X7,X8)は、自己相関が、リンクの方針を識別するのに役立つケースを説明します。自己相関なしで、PCMCIplusの出力は、マルコフ同値類を示すために無向リンクにになります。
4. PCMCIとPCアルゴリズムの比較
以下で、私たちは、PCMCIplusと標準のPCMCIメソッドを比較します。それは、時間遅延員が探索だけに取り組み、それをPCアルゴリズムに取り組みます。(時系列を適合します)
もちろん、データ上で標準PCMCIの比較は、実際、これが、PCMCIの仮定を変動させるので、同時性有向従属性は不正になることを含みます。同じtoyモデルの例を見ていきましょう。PCMCIには、私たちは、(任意のalpha_levelの閾値)p_matrixを基礎にして、graphを構築する必要があります。それは、同時性リンクに対称で、従って、方向性を示すことはできません。
tau_max = 3
alpha_level = 0.001
pcmci.verbosity = 0
results = pcmci.run_pcmci(tau_min=0, tau_max=tau_max, pc_alpha=None, alpha_level=alpha_level)
# Mark false links as grey
true_graph = toys.links_to_graph(links=links, tau_max=tau_max)
link_attribute = np.ones(results['val_matrix'].shape, dtype = 'object')
link_attribute[true_graph==""] = 'spurious'
link_attribute[true_graph!=""] = ''
# Symmetrize contemp. link attribute
for (i,j) in zip(*np.where(true_graph[:,:,0]!="")):
link_attribute[i,j,0] = link_attribute[j,i,0] = ''
tp.plot_time_series_graph(
figsize=(8, 8),
node_size=0.05,
val_matrix=results['val_matrix'],
graph=results['graph'],
link_attribute=link_attribute,
var_names=var_names,
)
plt.show()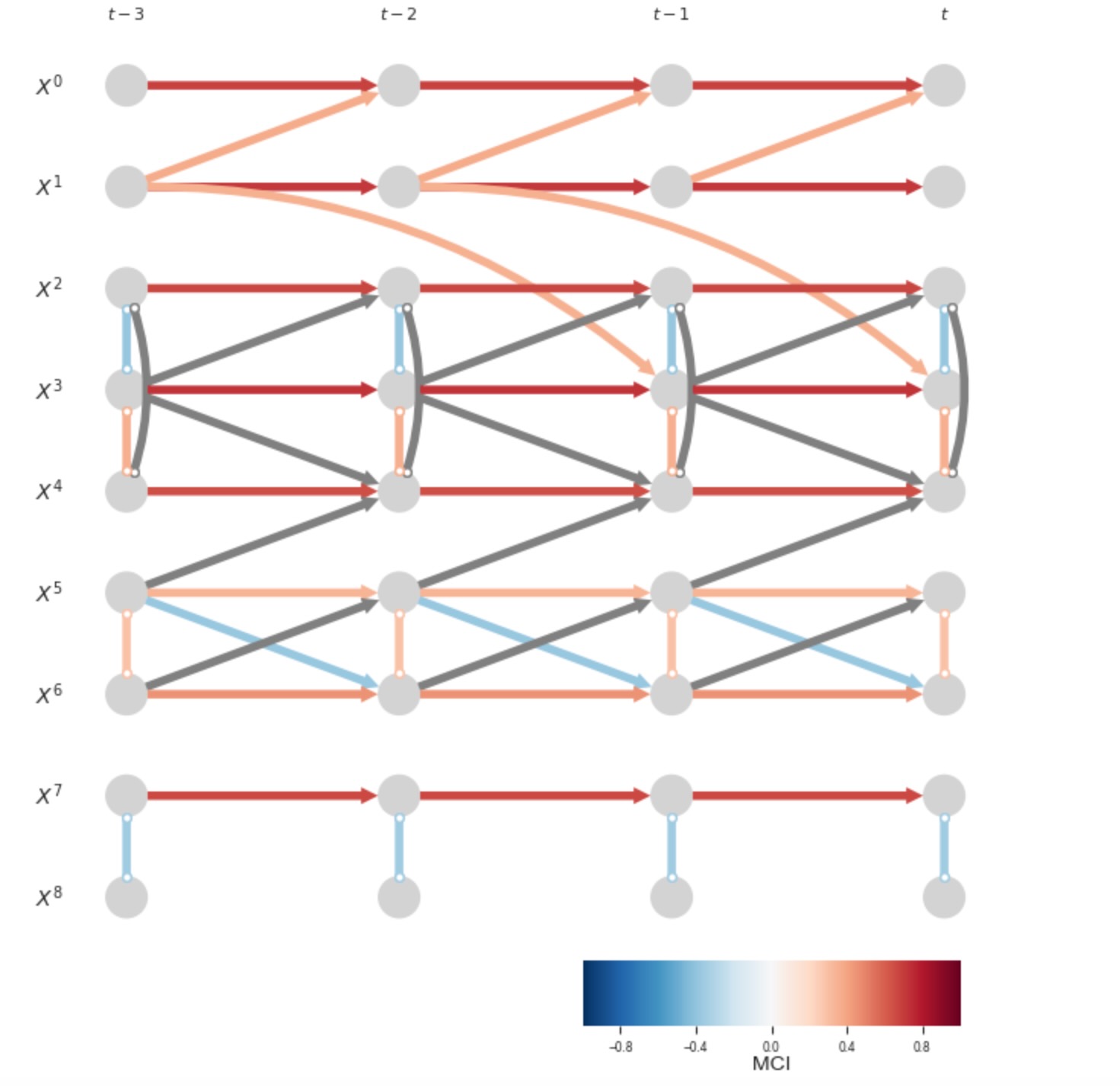
誤った有効性(灰色)は、ここで、同時性の親を通る間接の経路のために現れます。例えば、Xt-13 ー>Xt2は、経路Xt-13 -> Xt3 ->Xt2のために現れます。なぜなら、PCMCIは、関節リンクと、同時性の親を通って来るのでなく、遅延の親を通って来る共通ドライバだけを削除します。同様に、Xt2 <- Xt3 <- Xt4のために、誤った同時性リンクXt2 - Xt4を保持します。さらに、円の線によって示されるように、全ての同時性リンクは、無向を残します。
PCアルゴリズムとの比較は、前提の仮定が同じなので、公正になります。
tau_max = 3
pcmci.verbosity = 0
results = pcmci.run_pcalg(tau_min=0, tau_max=tau_max, pc_alpha=0.01)
tp.plot_time_series_graph(
figsize=(8, 8),
node_size=0.05,
val_matrix=results['val_matrix'],
graph=results['graph'],
link_attribute=link_attribute,
var_names=var_names,
link_colorbar_label='PC')
plt.show()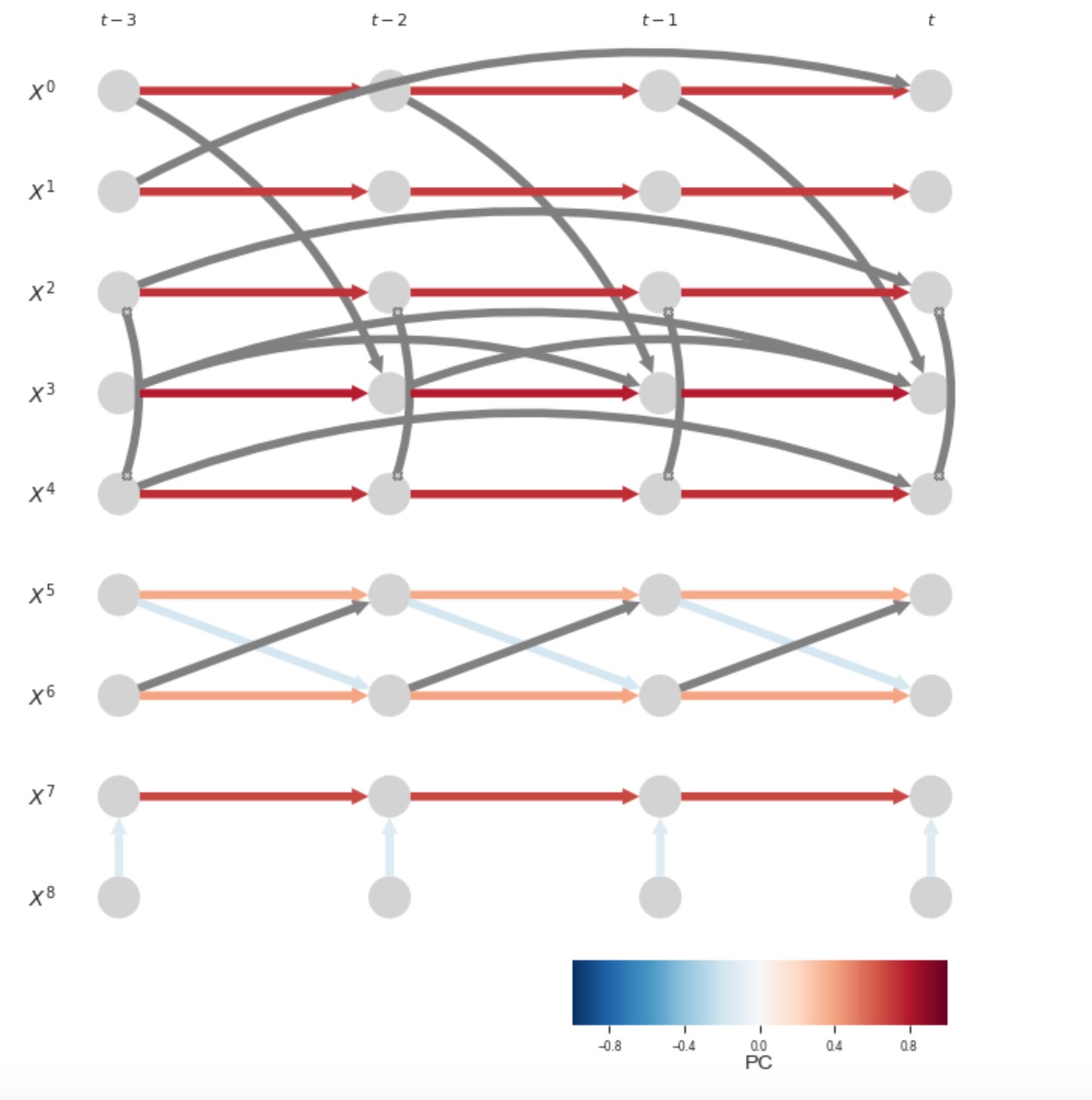
PCアルゴリズムは、まだここで、多重に誤ります。真のリンクは検出しません。以前に削除したリンクは、条件セットがそれ以上利用できないので、そのとき、誤った有効性を(x-xによって印づけられる衝突しているリンク)導きます。論文では、低い検出力は、主要な問題として識別されます。そして、このtoy例は、完全に議論されました。
たとえ、大きなサンプルサイズであっても、私たちは正しいグラフを得られません。リンクXt-ri -> Xtjの値は、任意の条件セットを通ってで対応する最も大きいp-値で決定されますが、そしてここでPCは何度も実行されますが、val_matrixの非常に小さい値に注意してください。
data_long, nonstationarity_indicator = toys.structural_causal_process(
links=links, T=100000, noises=noises, seed=seed)
parcorr = ParCorr(significance='analytic')
pcmci_long = PCMCI(
dataframe=pp.DataFrame(data_long, var_names=var_names),
cond_ind_test=parcorr,
verbosity=1)
tau_max = 3
pcmci_long.verbosity = 0
results = pcmci_long.run_pcalg(tau_min=0, tau_max=tau_max, pc_alpha=0.001)
tp.plot_time_series_graph(
figsize=(8, 8),
node_size=0.05,
val_matrix=results['val_matrix'],
graph=results['graph'],
link_attribute=link_attribute,
var_names=var_names,
link_colorbar_label='PC')
plt.show()