TIGRAMITEによる因果探索 (予測）

　TIGRAMITEは時系列分析Pythonモジュールです。PCMCIフレームワークを基礎にした離散、連続時系列からグラフィカルモデル(条件独立グラフ)を再構築し、結果の高品質の図を生成します。

　PCMCIはここに記述されています： J. Runge, P. Nowack, M. Kretschmer, S. Flaxman, D. Sejdinovic, Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 5, eaau4996 (2019) https://advances.sciencemag.org/content/5/11/eaau4996

　PCMCIのさらに進んだバージョンについては(例えば、PCMCI+, LPCMCI, etc)、一致するチュートリアルを参照してください。

　このチュートリアルは、最適化予測を得るためのPCMCIの使い方を説明しています。理論的バックグラウンドは、以下の論文を参照してください。: Runge, Jakob, Reik V. Donner, and Jürgen Kurths. 2015. “Optimal Model-Free Prediction from Multivariate Time Series.” Phys. Rev. E 91 (5): 052909. https://doi.org/10.1103/PhysRevE.91.052909.

　最後に、Nature Communication Perspective の論文は、概して因果推論のメソッドの概要を提供し、期待の持てるアプリケーションを識別し、方法論的な難問を議論します。(地球システムの科学の例)： https://www.nature.com/articles/s41467-019-10105-3

# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline     
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn

import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI

from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb

from tigramite.models import LinearMediation, Prediction

予測

　Tigramiteは、sklearnモデルを基礎にした予測を実行するためのtigramite.models.Predictionクラスを含んでいます。Predictionクラスは、PCMCIクラスからpredictorの選択を実行するために、run_pc_stableの周りのラッパーを含みます。以下のデータ生成過程を参照してください。

np.random.seed(42)
T = 200
links_coeffs = {0: [((0, -1), 0.6)],
                1: [((1, -1), 0.6), ((0, -1), 0.8)],
                2: [((2, -1), 0.5), ((1, -1), 0.7)],  # ((0, -1), c)],
                }
N = len(links_coeffs)
data, true_parents = toys.var_process(links_coeffs, T=T)
dataframe = pp.DataFrame(data, var_names = [r'$X^0$', r'$X^1$', r'$X^2$'])

　私たちは、cond_ind_model=ParCorr()とともにPredictionクラスを初期化します。2番目に、私たちは、ここで予測のために、sklean.linear_model.LnearRegression()を選択します。最後に、私たちは、data_transformを経由して、データをスケールします。クラスは予測のために、データを再スケールすることに注意します。パラメータtrain_indicesとtest_indicesは、データをトレーニングセットとテストセットに分割するのに使われます。ここで、私たちは、トレーニングとテストの指標の間で、少なくともtau_max(30以下で選択)のギャップを挿入します。なぜなら、私たちは、テスト指標を予測するために、遅延predictorを使います。テストセットは、新しいデータが後で供給されるので、オプションになります。トレーニングセットは、predictorsを選択するために使われ、モデルに適合されます。

pred = Prediction(dataframe=dataframe,
        cond_ind_test=ParCorr(),   #CMIknn ParCorr
        prediction_model = sklearn.linear_model.LinearRegression(),
#         prediction_model = sklearn.gaussian_process.GaussianProcessRegressor(),
        # prediction_model = sklearn.neighbors.KNeighborsRegressor(),
    data_transform=sklearn.preprocessing.StandardScaler(),
    train_indices= range(int(0.8*T)),
    test_indices= range(int(0.9*T), T),
    verbosity=1
    )

　ここで、私たちは、tau_maxの過去の最大遅延を理解するために対象の二つの変数のためにget_predictorsを使って、因果予測を推定します。私たちは、pc_alpha=Noneを使います。それは、Akaikeスコアを基礎にしてパラメータを最適化します。predictorは各範囲ごとに異なることに注意してください。例えば、Steps_ahead=1の予測範囲では、私たちは、モデルとその他から、因果の親を取得します。

target = 2
tau_max = 5
predictors = pred.get_predictors(
                  selected_targets=[target],
                  steps_ahead=1,
                  tau_max=tau_max,
                  pc_alpha=None
                  )
graph = np.zeros((N, N, tau_max+1), dtype='bool')
for j in [target]:
    for p in predictors[j]:
        graph[p[0], j, abs(p[1])] = 1

# Plot time series graph
tp.plot_time_series_graph(
    figsize=(6, 3),
#     node_aspect=2.,
    val_matrix=np.ones(graph.shape),
    graph=graph,
    var_names=None,
    link_colorbar_label='',
    ); plt.show()

##
## Step 1: PC1 algorithm with lagged conditions
##

Parameters:
independence test = par_corr
tau_min = 1
tau_max = 5
pc_alpha = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5]
max_conds_dim = None
max_combinations = 1



## Resulting lagged parent (super)sets:

    Variable $X^0$ has 1 link(s):
    [pc_alpha = 0.05]
        ($X^0$ -1): max_pval = 0.00000, min_val =  0.560

    Variable $X^1$ has 3 link(s):
    [pc_alpha = 0.3]
        ($X^0$ -1): max_pval = 0.00000, min_val =  0.685
        ($X^1$ -1): max_pval = 0.00000, min_val =  0.556
        ($X^2$ -1): max_pval = 0.22735, min_val = -0.099

    Variable $X^2$ has 3 link(s):
    [pc_alpha = 0.1]
        ($X^1$ -1): max_pval = 0.00000, min_val =  0.557
        ($X^2$ -1): max_pval = 0.00000, min_val =  0.418
        ($X^1$ -2): max_pval = 0.05793, min_val =  0.157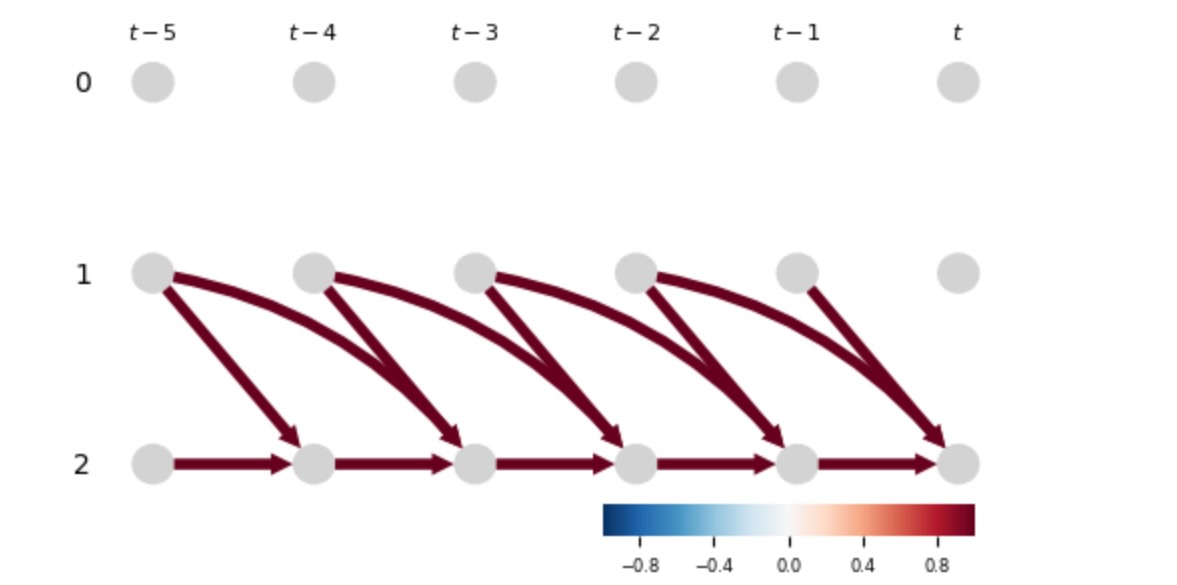

　get_predictorsは、PCMCIの最初のステップだけを基礎にしていることに注意してください。そしてMCIステップをスキップします。正誤の有効性率は、予測に関連していないので、そして、最初の単独ステップの方が速くなります。ここで、私たちは、steps_ahead=2を設定し、異なるpredictorを取得します。

tau_max = 20
steps_ahead = 2
target = 2

all_predictors = pred.get_predictors(
                  selected_targets=[target],
                  steps_ahead=steps_ahead,
                  tau_max=tau_max,
                  pc_alpha=None
                  )
graph = np.zeros((N, N, tau_max + 1), dtype='bool')
for j in [target]:
    for p in all_predictors[j]:
        graph[p[0], j, abs(p[1])] = 1

# Plot time series graph
tp.plot_time_series_graph(
    figsize=(18, 5),
    node_size=0.05,
    node_aspect=.3,
    val_matrix=np.ones(graph.shape),
    graph=graph,
    var_names=None,
    link_colorbar_label='',
    label_fontsize=24
    ); plt.show()

##
## Step 1: PC1 algorithm with lagged conditions
##

Parameters:
independence test = par_corr
tau_min = 2
tau_max = 20
pc_alpha = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5]
max_conds_dim = None
max_combinations = 1



## Resulting lagged parent (super)sets:

    Variable $X^0$ has 3 link(s):
    [pc_alpha = 0.3]
        ($X^0$ -2): max_pval = 0.00128, min_val =  0.296
        ($X^1$ -14): max_pval = 0.13889, min_val = -0.137
        ($X^2$ -5): max_pval = 0.25654, min_val = -0.106

    Variable $X^1$ has 5 link(s):
    [pc_alpha = 0.4]
        ($X^0$ -2): max_pval = 0.00000, min_val =  0.567
        ($X^1$ -2): max_pval = 0.00725, min_val =  0.246
        ($X^1$ -16): max_pval = 0.28612, min_val =  0.099
        ($X^0$ -10): max_pval = 0.28889, min_val = -0.098
        ($X^2$ -2): max_pval = 0.31115, min_val =  0.095

    Variable $X^2$ has 4 link(s):
    [pc_alpha = 0.05]
        ($X^1$ -2): max_pval = 0.00000, min_val =  0.720
        ($X^0$ -2): max_pval = 0.00006, min_val =  0.358
        ($X^2$ -2): max_pval = 0.01518, min_val =  0.222
        ($X^1$ -20): max_pval = 0.02435, min_val = -0.206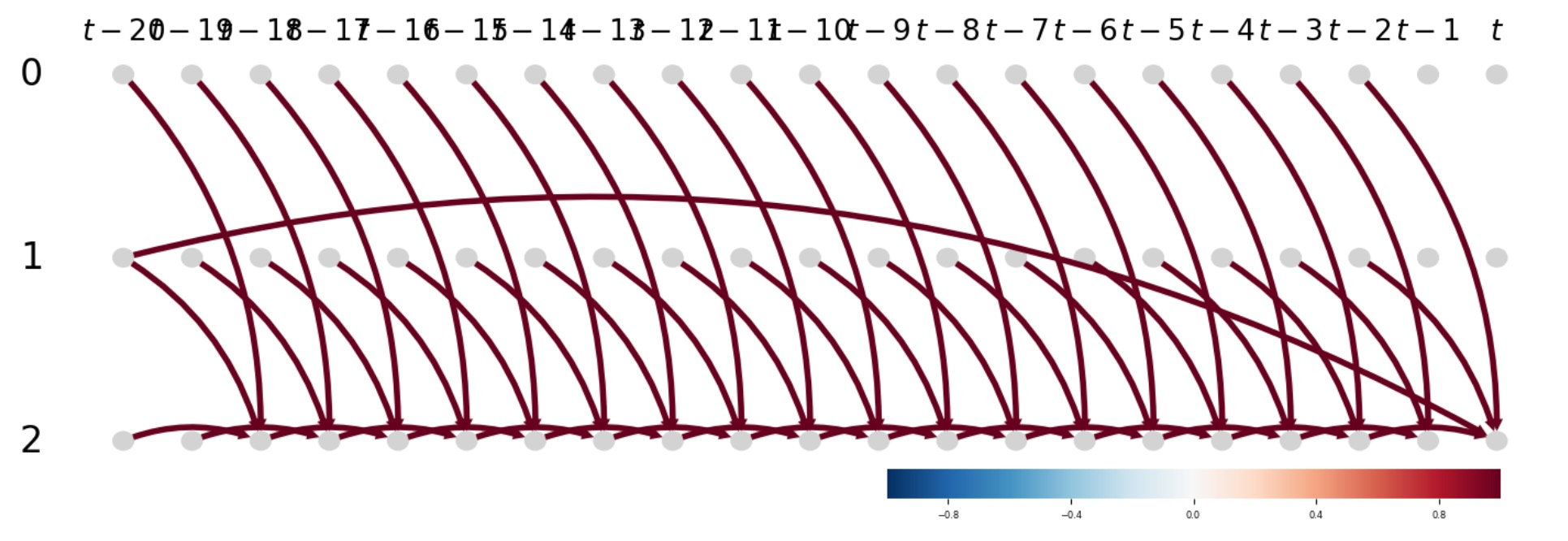

　これらのpredictorsは、ここで、以下のモデルで、オーバーフィット(過適合）を避けようとします。ここで、多重の対象変数がすぐに、適合するかどうか規定することができます。(全てのこれらのoredictorsは前もって推定されることが仮定されます)

pred.fit(target_predictors=all_predictors, 
                selected_targets=[target],
                    tau_max=tau_max)

　ここで、私たちは、テストサンプルで対象変数を予測する準備があります。

predicted = pred.predict(target)
true_data = pred.get_test_array(j=target)[0]

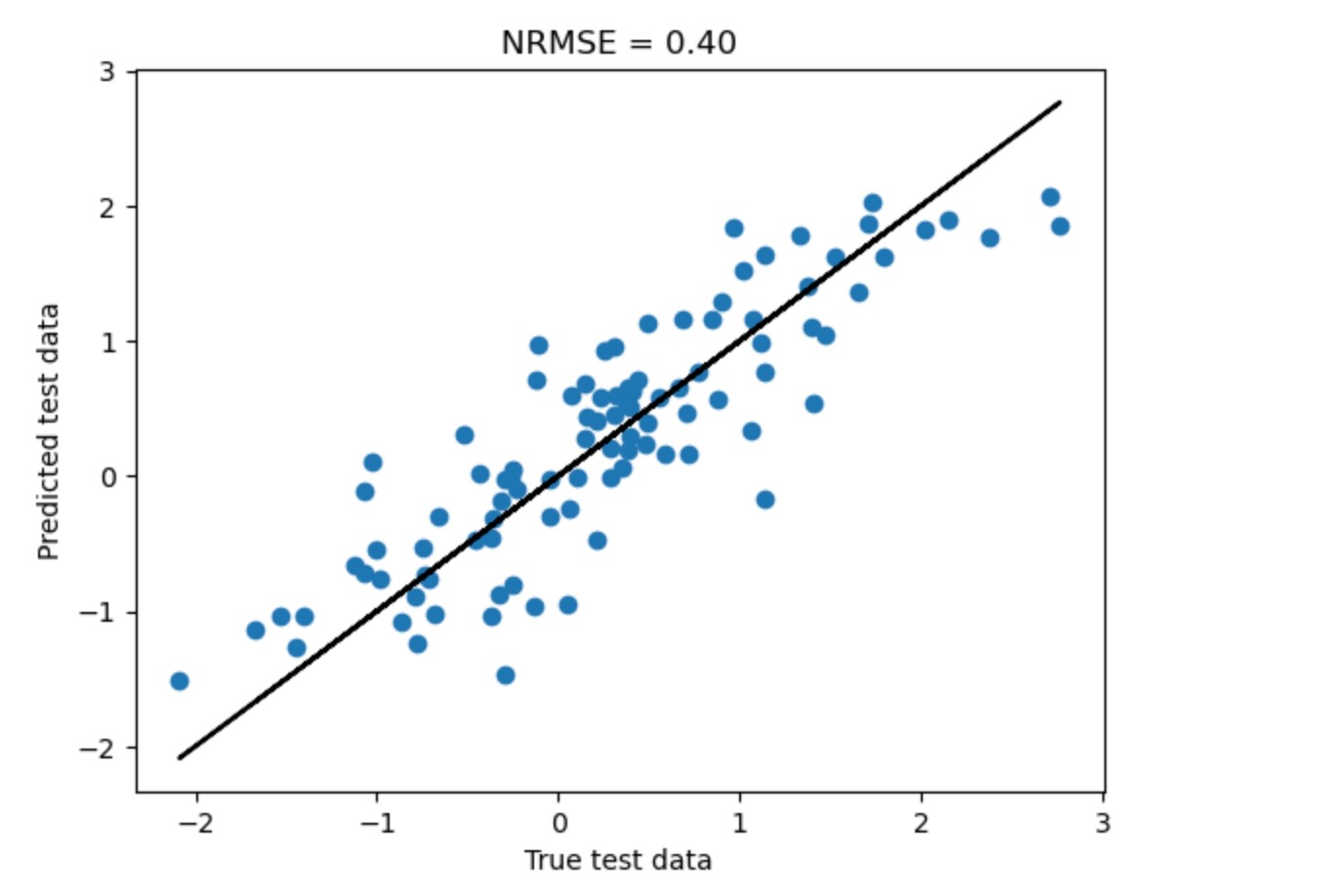
plt.scatter(true_data, predicted)
plt.title(r"NRMSE = %.2f" % (np.abs(true_data - predicted).mean()/true_data.std()))
plt.plot(true_data, true_data, 'k-')
plt.xlabel('True test data')
plt.ylabel('Predicted test data')
plt.show()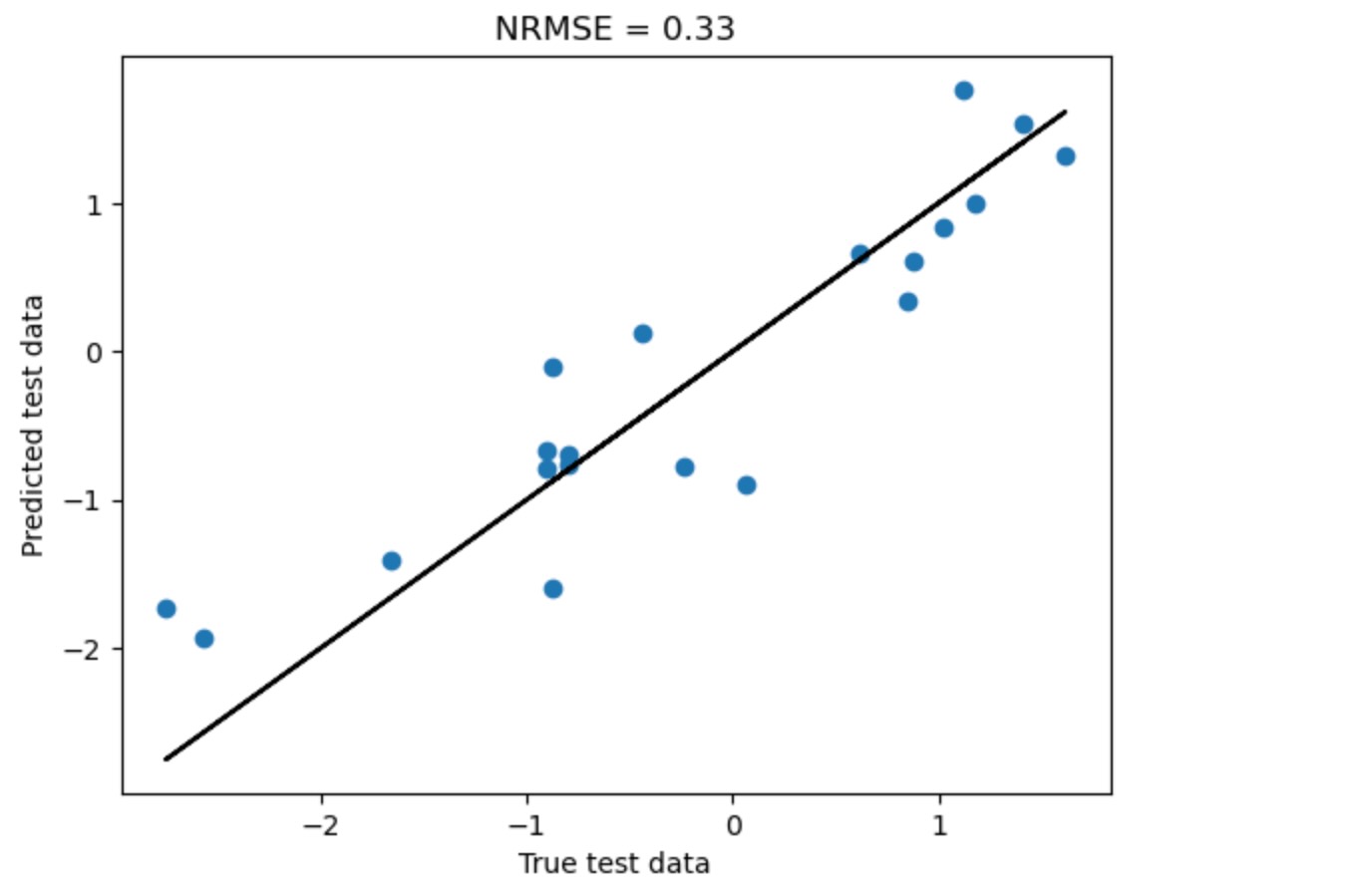

　私たちは、新しいデータフレームをnew_dataを供給することによって、他の新しいデータを予測することができます。

new_data = pp.DataFrame(toys.var_process(links_coeffs, T=200)[0])
predicted = pred.predict(target, new_data=new_data)
true_data = pred.get_test_array(j=target)[0]

plt.scatter(true_data, predicted)
plt.title(r"NRMSE = %.2f" % (np.abs(true_data - predicted).mean()/true_data.std()))
plt.plot(true_data, true_data, 'k-')
plt.xlabel('True test data')
plt.ylabel('Predicted test data')
plt.show()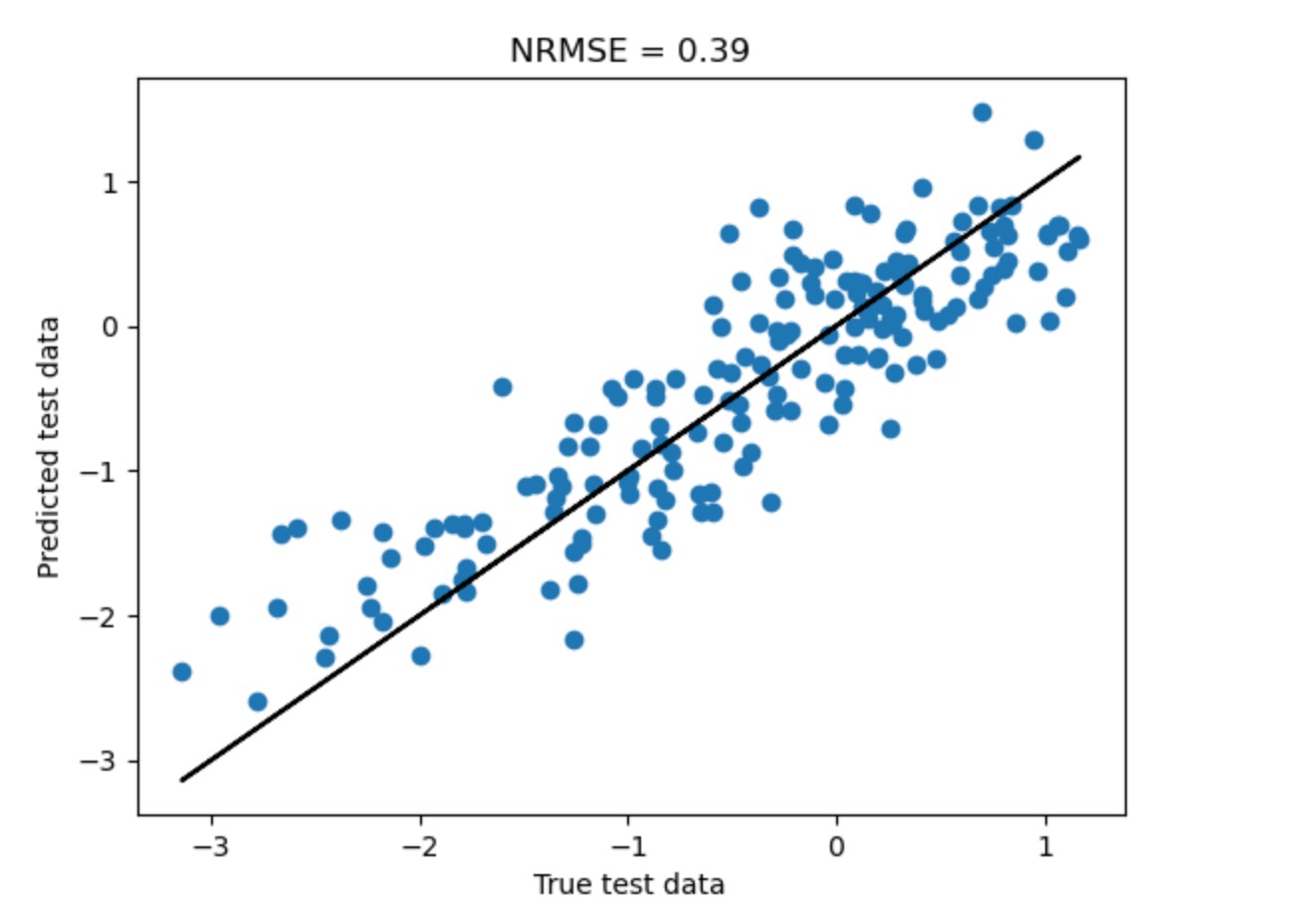

　この予測は、オーバーフィットに結びつく以前の全てのデータを使うよりずっとよくなります。

whole_predictors = {2:[(i, -tau) for i in range(3) for tau in range(1, tau_max+1)]}
pred.fit(target_predictors=whole_predictors, 
                selected_targets=[target],
                    tau_max=tau_max)

# new_data = pp.DataFrame(toys.var_process(links_coeffs, T=100)[0])
predicted = pred.predict(target, new_data=new_data)
# predicted = pred.predict(target)
true_data = pred.get_test_array(j=target)[0]

plt.scatter(true_data, predicted)
plt.plot(true_data, true_data, 'k-')
plt.title(r"NRMSE = %.2f" % (np.abs(true_data - predicted).mean()/true_data.std()))
plt.xlabel('True test data')
plt.ylabel('Predicted test data')
plt.show()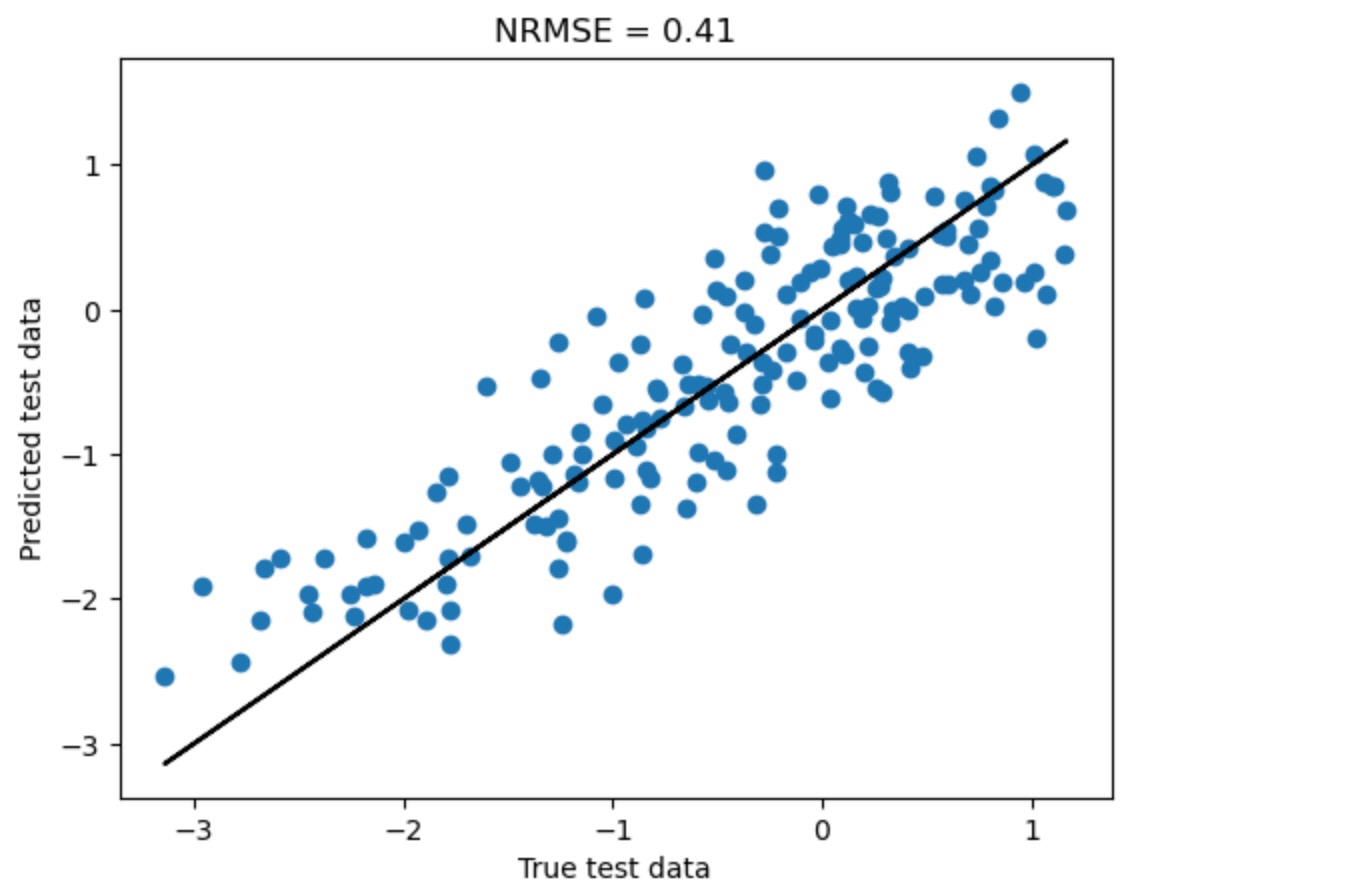

　前もって、私たちは、テストデータの再スケールを要求する適合の前に、データを再スケールします。私たちは、スケールされていないデータを切り離すことができます。

pred = Prediction(dataframe=dataframe,
        cond_ind_test=ParCorr(),
        prediction_model = sklearn.linear_model.LinearRegression(),
#     data_transform=sklearn.preprocessing.StandardScaler(),
    train_indices= list(range(int(0.8*T))),
    test_indices= list(range(int(0.9*T), T)),
    verbosity=1
    )
pred.fit(target_predictors=all_predictors, 
                selected_targets=[target],
                    tau_max=tau_max)
predicted = pred.predict(target)
# predicted = pred.predict(target)
true_data = pred.get_test_array(j=target)[0]

plt.scatter(true_data, predicted)
plt.plot(true_data, true_data, 'k-')
plt.title(r"NRMSE = %.2f" % (np.abs(true_data - predicted).mean()/true_data.std()))
plt.xlabel('True test data')
plt.ylabel('Predicted test data')
plt.show()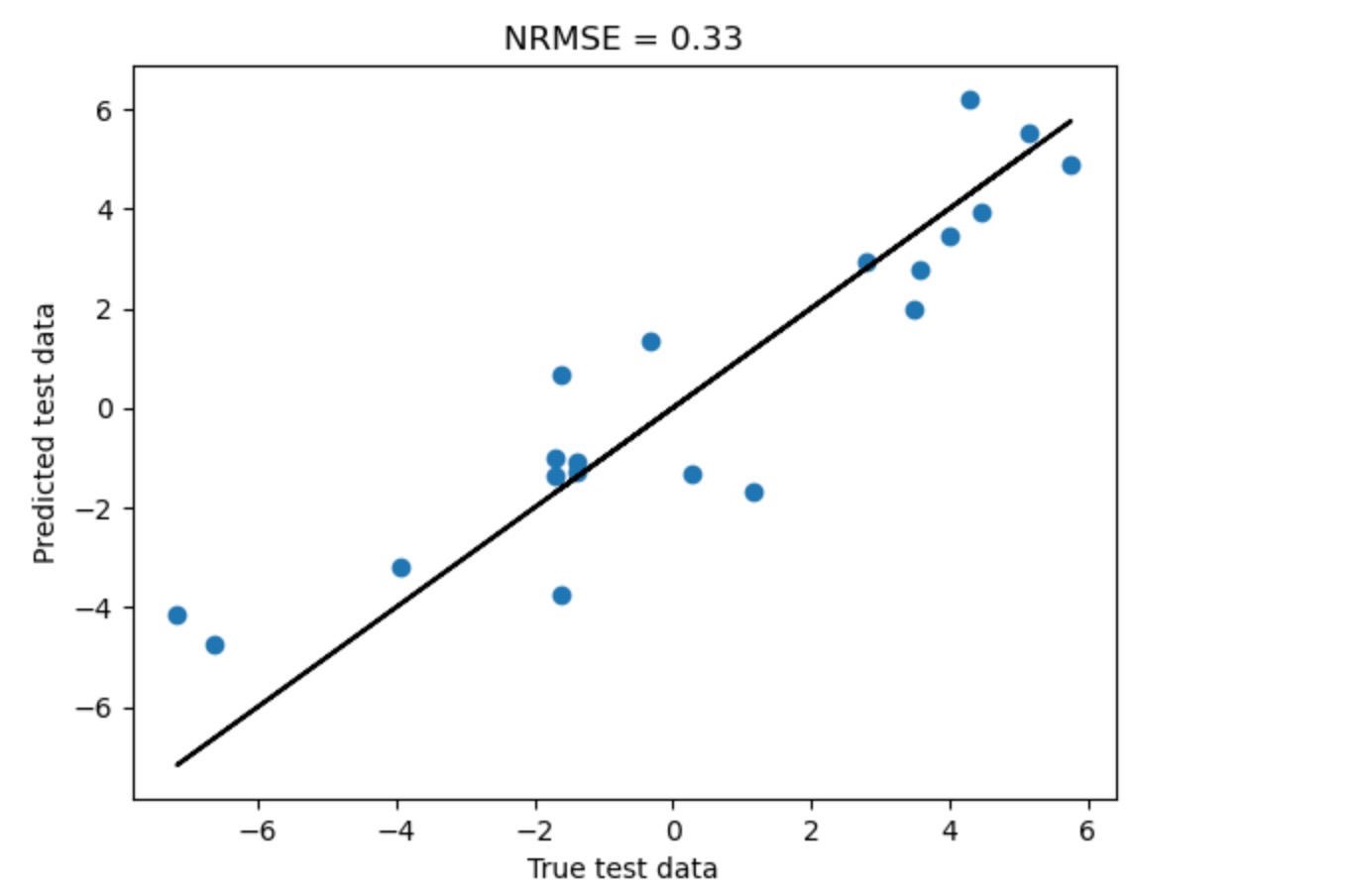

　xとy軸が異なるスケールであることに注意してください。

　最後に、GPDCpredictorの選択とともに、結合のガウス過程回帰をやってみましょう。ここで、私たちは、skleanのデフォルトがここではうまく働かないため、cond_ind_paramsとprediction_model_paramsを供給します。

tau_max = 10
steps_ahead = 2
target = 2
T = 500
dataframe = pp.DataFrame(toys.var_process(links_coeffs, T=T)[0])
pred = Prediction(dataframe=dataframe,
        cond_ind_test=GPDC(),   #CMIknn ParCorr
        prediction_model = sklearn.gaussian_process.GaussianProcessRegressor(alpha=0., 
                                 kernel=sklearn.gaussian_process.kernels.RBF() +
                                        sklearn.gaussian_process.kernels.WhiteKernel()),
        # prediction_model = sklearn.neighbors.KNeighborsRegressor(),
    data_transform=sklearn.preprocessing.StandardScaler(),
    train_indices= range(int(0.8*T)),
    test_indices= range(int(0.8*T), T),
    verbosity=1
    )

all_predictors = pred.get_predictors(
                  selected_targets=[target],
                  steps_ahead=steps_ahead,
                  tau_max=tau_max,
                  pc_alpha=0.2
                  )
pred.fit(target_predictors=all_predictors, 
                selected_targets=[target],
                    tau_max=tau_max)
predicted = pred.predict(target)
# predicted = pred.predict(target)
true_data = pred.get_test_array(j=target)[0]

plt.scatter(true_data, predicted)
plt.plot(true_data, true_data, 'k-')
plt.title(r"NRMSE = %.2f" % (np.abs(true_data - predicted).mean()/true_data.std()))
plt.xlabel('True test data')
plt.ylabel('Predicted test data')
plt.show()

##
## Step 1: PC1 algorithm with lagged conditions
##

Parameters:
independence test = gp_dc
tau_min = 2
tau_max = 10
pc_alpha = [0.2]
max_conds_dim = None
max_combinations = 1


Null distribution for GPDC not available for deg. of freed. = 380.

## Resulting lagged parent (super)sets:

    Variable 0 has 2 link(s):
        (0 -2): max_pval = 0.00000, min_val =  0.266
        (2 -6): max_pval = 0.18200, min_val =  0.095

    Variable 1 has 4 link(s):
        (0 -2): max_pval = 0.00000, min_val =  0.554
        (1 -2): max_pval = 0.01800, min_val =  0.136
        (0 -4): max_pval = 0.03800, min_val =  0.123
        (1 -3): max_pval = 0.05200, min_val =  0.116

    Variable 2 has 3 link(s):
        (1 -2): max_pval = 0.00000, min_val =  0.740
        (0 -2): max_pval = 0.00000, min_val =  0.420
        (2 -2): max_pval = 0.00000, min_val =  0.559