主要な参照:Elena Saggioro, Jana de Wiljes, Marlene Kretschmer, Jakob Runge; Reconstructing regime-dependent causal relationships from observational time series. Chaos 1 November 2020; 30 (11): 113115. https://doi.org/10.1063/5.0020538
以下のNature Review Earth and Environmentの論文は、一般的な因果推論の概要を与えます。
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearn
from sklearn.linear_model import LinearRegression
import tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toys
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.rpcmci import RPCMCI
from tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb以下で、私たちは、データを生成します。それは、因果的な構造下で、年間の夏場と冬場などで参照される二つのレジームの間で交互に現れます。特に、二つのレジームは、一つの因果的な影響が、二つのレジームの中で反対のサインであることが異なります。
重要なのは、レジーム-PCMCIが、レジームの周期的な構造を必要としないことです。それらは、時間を超えて、任意の分布にできます。しかし、レジームの数と持続性には、仮定があります。R-PCMCIの仮定には、論文を参照してください。
np.random.seed(43)
T = 500
var_names = [r'$X^1$', r'$X^2$', r'$X^3$']
data = np.random.randn(T, 3)
data_mask = np.zeros(data.shape)
for t in range(1, T):
if (t % 365) < 3*30 or (t % 365) > 8*30:
# Winter half year
data[t, 0] += 0.4*data[t-1, 0]
data[t, 1] += 0.3*data[t-1, 1] + 0.7*data[t-1, 0]
data[t, 2] += 0.3*data[t-1, 2] + 0.7*data[t-1, 0]
else:
# Summer half year
data_mask[[t, t-1]] = True
data[t, 0] += 0.4*data[t-1, 0]
data[t, 1] += 0.3*data[t-1, 1] - 0.7*data[t-1, 0]
data[t, 2] += 0.3*data[t-1, 2]
T, N = data.shape
# print data_mask[:100, 0]
datatime = np.arange(T)
dataframe_plotting = pp.DataFrame(data, mask=data_mask)
tp.plot_timeseries(dataframe_plotting, figsize=(8,3), grey_masked_samples='data'); plt.show()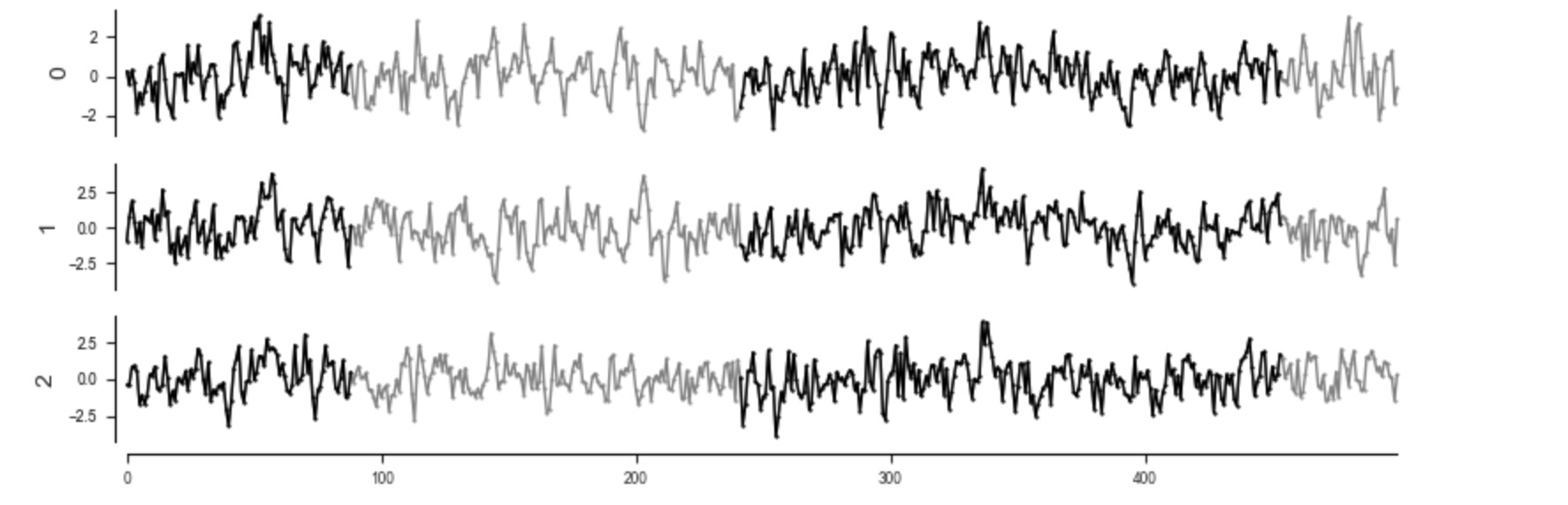
因果レジームが既知の場合の学習グラフ
最初に、マスキングされたレジームについての知識を明白に含んでいる、二つのレジームに属する因果グラフを再構築しましょう。dataset_challengeフォルダのマスキングのチュートリアルを参照してください。
# First mask out the summer
pcmci = PCMCI(dataframe=dataframe_plotting,
cond_ind_test=ParCorr(mask_type='y'))
results = pcmci.run_pcmci(tau_min=1, tau_max=2, pc_alpha=0.2, alpha_level=0.01)
tp.plot_graph(val_matrix=results['val_matrix'],
graph=results['graph'], var_names=var_names,
node_aspect=0.5, node_size=0.5
)
plt.show()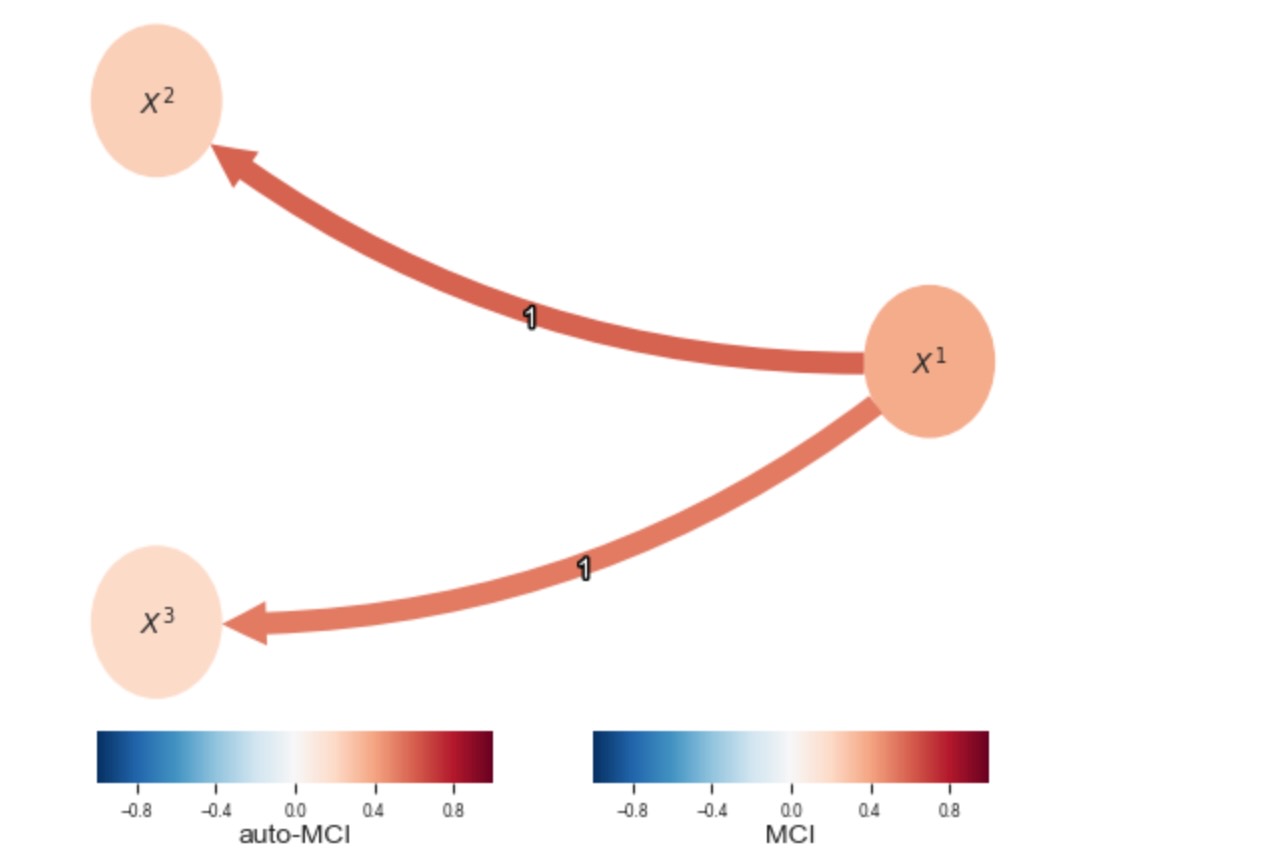
# Then mask out the winter
dataframe_plotting.mask[0] = dataframe_plotting.mask[0] == False
pcmci = PCMCI(dataframe=dataframe_plotting,
cond_ind_test=ParCorr(mask_type='y'))
results = pcmci.run_pcmci(tau_min=1, tau_max=2, pc_alpha=0.2, alpha_level=0.01)
tp.plot_graph(val_matrix=results['val_matrix'],
graph=results['graph'], var_names=var_names,
node_aspect=0.5, node_size=0.5
)
plt.show()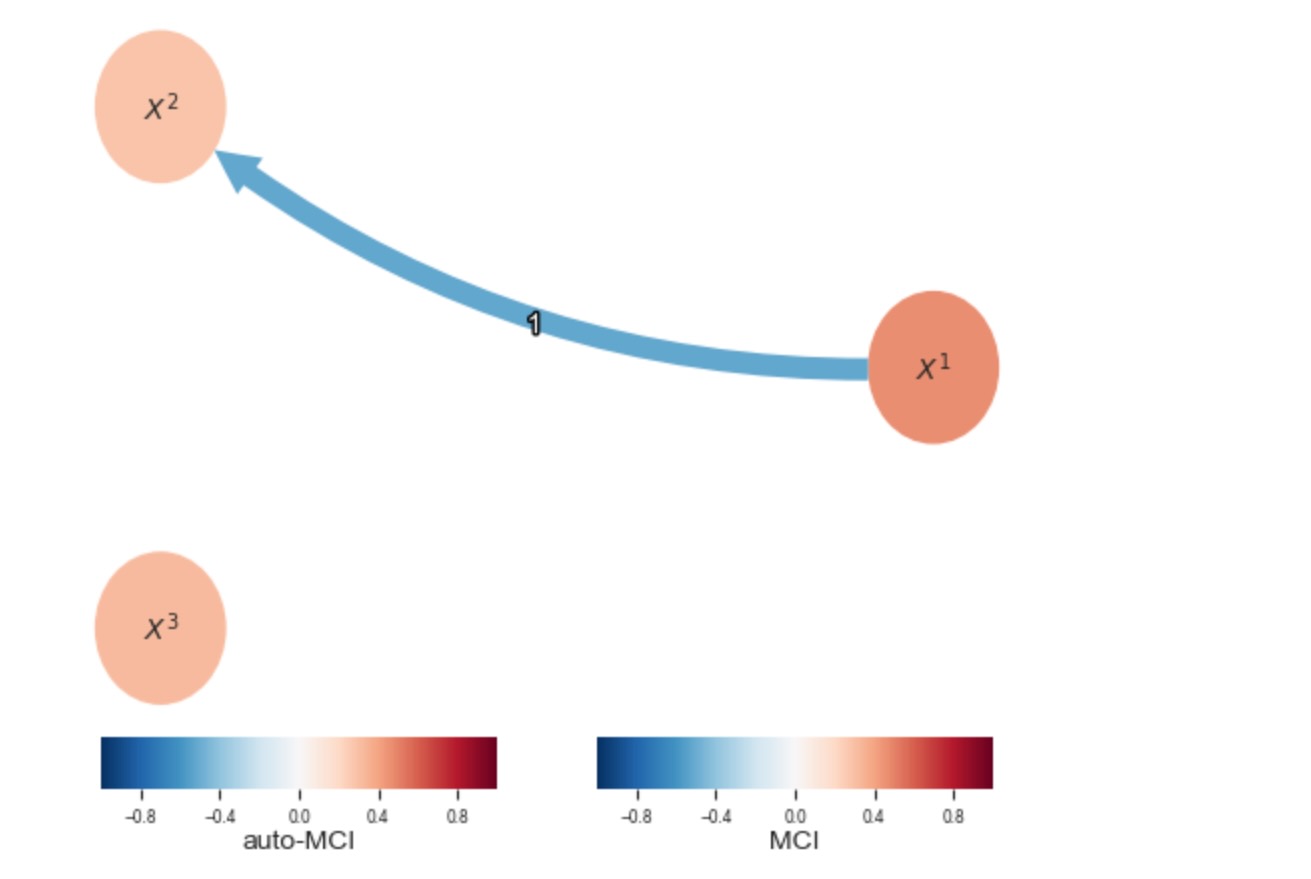
レジームの却下と全てのデータのグラフの学習
表示を見てください。
pcmci = PCMCI(dataframe=pp.DataFrame(data),
cond_ind_test=ParCorr())
results = pcmci.run_pcmci(tau_min=1, tau_max=2, pc_alpha=0.2, alpha_level=0.01)
tp.plot_graph(val_matrix=results['val_matrix'],
graph=results['graph'], var_names=var_names,
node_aspect=0.5, node_size=0.5
)
plt.show()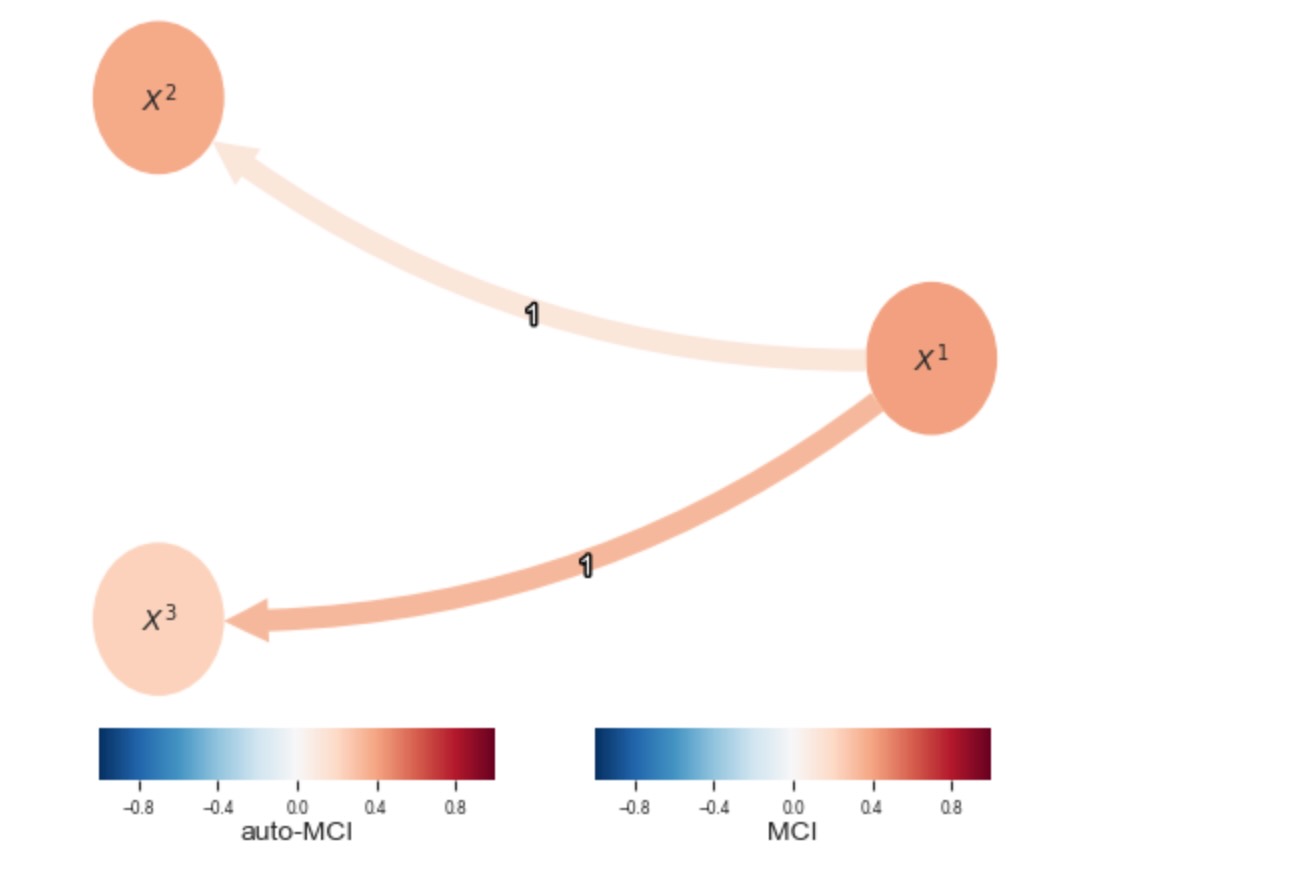
レジームの学習と対応する因果グラフ
ここで、マスキングにより仮定なしで因果レジームを自動的に検出するために、RPCMCIを実行します。
# Dataframe init. Note that for R-PCMCI no data mask can be used.
# The mask will internally be overwritten to learn regimes
dataframe = pp.DataFrame(data)
# Init RPCMCI with the dataframe, a conditional independence test for use in PCMCI,
# and a prediction_model which is used to predict each variable given its learned parents. This prediction
# is then used inside the regime learning optimization step.
rpcmci = RPCMCI(dataframe=dataframe,
cond_ind_test=ParCorr(),
prediction_model=LinearRegression(),
verbosity=1)
# RPCMCI parameters, see paper
num_regimes = 2
max_transitions = 4
switch_thres = 0.05
num_iterations = 20
max_anneal = 10
tau_min = 1
tau_max = 1
pc_alpha = 0.2
alpha_level = 0.01
n_jobs = -1 # uses joblib for parallelization, here all available cpus are used
# Run RPCMCI
results = rpcmci.run_rpcmci(
num_regimes=num_regimes, max_transitions=max_transitions,
switch_thres=switch_thres,
num_iterations=num_iterations, max_anneal=max_anneal,
tau_min=tau_min, tau_max=tau_max,
pc_alpha=pc_alpha, alpha_level=alpha_level,
n_jobs=n_jobs
)
if results is None:
print("All annealings resulted in errors. Increase annealing and tune other parameters!")
else:
print("Done!")Done!
regimes = results['regimes'].argmax(axis=0)
n_regimes = len(results['causal_results'])
# Create nice Mosaic plot
mosaic = [['data %s' %j for i in range(n_regimes)] for j in range(N+1)]
for n in range(N):
mosaic.append(['graph %s' %i for i in range(n_regimes)])
fig, axs = plt.subplot_mosaic(mosaic = mosaic, figsize=(20, 10))
for j in range(N):
ax = axs['data %s' %j]
ax.axhline(0., color='grey')
ax.plot(datatime, data[:,j])
for loc, spine in ax.spines.items():
if loc != 'left':
spine.set_color("none")
ax.xaxis.set_ticks([])
ax.set_xlim(0., T)
ax.set_ylabel(var_names[j])
# Regime variable
ax = axs['data %s' %N]
ax.plot(datatime, regimes.astype('int'), lw=3, color='black')
for loc, spine in ax.spines.items():
if loc != 'left':
spine.set_color("none")
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks(range(n_regimes))
ax.set_xlim(0., T)
ax.set_ylabel("Regime")
# Causal graphs for each regime
for w in range(n_regimes):
if w == 0: show_colorbar=True
else: show_colorbar = False
tp.plot_graph(graph=results['causal_results'][w]['graph'],
val_matrix=results['causal_results'][w]['val_matrix'],
show_colorbar=show_colorbar,
var_names=var_names,
fig_ax=(fig, axs['graph %s' %w]))
axs['graph %s' %w].set_title("Regime %d" %w, pad=-4)
fig.subplots_adjust(hspace=0.6)
plt.show()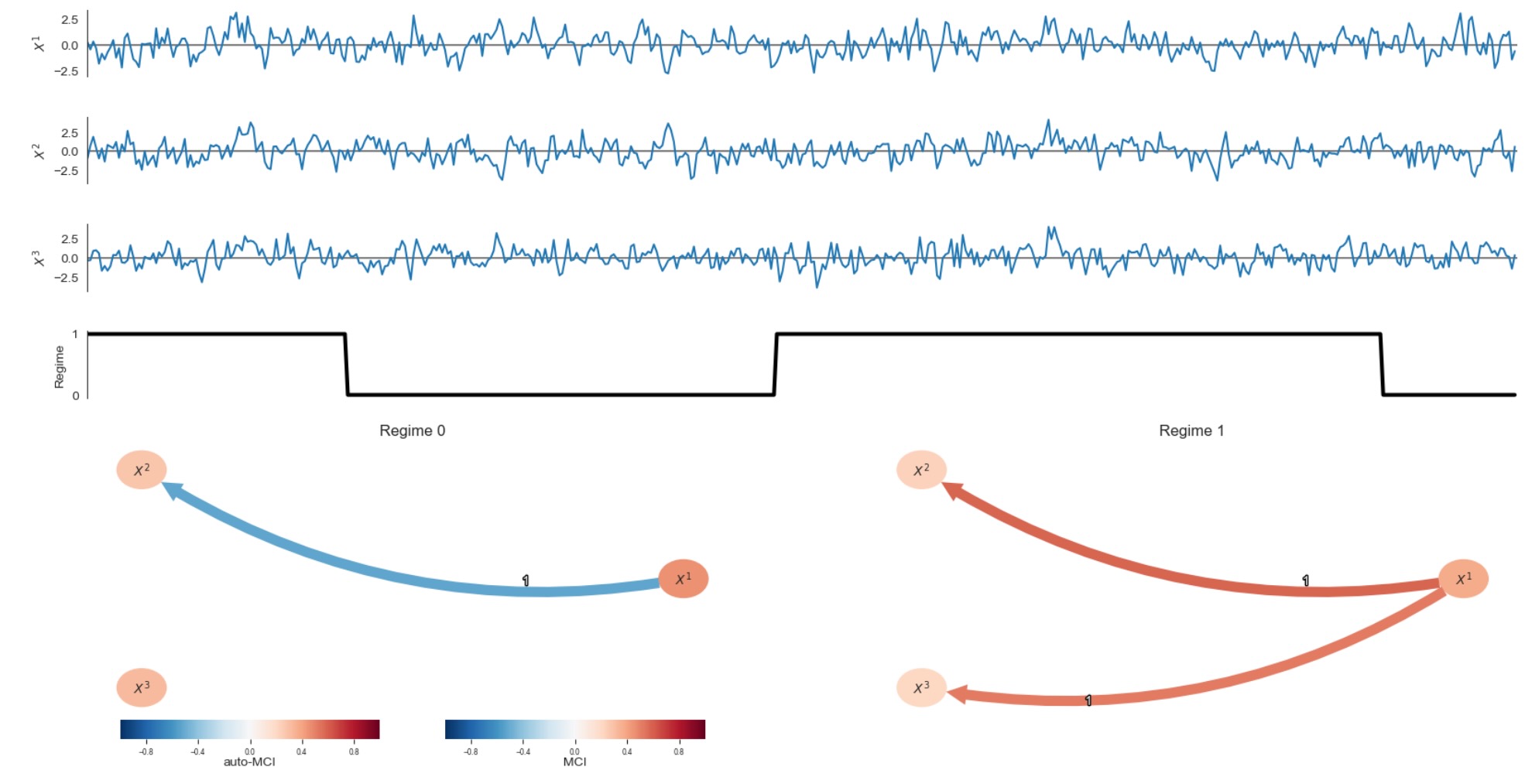
レジームはここでうまく再構築されます。任意の現実のデータの応用へは、私たちは、同じ性質を持った任意のtoyデータの構築を提案します。その後、どのパラメータがRPCMCIに最もよく働くか探索します。
私たちは、また、現在、レジームの種類の変化が、この方法で識別できる理論的な結果を持たないことを注記したいと思います。しかし、私たちは、数的な実験をデモします。それは、グラフの構造または、リンクの符号と大きさを変化させる働きをします。
